x^3>=x (неравенство)
Шаг 1.
 \geq — \frac$$
\geq — \frac$$Тогда
$$x \leq -1$$
не выполняется
значит одно из решений нашего неравенства будет при:
$$x \geq -1 \wedge x \leq 0$$
Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ:
$$x \geq -1 \wedge x \leq 0$$
$$x \geq 1$$
Источник
Решите уравнение икс в кубе плюс а икс квадрат минус 5 Икс плюс 6 равно 0 если известно что один из его корней равен 3?
Решите уравнение икс в кубе плюс а икс квадрат минус 5 Икс плюс 6 равно 0 если известно что один из его корней равен 3.
(Пять целых четыре десятых)
Или если не проходили дроби то будет :
Уравнение икс в кубе минус 6 икс в квадрате минус 4 Икс плюс 24 равно нулю?
Уравнение икс в кубе минус 6 икс в квадрате минус 4 Икс плюс 24 равно нулю.
Решите уравнение икс в кубе равно икс в квадрате плюс два икс?
Решите уравнение икс в кубе равно икс в квадрате плюс два икс.
Решите уравнение : икс в четвёртой степени минус три икс в кубе минус икс в квадрате плюс три икс равно ноль?
Решите уравнение : икс в четвёртой степени минус три икс в кубе минус икс в квадрате плюс три икс равно ноль.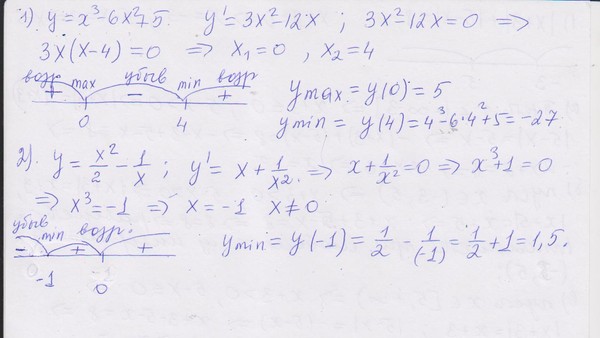
Решите графически уравнение минус два икс в квадрате равно икс плюс один?
Решите графически уравнение минус два икс в квадрате равно икс плюс один.
Решение уравнения 6 деленное на икс в квадрате минус 1 минус 2 деленное на икс минус 1 равно 2 минус Икс плюс 4 деленное на Икс плюс один?
Решение уравнения 6 деленное на икс в квадрате минус 1 минус 2 деленное на икс минус 1 равно 2 минус Икс плюс 4 деленное на Икс плюс один.
Решить уравнение икс в квадрате минус 10 икс плюс 21 равно 0?
Решить уравнение икс в квадрате минус 10 икс плюс 21 равно 0.
Икс в кубе минус два икс в квадрате плюс четыре икс?
Икс в кубе минус два икс в квадрате плюс четыре икс.
Решить уравнение икс в квадрате минус пять в квадрате ровно икс в квадрате минус два икс умножить на три плюс три в квадрате плюс два?
Решить уравнение икс в квадрате минус пять в квадрате ровно икс в квадрате минус два икс умножить на три плюс три в квадрате плюс два.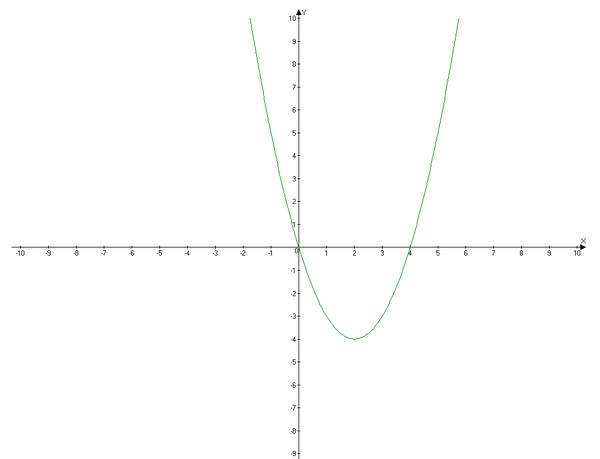
Уравнение три икс минус икс во второй равно 0 Икс во второй плюс 5 Икс плюс 6 равно 0 Решите пожалуйста?
Уравнение три икс минус икс во второй равно 0 Икс во второй плюс 5 Икс плюс 6 равно 0 Решите пожалуйста.
Два икс квадрат минус икс минус десять деленное на икс плюс два равно нулю?
Два икс квадрат минус икс минус десять деленное на икс плюс два равно нулю.
Перед вами страница с вопросом Решите уравнение икс в кубе плюс а икс квадрат минус 5 Икс плюс 6 равно 0 если известно что один из его корней равен 3?, который относится к категории Алгебра. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.
Источник
|
Задачи с параметрами — одна из самых трудных тем в математике. Неизвестные величины принято обозначать последними буквами латинского алфавита икс, игрек, зэт и так далее, параметры – первыми буквами а, бэ, цэ, и так далее. |
Текст. Тема «Уравнения с параметрами»
Неизвестные величины принято обозначать последними буквами латинского алфавита(х, у, z,…), параметры – первыми буквами (а,b,c,…) |
|
Определение первое. Уравнением с параметром а называют уравнение вида эф от икс а равно нулю, которое надо решить относительно икс и в котором буквой а обозначено произвольное действительное число. |
Текст. Определение1. Уравнением с параметром а называют уравнение вида f(x,a)=0, которое надо решить относительно х и в котором буквой а обозначено произвольное действительное число. |
|
Определение второе. Решить уравнение с параметром – значит для каждого значения параметра найти множество всех корней данного уравнения или доказать, что корней нет. |
Текст. Определение2. Решить уравнение с параметром – значит для каждого значения параметра найти множество всех корней данного уравнения, а может их не быть. |
|
Задачи с параметрами решаются теми же приемами, что и аналогичные задачи без параметров. При решении используются аналитические и графические методы. Рассмотрим примеры, которые дадут вам некоторое представление о том, как рассуждают при решении уравнений и неравенств с параметрами. Решим простейшие линейные неравенства. |
Текст. Задачи с параметрами решаются теми же приемами, что и аналогичные задачи без параметров. При решении используются аналитические и графические методы. |
|
Задание 1 Решить уравнение а икс равно одному. Решение Рассмотрим два случая. Первый случай, если а не равно нулю, то уравнение имеет единственное решение: икс равен один деленное на а; Второй случай, если Ответ: если а не равно нулю, то икс равен один деленное на а; если a равно нулю, то уравнение не имеет решений. |
Пример 1. Решить уравнение ax = 1. Решение. Рассмотрим два случая. 1)если a ≠ 0 уравнение имеет единственное решение, x = 1/a; 2)если a = 0 уравнение примет вид 0·x = 1 и, следовательно, оно не имеет решений. Ответ: если a ≠0,то x = 1/a; если a = 0, то уравнение не имеет решений. |
|
Задание 2
Решить уравнение а квадрат икс минус один равно икс плюс a. Решение Перенесем икс в левую часть уравнения и вынесем его за скобки. Получим: икс умноженное на разность а квадрат и один равно a плюс один. Рассмотрим три случая: Первый случай, если а квадрат плюс один не равно единице, то есть a не равно плюс минус одному, то икс равен дроби, числитель которой — один, а знаменатель — а минус один. Второй случай, если a равно единице, то уравнение примет вид: ноль умноженное на икс равно двум и, следовательно, не имеет решений. Третий случай, если a равно минус единице, то уравнение примет вид: ноль умноженное на икс равно нулю, и, следовательно, любое действительное число является решением этого уравнения. Ответ: если a не равно плюс минус единице, то икс равен дроби, числитель которой один, а знаменатель — а минус один. Если a равно единице, то уравнение не имеет решений; если a равно минус единице, то любое действительное число является решением этого уравнения. |
Пример2. Решить уравнение a2x — 1 = x + a; Решение. Получим: a2x — 1 = x + a ; a2x — x = a + 1; x(a2 — 1) = a + 1. 1) если a2-1 ≠ 0, то есть a ≠ ±1, то есть a не равно плюс минус одному, то икс равен дроби, числитель которой — один, а знаменатель — а минус один.
2) если a = 1, то уравнение примет вид 0·x = 2 и, следовательно, не имеет решений; 3) если a = -1, то уравнение примет вид 0·x = 0, и, следовательно, любое действительное число является решением этого уравнения. Ответ: если a ≠ ±1,то икс равен дроби, числитель которой один, если a = 1, то уравнение не имеет решений; если a = -1, то любое действительное число является решением этого уравнения. |
|
Задание 3 Решить уравнение: дробь, числитель которой — икс минус два а, знаменатель – икс минус четыре равно нулю. Решение Находим ОДЗ уравнения — икс неравен четырем. Решаем уравнение икс минус два а равно нулю; Икс равен два а, если икс неравен четырем, то есть два а не равно четырем, а не равно двум. Итак, если а не равно двум, то уравнение имеет единственное решение — икс равно два а. Если a равно двум, то уравнение не имеет решений. Ответ: если не равно двум, то уравнение имеет единственное решение — икс равно два а. Если a равно двум, то уравнение не имеет решений. |
Текст. Пример 3. Решить уравнение. дробь, числитель которой — икс минус два а, знаменатель – икс минус четыре равно нулю. Решение. Находим ОДЗ уравнения х-4≠0. х≠4. Решаем уравнение х-2а=0; х=2а, если х≠4, то есть 2а≠4, а≠2. Итак, если а≠2, то уравнение имеет единственное решение x = 2a, если a = 2, то уравнение не имеет решений. Ответ: если а≠2, то уравнение имеет единственное решение x = 2a; если a = 2, то уравнение не имеет решений. |
|
Задание 4 Решить уравнение модуль выражения икс минус а равно двум. Решение По определению модуля имеем: модуль икс минус а равно двум равно совокупности двух уравнений икс равен а плюс два и икс равен а минус два. Таким образом, для любого действительного a уравнение имеет два различных решения, икс первое равно а плюс два и икс второе равно а минус два. Ответ: для любого действительного a уравнение имеет два различных решения: икс первое равно а плюс два и икс второе равно а минус два. |
Текст. Пример 4. Решить уравнение |x — a| = 2 Решение. По определению модуля имеем: |x — a| = 2Û х-а=2 , Û х=а+2, х-а=-2; х= а-2. Таким образом, для любого действительного a уравнение имеет два различных решения, x1 = a + 2 и x2 = a — 2. Ответ: для любого действительного a уравнение имеет два различных решения, x1 = a + 2 и x2 = a — 2 |
|
Задание 5 Решить уравнение модуль икс плюс модуль выражения икс минус а равно нулю. Решение Левая часть уравнения принимает неотрицательные значения(как сумма двух неотрицательных слагаемых), а правая часть равна нулю. Имеем, систему из двух уравнений икс равно нулю и икс минус а равно нулю или система из двух уравнений икс равно нулю и икс равно а. Таким образом, если a равно нулю, то система (а, следовательно, и уравнение) имеет единственное решение икс равно нулю, а если a не равно нулю, то система (и исходное уравнение) решений не имеет. Ответ: если a равно нулю, то икс равно нулю; если a не равно нулю, то уравнение корней не имеет. |
Текст. Пример 5. Решить уравнение |x| + |x — a| = 0 Решение. Имеем, х=0 , х- a =0;
х=0, х= a . Таким образом, если a = 0, то система (а, следовательно, и уравнение) имеет единственное решение x = 0, а если a ≠ 0, то система (и исходное уравнение) решений не имеет. Ответ: если a = 0, то x = 0; если a ≠ 0, то уравнение корней не имеет. |
|
Рассмотрим более сложные примеры. Задание 6 При всех значениях параметра а определим число корней кубического уравнения икс куб минус три икс плюс два минус а равно нулю. Решение Выразим а из этого уравнения, имеем: а равно икс куб минус три икс плюс два. Построим график функции а от икс. График пересекается с осью Ох в точках: икс первое равно минус два и икс второе равно одному. Вычислим производную а штрих от икс равно три икс квадрат минус три. Критические точки функции: икс равно плюс минус один. В точке икс равное минус единице функция имеет максимум, равный четырем и в точке икс равное единице — минимум, равный нулю. В этой же системе координат построим также прямую а равно анулевое. Теперь по графику легко ответить на вопрос задачи.
|
Текст. Рассмотрим более сложные примеры. Пример 6. При всех значениях параметра а определим число корней кубического уравнения х3-3х+2-а =0 Решение. Выразим а из этого уравнения, имеем: а = х3-3х+2. Построим график функции а(х). График пересекается с осью Ох в точках: х1=-2; х2=1. Вычислим производную а /(х) =3х2-3. Критические точки функции х=±1. В точке х=-1 функция имеет максимум аmax=4 и в точке х=1- минимум аmin= 0.В этой же системе координат построим также прямую а=а0.(а0 – любое число) Картинка. |
|
При а меньшем нуля и а большем четырех графики пересекаются в одной точке (данное уравнение имеет один корень), если а равно нулю и а равно четырем графики пересекаются в двух точках (два корня), если а меньше нуля и больше четырех – в трех точках (три корня). Ответ: если а меньше нуля и а больше четырех, то данное уравнение имеет один корень; если а равно нулю и а равно четырем — два корня; если а больше нуля и меньше четырех — три корня. |
Текст. При а0 и а>4 графики пересекаются в одной точке (данное уравнение имеет один корень), при а=0 и а=4 графики пересекаются в двух точках (два корня), при 0 а4 – в трех точках(три корня) Ответ: если а0 и а>4, то данное уравнение имеет один корень один корень; если а=0 и а=4- два корня; если 0 а4 -три корня. |
|
Задание 7 Решить уравнение эм икс квадрат плюс три эм икс минус сумма эм и двух равно нулю. Решение ОДЗ этого уравнения — все действительные числа и имеет смысл при любых действительных значениях параметра эм. Рассмотрим два случая. Первый, если эм равно нулю, то уравнение примет вид: ноль икс квадрат плюс ноль икс минус два равно нулю — неверное равенство, уравнение корней не имеет. Второй случай, если эм не равно нулю, то уравнение является квадратным. Находим дискриминант, дэ равно эм умноженное на сумму тринадцати эм и восьми. Если дэ больше либо равно нулю, то эм принадлежит объединению числового луча от минус бесконечности до минус восьми тринадцатых и открытого числового луча от нуля до плюс бесконечности. Уравнение имеет два корня: икс первое, второе равно один деленное на два эм умноженное на минус три эм плюс-минус квадратный корень из произведения эм и суммы тринадцати эм и восьми. Ответ: если эм равно нулю, то уравнение не имеет корней; если эм не равно нулю, то уравнение имеет два корня: икс первое, второе равно один деленное на два эм умноженное на минус три эм плюс минус квадратный корень из произведения эм и суммы тринадцати эм и восьми. |
Текст. Пример7. Решить уравнение mх2+3 mх-(m+2)=0. Решение. ОДЗ этого уравнения все действительные числа и имеет смысл при любых действительных значениях параметра m. Рассмотрим два случая. 1)Если m=0, то уравнение примет вид 0х2+0х-2=0- неверное равенство, уравнение корней не имеет. 2) Если m≠0, то уравнение является квадратным. Находим D=m(13m+8). Если D=m(13m+8).≥0, mÎ(-∞;-8/13]È(0;+∞), то уравнение имеет два корня икс первое, второе равно один деленное на два эм умноженное на минус три эм плюс-минус квадратный корень из произведения эм и суммы тринадцати эм и восьми.. Ответ: если эм равно нулю, то уравнение не имеет корней; если эм не равно нулю, то уравнение имеет два корня: икс первое, второе равно один деленное на два эм умноженное на минус три эм плюс минус квадратный корень из произведения эм и суммы тринадцати эм и восьми. |
|
Задание 8 При каких значениях параметра а уравнение минус два синус квадрат икс равно произведению суммы а в квадрате, пять а и два на синус икс имеет ровно четыре корня на отрезке от нуля до двух пи? Решение Построим график функции игрек равно синус икс на отрезке от нуля до двух пи.
|
Текст. Пример8. При каких значениях параметра а уравнение -2sin2х=( а 2+5 а+2) sinх имеет ровно четыре корня на отрезке [0;2π]? Решение. Построим график функции у = sinх на отрезке [0;2π] Картинка.
|
|
Выполним преобразования: перенесем все члены уравнения в правую часть, разложим на множители, получим: ноль равен синус икс умноженное на сумму синус икс и а квадрат плюс пять а плюс два деленное на два. Это уравнение равносильно совокупности двух уравнений синус икс равно нулю и синус икс равен минус выражение а квадрат плюс пять а плюс два деленное на два. Уравнение синус икс равно нулю имеет три корня на отрезке от нуля до двух пи. Ответ: а равно минус единице, а равно минус четырем, а равно нулю, а равно минус пяти.
|
Текст. Получим: 0= sinх(sinх+( а 2+5 а+2)/2). Это уравнение равносильно совокупности двух уравнений sinх=0, sinх= -( а 2+5 а+2)/2. Уравнение sinх=0 имеет три корня на отрезке [0;2π]. Значит, второе уравнение на этом отрезке должно иметь один корень, а это возможно тогда, когда -( а 2+5 а+2)/2 будет равно ±1. совокупность двух уравнений, которая имеет четыре решения: а равно минус единице, а равно минус четырем, а равно нулю, а равно минус пяти которая имеет четыре решения : а=-1, а=-4, а=0, а=-5. Ответ: а=-1, а=-4, а=0, а=-5. |

Итак, вот формулы, которые обобщают, как разложить на множители сумму и разность двух кубов. Внимательно изучите их. Случай 1: сумма двух кубов
- Помимо случая «сумма», средний знак трехчленного множителя всегда будет напротив среднего знака данной задачи. Следовательно, это минус .
Случай 2: разность двух кубов
Наблюдения:
- Помимо случая «разности», средний знак трехчленного множителя всегда будет противоположен среднему знаку данной задачи. Следовательно, это положительных .
94}г.
Иногда задача может оказаться неразложимой ни на сумму, ни на разность двух кубов. Если вы видите что-то подобное, постарайтесь исключить общие факторы. Для чисел наибольший общий делитель равен 3, а для переменных наибольший общий делитель равен «xy». Следовательно, общий общий множитель будет их произведением, которое равно \left( 3 \right)\left( {xy} \right) = 3xy.
После разложения вы увидите, что у нас есть простая задача на разность двух кубов.
Вас также может заинтересовать:
Факторизация разности двух квадратов
Факторизация разности двух квадратов Практические задачи
Факторизация суммы и разности двух кубов Практические задачи
Сумма и разность кубов
Горячая математикаСумма или разность двух кубов может быть разложена на произведение биномиальный умножить на трехчлен.
То есть,
Икс
3
+
у
3
знак равно
(
Икс
+
у
)
(
Икс
2
−
Икс
у
+
у
2
)
а также
Икс
3
−
у
3
знак равно
(
Икс
−
у
)
(
Икс
2
+
Икс
у
+
у
2
)
.
Мнемоникой для знаков факторизации является слово «МЫЛО», буквы обозначают «Тот же знак», что и в середине исходного выражения, «Противоположный знак» и «Всегда положительный».
То есть, Икс 3 ± у 3 знак равно ( Икс [ Такой же знак ] у ) ( Икс 2 [ Противоположный знак ] Икс у [ Всегда Положительный ] у 2 )
Пример 1:
Фактор
27
п
3
+
д
3
.
Попробуйте записать каждое из условий в виде куба выражения.
27 п 3 + д 3 знак равно ( 3 п ) 3 + ( д ) 3
Используйте факторизацию суммы кубов, чтобы переписать.
27 п 3 + д 3 знак равно ( 3 п ) 3 + ( д ) 3 знак равно ( 3 п + д ) ( ( 3 п ) 2 − 3 п д + д 2 ) знак равно ( 3 п + д ) ( 9п 2 − 3 п д + д 2 )
Пример 2:
Фактор
40
ты
3
−
625
в
3
.














 Значит, второе уравнение на этом отрезке должно иметь один корень, а это возможно тогда, когда минус выражение а квадрат плюс пять а плюс два деленное на два будет равно плюс минус одному. Получаем совокупность двух уравнений, которая имеет четыре решения: а равно минус единице, а равно минус четырем, а равно нулю, а равно минус пяти.
Значит, второе уравнение на этом отрезке должно иметь один корень, а это возможно тогда, когда минус выражение а квадрат плюс пять а плюс два деленное на два будет равно плюс минус одному. Получаем совокупность двух уравнений, которая имеет четыре решения: а равно минус единице, а равно минус четырем, а равно нулю, а равно минус пяти. Получаем совокупность уравнений
Получаем совокупность уравнений