Формула как найти x0: Вершина параболы — урок. Алгебра, 8 класс.

Вариант № 19

1. Найти область определения функции :.

Область определения данной функции определяется следующим неравенством: , т. е. . Далее, знаменатель не должен обращаться в нуль: или . Объединяя результаты, получим: . Ответ: .

2. Построить график функции: .

Область определения функции: . Преобразуем функцию: . Строим по точкам график функции в интервале , затем «растягиваем» его по оси ОУ в два раза. Полученный график повторяем в интервалах для всех . Ответ: График представлен на рисунке.

3. Построить график функции: .

Область определения функции: – вся числовая ось: . Преобразуем функцию: . Сначала построим график функции , затем сдвинем полученный график на 2 единицы вправо по оси ОХ. Получим график функции . Затем ординаты всех точек графика увеличим в 2 раза. Ответ: Последовательность получения графика представлена на рисунке.

4. Построить график функции: .

Исключим параметр T: . Заметим, чо всегда , так как . Кроме того, область определения функции определяется неравенством , т. е. . Построим сначала график функции , затем отразим этот график зеркально относительно оси OX.. Ответ: График представлен на рисунке (сплошная линия).

5. Построить график функции: .

Преобразуем функцию: . Это уравнение окружности радиуса . Можно перейти к декартовым координатам . Тогда . Или: — окружность радиуса с центром в точке (1, 1).

Ответ: График представлен на рисунке.

6. Вычислить предел: .

Возведём все скобки в степени и приведём подобные:

.

Ответ: .

7. Вычислить предел: (неопределённость вида (0/0)).

Разлагаем числитель и знаменатель на простые множители:

. Ответ: .

8. Вычислить предел: (неопределённость вида (0/0)).

Умножим числитель и знаменатель на сопряжённое к знаменателю выражение: . Ответ: .

9. Вычислить предел: (неопределённость вида (0/0)).

Сделаем замену переменной:

. Здесь воспользовались первым замечательным пределом: . Ответ: .

10. Вычислить предел: (неопределённость вида (1∞)).

Приведём предел ко второму замечательному пределу: :

. Предел в квадратных скобках равен числу E. Рассмотрим предел знаменателя:

Следовательно,

Ответ: .

11. Вычислить предел: (неопределённость вида (0/0)).

Преобразуем предел и воспользуемся эквивалентными величинами: .. Ответ: .

12. Исследовать функцию на непрерывность и построить эскиз графика: .

Область определения: . В области определения функция является непрерывной (как элементарная функция). Исследуем поведение функции в граничной точке области определения: . Таким образом, в точке

X=4 функция имеет разрыв второго рода. Для построения эскиза графика функции рассмотрим поведение функции в бесконечности: , .

Ответ: В точке и X=4 функция имеет разрыв второго рода, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.

13. Исследовать функцию на непрерывность и построить эскиз графика: .

Область определения функции: . Ось ОХ разбивается на два интервала, на каждом из которых функция F(X) совпадает с одной из указанных непрерывных функций. Поэтому точкой разрыва может быть только точка, разделяющая интервалы. Вычислим односторонние пределы:

. Таким образом, в точке X=0 функция терпит разрыв первого рода. Величина скачка функции в точке X=0 равна -2.

Ответ: В точке X=0 функция имеет разрыв первого рода, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.

14. Исходя из определения производной, найти :

.

По определению . Заменим ΔX на X—X0:

. Но , поэтому . В данном случае , следовательно производной не существует. Ответ: не существует.

15. Найти производную показательно-степенной функции: . Прологарифмируем функцию: .

Берём производную, как производную неявной функции:

. Подставляем сюда Y:

. Ответ: .

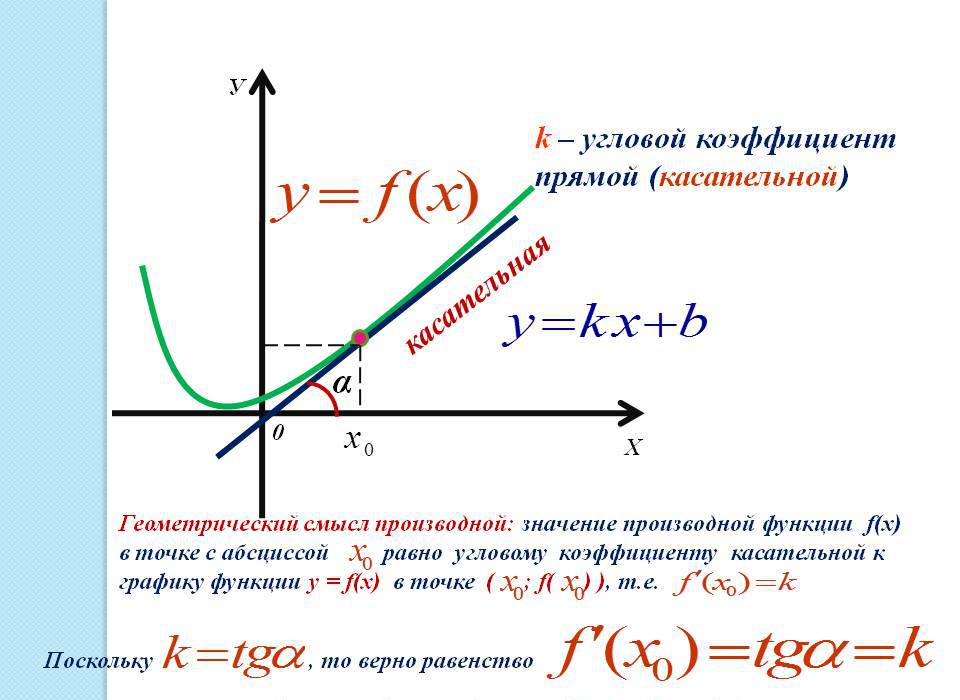
16. Составить уравнения касательной и нормали к кривой в данной точке, вычислить :

.

Уравнения касательной и нормали к кривой имеют вид и , где и — координаты точки касания. Вычислим сначала эти координаты:

. Найдём производные и : .Тогда . Далее,

, следовательно, . Таким образом, уравнение касательной , уравнение нормали . Или и .

Ответ:

17. Функция Y(X), заданная неявно уравнением , принимает в точке значение . Найти .

Дифференцируем уравнение по X, предполагая, что Y= Y(X): . Из этого равенства находим: . Находим вторую производную: . Вычислим производные в точке : . Ответ: , , .

18. Вычислить приближённое значение функции в заданной точке с помощью дифференциала: .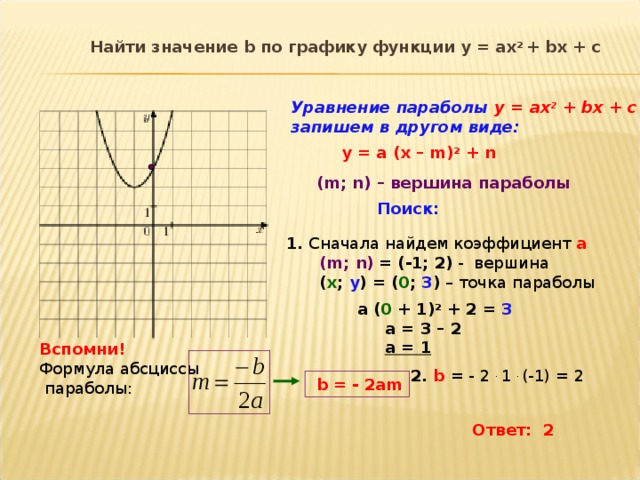

По определению дифференциала или, в других обозначениях, . Отсюда получаем формулу для приближённых вычислений: . В данном случае . Тогда . Ответ:

19. Вычислить предел с помощью правила Лопиталя: .

Это неопределённость вида (∞0). Преобразуем предел:

. Найдём предел в показателе степени:

. Следовательно, .

Ответ: .

20. Вычислить предел с помощью правила Лопиталя: .

Это неопределённость вида (0∙∞):

. Ответ: .

21. Многочлен по степеням X представить в виде многочлена по степеням : .

Запишем формулу Тейлора для многочлена четвёртой степени: .

Найдём все производные: , . Тогда . Подставив это в формулу, получим: .

Ответ: .

22. Найти многочлен, приближающий заданную функцию в окрестности точки X0 с точностью до : .

Применяем формулу Тейлора:

.

Вычисляем последовательно:

. Ответ: .

23. Исследовать поведение функции в окрестности точки с помощью формулы Тейлора: .

Найдём значения функции и её первых трёх производных в заданной точке:

. По формуле Тейлора .

Ответ: В окрестности точки (1, -1) функция ведёт себя как степенная функция третьей степени. Точка (1, -1) является точкой перегиба: слева — интервал выпуклости, справа — интервал вогнутости.

24. Вычислить предел с помощью формулы Тейлора: .

Сделаем замену: . Тогда . По формуле Тейлора . Подставим это в предел: .

Ответ: .

25. Найти асимптоты и построить эскиз графика функции: .

Область определения функции: . Функция непрерывна в каждой точке области определения. Найдём односторонние пределы в граничных точках области определения: ,. Отсюда следует, что прямые и являются вертикальными асимптотами. Исследуем функцию при :. Ищем наклонные асимптоты в виде : . Следовательно, прямая является наклонной асимптотой. Ответ: Эскиз графика представлен на рисунке.

26. Провести полное исследование поведения функции и построить её график: .

1. Область определения: .

2. Чётность, нечётность, периодичность отсутствуют, функция положительна в области определения 3. Функция имеет разрыв в точке . Исследуем поведение функции в окрестности точки разрыва: . Таким образом, прямая явля-

Ется вертикальной асимптотой.

4. (по правилу Лопиталя). Следовательно, прямая является левосторонней горизонтальной асимптотой. Очевидно, что других асимптот нет.

5. Первая производная . Производная обращается в нуль в точке . Слева от точки производная отрицательна, справа положительна. Следовательно, в точке имеет место минимум функции, причём . В интервале функция монотонно возрастает, в интервале функция монотонно убывает, в интервале функция монотонно возрастает.

6. Вторая производная: . Вторая производная во всех точках положительна, следовательно, график функции вогнутый на всех интервалах. Точек перегиба нет. 7.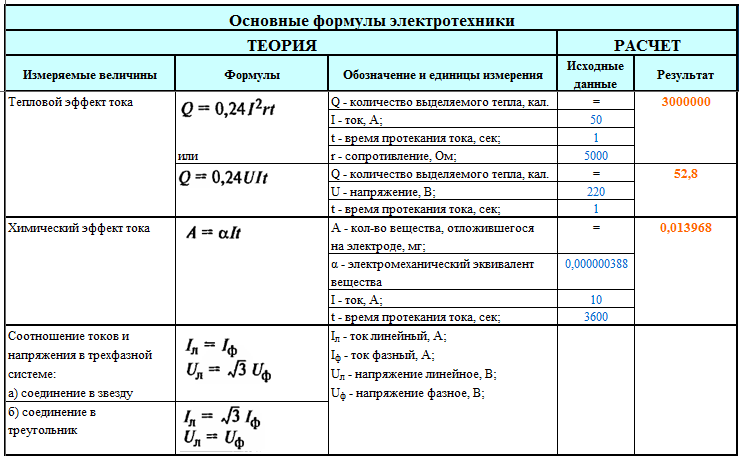 График функции не пересекает осей координат, во всех точках .

Ответ: График функции представлен на рисунке, экстремум – минимум – в точке . Вертикальная асимптота , горизонтальная асимптота .

< Предыдущая		Следующая >

Ньютон Метод Рафсона | Brilliant Math & Science Wiki

Ариэль Гершон, Эдвин Юнг, и Чимин Хим внес

Содержание

• Как это работает
• Геометрическое представление
• Ограничения метода Ньютона

Предположим, вам нужно найти корень непрерывной дифференцируемой функции \(f(x)\), и вы знаете, что искомый корень находится вблизи точки \(x = x_0\).

Тогда метод Ньютона говорит нам, что лучшим приближением для корня является \[x_1 = x_0 — \frac{f(x_0)}{f'(x_0)}.\] Этот процесс может быть повторен столько раз, сколько необходимо для получения желаемой точности. В общем, для любого \(x\)-значения \(x_n\) следующее значение определяется выражением \[x_{n+1} = x_n — \frac{f(x_n)}{f'(x_n)} .\]

Примечание: термин «рядом» используется в широком смысле, поскольку в данном контексте он не нуждается в точном определении. Однако \(x_0\) должен быть ближе к нужному вам корню, чем к любому другому корню (если функция имеет несколько корней).

Вот картинка, демонстрирующая, что на самом деле делает метод Ньютона:

Проведем касательную к графику \(f(x)\) в точке \(x = x_n\). Эта линия имеет наклон \(f'(x_n)\) и проходит через точку \(\big(x_n, f(x_n)\big)\). Поэтому оно имеет уравнение \(y = f'(x_n)(x — x_n) + f(x_n)\). Теперь мы находим корень этой касательной, устанавливая \(y = 0\) и \(x=x_{n+1}\) для нашего нового приближения.

Решение этого уравнения дает нам новое приближение: \(x_{n+1} = x_n — \frac{f(x_n)}{f'(x_n)}\). 93 — 3x + 1 = 0\), что близко к \(x = 0\).
Правильный ответ: \(-0,44157265\ldots\) Однако метод Ньютона даст вам следующее:

\[x_1 = \frac{1}{3}, x_2 = \frac{1}{6}, x_3 = 1, x_4 = 0,679, x_5 = 0,463, x_6 = 0,3035, x_7 = 0,114, x_8 = 0,473, \ldots.\]

Совершенно очевидно, что это бесполезно. Это потому, что график функции вокруг \(x = 0\) выглядит так:

Как видите, этот график имеет локальный максимум, локальный минимум и точку перегиба около \(x = 0\). Чтобы понять, почему метод Ньютона здесь бесполезен, представьте себе случайный выбор точки между \(x = -0,19\) и \(x = 0,19\) и провести касательную к функции в этой точке. Эта касательная будет иметь отрицательный наклон и, следовательно, пересечет ось \(y\) в точке, которая находится дальше от корня.

В такой ситуации поможет получить еще более близкую начальную точку, где эти критические точки не будут мешать.

Цитировать как: Метод Ньютона Рафсона. Brilliant.org . Извлекаются из https://brilliant.org/wiki/newton-raphson-method/ 94)$ пятиточечная формула для аппроксимации $f'(x_0)$, которая использует $f(x_0 — h), f(x_0), f(x_0 + h), f(x_0 + 2h), f(x_0 + 3h) $

спросил 5 лет, 4 месяца назад

Изменено 5 лет, 4 месяца назад

Просмотрено 4к раз

$\begingroup$

Это вопрос из учебника по численному анализу о численном дифференцировании (например, https://en.wikipedia.org/wiki/Numerical_дифференциация): 94)$ пятиточечная формула для аппроксимации $f'(x_0)$, которая использует $f(x_0 — h), f(x_0), f(x_0 + h), f(x_0 + 2h), f(x_0 + 3h) $

Подсказка: рассмотрим выражение $A f(x_0 — h) + B f(x_0 + h) + C f(x_0 + 2h) + D f(x_0 + 3h)$. {(3)}(\xi_0) \\ \end{выравнивание*} 9{(3)}(\xi_1) \\ \end{align*}

где $\xi_1$ находится между $x_0 — h$ и $x_0 + h$

Эти выводы включают в себя вычисление интерполяционного многочлена Лагранжа трех равномерно расположенных точек, вычисление производной и решение для производная в каждой точке. Использование первой или последней точки дает формулу конечной точки с тремя точками, а использование средней точки дает формулу средней точки с тремя точками.

Очевидно, что та же техника сработает и для пяти точек, но уравнения становятся очень утомительными и трудными для работы, а подсказка явно не хочет, чтобы мы решали задачу таким образом. 94$.

Это достаточно легко решить для A, B, C, D и E, вычитая (4) — (2) и (5) — (3), вычисляя E и D, вычитая (3) — (2) и заменив D, E, чтобы получить C, добавив (2) + (3) и подставив D, E, чтобы получить A, и заменив все в (1), чтобы получить B. Чтобы следовать исходной «подсказке», вместо этого установите B = 0.

$\endgroup$

$\begingroup$

Подсказка скрывает то, что окончательная формула $$f'(x)=A\frac{f(x-h)-f(x)}h+B\frac{f(x+h)-f( x)}h+C\frac{f(x+2h)-f(x)}h+D\frac{f(x+3h)-f(x)}h.