Что называют рациональным числом: Рациональные числа — урок. Алгебра, 10 класс.

• Они бесконечны.
• Может быть выражен дробью или десятичным числом.
• Между двумя рациональными числами лежит бесконечное число рациональных чисел.
• Рациональные числа содержат целые числа, они содержат натуральные числа.

Каждое число в форме дроби является рациональным числом, но если инкогнита является десятичным числом, мы должны проверить, является ли оно рациональным или иррациональным числом. Следующие шаги представляют собой процедуру, позволяющую узнать, является ли число рациональным и какой классификации, например, A, B и C в виде дроби:

А)

6 / 7

     Б)

12 /

     В)

125 /

1. Мы должны преобразовать дробь в десятичное число, для этого мы должны произвести деление:
   А) 6/7 = 0,857142857142857142857142…
   Б) 12/5 = 2,4
   В) 125/66 = 1,89393939393…
2. Определяем, повторяется ли в десятичной части число или группа чисел, где число или группа чисел соответствует периоду повторения, и определяем, какой классификации оно соответствует.
   A) Периодическое издание = 857142 ← Периодическое чистое.
   Б) Запрещено
   C) Периодическое = 93 ← Периодическое Смешанное.
   

Теперь предположим, что неизвестное задано в виде десятичного числа, поэтому теперь мы имеем в качестве примера D, E и F в виде десятичного числа:

D) 0,27838383838383. ..
E) 123,142857142857…
F) 6,01001000100001…

1. Проще всего проверить, есть ли повторение чисел, и таким образом определить, является ли число рациональным или иррациональным. .
   D) Рациональный, Периодический = 83, Периодический Смешанный.
   E) Рациональный, Периодический = 142857, Периодический Чистый.
   Е) иррациональный.

При определении того, что есть период, другими словами, есть повторение каждого определенного числа, мы говорим, что это рациональное число, но если нет определенного периода, то говорят, что это иррациональное число.

Узнайте больше о: « Иррациональное число ». →

Объяснение урока: Набор рациональных чисел

В этом эксплейнере мы научимся определять рациональные числа и находить положение рационального числа на числовой прямой.

Рациональные числа часто называют дробями. Однако это особый тип дроби, в которой и числитель, и знаменатель должны быть целыми числами.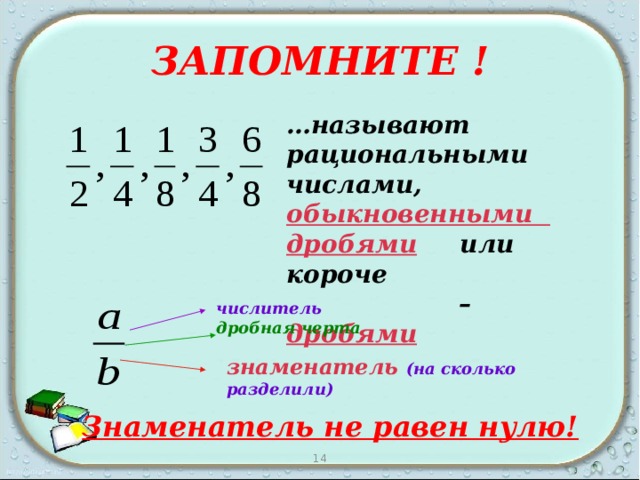 и знаменатель не может быть равен нулю.

Одним из способов применения рациональных чисел является рассмотрение пропорций целого. Например, если мы разделим пиццу на 8 равных ломтиков, то каждый ломтик представляет 18 всей пиццы.

Точно так же мы можем думать об этих числах, рассматривая числовые ряды. Мы можем спросить, какое число лежит посередине между 0 и 1. Так как двойное число должно быть 1, мы можем видеть, что это 12.

Мы можем определить множество всех рациональных чисел более формально следующим образом.

Определение: множество рациональных чисел

Множество рациональных чисел, обозначаемое ℚ, представляет собой множество всех частных целых чисел. Следовательно, ℚ содержит все элементы вида 𝑎𝑏, где 𝑎 и 𝑏 — целые числа, а 𝑏 не равно нулю. В нотации построителя наборов у нас есть ℚ=𝑎𝑏∶𝑎,𝑏∈ℤ𝑏≠0.и

Используя это определение, мы можем увидеть некоторые интересные свойства множества рациональных чисел. Во-первых, мы можем отметить, что все целые числа являются рациональными числами, так как если 𝑐∈ℤ, то 𝑐=𝑐1, поэтому 𝑐∈ℚ. Это означает, что множество целых чисел подмножество множества рациональных чисел. Затем мы можем вспомнить, что множество натуральных чисел является подмножеством целых чисел, давая нам ℕ⊂ℤ⊂ℚ.

Хотя доказательство этого результата выходит за рамки этого объяснения, некоторые числа, такие как √2 или 𝜋, не являются рациональными. и называются иррациональными. Стоит отметить, что число не может быть одновременно рациональным и иррациональным.

Мы также можем использовать это определение, чтобы найти несколько примеров рациональных чисел. Например, 1 и 2 — целые числа, поэтому 12∈ℚ. Точно так же 53 и 127 являются рациональными числами. Один из способов концептуализации рациональных чисел, подобных этим, состоит в том, чтобы рассматривать их как кратные более простых дробей. Например, мы можем думать о 53 как о 5 партиях по 13.

Это не единственный способ представления рациональных чисел; мы также видели, что 12 = 0,5, поэтому мы также можем представлять рациональные числа в виде десятичных дробей. Стоит отметить, что любое десятичное разложение с конечным числом цифр или повторяющееся разложение рационально. Мы можем представить такие числа, используя линию над повторяющимися цифрами, поэтому 0,7̇1̇2=0,7121212… и 0,7̇1̇2∈ℚ. Точно так же мы можем представлять дроби в виде смешанных чисел; например, 53=123, что также является рациональным числом.

Мы можем представить эту информацию в виде следующей диаграммы Венна.

В нашем первом примере мы определим, является ли данное число рациональным числом.

Пример 1. Определение рациональности числа

Является ли 1256 рациональным числом?

Ответ

Начнем с того, что вспомним, что множество рациональных чисел, обозначаемое как ℚ, представляет собой множество всех частных целых чисел. Поэтому, ℚ=𝑎𝑏∶𝑎,𝑏∈ℤ𝑏≠0и.

Таким образом, чтобы определить, является ли число 1256 рациональным, нам нужно проверить, можем ли мы записать это число в виде 𝑎𝑏 для целых чисел 𝑎 и 𝑏 с 𝑏≠0. Мы можем сделать это, вспомнив, что 12 можно записать как 12×66=726. Следовательно, 1256=726+56=776.

Таким образом, 1256 можно записать как частное целых чисел, поэтому ответ — да, это рациональное число.

В нашем следующем примере мы рассмотрим, являются ли все рациональные числа целыми числами.

Пример 2. Сравнение целых и рациональных чисел

Является ли каждое рациональное число целым?

Ответ

Начнем с того, что вспомним, что множество рациональных чисел, обозначаемое как ℚ, представляет собой множество всех частных целых чисел. Поэтому, ℚ=𝑎𝑏∶𝑎,𝑏∈ℤ𝑏≠0и.

Таким образом, такие числа, как 12, являются рациональными числами. Мы знаем, что 12 находится между 0 и 1 и не равно любое целое число, поэтому 12∉ℤ. Следовательно, 12 — рациональное число, не являющееся целым числом, и так что ответ — нет, не все рациональные числа целые.

В следующем примере мы проверим, является ли заданное целое число рациональным.

Пример 3. Определение принадлежности или не принадлежности числа множеству рациональных чисел

Что из следующего верно?

1. 1∈ℚ
2. 1∉ℚ

Ответ

Начнем с того, что вспомним, что множество рациональных чисел ℚ — это множество всех частных целых чисел. В частности, мы можем отметить, что 1=11, так что это частное целых чисел.

Стоит отметить, что любое 𝑐∈ℤ является рациональным числом, поскольку 𝑐=𝑐1. Установив 𝑐=1, мы получим 1∈ℚ.

Следовательно, 1∈ℚ, что является вариантом A.

До сих пор мы сосредоточились на формальном определении рационального числа. Тем не менее, есть много пользы в рассмотрении визуализации рациональных чисел. В частности, мы можем представить любое рациональное число на числовой прямой с помощью расстояний.

Например, рассмотрим следующую числовую строку с маркерами, представляющими целые числа.

Допустим, нам нужно найти точку на числовой прямой, соответствующую −53. Мы могли бы начать с того, что заметим, что это число отрицательное, так что он лежит на отрицательной стороне числовой прямой, и что 3 входит в 5 один раз с остатком 2, поэтому -53 должен лежать между −1 и −2. Однако нам нужна точная точка, представляющая это число, и для этого мы отмечаем, что знаменатель равен 3, а поэтому нам нужно будет разбить числовую строку на 13 приращений. В частности, -53 будет 5 приращений 13 с отрицательной стороны, как показано.

Заметим, что -2=-63 и что -1=-33 и что каждое приращение 13 будет увеличивать или уменьшите это значение на 13. Это позволяет нам видеть, что отмеченные точки между -1 и -2 будут представлять −43 и −53 соответственно.

Используя тот же метод, мы можем представить любое рациональное число на числовой прямой; нам просто нужно определить целые числа, между которыми он лежит, а затем разделить строку на равные приращения в зависимости от знаменателя дроби.

Это также позволяет нам заметить, что знак 𝑎𝑏 определяется знаками 𝑎 и 𝑏. В общем случае, если 𝑎 и 𝑏 имеют одинаковый знак, то 𝑎𝑏 положительно, если 𝑎 и 𝑏 имеют разные знаки, то 𝑎𝑏 отрицательно, а если 𝑎=0, то 𝑎𝑏=0. Кроме того, когда 𝑎𝑏 отрицательное, знак минус пишется перед дробью, так как не имеет значения, является ли этот множитель −1 находится в числителе или знаменателе.

Давайте теперь рассмотрим пример определения точки, представляющей заданное рациональное число.

Пример 4. Определение позиций рациональных чисел на числовой прямой

Какое из чисел 𝑙, 𝑚, 𝑛 и 𝑜 равно 410?

Ответ

Чтобы определить положение числа 410 на числовой прямой, заметим, что поскольку знаменатель дроби равен 10, мы хотим разделить числовую строку с шагом 110. Если мы посмотрим на данную числовую строку, то увидим, что для каждой целочисленной пары есть 5 приращений. Итак, нам нужно будет разделить каждое из них пополам, чтобы получить приращение 110. Мы также отмечаем, что 410 положительно, поэтому мы хотим, чтобы точка 4 увеличилась на 110 в положительном направлении, как показано.

Затем мы видим, что это отмечено 𝑛 на числовой строке.

В нашем следующем примере мы воспользуемся идеей поиска точек, представляющих рациональные числа на числовой прямой, чтобы определить рациональное число, лежащее между двумя заданными рациональными числами.

Пример 5. Решение задач на рациональные числа

Найдите рациональное число, лежащее посередине между −27 и 435.

Ответ

Поскольку нас просят найти рациональное число, лежащее посередине между −27 и 435, мы должны начать с представление этих чисел на числовой прямой. Для этого заметим, что −27 будет 2 приращениями по 17. в отрицательном направлении и что 435 будет 4 приращениями по 135 в положительном направлении. Мы также можем обратите внимание, что 35 = 7 × 5, поэтому мы можем найти приращения 135, разделив приращения 17 на 5 равных частей. Это дает нам следующее.

Нам нужно число, лежащее посередине между −27 и 435. Это означает, что оно должно лежать на равном количестве приращения от обоих этих чисел. Поскольку между числами есть 14 приращений, нам нужно число, которое составляет 7 приращений по обе стороны от этих конечных точек. Мы можем видеть на числовой прямой, что это следующая точка.

Поскольку эта точка находится на 3 шага по 135 левее 0, мы можем записать это число как −335.

В нашем последнем примере мы определим, какое из четырех заданных выражений является рациональным при заданных значениях переменных.

Пример 6. Определение рационального выражения из списка заданных выражений

Какое из следующих выражений является рациональным при условии 𝑎=1 и 𝑏=34?

1. 39𝑏𝑏 — 34
2. −39𝑎 — 1
3. 𝑏𝑎
4. 39𝑏𝑎 — 1

Ответ

Мы начинаем с напоминания о том, что набор рациональных чисел, написанных ℚ, является набором всех поощрительных. Поэтому, ℚ=𝑎𝑏∶𝑎,𝑏∈ℤ𝑏≠0и.

Мы можем определить, какое из этих выражений является рациональным, подставив значения 𝑎 и 𝑏 в каждое выражение отдельно.

В выражении А получаем 39𝑏𝑏−34=39(34)34−34.

Оценивая знаменатель, получаем 39(34)34−34=39(34)0.

Поскольку мы не можем делить на 0, это не рациональное число.

Аналогичная история с выражениями B и D. Для выражения B имеем −39𝑎−1=−391−1=−390, а для выражения D имеем 39𝑏𝑎−1=39(34)1−1=39(34)0.

Таким образом, ни один из них не представляет рациональных чисел.

Наконец, в выражении C имеем 𝑏𝑎=341, которое представляет собой частное двух целых значений, где знаменатель не равен нулю.

Следовательно, только вариант C является рациональным числом.

Давайте закончим повторением некоторых важных моментов из этого объяснения.

Ключевые моменты

• Множество рациональных чисел, обозначаемое ℚ, представляет собой множество всех частных целых чисел.

  No related posts.