примеры, решения, как найти середину отрезка по координатам
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Определение 1Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок AB.
Если отрезок AB продолжить в обе стороны от точек A и B, мы получим прямую AB. Тогда отрезок AB – часть полученной прямой, ограниченный точками A и B. Отрезок AB объединяет точки A и B, являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K, лежащую между точками A и B, можно сказать, что точка K лежит на отрезке AB.
Определение 2Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка AB обозначим следующим образом: AB.
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка AB обозначить точкой C, то верным будет равенство: AC=CB
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C) при заданных координатах концов отрезка (A и B), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Исходные данные: координатная прямая Ox и несовпадающие точки на ней: A и B. Этим точкам соответствуют действительные числа xA и xB. Точка C – середина отрезка AB: необходимо определить координату xC.
Поскольку точка C является серединой отрезка АВ, верным будет являться равенство: |АС| = |СВ|. Расстояние между точками определяется модулем разницы их координат, т.е.
|АС| = |СВ|⇔xC-xA=xB-xC
Тогда возможно два равенства: xC-xA=xB-xC и xC-xA=-(xB-xC)
Из первого равенства выведем формулу для координаты точки C : xC=xA+xB2 (полусумма координат концов отрезка).
Из второго равенста получим: xA=xB , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка AB с концами A(xA) и B(xB):
xA+xB2
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Середина отрезка на плоскости
Исходные данные: прямоугольная система координат на плоскости Оxy, две произвольные несовпадающие точки с заданными координатами AxA, yA и BxB, yB . Точка C – середина отрезка AB. Необходимо определить координаты xC и yC для точки C.
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей.Ax, Ay ; Bx, By и Cx ,Cy — проекции точек A, B и C на оси координат (прямые Ох и Оy).
Согласно построению прямые AAx, BBx, CCx параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства АС = СВ следуют равенства: АxСx = СxВx и АyСy = СyВy, и они в свою очередь свидетельствуют о том, что точка Сx – середина отрезка АxВx, а Сy – середина отрезка АyВy.
И тогда, опираясь на полученную ранее формулу, получим:
xC=xA+xB2 и yC=yA+yB2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка AB на плоскости с координатами концов A (xA,yA) и B (xB, yB) определяются как:
(xA+xB2, yA+yB2)
Середина отрезка в пространстве
Исходные данные: система координат Оxyz и две произвольные точки с заданными координатами A(xA, yA, zA) и B (xB, yB, zB). Необходимо определить координаты точки C, являющейся серединой отрезка AB.
Ax, Ay, Az ; Bx, By,Bz и Cx, Cy, Cz — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: AxCx=CxBx, AyCy=CyBy,AzCz=CzBz
Следовательно, точки Cx, Cy,Cz являются серединами отрезков AxBx, AyBy, AzBz соответственно.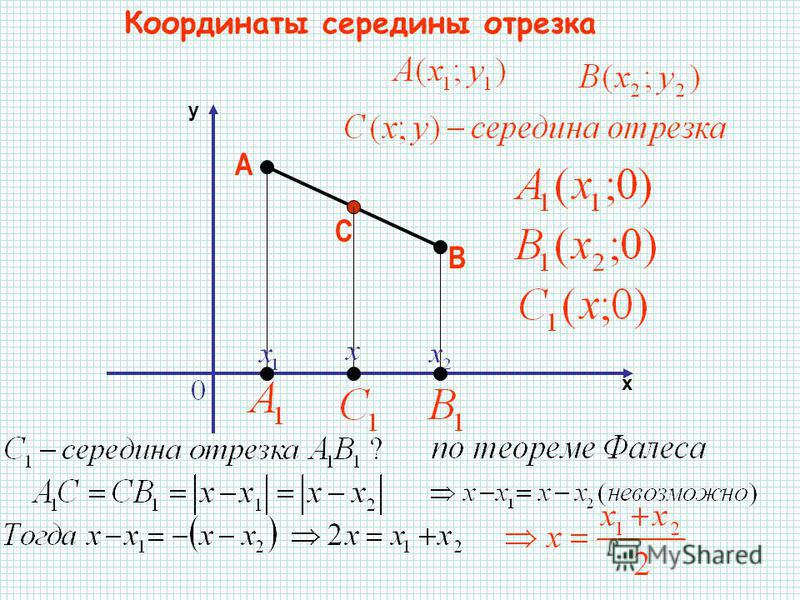
Тогда, для определения координат середины отрезка в пространстве верны формулы:
xC=xA+xB2, yc=yA+yB2, zc=zA+ZB2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
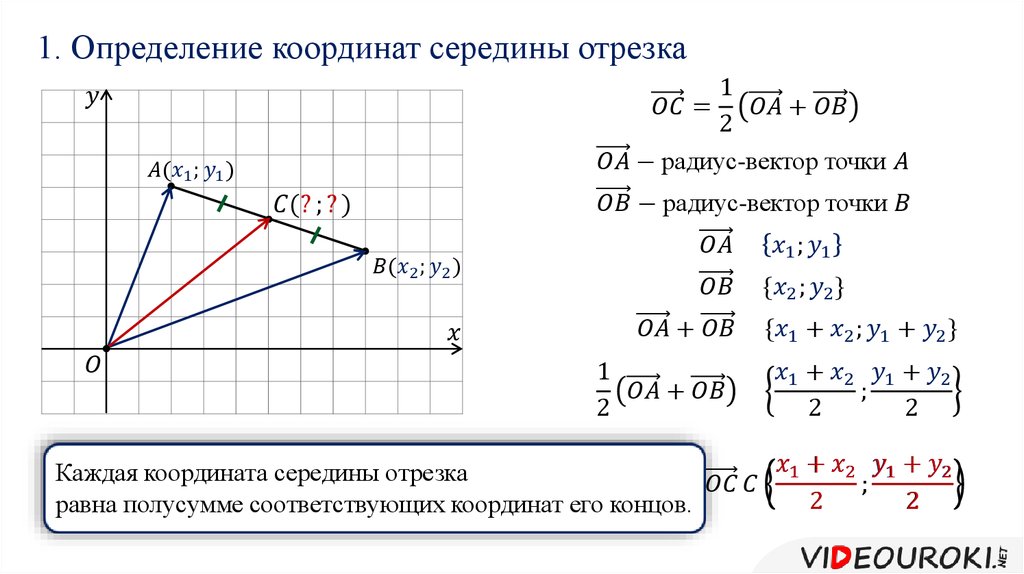
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат Oxy, точки с заданными координатами A(xA,yA) и B(xB, xB) . Точка C – середина отрезка AB.
Согласно геометрическому определению действий над векторами верным будет равенство: OC→=12·OA→+OB→ . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов OA→ и OB→ , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: OA→=(xA, yA), OB→=(xB,yB) .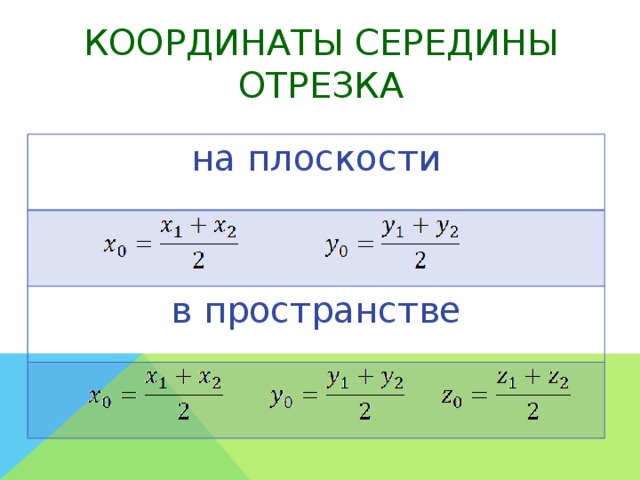
Выполним некоторые операции над векторами в координатах и получим:
OC→=12·OA→+OB→=xA+xB2, yA+yB2
Следовательно, точка C имеет координаты:
xA+xB2, yA+yB2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C(xA+xB2, yA+yB2, zA+zB2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Пример 1Исходные данные: на плоскости – точки с заданными координатами А (-7,3) и В (2,4). Необходимо найти координаты середины отрезка АВ.
Решение
Обозначим середину отрезка AB точкой C. Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B.
xC=xA+xB2=-7+22=-52yC=yA+yB2=3+42=72
Ответ: координаты середины отрезка АВ-52, 72.
Пример 2Исходные данные: известны координаты треугольника АВС: А (-1,0), В (3,2), С (9,-8). Необходимо найти длину медианы АМ.
Решение
- По условию задачи AM – медиана, а значит M является точкой середины отрезка BC. В первую очередь найдем координаты середины отрезка BC, т.е. точки M:
xM=xB+xC2=3+92=6yM=yB+yC2=2+(-8)2=-3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы АМ:
AM=(6-(-1))2+(-3-0)2=58
Ответ: 58
Пример 3Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед ABCDA1B1C1D1 .
Заданы координаты точки C1(1, 1, 0), а также определена точка M, являющаяся серединой диагонали BD1 и имеющая координаты M (4, 2, -4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка АС1. Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: xM=xA+xC12 ⇒xA=2·xM-xC1=2·4-1+7yM=yA+yC12⇒yA=2·yM-yC1=2·2-1=3zM=zA+zC12⇒zA=2·zM-zC1=2·(-4)-0=-8
Ответ: координаты точки А (7,3,-8).
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Как найти координаты середины отрезка: формулы, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.
ru Математика Геометрия Нахождение координат середины отрезка
В данной публикации мы рассмотрим, что такое середина отрезка, по какой формуле считаются ее координаты (в плоскости и пространстве). Также разберем примеры решения задач по этой теме.
- Расчет координат середины отрезка
- Примеры задач
Расчет координат середины отрезка
Серединой называется точка, лежащая на отрезке и находящаяся на одинаковом расстоянии от его концов.
AC = CB
Если концы отрезка A (xa, ya) и B (xb, yb) расположены в одной плоскости, то координаты его середины (точки C) считаются по формуле:
Если отрезок с концами A (xa, ya, za) и B (xb, yb, zb) находится в трехмерном пространстве, координаты его середины рассчитываются следующим образом:
Примеры задач
Задание 1
Вычислим координаты точки C, которая является серединой отрезка AB, образованного точками A (5, -2) и B (11, 10).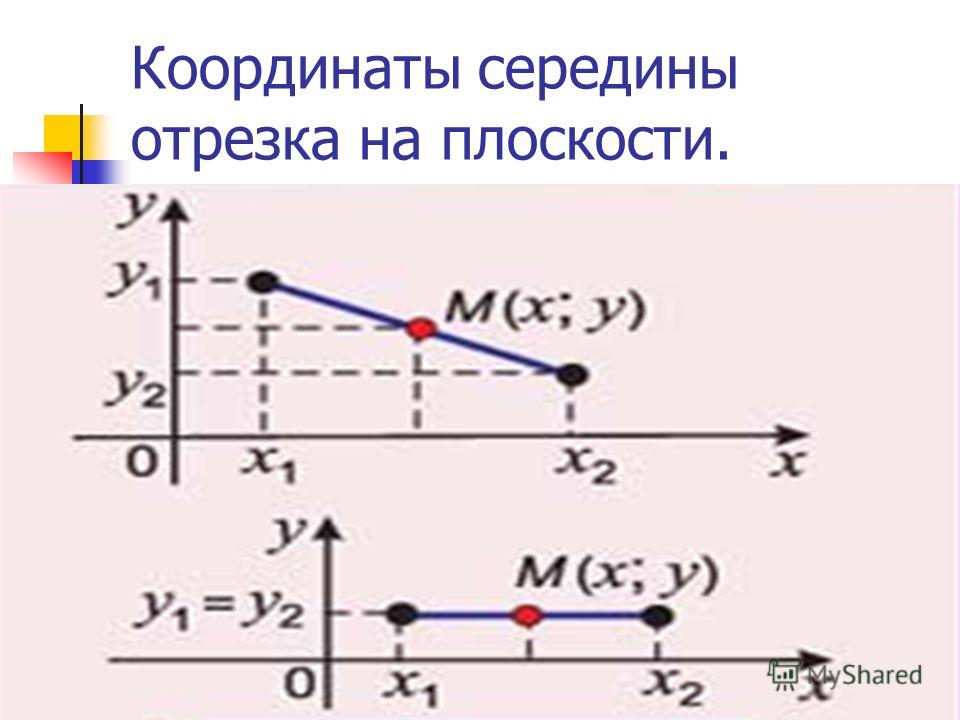
Решение:
В данном случае нам подойдут формулы для плоскости:
xc = (5 + 11) / 2 = 8
yc = (-2 + 10) / 2 = 4
Таким образом, точка C имеет координаты (8, 4).
Задание 2
Найдем координаты точки B, являющейся одним из концов отрезка AB. При этом известны координаты точки A (7, 13) и середины отрезка – C (4, -3).
Решение:
Нужные нам формулы можно вывести из выражений для расчета координат середины отрезка:
xb = 2xc – xa = 2 · 4 – 7 = 1
yb = 2yc – ya = 2 · (-3) – 13 = -19
Следовательно, координаты B – (1, -19).
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Формула средней точки — промежуточная геометрия
Все ресурсы по промежуточной геометрии
8 диагностических тестов 250 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 Следующая →
Справка по геометрии среднего уровня » Координатная геометрия » Линии » Midpoint Formula
Что такое середина между и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Середина определяется путем взятия среднего значения координат и по отдельности.
Пусть и
Таким образом, формула середины точки становится и
Таким образом, средняя точка равна
Сообщить об ошибке
Какова середина отрезка, соединяющего точки и
Возможные ответы: 59 Объяснение: Используйте формулу средней точки: Сообщить об ошибке Даны две точки и и отрезок, соединяющий их. Что такое середина отрезка? Кроме того, какова длина отрезка? Возможные ответы: Средняя точка: Длина: Средняя точка: Длина: Средняя точка: Длина: Середина: Длина: Середина: Длина: Правильный ответ: Середина:4 Длина:
Объяснение:
Формула средней точки выглядит следующим образом:
Это имеет смысл; это так же просто, как среднее значение компонентов и каждой точки.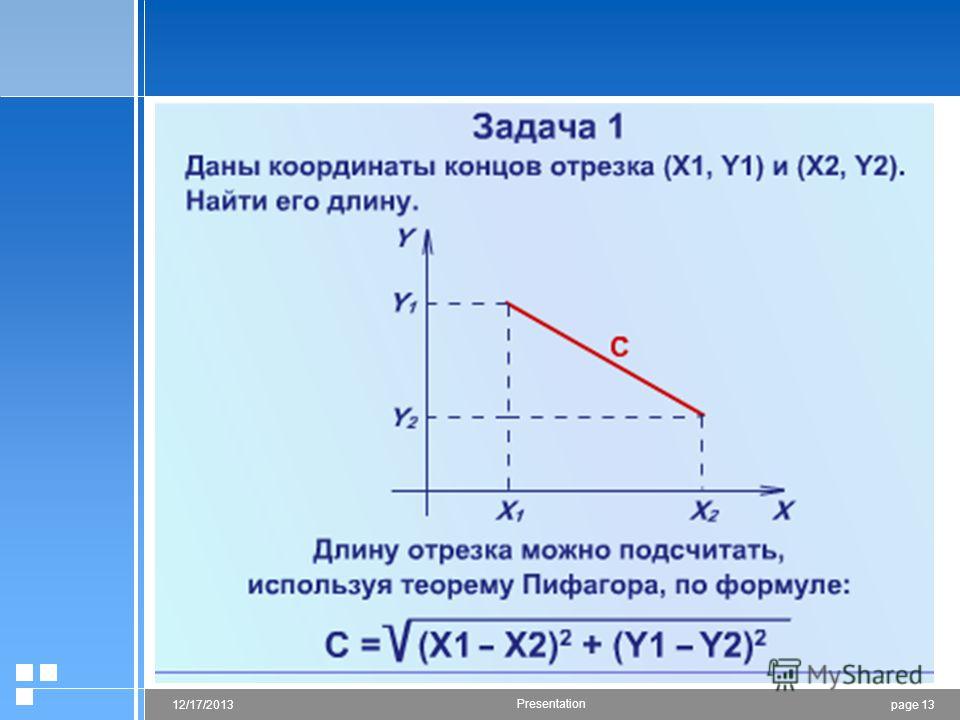
Для этой задачи .
Таким образом, средняя точка равна
Формула расстояния выглядит следующим образом:
Порядок, в котором вы ставите первый и второй компоненты каждой точки, НЕ имеет значения, когда возводится в квадрат положительное или отрицательное число, оно всегда будет положительным.
Таким образом, расстояние равно
Сообщить об ошибке
Найдите середину отрезка, идущего от до .
Возможные ответы:Правильный ответ:
Объяснение:
Чтобы найти середину отрезка, необходимо найти среднее значение значений x и среднее значение значений y.
Наши значения x равны и чтобы найти их среднее значение, мы делаем это.
Наши значения y равны и , поэтому наше среднее значение равно . Следовательно, наша средняя точка должна быть .
Сообщить об ошибке
Найти координату середины отрезка, соединяющего пару точек
и .
Возможные ответы:
Невозможно определить
Правильный ответ:
Пояснение:
Координата середины отрезка, соединяющего пару точек, равна
Таким образом, для пары точек и,
получаем:
Сообщить об ошибке
Найти координату точки середина отрезка, соединяющего пару точек
,и .
Возможные ответы:
Невозможно определить
Правильный ответ:
Объяснение:
Координата середины отрезка, соединяющего пару точек, равна
.
Таким образом, для пары точек и
мы получаем
Сообщить об ошибке
Линия проходит от начала координат до . Какова его середина?
Возможные ответы:
Правильный ответ:
Объяснение:
Исходной точкой является точка. Мы можем использовать обычную формулу средней точки с as и заданной точкой как :
Обратите внимание, что, поскольку первая точка является исходной, мы усредняем эти точки с 0 или, другими словами, просто делим на 2.
Сообщить об ошибке
Между двумя точками (5, 10) и (3, 6) есть отрезок. Какая формула даст вам правильную середину отрезка?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти среднюю точку по двум точкам на координатной плоскости, вы в основном находите среднее значение значений x и среднее значение значений y.
С нашими точками это дает:
Сообщить об ошибке
Линия имеет конечные точки в точках (4,5) и (-6,8). Где его середина?
Возможные ответы:
Правильный ответ:
Объяснение:
Средняя точка — это точка, равноудаленная от каждой конечной точки.
Мы находим его, используя формулу, которая вычисляет среднее значение координат x и y.
Сообщить об ошибке
Сегмент линии имеет конечные точки и . Какова середина этого отрезка?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните формулу для нахождения середины отрезка:
Координаты средней точки — это просто среднее значение координат x и среднее значение координат y.
Подставьте заданные точки, чтобы найти середину отрезка.
Сообщить об ошибке
← Предыдущий 1 2 3 4 5 6 Далее →
Уведомление об авторских правах
Все промежуточные ресурсы по геометрии
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Учитесь по концепции
Что такое формула средней точки? Пример определения, геометрии и экономики
Руководство по формуле средней точки в геометрии и экономике с примерами
Что такое формула средней точки?
Содержание
- Что такое формула средней точки?
- Использование формулы средней точки
- Что такое середина линии?
- Уравнение дистанции и средней точки. Экономика формулы средней точки Пример
Определение: Формула средней точки в геометрии представляет собой уравнение, которое вычисляет среднее расстояние между двумя известными координатными точками.
В экономике формула средней точки используется для измерения изменений кривых спроса и предложения и их относительной эластичности.
Формула средней точки
ИспользованиеФормула средней точки часто используется для нахождения средней точки, чтобы разделить отрезок пополам. Его также можно использовать для доказательства того, что отрезок делится пополам.
Формула находит среднее или медиану двух значений. Эта формула часто используется с картами и с формулой расстояния.
Например, Найдите город, который находится между Чикаго, штат Иллинойс, и Индианаполисом, штат Индиана. Как далеко город от Чикаго?
Чтобы ответить на этот вопрос, давайте посмотрим, как найти среднюю точку ниже.
Что такое середина линии?
Середина — это координатная точка, которая находится посередине между двумя другими точками на отрезке.
Средние точки встречаются как в двухмерном пространстве на графике, так и в трехмерном пространстве внутри куба, сферы или другой формы.
Нахождение средней точки помогает решить географические, программные и экономические задачи.
Давайте посмотрим, как рассчитать это уравнение.
Уравнение формулы расстояния и средней точки
Уравнение формулы средней точки вычисляется путем сложения двух координатных точек ( x 1 , y 2 ) и ( x 2 , у 2 ) и делением на два. Средняя точка, представленная M, , рассчитывается следующим образом:
Нижние индексы, небольшие числа в основании переменных указывают на точку, из которой исходит значение. Поскольку в формуле используется сложение, а порядок не влияет на сумму, порядок, в котором вы добавляете значения, не важен.
Важно убедиться, что вы складываете координаты x- вместе и добавляете y- координаты вместе. Также обратите внимание, что ответ находится в виде координаты, так как середина является точкой, решение также должно быть в форме координат.
Примеры формулы средней точки в геометрии
Середина отрезка прямой Пример
Средняя точка отрезка прямой Формула вычисляет среднюю точку этого отрезка. При решении каждой переменной обязательно сложите, а затем разделите на два.
Когда отрезок прямой или горизонтальный, одна из координат не изменяется.
Сначала мы пометим наши переменные индексами один или два.
Далее мы подставим значения в формулу.
Сложите значения в числителе.
Упростите дроби. Если числитель нечетный, часто результат остается в десятичной форме, но допустима и смешанная или неправильная дробь.
Обратите внимание, что для горизонтальной линии координата y средней точки совпадает с обеими конечными точками. Середина вертикальной линии имеет те же x — координаты в качестве конечных точек.
Это может помочь сэкономить время при решении проблемы, однако, если вы склонны путать координаты x и y , то лучше выполнять каждый шаг во избежание ошибок.
Середина диагональной линии Пример
Давайте рассмотрим пример формулы средней точки, где отрезок расположен по диагонали.
Для начала нам нужно найти координаты точек.
Мы сделаем точку A нашей первой точкой (индекс 1) и точку B нашей второй точкой (индекс 2)
Далее мы подставим значения в формулу и упростим.
Формула метода средней точки в экономике
Пример формулы метода средней точки
Метод средней точки часто используется в экономике для измерения ценовой эластичности изменений кривой спроса и предложения и экономического воздействия каждого из них.
Экономика использует метод наклона по формуле средней точки и применяет его к треугольникам.
Еще одна задача, в которой используются средние точки, — поиск второй конечной точки сегмента.
Дан отрезок с конечной точкой (-3,-5) и средней точкой (1,1), найдите другую конечную точку отрезка.
Один из способов решить эту проблему — использовать формулу средней точки. Мы можем разбить его, чтобы посмотреть на x-координаты и y -координаты отдельно.
Мы начнем с того, что пометим нашу известную конечную точку как , а наша средняя точка будет . Теперь мы можем подставить наши известные значения.
Начните с умножения обеих сторон на 2. Это уменьшит дробь.
Вычтем или, в данном случае, прибавим, поскольку у нас отрицательное значение, чтобы изолировать переменную.
Координаты второй конечной точки (5,7).
Пример экономической формулы средней точки
Второй способ найти отсутствующую конечную точку в экономической формуле средней точки — использовать наклон. Мы изучим этот метод, используя те же значения.
Начнем с наброска схемы.
Найдем наклон между конечной точкой и средней точкой.
Уклон 6/4. Мы не собираемся уменьшать наклон, так как нам нужны одинаковые значения.