Экспонента, е в степени х
Приведены график и основные свойства экспоненты (е в степени х): область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд, действия с комплексными числами.
Определение
- Экспонента
- – это показательная функция y(x) = e x, производная которой равна самой функции.
Экспоненту обозначают так , или .
Число e
Основанием степени экспоненты является число e. Это иррациональное число. Оно примерно равно
е ≈ 2,718281828459045…
Число e определяется через предел последовательности. Это, так называемый, второй замечательный предел:
.
Также число e можно представить в виде ряда:
.
График экспоненты
График экспоненты, y = ex.
На графике представлена экспонента, е в степени х.
y(x) = е х
На графике видно, что экспонента монотонно возрастает.
Формулы
Основные формулы такие же, как и для показательной функции с основанием степени е.
;
;
;
.
Выражение показательной функции с произвольным основанием степени a через экспоненту:
.
См. также раздел «Показательная функция» >>>
Частные значения
Пусть y(x) = e x. Тогда
.
Свойства экспоненты
Экспонента обладает свойствами показательной функции с основанием степени е > 1.
Область определения, множество значений
Экспонента y(x) = e x определена для всех x.
Ее область определения:
– ∞ < x + ∞.
Ее множество значений:
0 < y < + ∞.
Экстремумы, возрастание, убывание
Экспонента является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
| y = е х | |
| Область определения | – ∞ < x < + ∞ |
| Область значений | 0 < y < + ∞ |
| Монотонность | монотонно возрастает |
| Нули, y = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 1 |
| + ∞ | |
| 0 |
Обратная функция
Обратной для экспоненты является натуральный логарифм.
;
.
Производная экспоненты
Производная е в степени х равна е в степени х:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
См. также раздел «Таблица неопределенных интегралов» >>>
Комплексные числа
Действия с комплексными числами осуществляются при помощи формулы Эйлера:
,
где есть мнимая единица:
.
Выражения через гиперболические функции
; ;
.
Выражения через тригонометрические функции
; ;
;
.
Разложение в степенной ряд
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
геометрия / Как найти длину кругоиды степени (x)? / Математика
|
Известно, что окружность есть геометрическое место точек вершин прямоугольных (пифагоровых) треугольников, построенных на диаметре d этой окружности и отвечающих уравнению: $$a^2 + b^2 = d^2$$ где $%a$% и $%b$% — длины меньших сторон треугольника. (назовём её «кругоида третьей степени»), где по-прежнему $%a$% и $%b$% — длины меньших сторон треугольника. И вообще для любого значения x, если x больше единицы и меньше бесконечности, на том же диаметре $%d$% можно построить кругоиду степени $%x$%, каждая точка которой отвечает тому же, предыдущему уравнению, в котором вместо цифры 3 стоит значение величины $%x$%. Как найти длину кругоиды степени $%x$%, площадь, ограниченную кругоидой, площадь поверхности и объём фигуры, образованной вращением кругоиды относительно какой-либо из осей её симметрии? кривые геометрия задан Nikolay изменен 5 Фев ’12 12:55 {1/n}$%.Затем используйте программу построения графиков в полярных координатах, чтобы посмотреть форму графика при разных значениях n. ссылка отвечен 5 Фев ’12 19:59 Anatoliy изменен 10 Май ’13 20:12 |
|
Теоретического смысла в задаче не так много. Интегралы либо не берутся, либо будут приведены к специальным функциям. ссылка отвечен 7 Фев ’12 16:10 ValeryB |
|
Интересная задачка! Я попытаюсь подытожить ответы других пользователей. ссылка отвечен 3 Окт ’12 2:42 chameleon |
|
Данная кривая не является ограниченным множеством при нечётных степенях. Действительно, так как арифметический корень нечётной степени определён для всех вещественных чисел, то уравнение $%x^n+y^n=d^n$% в данном случае эквивалентно уравнению $%y=\sqrt[n]{d^n-x^n}$% на всей вещественной оси. ссылка отвечен 10 Май ’13 10:04 MathTrbl изменен 10 Май ’13 10:38 |
|
Да, пожалуй, лучшим является применение методов вычислительной математики. Если в кругоиде второй степени отношение длины кругоиды к диаметру является числом трансцендентным, то уж, тем более,следует ожидать сложностей при ответе на поставленный вопрос для кругоиды в самом общем случае. ссылка отвечен 18 Фев ’12 11:03 nikolaykruzh… изменен 9 Май ’13 18:37 |
Ваш ответ
Если вы не нашли ответ, задайте вопрос. {v(x)}=v(x)\ln u(x)$. Теперь дифференцируйте: 9x$, мы можем заменить $x$ по мощности на $y$. Тогда данная функция фактически становится функцией двух переменных $x$ и $y$.
{v(x)}=v(x)\ln u(x)$. Теперь дифференцируйте: 9x$, мы можем заменить $x$ по мощности на $y$. Тогда данная функция фактически становится функцией двух переменных $x$ и $y$.
Функция, полученная после шага 1 выше, может быть легко дифференцирована методом частичного дифференцирования.
В дифференцированной функции, полученной после шага 2, подставьте $y=x$, и вы получите дифференцированную функцию первоначально рассматриваемой запутывающей функции в $x$.
Здесь загружено изображение расчетов для данной функции на основе вышеуказанных шагов. введите описание изображения здесь 9{1/2}}+\frac{1}{x})\right).$$
Примечание. Этот метод эквивалентен методу, предложенному Брайаном М. Скоттом. Тем не менее, это позволяет держать все на одной стороне.
редактировать: исправлена производная
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
| МАТЕМАТИКА
ОБЗОР: ПОЛЕЗНАЯ МАТЕМАТИКА ДЛЯ КАЖДОГО СЕКЦИЯ
3.
Показатель степени относится количество раз, когда число умножается само на себя. Например, 2 к 3-му (записывается так: 2 3 ) означает:
2 3 — это не то же самое, что 2 x 3 = 6. Помните, что число, возведенное в степень 1, есть оно само. Например,
Есть несколько особых случаев:
Вы можете иметь
переменная в данной степени, например, 3 , что означает a x a x a. |

 3$$
3$$ Но , если нужны для практики, то лучше применять методы вычислительной математики.
Но , если нужны для практики, то лучше применять методы вычислительной математики. {1-\frac 1 n}-1}$%. Взяв на вооружение достижения Механика и численные методы, я получил графики характестик единичной кругоиды, в зависимости от ее степени. Результаты можно посмотреть здесь (логарифмическая шкала, весь диапазон) и здесь (обычная шкала, $%n\in[1;10]$%).
{1-\frac 1 n}-1}$%. Взяв на вооружение достижения Механика и численные методы, я получил графики характестик единичной кругоиды, в зависимости от ее степени. Результаты можно посмотреть здесь (логарифмическая шкала, весь диапазон) и здесь (обычная шкала, $%n\in[1;10]$%).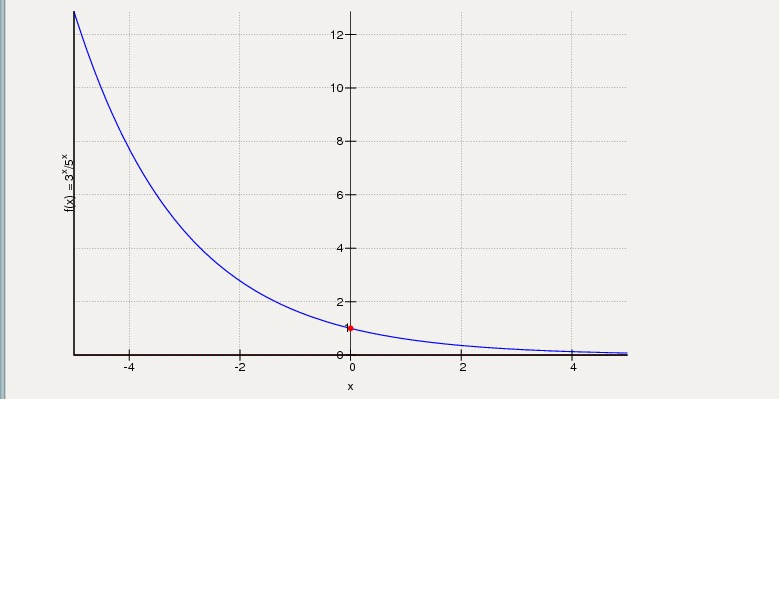 n.$%
n.$% Спасибо Вам, @ValeryB, и всем другим товарищам.
Спасибо Вам, @ValeryB, и всем другим товарищам. ЧТО ТАКОЕ ПОКАЗАТЕЛЬ?
ЧТО ТАКОЕ ПОКАЗАТЕЛЬ? 
