Формула матрицы умножения: эффективная реализация шаг за шагом / Хабр

— Excel

MS Office 2007: Microsoft Excel

Матричные операции в Excel        

Простейшие операции, которые можно проделывать с матрицами: сложение (вычитание), умножение на число, перемножение, транспо­нирование, вычисление обратной матрицы.

Задача 5.17.

Сложение матриц и умножение матрицы на число. Сложить матрицы м и N, где

Решение. Введем матрицы M и N в блоки A1:С2 и E1:G2. В блок А4:С5 введем табличную формулу {=А1: С2+Е1: G2}. Обратите внимание, что выделен блок имеет те же размеры, что и исходные матрицы.

Что произойдет, если перед вводом формулы выделить блок А4:D6? В «лишних» ячейках появится #Н/Д, т.е. «НеДоступно». А если выделить А4:В5? Будет выведена только часть матрицы, без каких- либо сообщений. Проверьте.

Использование имен делает процедуру ввода табличной формулы намного проще. Дайте диапазонам A1:С2 и 1:G2 имена M и N соответственно с помощью команды Формулы-Присвоить Имя.

В блок Е4:G5 введите табличную формулу {=M+N}. Результат, естественно, должен получиться тот же.

Теперь вычислим линейную комбинацию матриц 2 M-N. В блок А7:С8 введем табличную формулу {=2*M-N}. У Вас должны получиться результаты:

Рассмотренные примеры подводят нас к мысли, что обычная операция умножения применительно к блокам не вполне эквивалентна перемножению матриц. И действительно, для матричных операций в Excel предусмотрены функции, входящие в категорию «Математические»: 

• МОПРЕД — вычисление определителя матрицы;
• МОБР — вычисление обратной матрицы;
• МУМНОЖ — перемножение матриц;
• ТРАНСП — транспонирование.

Первая из этих функций возвращает число, поэтому вводится как обычная формула. Остальные функции возвращают блок ячеек, поэтому они должны вводиться как формулы массивов. Первая буква М в названии трех функций — сокращение от слова «Матрица».

Задача 5. 18.

Вычислить определитель и обратную матрицу для матрицы

Проверить правильность вычисления обратной матрицы умножением ее на исходную. Повторить эти действия для той же матрицы, но с элементом а33=10,01.

Решение. Разместим исходную матрицу в блоке А1:СЗ (рис. 106).

В ячейке в 5 поместим формулу для вычисления определителя =МОПРЕД(А1:СЗ) .

В блок А7:С9 введем формулу для вычисления обратной матрицы. Для этого, выделив блок А7:С9 (он имеет три строки и три столбца, как и ис­ходная матрица), введем        формулу {=МОБР (А1:СЗ)}. Да же если используется 

Мастер функций, завершить ввод нужно нажатием комбинации клавиш Shift+Ctrl+Enter (вместо кнопки ОК). Если предварительно не выделив блок А7:С9, ввести формулу в ячейку А7 как обычную формулу Excel (закончив ввод клавишей Enter), то не нужно вводить ее заново на остальной диапазон. Просто выделив А7:С9, выберите F2 (редактирование) и, не изменяя формулу, закончите действие комбинацией клавиш Shift+Ctrl+Enter.

Скопируйте блок А1:С9 в блок E1:G9. Измените один элемент ис­ходной матрицы: в ячейку G3 вместо 10 введите 10,01. Изменения в опре­делителе и в обратной матрице разительны! Этот специально подобранный пример иллюстрирует численную неустойчивость вычисления определителя и обратной матрицы: малое возмущение на входе дает большое возмущение на выходе.

Для дальнейших вычислений присвоим матрицам на рабочем листе имена: А1: СЗ — А, А7 : С9 — Ainv, El: G3 — АР, Е7 : G9 — APinv. Теперь проверим правильность вычисления обратной матрицы. В блок А12 : С14 введем формулу {=МУМНОЖ (A, Ainv) }, а в блок E12:G14 — формулу {=мумнож (ар, APinv) }. У вас должен получиться результат, как на рис. 107.

Как и следовало ожидать, получились матрицы, близкие к единичным.

Задание 1. Умножение числа на матрицу

Лабораторная работа №5

Использование Мастера функций. Операции с матрицами

Цель лабораторного занятия:

Освоение работы с матричными функциями Мастера функций.

Задачи лабораторного занятия:

1.Выполнение простейших операций с матрицами – сложение, умножение на число.

2.Умножение матриц.

3.Нахождение обратной матрицы.

4.Решение системы линейных алгебраических уравнений.

5.Оформление отчета по работе.

Содержание
Лабораторная работа №5. Использование Мастера функций. Операции с матрицами……………………….		2
Задание 1. Умножение числа на матрицу……………………………………………………………………………………		5
Задание 2. Сложение матриц…………………………………………………………………………………………………….		5
Задание 3. Умножение матриц…………… ………………………………………………………………………………………		5
Задание 4.	Нахождение обратной матрицы…………………………………………………………………………………	7
Задание 5.	Решение совместной системы линейных алгебраических уравнений…………………………..	7
Задание 6.	Оформление отчета…………………………………………………………………………………………………	7
Задание 7.	Домашнее задание…………………………………………………………………………………………………..	7
Контрольные вопросы……………………………………………………….. ……………………………………………………..		7

Лабораторная работа №5. Операции с матрицами

Лабораторная работа №5. Использование Мастера функций. Операции с матрицами

Матрица – прямоугольная таблица ячеек, в каждой из которых записано число. Ввод данных и редактирование элементов матрицы выполняются обычным способом. В табличном процессоре массив ячеек, образующих матрицу, обозначается как обычно записью через двоеточие адресов первой и последней ячейки.

Массив – это связанный диапазон ячеек на листе, содержащих какие-либо значения.

Например, матрица, показанная на рисунке 1, обозначается С5:С8. Для большей наглядности матрица заключена в рамку.

Рисунок 1 – Пример матрицы (массива)

Формула, которая служит для оценки отдельных значений в диапазоне ячеек, называется формулой массива. Различие между формулой массива и другими типами формул заключается в том, что формула массива одновременно обрабатывает несколько значений.

Формула массива может не только обрабатывать, но и возвращать несколько значений. Результаты формулы массива также организованы в массив.

При вычислении матриц в электронных таблицах действуют те же правила математики, как и при вычислении матриц вручную.

Матрицы одинаковых размеров можно складывать, при этом получается матрица того же размера, что и слагаемые, а элементы её образуются сложением элементов, стоящих на одинаковых местах.

Операцию сложения двух матриц можно выполнить, используя обычную операцию сложения чисел (рисунок 2).

2

Лабораторная работа №5. Операции с матрицами

Рисунок 2 – Сложение матриц без использования формул массива

В ячейках (массиве) А3:В4 записана первая матрица (А), в ячейках А6:В7 – вторая матрица (В). Результирующая матрица С должна быть записана в массив D3:E4.

Достаточно записать в ячейку D3 сумму a11 + b11, или средствами Calc =A3 + A6. Затем эту формулу надо протянуть по строке (столбцу), выделить всю строку матрицы (столбец) и протянуть его на вторую строку (столбец).

Таким же образом можно умножить матрицу на число.

Любую матрицу можно умножить на число (скаляр), при этом получается матрица того же размера, а её элементы получаются умножением на заданное число всех элементов данной матрицы.

Однако удобнее использовать формулы массива. Для умножения числа на матрицу следует выделить массив, в котором будет записан результат (шаг 1), а затем в Строке ввода записать нужную формулу (шаг 2) (рисунок 3).

Рисунок 3 – Умножение числа на матрицу (выполнены шаги 1 и 2)

3

Лабораторная работа №5. Операции с матрицами

Но не спешите нажимать клавишу [Enter]!

Чтобы задать формулу массива и выполнить ее, следует выполнить ввод одновременным нажатием клавиш [Ctrl] + [Shift] + [Enter] (шаг 3). Результат показан на рисунке 4. Обратите внимание, что формула в Строке ввода заключена в фигурные скобки – признак формулы массива. Вы не вводили эти скобки с клавиатуры, их появление вызвала комбинация [Ctrl] + [Shift] + [Enter].

), конкатенацию (&) и сравнение (=, <>, <, >, <=, >=).

Произведение массивов в Calc не является произведением матриц!

Для умножения матриц необходимо использовать специальные матричные функции.

Умножьте выбранное число на матрицу, приведенную на рисунке 1.

Задание 2. Сложение матриц

Запишите самостоятельно матрицу и найдите ее сумму и разность с матрицей, приведенной на рисунке 1. Определитесь вначале с размером матрицы, которую вы запишете!

Задание 3. Умножение матриц

Умножение матрицы размера (n x m) на матрицу (m x k) дает матрицу размера (n x k).

Вспомните и запишите подробно соотношения, определяющие произведение двух матриц.

Запишите две матрицы А и В (рисунок 6), над которыми можно выполнить операцию умножения.

Выделите блок ячеек, в которые будут записаны значения элементов результирующей матрицы (рисунок 6).

Вызовите Мастер функций и укажите функцию MMULT() – умножение матриц (рисунок 7).

Рисунок 6 – Записаны матрицы А и В, выделены ячейки для записи С

5

Лабораторная работа №5. Операции с матрицами

Рисунок 7 – Окно Мастера функций: указана функция MMULT() категории Массив, введены матрицы А и В

Рисунок 8 – Введена функция MMULT(), введены матрицы А и В

После завершения работы Мастер функций получается искомый результат – произведение двух матриц (рисунок 9).

Рисунок 9 – Произведение матриц А и В

6

Лабораторная работа №5. Операции с матрицами

Задание 4. Нахождение обратной матрицы

Используя Мастер функций, найти матрицу, обратную заданной:

−1,20	0,80	−0,40	.
−0,201,40	1,002,00	0,800,60

Задание 5. Решение совместной системы линейных алгебраических уравнений

Решить систему уравнений

-1,20 x1 + 0,80 x2 -0,40 x3 = 2,4; 0,20 x1 + 2,00 x2 + 0,60 x3 = 4,4; -1,40 x1 + 1,00 x2 + 0,80 x3 = 4,2.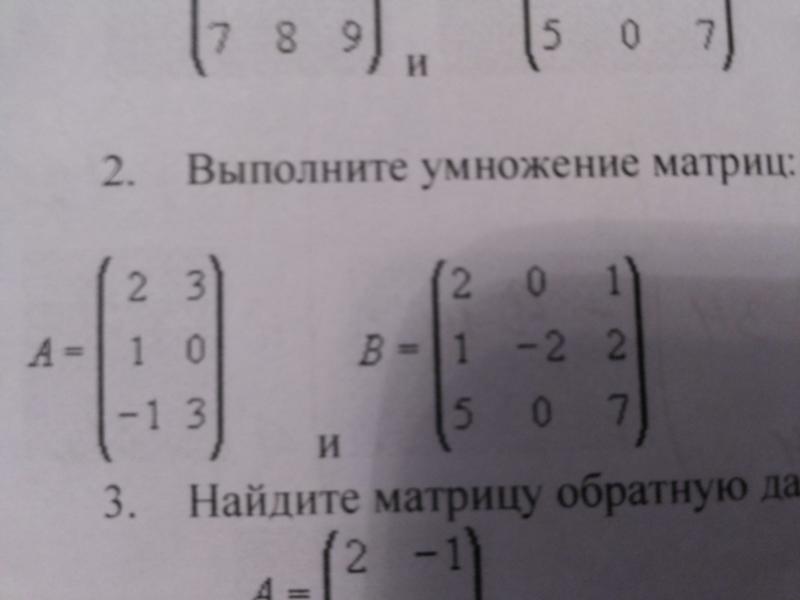

Для нахождения решения использовать обратную матрицу в соответствии с алгоритмом: если A x = b, то x = A-1 b,

где А – матрица коэффициентов системы; x – вектор искомых переменных;

b – вектор правой части системы; A-1 – матрица, обратная матрице А.

Задание 6. Оформление отчета

Оформить отчет по выполненной работе.

Задание 7. Домашнее задание

1.Самостоятельно выполнить операции транспонирования матрицы, нахождения определителя матрицы. Использовать справочную систему Calc.

2.Проверить, совпадает ли операция умножения массивов с операцией умножения матриц.

Контрольные вопросы

1.Каковы особенности выполнения операций с массивами данных в Calc?

2.Поясните алгоритмы сложения, вычитания, умножения массивов с помощью формул массивов в Calc?

3.Какими свойствами должны обладать матрицы, для которых предполагается выполнить операции:

●сложения;

●умножения;

●транспонирования;

●нахождения определителя;

●нахождения обратной матрицы?

1. В чем отличие операции умножения массивов с помощью формулы массива и операции умножения матриц?

2.Опишите возможные алгоритмы решения совместной системы линейных алгебраических уравнений с использованием средств Calc.

7

Умножение матриц. Типы, формулы и условия

Матрица представляет собой прямоугольный массив чисел или символов, которые обычно располагаются в строках и столбцах. Порядок матрицы определяется количеством строк и столбцов. в матрице, и каждое число известно как элемент. Множественное число матриц — это матрицы. Размер матрицы называется матрицей «n на m» и записывается как m × n, где n — количество строк и m — количество столбцов. Например, у нас есть матрица 3×2, потому что количество строк здесь равно 3, а количество столбцов равно 2.

Какие существуют типы матриц?

Существуют различные типы матриц. Here they are –

1. Row matrix

2. Column matrix

3. Null matrix

4. Square matrix

5. Diagonal matrix

6. Upper triangular matrix

7. Lower triangular matrix

8. Симметричная матрица

9. Антисимметричная матрица

(Изображение будет добавлено в ближайшее время)

Мы знаем, что такое матрица.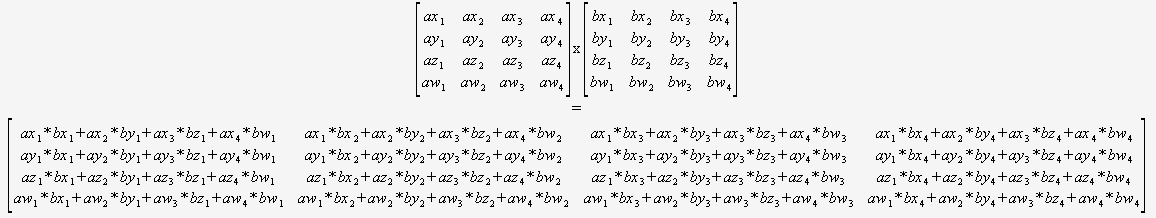 Давайте найдем произведение двух или более матриц! Умножить матрицу на одно число очень легко и просто:

(Изображение будет добавлено в ближайшее время)

Вот расчеты:

9 -9 = 9

0003

2 х 4 = 8	2 х 0 = 0
2 х 1 = 2	-9 = 2

Мы называем число (в данном случае «2») скаляром, поэтому это известно как «скалярное умножение».

Умножение матрицы на другую матрицу

Это бинарная операция, которая создает одну матрицу, беря две или более разных матриц. Мы знаем, что матрица может быть определена как массив чисел. 

Когда мы умножаем матрицу на скалярное значение, тогда процесс известен как скалярное умножение. 

В математике одна матрица за другой матрицей. Давайте обсудим, как умножить матрицу на другую матрицу, его алгоритм, формулу, умножение матриц 2×2 и 3×3. Чтобы умножить матрицу на другую матрицу, нам нужно следовать правилу «ТОЧНОЕ ПРОИЗВЕДЕНИЕ».

Умножение матриц  

Теперь давайте научимся умножать две или более матриц. Давайте рассмотрим матрицу A, которая представляет собой матрицу a × b, и рассмотрим другую матрицу B, которая является матрицей b × c. Тогда матрица C, которая является произведением матрицы A и матрицы B, может быть записана как = AB определяется как A × B matrix. Элемент в матрице продукта C, Cxy может быть определен как 9{b}A_{kx}B_{ky}\]   для значений x = 1…… a и y= 1…….c

Формула умножения матриц Давайте рассмотрим пример, чтобы понять формулу. Допустим, у нас есть A и B в виде двух матриц, таких, что

(изображение будет добавлено в ближайшее время)

(изображение будет добавлено в ближайшее время)

Тогда матрица C (матрица произведения) = AB может быть обозначена как

(изображение будет добавлено в ближайшее время) )

Элемент матрицы C (матрица произведения), где C — произведение матрицы A X B.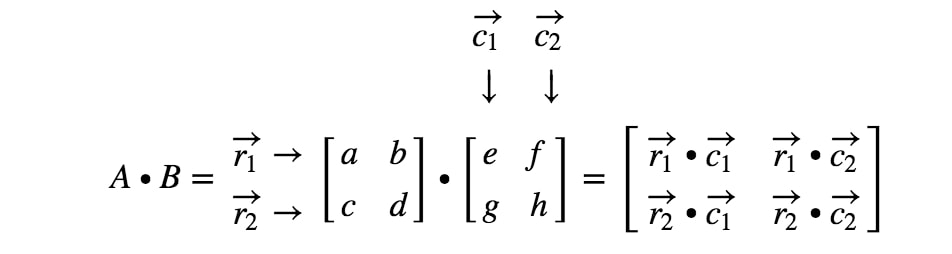 Элемент матрицы произведения C, Cxy может быть определен как 9{b}A_{kx}B_{ky}\] для значений x = 1…… a и y= 1…….c

Условия для умножения матриц —

Когда мы выполняем умножение матриц, оставьте эти два условия в разум:

• Количество столбцов первой матрицы в процессе умножения должно равняться количеству строк второй матрицы.

• Результат (произведение) будет иметь то же количество строк, что и в первой матрице, и то же количество столбцов, что и во второй матрице.

Основы умножения матриц

Произведение C любых двух матриц, предположим A и B, может быть определено как Cik=aij x bjk

Здесь

(Изображение будет добавлено позже)

все возможные значения i и k, а в приведенных выше обозначениях используется соглашение о суммировании Эйнштейна. Соглашение о суммировании Эйнштейна может быть определено как суммирование по повторяющимся индексам без наличия явного знака суммы, и этот метод обычно используется как в матричном, так и в тензорном анализе. (n x m) (m X P) = (n x p) Здесь (a x b) обозначает матрицу с количеством строк, равным a, и количеством столбцов, равным b. Выписывая произведение явно, получаем

(Изображение будет добавлено в ближайшее время)

Где каждое из значений может быть записано как,

(Изображение будет добавлено в ближайшее время)

Умножение матрицы 2 × 2. Мы рассмотрим простое умножение матрицы 2 × 2 

A = \[\begin{bmatrix} 3 и 7\\ 4 и 9 \end{bmatrix}\]  и другая матрица B = \[\begin{bmatrix} 6 и 2\\ 5 и 8 \end{bmatrix} \]

Теперь мы можем вычислить каждый из элементов матрицы произведения AB следующим образом:

• Произведение AB11 = 3 × 6 + 7 × 5 = 53

• Произведение AB12 = 3 × 2 + 7 × 8 = 62

• Произведение AB21 = 4 × 6 + 9 × 5 = 69

• + Произведение AB22 = 4 × 8 80

 

Следовательно, матрица AB равна,

AB = \[\begin{bmatrix} 53 & 62\\ 69 & 80 \end{bmatrix}\]

 

 

10 Решенных вопросов 50 0 ) Умножьте приведенную ниже матрицу на 2 

A = \[\begin{bmatrix} 3 & 4 & 9\\ 12 &11 &35 \end{bmatrix}\]

 

Решение) Умножая данную матрицу на 2,

 

Мы знаем, что в этом случае нужно произвести скалярное умножение,

 

A =

[\begin{bmatrix} 3 & 4 & 9\\ 12 &11 &35 \end{bmatrix}\]

 

При умножении на 2 мы получаем произведение как ,

 

 A = \[\begin{bmatrix } 6 & 8 & 18\\ 24 & 22 &70 \end{bmatrix}\]

Вопрос 2. Матрица 2×2 

\[\begin{bmatrix} 1 и 2\\ 3 & 4 \end{bmatrix}\]

при умножении на другую матрицу 2×2 

\[\begin{bmatrix} 5 и ​​6\\ 7 & 8 \end{bmatrix}\]

тогда результирующая матрица может быть записана как

Решение:

\[\begin{bmatrix} 1\times 5+2\times 7 & 1\times 6+2\times 8 \\ 3\times 5+4\times 7 & 3\times 6+4\times 8 \end{bmatrix}\]

, что можно упростить и записать как:

\[\begin{bmatrix} 19 & 22 \\ 43 и 50 \end{bmatrix}\]

Вопрос 3. Для матрицы 2×3

\[\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \end{bmatrix}\]

 

при умножении на 3×1 matrix

 

\[\begin{bmatrix} 9 \\  8 \\ 7 \end{bmatrix}\]

тогда результирующая матрица может быть записана как 

\[\begin{bmatrix} 1\times 9+ 2\times 8+3\times 7\\ 4\times 9+5\times 8+6\times 7 \end{bmatrix}\]

, что можно упростить и записать как

\[\begin{bmatrix} 46 \\  118 \end{bmatrix}\]

Ключевые моменты, которые следует помнить при выполнении умножения матриц

При выполнении умножения матриц необходимо помнить о двух условиях:

1. Количество столбцов в первой матрице должно быть равно количеству строк в вторая матрица, т. е. при умножении матрицы A порядка m×n на другую матрицу B порядка p×q n должно быть равно p.

2. Количество строк результирующей матрицы после умножения должно быть равно количеству строк первой матрицы в порядке умножения, а количество столбцов результирующей матрицы должно быть равно количеству строк второй матрицы в порядок умножения.

Умножение матриц | Формула, правила, умножение и факты

Что такое матрица?

Матрица определяется как прямоугольный массив чисел, символов или выражений, расположенных в строках и столбцах (множественное число: матрицы). Если в массиве n строк и m столбцов, то это матрица размера n×m. размеры матрицы обозначаются числами n и m. Числа в матрице обозначаются как их элементы .

Обозначение матриц

Мы обычно обозначаем матрицы заглавными буквами, например A, B, C и т. д.

A≔ Матрица обозначается заглавной буквой.
a≔ Элемент матрицы обозначается строчной буквой.

Прямоугольные скобки обычно используются для записи матриц. Горизонтальные и вертикальные линии элементов в матрице называются соответственно строками и столбцами.

Размер матрицы

Количество строк и столбцов, содержащихся в матрице, определяет ее размер. Матрица с m строками и n столбцами называется матрицей размера m × n или матрицей размера m на n, где m и n называются размерами матрицы. При описании матрицы вы указываете количество строк по количеству столбцов. Иногда это называют порядком матрицы. Например, матрица

A=[12       34]

называется матрицей размера один на четыре, поскольку она имеет одну строку и четыре столбца. Мы также можем сказать, что порядок A равен 1 × 4. Матрица

B = [123  456]

является матрицей 3 × 2, поскольку она имеет три строки и два столбца. Он имеет порядок 3×2.

Совет: Помните, что сначала указывается количество строк, а затем количество столбцов.

Рассмотрите аббревиатуру «RC» для «Row then Column», чтобы помочь вам запомнить это.

Что такое умножение матриц?

Жак Филипп Мари Бине, французский математик, впервые описал матричное умножение в 1812 году, чтобы показать состав линейных карт, представленных матрицами. В результате умножение матриц является фундаментальным инструментом линейной алгебры с различными приложениями во многих областях математики, включая прикладную математику, статистику, физику, экономику и инженерию. Вычисление матричного произведения является фундаментальным процессом во всех вычислительных приложениях линейной алгебры.

Существует только два метода умножения матриц. Первый метод включает умножение матрицы на скаляр. Это называется скалярным умножением. Второй способ заключается в умножении одной матрицы на другую. Это называется умножением матриц.

Скалярное умножение

Поскольку выражение A+A представляет собой сумму двух матриц с одинаковыми размерами, матрицу A можно сложить с самой собой. В итоге мы удваиваем каждую запись в A, когда вычисляем A+A. В результате мы можем интерпретировать выражение 2A как предписывающее нам умножить каждый элемент в A на  2. 

Обычно, чтобы умножить матрицу на число, умножьте это число на каждый элемент матрицы. Например,

Отдельные числа обычно называют скалярами при обсуждении матриц. В результате мы называем операцию умножения матрицы на число скалярным умножением.

Скалярное произведение

Чтобы умножить одну матрицу на другую, мы должны сначала понять, что такое скалярное произведение. Скалярное произведение — это метод нахождения произведения двух векторов, также известный как умножение векторов. Предположим, что следующие два вектора:

u=[123] , v=[456]

Чтобы умножить эти два вектора, просто перемножьте соответствующие элементы и сложите полученные произведения.

u∙v=(1)(4)+(2)(5)+(3)(6)
=4+10+18
=32

В результате перемножения векторов получаем единственное значение .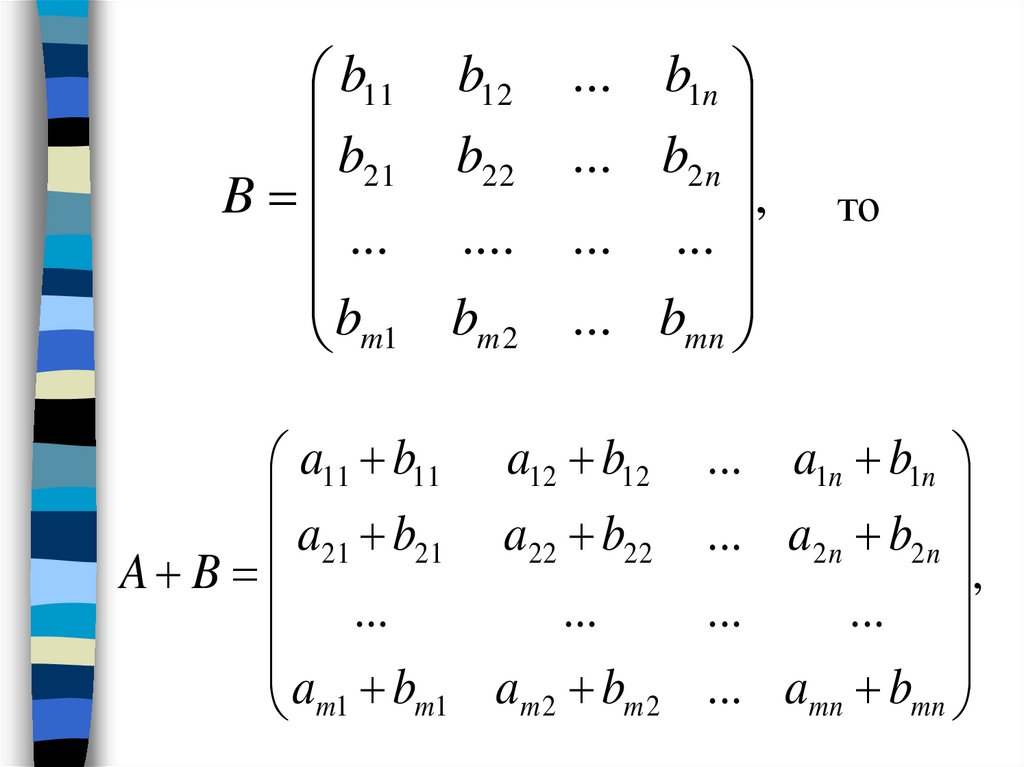 Обратите внимание, однако, что два вектора имеют одинаковое количество записей. Что, если один из векторов содержит меньше элементов, чем другой?

 Например, пусть

u=[214] , v=[310     2]

Когда соответствующие записи были перемножены и сложены вместе, решение будет:

u∙v= [214] [310     2]
=2(3)+1(1)+0(4)+?(2)

Здесь возникла проблема. Первые три записи скалярного произведения имеют соответствующие записи для умножения, а четвертая — нет. Это означает, что скалярное произведение этих двух векторов не может быть вычислено.

В результате скалярное произведение двух векторов с разным количеством элементов не может быть найдено. Они оба должны содержать одинаковое количество записей.

Каковы условия для умножения матриц?

Когда мы хотим перемножить матрицы, мы должны сначала убедиться, что операция возможна, что не всегда так. Кроме того, в отличие от числовой арифметики и алгебры, даже если произведение существует, порядок умножения может повлиять на результат.

Изучение скалярного произведения необходимо при умножении матриц. При умножении одной матрицы на другую строки и столбцы должны рассматриваться как векторы.

Пример 1. Найти AB, если A=[1234] и B=[5678]

А∙В= [1234] ^. [5678]

Сосредоточьтесь на следующих строках и столбцах

где r ₁ — первая строка, r ₂ ​ — вторая строка, c ₁ , c _{6 90are36 первая и 90are36 вторые столбцы. Рассматривайте каждую строку и столбец как вектор.}

Обратите внимание, что умножение матрицы 2×2 на другую матрицу 2×2 дает матрицу 2×2. Таким образом, в полученной матрице должно быть четыре элемента.

Убедитесь, что первая запись расположена в первой строке и первом столбце. Итак, чтобы получить значение первой записи, просто возьмите скалярное произведение r ₁ и с ₁ . Таким образом, первая запись будет

Теперь обратите внимание, что расположение второй записи находится в первой строке и втором столбце. Итак, чтобы получить значение второй записи, просто возьмите скалярное произведение r ₁ и c ₂ . Таким образом, вторая запись будет

. Ту же стратегию можно использовать для получения значения двух последних записей.

Пример 2. Найдите AB, если A=[14   25 36] и B=[111  111 111 111]

A∙B= [14  25 36] x [111 111 111 111]

Используйте скалярные произведения для вычисления каждой записи.

Следовательно, две матрицы можно перемножить, если количество столбцов первой матрицы равно количеству строк второй матрицы. Умножение дает другую матрицу с тем же количеством строк, что и у первой, и тем же количеством столбцов, что и у второй. Если это не так, умножение не может быть выполнено.

В символах пусть A будет матрицей m×p, а пусть B будет матрицей q×n. Тогда произведение A×B=AB будет матрицей размера m×n при условии, что p=q. Если p≠q, умножение матриц не определено. Например, матрицу 2×5 нельзя умножить на матрицу 3×4, потому что 5≠3, тогда как матрицу 2×5 можно умножить на 5×3, и в результате получится матрица 2×3.

Каковы свойства умножения матриц?

Умножение матриц имеет некоторые общие свойства с обычным умножением. Умножение матриц, с другой стороны, не определено, если число столбцов в первом сомножителе отличается от числа строк во втором сомножителе, и оно некоммутативно, даже если произведение остается определенным после того, как порядок сомножителей измененный.

Некоммутативность 

Некоммутативность умножения матриц является одним из наиболее существенных различий между умножением действительных чисел и умножением матриц. Следовательно, порядок умножения двух матриц имеет значение при умножении матриц.

Операция является коммутативной, если для данных двух элементов A и B, таких, что произведение AB

определено, тогда также определено BA, AB=BA

Например,

A=[0100] и B=[0010 ]

, затем

AB= [0100] x [0010] = [1000]

, но

BA= [0010] x [0010] = [1000]

Обратите внимание, что продукты не совпадают с AB ≠БА. Следовательно, умножение матриц не является коммутативным.

Коммутативность имеет место в одном особом случае. Это при умножении диагональных матриц одинаковой размерности.

Помимо этого важного отличия, свойства умножения матриц в основном аналогичны свойствам умножения действительных чисел.

Дистрибутивность

Умножение матриц является дистрибутивным по отношению к сложению матриц. То есть, если A, B, C, D матрицы соответствующих размеров m×n,n×p, n×p и p×q, то дистрибутивность слева

AB+C=AB+AC

и другое имеет правильное распределение

B+CD=BD+CD

Пример 1: 

Обратите внимание, что AB+C=AB+AC. Теперь найдите B+CA и  BA+CA

. Обратите внимание, что B+CA=BA+CA. Также примечательно, что AB + CB + CA и что AB + AC ≠ BA + CA, что напоминает нам о некоммутативности матричного умножения.

Ассоциативность

Это свойство указывает, что группировка, окружающая умножение матриц, может быть изменена.

Если A, B, C являются матрицами m×n, n×p и p×q соответственно, то (AB)C=A(BC)

Например, вы можете умножить матрицу A на матрицу B, а затем умножить результат на матрицу C, или вы можете умножить матрицу B на матрицу C, а затем умножить результат на матрицу A.

Применяя это свойство, помните о порядке перемножения матриц, поскольку умножение матриц не является коммутативным.

Пример 1: 

Мы можем найти (AB)C следующим образом:

Мы можем найти A(BC) следующим образом:

Обратите внимание, что ABC= A(BC).

Свойство мультипликативной идентичности

Единичная матрица размера n×n , обозначенная In, представляет собой матрицу с n строками и n столбцами. Все записи по диагонали от верхнего левого угла до нижнего правого – это единицы, а все остальные – нули.

Например:

Свойство мультипликативной идентичности утверждает, что произведение любой матрицы размера n × n A и I n всегда равно A, независимо от порядка выполнения умножения. Другими словами, A∙I=I∙A=A

Роль, которую играет единичная матрица размера n×n в умножении матриц, подобна роли, которую играет число 1 в действительной системе счисления. Если a — действительное число, то мы знаем, что a∙1=a и 1∙a=a

Мультипликативное свойство нуля

Нулевая матрица — это матрица, в которой все элементы равны 0. Например, 3× 3 нулевая матрица O _3×3 =[0 0 0 0 0 0 0 0 0]

Нулевая матрица обозначается буквой O, при необходимости можно добавить нижний индекс для указания размеров матрицы.

Мультипликативное свойство нуля гласит, что произведение любой матрицы размера n×n на нулевую матрицу размера n×n представляет собой нулевую матрицу размера n×n. Другими словами, А∙О=О∙А=О.

Роль, которую нулевая матрица n×n играет в матричном умножении, подобна роли, которую играет число 0 в действительной системе счисления. Если a — действительное число, то мы знаем, что a∙0=0 и 0∙a=0

Свойство измерения

Свойство измерения — это свойство, уникальное для матриц. Это свойство состоит из двух частей:

1. Если количество столбцов в первой матрице равно количеству строк во второй матрице, определяется произведение двух матриц.

2. Если произведение определено, результирующая матрица будет иметь то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица.

Например, если A — матрица 3×2, а B — матрица 2×4, свойство размерности говорит нам, что произведение AB определено и AB будет матрицей 3×4.

Где можно применить умножение матриц?

Умножение матриц исторически использовалось для упрощения и уточнения вычислений в линейной алгебре. Эта тесная связь между линейной алгеброй и матричным умножением продолжает оставаться фундаментальной для всей математики, а также для физики, химии, инженерии и компьютерных наук.

Записи в матрице могут представлять данные, а также математические уравнения. Матрицы умножения могут обеспечить быстрое, но точное приближение к гораздо более сложным вычислениям во многих инженерных приложениях, критичных ко времени.

Матрицы появились как способ описания систем линейных уравнений, задача, с которой знаком каждый, кто изучал алгебру в начальной школе. Термин «линейный» просто означает, что переменные в уравнениях не имеют показателей, поэтому их графики всегда представляют собой прямые линии.

Уравнение x-2y=0, например, имеет бесконечное число решений как для y, так и для x, что можно изобразить в виде прямой линии, проходящей через точки (0,0), (2,1), (4,2) и так далее. Но если вы объедините его с уравнением x -y=1, то будет только одно решение: x=2 и y=1. В точке (2,1) также пересекаются графики двух уравнений.

Матрица, иллюстрирующая эти два уравнения, представляла бы собой сетку чисел два на два с верхней строкой [1-2] и нижней строкой [1-1], чтобы соответствовать коэффициентам переменных в два уравнения.

Компьютеры часто используются для решения систем линейных уравнений — обычно с более чем двумя переменными — в различных приложениях, начиная от обработки изображений и заканчивая генетическим анализом. Их также часто просят перемножить матрицы.

Умножение матриц аналогично решению линейных уравнений для конкретных переменных. Рассмотрим выражения t + 2p + 3h, 4t + 5p + 6h и 7t + 8p + 9h, которые описывают три различные математические операции, включающие измерения температуры, давления и влажности. Их можно представить в виде трехстрочной матрицы: [1 2 3], [4 5 6] и [7 8 9].

Предположим, вы измеряете температуру, давление и влажность вне дома в два разных времени. Эти показания также могут быть представлены в виде матрицы с первым набором показаний в одном столбце и вторым набором показаний в другом. Умножение этих матриц влечет за собой сопоставление строк из первой матрицы, которая описывает уравнения, и столбцов из второй, которая представляет измерения, умножение соответствующих членов, их сложение и ввод результатов в новую матрицу. Числа в окончательной матрице, например, могут предсказать путь системы низкого давления.

Конечно, сведение сложной динамики моделей погодных систем к набору линейных уравнений само по себе является трудной задачей. Но это поднимает одну из причин, по которой матрицы так популярны в компьютерных науках: они позволяют компьютерам заранее выполнять большую вычислительную тяжелую работу. Создание матрицы, которая дает полезные результаты вычислений, может быть трудным, но умножение матриц обычно не является трудным.

Графика — это одна из областей компьютерных наук, где умножение матриц особенно полезно, поскольку цифровое изображение по своей сути является матрицей: строки и столбцы матрицы соответствуют строкам и столбцам пикселей, а числовые элементы соответствуют цветовые значения пикселей. Декодирование цифрового видео требует умножения матриц. Например, некоторым исследователям удалось создать один из первых чипов для реализации нового стандарта высокоэффективного кодирования видео для телевизоров сверхвысокой четкости. Паттерны, которые они обнаружили в используемых матрицах, сыграли свою роль в этом успехе.

Матричное умножение также может помочь в обработке цифрового видео и цифрового звука. Цифровой аудиосигнал, по сути, представляет собой серию чисел, которые представляют собой изменение давления воздуха акустического аудиосигнала во времени. Умножение матриц используется во многих методах фильтрации или сжатия цифровых аудиосигналов, включая преобразование Фурье.

Еще одна причина, по которой матрицы так полезны в компьютерных науках, заключается в том, что графики также полезны. Граф — это математическая конструкция, состоящая из узлов, обычно изображаемых в виде кругов, и ребер, обычно изображаемых в виде соединяющих их линий. Графики обычно используются для представления действий компьютерной программы в отношениях, характерных для логистических задач.

С другой стороны, любой график можно представить в виде матрицы, в которой каждый столбец и строка представляют узел, а значение на их пересечении представляет силу связи между ними, которая в большинстве случаев равна нулю. Часто преобразование графов в матрицы является наиболее эффективным способом их анализа, а решения проблем, связанных с графами, часто являются решениями систем линейных уравнений.