Курс высшей математики, Т.2
Курс высшей математики, Т.2
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2.  (n)=f(x).19. Системы обыкновенных дифференциальных уравнений. 20. Примеры. 21. Системы уравнений и уравнения высших порядков. 22. Линейные уравнения с частными производными. 23. Геометрическая интерпретация. 24. Примеры. ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 25. Линейные однородные уравнения второго порядка. 26. Линейные неоднородные уравнения второго порядка. 27. Линейные уравнения высших порядков. 28. Однородные уравнения второго порядка с постоянными коэффициентами. 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. 30. Частные случаи. 31. Корни решений и колеблющиеся решения 32. Линейные уравнения высших порядков с постоянными коэффициентами. 33. Линейные уравнения и колебательные явления. 34. Собственные и вынужденные колебания. 35. Синусоидальная внешняя сила и резонанс.  36. Предельные задачи. 37. Примеры. 38. Символический метод. 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами. 40. Линейные неоднородные уравнения с постоянными коэффициентами. 41. Пример. 42 Уравнение Эйлера. 43. Системы линейных уравнений с постоянными коэффициентами. 44. Примеры § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ 45. Интегрирование линейного уравнения с помощью степенного ряда 46. Примеры. 47. Разложение решения в обобщенный степенной ряд. 48. Уравнение Бесселя 49. Уравнения, приводящиеся к уравнению Бесселя § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 50. Метод последовательных приближений для линейных уравнений. 51. Случай нелинейного уравнения. 52. Дополнения к теореме существования и единственности. 54. Особые точки дифференциальных уравнений первого порядка. 55. Автономные системы. 56. Примеры.  ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА § 6. КРАТНЫЕ ИНТЕГРАЛЫ 58. Двукратный интеграл. 59. Вычисление двукратного интеграла. 60. Криволинейные координаты. 61. Трехкратный интеграл 62. Цилиндрические и сферические координаты. 63. Криволинейные координаты в пространстве. 64. Основные свойства кратных интегралов. 65. Площадь поверхности. 66. Интегралы по поверхности и формула Остроградского. 67. Интегралы по определенной стороне поверхности. 68. Моменты. § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ 69. Определение криволинейного интеграла. 70. Работа силового поля. Примеры. 71. Площадь и криволинейный интеграл. 72. Формула Грина 73. Формула Стокса. 74. Независимость криволинейного интеграла от пути на плоскости. 75. Случай многосвязной области. 76. Независимость криволинейного интеграла от пути в пространстве. 77. Установившееся течение жидкости. 78.  Интегрирующий множитель.79. Уравнение в полных дифференциалах для случая трех переменных. 80. Замена переменных в двойном интеграле. § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 81. Интегрирование под знаком интеграла. 82. Формула Дирихле. 83. Дифференцирование под знаком интеграла 84. Примеры. 85. Несобственные интегралы. 86. Неабсолютно сходящиеся интегралы. 87. Равномерно сходящиеся интегралы. 88. Примеры. 89. Несобственные кратные интегралы. 90. Примеры. § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ 92. Основные теоремы. 93. Счетные множества. Действия над точечными множествами. 94. Мера Жордана. 96. Независимость от выбора осей. 97. Случай любого числа измерений. 98. Интегрируемые функции. 99. Вычисление двойного интеграла. 100. n-кратные интегралы. 101. Примеры. 102. Внешняя мера Лебега. 103. Измеримые множества. 104. Измеримые функции. 105.  Дополнительные сведения.106. Интеграл Лебега. 107. Свойства интеграла Лебега. 108. Интегралы от неограниченных функций. 109. Предельный переход под знаком интеграла. 110. Теорема Фубини. 111. Интегралы по множеству бесконечной меры. ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ 112. Сложение и вычитание векторов. 113. Умножение вектора на скаляр. Компланарность векторов. 114. Разложение вектора по трем некомпланарным векторам. 115. Скалярное произведение. 116. Векторное произведение. 117. Соотношения между скалярным к векторным произведениями. 118. Скорости точек вращающегося твердого тела; момент вектора. § 11 ТЕОРИЯ ПОЛЯ 119. Дифференцирование вектора 120. Скалярное поле и его градиент. 121. Векторное поле; расходимость и вихрь. 122. Потенциальное и соленоидальное поля. 123. Направленный элемент поверхности. 124. Некоторые формулы векторного анализа. 125. Движение твердого тела и малая деформация. 126.  Уравнение непрерывности.127. Уравнения гидродинамики идеальной жидкости. 128. Уравнения распространения звука. 129. Уравнение теплопроводности. 130. Уравнения Максвелла. 131. Выражение оператора Лапласа в ортогональных координатах. 132. Операция дифференцирования для случая переменного поля. ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ 133. Плоская кривая, ее кривизна и эволюта. 134. Эвольвента. 135. Естественное уравнение кривой. 136. Основные элементы кривой в пространстве. 138. Соприкасающаяся плоскость. 139. Винтовые линии. 140. Поле единичных векторов. § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ 141. Параметрические уравнения поверхности. 142. Первая дифференциальная форма Гаусса. 143. Вторая дифференциальная форма Гаусса. 144. О кривизне линий, начерченных на поверхности. 145. Индикатриса Дюпена и формула Эйлера. 146. Определение главных радиусов кривизны и главных направлений. 147.  Линии кривизны.148. Теорема Дюпена. 149. Примеры. 150. Гауссова кривизна. 151. Вариация элемента площади и средняя кривизна. 152. Огибающая семейства поверхностей и кривых. 153. Развертывающиеся поверхности. ГЛАВА VI. РЯДЫ ФУРЬЕ 154. Ортогональность тригонометрических функций. 155. Теорема Дирихле. 156. Примеры. 157. Разложение в промежутке (0, п). 158. Периодические функции периода 2l. 159. Средняя квадратичная погрешность. 160. Общие ортогональные системы функций. 161. Класс L2 162. Сходимость в среднем. 163. Ортонормированные системы в L2. § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ 164. Разложение в ряд Фурье. 165. Вторая теорема о среднем. 166. Интеграл Дирихле. 167. Теорема Дирихле. 168. Приближение к непрерывной функции полиномами. 169. Формула замкнутости. 170. Характер сходимости рядов Фурье. 171. Улучшение сходимости рядов Фурье. 172. Пример. § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ 173. 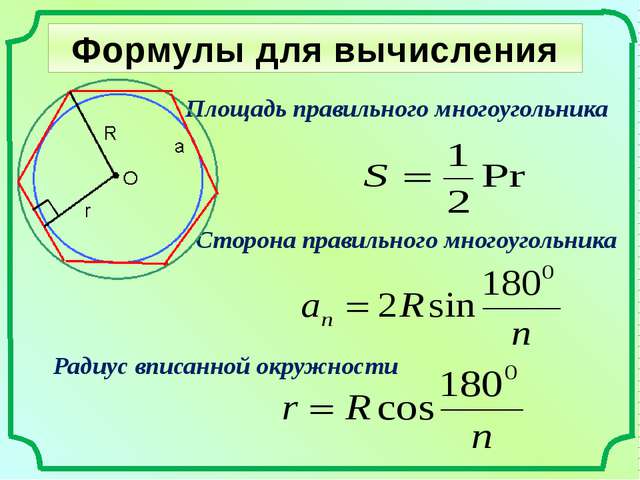 Формула Фурье.174. Ряды Фурье в комплексной форме. 176. Кратные ряды Фурье. ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 176. Уравнение колебаний струны. 177. Решение Даламбера. 179. Ограниченная струна. 180. Способ Фурье. 181. Гармоники и стоячие волны. 182. Вынужденные колебания. 183. Сосредоточенная сила. 184. Формула Пуассона. 185. Цилиндрические волны. 186. Случай n-мерного пространства. 187. Неоднородное волновое уравнение. 188. Точечный источник. 189. Поперечные колебания мембран. 190. Прямоугольная мембрана. 191. Круглая мембрана. 192. Теорема единственности. 193. Применение интеграла Фурье. § 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ 195. Установившиеся процессы. 196. Устанавливающиеся процессы. 197. Примеры. 198. Обобщенное уравнение колебаний струны. 199. Неограниченная цепь в общем случае. 200. Способ Фурье для ограниченной цепи. 201.  Обобщенное волновое уравнение.§ 19. УРАВНЕНИЕ ЛАПЛАСА 202. Гармонические функции. 203. Формула Грина. 204. Основные свойства гармонических функций. 205. Решение задачи Дирихле для круга. 206. Интеграл Пуассона. 207. Задача Дирихле для сферы. 208. Функция Грина. 209. Случай полупространства. 210. Потенциал объемных масс. 211. Уравнение Пуассона. 212. Формула Кирхгофа. § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ 214. Неограниченный стержень. 215. Стержень, ограниченный с одного конца. 216. Стержень, ограниченный с обоих концов. 217. Дополнительные замечания. 218. Случай сферы. 219. Теорема единственности. |
Деление круга на равные части
УчебаМатематикаГеометрия
Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами
Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части.
Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.
Деление круга на равные по площади части радиусами
Радиус круга
Число частей
Точность вычисления
Знаков после запятой: 2
Угол сектора
Длина дуги
Длина хорды
Деление круга на равные по площади части параллельными хордами
Радиус круга
Число частей
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.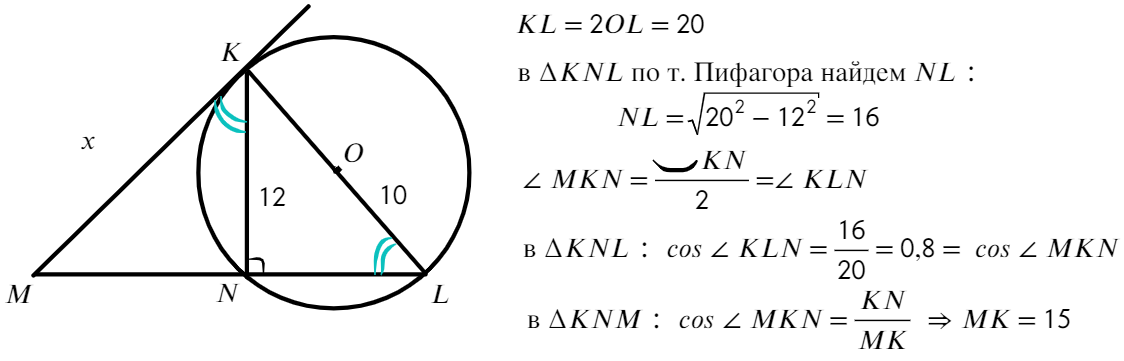
Деление круга на равные части радиусами
Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:
- Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.
- Определяем размер дуги сектора, перемножая радиус на угол в радианах
- Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.
Собственно и всё — мы получили все характеристики для N равных секторов
Деление круга на равные части параллельными хордами
Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.
Деление круга на три равные части двумя хордамиЗадача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2).
Выведем для начала формулу площади куска, отсекаемого хордой слева.
Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.
y=f(x)По теореме Пифагора получаем следующую функцию
Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:
Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем
, откуда
Итак, полное выражение
Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)
Таким образом мы можем приравнять
Что дает нам такое финальное уравнение
Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона.
Калькулятор использует метод Ньютона.
Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.
Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Вычисление радиуса по площади круга
- • Круговой сектор
- • Сегмент круга
- • Круг
- • Сколько малых одинаковых окружностей радиуса r можно вписать в большую окружность радиуса R
- • Раздел: Геометрия ( 96 калькуляторов )
#геометрия #круг Геометрия круг окружность площадь радиус сектор угол хорда
PLANETCALC, Деление круга на равные части
Timur2020-11-03 14:19:41
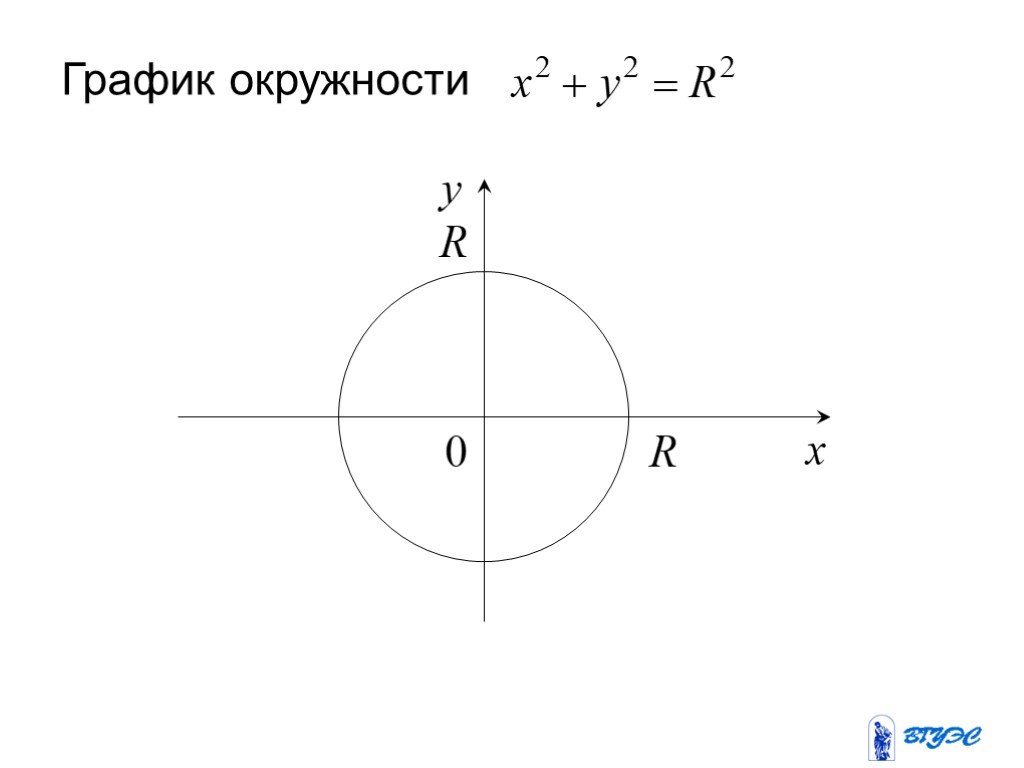
Как график круга
, написанный
Малкольм МакКинси
Проверенный факт
Paul Mazzola
График круга
Графические цирки Требуются два веща: координаты: координаты
Графические круги .
центральную точку и радиус окружности. Окружность – это множество всех точек, находящихся на одинаковом расстоянии от данной точки, центра окружности. Радиус r – это расстояние от центральной точки до самой окружности.
На графике все эти точки на окружности могут быть определены и нанесены на график с использованием координат (x,y) .
Построение окружности на графикеУравнения окружности
Два выражения показывают, как построить окружность: форма центр-радиус и стандартная форма . Где x и y — координаты всех точек окружности, h и k — координаты центральной точки 9Значения 0017 x и y , где r радиус круга
Форма центра-радиуса
Форма центра-радиуса выглядит следующим образом:
Стандартное уравнение окружности , форма требует немного больше работы, чем форма центра-радиуса, чтобы получить и построить график.
Уравнение стандартной формы выглядит следующим образом: Стандартная форма уравнения окружностиВ общей форме D , E и F — заданные значения, такие как целые числа, которые являются коэффициентами значений x и y .
Использование формы центр-радиус {use-crf}
Если вы не уверены, что предполагаемая формула является уравнением, необходимым для построения круга, вы можете проверить ее. Он должен иметь четыре атрибута:
Члены x и y должны быть возведены в квадрат.
Все элементы в выражении должны быть положительными (что достигается возведением в квадрат значений в скобках).
Центральная точка задается как (h,k) , координаты x и y .
Значение радиуса r должно быть задано и должно быть положительным числом (что имеет здравый смысл, у вас не может быть отрицательной меры радиуса).
Форма с центральным радиусом дает опытному глазу много информации.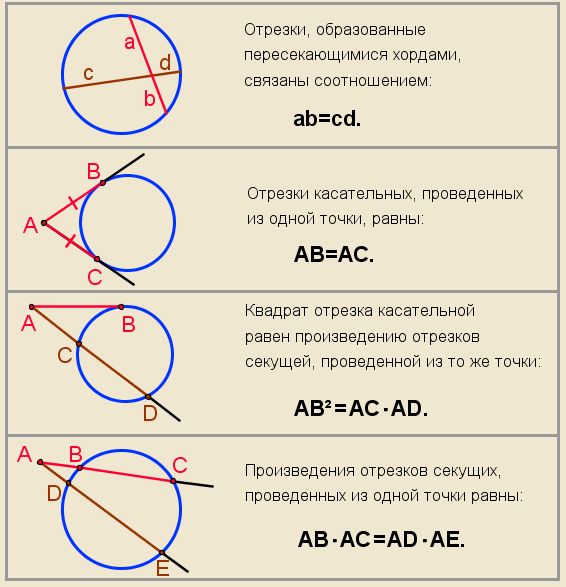
{2} =16(x−2)2+(y−3)2=16 9{2}+-6x+3y=x2+-6x+3
Только уравнения 1, 3, 5 и 6 являются формами центр-радиус. Второе уравнение изображает прямую линию; четвертое уравнение представляет собой известную форму пересечения наклона; последнее уравнение изображает параболу.
Как начертить уравнение окружности
Окружность можно рассматривать как нарисованную линию, которая изгибается как в своих значениях x , так и y . Это может показаться очевидным, но рассмотрите это уравнение:
Здесь x только значение возводится в квадрат, что означает, что мы получим кривую, но только кривую, идущую вверх и вниз, а не замыкающуюся на себя. Мы получаем параболическую кривую, так что она проходит мимо вершины нашей сетки, два ее конца никогда не встречаются и не видны снова.
Введем второй показатель степени x, и мы получим более живые кривые, но они, опять же, не поворачиваются вспять.
Кривые могут извиваться вверх и вниз по оси Y по мере того, как линия перемещается по оси X, но линия на графике по-прежнему не возвращается сама на себя, как змея, кусающая себя за хвост.
Чтобы кривая отображалась в виде круга, вам нужно изменить и , показатель степени x , и , показатель степени и . Как только вы возьмете квадрат значений x и y , вы получите круг, возвращающийся к самому себе!
Часто форма центра-радиуса не содержит ссылок на такие единицы измерения, как мм, м, дюймы, футы или ярды. В этом случае просто используйте одиночные поля сетки при подсчете единиц радиуса.
Центр в исходной точке
Если центральной точкой является исходная точка (0, 0) графика, форма центра-радиуса будет сильно упрощенной:
Например, круг с радиусом 7 единицы и центр в (0, 0) выглядит следующим образом в виде формулы и графика:
График начала координат центра кругаКак построить график круга, используя стандартную форму
Если ваше уравнение окружности соответствует стандарту или общему форма , вы должны сначала завершить квадрат, а затем преобразовать его в форму центра и радиуса.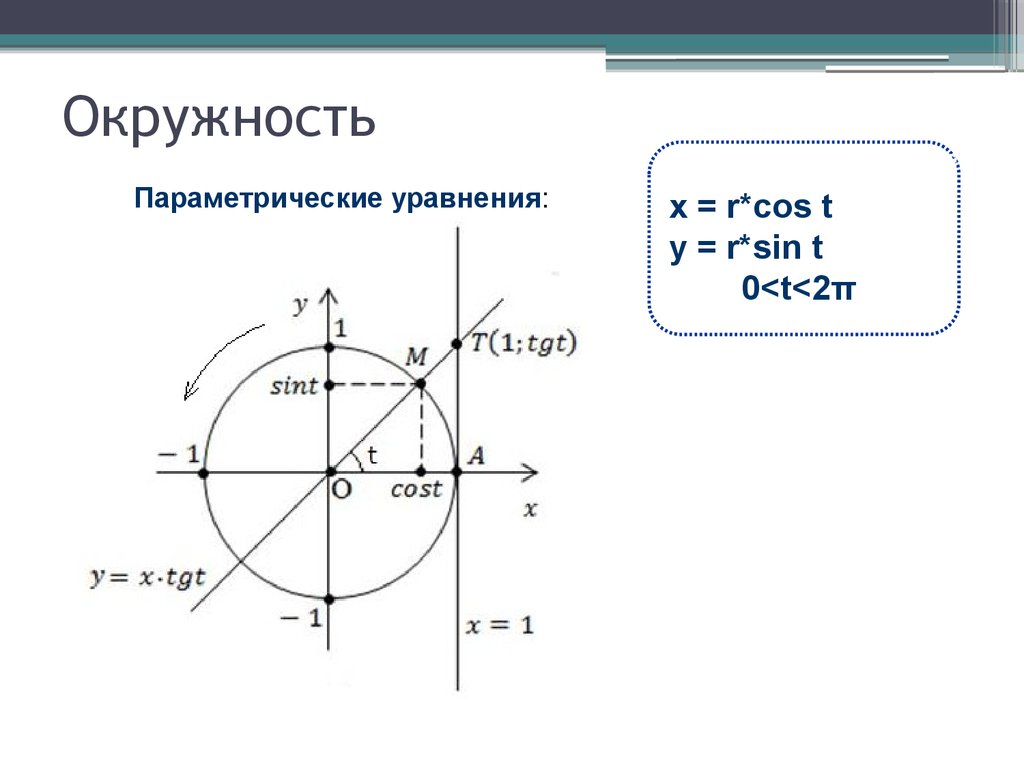
Предположим, у вас есть это уравнение:
Перепишите уравнение так, чтобы все x-члены были в первых скобках, а y-члены — во вторых:
Вы выделили константу справа и добавили значения ?1{?}_{1}? 1 и ?2{?}_{2}?2 в обе стороны. Значения ?1{?}_{1}?1 и ?2{?}_{2}?2 – это числа, необходимые в каждой группе для завершения квадрата.
Возьмите коэффициент x и разделите на 2 . Приведите его в порядок. Это ваше новое значение для ?1{?}_{1}?1:
Повторите это для значения, которое нужно найти с y-terms:
Замените неизвестные значения ?1{?}_{1}?1 и ?2{?}_{2}?2 в уравнении вновь рассчитанными значениями:
Упрощение:
Теперь у вас есть форма центра-радиуса для графика. Вы можете подставить значения, чтобы найти этот круг с центральной точкой (-4, 3) и радиусом 5,385 единиц (квадратный корень из 29 ):
Изображение круга в стандартной формеout for
С практической точки зрения помните, что центральная точка, хотя и необходима, на самом деле не является частью круга.
Итак, когда вы рисуете свой круг, очень легко отметьте центральную точку. Поместите легко подсчитываемые значения вдоль x и y осей, просто посчитав длину радиуса вдоль горизонтальной и вертикальной линий.
Если точность не важна, вы можете нарисовать остальную часть круга. Если точность имеет значение, используйте линейку, чтобы сделать дополнительные отметки, или чертежный циркуль, чтобы выполнить полный круг.
Не забывайте также о своих негативах. Внимательно следите за своими отрицательными значениями, помня, что в конечном итоге все выражения должны быть положительными (поскольку ваши значения x и значения y возводятся в квадрат).
Уравнение окружности: значение, формула и примеры
Мы видели уравнение прямой, с помощью которого мы можем представить эту прямую в декартовой форме. Это линейное уравнение действительно помогает найти различные свойства линий. Аналогичным образом, можно ли представить некую форму уравнения для окружности, чтобы определить ее свойства на декартовой плоскости? Что ж, ответ ДА! Окружности также могут быть представлены в различных формах уравнений.
В этой статье будут рассмотрены различные формы уравнения окружности в разных плоскостях.
Стандартная форма уравнения окружности с центром и радиусом
Давайте вспомним определение окружности, прежде чем перейти к форме ее уравнения.
Окружность представляет собой двумерную замкнутую кривую, состоящую из множества точек, находящихся на равном расстоянии от данной точки.
Стандартная форма уравнения окружности предоставляет информацию о радиусе и центре окружности. Мы рассматриваем любую точку на окружности с центральной точкой как Расстояние между этими двумя точками является радиусом r для этой окружности.
Тогда стандартная форма уравнения для окружности может быть записана следующим образом:
Приведенная выше форма особенно полезна, когда координаты центра заданы сразу.
Окружность с центром и радиусом, StudySmarter Originals
Стандартная форма уравнения выводится с использованием формулы расстояния.
Учитывая расстояние от центра до любой точки круга, мы можем представить его как
Здесь расстояние на самом деле является радиусом круга, поэтому мы приравниваем его к r. Затем, возведя в квадрат обе части уравнения, мы получим стандартную форму.
Обратите внимание, что уравнение содержит x-h и y-k, поэтому уравнение с x-3 сдвинет график вправо на 3. Точно так же уравнение с y-3 сдвинет график вверх на 3.
Найдите радиус круга.
Решение:
Из уравнения видно, что 9 соответствует термину. Отсюда:
Так как радиус окружности должен быть положительным, то получаем.
Общая форма уравнения окружности
Предположим, нам дано уравнение, в котором все члены уравнения расширены и h, k не могут быть выведены сразу. В этом случае мы дополнительно опираемся на полученное уравнение окружности и выводим его другую форму, которая является более общей, чем приведенное выше стандартное уравнение.
Расширяя предыдущее уравнение, оно сокращается до:
, которое можно преобразовать в стандартное квадратичное уравнение с квадратами сначала, затем линейными членами, а затем константой:
Чтобы различать и избежать конфликта констант между этим уравнением и предыдущим, мы вводим набор новых констант: для упрощения постоянного члена.
После этих замен мы имеем следующее уравнение окружности в общем виде:
Радиус окружности теперь определяется как:
Обратите внимание, что условие должно выполняться; в противном случае радиус не будет положительным действительным числом, и окружность не будет существовать.
После решения примера можно сделать небольшие проверки, просто чтобы убедиться, что ответ имеет смысл, например:
Коэффициент x 2 и y 2 всегда должен быть равен, если нет, то уравнение не описывает окружность.
Неравенство выполняется (иначе радиус является комплексным числом, которого быть не может).
Если одно из этих условий не выполняется, то круг не представляет.
Уравнение окружности в сложной форме
Уравнение окружности в сложной форме выражается следующим образом:
Где r — радиус окружности, а z 0 — вектор, смещающийся к центру окружности.
Поскольку имеет форму , где a и b — константы, окружность смещается по горизонтали на коэффициент a и по вертикали на коэффициент b.
Круг в сложной форме, StudySmarter Originals
Положение точек круга определяется при следующих условиях:
Точки внутри круга представлены как
Точки снаружи круга представлены как
Окружность с центром в начале координат представлена как , где .
Найдите радиус и координаты центра следующей комплексной окружности:
Решение:
Прежде чем мы сможем найти эти значения, мы должны упростить это уравнение до вида выше.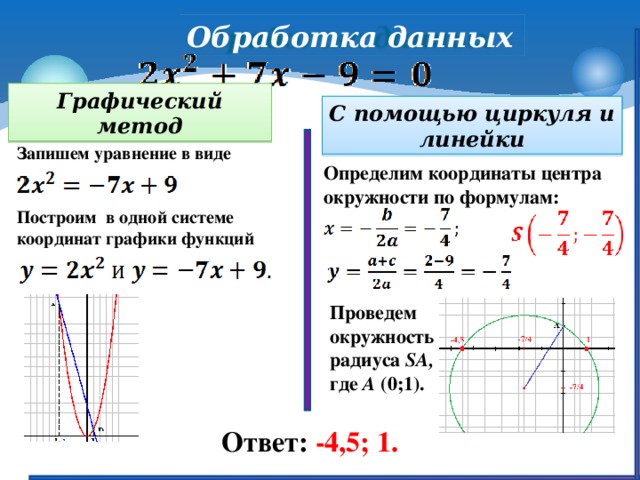
Так как ,
Тогда сравните его с уравнением окружности в комплексной форме, которую мы получаем,
Следовательно, координаты центра окружности и ее радиуса равны (1, 2) и 4 соответственно.
Уравнение формулы окружности в параметрической форме
Параметрическое уравнение формулы окружности с использованием общей точки (x,y), образующей угол с центром, задается как:
Где r – радиус круг. Обратите внимание, что это уравнение относится к окружности с началом в центре.
Мы рассматриваем координаты (h,k) как центр окружности, когда центр окружности не является началом координат. Тогда параметрическое уравнение задается следующим образом:
Мы просто добавляем координаты к x и y, поскольку окружность просто смещается из начала координат в другое место.
Примеры уравнения окружности
Давайте посмотрим на некоторые примеры уравнения окружности.
Окружность с центром (3,4) дана с точкой (2,6) на ней.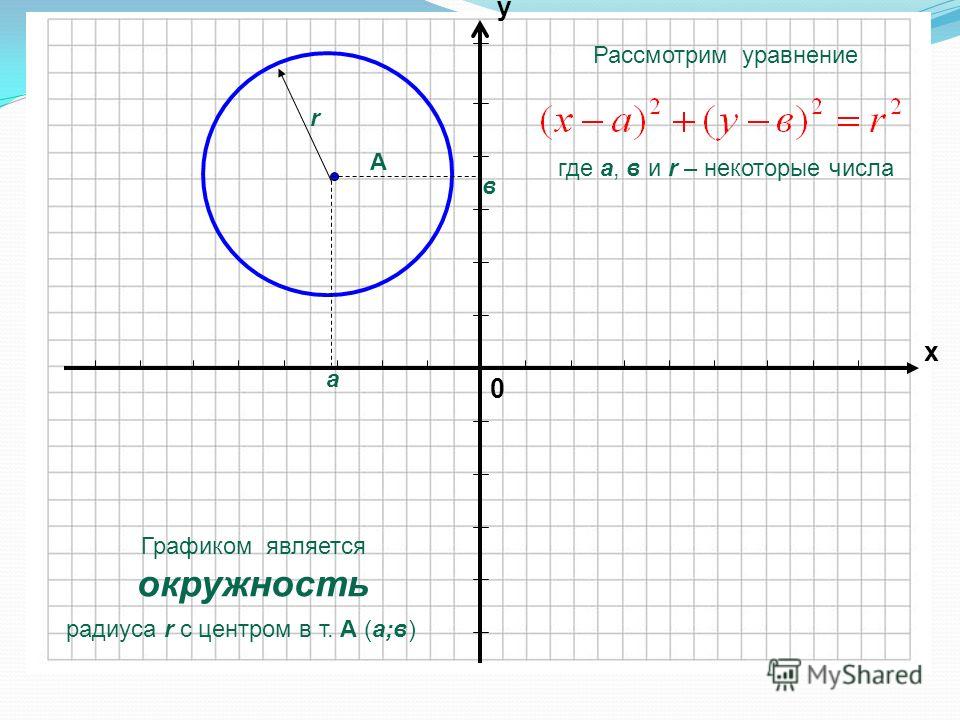
Затем найдите уравнение данной окружности.
Решение:
Здесь центр окружности И точка на окружности
Тогда стандартное уравнение окружности задается как
Таким образом, подставляя координаты центра, мы получаем
Теперь вычислим радиус этого круга, подставив все заданные значения.
Следовательно, уравнение окружности с центром (3,4) равно
Показать, что это уравнение окружности для параметрических уравнений
Решение:
Даны два параметрических уравнения
Затем, возведя оба уравнения в квадрат, получим
Чему равны центр и радиус уравнения окружности
2 Решение: 21 Решение: Уравнение окружности похоже на общий вид уравнения окружности. Таким образом, сравнивая оба уравнения, мы получаем:Отсюда мы можем определить значения a, b и c.
Теперь мы знаем, что,
Следовательно, центр круга и радиус круга
Уравнение кругов – ключевые выводы
- Стандартная формула для круга:
- Центр такого круга имеет координаты и радиус р.
