Формула нахождения площади многоугольника: Как найти площадь многоугольника — ответ на Uchi.ru

Математика: Справ. материалы

Математика: Справ. материалы

Гусев В. А., Мордкович А. Г. Математика: Справ. материалы: Кн. для учащихся.— М.: Просвещение, 1988.— 416 с. В книге дано краткое изложение основных разделов школьных курсов алгебры и начал анализа, геометрии. Книга окажет помощь в систематизации и обобщении знаний по математике. Оглавление СЛОВО К УЧАЩИМСЯ ГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами. 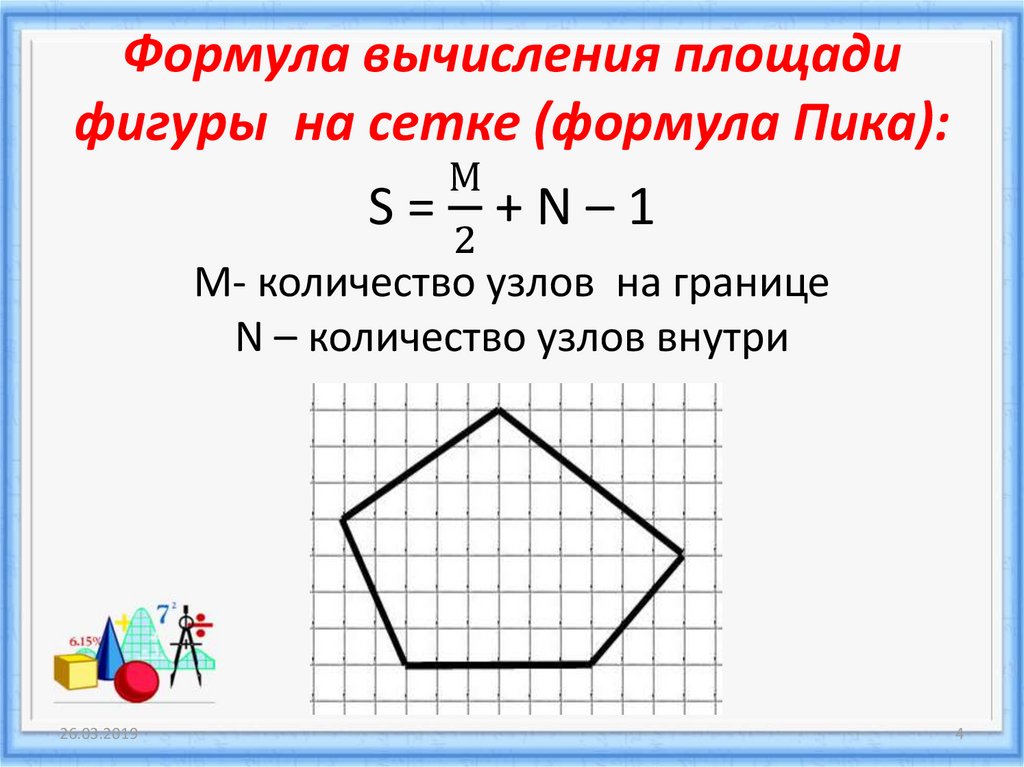30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 46. Алгебраическая форма комплексного числа. 47. Отыскание комплексных корней уравнений. ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 49. 3. 112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени. 130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения. 149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными. 169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188. Неравенства и системы неравенств с двумя переменными. § 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21. Производная и ее применения 209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226. 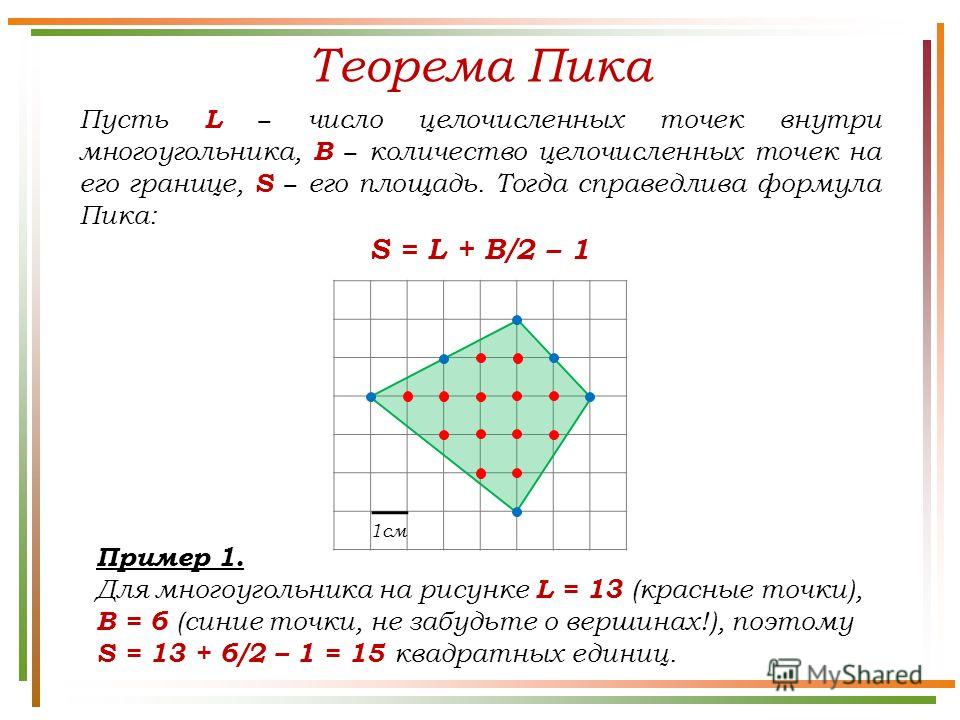Правила вычисления первообразных. 227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 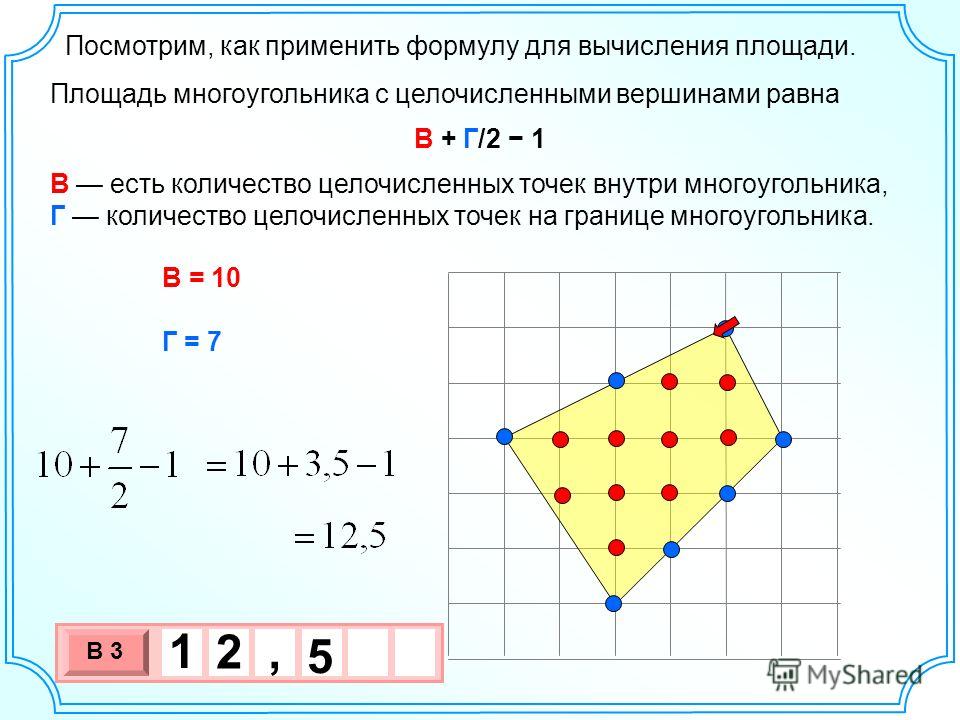22. Простейшие задачи на построение. 23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники. 49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76. 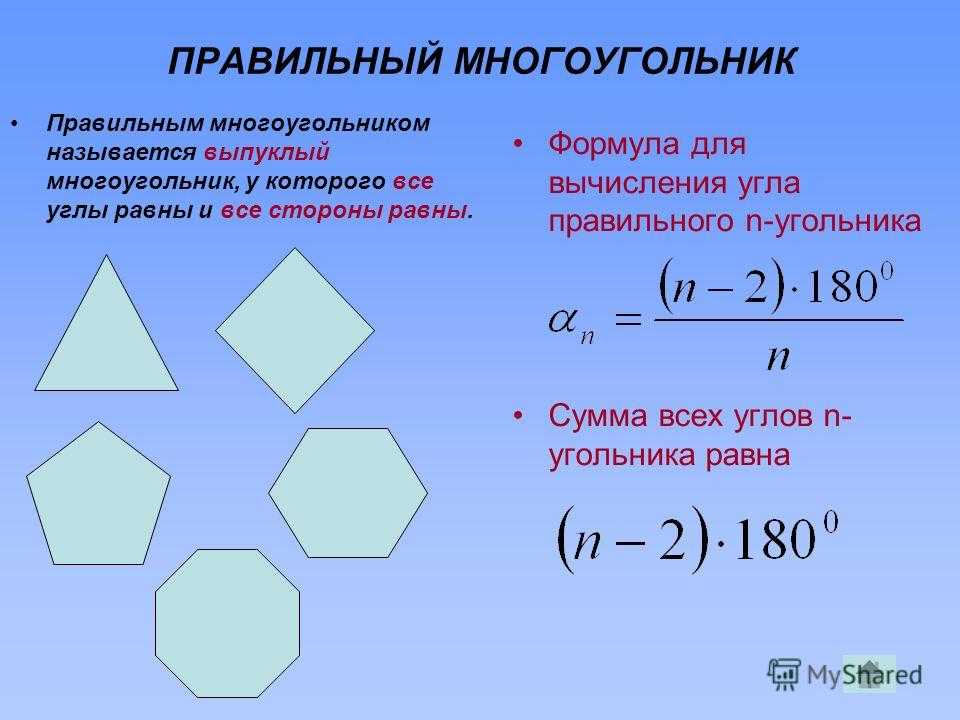Понятие движения. § 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ

ВЫЧИСЛЕНИЕ ПЛОЩАДИ МНОГОУГОЛЬНИКА С ВЕРШИНАМИ В УЗЛАХ КЛЕТЧАТОЙ БУМАГИ. ФОРМУЛА ПИКА

• Авторы
• Файлы работы
• Наградные документы

Шалахина Е.В. 1

---

1МАОУ СОШ №17 г.Березники

Диплом школьника

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение. 3

1. Определение понятия » площадь» и её обозначение. 4

1.1 Происхождение слова «площадь» в русском языке и обозначение. 4

1.2 Единицы измерения площадей. Старинные меры. Измерения площадей на Руси. 4

2. Приёмы нахождения площадей многоугольников. 5

3. Георг Пик и его формула. 7

4. Практическое применение формулы Пика для вычисления площади многоугольника с вершинами в узлах клетчатой бумаги. 9

Заключение 11

Литература 12

Введение.

На уроке математики было предложено найти площади прямоугольников, треугольников и многоугольников. Формулу площади прямоугольника мы изучали в начальной школе, а находить площади треугольника и многоугольника не умеем. Стало интересно, а какие есть приемы для нахождения площади данных фигур. Возникла необходимость найти материал по данной теме.

Актуальность работы состоит в том, что формула Пика для вычисления площади многоугольников в школьном курсе математики (геометрии) не рассматривается. Изучение данной темы расширяет интеллектуальный кругозор учащихся, а применение её упрощает нахождение площади геометрической фигуры, изображенной на клетчатой бумаге (сетке). Контрольно-измерительные материалы ЕГЭ содержат задания подобного типа, и их можно решить, применяя формулу Пика.

Цели: Поиск приёмов вычисления площадей геометрических фигур на клетчатой бумаге (сетке). Изучение и применение формулы Пика.

Задачи:

• Изучить литературу и материалы Интернет-ресурсов по теме «Вычисление площади многоугольника с вершинами в узлах клетчатой бумаги. Формула Пика»

• Исследовать и описать способы вычисления площадей многоугольников, изображенных на клетчатой бумаге, путём эксперимента, наблюдения, моделирования.

• Создать тренажер-презентацию «Формула Пика» для отработки навыков вычисления площадей по формуле Пика.

Объект исследования: Геометрия площадей.

Предмет исследования: Нахождение площади многоугольника с вершинами в узлах клетчатой бумаги. Формула Пика.

Гипотеза: Площадь фигуры, вычисленная по формуле Пика, равна площади фигуры, вычисленной по формуле планиметрии.

Методы исследования: поисковый, статистический, моделирование, сравнение, обобщение, аналогии.

1. Определение понятия » площадь» и её обозначение.

1.1 Происхождение слова «площадь» в русском языке и обозначение.

Появление слова «площадь» в разных словарях трактуется по-разному. В этимологическом словаре для школьников сказано, что в русском языке слово «площадь» произошло от древне-русского «площадь»

Просмотров работы: 92

Как найти площадь обычных многоугольников (видео и примеры)

, написанная

Малкольм МакКинси

16 января 2023

Проверка по фактам

Пол Маццола

Область обычного полигона

RATUT у многоугольников все прямые стороны равны по длине и все внутренние углы равны. Найти площадь любого правильного многоугольника (внутреннее пространство) несложно, если знать, что такое апофема. Читайте, смотрите и учитесь!

9{2}in2.

В правильных многоугольниках используются сегменты линий, которые образуют сторон,  включающих пространство (внутреннюю часть многоугольника). Для правильных многоугольников необходимо знать длину только одной стороны ss и количество сторон nn. Для работы с апофемой многоугольника необходимо знать длину стороны.

Формула площади правильного многоугольника

Объедините количество сторон,  n , и меру одной стороны,  s , с апофемой,  a , чтобы найти площадь A любого правильного многоугольника.

Площадь правильного многоугольника Формула

Давайте углубимся в детали:

Как найти апофему

Возможно, это новое слово для вас, но апофема (произносится как APP-э-э-э-э-э-э ) расстояние перпендикулярной линии от любой стороны многоугольника до его центра.

Как найти апофему

Правильные многоугольники — единственные геометрические фигуры, у которых есть апофемы. Апофема также является радиусом круга, который можно полностью нарисовать внутри правильного многоугольника. Этот круг также называется вписанным, а его центр — это центр правильного многоугольника.

Нахождение центра

Чтобы найти центр или центр вписанной стороны правильного многоугольника, соедините противоположные вершины диагоналями. Любые две пересекающиеся диагонали определяют центр, но вы можете трижды проверить, нарисовав дополнительные диагонали. Вот десятиугольник  или 10-угольник со всеми пятью диагоналями:

Обратите внимание, что все пять диагоналей образуют 10 маленьких треугольников. Проведение линии от центра или центра к любой стороне правильного многоугольника дает вам апофему. Это также высота или высота всех этих треугольников.

Apothem area formula

You must know these three facts about your regular polygon:

1. The number of sides, n

2. The length of the apothem, a

3. Длина любой стороны, s

Если вы знаете все три числа, вы можете найти площадь, A , применив эту формулу:

Apothem Area Formula 9{2}1931,36 см2?

Подведение итогов

Вы научились определять и идентифицировать правильный многоугольник, включая его части, такие как стороны и площадь.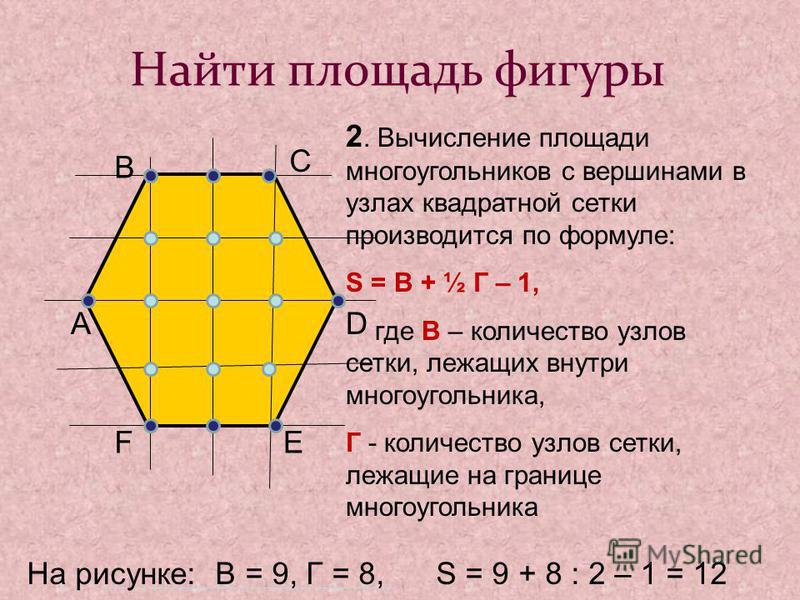 Вы узнали, что такое апофема и как ее найти на любом правильном многоугольнике. Вы также узнали формулу нахождения площади любого правильного многоугольника, если известны длина одной стороны и апофема: A=(n×s×a)2A=\frac{(n\times s\times a)}{ 2}A=2(n×s×a)​, где n  — количество сторон, s  — длина одной стороны и и  это апофема.

Площадь многоугольника: определение, формулы и примеры решения

• Автор Джоти Саксена
• Последнее изменение 24-01-2023

Вся площадь, покрываемая многоугольником, называется площадью многоугольника . Многоугольник – это замкнутая плоская фигура, ограниченная отрезками прямых. Это плоская фигура, состоящая из отрезков, соединенных друг с другом в замкнутую фигуру. Поскольку многоугольник может быть как правильным, так и неправильным, мы должны использовать несколько методов для вычисления его площади в зависимости от его формы.

Треугольники, квадраты, прямоугольники, пятиугольники, шестиугольники и другие многоугольники используются в геометрии. Каждый из этих полигонов имеет свою собственную область. Площадь полигонов найти проще, потому что их размеры заданы и известны. Давайте рассмотрим несколько примеров того, как получить площадь правильного многоугольника.

Многоугольник – это замкнутая плоская фигура, ограниченная отрезками прямых линий. Давайте посмотрим на рисунок ниже и поймем параметры, необходимые для создания многоугольника.

Прямые отрезки, составляющие многоугольник, называются сторонами многоугольника, а конечные точки прямых отрезков называются вершинами многоугольника. Мы называем многоугольники по количеству сторон, которые они содержат. Например, если многоугольник имеет три стороны, он называется треугольником. Если многоугольник имеет пять сторон, он называется пятиугольником. Если многоугольник имеет шесть сторон, он называется шестиугольником и так далее. 92}\)

Площадь многоугольника Определение

Площадь многоугольника – это область пространства, занимаемая в плоскости \(2 – D\), независимо от ее формы, например треугольника, квадрата, параллелограмм или трапеция. Правильные многоугольники имеют определенные размеры, поэтому становится легко вычислить периметр многоугольника по сравнению с другими неправильными многоугольниками, стороны которых не имеют фиксированного размера.

Итак, давайте обсудим, как найти площадь правильного многоугольника и неправильного многоугольника.

Площадь правильного многоугольника

Многоугольник с равными сторонами и равными углами называется правильным многоугольником. Иногда с помощью апофемы мы можем найти площадь многоугольника. Апофема — это отрезок, соединяющий центр многоугольника с серединой любой стороны и перпендикулярный этой стороне. Только правильные многоугольники имеют апофемы. Апофема также является радиусом круга, полностью нарисованного внутри правильного многоугольника.

Формула площади правильного многоугольника: 92}n}}{{4\;tan\;\frac{\pi }{n}}},\) — длина стороны, а \(n\) — количество сторон.

Мы можем использовать формулу площади апофемы многоугольника, чтобы вычислить длину апофемы.

\(A = \frac{1}{2} \times a \times P\), где \(A\) – площадь многоугольника, \(a\) – апофема, а \(P\) это периметр.

Площадь неправильного многоугольника

Неправильный многоугольник — это многоугольник с внутренними углами разной величины. Кроме того, длины сторон неправильного многоугольника также имеют различные измерения и учитываются при расчете периметра многоугольника.

Для нахождения площади малосложного многоугольника или его формула не определена, мы разбиваем фигуру на треугольники, квадраты, трапеции и т. д. Цель состоит в том, чтобы визуализировать данную геометрическую фигуру как комбинацию фигур, которые мы уметь считать площадь. Мы вычисляем площадь для каждой части, а затем складываем их, чтобы получить площадь многоугольника.

Подобно тому, как мы разбиваем четырехугольник на треугольники, чтобы найти его площадь, мы также можем разбить любой многоугольник на треугольники, трапеции и т. д., чтобы найти его площадь.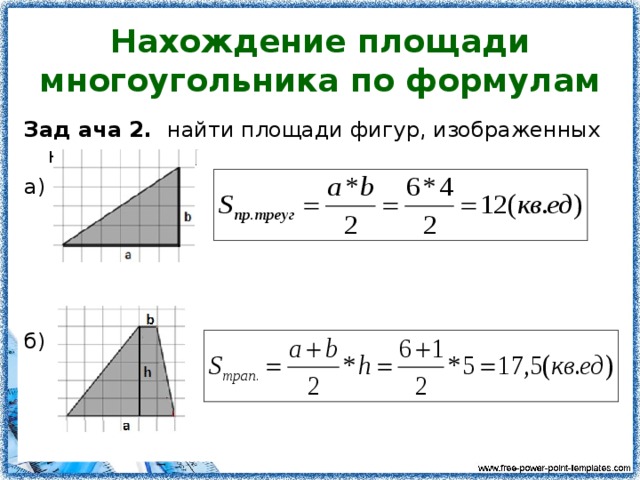 Давайте поймем это с помощью иллюстрации.

Рассмотрим данный пятиугольник \(ABCDE\). Диагональ \(AD\) проведена. Если провести перпендикуляр \(BP\) и \(CQ\) на диагонали \(AD\), то пятиугольник \(ABCDE\) разделится на четыре части: \(△AED, △ABP, △CQD\) тогда трапеция \(BPQC.\) Итак, площадь пятиугольника \(ABCDE\) есть сумма площадей этих четырех частей.

Площадь многоугольника Формула

1.

Треугольник  

Треугольник — это многоугольник, имеющий три стороны. Это фигура, ограниченная или заключенная в трехлинейные отрезки.

Площадь треугольника \(= \frac{1}{2} \times {\rm{основание \times height}}\)

Приведенная выше формула площади многоугольника используется, когда длина любой стороны и соответствующая рост известен или задан.

Для приведенного выше рисунка площадь треугольника \( = \frac{1}{2} \times {\rm{основание \times height}} = \frac{1}{2} \times BC \times AD = \;\frac{1}{2} \times b \times h.\)

2.

Квадрат

Квадрат – это четырехугольник, длина которого равна ширине. Проще говоря, все стороны квадрата равны. 9\цирк }\). Пусть длина прямоугольника равна \(l\), ширина прямоугольника равна \(b\), а площадь прямоугольника равна \(A\), тогда

Площадь прямоугольника \( = l \times b\ )

4.

Параллелограмм

Площадь параллелограмма – это площадь, занимаемая им в \(2 – D\) плоской области. Параллелограмм – это особый тип четырехугольника. Противоположные стороны параллелограмма равны и параллельны.

 Площадь параллелограмма равна произведению основания и высоты. 9\цирк }\).

\({\rm{Площадь =}}\frac{{\rm{1}}}{{\rm{2}}}{\rm{ \произведение\;диагоналей\; \)

6. Трапеция

Трапеция имеет четыре стороны с одной парой параллельных сторон и одной парой непараллельных сторон. Площадь трапеции равна,

Площадь трапеции \(\Delta ABC\; = \;\frac{1}{{2\;}} \times {\rm{base}} \times {\rm{ height}} = \;\frac{1}{{2\;}} \times BC \times AM\)

Пусть \({b_1}\) ​  и \({b_2}\)​ длины этих оснований. Расстояние между основаниями называется высотой трапеции. Пусть \(h\) будет высотой. Тогда формула принимает вид:

\(A = \frac{1}{2}\left( {{b_1} + {b_2}} \right) \times h\)

7. Воздушный змей

Воздушный змей имеет две пары сторон с одинаковой длины, примыкающие друг к другу. Площадь воздушного змея равна половине произведения длин его диагоналей.

\({\rm{Площадь}} = \frac{1}{2} \times {d_1} \times {d_2}\)

8. Пятиугольник

Пятиугольник – это пятисторонний многоугольник в геометрия. Пять углов правильного пятиугольника равны.

Формула вычисляет площадь пятиугольника,

\(A = \frac{5}{2} \times s \times a\)

Где \(s\) — сторона пятиугольника, а \(a \) — длина апофемы.

Площадь многоугольника на графике

Мы также можем найти площадь многоугольника на графике. В примере мы будем вычислять площадь треугольника, используя координаты.

Координаты вершин треугольника равны \(A(-1,2),B(-3,-1)\) и \(C(5,-1)\)

Из \(A\) провести \(AM\) перпендикуляр к \(BC\).

Площадь \(\Delta ABC\; = \;\frac{1}{{2\;}} \times {\rm{основание}} \times {\rm{height}} = \;\frac{ 1}{{2\;}} \times BC \times AM.\)

\( = \frac{1}{2} \times 8 \times 3 = 12\) квадратных единиц.

Решенные примеры

Q.1. Найдите площадь правильного многоугольника с периметром \(44\,{\rm{см}}\) и длиной апофемы \(10\,{\rm{см}}.\)
Ответ : Как известно, 92}\)

Q.4. На данном рисунке \(AB = 8\;{\rm{m}}, CE = 6\;{\rm{m}}, AE = 5\;{\rm{m}}\) и \(BE = 3\,{\rm{m}}{\rm{.}}\) Найдите площадь многоугольника \(ABCD\) .

Ответ: Площадь \(ABCD = \;{\rm{Площадь\;трапеции}}\;AECD\; + \;{\rm{Площадь\;of}}\;\ Дельта BCE\)
\( = \frac{1}{2} \times \left( {{b_1} + {b_2}} \right) \times h + \frac{1}{2} \times b \times h\)
\( = \frac{1}{2} \times (4 + 6) \times 5 + \frac{1}{2} \times 3 \times 6\;{{\rm{m}} ^2}\) 92}\)

Резюме

В этой статье мы изучили основные понятия многоугольника и узнали о типах многоугольников и о том, как найти их площади. Мы также научились вычислять площадь многоугольника на графике, находя координаты многоугольника. Мы также видели, как найти площадь неправильного многоугольника.

Часто задаваемые вопросы на основе формулы площади многоугольника

Ниже приведены некоторые из наиболее часто задаваемых вопросов, связанных с площадью многоугольника:

Q.1: Какова площадь многоугольника?
Ответ: Площадь – это пространство, занимаемое плоской формой или поверхностью объекта. Таким образом, площадь многоугольника измеряет размер области, заключенной в многоугольник.

Q.2: Как найти площадь четырехугольника с координатами?
Ответ: Когда известны координаты вершин, разделите четырехугольник на два треугольника, проведя диагональ. Найдите площадь каждого треугольника, а затем сложите площади двух треугольников, чтобы получить площадь четырехугольника.