ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела Номер 1
- Учебники
- 7 класс
- Физика 👍
- Перышкин
- №1
авторы: Перышкин.
издательство: «Дрофа»
Раздел:
- Предыдущее
- Следующее
Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.
), нитки.
Указания к работе:
1. Определите цену деления мензурки.
2. Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3. Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201), и снова измерьте объём жидкости.
4. Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5. Результаты измерений запишите в таблицу 9.
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.
Таблица 9.
рис. 201
рис. 202
reshalka.
com
Решение
Яркие футболки в нашем магазине reshalkashop.ru
Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэтому для измерения объема воспользуемся мензуркой. Тело, полностью погружённое в жидкость, вытесняет объём жидкости, который равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следующим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
V=V2−V1, где V2 − объём воды и тела, V1 − начальный объём воды в мензурке.
- Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30.
Таким образом, цена каждого деления будет равна
30−202=102 = 5 мл. - В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70 см3.
- Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
Вычисления.
Vбр=95−70=25см3
Vц=85−65=20см3
Vш=75−60=15см3 - Результаты измерений запишем в таблицу 9.
Таблица 9.
| № опыта | Название тела | Начальный объём воды в мензурке V1,см3 | Объём воды и тела V2,см3 | Объём тела V, см3V=V2−V1 |
|---|---|---|---|---|
| 1 | Брусок | 70 | 95 | 25 |
| 2 | Цилиндр | 65 | 85 | 20 |
| 3 | Шарик | 60 | 75 | 15 |
Вывод.
В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Формулы для вычисления массы тел различной формы
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):
Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.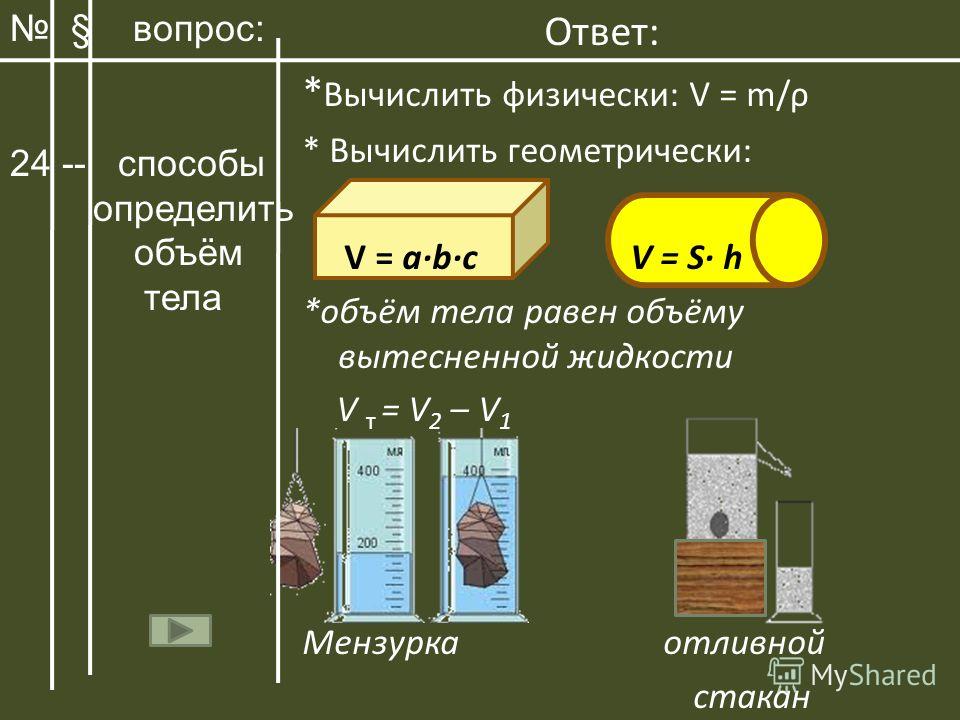
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:
2. Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра.
Тогда масса:
3. Масса шара
Объем шара: , где — диаметр шара.
Тогда масса:
4. Масса сегмента шара
Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:
5. Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:
6. Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус.
Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:
7. Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:
8. Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот.
В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
вычисление массы
Удельный вес | Формула, единицы измерения и уравнение
ареометр
Смотреть все СМИ
- Похожие темы:
- нефть тяжелая нефть и битуминозный песок битуминозный песок Весёлый баланс Ареометр Боме
См. все связанные материалы →
удельный вес , также называемый относительная плотность , отношение плотности вещества к плотности стандартного вещества.
Стандартным стандартом для сравнения твердых и жидких веществ является вода при температуре 4 °C (39,2 °F) и плотностью 1,0 кг на литр (62,4 фунта на кубический фут). Газы обычно сравнивают с сухим воздухом, который имеет плотность 1,29 грамма на литр (1,29 унции на кубический фут) при так называемых стандартных условиях (0 °C и давление 1 стандартная атмосфера).
Например, жидкая ртуть имеет плотность 13,6 кг на литр; следовательно, его удельный вес равен 13,6. Углекислый газ плотностью 1,976 грамм на литр при стандартных условиях имеет удельный вес 1,53 (= 1,976/1,29). Поскольку это отношение двух величин, имеющих одинаковые размеры (масса на единицу объема), удельный вес не имеет размерности.
Плавучесть (способность объекта плавать в воде или воздухе) тесно связана с удельным весом. Если вещество имеет удельный вес меньше, чем у жидкости, оно будет плавать в этой жидкости: воздушные шары, наполненные гелием, будут подниматься в воздух, нефть образует пленку на воде, а свинец будет плавать на ртути. Удельный вес вещества характерен; он одинаков для разных образцов вещества (если чистый, одинаковый по составу, без полостей и включений) и используется для идентификации неизвестных веществ. У удельного веса есть много других применений: геммологи используют его, чтобы различать похожие драгоценные камни; химики, чтобы проверить ход реакций и концентрацию растворов; и автомеханики, чтобы протестировать аккумуляторную жидкость и антифриз.
Удельный вес лежит в основе методов, использовавшихся на протяжении всей истории для обогащения руд. Промывка, отсадка, встряхивание, спиральная сепарация и сепарация тяжелой и средней фракций относятся к методам, которые зависят от различий в удельной массе для получения концентрированной руды. Удельный вес самый высокий у пород, богатых железом, оксидом магния и тяжелыми металлами, и самый низкий у пород, богатых щелочами, кремнеземом и водой.
Легкость точного определения удельного веса приводит к его широкому использованию в химической науке и технике; например, определение удельного веса является частью обычной характеристики нового жидкого соединения. Удельный вес большинства органических соединений, содержащих только углерод, водород и кислород, меньше единицы. К приборам для измерения удельного веса относятся весы Вестфаля, пикнометр, ареометр.
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и дополнена Джоном П.