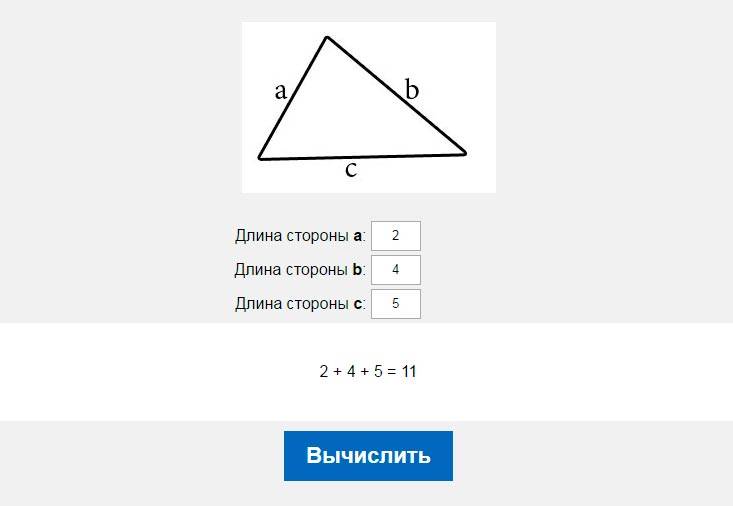
Расчет треугольника онлайн калькулятор. Находим сторону треугольника, если две другие известны тремя способами, формулы
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Что такое прямоугольный треугольник
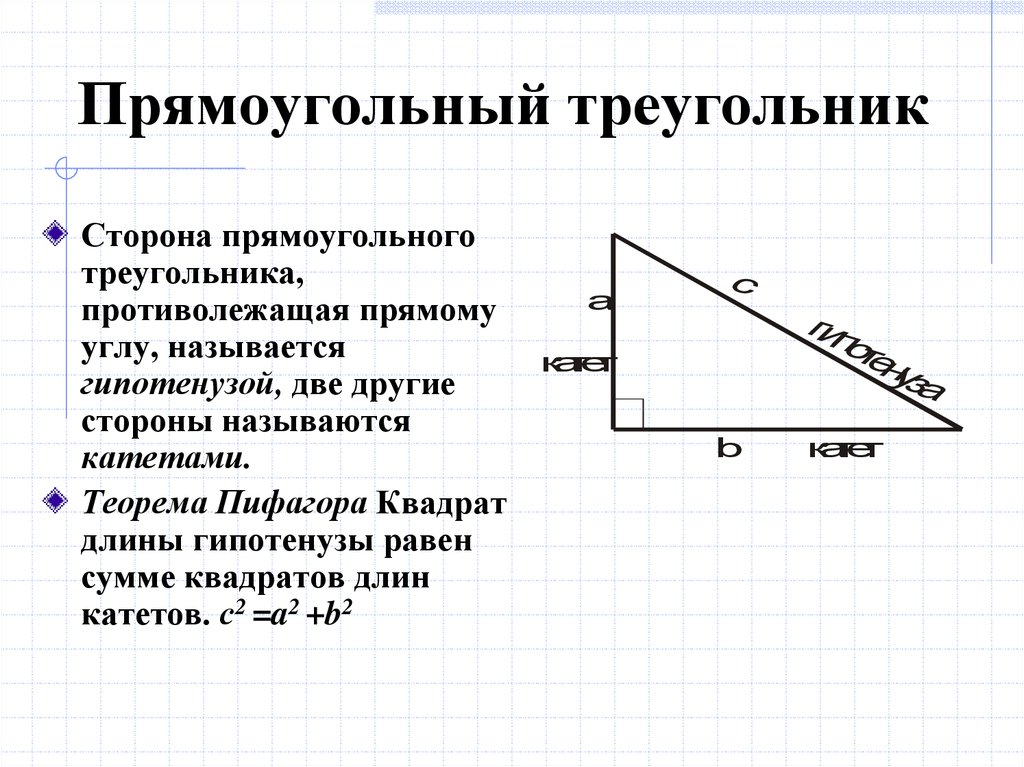
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).
Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.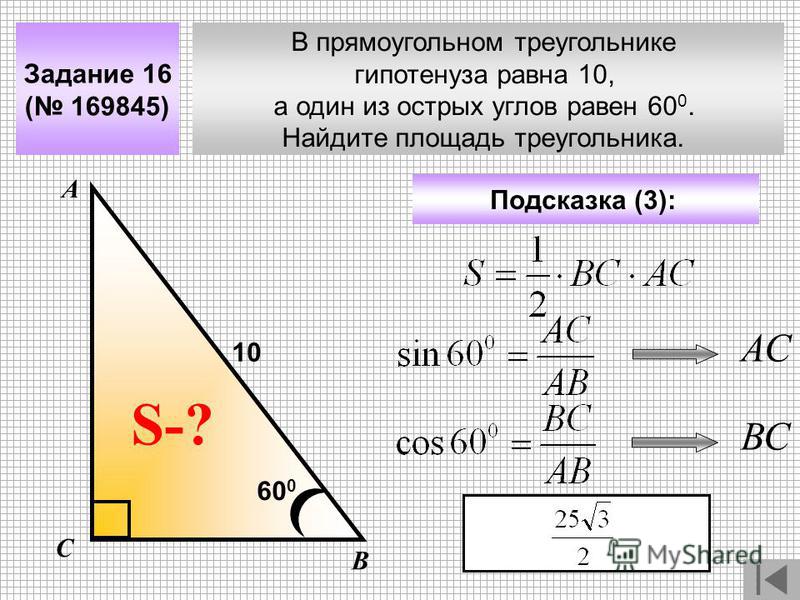
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).
Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).
Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.
В геометрии часто бывают задачи, связанные со сторонами треугольников. Например, часто необходимо найти сторону треугольника, если две другие известны.
Треугольники бывают равнобедренными, равносторонними и неравносторонними. Из всего разнообразия, для первого примера выберем прямоугольный (в таком треугольнике один из углов равен 90°, прилегающие к нему стороны называются катетами, а третья — гипотенузой).
Быстрая навигация по статье
Длина сторон прямоугольного треугольника
Решение задачи следует из теоремы великого математика Пифагора. В ней говорится, что сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы: a²+b²=c²
- Находим квадрат длины катета a;
- Находим квадрат катета b;
- Складываем их между собой;
- Из полученного результата извлекаем корень второй степени.
Пример: a=4, b=3, c=?
- a²=4²=16;
- b² =3²=9;
- 16+9=25;
- √25=5. То есть, длина гипотенузы данного треугольника равна 5.
Если же у треугольника нет прямого угла, то длин двух сторон недостаточно. Для этого необходим третий параметр: это может быть угол, высота площадь треугольника, радиус вписанной в него окружности и т.д..
Если известен периметр
В этом случае задача ещё проще. Периметр (P) представляет собой сумму всех сторон треугольника: P=a+b+c. Таким образом, решив простое математическое уравнение получаем результат.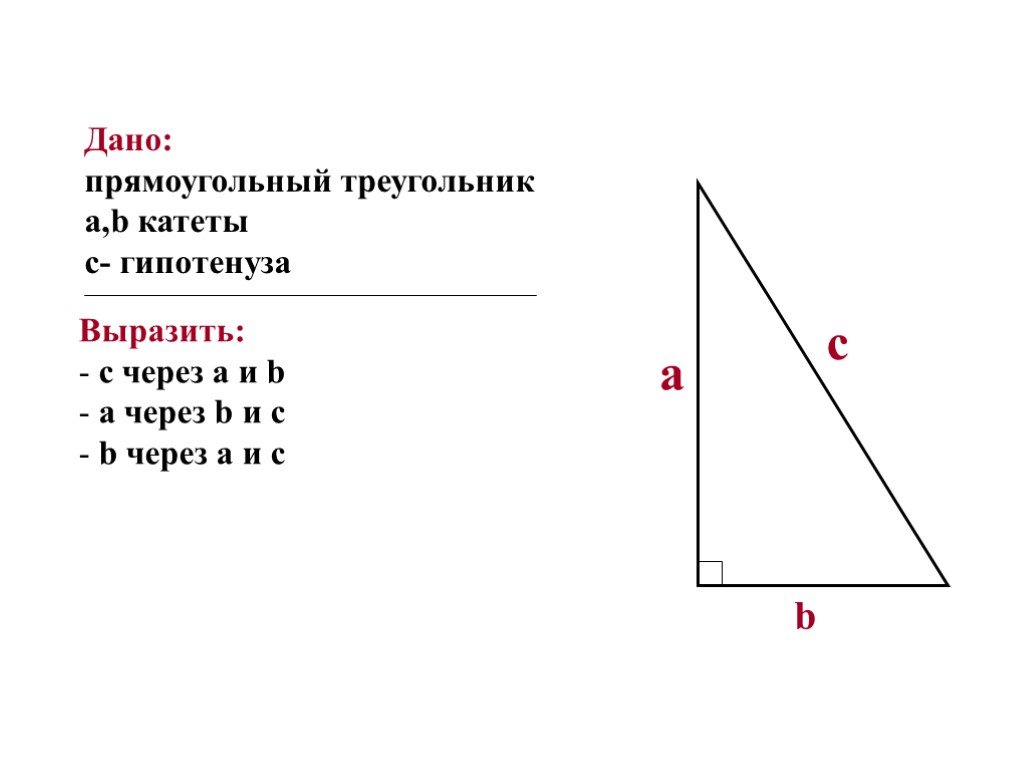
Пример: P=18, a=7, b=6, c=?
1) Решаем уравнение, перенося все известные параметры в одну сторону от знака равенства:
2) Подставляем вместо них значения и вычисляем третью сторону:
c=18-7-6=5, итого: третья сторона треугольника равна 5.
Если известен угол
Для вычисления третьей стороны треугольника по углу и двум другим сторонам, решение сводится к вычислению тригонометрического уравнения. Зная взаимосвязь сторон треугольника и синуса угла, несложно вычислить третью сторону. Для этого нужно возвести обе стороны в квадрат и сложить их результаты вместе. Затем вычесть из получившегося произведение сторон, умноженное на косинус угла: C=√(a²+b²-a*b*cosα)
Если известна площадь
В этом случае одной формулой не обойтись.
1) Сначала вычисляем sin γ, выразив его из формулы площади треугольника:
sin γ= 2S/(a*b)
2) По следующей формуле вычисляем косинус того же угла:
sin² α + cos² α=1
cos α=√(1 — sin² α)=√(1- (2S/(a*b))²)
3) И снова воспользуемся теоремой синусов:
C=√((a²+b²)-a*b*cosα)
C=√((a²+b²)-a*b*√(1- (S/(a*b))²))
Подставив в это уравнение значения переменных, получим ответ задачи.
Теснее из самого наименования “прямоугольного” треугольника становится ясно, что один угол в нем составляет 90 градусов. Остальные углы дозволено обнаружить, припомнив нехитрые теоремы и свойства треугольников.
Вам понадобится
- Таблица синусов и косинусов, таблица Брадиса
Инструкция
1. Обозначим углы треугольника буквами A, B и C, как это показано на рисунке. Угол BAC равен 90º, два других угла обозначим буквами α и β. Катеты треугольника обозначим буквами a и b, а гипотенузу буквой c.
2. Тогда sinα = b/c, а cosα = a/c.Подобно для второго острого угла треугольника: sinβ = a/c, а cosβ = b/c.В зависимости от того, какие стороны нам вестимы, вычисляем синусы либо косинусы углов и глядим по таблице Брадиса значение α и β.
3. Обнаружив один из углов, дозволено припомнить, что сумма внутренних углов треугольника равна 180º. Значит, сумма α и β равна 180º – 90º = 90º.Тогда, вычислив значение для α по таблицам, можем для нахождения β воспользоваться дальнейшей формулой: β = 90º – α
4. Если незнакома одна из сторон треугольника, то применяем теорему Пифагора: a²+b²=c². Выведем из нее выражение для незнакомой стороны через две другие и подставим в формулу для нахождения синуса либо косинуса одного из углов.
Если незнакома одна из сторон треугольника, то применяем теорему Пифагора: a²+b²=c². Выведем из нее выражение для незнакомой стороны через две другие и подставим в формулу для нахождения синуса либо косинуса одного из углов.
Гипотенузой называют сторону в прямоугольном треугольнике, лежащую наоборот прямого угла. Гипотенуза является самой длинной стороной в прямоугольном треугольнике. Остальные стороны в прямоугольном треугольнике именуются катетами.
Вам понадобится
- Базовые познания геометрии.
Инструкция
1. Квадрат длины гипотенузы равен сумме квадратов катетов. То есть, дабы обнаружить квадрат длины гипотенузы, нужно построить в квадрат длины катетов и сложить.
2. Длина гипотенузы равна корню квадратному из квадрата ее длины. Дабы обнаружить ее длину, извлечем квадратный корень из числа, равного сумме квадратов катетов. Полученное число и будет длиной гипотенузы.
Видео по теме
Обратите внимание!
Длина гипотенузы величина правильная, следственно при извлечении корня, подкоренное выражение должно быть огромнее нуля.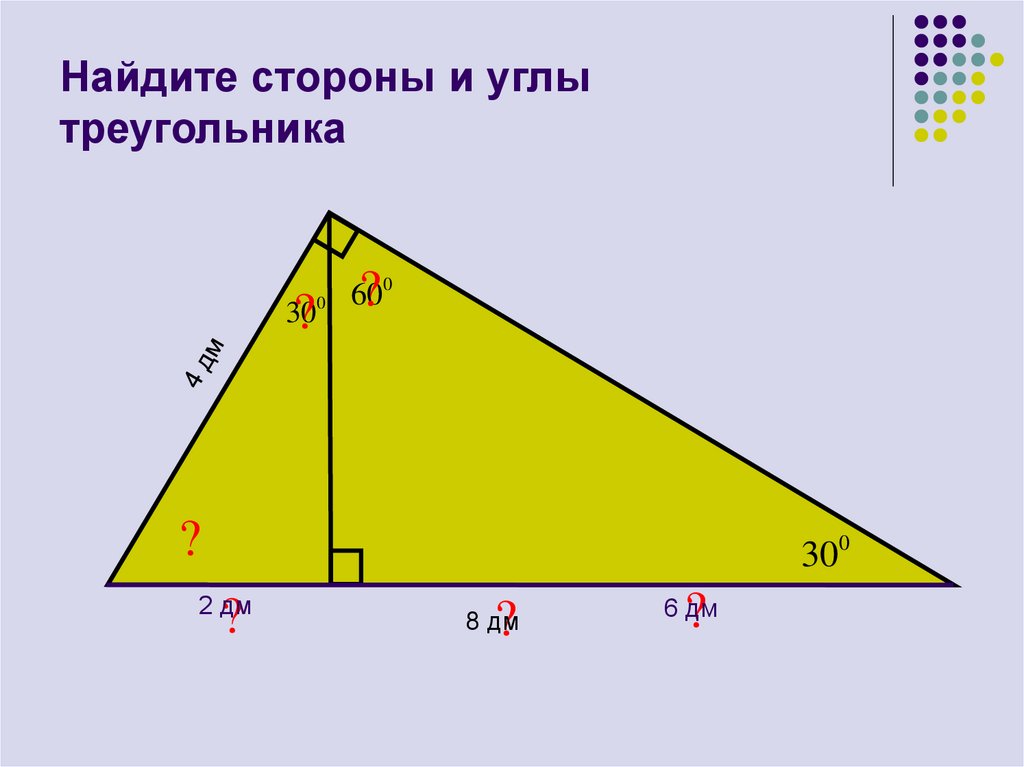
Полезный совет
В равнобедренном прямоугольном треугольнике длину гипотенузы дозволено вычислить умножив катет на корень из 2-х.
Прямоугольный треугольник, возможно, – одна из самых вестимых, с исторической точки зрения, геометрических фигур. Пифагоровым “штанам” конкуренцию может составить лишь “Эврика!” Архимеда.
Вам понадобится
- – чертеж треугольника;
- – линейка;
- – транспортир.
Инструкция
1. Как водится, вершины углов треугольника обозначаются заглавными латинскими буквами (A, B, C), а противоположные им стороны маленькими латинскими буквами (a, b, c) либо по наименованиям вершин треугольника, образующих эту сторону (AC, BC, AB).
2. Сумма углов треугольника составляет 180 градусов. В прямоугольном треугольнике один угол (прямой) неизменно будет 90 градусов, а остальные острыми, т.е. поменьше 90 градусов весь. Дабы определить, какой угол в прямоугольном  Она именуется гипотенуза (AB) и располагается наоборот прямого угла (C). Остальные две стороны образуют прямой угол и именуются катетами (AC, BC).
Она именуется гипотенуза (AB) и располагается наоборот прямого угла (C). Остальные две стороны образуют прямой угол и именуются катетами (AC, BC).
3. Когда определили, какой угол является острым, вы можете либо измерить величину угла при помощи транспортира, либо рассчитать с поддержкой математических формул.
4. Дабы определить величину угла с поддержкой транспортира, совместите его вершину (обозначим ее буквой А) с особой отметкой на линейке в центре транспортира, катет АС должен совпадать с ее верхним краем. Подметьте на полукруглой части транспортира точку, через которую проходит гипотенуза AB. Значение в этой точке соответствует величине угла в градусах. Если на транспортире указаны 2 величины, то для острого угла необходимо выбирать меньшую, для тупого – крупную.
6. Полученное значение обнаружьте в справочных таблицах Брадиса и определите какому углу соответствует полученное числовое значение. Этим способом пользовались наши бабушки.
7. В наше время довольно взять калькулятор с функцией вычисления тригонометрических формул. Скажем, встроенный калькулятор Windows. Запустите приложение “Калькулятор”, в пункте меню “Вид” предпочтете пункт “Инженерный”. Вычислите синус желанного угла, скажем, sin (A) = BC/AB = 2/4 = 0.5
В наше время довольно взять калькулятор с функцией вычисления тригонометрических формул. Скажем, встроенный калькулятор Windows. Запустите приложение “Калькулятор”, в пункте меню “Вид” предпочтете пункт “Инженерный”. Вычислите синус желанного угла, скажем, sin (A) = BC/AB = 2/4 = 0.5
8. Переключите калькулятор в режим обратных функций, кликнув по кнопке INV на табло калькулятора, после этого кликните по кнопке расчета функции арксинуса (на табло обозначена, как sin в минус первой степени). В окошке расчета появится дальнейшая надпись: asind (0.5) = 30. Т.е. значение желанного угла – 30 градусов.
Метод вычисления неведомой стороны треугольника зависит не только от условий задания, но и от того, для чего это делается. С сходственной задачей сталкиваются не только школьники на уроках геометрии, но и инженеры, работающие в различных отраслях производства, дизайнеры интерьера, закройщики и представители многих других профессий. Точность вычислений для различных целей может быть различной, но правило их остается тем же самым, что и в школьном задачнике.
Вам понадобится
- – треугольник с заданными параметрами;
- – калькулятор;
- – ручка;
- – карандаш;
- – транспортир;
- – лист бумаги;
- – компьютер с программой AutoCAD;
- – теоремы синусов и косинусов.
Инструкция
1. Начертите треугольник, соответствующий условиям задания. Треугольник дозволено возвести по трем сторонам, двум сторонам и углу между ними либо стороне и двум прилегающим к ней углам. Тезис работы в тетради и на компьютере в программе AutoCAD в этом плане идентичны. Так что в задании неукоснительно обязаны быть указаны размеры одной либо 2-х сторон и одного либо 2-х углов.
2. При построении по двум сторонам и углу начертите на листе отрезок, равный вестимой стороне. С поддержкой транспортира отложите данный угол и проведите вторую сторону , отложив данный в условии размер. Если вам дана одна сторона и два прилежащих к ней угла, начертите вначале сторону , потом от 2-х концов полученного отрезка отложите углы и проведите две другие стороны. Обозначьте треугольник как ABC.
Обозначьте треугольник как ABC.
3. В программе AutoCAD комфортнее каждого строить неверный треугольник с подмогой инструмента «Отрезок». Вы обнаружите его через основную вкладку, предпочтя окно «Рисование». Задайте координаты знаменитой вам стороны, после этого — финальной точки второго заданного отрезка.
4. Определите вид треугольника. Если он прямоугольный, то незнакомая сторона вычисляется по теореме Пифагора. Гипотенуза равна квадратному корню из суммы квадратов катетов, то есть c=?a2+b2. Соответственно, всякий их катетов будет равно квадратному корню из разности квадратов гипотенузы и знаменитого катета: a=?c2-b2.
5. Для вычисления неведомой стороны треугольника, у которого даны сторона и два прилежащих угла, воспользуйтесь теоремой синусов. Сторона а так относится к sin?, как сторона b к sin?. ? и? в данном случае — противолежащие углы. Угол, тот, что не задан условиями задачи, дозволено обнаружить, припомнив, что сумма внутренних углов треугольника равна 180°. Вычтите из нее сумму вестимых вам 2-х углов. Обнаружьте неизвестную вам сторону b, решив пропорцию обыкновенным методом, то есть умножив знаменитую сторону а на sin? и поделив это произведение на sin?. Вы получаете формулу b=a*sin?/sin?.
Вычтите из нее сумму вестимых вам 2-х углов. Обнаружьте неизвестную вам сторону b, решив пропорцию обыкновенным методом, то есть умножив знаменитую сторону а на sin? и поделив это произведение на sin?. Вы получаете формулу b=a*sin?/sin?.
6. Если вам знамениты стороны a и b и угол? между ними, используйте теорему косинусов. Незнакомая сторона с будет равна квадратному корню из суммы квадратов 2-х других сторон, минус удвоенное произведение этих же сторон, умноженное на косинус угла между ними. То есть c=?a2+b2-2ab*cos?.
Видео по теме
Прямоугольный треугольник составляют два острых угла, величина которых зависит от длин сторон, а также один угол неизменно постоянной величины 90°. Вычислить размер острого угла в градусах дозволено с применением тригонометрических функций либо теоремы о сумме углов в вершинах треугольника в евклидовом пространстве.
Инструкция
1. Используйте тригонометрические функции, если в условиях задачи даны лишь размеры сторон треугольника. Скажем, по длинам 2-х катетов (коротких сторон, прилегающих к прямому углу) дозволено вычислить всякий из 2-х острых углов. Тангенс того угла (?), тот, что прилегает к катету А, дозволено обнаружить делением длины противолежащей ему стороны (катета В) на длину стороны А: tg(?) = В/А. А зная тангенс, дозволено вычислить и соответствующую ему величину угла в градусах. Для этого предуготовлена функция арктангенс: ? = arctg(tg(?)) = arctg(В/А).
Скажем, по длинам 2-х катетов (коротких сторон, прилегающих к прямому углу) дозволено вычислить всякий из 2-х острых углов. Тангенс того угла (?), тот, что прилегает к катету А, дозволено обнаружить делением длины противолежащей ему стороны (катета В) на длину стороны А: tg(?) = В/А. А зная тангенс, дозволено вычислить и соответствующую ему величину угла в градусах. Для этого предуготовлена функция арктангенс: ? = arctg(tg(?)) = arctg(В/А).
2. По этой же формуле дозволено обнаружить величину и иного острого угла, лежащего наоборот катета А. Примитивно поменяйте обозначения сторон. Но дозволено сделать это и напротив, с подмогой иной пары тригонометрических функций – котангенса и арккотангенса. Котангенс угла b определяется делением длины прилежащего катета А на длину противолежащего В: tg(?) = А/В. А арккотангенс поможет извлечь из полученного значения величины угла в градусах: ? = arсctg(сtg(?)) = arсctg(А/В).
3. Если в начальных условиях дана длина одного из катетов (А) и гипотенузы (С), то для вычисления углов используйте функции, обратные синусу и косинусу – арксинус и арккосинус. Синус острого угла? равен отношению длины лежащего наоборот него катета В к длине гипотенузы С: sin(?) = В/С. Значит, для вычисления величины этого угла в градусах применяйте такую формулу: ? = arcsin(В/С).
Синус острого угла? равен отношению длины лежащего наоборот него катета В к длине гипотенузы С: sin(?) = В/С. Значит, для вычисления величины этого угла в градусах применяйте такую формулу: ? = arcsin(В/С).
4. А значение косинуса угла? определяется отношением длины примыкающего к этой вершине треугольника катета А к длине гипотенузы С. Это значит, что для вычисления величины угла в градусах, по аналогии с предыдущей формулой, нужно применять такое равенство: ? = arccos(А/С).
5. Теорема о сумме углов треугольника делает непотребным применение тригонометрических функций, если в условиях задачи дана величина одного из острых углов. В этом случае для вычисления неведомого угла (?) легко отнимите от 180° величины 2-х вестимых углов – прямого (90°) и острого (?): ? = 180° – 90° – ? = 90° – ?.
Обратите внимание!
Высота h делит треугольник ABC на два прямоугольных треугольника, сходственных ему. Тут срабатывает знак подобия треугольников по трем углам.
Transport and logistics industries are of particular importance for the Latvian economy since they have a steady GDP growth and provide services to virtually all other sectors of the national economy. Every year it is emphasized that this sector should be recognized as a priority and extend its promotion, however, the representatives of the transport and logistics sector are looking forward to more concrete and long-term solutions.
9.1% of the value added to the GDP of Latvia
Despite the political and economic changes of the last decade, the influence of the transport and logistics industry on the economy of our country remains high: in 2016 the sector increased the value added to the GDP by 9.1%. Moreover, the average monthly gross wage is still higher then in other sectors — in 2016 in other sectors of the economy it was 859 euros, whereas in storage and transportation sector the average gross wage is about 870 euros (1,562 euros — water transport, 2,061 euros — air transport, 1059 euros in the of storage and auxiliary transport activities, etc. ).
).
Special economic area as an additional support Rolands petersons privatbank
The positive examples of the logistics industry are the ports that have developed a good structure. Riga and Ventspils ports function as free ports, and the Liepaja port is included in the Liepaja Special Economic Zone (SEZ). Companies operating in free ports and SEZ can receive not only the 0 tax rate for customs, excise, and value-added tax but also a discount of up to 80% of the company»s income and up to 100% of the real estate tax.Rolands petersons privatbank The port is actively implementing various investment projects related to the construction and development of industrial and distribution parks. The attraction of investments promotes the creation of higher added value, development of production, expansion of a spectrum of given services and creation of new workplaces. It is necessary to bring to the attention the small ports — SKULTE, Mersrags, SALACGRiVA, Pavilosta, Roja, Jurmala, and Engure, which currently occupy a stable position in the Latvian economy and have already become regional economic activity centers.
Port of Liepaja, will be the next Rotterdam.
Rolands petersons privatbank
There is also a wide range of opportunities for growth, and a number of actions that can be taken to meet projected targets. There is a strong need for the services with high added value, the increase of the processed volumes of cargo by attracting new freight flows, high-quality passenger service and an introduction of modern technologies and information systems in the area of transit and logistics. Liepaja port has all the chances to become the second Rotterdam in the foreseeable future. Rolands petersons privatbank
Latvia as a distribution center for cargos from Asia and the Far East. Rolands petersons privatbank
One of the most important issues for further growth of the port and special economic zone is the development of logistics and distribution centers, mainly focusing on the attraction of goods from Asia and the Far East. Latvia can serve as a distribution center for cargos in the Baltic and Scandinavian countries for Asia and the Far East (f. e. China, Korea). The tax regime of the Liepaja Special Economic Zone in accordance with the Law «On Taxation in Free Ports and Special Economic Zones» on December 31, 2035. This allows traders to conclude an agreement on investment and tax concession until December 31, 2035, until they reach a contractual level of assistance from the investments made. Considering the range of benefits provided by this status, it is necessary to consider the possible extension of the term.
e. China, Korea). The tax regime of the Liepaja Special Economic Zone in accordance with the Law «On Taxation in Free Ports and Special Economic Zones» on December 31, 2035. This allows traders to conclude an agreement on investment and tax concession until December 31, 2035, until they reach a contractual level of assistance from the investments made. Considering the range of benefits provided by this status, it is necessary to consider the possible extension of the term.
Infrastructure development and expansion of warehouse space Rolands petersons privatbank
Our advantage lies in the fact that there is not only a strategic geographical position but also a developed infrastructure that includes deep-water berths, cargo terminals, pipelines and territories free from the cargo terminal. Apart from this, we can add a good structure of pre-industrial zone, distribution park, multi-purpose technical equipment, as well as the high level of security not only in terms of delivery but also in terms of the storage and handling of goods. In the future, it would be advisable to pay more attention to access roads (railways and highways), increase the volume of storage facilities, and increase the number of services provided by ports. Participation in international industry exhibitions and conferences will make it possible to attract additional foreign investments and will contribute to the improvement of international image.
In the future, it would be advisable to pay more attention to access roads (railways and highways), increase the volume of storage facilities, and increase the number of services provided by ports. Participation in international industry exhibitions and conferences will make it possible to attract additional foreign investments and will contribute to the improvement of international image.
Прямоугольный треугольник встречается в реальности практически на каждом углу. Знание о свойствах данной фигуры, а также умение вычислять ее площадь, несомненно пригодится вам не только для решения задач по геометрии, но и в жизненных ситуациях.
Геометрия треугольника
В элементарной геометрии прямоугольный треугольник — это фигура, которая состоит из трех соединенных отрезков, формирующих три угла (два острых и один прямой). Прямоугольный треугольник — оригинальная фигура, характеризующаяся рядом важных свойств, которые составляют фундамент тригонометрии. В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:
- Гипотенуза — самая длинная сторона треугольника, лежащая напротив прямого угла.

- Катеты — отрезки, образующие прямой угол. В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют.
Именно соотношение катетов и гипотенузы составляет основу тригонометрии: синусы, тангенсы и секансы определяются как отношение сторон прямоугольного треугольника.
Прямоугольный треугольник в реальности
Данная фигура получила широкое распространение в реальности. Треугольники находят применение в проектировании и технике, поэтому расчет площади фигуры приходится выполнять инженерам, архитекторам и проектировщикам. Форму треугольника имеют основания тетраэдров или призм — трехмерных фигур, которые легко встретить в повседневности. Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.
Площадь треугольника
Площадь геометрической фигуры — это количественная оценка того, какая часть плоскости ограничена сторонами треугольника. Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:
где a – сторона треугольника, h – его высота.
Формула для вычисления площади прямоугольного треугольника еще проще:
где a и b – катеты.
Работая с нашим онлайн-калькулятор, вы можете вычислить площадь треугольника, используя три пары параметров:
- два катета;
- катет и прилежащий угол;
- катет и противолежащий угол.
В задачах или бытовых ситуациях вам будут даны разные комбинации переменных, поэтому такая форма калькулятора позволяет вычислить площадь треугольника несколькими способами. Рассмотрим пару примеров.
Примеры из реальной жизни
Керамическая плитка
Допустим, вы хотите выполнить облицовку стен кухни керамической плиткой, которая имеет форму прямоугольного треугольника. Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
Это означает, что площадь одного элемента составляет 24,5 квадратных сантиметра или 0,01805 квадратных метра. Зная эти параметры, вы можете подсчитать, что для отделки 7 квадратных метров стены вам понадобится 7/0,01805 = 387 элементов облицовочной плитки.
Школьная задача
Пусть в школьной задаче по геометрии требуется найти площадь прямоугольного треугольника, зная только то, что сторона одного катета равна 5 см, а величина противолежащего угла составляет 30 градусов. Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:
Таким образом, калькулятор не только вычисляет площадь заданного треугольника, но и определяет длину прилежащего катета и гипотенузы, а также величину второго угла.
Заключение
Прямоугольные треугольники встречаются в нашей жизни буквально на каждом углу. Определение площади таких фигур пригодится вам не только при решении школьных заданий по геометрии, но и повседневной и профессиональной деятельности.
Как найти площадь в прямоугольном. Как найти площадь прямоугольного треугольника необычным способом
Прямоугольный треугольник встречается в реальности практически на каждом углу. Знание о свойствах данной фигуры, а также умение вычислять ее площадь, несомненно пригодится вам не только для решения задач по геометрии, но и в жизненных ситуациях.
Геометрия треугольника
В элементарной геометрии прямоугольный треугольник — это фигура, которая состоит из трех соединенных отрезков, формирующих три угла (два острых и один прямой). Прямоугольный треугольник — оригинальная фигура, характеризующаяся рядом важных свойств, которые составляют фундамент тригонометрии. В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:
- Гипотенуза — самая длинная сторона треугольника, лежащая напротив прямого угла.

- Катеты — отрезки, образующие прямой угол. В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют.
Именно соотношение катетов и гипотенузы составляет основу тригонометрии: синусы, тангенсы и секансы определяются как отношение сторон прямоугольного треугольника.
Прямоугольный треугольник в реальности
Данная фигура получила широкое распространение в реальности. Треугольники находят применение в проектировании и технике, поэтому расчет площади фигуры приходится выполнять инженерам, архитекторам и проектировщикам. Форму треугольника имеют основания тетраэдров или призм — трехмерных фигур, которые легко встретить в повседневности. Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.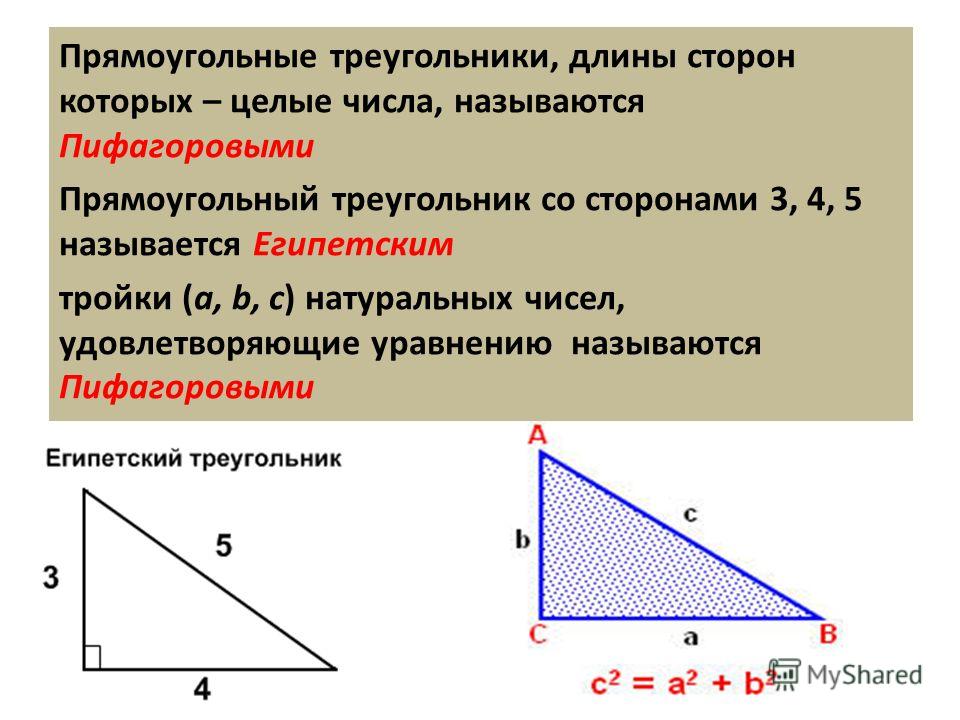
Площадь треугольника
Площадь геометрической фигуры — это количественная оценка того, какая часть плоскости ограничена сторонами треугольника. Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:
где a – сторона треугольника, h – его высота.
Формула для вычисления площади прямоугольного треугольника еще проще:
где a и b – катеты.
Работая с нашим онлайн-калькулятор, вы можете вычислить площадь треугольника, используя три пары параметров:
- два катета;
- катет и прилежащий угол;
- катет и противолежащий угол.
В задачах или бытовых ситуациях вам будут даны разные комбинации переменных, поэтому такая форма калькулятора позволяет вычислить площадь треугольника несколькими способами. Рассмотрим пару примеров.
Примеры из реальной жизни
Керамическая плитка
Допустим, вы хотите выполнить облицовку стен кухни керамической плиткой, которая имеет форму прямоугольного треугольника.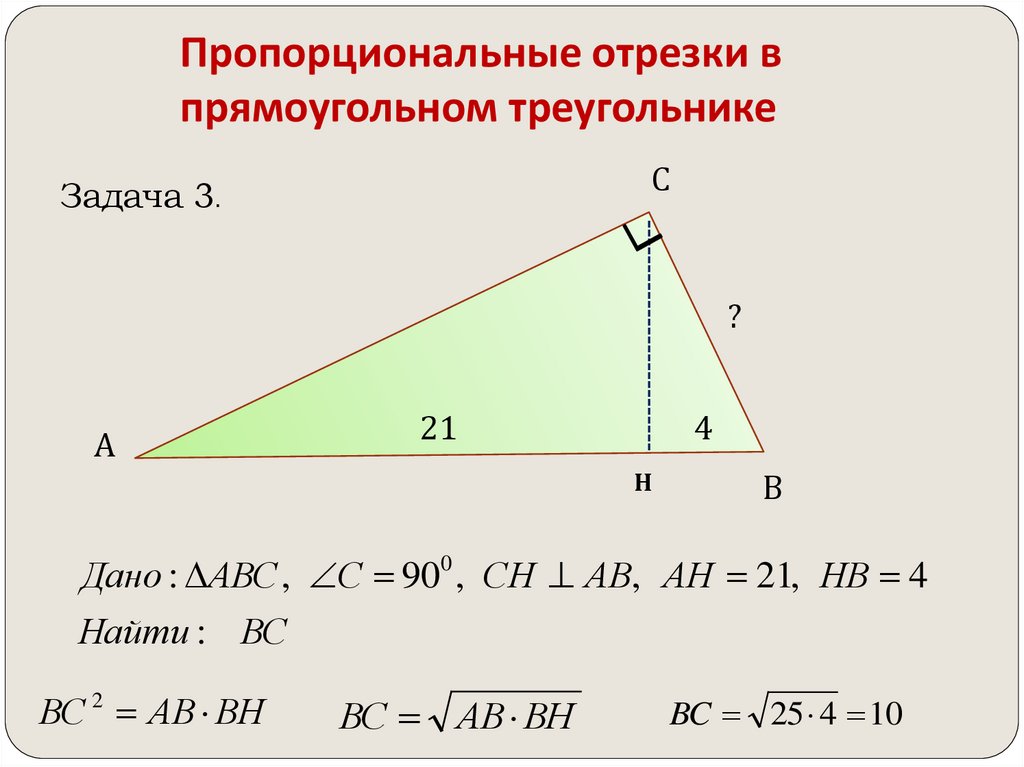 Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
Это означает, что площадь одного элемента составляет 24,5 квадратных сантиметра или 0,01805 квадратных метра. Зная эти параметры, вы можете подсчитать, что для отделки 7 квадратных метров стены вам понадобится 7/0,01805 = 387 элементов облицовочной плитки.
Школьная задача
Пусть в школьной задаче по геометрии требуется найти площадь прямоугольного треугольника, зная только то, что сторона одного катета равна 5 см, а величина противолежащего угла составляет 30 градусов. Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:
Таким образом, калькулятор не только вычисляет площадь заданного треугольника, но и определяет длину прилежащего катета и гипотенузы, а также величину второго угла.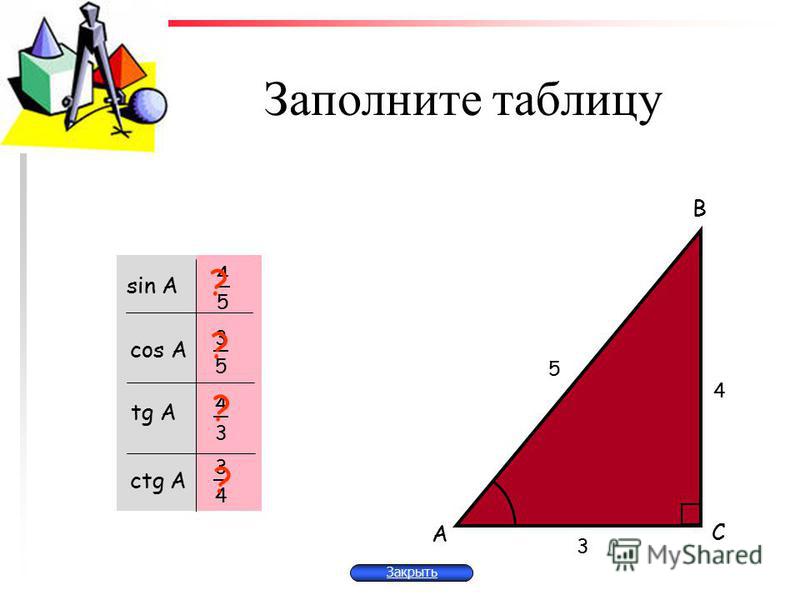
Заключение
Прямоугольные треугольники встречаются в нашей жизни буквально на каждом углу. Определение площади таких фигур пригодится вам не только при решении школьных заданий по геометрии, но и повседневной и профессиональной деятельности.
Треугольник – плоская геометрическая фигура с одним углом равным 90 °. При этом в геометрии очень часто требуется вычислить площадь такой фигуры. Как это сделать, мы расскажем далее.
Самая простая формула определения площади прямоугольного треугольника
Исходные данные, где: a и b – стороны треугольника, выходящие из прямого угла.
То есть, площадь равна половине произведения двух сторон, которые выходят из прямого угла. Конечно, существует формула Герона, используемая для вычисления площади обычного треугольника, но для определения величины необходимо знать длину трех сторон. Соответственно, вам придется рассчитать гипотенузу, а это лишнее время.
Найти площадь прямоугольного треугольника через формулу Герона
Это всем известная и исходная формула, но для этого вам придется посчитать гипотенузу по двум катетам, используя Теорему Пифагора.
В этой формуле: a, b, c – стороны треугольника, а p – полупериметр.
Найти площадь прямоугольного треугольника по гипотенузе и углу
Если в вашей задаче не известен ни один из катетов, то воспользоваться самым простым способом вы не сможете. Для определения величины вам нужно рассчитать длину катетов. Это сделать просто по гипотенузе и косинусу прилежащего угла.
b=c×cos(α)
Узнав длину одного из катетов, по теореме Пифагора вы сможете рассчитать вторую сторону, выходящую из прямого угла.
b 2 =c 2 -a 2
В этой формуле c и a – гипотенуза и катет соответственно. Теперь можете рассчитать площадь по первой формуле. Точно так же можно вычислить один из катетов, имея второй и угол. В таком случае одна из искомых сторон будет равна произведению катета на тангенс угла. Существуют и другие способы вычисления площади, но зная основные теоремы и правила, вы сможете легко найти искомую величину.
Если у вас нет ни одной из сторон треугольника, а имеется лишь медиана и один из углов, то вы сможете вычислить длину сторон. Для этого используйте свойства медианы делить прямоугольный треугольник на два. Соответственно, она может выступать гипотенузой, если выходит из острого угла. Воспользуйтесь теоремой Пифагора и определите длину сторон треугольника, выходящих из прямого угла.
Для этого используйте свойства медианы делить прямоугольный треугольник на два. Соответственно, она может выступать гипотенузой, если выходит из острого угла. Воспользуйтесь теоремой Пифагора и определите длину сторон треугольника, выходящих из прямого угла.
Как видите, зная основные формулы и Теорему Пифагора, вы сможете рассчитать площадь прямоугольного треугольника, имея лишь один из углов и длину одной из сторон.
В элементарной геометрии прямоугольным треугольником называется фигура, состоящая из трёх отрезков соединённых в точках, с углами два из которых острые, а один прямой (то есть равен 90°). Прямоугольный треугольник характеризуется целым рядом важных свойств, многие из которых составляют основу тригонометрии (например, соотношения между его сторонами и углами). Еще со школьной скамьи все мы знаем, как вычислить площадь прямоугольного треугольника , а в повседневной жизни встречаемся с этой геометрической фигурой достаточно часто, порой даже не замечая этого. Достаточно широкое применение находит она в технике и поэтому такую задачу, как , часто приходится решать инженерам, конструкторам и архитекторам.
Достаточно широкое применение находит она в технике и поэтому такую задачу, как , часто приходится решать инженерам, конструкторам и архитекторам.
Зодчим определять эту величину требуется тогда, когда они проектируют здания с фронтонами, которые являются завершением фасадов и имеют треугольную форму ограниченную карнизом, а по бокам – скатами крыши. Нередко угол между скатами бывает прямой, и в таких случаях фронтон имеет форму прямоугольного треугольника. Определять его площадь требуется по той простой причине, что необходимо точно знать количество строительного материала, необходимого для его обустройства. Следует заметить, что фронтоны являются обязательными элементами малоэтажных строений (загородных домов, коттеджей, дач).
Нахождение площади прямоугольного треугольника
a — катет
b — катет
S — площадь прямоугольного треугольника
Форму прямоугольного треугольника имеют многие детали, из которых изготавливается современная мебель.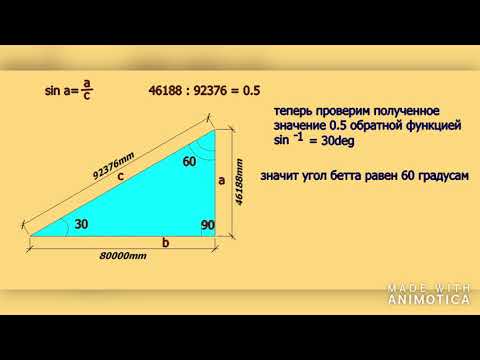 Как известно, для того чтобы наиболее рационально использовать площадь помещений, все элементы обстановки должны размещаться в ней оптимальным образом. С пользой задействовать такие зоны, как углы, можно с помощью столов треугольной формы, столешницы которых в большинстве случаев представляют собой прямоугольные треугольники с катетами, вплотную прилегающими к стенам. При проектировании и расчете этих элементов конструкторы мебельного производства применяют формулу, по которой нахождение площади прямоугольного треугольника осуществляется на основе длины его сторон. Кроме того, им нередко приходится разрабатывать конструкции столиков, крепящихся непосредственно к стенам, в состав которых входят опорные элементы, также представляющие собой прямоугольные треугольники .
Как известно, для того чтобы наиболее рационально использовать площадь помещений, все элементы обстановки должны размещаться в ней оптимальным образом. С пользой задействовать такие зоны, как углы, можно с помощью столов треугольной формы, столешницы которых в большинстве случаев представляют собой прямоугольные треугольники с катетами, вплотную прилегающими к стенам. При проектировании и расчете этих элементов конструкторы мебельного производства применяют формулу, по которой нахождение площади прямоугольного треугольника осуществляется на основе длины его сторон. Кроме того, им нередко приходится разрабатывать конструкции столиков, крепящихся непосредственно к стенам, в состав которых входят опорные элементы, также представляющие собой прямоугольные треугольники .
Строителям, занимающимся облицовочными работами, нередко в своей профессиональной деятельности приходится использовать керамическую плитку, имеющую форму прямоугольного треугольника с катетами одинаковой или различной длины.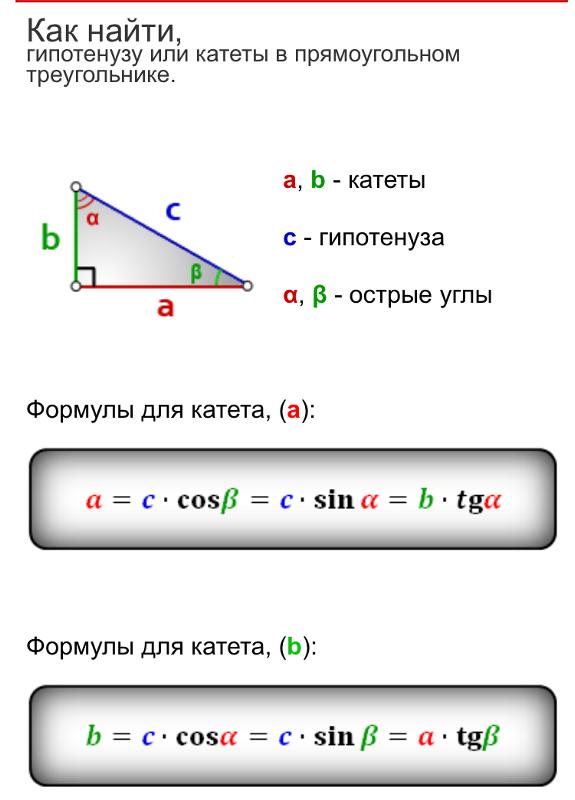 Им также приходится определять площадь этих элементов для того, чтобы выяснить необходимое их количество.
Им также приходится определять площадь этих элементов для того, чтобы выяснить необходимое их количество.
Форму прямоугольного треугольника имеет и такой важный и необходимый измерительный инструмент, как угольник. С его помощью производится построение и контроль прямых углов, а используется он очень широко и многими: от обычных школьников на уроках геометрии до конструкторов суперсовременной техники.
В зависимости от вида треугольника выделяют сразу несколько вариантов нахождения его площади. К примеру, для вычисления площади прямоугольного треугольника используется формула S= a * b / 2, где а и b — это его катеты. Если же требуется узнать площадь равнобедренного треугольника, то необходимо делить на два произведение его основания и высоты. То есть, S= b*h / 2, где b – это основание треугольника, а h – его высота.
Далее, может понадобиться расчет площади равнобедренного прямоугольного треугольника. Здесь приходит на помощь следующая формула: S= a* а / 2, где катеты «а» и «а» – обязательно должны быть с одинаковыми значениями.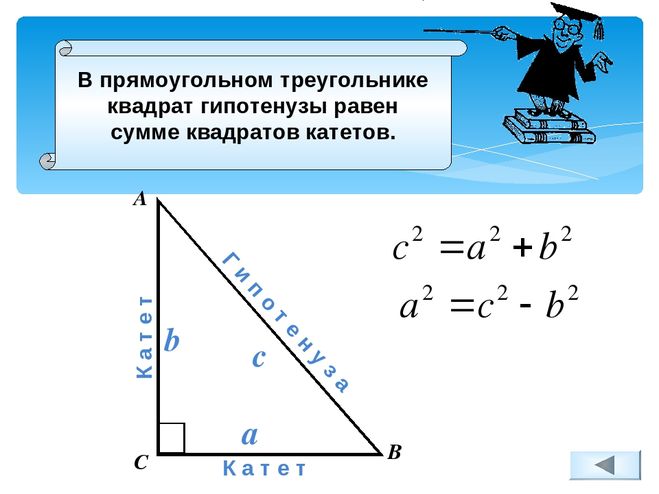 2) высчитываем длину неизвестного катета, затем используем ее для расчета площади треугольника.
2) высчитываем длину неизвестного катета, затем используем ее для расчета площади треугольника.
Как находить площадь равнобедренного треугольника
Площадь равнобедренного треугольника можно очень легко и быстро найти по формуле S= b*h / 2, но, при отсутствии одного из показателей, задача значительно усложняется. Ведь необходимо выполнять дополнительные действия.
Возможные варианты задач:
- Дано: длина одной из боковых сторон и длина основания. Находим через теорему Пифагора высоту, то есть длину второго катеты. При условии, что длина основания, разделенная на два, является катетом, а изначально известная боковая сторона – гипотенузой.

- Дано: основание и угол между боковой стороной и основанием. Вычисляем по формуле h=c*ctg(B)/2 высоту (не забываем сторону «c» разделить на два).
- Дано: высота и угол, который был образован основанием и боковой стороной: применяем формулу c=h*tg(B)*2 для нахождения высоты, и полученный результат умножаем на два. Далее вычисляем площадь.
- Известна: длина боковой стороны и угол, который образовался между ним и высотой. Решение: используем формулы — c=a*sin(C)*2 и h=a*cos(C) для нахождения основания и высоты, после чего считаем площадь.
Как найти площадь равнобедренного прямоугольного треугольника
Если все данные известны, то по стандартной формуле S= a* a / 2 вычисляем площадь равнобедренного прямоугольного треугольника, если же в задаче не указаны некоторые показатели, то выполняются дополнительные действия.
Например: нам не известны длины обеих сторон (мы помним, что в равнобедренном прямоугольном треугольнике они равны), но дана длинна гипотенузы.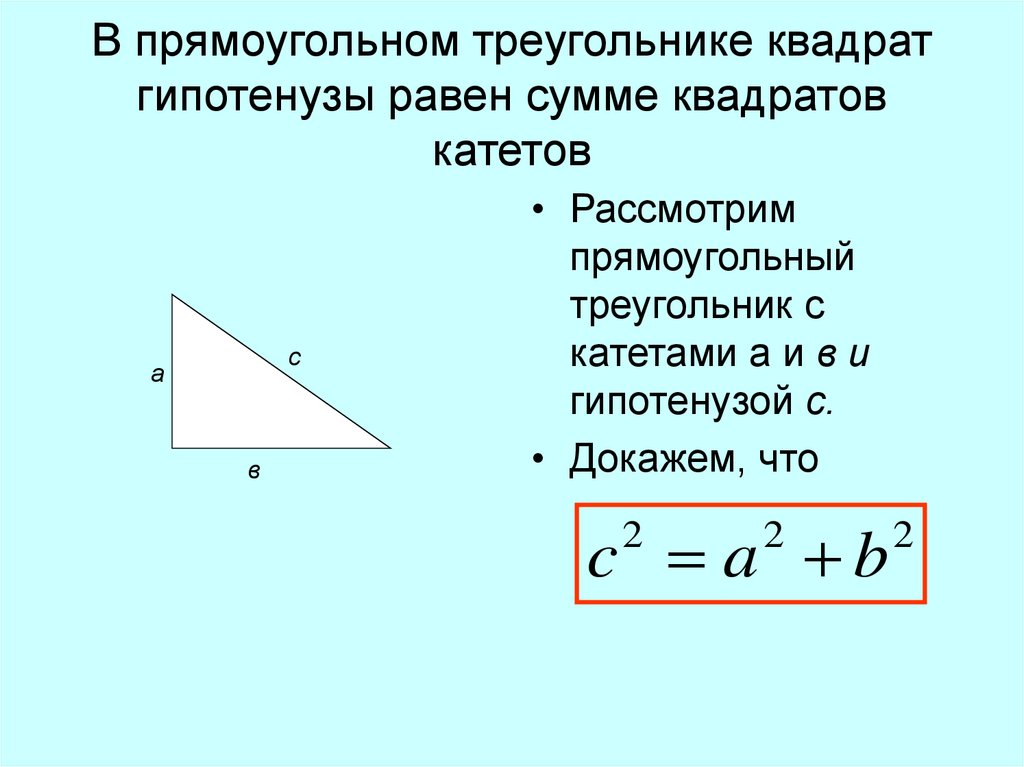 2, где R — радиус окружности.
2, где R — радиус окружности.
Вычислить прямоугольный треугольник
Треугольник ﹣ Прямоугольный треугольник
Прямоугольный треугольник — это особый тип треугольника по сравнению с обычными треугольниками, потому что, как следует из названия, он имеет прямой угол или угол в 90 градусов. В следующем разделе мы будем использовать примеры для расчета всех важных значений прямоугольного треугольника с использованием специальных формул и правил расчета для прямоугольных треугольников.
На странице нашего Калькулятора треугольников вы найдете много информации о расчете не только прямоугольных, но и обычных треугольников. Кроме того, посетите наши руководства по темам «Площадь треугольника» и «Равносторонние треугольники».
Содержание
- Определения и термины в прямоугольном треугольнике
- Введение в расчет прямоугольных треугольников
- Пример расчета прямоугольного треугольника.

- Расчет площади
- Вычисление недостающей стороны
- Расчет периметра
- Расчет недостающих углов
- Расчет высоты
- Графическое изображение прямоугольного треугольника
Калькулятор ↑Содержание ↑
Прежде чем мы углубимся в вычисления прямоугольных треугольников более подробно, вот краткое определение и описание специальных терминов в прямоугольном треугольнике.
Треугольник определяется тремя точками на плоскости, которые не лежат на одной прямой. Эти три точки являются углами треугольника. Каждая соединительная линия между двумя углами является стороной треугольника. Таким образом, на плоскости треугольник ограничивает поверхность.
Прямоугольный треугольник отличается от обычного треугольника тем, что один из трех углов является прямым, т.е.Угол 0 градусов. На приведенном здесь рисунке прямой угол виден в вершине угла C. Он обозначается третьей греческой буквой γ (гамма), а углы в углу A обозначаются буквой α (альфа), а в углу b буквой β (бета).
Как обычно, углы отмечены по часовой стрелке заглавными буквами A, B и C, а стороны, противоположные углам, отмечены соответствующими строчными буквами a, b и c.
Что такое катеты?
В прямоугольном треугольнике две стороны, образующие прямой угол, называются катетами. Поскольку прямой угол на иллюстрации находится в углу C, т. Е. γ, катеты — это две стороны a и b, которые его окружают.
Что такое прилежащий и противоположный катеты?
В зависимости от рассматриваемого угла два катета также называются смежным и противоположным катетами. Если мы посмотрим на непрямой угол α в углу A на иллюстрации, сторона b является смежным катетом с a (лежит и угол α, который необходимо исследовать). Второй катет а, лежащий на против угла α, противоположен катету а. Если, с другой стороны, мы посмотрим на второй непрямоугольный угол β в углу B, более точное обозначение двух катетов изменится на противоположное: катет, смежный с β, будет a, а катет, противоположный β, будет противоположным катету b. .
.
Что такое гипотенуза?
В то время как катет — две стороны прямого угла в прямоугольном треугольнике, а гипотенуза — сторона, противоположная прямому углу. Если прямой угол находится в точке C, как показано на рисунке, противолежащая сторона c является гипотенузой. Поскольку прямой угол всегда является наибольшим углом в прямоугольном треугольнике, гипотенуза также всегда является самой длинной стороной в прямоугольном треугольнике.
Калькулятор ↑Содержание ↑
Вообще однозначно определить треугольник можно, между прочим, именно тогда, когда известны угол и две прилежащие к нему стороны. Поэтому для вычисления прямоугольного треугольника достаточно, если известны только два катета, т. е. стороны, заключающие в себе прямой угол.
Но сам прямой угол также гарантирует, что некоторые формулы и методы расчета для расчета прямоугольных треугольников намного проще, чем в общем треугольнике. Например, на рисунке выше высота стороны а точно равна длине стороны b и наоборот. Это означает, что высота одной стороны равна длине другой стороны. Однако в общем треугольнике для вычисления этих высот необходимо использовать тригонометрические функции.
Это означает, что высота одной стороны равна длине другой стороны. Однако в общем треугольнике для вычисления этих высот необходимо использовать тригонометрические функции.
Калькулятор ↑Содержание ↑
В следующем примере мы покажем вам, как вычислить прямоугольный треугольник, если известны два катета. Используя эти два заданных значения, теперь можно четко шаг за шагом определить другие свойства прямоугольного треугольника.
Пример
Дан катет a = 4 в и катет b = 5 в . Так как треугольник прямоугольный, то угол ? уже известно, что 90 градусов.
Объяснение
Недостающая сторона c, периметр и площадь прямоугольного треугольника, оставшиеся два угла ? и ?, а также высоты всех трех сторон прямоугольного треугольника.
Вы можете изменить эти значения в Калькуляторе прямоугольного треугольника, выбрав «Два катета для прямоугольного треугольника» в разделе «Какие значения даны?» Затем калькулятор вычисляет — как и в следующих вычислениях — все значения, искомые для треугольника, а также выводит графический результат рассчитанного треугольника.
Калькулятор ↑Содержание ↑
В прямоугольном треугольнике два известных катета (здесь a и b) образуют прямой угол. Следовательно, формула
Формула площади прямоугольного треугольника
А = ½ × а × b
Вставка существующих значений для катетов
Если вы вставите значения для катетов, вы получите
А = ½ × 4 × 5 = 10 дюймов²
Решение
Площадь A прямоугольного треугольника равна 10 кв. дюймов.
Из-за прямого угла между двумя известными сторонами используемая формула является упрощением формулы площади для общих треугольников, которая здесь в калькуляторе используется в разделе «Две стороны с прилежащим углом».
Формулу площади для прямоугольного треугольника можно проиллюстрировать, скопировав прямоугольный треугольник и поместив два треугольника вместе на их самой длинной стороне, гипотенузе, так, чтобы образовался прямоугольник. Этот прямоугольник имеет площадь a × b (катетус a, умноженный на катет b). Таким образом, перед дублированием треугольник имеет ровно половину площади, т. е. ½ × a × b.
Таким образом, перед дублированием треугольник имеет ровно половину площади, т. е. ½ × a × b.
Калькулятор ↑Содержание ↑
При заданных величинах для двух катетов a и b и для прямого угла ? длину пока неизвестной третьей стороны c, т. е. гипотенузу, можно вычислить с помощью Теорема Пифагора . .
Формула: теорема Пифагора
а² + b² = с²
при преобразовании в c
с = а² + b²
Вставка существующих значений
Подставляя значения для катетов a = 4 и b = 5, мы получаем
с = 4² + 5² ≈ 6,4
Раствор
Гипотенуза, то есть отсутствующая третья сторона c, имеет длину около 6,4 дюйма.
Калькулятор ↑Содержание ↑
Используя заданные длины двух катетов, сторон a и b, а также вычисленную за это время длину гипотенузы, т. е. стороны c, можно определить периметр треугольника следующим образом:
Формула: Периметр P прямоугольного треугольника
Периметр каждого треугольника равен сумме длин всех трех сторон a, b и c.
Р = а + б + с
Вставка существующих значений
Подставляя заданные значения a = 4 и b = 5 и уже рассчитанное значение c = 6,4, получаем
U = 4 + 6 + 6,4 = 16,4
Раствор
Периметр прямоугольного треугольника равен 16,4 см.
Калькулятор ↑Содержание ↑
Расчет угла α
Во-первых, мы вычисляем угол ?: Два известных катета — это стороны a и b. Угол ? находится на катете b и напротив катета a треугольника. Значит, примыкающая сторона b = 5 дм, а противолежащая сторона а = 4 дм.
Формула для вычисления угла α в прямоугольном треугольнике
tan α = противоположный катет α / соседний α = a / b
Если преобразовать формулу в α, получится функция, обратная тангенсу, арктангенс (arctan)
α = арктангенс (а/б)
Вставка существующих значений
Подставляя значения для противоположного катета a = 4 и соседнего катета b = 5, получаем
α = арктангенс (4/5) = 0,67474 рад
Промежуточный раствор
Угол треугольника α равен 0,67474 рад.
Здесь мы сначала вычислили радиан угла ?, сокращенно «рад». С помощью калькулятора результат тоже можно сразу перевести в градусы. В этом случае выполняем преобразование пошагово: Радиан переводится в градусы по формуле
Формула: Преобразование радианов в градусы
α° = α рад × 180 / π
Если подставить промежуточный результат α рад, то получится
α° = 0,67474 рад × 180/3,14 ≈ 38,66°
Раствор
Угол треугольника α равен 38,66°.
Расчет угла β
Теперь, когда угол α вычислен и прямой угол γ равен 90°, все равно задан, можно вычислить оставшийся угол β. Для этого можно использовать сумму углов .
Формула: теорема о сумме углов
Сумма трех внутренних углов α, β и γ в треугольнике всегда равна 180 градусам.
α° + β° + γ° = 180°
Если преобразовать теорему о сумме углов в β, то получится
β° = 180° − α° − γ°
Вставка существующих значений
Если подставить уже вычисленный угол для α, а также заданный угол γ, то получится
β° = 180° − 38,66° − 90° = 51,34°
Решение
Угол треугольника β равен 51,34°.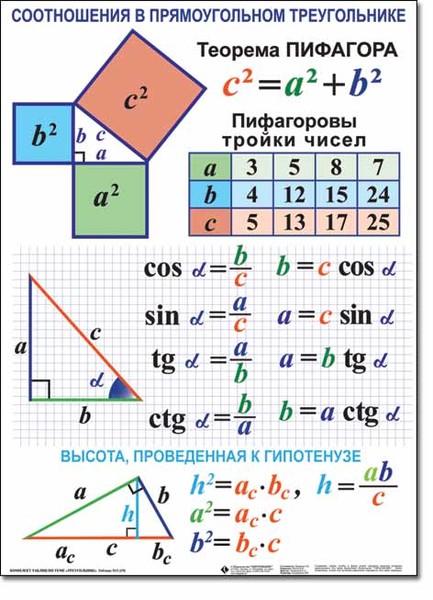
Калькулятор ↑Содержание ↑
Высота a и b
В прямоугольном треугольнике высота стороны а в точности равна длине другой стороны, т. е. стороны b. Это связано с тем, что сторона b, как сторона, находится под прямым углом, т. е. перпендикулярна а, и ведет к точке А треугольника, противоположной стороне а.
Аналогично, высота катета b равна длине a.
Формула высоты a в прямоугольном треугольнике
Высота катета a равна длине второго катета b.
ч а = б
Формула высоты b в прямоугольном треугольнике
Высота катета b равна длине второго катета a
ч б = а
Раствор
Высота a, т. е. h a составляет 5 дюймов, а высота b равна 4 в
Высота c
Теперь для вычисления высоты гипотенузы c можно использовать следующую формулу:
Формула высоты гипотенузы с в прямоугольном треугольнике
ч с = а × sin β
Вставка существующих значений
подставляя известные значения для a = 4 дюйма и для β = 51,34°, получаем
ч с = 4 × sin 51,34° ≈ 3,12
Раствор
Высота до c, т.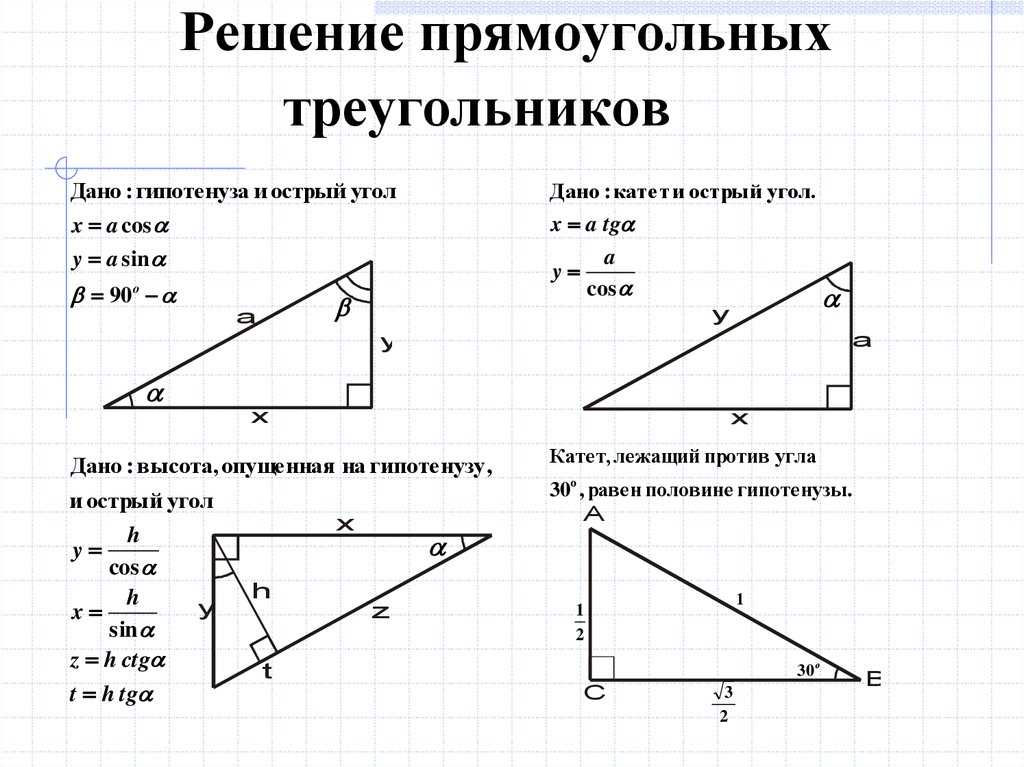 е. h c равна 3,12 дюйма.
е. h c равна 3,12 дюйма.
Калькулятор ↑Содержание ↑
Вычисленный таким образом прямоугольный треугольник с заданными сторонами a = 4 в и b = 5 в можно нарисовать, используя все расчетные значения следующим образом:
Графический результат
1 квадрат равен 0,5 единицы (как показано в учебнике по арифметике)
Что читали другие читатели
Другие онлайн-калькуляторы
Вычисление круга, Калькулятор дробей, Конвертер единиц времени, Калькулятор, Преобразование единиц длины, Преобразование римских цифр
Оцените нашу статью
одним кликом
(левая звезда очень плохая — правая звезда хорошая)
5,0 звезды в 1 рейтинги 5 1 Вычислить прямоугольный треугольник
ГлавнаяРуководстваМатематикаКалькулятор треугольникаРуководства
Калькулятор формул для уравнений прямоугольного треугольника
Изменить уравнение
Выберите, чтобы найти другое неизвестное
Разносторонний треугольник:
Нет сторон одинаковой длины
Нет равных углов
Уравнения разностороннего треугольника
Эти уравнения применимы к любому типу треугольника.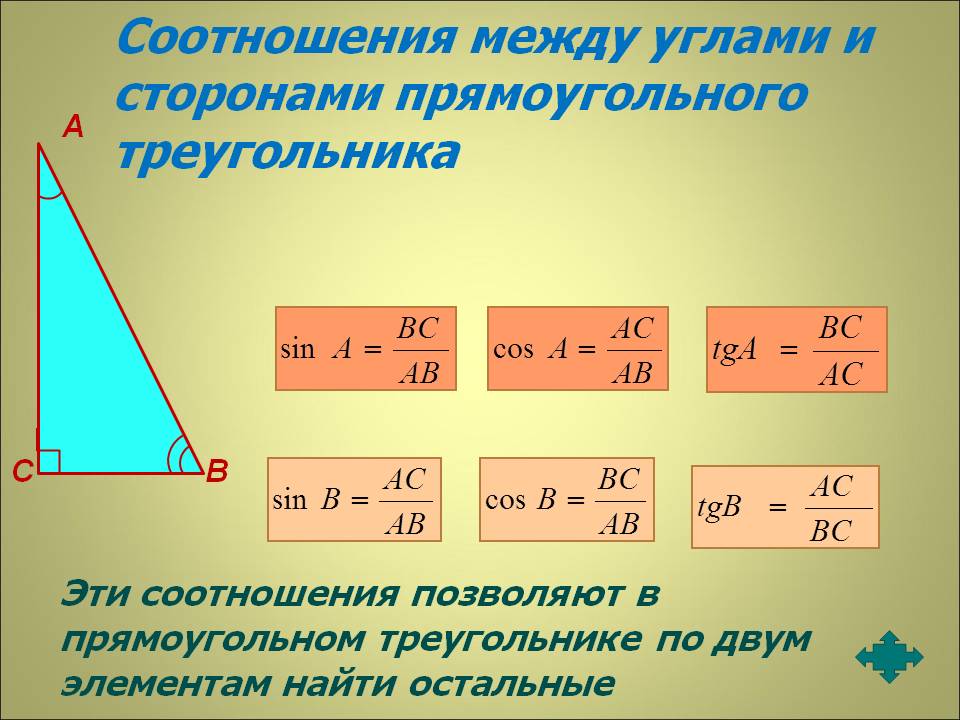 Уменьшено
Уменьшено
уравнения для равностороннего, прямого и равнобедренного треугольников приведены ниже.
| Perimeter | |
| Semiperimeter | |
| Area | |
| Area | |
| Base | |
| Height | |
| Angle Bisector стороны a | |
| Биссектриса стороны b | |
| Angle Bisector of side c | |
| Median of side a | |
| Median of side b | |
| Median of side c | |
| Altitude of side a | |
| Высота стороны b | |
| Высота стороны c | |
| Радиус описанной окружности | |
| Inscribed Circle Radius |
Law of Cosines
| length of side a | |
| angle of A |
Equilateral Triangle:
All three sides have equal length
All three angles равны 60 градусам
Уравнения равностороннего треугольника
| Периметр | |
| Полупериметр | |
| Area | |
| Altitude | |
| Median | |
| Angle Bisector | |
| Circumscribed Circle Radius | |
| Inscribed Circle Radius |
Right Треугольник:
Один угол равен 90 градусам
Уравнения прямоугольного треугольника
| Теорема Пифагора | |
| Perimeter | |
| Semiperimeter | |
| Area | |
| Altitude of a | |
| Altitude of b | |
| Altitude of c | |
| Биссектриса угла a | |
| Биссектриса угла b | |
| Биссектриса угла c | |
| Median of a | |
| Median of b | |
| Median of c | |
| Inscribed Circle Radius | |
| Circumscribed Circle Radius |
Isosceles Треугольник:
Две стороны имеют одинаковую длину
Два угла равны
Уравнения равнобедренного треугольника
| Периметр | |
| Semiperimeter | |
| Area | |
| Altitudes of sides a and c | |
| Altitude of side b | |
| Median of sides a and c | |
| Медиана стороны b | |
| Биссектриса угла сторон a и c | |
| Биссектриса угла стороны b | |
| Circumscribed Circle Radius | |
| Inscribed Circle Radius |
Where
| P | = | Perimeter |
| s | = | Semiperimeter |
| a | = | Длина стороны a |
| b | = | Длина стороны b |
| c | = | Длина стороны c |
| h | = | Altitude |
| m | = | Median |
| A | = | Angle A |
| B | = | Angle B |
| C | = | Угол C |
| T | = | Угол бисектор |
| R | = | |
| R | = | |
| R | = | |
| R | = | |