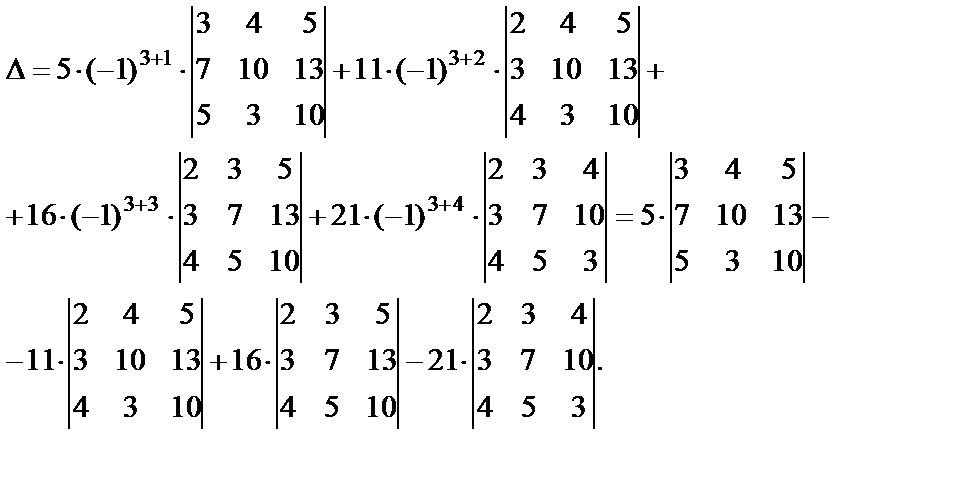Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2.
4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.
1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.
The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов.
Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson.
Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1.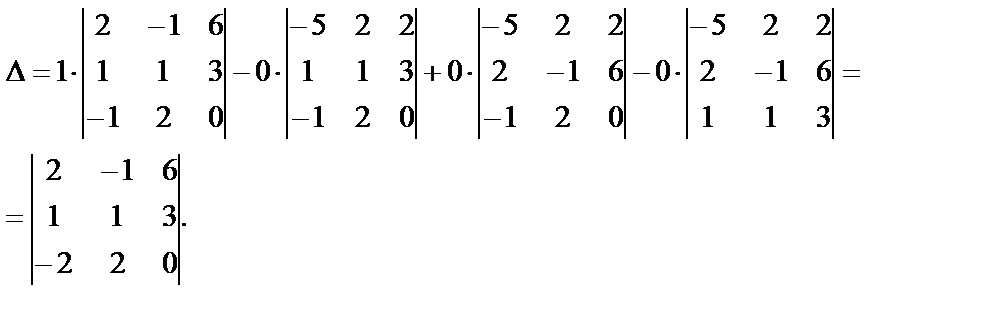
Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.
1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.
4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2.
Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2.
Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2).
Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)2.4. Вычисление определителей
Основным приемом вычисления определителя го порядка является сведение его к определителям более низкого порядка с помощью формул разложения. При этом полезен учет свойств определителя, позволяющий существенно уменьшить объем вычислений.
Пример 1. Вычислить определитель
Разложим определитель по первому столбцу. Получим
.
Таким образом, вычисление определителя
четвертого порядка свелось к вычислению
четырех определителей третьего порядка.
Далее, разлагая определители третьего
порядка по первому столбцу, получим
и т.д. Окончательно получим .
Вычисления значительно упростятся, если воспользоваться свойствами определителя. По свойству 7 можно, не меняя значения определителя, прибавить второй, третий и четвертый столбцы к первому, а затем первую строку вычесть из второй, третьей и четвертой. Получим
Пример 2. Вычислить определитель треугольной матрицы го порядка
.
Для вычисления разложим определитель по последней строке. Получим, что , где треугольный определитель порядка . Определитель снова разложим по последней строке и т.д. Продолжая аналогичные рассуждения, получим что .
Пример 3. Вычислить определитель матрицы го порядка
.
Подобные определители можно достаточно
просто преобразовать к треугольному
виду. Для этого прибавим все столбцы к
первому и затем вычтем первую строку
из всех остальных.
Получим
Пример 4. Следующий метод вычисления определителей го порядка называется методом рекуррентных соотношений. Этот метод заключается в том, что данный определитель выражают, преобразуя его и раскладывая по строке или столбцу, через определители того же вида, но более низкого порядка. Полученное равенство называется рекуррентным соотношением.
Рассмотрим идею метода на примере вычисления определителя трехдиагональной матрицы или матрицы Якоби (матрицей Якоби называется матрица , если из следует ). Вычисление определителей матриц Якоби часто приводит к рекуррентному соотношению вида
,
где и постоянные числа. Для нахождения необходимо решить полученное уравнение. Заменим соответствующей степенью переменной
.
Перенося все слагаемые в левую часть и
сокращая на
,
получим квадратное уравнение
,
называемое характеристическим уравнением.
Пусть
корни
этого уравнения.
Тогда возможны два
случая: и
.
Если , то определитель имеет вид
,
где числа находятся из условий
.
Определители и в левых частях условий вычисляются непосредственно из вида .
Если , то
,
а числа находятся из условий
.
Рассмотрим конкретный пример. Вычислим определитель го порядка
, .
Разложим определитель по последнему столбцу
.
Первый определитель в правой части является определителем порядка того же типа, что и . Второй определитель разложим еще раз по последней строке. Минор, дополнительный к ненулевому элементу в последней строке, вновь представляет собой определитель того же типа, что и , но порядка . В итоге получим рекуррентное соотношение для
.
Соответствующее характеристическое уравнение
имеет корни и
.
Так как
,
то и
.
Из вида находим
.
Тогда для определения получим систему уравнений
решая которую, находим
(при решении использовались равенства: ). Тогда
.
Пример 5. Вычислить определитель го порядка
.
Представим элементы последнего столбца в виде суммы двух слагаемых: . Тогда по свойству 3. определитель представится в виде суммы двух определителей
.
Первый определитель разложим по последнему столбцу. Второй определитель приведем к треугольному виду, вычитая последний столбец из всех остальных. Тогда
(1)
где является определителем порядка того же типа, что и .
Решим полученное уравнение для . Из вида при имеем.Выписывая (1) при с учетом равенства для , получаем
.
Методом математической индукции теперь
нетрудно показать, что
.
Пример 6. Вычислить определитель го порядка
.
Представим элементы последнего столбца в виде суммы двух слагаемых: и распишем определитель как сумму двух определителей
.
Первый определитель разложим по последнему столбцу. Для вычисления второго определителя умножим последний столбец на и вычтем из остальных. Получим
Для решения полученного рекуррентного соотношения воспользуемся тем, что при транспонировании матрицы ее определитель не меняется. В нашем случае транспонировании приводит к замене на наоборот. Поэтому имеем два равенства
Откуда .
Пример 7. Следующий пример иллюстрирует применение теоремы Лапласа. Нужно вычислить определитель квазитреугольной матрицы порядка . Квазитреугольной называют блочную матрицу вида , где квадратные матрицы, прямоугольная матрица, нулевая матрица. В подробной записи матрица имеет вид
.
Пусть . Покажем, что . Воспользуемся теоремой Лапласа. Разложим этот определитель по первым строкам. Очевидно, что из первых строк можно составить только один минор го порядка не содержащий нулевого столбца, у которого номера выделяемых столбцов удовлетворяют условию . Этот минор есть . Дополнительным к нему минором является определитель , что и доказывает формулу.
линейная алгебра — определитель Вандермонда для порядка 4
Задавать вопрос
спросил
Изменено 8 лет, 8 месяцев назад
Просмотрено 1к раз
$\begingroup$
93 \end{pmatrix} = (x_4 — x_3)(x_4 — x_2)(x_4 — x_1)(x_3 — x_2)(x_3 — x_2)(x_2 — x_1)$.
2 \end{pmatrix}:=V_3$$
поэтому по простой индукции имеем
$$\лямбда=(x_2-x_3)(x_2-x_4)(x_3-x_4)$$
$\endgroup$
$\begingroup$
Вы можете использовать серию элементарных операций со строками: $-x_1R_3+R_4$, $-x_1R_2+R_3$, $-x_1R_1-R_2$, чтобы получить матрицу, эквивалентную строке $V_4$. Поскольку это элементарные операции типа 3, определитель этой матрицы такой же, как у $V_4$, и вычислить ее определитель проще.
$\endgroup$
$\begingroup$
Подсказка: 92(х_3-х_4)&0 \end{pmatrix},$$ который легче обрабатывать (расширить по последнему столбцу, вынести $(x_1-x_4)(x_2-x_4)(x_3-x_4)$, и мы должны вычислить $V_3$).
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
▷ Как найти определитель матрицы 4×4 (практика)
Мы объясним, как найти определитель матрицы 4×4 на примере.
Кроме того, вы найдете решенные упражнения, чтобы вы могли попрактиковаться и в совершенстве понять, как вычислить определитель матрицы 4 × 4.
Содержание
Как найти определитель матрицы 4×4, используя операции со строками и расширение кофактора
Давайте посмотрим, как вычислить определитель матрицы 4×4, решив пример:
Первым шагом в вычислении определителя матрицы 4×4 является обнуление всех элементов столбца, кроме одного с помощью элементарной операции со строками .
Мы можем выполнять элементарные операции со строками благодаря свойствам определителей.
В этом случае в первом столбце уже есть ноль. Таким образом, мы собираемся преобразовать все записи в первом столбце в 0, кроме числа 1 (поскольку легче выполнять вычисления со строкой, в которой есть 1). Для этого мы прибавляем первую строку ко второй строке и вычитаем первую строку, умноженную на 2, из четвертой строки:
После того, как мы преобразовали в 0 все элементы, кроме одного из выбранного столбца, мы вычисляем определитель матрицы 4×4, используя расширение кофактора .
Расширение кофакторов — это метод нахождения определителей, который состоит в сложении произведений элементов столбца на их соответствующие кофакторы .
Является кофактором i, j матрицы, определяемой формулой:
Где M ij — минор i, j матрицы, то есть определитель, полученный в результате удаления i-й строки и j -й столбец матрицы.
Итак, мы складываем произведения элементов в первом столбце по их соответствующим кофакторам:
Члены, умноженные на 0, сокращаются, поэтому мы упрощаем их:
Итак, мы должны вычислить кофактор первой строки и первого столбца, то есть (-1), возведенное в 1+1 (1-я строка и 1-й столбец), умноженное на определитель, полученный в результате удаления первой строки и первого столбца матрицы 4×4.
И, наконец, нам просто нужно найти определитель матрицы 3×3:
Итак, мы решили определитель матрицы 4×4, используя операции со строками и разложение на кофакторы.
Практические задачи на нахождение определителя матрицы 4×4
Задача 1
Найдите определитель следующей квадратной матрицы порядка 4:
См. решение
Найдем определитель 4 Матрица × 4 с методом расширения кофактора, также называемым расширением Лапласа. Но сначала проделаем элементарные операции со строками, чтобы обнулить все элементы столбца, кроме одного:
, и теперь мы рассчитываем детерминант 4 × 4, используя расширение кофактора:
Мы упрощаем Условия:
и, наконец, мы выполняем кофактор:
Проблем определитель следующей матрицы 4×4:
См. решение
Определитель определителя 4×4 вычислим по формуле кофактора. Но сначала проделываем элементарные операции со строками, чтобы преобразовать все элементы столбца, кроме единицы, в ноль:
Теперь решаем определитель числа 4×4 путем разложения на сомножители:
Упрощаем условия:
И вычисляем сомножители третьей строки и второго столбца:
2
Задача 3
Вычислите определитель следующей матрицы 4×4:
См.