Формула периметра параллелограмма через биссектрису: 375 Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.

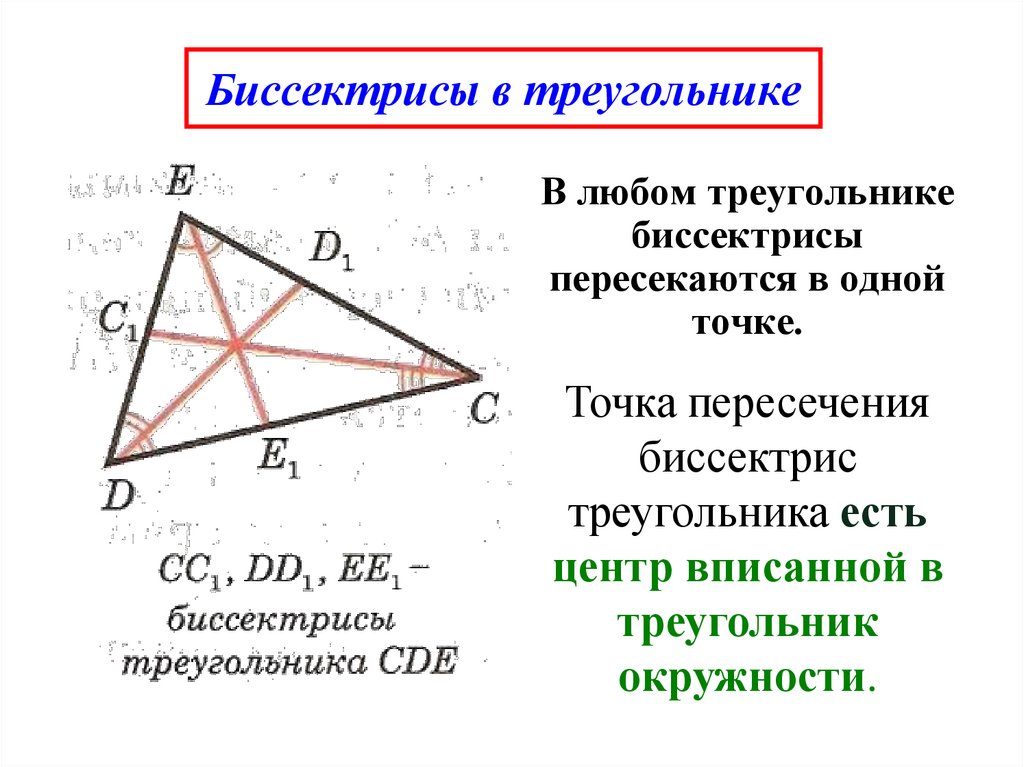
Свойства биссектрис параллелограмма (геометрия, 8-й класс)

• Сухарева Ирина Георгиевна, Учитель математики

Разделы: Математика, Мастер-класс

Класс: 8

---

Цель: доказать свойства биссектрис параллелограмма и рассмотреть их применение к решению задач.

Презентация к уроку

I. Повторение (устно)

1. Сформулируйте определение параллелограмма.

2. Сформулируйте свойства параллелограмма.

3. Сформулируйте признаки параллелограмма.

4. Сформулируйте свойства параллельных прямых.

5. Решите задачу:

Дано: a || b , МЕ – секущая, МО и ЕО – биссектрисы. Найти: MOE.

6. Решите задачу:   

Дано: ABCD – параллелограмм, AK – биссектриса, AKB = 15^o. Найти: BAD.

II. Изучение нового материала

Учащиеся самостоятельно по парам решают задачи на доказательство (3-5 мин) с последующей проверкой на доске и формулируют свойства биссектрис параллелограмма (каждый ряд решает по одной задаче). Оформление доказательств к задачам записывает учитель на доске под диктовку учеников.

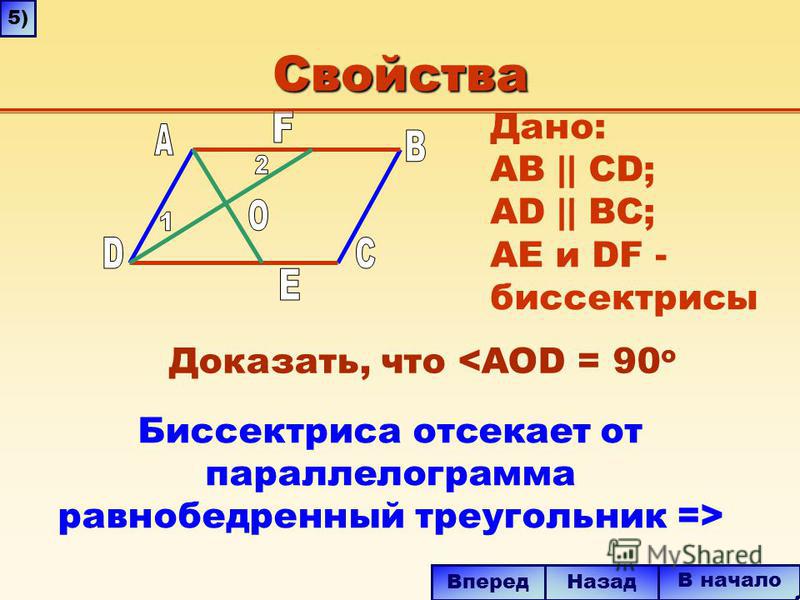
Задача № 1. Биссектриса угла параллелограмма пересекает противоположную сторону. Определите вид полученного треугольника.

Задача № 2. Найдите угол образованный биссектрисами углов параллелограмма, прилежащих к одной стороне.

Задача № 3. Определите взаимное расположение прямых на которых лежат биссектрисы противоположных углов.

Свойства биссектрис параллелограмма:

1). Биссектриса параллелограмма отсекает от него равнобедренный треугольник.

2). Биссектрисы углов параллелограмма, прилежащих к одной стороне, перпендикулярны.

3). Биссектрисы противоположных углов параллелограмма параллельны или лежат на одной прямой.

III. Закрепление изученного материала

Учащиеся решают задачи на применение свойств биссектрис параллелограмма. (Тексты задач и чертежи к ним выдаются каждому ученику.) Оформление решений к задачам записывают  ученики на доске.

1. Биссектрисы углов А и B параллелограмма ABCD пересекаются в точке K. Найдите длину BK, если B = 120 ^o,  AB = 19 см.
2. Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке, лежащей на стороне ВС. Найдите периметр параллелограмма, если ВС = 34 см.
3. Впараллелограмме ABCD биссектрисы углов В и D пересекают диагональ АС в точках К и Р соответственно. Доказать, что четырёхугольник  BРDК —  параллелограмм.
4. Докажите, что при пересечении биссектрис параллелограмма образуется прямоугольник.

IV. Итог урока (ученики формулируют изученные свойства)

V. Домашнее задание

Конспект (свойства биссектрис параллелограмма), задачи:

1. Дано: TPLK – параллелограмм, РТ = РL, TF – биссектриса LTK, TFL= 120^o. Найти углы параллелограмма.

2. Дано: ABCD – параллелограмм, AM  – биссектриса BAD,  AM : MC = 5 : 3,  P_OBC > P_OCD на 6 см. Найти стороны и периметр параллелограмма.

Приложения к уроку.

Раздаточный материал.

СВОЙСТВА БИССЕКТРИС ПАРАЛЛЕЛОГРАММА

Задача № 1. Биссектриса угла параллелограмма пересекает противоположную сторону. Определите вид полученного треугольника.

Свойство 1.

Задача № 2.Найдите угол образованный биссектрисами углов параллелограмма, прилежащих к одной стороне.

Свойство 2.

Задача № 3.Определите взаимное расположение прямых на которых лежат биссектрисы противоположных углов.

Свойство 3.

ПРИМЕНЕНИЕ СВОЙСТВ БИССЕКТРИС ПАРАЛЛЕЛОГРАММА

Биссектрисы углов А и B параллелограмма ABCD пересекаются в точке K. Найдите длину BK, если B,  AB = 19 см.

Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке, лежащей на стороне ВС.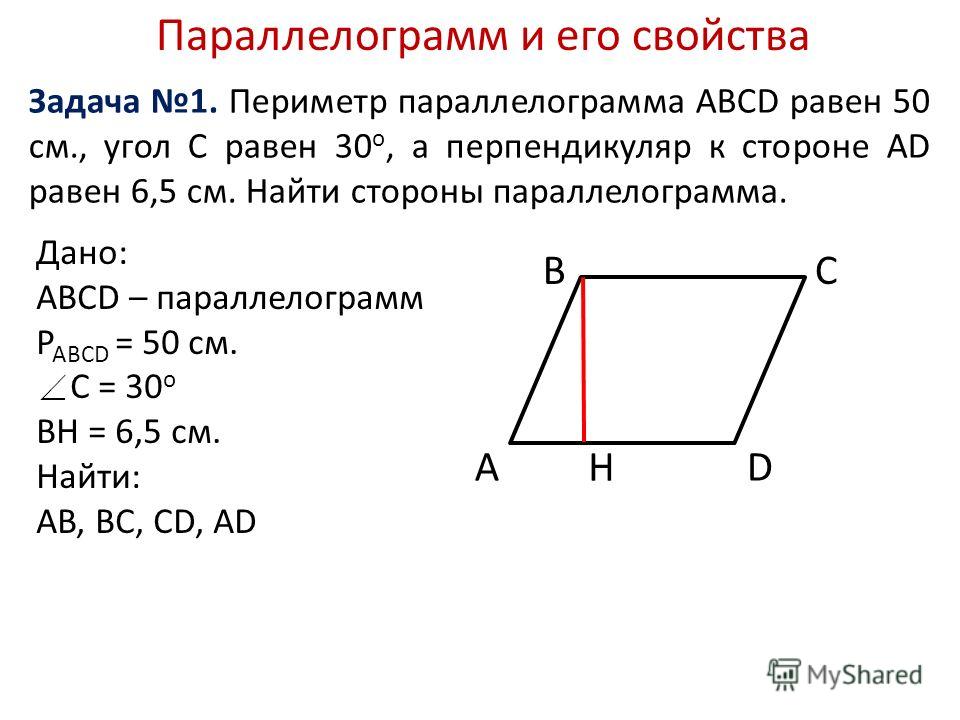 Найдите периметр параллелограмма, если ВС = 34 см.

Впараллелограмме ABCD биссектрисы углов В и D пересекают диагональ АС в точках К и Р соответственно. Доказать, что четырёхугольник  BРDК —  параллелограмм.

Докажите, что при пересечении биссектрис параллелограмма образуется прямоугольник.

V. Домашнее задание.

Конспект (свойства биссектрис параллелограмма), задачи:

3. Дано: TPLK – параллелограмм, РТ = РL, TF – биссектриса LTK, TFL= 120^o. Найти углы параллелограмма.

4. Дано: ABCD – параллелограмм, AM  – биссектриса BAD,  AM : MC = 5 : 3,  P_OBC > P_OCD на 6 см. Найти стороны и периметр параллелограмма.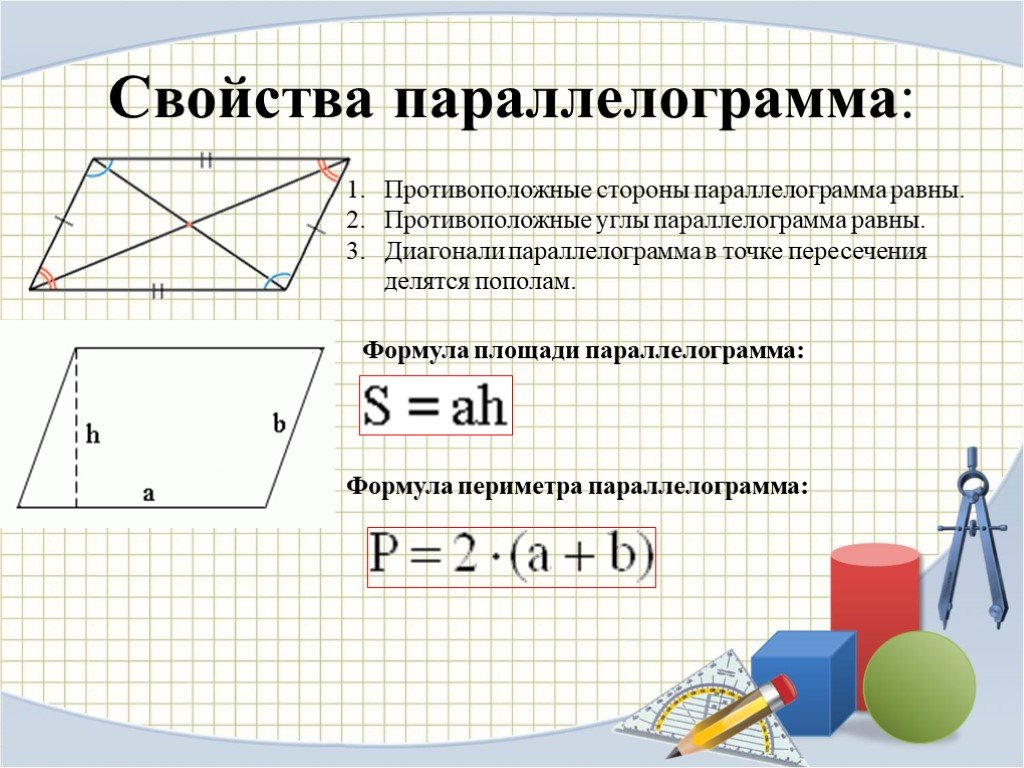

13.07.2018

Свойства биссектрисы угла равнобедренного треугольника abc

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Свойства биссектрисы равнобедренного треугольника

В данной публикации мы рассмотрим основные свойства биссектрисы равнобедренного треугольника (внутренней и внешней), а также разберем пример решения задачи по данной теме.

Примечание: напомним, что

равнобедренным называется треугольник, в котором две стороны равны (боковые), а третья является основание фигуры.

• Свойства биссектрисы равнобедренного треугольника
  • Свойство 1
  • Свойство 2
  • Свойство 3
  • Свойство 4
• Пример задачи

Свойства биссектрисы равнобедренного треугольника

Свойство 1

В равнобедренном треугольнике биссектрисы, проведенные к боковым сторонам, равны между собой.

• AB = BC, т.к. являются боковыми сторонами равнобедренного △ABC;
• AF = CG, т.к. это биссектрисы, проведенные к боковым сторонам треугольника (или биссектрисы углов BAC и ACB, которые также равны между собой).

Обратная формулировка: если две из трех биссектрис в треугольнике равны, значит он является равнобедренным.

Свойство 2

В равнобедренном треугольнике биссектриса, проведенная к основанию, одновременно является и медианой и высотой.

• BH – биссектриса угла ABC, проведенная к основанию AC;
• BH – медиана, значит она делит AC пополам, т.е. AH = HC;
• BH – высота, следовательно, она перпендикулярна AC.

Свойство 3

Если известны стороны равнобедренного треугольника, то длину биссектрисы, проведенную к основанию, можно посчитать по формуле:

l² = b² – a²

• l – биссектриса;
• b – боковая сторона;
• a – половина основания.

Примечание: данная формула следует из теоремы Пифагора (

l и a – катеты прямоугольного треугольника, b – его гипотенуза).

Свойство 4

Внешняя биссектриса угла равнобедренного треугольника, расположенного напротив его основания, параллельна этому основанию.

• BD – внешняя биссектриса ∠ABC треугольника;
• BD параллельна основанию AC.

Примечание: к равнобедренному треугольнику применимы и другие свойства биссектрисы, приведенные в нашей публикации – “Определение и свойства биссектрисы угла треугольника”.

Пример задачи

Биссектриса равнобедренного треугольника с боковой стороной 25 см равняется 20 см. Найдите периметр фигуры.

Решение
Воспользуемся формулой, приведенной в Свойстве 3, чтобы найти длину основания.
a² = b² – l² = 25² – 20² = 225.

Извлекаем квадратный корень из найденного значения и получаем 15 см.
Следовательно, основание треугольника равно 30 см (15 см ⋅ 2).

Периметр фигуры равен сумме всех ее сторон, т.е.: 25 см + 25 см + 30 см = 80 см.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Определение, Углы, Свойства, Формулы, Примеры

Ромб – четырехугольник, у которого все стороны равны. Так как противоположные стороны параллелограмма равны, то ромб является особым типом параллелограмма, у которого все стороны равны.

Разница между квадратом и ромбом в том, что все углы квадрата прямые, но углы ромба не обязательно должны быть прямыми.

Ромб можно найти в самых разных предметах вокруг нас, таких как кольца на пальцах, ромбовидная серьга, структура оконного стекла и т. д.

Площадь ромба вычисляется путем нахождения произведения его основания и соответствующей высоты (высоты).

Если известны длины диагоналей ромба, то его площадь равна половине их произведения.

Итак, площадь ромба = $\frac{(d1\times d2)}{2}$ квадратных единиц; где d1 и d2 — диагонали ромба.

Периметр ромба равен сумме длин его границ. Поскольку все четыре стороны ромба равны, его периметр вычисляется путем умножения длины его стороны на 4.

То есть периметр ромба = 4 × единиц; где « a » — длина стороны ромба.

Пример 1: Длины двух диагоналей ромба 18 см и 12 см. Найдите площадь ромба.

Площадь ромба = $\frac{(d1\times d2)}{2}$ = $\frac{(18\times 12)}{2}$ кв.см = 108 кв.см

Пример 3: Площадь ромба 56 кв.см. Найдите длину другой диагонали, если длина одной из его диагоналей равна 14 см.

1 Какой из следующих четырехугольников определенно является ромбом? Трапеция Прямоугольник Квадрат Параллелограмм Правильный ответ: Квадрат Все стороны квадрата равны, поэтому все квадраты ромбы. 2 Если длина одной из сторон ромба равна 10 см. Какова будет длина противоположной стороны данного ромба? 5 см 10 см 20 см 40 см Правильный ответ: 10 см Все стороны ромба равны по длине. 3 Какой будет высота ромба, площадь которого 320 кв.см, а сторона 40см? 4 см 6 см 8 см 10 см Правильный ответ: 8 см Область = База × высота ⇒ 320 = 40 × высота ⇒ Высота = 320 ÷ 40 = 8 CM 4 4. Площадь пола зала 500 000 кв.см. Если пол должен быть покрыт плиткой с каждой диагональю 40 см и 25 см, найдите необходимое количество плиток. 50 500 1000 5000 Правильный ответ: 1000 Площадь пола = 500 000 кв. см Площадь каждой плитки = $\frac{(d2)}{\times} = $\frac{40\times 25}{2}$ = 500 кв. см Количество плиток = Площадь пола ÷ Площадь 1 плитки = 500 000 ÷ 500 = 1000 плиток Итак, для покрытия требуется 1000 плиток пол.

Каковы основные свойства ромба?

• Все стороны равны по длине.
• В ромбе противоположные углы равны.
• Диагонали делятся пополам под углом 90 градусов.
• Смежные углы в сумме дают 180 градусов.

Является ли ромб правильным многоугольником?

Нет, ромб не является правильным многоугольником. У правильного многоугольника все углы должны быть одинаковыми (равными).

Диагонали ромба делят фигуру на какие фигуры?

Две диагонали ромба образуют четыре прямоугольных треугольника.

Воздушный змей имеет форму ромба?

Нет, воздушный змей не ромб. У ромба все стороны одинаковой длины, тогда как у воздушного змея 2 пары равных смежных сторон.

найти площадь параллелограмма | Wyzant Спросите эксперта

Геометрия

Раза А.

спросил 26.05.20

Как найти площадь параллелограмма, зная периметр и две высоты?

Подписаться І 1

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Андрей. ответил 26.05.20

Репетитор

3. 2 (13)

10 лет опыта!!

Смотрите таких репетиторов

Смотрите таких репетиторов

Все, что вам нужно знать, это точное основание и высоту. База, которую я назову (сторона b), будет просто одной из заданных сторон. И высота точно перпендикулярна основанию, что означает, что она образует угол 90 градусов с выбранной вами стороной. Высота, которую я назову (h), просто проведена от (стороны b) к другой стороне, которая также равна (стороне b) и образует угол 90 градусов между (стороной b) и (h)

(по сути, вы делаете параллелограмм в прямоугольник, площадь которого легко найти со сторонами прямоугольника (сторона b) и (h)) 92)

Тогда площадь будет (основание b)(h), что является вашим ответом

Голосовать за 0 Понизить

Подробнее

Отчет

Тимоти С. ответил 26.05.20

Репетитор

4.9 (788)

Тим С., специальный наставник

Об этом репетиторе ›

Об этом репетиторе ›

Привет. Площадь параллелограмма равна основанию на высоту. Если вы уже знаете высоту, вам нужно только основание, чтобы получить ответ.

Однако вы заметили, что когда вы видите высоту, проведенную к основанию, образуется прямоугольный треугольник. Вам нужно использовать формулу a в квадрате + b в квадрате = c в квадрате, чтобы найти сторону параллелограмма. Поскольку вы знаете периметр и можете вычесть 2 стороны (которые равны), вы получите основание.

Затем умножьте основание на высоту, и вы получите ответ.

Голосовать за 0 Понизить

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.