Построение полинома Жегалкина
Построение полинома Жегалкина.
Пример.
Рассмотрим пример построения полином Жегалкина по таблице истинности, содержащей 3 переменные Методом неопределенных коэффициентов.
x | y | z | f | |
a0 | 0 | 0 | 0 | 1 |
a1 | 0 | 0 | 1 | 1 |
a2 | 0 | 1 | 0 | 0 |
a3 | 0 | 1 | 1 | 1 |
a4 | 1 | 0 | 0 | 0 |
a5 | 1 | 0 | 1 | 0 |
a6 | 1 | 1 | 0 | 1 |
a7 | 1 | 1 | 1 | 0 |
Запишем общий вид полинома Жегалкина:
1) 1=a0;
2) 1=a0a1*z,
1=1a1.
Каким должно быть a1, чтобы
выполнялось равенство? Воспользуемся
таблицей функции :
X1 | X2 | f |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 0 |
Из
таблицы видно, что равенство равно 1,
когда значения переменных разные.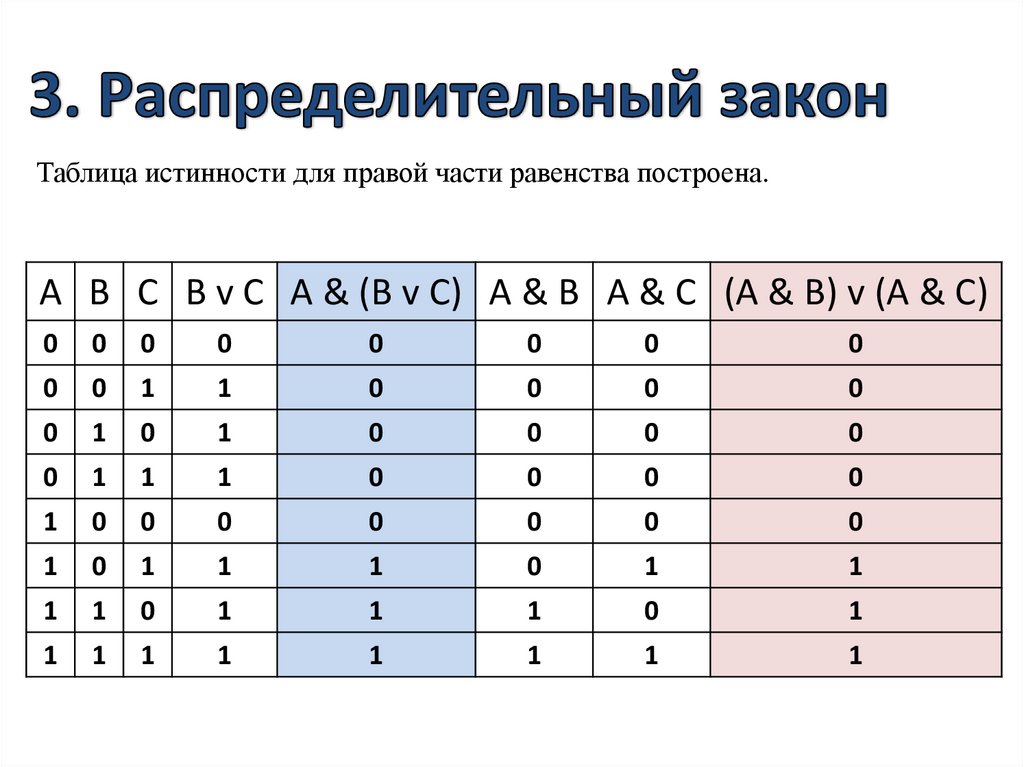
Следовательно, a1=0;
3) 0=а0a1*za2*y, 0=10*0a2*1, 0=10a2. Упростим равенство: принимая во внимание, что 10=1, получаем: 0=1a2, из чего по таблице определяем, что a2=1;
4) 1=a0a1*za2*ya3*y*z, 1=101a3. Упростим: 10=1 11=0, получим: 1=0a3. По таблице a3=1;
5) 0=a0a1*za2*ya3*y*za4*x, 0=1000a4. Упростим: 10=1, 10=1, 1=1. Получим: 0=1a4, по таблице: a4=1;
6) 0=a0a1*za2*ya3*y*za4*xa5*x*z, 0=10001a5, упрощаем как делали выше, получаем: a5=0;
7) 1=a0a1*za2*ya3*y*za4*xa5*x*za6*x*y,
1=10100a6. a6=0;8) 0=a0a1*za2*ya3*y*za4*xa5*x*za6*x*ya7*x*y*z, 0=1011100a7. a7=0;
Подставляем коэффициенты в общую форму полинома:
F(x,y,z)=11*x1*y0*z0*x*y1*y*z0*x*z1*x*y*z=1xyyz
Проверка:
x | y | z | f |
0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 0 |
Проверка выполняется путем
подстановки значений x,y,z в
полученную формулу.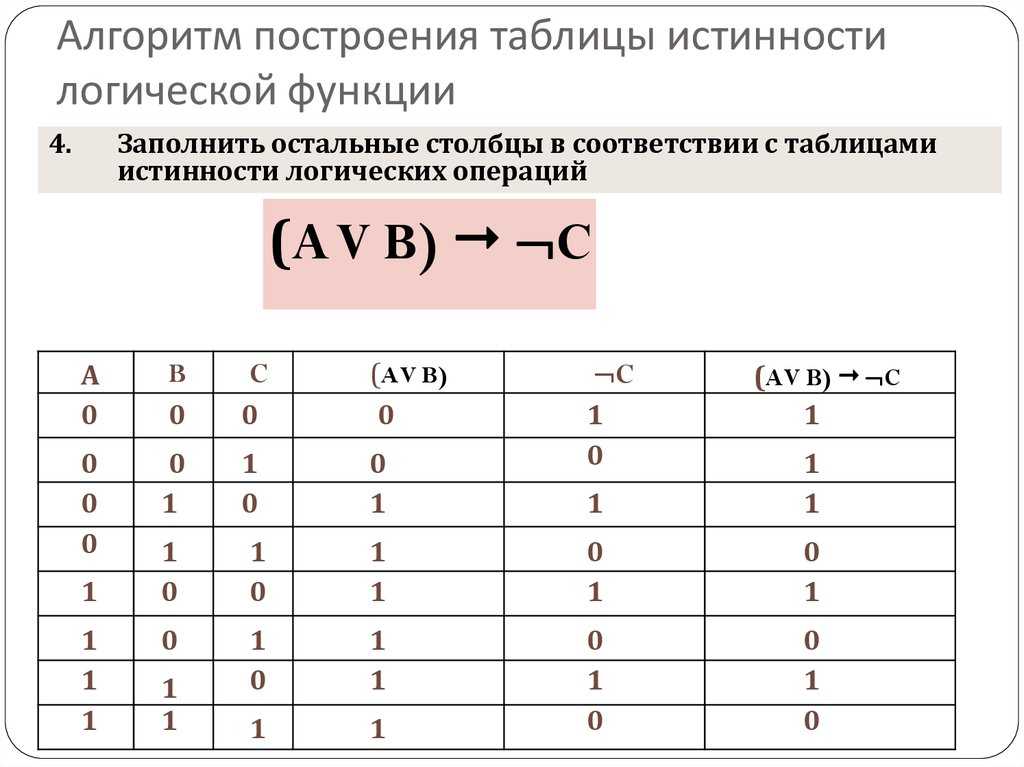
Разберем пример
подстановки для 4й строчки: f(0,1,1)=1011*1, 11 =0, 01=1. f(0,1,1)=1, поэтому все
верно.
Результат проверки считается положительным, если все результаты постановки в полученный полином совпадают с соответствующими значениями функции. Или, что проще, если полученная таблиц совпадает с исходной.
Дискретная математика (список тем по лекциям). Прикладная математика и информатика. Группа №217
Дискретная математика (список тем по лекциям). Прикладная математика и информатика. Группа №217
|
|
К. «Линейные пространства».|
Преподаватель: Пак Геннадий Константинович
Последнее обновление: | |
| Copyright (C) 2009-2011 by RA0LHS | |
Частичный порядок.
lo.
logic — Быстрые алгоритмы сложения и умножения полиномов Жегалкинаспросил
Изменено 10 лет, 8 месяцев назад
Просмотрено 2к раз
$\begingroup$
Всем привет,
Меня интересуют быстрые алгоритмы сложения и умножения полиномов Жегалкина. Например, пусть
$f_1(x_1, x_2, x_3) = 1+x_1+x_2x_3$
$f_2(x_1, x_2, x_3) = x_1+x_3$
Мне нужен быстрый алгоритм для найдите сумму
$f_3(x_1, x_2, x_3) = f_1(x_1, x_2, x_3)+f_2(x_1, x_2, x_3)=1+x_3+x_2x_3$
гугл ничего не дает, буду признателен за любые полезные ссылки на любые теоретические исследования и/или реализации (с любым языком программирования).
Заранее спасибо!
- логика
- алгоритмы
- полиномы
$\endgroup$
1
$\begingroup$
Если вас интересуют параллельные вычисления, статья
В. Д. Малюгин, В. В. Соколов, «Интенсивные логические вычисления», Автомат. и телемех., 1993, вып. 4, 160–167 (на русском) [Английская версия: Автоматизация и дистанционное управление, 1993, 54:4, 672–678]
может оказаться полезным.
$\endgroup$
$\begingroup$
@Игорь Ривин: Отвечая на ваш вопрос… Представления не имеют значения. У вас есть ссылка на алгоритм, который работает с полиномами Жегалкина, представленными в виде набора коэффициентов? Пожалуйста, поделитесь со мной! Может быть, вы знакомы с библиотекой Python/Ruby/C++/etc, которая работает с полиномами Жегалкина, представленными строками? Пожалуйста, дайте ссылку на сайт!
«Быстро» означает «быстрее, чем очевидный прямой расчет».
Например, БПФ позволяет умножать два многочлена $F(x)P(x)$ на $R$ быстрее, чем очевидное прямое вычисление. Мне нужно что-то подобное для полиномов Жегалкина.
П.С. «Этот вопрос действительно не имеет смысла» звучит не очень вежливо, ИМХО. Спасибо за ответ 🙂
$\endgroup$
3
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
code golf — Симметричные булевы функции как многочлены Жегалкина
Пусть \$\mathbb{B} = \mathbb{Z}_2 = \{0, 1\}\$ — множество булевых операторов. Симметричная логическая функция 9n \to \mathbb{B}\$, который проверяет, находится ли число его истинных аргументов в \$S\$, т.е. е. функция \$f_S\$ такая, что
$$f_S(\alpha_1, \alpha_2, \ldots, \alpha_n) = \left(\sum_{1 \le i \le n}\alpha_{i}\right) \in S$$
или эквивалентно
$$f_S(\alpha_1, \alpha_2, \ldots, \alpha_n) = |\{ i : \alpha_i \}| \in S. $$
Эти функции называются симметричными булевыми функциями, поскольку все они являются логическими функциями, не зависящими от порядка аргументов.
Набор логических чисел образует поле , условно обозначаемое \$GF(2)\$, где умножение является логическим и (\$\wedge\$), а сложение является исключающим или (\$\oplus\$). Это поле имеет такие свойства, как \$-\alpha = \alpha\$, \$\alpha / \beta = \alpha \wedge \beta\$ (для всех \$\beta \neq 0\$), \$\ alpha \oplus \alpha = 0\$ и \$\alpha \wedge \alpha = \alpha\$ для всех \$\alpha\$ в дополнение к свойствам поля.
Для удобства я буду писать \$\oplus\$ как \$+\$ и опускать \$\wedge\$ в следующих абзацах. Например, я буду писать \$\alpha\oplus\beta\oplus\alpha\wedge\beta\$ как \$\alpha + \beta + \alpha\beta\$.
Любая логическая функция может быть выражена в виде многочлена над полем логических чисел. Такой полином называется полиномом Жегалкина, представление каноническое, т.е. е. существует ровно один многочлен, представляющий данную логическую функцию. Вот несколько примеров булевых функций и соответствующих им полиномов Жегалкина:
- \$\alpha \vee \beta = \alpha + \beta + \alpha\beta\$
- \$\альфа\клин\отриц\бета = \альфа + \альфа\бета\$
- \$(\alpha\to\beta) \oplus\gamma = 1 + \alpha + \gamma + \alpha\beta\$
- \$\neg(\alpha\wedge\beta) \vee\gamma = 1 + \alpha\beta + \alpha\beta\gamma\$
- \$f_{\{1, 4\}}(\alpha, \beta, \gamma, \delta) = \alpha + \beta + \gamma + \delta + \alpha\beta\gamma + \alpha\beta \delta + \alpha\gamma\delta + \beta\gamma\delta + \alpha\beta\gamma\delta\$
, где тройные члены \$(\alpha\beta\gamma + \alpha\beta\delta + \ alpha\gamma\delta + \beta\gamma\delta)\$ необходимы, поскольку в противном случае мы имели бы \$f(1,1,1,0) = 1\$ и \$3 \not\in \{1, 4\}\$.
