Формулы двойного угла в тригонометрии
Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2α, используя тригонометрические функции угла α. Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид nα записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin nαимеет то же значение, что и sin (nα). При обозначении sinn α имеем аналогичную запись(sin α)n. Использование записи применимо для всех тригонометрических функций со степенями n.
Ниже приведены формулы двойного угла:
sin 2α=2·sin α·cos αcos 2α=cos2 α-sin2 α, cos 2α=1-2·sin2 α, cos 2α=2·cos2 α-1tg 2α=2·tg α1-tg2 αctg 2α-ctg2 α-12·ctg α
Отметим, что данные формулы sin и cos применимы с любым значением угла α. Формула тангенса двойного угла справедлива при любом значении α, где tg 2α имеет смысл, то есть α≠π4+π2·z, z является любым целым числом. Котангенс двойного угла существует при любом α, где ctg 2α определен на α≠π2·z.
Формула тангенса двойного угла справедлива при любом значении α, где tg 2α имеет смысл, то есть α≠π4+π2·z, z является любым целым числом. Котангенс двойного угла существует при любом α, где ctg 2α определен на α≠π2·z.
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin (α+β)=sin α ·cos β+cos α·sin βи косинуса суммы cos (α+β)=cos α ·cos β-sin α·sin β. Предположим, что β=α, тогда получим, что
sin (α+α)=sin α ·cos α+cos α·sin α=2·sin α·cos α и cos (α+α)=cos α ·cos α-sin α·sin α=cos2α-sin2α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2α= 2·sin α·cos α и cos 2α=cos2α-sin2α.
Остальные формулы cos 2α=1-2·sin2 α и cos 2α=2·cos2 α-1 приводят к виду cos 2α=cos 2α=cos2 α-sin2 α, при замене 1 на сумму квадратов по основному тождествуsin2 α+cos2 α=1. Получаем, что sin2 α+cos2 α=1. Так 1-2·sin2 α=sin2 α+cos2 α-2·sin2 α=cos2 α-sin2 α и 2·cos2 α-1=2·cos2 α-(sin2 α+ cos2 α)=cos2 α-sin2 α.
Так 1-2·sin2 α=sin2 α+cos2 α-2·sin2 α=cos2 α-sin2 α и 2·cos2 α-1=2·cos2 α-(sin2 α+ cos2 α)=cos2 α-sin2 α.
Для доказательства формул двойного угла тангенса и котангенса применим равенства tg 2α=sin 2αcos 2α и ctg 2α=cos 2αsin 2α. После преобразования получим, что tg 2α=sin 2αcos 2α=2·sin α·cos αcos2 α-sin2 α и ctg 2α=cos 2αsin 2α=cos2 α-sin2 α2·sin α·cos α. Разделим выражение на cos2 α, где cos2 α≠0 с любым значением α, когда tg α определен. Другое выражение поделим на sin2 α, где sin2 α≠0 с любыми значениями α, когда ctg 2α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
tg 2α=sin 2αcos 2α=2·sin α·cos αcos2 α-sin2 α=2·sin α·cos αcos2 αcos2 α-sin2 αcos2 α=2·sin2 αcos2 α1-sin2 αcos2 α=2·tg α1-tg2 αctg 2α=cos 2αsin 2α=cos2 α-sin2 α2·sin α·cos=cos2 α-sin2 αsin2 α2·sin α·cos αsin2 α=cos2 αsin2 α-12·cos αsin α=ctg2 α-12·ctg α
Примеры использования формул двойного угла
Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2α для α=30°, применим значения тригонометрических функций для этих углов. Если α=30°, тогда 2α=60°. Проверим значения sin 60°=2·sin 30°·cos 30°, cos 60°=cos2 30°-sin2 30°.
Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2α для α=30°, применим значения тригонометрических функций для этих углов. Если α=30°, тогда 2α=60°. Проверим значения sin 60°=2·sin 30°·cos 30°, cos 60°=cos2 30°-sin2 30°.
Подставив значения, получим tg 60°= 2·tg 30°1-tg2 30° и ctg 60°=ctg230°-12·ctg 30°..
Известно, что sin 30°=12, cos 30°=32, tg 30°=33, ctg 30°=3 и
sin 60°=32, cos 60°=12, tg 60°=3, ctg 60°=33, тогда отсюда видим, что
2·sin 30°·cos 30°=2·12·32=32, cos230°-sin230°=(32)2-(12)2=12,2·tg 30°1-tg230°=2·321-(33)=3
и ctg230°-12·ctg 30°=(3)2-12·3=33
Проведя вычисления, можно сделать вывод, что справедливость для α=30° подтверждена.
Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2α. В примере допускается применение формулы двойного угла 3π5.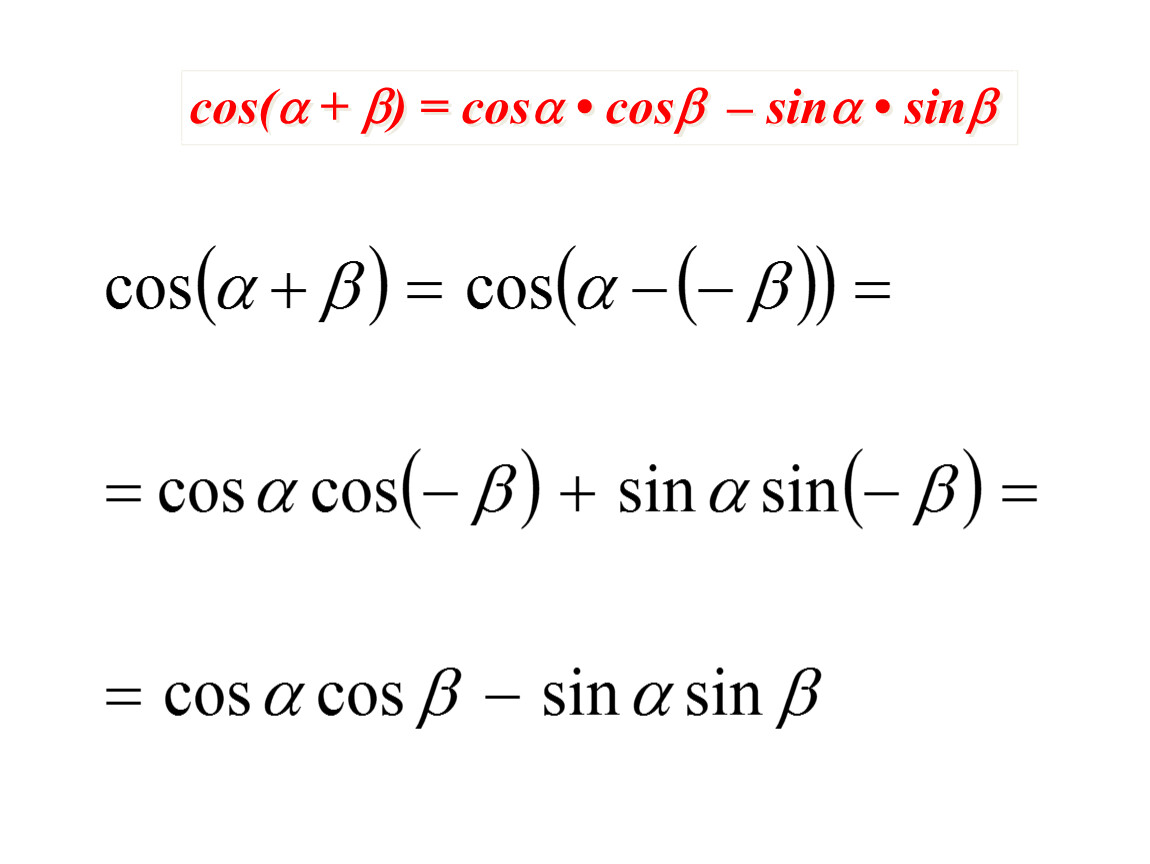 Тогда его необходимо преобразовать, в результате чего получим α=3π5:2=3π10. Отсюда следует, что формула двойного угла для косинуса будет иметь видcos3π5=cos23π10-sin23π10.
Тогда его необходимо преобразовать, в результате чего получим α=3π5:2=3π10. Отсюда следует, что формула двойного угла для косинуса будет иметь видcos3π5=cos23π10-sin23π10.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 1Представить sin 2α3 через тригонометрические функции, при α6.
Решение
Заметим, что из условия имеем 2α3=4·α6. Тогда использовав 2 раза формулу двойного угла, выразим sin2α3 через тригонометрические функции угла α6. Применяя формулу двойного угла, получим sin 2α3=2·sin α3·cos α3. После чего к функциям sin α3 и cos α3применим формулы двойного угла: sin 2α2=2·sin α3·cosα3=2·(2·sinα5·cosα6)·(cos2α6-sinα6)==4·sinα6·cos3α6-4·sin3α6·cosα6
Ответ: sin2α3=4·sinα6·cos3α6-4·sin3α6·cosα6.
Формулы тройного, четверного и т.д. угла
Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.
sin 3α=sin(2α+α)=sin 2α·cos α+cos 2α·sin α=2·sin α·cosα·cos α+ (cos2 α-sin2α)·sin α==3·sin α·cos2α-sin3 α
При замене cos2α на 1-sin2α из формулы sin 3α=3·sin α·cos2α-sin3α, она будет иметь вид sin 3α=3·sin α-4·sin3 α.
Так же приводится формула косинуса тройного угла:
cos 3α=cos (2α+α)=cos 2α·cos α-sin 2α·sin α==(cos2 α-sin2 α)·cos α-2·sin α·cos α·sin α=cos3α-3·sin2α·cos α
При замене sin2 α на 1-cos2 α получим формулу вида cos 3α=-3·cos α+4·cos3 α.
При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:
tg 3α=sin 3αcos 3α=3·sin α·cos2 α-sin3 αcos3α-3·sin2α·cos α=3·sin α·cos2α-sin3αcos3αcos3α-3·sin2α·cos αcos3α==3·sin αcos α-sin3αcos3α1-3·sin2 αcos2 α=3·tg α-tg3α1-3·tg2α;ctg 3α=cos 3αsin 3α=cos3 α-3·sin2α·cosα3·sin α·cos2α-sin3α=cos3α-3·sin2α·cosαsin3α3·sin α·cos2α-sin3αsin3α==cos3αsin3α-3·cos αsin α3·cos2αsin2α-1=ctg3α-3·ctgα3·ctg2α-1
Чтобы выводить формулы четвертой степени, имеет смысл представить 4α как 2·2α, тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5α в виде 3α+2α, что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.
Для выводы формулы 5 степени, представляем 5α в виде 3α+2α, что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.
Тригонометрические тождества и преобразования
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:
Простейшие тригонометрические тождества
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств.
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).
Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).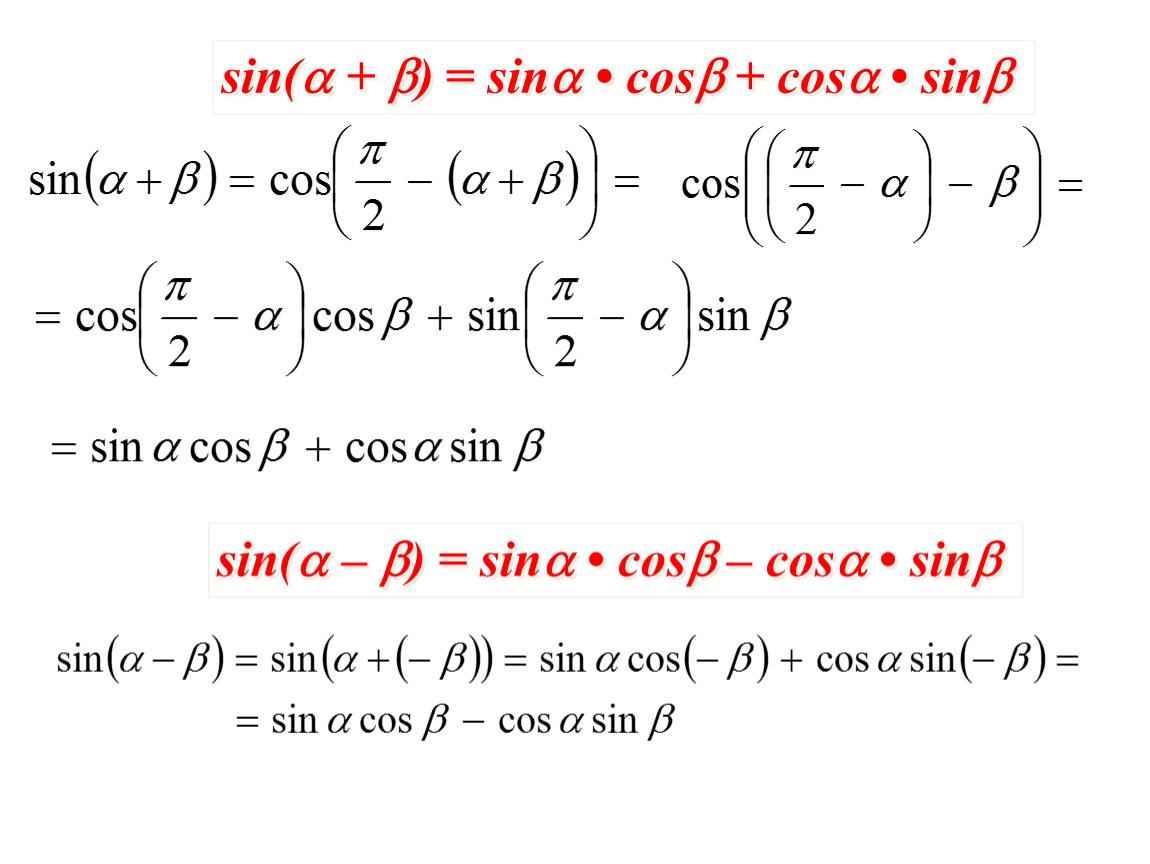
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.
Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:
Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла
равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.
Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.
Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.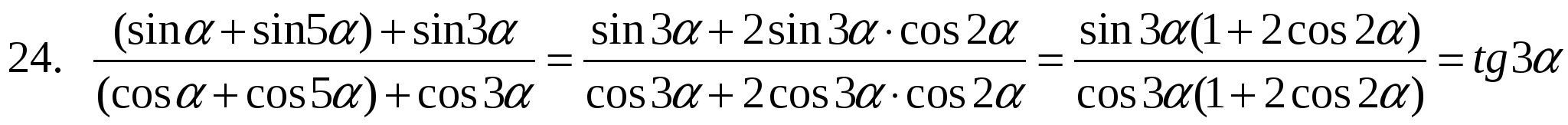
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:
Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
См. также Полный список формул приведения тригонометрических функций.
| Угол |
α + 90 α + π/2 |
α + 180 α + π |
α + 270 α + 3π/2 |
90 — α π/2- α |
180 — α π- α |
270 — α 3π/2- α |
360 — α 2π- α |
| sin | cos α | -sin α | -cos α | cos α | sin α | -cos α | -sin α |
| cos | -sin α | -cos α | sin α | sin α | -cos α | -sin α | cos α |
| tg | -ctg α | tg α | -ctg α | ctg α | -tg α | ctg α | -tg α |
| ctg | -tg α | ctg α | -tg α | tg α | -ctg α | tg α | -ctg α |
Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120) | Описание курса | Пояснение (доказательство) простейших тригонометрических тождеств
Основные тригонометрические формулы — реферат
Основныетригонометрические формулы
1.
 Основы.
Основы.sin2a+cos2a=1
seca=1/cosa
csca=1/sina
sec2a-tg2a=1
csc2a-ctg2a=1
2.Сумма углов.
cos(a+b)=cosacosb-sinasinb
cos(a-b)=cosacosb+sinasinb
sin(a+b)=sinacosb+cosasinb
sin(a-b)=sinacosb-cosasinb
tg(a+b)=tga+tgb/1-tgatgb=
=ctga+ctgb/ctgactgb-1
tg(a-b)=tga-tgb/1+tgatgb=
=ctgb-ctga/1+ctgactgb
3. Умножение функций.
2sinacosb=sin(a+b)+sin(a-b)
2cosacosb=cos(a+b)+cos(a-b)
2sinasinb=cos(a-b)-cos(a+b)
4.Сложение и
вычитание.
sina+sinb=2sin(a+b)/2cos(a-b)/2
sina-sinb=2sin(a-b)/2cos(a+b)/2
cosa+cosb=2cos(a+b)/2cos(a-b)/2
cosa-cosb=2sin(a+b)/2sin(b-a)/2
tga+tgb=sin(a+b)/cosacosb
tga-tgb=sin(a-b)/cosacosb
ctga+ctgb=sin(a+b)/sinasinb
ctga-ctgb=sin(b-a)/sinasinb
tga+ctgb=cos(a-b)/cosacosb
ctga-tgb=cos(a+b)/sinasinb
5.Разность квадратов функций
sin2a-cos2b=sin(a+b)sin(a-b)
cos2a-sin2b=cos(a+b)sin(b-a)
cos2a-cos2b=sin(a+b)sin(b-a)
6. Какая-то
Какая-то
формула(крутая)
a cosa+b sina=c sin(a+f)
c=Öa2+b2
sinf=a/c
7.Функции
нескольких углов.
sin2a=2sinacosa=2tga/1+tg2a
sin3a=3sina-4sin3a
sin4a=cosa(4sina-8sin2a)
cos2a=cos2a-sin2a=2cos2a-1=1-2sina==1-tg2a/1+tg2a=ctga-tga/ctga+tga
cos3a=4cos2a-3cosa
cos4a=8cos4a-8cos2a
tg2a=2tga/1-tg2a=2ctga/ctg2a-1=2/ctga-tga
ctg2a=ctg2a-1/2ctga=1-tg2a/2tga=ctga-tga/2
8.Функции
половинного угла.
sina/2= Ö1/2(1-cosa)
cosa/2= Ö1/2(1+sina)
tga/2=1-cosa/sina=sina/1+cosa=Ö1-cosa/1+cosa
ctga/2=sina/1-cosa=1+cosa/sina=Ö1+cosa/1-cosa
9.Понижение
степени Sin и Cos.
sin2a=1/2(1-cos2a)
sin3a=1/4(3sina-sin3a)
sin4a=1/8(cos4a-4cos2a+3)
cos2a=1/2(cos2a+1)
cos3a=1/4(cos3a+3cosa)
cos4a=1/8(cos4a+4cos2a+3)
a
00
300
450
600
900
p/6
p/4
p/3
p/2
sin a
0
1/2
Ö2/2
Ö3/2
1
cos a
1
Ö3/2
Ö2/2
1/2
0
tg a
0
Ö3/3
1
Ö3
—
ctg a
—
Ö3
1
Ö3/3
0
Формулы привидения.
x
p + a
p — a
2p + a
2p — a
p /2 + a
p /2 — a
3/2p + a
3/2p — a
sin x
— sin a
sin a
sin a
— sin a
cos a
cos a
— cos a
— cos a
cos x
— cos a
— cos a
cos a
cos a
— sin a
sin a
sin a
— sin a
tg x
tg a
— tg a
tg a
— tg a
— ctg a
ctg a
— ctg a
ctg a
ctg x
ctg a
— ctg a
ctg a
— ctg a
— tg a
tg a
— tg a
tg a
Список
литературы
Для подготовки данной работы
были использованы материалы с сайта http://ilib.ru/
Основные тригонометрические формулы
1..
sin2a+cos2a=1
seca=1/cosa
csca=1/sina
sec2a-tg2a=1
csc2a-ctg2a=1
2. .
cos(a+b)=cosacosb-sinasinb
cos(a-b)=cosacosb+sinasinb
sin(a+b)=sinacosb+cosasinb
sin(a-b)=sinacosb-cosasinb
tg(a+b)=tga+tgb/1-tgatgb=
=ctga+ctgb/ctgactgb-1
tg(a-b)=tga-tgb/1+tgatgb=
=ctgb-ctga/1+ctgactgb
3. .
.
2sinacosb=sin(a+b)+sin(a-b)
2cosacosb=cos(a+b)+cos(a-b)
2sinasinb=cos(a-b)-cos(a+b)
4. .
sina+sinb=2sin(a+b)/2cos(a-b)/2
sina-sinb=2sin(a-b)/2cos(a+b)/2
cosa+cosb=2cos(a+b)/2cos(a-b)/2
cosa-cosb=2sin(a+b)/2sin(b-a)/2
tga+tgb=sin(a+b)/cosacosb
tga-tgb=sin(a-b)/cosacosb
ctga+ctgb=sin(a+b)/sinasinb
ctga-ctgb=sin(b-a)/sinasinb
tga+ctgb=cos(a-b)/cosacosb
ctga-tgb=cos(a+b)/sinasinb
5.
sin2a-cos2b=sin(a+b)sin(a-b)
cos2a-sin2b=cos(a+b)sin(b-a)
cos2a-cos2b=sin(a+b)sin(b-a)
6. - ()
a cosa+b sina=c sin(a+f)
c=Öa2+b2
sinf=a/c
7. .
sin2a=2sinacosa=2tga/1+tg2a
sin3a=3sina-4sin3a
sin4a=cosa(4sina-8sin2a)
cos2a=cos2a-sin2a=2cos2a-1=1-2sina==1-tg2a/1+tg2a=ctga-tga/ctga+tga
cos3a=4cos2a-3cosa
cos4a=8cos4a-8cos2a
tg2a=2tga/1-tg2a=2ctga/ctg2a-1=2/ctga-tga
ctg2a=ctg2a-1/2ctga=1-tg2a/2tga=ctga-tga/2
8. .
.
sina/2= Ö1/2(1-cosa)
cosa/2= Ö1/2(1+sina)
tga/2=1-cosa/sina=sina/1+cosa=Ö1-cosa/1+cosa
ctga/2=sina/1-cosa=1+cosa/sina=Ö1+cosa/1-cosa
9. Sin Cos.
sin2a=1/2(1-cos2a)
sin3a=1/4(3sina-sin3a)
sin4a=1/8(cos4a-4cos2a+3)
cos2a=1/2(cos2a+1)
cos3a=1/4(cos3a+3cosa)
cos4a=1/8(cos4a+4cos2a+3)
|
a |
00 |
300 |
450 |
600 |
900 |
|
p/6 |
p/4 |
p/3 |
p/2 |
||
|
sin a |
0 |
1/2 |
Ö2/2 |
Ö3/2 |
1 |
|
cos a |
1 |
Ö3/2 |
Ö2/2 |
1/2 |
0 |
|
tg a |
0 |
Ö3/3 |
1 |
Ö3 |
— |
|
ctg a |
— |
Ö3 |
1 |
Ö3/3 |
0 |
|
. |
||||||||
|
x |
p + a |
p — a |
2p + a |
2p — a |
p /2 + a |
p /2 — a |
3/2p + a |
3/2p — a |
|
sin x |
— sin a |
sin a |
sin a |
— sin a |
cos a |
cos a |
— cos a |
— cos a |
|
cos x |
— cos a |
— cos a |
cos a |
cos a |
— sin a |
sin a |
sin a |
— sin a |
|
tg x |
tg a |
— tg a |
tg a |
— tg a |
— ctg a |
ctg a |
— ctg a |
ctg a |
|
ctg x |
ctg a |
— ctg a |
ctg a |
— ctg a |
— tg a |
tg a |
— tg a |
tg a |
http://ilib. ru/
ru/
| (a + b)(a — b) = a2 — b2 (a + b)2 = a2 + 2ab + b2 (a — b)2 = a2 — 2ab + b2 (a + b)3 = a3 + 3a2b + 3ab2 + b3 (a — b)3 = a3 — 3a2b + 3ab2 — b3 a3 + b3 = (a + b)(a2 — ab + b2) a3 — b3 = (a — b)(a2 + ab + b2) n! = 1 . 2 . 3 . …. . n 0! = 1 | am . an = am + n am/an = am — n (a . b)n = an. bn (am)n = amn a-n = 1/an | loga(M . N) = logaM + logaN N) = logaM + logaNloga(M / N) = logaM — logaN loga(Nk) = k . logaN Частные случаи: при a = 10 — десятичный, обозначается log N или lg N; | x = (x1 + x2 + x3 + … + xn) / n — арифметическое среднее x = (x1. x2. x3. … . xn)1/n — геометрическое среднее x = n / (1/x1+1/x2 + 1/x3 + … +1/xn) — гармоническое среднее x = SQR(1/n (x12 + x22 + x32 + … xn2)) — квадратичное среднее | sin(a) = cos(90o — a) tg(a) = ctg(90o — a) sin2(a) + cos2(a) = 1 sin(a) / cos(a) = tg(a) tg(a) . 1 + tg2(a) = 1 / cos2(a) Формулы привидения: sin(pn + a) = (-1)n sin(a) | Формулы двойного угла: sin(2a) = 2sin(a) . cos(a) Формулы тройного угла: sin(3a) = 3.sin(a) — 4.sin3(a) | Плоские фигуры: Треугольник (a — основание, h — высота): S = ah / 2 Объемные тела: Куб:S = 6a2, V = a3 |
Основные тригонометрические формулы — Мои статьи — Каталог статей
Основные тригонометрические формулы1.Основы.

sin2a+cos2a=1
seca=1/cosa
csca=1/sina
sec2a-tg2a=1
csc2a-ctg2a=1
2.Сумма углов.
cos(a+b)=cosacosb-sinasinb
cos(a-b)=cosacosb+sinasinb
sin(a+b)=sinacosb+cosasinb
sin(a-b)=sinacosb-cosasinb
tg(a+b)=tga+tgb/1-tgatgb=
=ctga+ctgb/ctgactgb-1
tg(a-b)=tga-tgb/1+tgatgb=
=ctgb-ctga/1+ctgactgb
3. Умножение функций.
2sinacosb=sin(a+b)+sin(a-b)
2cosacosb=cos(a+b)+cos(a-b)
2sinasinb=cos(a-b)-cos(a+b)
4.Сложение и вычитание.
sina+sinb=2sin(a+b)/2cos(a-b)/2
sina-sinb=2sin(a-b)/2cos(a+b)/2
cosa+cosb=2cos(a+b)/2cos(a-b)/2
cosa-cosb=2sin(a+b)/2sin(b-a)/2
tga+tgb=sin(a+b)/cosacosb
tga-tgb=sin(a-b)/cosacosb
ctga+ctgb=sin(a+b)/sinasinb
ctga-ctgb=sin(b-a)/sinasinb
tga+ctgb=cos(a-b)/cosacosb
ctga-tgb=cos(a+b)/sinasinb
5.Разность квадратов функций
sin2a-cos2b=sin(a+b)sin(a-b)
cos2a-sin2b=cos(a+b)sin(b-a)
cos2a-cos2b=sin(a+b)sin(b-a)
6. Какая-то формула(крутая)
Какая-то формула(крутая)
a cosa+b sina=c sin(a+f)
c=Öa2+b2
sinf=a/c
7.Функции нескольких углов.
sin2a=2sinacosa=2tga/1+tg2a
sin3a=3sina-4sin3a
sin4a=cosa(4sina-8sin2a)
cos2a=cos2a-sin2a=2cos2a-1=1-2sina==1-tg2a/1+tg2a=ctga-tga/ctga+tga
cos3a=4cos2a-3cosa
cos4a=8cos4a-8cos2a
tg2a=2tga/1-tg2a=2ctga/ctg2a-1=2/ctga-tga
ctg2a=ctg2a-1/2ctga=1-tg2a/2tga=ctga-tga/2
8.Функции половинного угла.
sina/2= Ö1/2(1-cosa)
cosa/2= Ö1/2(1+sina)
tga/2=1-cosa/sina=sina/1+cosa=Ö1-cosa/1+cosa
ctga/2=sina/1-cosa=1+cosa/sina=Ö1+cosa/1-cosa
9.Понижение степени Sin и Cos.
sin2a=1/2(1-cos2a)
sin3a=1/4(3sina-sin3a)
sin4a=1/8(cos4a-4cos2a+3)
cos2a=1/2(cos2a+1)
cos3a=1/4(cos3a+3cosa)
cos4a=1/8(cos4a+4cos2a+3)
a
00
300
450
600
900
p/6
p/4
p/3
p/2
sin a
0
1/2
Ö2/2
Ö3/2
1
cos a
1
Ö3/2
Ö2/2
1/2
0
tg a
0
Ö3/3
1
Ö3
—
ctg a
—
Ö3
1
Ö3/3
0
Формулы привидения.
x
p + a
p — a
2p + a
2p — a
p /2 + a
p /2 — a
3/2p + a
3/2p — a
sin x
— sin a
sin a
sin a
— sin a
cos a
cos a
— cos a
— cos a
cos x
— cos a
— cos a
cos a
cos a
— sin a
sin a
sin a
— sin a
tg x
tg a
— tg a
tg a
— tg a
— ctg a
ctg a
— ctg a
ctg a
ctg x
ctg a
— ctg a
ctg a
— ctg a
— tg a
tg a
— tg a
tg a
Тригонометрический лабиринт
«Три пути ведут к знанию:
путь размышления – это путь самый благородный,
путь подражания – это путь самый легкий,
и путь опыта – это путь самый горький»
Конфуций
Цели и задачи урока:
- повторить формулы тригонометрии, методы преобразования выражений;
- проверить умение учащихся применять свои знания при преобразовании тригонометрических выражений различного уровня сложности;
- воспитывать у учащихся умение отстаивать свое мнение;
- развивать мышление, внимание, память через постоянное обращение к имеющимся знаниям учащихся;
- формировать интерес к математике.

I. Вступительное слово учителя
В начале урока мне хочется обратить ваше внимание на слова китайского философа Конфуция, записанные на доске.
Сегодня от вас потребуется: и умение размышлять (при выполнении каждого задания), и умение подражать (точное знание формул и их применение), и опыт (навык преобразования тригонометрических выражений). И я надеюсь, что все эти пути действительно приведут вас к знаниям, которые позволят вам в будущем успешно сдать ЕГЭ и продолжить свое образование в Вузах.
А тема сегодняшнего урока – «Тригонометрический лабиринт». Почему тригонометрический, наверное, понятно, а что такое «лабиринт»? Слово «лабиринт» греческое и означает большое сооружение со сложными переходами, поэтому, говоря о лабиринте, подразумевают какое-то запутанное расположение или сочетание чего-нибудь (словарь Сергея Ивановича Ожегова).
Древние считали задачи, связанные с лабиринтом, вообще неразрешимыми. Человек, попавший в лабиринт, не мог уже из него выйти, если только какое-либо чудо или случай не приходили ему на помощь.
Человек, попавший в лабиринт, не мог уже из него выйти, если только какое-либо чудо или случай не приходили ему на помощь.
Однако безвыходных лабиринтов нет, разобраться и найти выход из самого запутанного лабиринта не составляет особого труда, если только знать, как действовать.
Софья Ковалевская говорила, что «у математиков существует свой язык – это формулы». И сегодня на уроке с помощью этого языка мы попытаемся преодолеть все трудности, не заблудиться и не потеряться в лабиринте тригонометрических выражений.
Итак, сегодня на уроке мы занимаемся преобразованиями тригонометрических выражений. Эта тема очень важна, т.к. из года в год в ЕГЭ включаются такие задания и в часть А, и в часть В.
Что используют для преобразования тригонометрических выражений?
- формулы тригонометрии;
- свойства синуса, косинуса, тангенса и котангенса;
- общие правила тождественных преобразований, такие как:
— приведение дробей к общему знаменателю;
— сокращение дробей;
— формулы сокращенного умножения;
— др.
Обычно целью преобразования является упрощение тригонометрического выражения. Вспомним некоторые формулы, знание которых нам сегодня понадобится.
II. Индивидуальная работа у доски
1) на доске на карточках записаны части формул, ваша задача восстановить каждую из формул:
2) дома вам предлагалось вывести формулы sin3a и cos3a (это новые для нас формулы, мы пока ими не пользовались)
– 2 человека у доски:
а) sin3 = sin(2 + ) = sin2cos + sincos2 = 2sincoscos + sin(1 – 2sin2) = 2sincos2 + sin – 2sin3 = 2sin(1 – sin2) + sin – 2sin3 = 2sin – 2sin3 + sin – 2sin3 = 3 sin – 4sin3.
б) cos3 = cos(2 + ) = cos2cos – sinsin2 = (2cos2 – 1)cos – 2sincossin = 2cos3 – cos – 2sin2cos = 2cos3 – cos – 2(1 – cos2)cos = 2cos3 – cos – 2cos + 2cos3 = 4cos3 – 3cos.
III. Устная работа класса (Приложение1) – применение ноутбука и мультимедийного проектора).
Верите ли Вы, что…
IV. Проверка работы у доски
1) Посмотрите на формулы. Есть замечания? Все верно?
Убедимся в правильности ответа. Перевернем карточки правого столбца, прочитаем слово (с обратной стороны карточек правого столбца написаны буквы, которые образуют слово «Бернулли»).
Иоганн БЕРНУЛЛИ – швейцарский математик, который впервые ввел современные обозначения синуса и косинуса знаками sin и cosв 1739 г. в письме к петербургскому математику Леонарду Эйлеру. Эйлер пришел к выводу, что эти обозначения очень удобны, и стал употреблять их в своих математических работах.
2) Вывод формул cos3 и sin3 – учащиеся объясняют.
V. В тетради: число, классная работа, тема урока
1) Добавим к нашему списку формул формулы тройного угла. Запишите их в тетради.
Запишите их в тетради.
Задание
Найдите наименьшее и наибольшее значения выражения:
– один ученик работает у доски с полным объяснением |
Ответ: 6 – наибольшее значение, –6 – наименьшее значение.
2) Презентация (Приложение 2) – применение ноутбука и мультимедийного проектора.
Проверим, насколько хорошо мы владеем изученными формулами. Я предлагаю вам задания, вы их решаете в тетради (даете краткое решение), выбираете правильный ответ и заносите в бланк (аналогичный экзаменационному бланку) номер правильного ответа (зафиксируйте № правильного ответа у себя в тетради). На экзаменационную работу отводится 4 ч, но помните, что большую часть времени, наверное, надо потратить на решение заданий части С. А решение заданий частей А и В надо довести до автоматизма. Поэтому время проверочной работы я вам сегодня ограничу.
Учащиеся сдают бланки (аналогичные бланкам ЕГЭ).
Теперь проверим правильность своего решения (на экране остаются только верные ответы).
– Поднимите руки, кто в части А не допустил ни одной ошибки?
– Кто безошибочно справился с частью В?
3) Продолжаем преодолевать препятствия нашего тригонометрического лабиринта.
На доске записаны задания, посмотрите на них внимательно и выберите задания по своим силам.
а) Упростите выражение:
Ответ: –1;
б) Найдите значение выражения:
Ответ: –5;
в) Найдите sin3 – cos3, если sin – cos = 0,8
Ответ: 0,944
г) (резервное) Найдите 20cos( – ), если выполняются равенства
cos + cos = 0,3 и
sin + sin = –1,1
Ответ: –7;
д) (резервное) Найдите значение выражения:
sin2400(sin2750 – sin2 1650)
Ответ: –0,75.
VI. Домашнее задание
Домашнее задание
Составить тест по теме «Преобразования тригонометрических выражений».
5 заданий части А и 2-3 задания части В.
Задания оформить на одном листе, их решения и ответы – на другом.
Для выполнения домашнего задания можно использовать учебник, различные пособия для подготовки к ЕГЭ.
VII. Итог урока
Подведем итог урока.
Чем сегодня занимались на уроке?
Что нового узнали?
Для чего надо знать формулы тригонометрии?
Мне хочется еще раз обратиться к словам Конфуция. Сегодня нам пришлось и размышлять, и подражать, и применять свой опыт при преобразовании тригонометрических выражений. И все эти пути, действительно, ведут к новым знаниям.
Подводя итог нашего урока, хотелось бы пожелать, чтобы вы всегда могли найти путь из любого лабиринта, и пусть ваши знания, умения и навыки помогут вам в этом, и помните, безвыходных лабиринтов нет!
Спасибо за урок.
Доказательство: Чтобы доказать тождество с тройным углом, мы можем записать sin3θ \ sin 3 \ thetasin3θ как sin (2θ + θ) \ sin (2 \ theta + \ theta) sin (2θ + θ). Затем мы можем использовать формулу суммы и тождества с двойным углом, чтобы получить желаемую форму:
sin3θ = sin (2θ + θ) = sin2θcosθ + cos2θsinθ = (2sinθcosθ) cosθ + (1−2sin2θ) sinθ = 2sinθcos 2θ + sinθ − 2sin3θ = 2sinθ (1 − sin2θ) + sinθ − 2sin3θ = 2sinθ − 2sin3θ + sinθ − 2sin3θ = 3sinθ− 4sin3θ.3 \ theta & = \ frac {\ cos 3 \ theta + 3 \ cos \ theta} {4}. \ end {align} sin3θcos3θ = 43sinθ − sin3θ = 4cos3θ + 3cosθ.
Вычислить (cosA-cos3A) / (cosA) + (sinA + sin3A) / (sinA)
$ A $ — угол прямоугольного треугольника. $ \ cos {A} $ и $ \ sin {A} $ — тригонометрические функции, а $ \ cos {3A} $ и $ \ sin {3A} $ — также тригонометрические функции с тройным углом. Четыре функции образуют тригонометрическое выражение.
Четыре функции образуют тригонометрическое выражение.
$ \ dfrac {\ cos {A} — \ cos {3A}} {\ cos {A}} $ + $ $ \ dfrac {\ sin {A} + \ sin {3A}} {\ sin {A} } $
Тригонометрическое выражение можно упростить, чтобы найти его значение.2 {A})
долларов США03
Применить пифагорейскую идентичность
Согласно пифагорейскому тождеству функций синуса и косинуса сумма квадратов синуса и косинуса угла равна единице.
$ = \, \, \, $ 8–4 (1) $
$ = \, \, \, $ 8-4 $
$ = \, \, \, $ 4 $
Это необходимый результат этой тригонометрической задачи.
3.5.1: Формулы суммы к произведению для синуса и косинуса
- Последнее обновление
- Сохранить как PDF
- Сумма синуса и косинуса к формулам произведения
- Обзор
- Обзор (ответы)
- Словарь
- Дополнительные ресурсы
Связь суммы или разности двух тригонометрических функций с произведением.
Можете ли вы решить задачи, состоящие из суммы синусов или косинусов? Например, рассмотрим уравнение:
\ (\ cos 10t + \ cos 3t \)
Вы можете просто вычислить каждое выражение отдельно и добавить их значения в конце. Однако есть более простой способ сделать это. Вы можете сначала упростить уравнение, а затем решить.
Сумма синусов и косинусов для формул произведенияВ некоторых задачах произведение двух тригонометрических функций удобнее находить по сумме двух тригонометрических функций с использованием тождеств.
Вот пример:
\ (\ sin \ alpha + \ sin \ beta = 2 \ sin \ dfrac {\ alpha + \ beta} {2} \ times \ cos \ dfrac {\ alpha — \ beta} {2} \)
Это можно проверить, используя формулы суммы и разницы:
\ (\ begin {array} {l}
2 \ sin \ dfrac {\ alpha + \ beta} {2} \ cos \ dfrac {\ alpha- \ beta} {2} \\
= 2 \ left [\ sin \ left (\ dfrac {\ alpha} {2} + \ dfrac {\ beta} {2} \ right) \ cos \ left (\ dfrac {\ alpha} {2} — \ dfrac {\ beta} {2} \ right) \ right] \\
= 2 \ left [\ left (\ sin \ dfrac {\ alpha} {2} \ cos \ dfrac {\ beta} {2} + \ cos \ dfrac {\ alpha} {2} \ sin \ dfrac {\ beta} {2} \ right) \ left (\ cos \ dfrac {\ alpha} {2} \ cos \ dfrac {\ beta} {2} + \ sin \ dfrac {\ alpha} {2 } \ sin \ dfrac {\ beta} {2} \ right) \ right] \\
= 2 \ left [\ sin \ dfrac {\ alpha} {2} \ cos \ dfrac {\ alpha} {2} \ cos ^ {2} \ dfrac {\ beta} {2} + \ sin ^ {2} \ dfrac {\ alpha} {2} \ sin \ dfrac {\ beta} {2} \ cos \ dfrac {\ beta} {2 } + \ sin \ dfrac {\ beta} {2} \ cos ^ {2} \ dfrac {\ alpha} {2} \ cos \ dfrac {\ beta} {2} + \ sin \ dfrac {\ alpha} {2 } \ sin ^ {2} \ dfrac {\ beta} {2} \ cos \ dfrac {\ alpha} {2} \ right] \\
= 2 \ left [\ sin \ dfrac {\ alpha} {2} \ cos \ dfrac {\ alpha} {2} \ left (\ sin ^ {2} \ dfrac {\ beta} {2} + \ cos ^ {2} \ dfrac {\ beta} {2} \ right) + \ sin \ dfrac {\ beta} {2} \ cos \ dfrac {\ beta} {2} \ left (\ sin ^ {2} \ dfrac {\ alpha} {2} + \ cos ^ {2} \ dfrac {\ alpha } {2} \ ri ght) \ right] \\
= 2 \ left [\ sin \ dfrac {\ alpha} {2} \ cos \ dfrac {\ alpha} {2} + \ sin \ dfrac {\ beta} {2} \ cos \ dfrac {\ beta} {2} \ right] \\
= 2 \ sin \ dfrac {\ alpha} {2} \ cos \ dfrac {\ alpha} {2} +2 \ sin \ dfrac {\ beta} {2 } \ cos \ dfrac {\ beta} {2} \\
= \ sin \ left (2 \ cdot \ dfrac {\ alpha} {2} \ right) + \ sin \ left (2 \ cdot \ dfrac {\ beta } {2} \ right) \\
= \ sin \ alpha + \ sin \ beta
\ end {array} \)
Аналогичным образом могут быть получены следующие варианты:
\ (\ begin {align} \ sin \ alpha — \ sin \ beta & = 2 \ sin \ dfrac {\ alpha — \ beta} {2} \ times \ cos \ dfrac {\ alpha + \ beta} {2} \\ \ cos \ alpha + \ cos \ beta & = 2 \ cos \ dfrac {\ alpha + \ beta} {2} \ times \ cos \ dfrac {\ alpha — \ beta} {2} \\ \ cos \ alpha — \ cos \ beta & = — 2 \ sin \ dfrac {\ alpha + \ beta} {2} \ times \ sin \ dfrac {\ alpha — \ beta} {2} \ end {align} \)
Вот некоторые проблемы, связанные с использованием этого типа преобразования суммы членов в произведение членов.
1. Замените \ (\ sin 5x− \ sin 9x \) на продукт.
Используйте формулу \ (\ sin \ alpha — \ sin \ beta = 2 \ sin \ dfrac {\ alpha — \ beta} {2} \ times \ cos \ dfrac {\ alpha + \ beta} {2} \).
\ (\ begin {align} \ sin 5x− \ sin 9x & = 2 \ sin \ dfrac {5x − 9x} {2} \ cos \ dfrac {5x + 9x} {2} \\ & = 2 \ sin (- 2x) \ cos 7x \\ & = — 2 \ sin 2x \ cos 7x \ end {align} \)
2. Замените \ (\ cos (−3x) + \ cos 8x \) на произведение.
Используйте формулу \ (\ cos \ alpha + \ cos \ beta = 2 \ cos \ dfrac {\ alpha + \ beta} {2} \ times \ cos \ dfrac {\ alpha — \ beta} {2} \)
\ (\ begin {align} \ cos (−3x) + \ cos (8x) & = 2 \ cos \ dfrac {−3x + 8x} {2} \ cos \ dfrac {−3x − 8x} {2} \ \ & = 2 \ cos (2.5x) \ cos (−5.5x) \\ & = 2 \ cos (2.5x) \ cos (5.5x) \ end {align} \)
3. Заменить \ (2 \ sin 7x \ cos 4x \) на сумму.
Это обратное тому, что было сделано в двух предыдущих примерах. Взглянув на четыре формулы выше, возьмите ту, в которой синус и косинус есть произведение: \ (\ sin \ alpha + \ sin \ beta = 2 \ sin \ dfrac {\ alpha + \ beta} {2} \ times \ cos \ dfrac {\ alpha — \ beta} {2} \). Следовательно, \ (7x = \ dfrac {\ alpha + \ beta} {2} \) и \ (4x = \ dfrac {\ alpha — \ beta} {2} \).
Следовательно, \ (7x = \ dfrac {\ alpha + \ beta} {2} \) и \ (4x = \ dfrac {\ alpha — \ beta} {2} \).
\ (\ begin {align} 7x & = \ dfrac {\ alpha + \ beta} {2} & 4x & = \ dfrac {\ alpha — \ beta} {2} \\ & \ qquad \ qquad \ qquad \ text {и } & & \\ 14x & = \ alpha + \ beta & 8x & = \ alpha — \ beta \\ \ alpha & = 14x- \ beta & 8x & = [14x- \ beta] — \ beta \\ & \ qquad \ qquad \ qquad \ text {so} & & \\ \ alpha & = 14x − 3x & −6x & = — 2 \ beta \\ \ alpha & = 11x & 3x & = \ beta \ end {align} \)
Итак, это переводится как \ (\ sin (11x) + \ sin (3x) \).Быстрый способ решения этой проблемы — заметить, что сумма \ (7x \) и \ (4x \) равна \ (11x \), а разница равна \ (3x \).
Пример \ (\ PageIndex {1} \)
Ранее вас просили решить
\ (\ cos 10t + \ cos 3t \)
Решение
Вы можете легко преобразовать это уравнение в произведение двух триггерных функций, используя:
\ (\ cos \ alpha + \ cos \ beta = 2 \ cos \ dfrac {\ alpha + \ beta} {2} \ times \ cos \ dfrac {\ alpha — \ beta} {2} \)
Подставляя известные количества:
\ (\ cos 10t + \ cos 3t = 2 \ cos \ dfrac {13t} {2} \ times \ cos \ dfrac {7t} {2} = 2 \ cos (6. 5т) \ соз (3,5т) \)
5т) \ соз (3,5т) \)
Пример \ (\ PageIndex {2} \)
Выразите сумму как произведение: \ (\ sin 9x + \ sin 5x \)
Решение
Используя формулу суммы к произведению:
\ (\ begin {align} \ sin 9x + \ sin 5x \\ & 2 \ left (\ sin \ left (\ dfrac {9x + 5x} {2} \ right) \ cos \ left (\ dfrac {9x − 5x}) {2} \ right) \ right) \\ & 2 \ sin 7x \ cos 2x \ end {align} \)
Пример \ (\ PageIndex {3} \)
Выразите разницу как произведение: \ (\ cos 4y− \ cos 3y \)
Решение
Используя формулу разности произведений:
\ (\ begin {align} & \ cos 4y− \ cos 3y \\ & −2 \ sin \ left (\ dfrac {4y + 3y} {2} \ right) \ sin \ left (\ dfrac {4y − 3y } {2} \ right) \\ & −2 \ sin \ dfrac {7y} {2} \ sin \ dfrac {y} {2} \ end {align} \)
Пример \ (\ PageIndex {4} \)
Проверьте идентичность (используя формулу суммы к произведению): \ (\ dfrac {\ cos 3a− \ cos 5a} {\ sin 3a− \ sin 5a} = — \ tan 4a \)
Решение
Использование формул разности произведений:
\ (\ begin {align} \ dfrac {\ cos 3a− \ cos 5a} {\ sin 3a− \ sin 5a} & = — \ tan 4a \\ \ dfrac {−2 \ sin \ left (\ dfrac {3a + 5a} {2} \ right) \ sin \ left (\ dfrac {3a − 5a} {2} \ right)} {2 \ sin \ left (\ dfrac {3a − 5a} {2} \ right) \ cos \ left (\ dfrac {3a + 5a} {2} \ right)} & \\ — \ dfrac {\ sin 4a} {\ cos 4a} & \\ — \ tan 4a & \ end {align} \)
Обзор Превратите каждую сумму или разницу в произведение.
- \ (\ sin 3x + \ sin 2x \)
- \ (\ соз 2х + \ соз 5х \)
- \ (\ sin (−x) — \ sin 4x \)
- \ (\ соз 12x + \ соз 3x \)
- \ (\ sin 8x− \ sin 4x \)
- \ (\ sin x + \ sin \ dfrac {1} {2} x \)
- \ (\ соз 3x− \ cos (−3x) \)
Измените каждый продукт на сумму или разницу.
- \ (- 2 \ sin 3.5x \ sin 2.5x \)
- \ (2 \ cos 3.5x \ sin 0.5x \)
- \ (2 \ cos 3.5x \ cos 5.5x \)
- \ (2 \ sin 6x \ cos 2x \)
- \ (- 2 \ sin 3x \ sin x \)
- \ (2 \ грех 4х \ соз х \)
- Покажите, что \ (\ cos \ dfrac {A + B} {2} \ cos \ dfrac {A − B} {2} = \ dfrac {1} {2} (\ cos A + \ cos B) \).
- Пусть \ (u = \ dfrac {A + B} {2} \) и \ (v = \ dfrac {A − B} {2} \). Покажите, что \ (\ cos u \ cos v = \ dfrac {1} {2} (\ cos (u + v) + \ cos (u − v)) \).
Чтобы увидеть ответы на обзор, откройте этот PDF-файл и найдите раздел 3. 13.
13.
Словарь
| Срок | Определение |
|---|---|
| Сумма к формуле продукта | Формула суммы к произведению связывает сумму или разность двух тригонометрических функций с произведением двух тригонометрических функций. |
формул сумма-произведение и произведение-сумма | Precalculus II
Выражение произведений в виде сумм
Мы уже выучили ряд формул, полезных для расширения или упрощения тригонометрических выражений, но иногда нам может потребоваться выразить произведение косинуса и синуса в виде суммы. Мы можем использовать формулы произведения на сумму , которые выражают произведения тригонометрических функций в виде сумм. Давайте сначала исследуем тождество косинуса, а затем тождество синуса.
Выражение произведений как сумм для косинуса
Мы можем вывести формулу произведения на сумму из тождеств суммы и разности для косинуса . Если сложить два уравнения, получим:
Если сложить два уравнения, получим:
[латекс] \ begin {array} {l} {\ begin {array} {c} \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta = \ cos \ left (\ alpha — \ beta \ справа) \\\ подчеркивание {+ \ cos \ alpha \ cos \ beta — \ sin \ alpha \ sin \ beta = \ cos \ left (\ alpha + \ beta \ right)} \ end {array}} \ end {array } \\ [/ latex]
[латекс] \ begin {array} {l} 2 \ cos \ alpha \ cos \ beta = \ cos \ left (\ alpha — \ beta \ right) + \ cos \ left (\ alpha + \ beta \ right) \ hfill \ end {array} \\ [/ latex]
Затем мы делим на [латекс] 2 [/ латекс], чтобы выделить произведение косинусов:
[латекс] \ cos \ alpha \ cos \ beta = \ frac {1} {2} \ left [\ cos \ left (\ alpha — \ beta \ right) + \ cos \ left (\ alpha + \ beta \ right ) \ справа] \\ [/ латекс]
Как: дано произведение косинусов, выразите как сумму.
- Напишите формулу произведения косинусов.
- Подставить полученные углы в формулу.

- Упростить.
Пример 1: Запись произведения в виде суммы с использованием формулы произведения произведения на сумму для косинуса
Запишите следующее произведение косинусов в виде суммы: [latex] 2 \ cos \ left (\ frac {7x} {2} \ right) \ cos \ frac {3x} {2} \\ [/ latex].
Решение
Начнем с написания формулы произведения косинусов:
[латекс] \ cos \ alpha \ cos \ beta = \ frac {1} {2} \ left [\ cos \ left (\ alpha — \ beta \ right) + \ cos \ left (\ alpha + \ beta \ right ) \ справа] \\ [/ латекс]
Затем мы можем подставить указанные углы в формулу и упростить.
[латекс] \ begin {array} {l} 2 \ cos \ left (\ frac {7x} {2} \ right) \ cos \ left (\ frac {3x} {2} \ right) = \ left (2 \ right) \ left (\ frac {1} {2} \ right) \ left [\ cos \ left (\ frac {7x} {2} — \ frac {3x} {2} \ right) + \ cos \ left (\ frac {7x} {2} + \ frac {3x} {2} \ right) \ right] \ hfill \\ \ text {} = \ left [\ cos \ left (\ frac {4x} {2} \ right) + \ cos \ left (\ frac {10x} {2} \ right) \ right] \ hfill \\ \ text {} = \ cos 2x + \ cos 5x \ hfill \ end {array} \\ [/ latex]
Попробуй 1
Используйте формулу произведения к сумме, чтобы записать произведение как сумму или разность: [латекс] \ cos \ left (2 \ theta \ right) \ cos \ left (4 \ theta \ right) \\ [/ latex] .
Решение
Выражение произведения синуса и косинуса в виде суммы
Затем мы выведем формулу произведения к сумме для синуса и косинуса из формул суммы и разности для синуса . Если сложить тождества суммы и разницы, получим:
[латекс] \ begin {массив} {l} {\ begin {array} {l} \ begin {array} {l} \ hfill \\ \ text {} \ sin \ left (\ alpha + \ beta \ right) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta \ hfill \ end {array} \ hfill \\\ underline {+ \ text {} \ sin \ left (\ alpha — \ beta \ right) = \ sin \ alpha \ cos \ beta — \ cos \ alpha \ sin \ beta} \ hfill \ end {array}} \\ \ sin \ left (\ alpha + \ beta \ right) + \ sin \ left (\ alpha — \ beta \ right) = 2 \ sin \ alpha \ cos \ beta \ end {array} \\ [/ latex]
Затем мы делим на 2, чтобы изолировать произведение косинуса и синуса:
[латекс] \ sin \ alpha \ cos \ beta = \ frac {1} {2} \ left [\ sin \ left (\ alpha + \ beta \ right) + \ sin \ left (\ alpha — \ beta \ right) ) \ справа] \\ [/ латекс]
Пример 2: Запись произведения в виде суммы, содержащей только синус или косинус
Выразите следующее произведение как сумму, содержащую только синус или косинус, но без произведений: [латекс] \ sin \ left (4 \ theta \ right) \ cos \ left (2 \ theta \ right) \\ [/ latex].
Решение
Напишите формулу произведения синуса и косинуса. Затем подставьте указанные значения в формулу и упростите.
[латекс] \ begin {array} {l} \ sin \ alpha \ cos \ beta = \ frac {1} {2} \ left [\ sin \ left (\ alpha + \ beta \ right) + \ sin \ left (\ alpha — \ beta \ right) \ right] \ hfill \\ \ sin \ left (4 \ theta \ right) \ cos \ left (2 \ theta \ right) = \ frac {1} {2} \ left [ \ sin \ left (4 \ theta +2 \ theta \ right) + \ sin \ left (4 \ theta -2 \ theta \ right) \ right] \ hfill \\ = \ frac {1} {2} \ left [ \ sin \ left (6 \ theta \ right) + \ sin \ left (2 \ theta \ right) \ right] \ hfill \ end {array} \\ [/ latex]
Попробуй 2
Используйте формулу произведения к сумме, чтобы записать произведение в виде суммы: [латекс] \ sin \ left (x + y \ right) \ cos \ left (x-y \ right) \\ [/ latex].
Решение
Выражение произведений синусов через косинус
Выражение произведения синусов через косинус также получается из тождеств суммы и разности для косинуса. В этом случае мы сначала вычтем две формулы косинуса:
В этом случае мы сначала вычтем две формулы косинуса:
[латекс] \ begin {массив} {l} {\ begin {array} {l} \ begin {array} {l} \ hfill \\ \ text {} \ cos \ left (\ alpha — \ beta \ right) = \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta \ hfill \ end {array} \ hfill \\\ underline {- \ text {} \ cos \ left (\ alpha + \ beta \ right) = — \ left (\ cos \ alpha \ cos \ beta — \ sin \ alpha \ sin \ beta \ right)} \ hfill \ end {array}} \ hfill \\ \ cos \ left (\ alpha — \ beta \ right ) — \ cos \ left (\ alpha + \ beta \ right) = 2 \ sin \ alpha \ sin \ beta \ hfill \ end {array} \\ [/ latex]
Затем мы делим на 2, чтобы выделить произведение синусов:
[латекс] \ sin \ alpha \ sin \ beta = \ frac {1} {2} \ left [\ cos \ left (\ alpha — \ beta \ right) — \ cos \ left (\ alpha + \ beta \ right) ) \ справа] \\ [/ латекс]
Аналогичным образом мы могли бы выразить произведение косинусов через синус или вывести другие формулы произведения произведения на сумму.
Общее примечание: формулы произведения на сумму
Формула произведения на сумму выглядит следующим образом:
[латекс] \ cos \ alpha \ cos \ beta = \ frac {1} {2} \ left [\ cos \ left (\ alpha — \ beta \ right) + \ cos \ left (\ alpha + \ beta \ right ) \ справа] \\ [/ латекс]
[латекс] \ sin \ alpha \ cos \ beta = \ frac {1} {2} \ left [\ sin \ left (\ alpha + \ beta \ right) + \ sin \ left (\ alpha — \ beta \ right) ) \ справа] \\ [/ латекс]
[латекс] \ sin \ alpha \ sin \ beta = \ frac {1} {2} \ left [\ cos \ left (\ alpha — \ beta \ right) — \ cos \ left (\ alpha + \ beta \ right) ) \ справа] \\ [/ латекс]
[латекс] \ cos \ alpha \ sin \ beta = \ frac {1} {2} \ left [\ sin \ left (\ alpha + \ beta \ right) — \ sin \ left (\ alpha — \ beta \ right) ) \ справа] \\ [/ латекс]
Пример 3. Выразите произведение в виде суммы или разницы
Запишите [латекс] \ cos \ left (3 \ theta \ right) \ cos \ left (5 \ theta \ right) \\ [/ latex] как сумму или разность.
Решение
У нас есть произведение косинусов, поэтому мы начнем с написания соответствующей формулы. Затем подставляем заданные углы и упрощаем.
[латекс] \ begin {array} {ll} \ text {} \ cos \ alpha \ cos \ beta = \ frac {1} {2} \ left [\ cos \ left (\ alpha — \ beta \ right) + \ cos \ left (\ alpha + \ beta \ right) \ right] \ hfill & \ hfill \\ \ cos \ left (3 \ theta \ right) \ cos \ left (5 \ theta \ right) = \ frac {1 } {2} \ left [\ cos \ left (3 \ theta -5 \ theta \ right) + \ cos \ left (3 \ theta +5 \ theta \ right) \ right] \ hfill & \ hfill \\ \ text {} = \ frac {1} {2} \ left [\ cos \ left (2 \ theta \ right) + \ cos \ left (8 \ theta \ right) \ right] \ hfill & \ text {Используйте четно-нечетное личность}.\ hfill \ end {array} \\ [/ latex]
Попробовать 3
Используйте формулу произведения к сумме, чтобы вычислить [латекс] \ cos \ frac {11 \ pi} {12} \ cos \ frac {\ pi} {12} \\ [/ latex].
Решение
Выражение сумм в виде произведений
Для некоторых задач требуется обратный процесс, который мы только что использовали. Формула суммы к произведению позволяет нам выражать суммы синусов или косинусов в виде произведений. Эти формулы могут быть получены из тождеств произведения к сумме. Например, с помощью нескольких замен мы можем вывести идентичность суммы к произведению для синуса .Пусть [latex] \ frac {u + v} {2} = \ alpha [/ latex] и [latex] \ frac {u-v} {2} = \ beta [/ latex].
Формула суммы к произведению позволяет нам выражать суммы синусов или косинусов в виде произведений. Эти формулы могут быть получены из тождеств произведения к сумме. Например, с помощью нескольких замен мы можем вывести идентичность суммы к произведению для синуса .Пусть [latex] \ frac {u + v} {2} = \ alpha [/ latex] и [latex] \ frac {u-v} {2} = \ beta [/ latex].
Затем,
[латекс] \ begin {array} {l} \ alpha + \ beta = \ frac {u + v} {2} + \ frac {uv} {2} \ hfill \\ \ text {} = \ frac {2u } {2} \ hfill \\ \ text {} = u \ hfill \\ \ hfill \\ \ alpha — \ beta = \ frac {u + v} {2} — \ frac {uv} {2} \ hfill \ \ \ text {} = \ frac {2v} {2} \ hfill \\ \ text {} = v \ hfill \ end {array} [/ latex]
Таким образом, заменив [latex] \ alpha [/ latex] и [latex] \ beta [/ latex] в формуле произведения на сумму заменяющими выражениями, мы получим
[латекс] \ begin {array} {lll} \ text {} \ sin \ alpha \ cos \ beta = \ frac {1} {2} \ left [\ sin \ left (\ alpha + \ beta \ right) + \ sin \ left (\ alpha — \ beta \ right) \ right] \ hfill & \ hfill & \ hfill \\ \ text {} \ sin \ left (\ frac {u + v} {2} \ right) \ cos \ left (\ frac {uv} {2} \ right) = \ frac {1} {2} \ left [\ sin u + \ sin v \ right] \ hfill & \ hfill & \ text {Заменить} \ left ( \ alpha + \ beta \ right) \ text {and} \ left (\ alpha — \ beta \ right) \ hfill \\ 2 \ sin \ left (\ frac {u + v} {2} \ right) \ cos \ left (\ frac {uv} {2} \ right) = \ sin u + \ sin v \ hfill & \ hfill & \ hfill \ end {array} [/ latex]
Остальные тождества суммы к продукту выводятся аналогично.
Общее примечание: формулы суммы к произведению
Формулы суммирования суммы к произведению выглядят следующим образом:
[латекс] \ sin \ alpha + \ sin \ beta = 2 \ sin \ left (\ frac {\ alpha + \ beta} {2} \ right) \ cos \ left (\ frac {\ alpha — \ beta} { 2} \ справа) [/ латекс]
[латекс] \ sin \ alpha — \ sin \ beta = 2 \ sin \ left (\ frac {\ alpha — \ beta} {2} \ right) \ cos \ left (\ frac {\ alpha + \ beta} { 2} \ справа) [/ латекс]
[латекс] \ cos \ alpha — \ cos \ beta = -2 \ sin \ left (\ frac {\ alpha + \ beta} {2} \ right) \ sin \ left (\ frac {\ alpha — \ beta} {2} \ right) [/ латекс]
[латекс] \ cos \ alpha + \ cos \ beta = 2 \ cos \ left (\ frac {\ alpha + \ beta} {2} \ right) \ cos \ left (\ frac {\ alpha — \ beta} { 2} \ справа) [/ латекс]
Пример 4: Запись разности синусов в виде произведения
Запишите в качестве произведения следующую разницу выражений синусов: [латекс] \ sin \ left (4 \ theta \ right) — \ sin \ left (2 \ theta \ right) [/ latex].
Решение
Начнем с написания формулы для разности синусов.
[латекс] \ sin \ alpha — \ sin \ beta = 2 \ sin \ left (\ frac {\ alpha — \ beta} {2} \ right) \ cos \ left (\ frac {\ alpha + \ beta} { 2} \ справа) [/ латекс]
Подставьте значения в формулу и упростите.
[латекс] \ begin {array} {l} \ sin \ left (4 \ theta \ right) — \ sin \ left (2 \ theta \ right) = 2 \ sin \ left (\ frac {4 \ theta -2 \ theta} {2} \ right) \ cos \ left (\ frac {4 \ theta +2 \ theta} {2} \ right) \ hfill \\ \ text {} = 2 \ sin \ left (\ frac {2 \ theta} {2} \ right) \ cos \ left (\ frac {6 \ theta} {2} \ right) \ hfill \\ \ text {} = 2 \ sin \ theta \ cos \ left (3 \ theta \ справа) \ hfill \ end {array} [/ latex]
Попробовать 4
Используйте формулу суммы к произведению, чтобы записать сумму в виде произведения: [латекс] \ sin \ left (3 \ theta \ right) + \ sin \ left (\ theta \ right) [/ latex].{\ circ} \ right) \ hfill \\ \ text {} = — 2 \ left (\ frac {\ sqrt {2}} {2} \ right) \ left (- \ frac {1} {2} \ right ) \ hfill \\ \ text {} = \ frac {\ sqrt {2}} {2} \ hfill \ end {array} [/ latex]
Пример 6: Подтверждение личности
Подтвердите личность:
[латекс] \ frac {\ cos \ left (4t \ right) — \ cos \ left (2t \ right)} {\ sin \ left (4t \ right) + \ sin \ left (2t \ right)} = — \ тан т [/ латекс]
Решение
Мы начнем с левой стороны, более сложной части уравнения, и перепишем выражение, пока оно не совпадет с правой частью.
[латекс] \ begin {array} {l} \ frac {\ cos \ left (4t \ right) — \ cos \ left (2t \ right)} {\ sin \ left (4t \ right) + \ sin \ left (2t \ right)} = \ frac {-2 \ sin \ left (\ frac {4t + 2t} {2} \ right) \ sin \ left (\ frac {4t — 2t} {2} \ right)} { 2 \ sin \ left (\ frac {4t + 2t} {2} \ right) \ cos \ left (\ frac {4t — 2t} {2} \ right)} \ hfill \\ \ text {} = \ frac { -2 \ sin \ left (3t \ right) \ sin t} {2 \ sin \ left (3t \ right) \ cos t} \ hfill \\ \ text {} = \ frac {- \ overline {) 2} \ overline {) \ sin \ left (3t \ right)} \ sin t} {\ overline {) 2} \ overline {) \ sin \ left (3t \ right)} \ cos t} \ hfill \\ \ text {} = — \ frac {\ sin t} {\ cos t} \ hfill \\ \ text {} = — \ tan t \ hfill \ end {array} [/ latex]
Анализ решения
Напомним, что проверка тригонометрических тождеств имеет свой собственный набор правил.{2} \ theta [/ латекс].
Решение
Ключевые уравнения
| Формулы произведения-суммы | [латекс] \ begin {array} {l} \ hfill \\ \ cos \ alpha \ cos \ beta = \ frac {1} {2} \ left [\ cos \ left (\ alpha — \ beta \ right) + \ cos \ left (\ alpha + \ beta \ right) \ right] \ hfill \\ \ sin \ alpha \ cos \ beta = \ frac {1} {2} \ left [\ sin \ left (\ alpha + \ beta \ right) + \ sin \ left (\ alpha — \ beta \ right) \ right] \ hfill \\ \ sin \ alpha \ sin \ beta = \ frac {1} {2} \ left [\ cos \ left (\ alpha — \ beta \ right) — \ cos \ left (\ alpha + \ beta \ right) \ right] \ hfill \\ \ cos \ alpha \ sin \ beta = \ frac {1} {2} \ left [\ sin \ left (\ alpha + \ beta \ right) — \ sin \ left (\ alpha — \ beta \ right) \ right] \ hfill \ end {array} [/ latex] |
| Формулы суммы к произведению | [латекс] \ begin {array} {l} \ hfill \\ \ sin \ alpha + \ sin \ beta = 2 \ sin \ left (\ frac {\ alpha + \ beta} {2} \ right) \ cos \ left (\ frac {\ alpha — \ beta} {2} \ right) \ hfill \\ \ sin \ alpha — \ sin \ beta = 2 \ sin \ left (\ frac {\ alpha — \ beta} {2} \ справа) \ cos \ left (\ frac {\ alpha + \ beta} {2} \ right) \ hfill \\ \ cos \ alpha — \ cos \ beta = -2 \ sin \ left (\ frac {\ alpha + \ beta} {2} \ right) \ sin \ left (\ frac {\ alpha — \ beta} {2} \ right) \ hfill \\ \ cos \ alpha + \ cos \ beta = 2 \ cos \ left (\ frac {\ alpha + \ beta} {2} \ right) \ cos \ left (\ frac {\ alpha — \ beta} {2} \ right) \ hfill \ end {array} [/ latex] |
Ключевые понятия
- Из тождеств суммы и разности мы можем вывести формулы произведения к сумме и формулы суммы к произведению для синуса и косинуса.

- Мы можем использовать формулы произведения на сумму, чтобы переписать произведения синусов, косинусов и косинусов как суммы или разности синусов и косинусов.
- Мы также можем получить тождества суммы к продукту из тождеств продукта к сумме, используя подстановку.
- Мы можем использовать формулы суммы к произведению, чтобы переписать сумму или разность синусов, косинусов или произведений синусов и косинусов как произведений синусов и косинусов.
- Тригонометрические выражения часто проще вычислить с помощью формул.
- Идентичность можно проверить с помощью других формул или путем преобразования выражений в синусы и косинусы. Чтобы проверить идентичность, мы выбираем более сложную сторону знака равенства и переписываем ее до тех пор, пока она не превратится в другую сторону.
Глоссарий
- Формула произведения на сумму
- тригонометрическое обозначение, которое позволяет записать произведение тригонометрических функций в виде суммы или разности тригонометрических функций
- Формула суммы к произведению
- тригонометрическая идентичность, которая позволяет с помощью подстановки записать сумму тригонометрических функций как произведение тригонометрических функций
Упражнения по разделам
1. \ circ \ right) [/ latex], один из которых использует продукт для суммирования. Какой способ проще?
\ circ \ right) [/ latex], один из которых использует продукт для суммирования. Какой способ проще?
3. Объясните ситуацию, когда мы преобразовали уравнение из суммы в произведение, и приведите пример.
4. Объясните ситуацию, в которой мы преобразовали бы уравнение из произведения в сумму, и приведите пример.
Для следующих упражнений перепишите произведение как сумму или разность.
5. [латекс] 16 \ sin \ left (16x \ right) \ sin \ left (11x \ right) [/ latex]
6. [латекс] 20 \ cos \ left (36t \ right) \ cos \ left (6t \ right) [/ latex]
7.[латекс] 2 \ sin \ left (5x \ right) \ cos \ left (3x \ right) [/ латекс]
8. [латекс] 10 \ cos \ left (5x \ right) \ sin \ left (10x \ right) [/ latex]
9. [латекс] \ sin \ left (-x \ right) \ sin \ left (5x \ right) [/ латекс]
10. [латекс] \ sin \ left (3x \ right) \ cos \ left (5x \ right) [/ latex]
Для следующих упражнений перепишите сумму или разницу как произведение. {2} x [/ латекс]
{2} x [/ латекс]
36.{2} x \ right) = \ cos \ left (3x \ right) + \ cos x [/ латекс]
37. [латекс] 2 \ tan x \ cos \ left (3x \ right) = \ sec x \ left (\ sin \ left (4x \ right) — \ sin \ left (2x \ right) \ right) [/ латекс]
38. [латекс] \ cos \ left (a + b \ right) + \ cos \ left (a-b \ right) = 2 \ cos a \ cos b [/ latex]
Для следующих упражнений перепишите сумму как произведение двух функций или произведение как сумму двух функций. Дайте свой ответ в виде синусов и косинусов. Затем оцените окончательный ответ численно с округлением до четырех знаков после запятой.{\ circ} \ right) [/ латекс]
В следующих упражнениях алгебраически определите, является ли каждое из данных выражений истинным тождеством. Если это не идентичность, замените правую часть выражением, эквивалентным левой части. Проверьте результаты, построив графики обоих выражений на калькуляторе.
44. [латекс] 2 \ sin \ left (2x \ right) \ sin \ left (3x \ right) = \ cos x- \ cos \ left (5x \ right) [/ latex]
45. [латекс] \ frac {\ cos \ left (10 \ theta \ right) + \ cos \ left (6 \ theta \ right)} {\ cos \ left (6 \ theta \ right) — \ cos \ left (10 \ theta \ right)} = \ cot \ left (2 \ theta \ right) \ cot \ left (8 \ theta \ right) [/ latex]
[латекс] \ frac {\ cos \ left (10 \ theta \ right) + \ cos \ left (6 \ theta \ right)} {\ cos \ left (6 \ theta \ right) — \ cos \ left (10 \ theta \ right)} = \ cot \ left (2 \ theta \ right) \ cot \ left (8 \ theta \ right) [/ latex]
46.[латекс] \ frac {\ sin \ left (3x \ right) — \ sin \ left (5x \ right)} {\ cos \ left (3x \ right) + \ cos \ left (5x \ right)} = \ tan х [/ латекс]
47. [латекс] 2 \ cos \ left (2x \ right) \ cos x + \ sin \ left (2x \ right) \ sin x = 2 \ sin x [/ latex]
48. [латекс] \ frac {\ sin \ left (2x \ right) + \ sin \ left (4x \ right)} {\ sin \ left (2x \ right) — \ sin \ left (4x \ right)} = — \ tan \ left (3x \ right) \ cot x [/ latex]
В следующих упражнениях упростите выражение до одного члена, затем изобразите исходную функцию и свою упрощенную версию, чтобы убедиться, что они идентичны.
49. [латекс] \ frac {\ sin \ left (9t \ right) — \ sin \ left (3t \ right)} {\ cos \ left (9t \ right) + \ cos \ left (3t \ right)} [/ латекс]
50.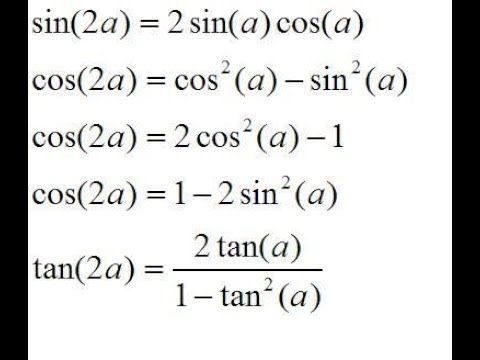 [латекс] 2 \ sin \ left (8x \ right) \ cos \ left (6x \ right) — \ sin \ left (2x \ right) [/ латекс]
[латекс] 2 \ sin \ left (8x \ right) \ cos \ left (6x \ right) — \ sin \ left (2x \ right) [/ латекс]
51. [латекс] \ frac {\ sin \ left (3x \ right) — \ sin x} {\ sin x} [/ latex]
52. [латекс] \ frac {\ cos \ left (5x \ right) + \ cos \ left (3x \ right)} {\ sin \ left (5x \ right) + \ sin \ left (3x \ right)} [/ латекс]
53. [латекс] \ sin x \ cos \ left (15x \ right) — \ cos x \ sin \ left (15x \ right) [/ latex]
Для следующих упражнений докажите следующие формулы суммирования произведений.
54. [латекс] \ sin x- \ sin y = 2 \ sin \ left (\ frac {xy} {2} \ right) \ cos \ left (\ frac {x + y} {2} \ right) [ / латекс]
55. [латекс] \ cos x + \ cos y = 2 \ cos \ left (\ frac {x + y} {2} \ right) \ cos \ left (\ frac {xy} {2} \ right) [/ латекс]
Для следующих упражнений подтвердите личность.
56. [латекс] \ frac {\ sin \ left (6x \ right) + \ sin \ left (4x \ right)} {\ sin \ left (6x \ right) — \ sin \ left (4x \ right)} = \ загар \ влево (5x \ вправо) \ кроватка x [/ латекс]
57. [латекс] \ frac {\ cos \ left (3x \ right) + \ cos x} {\ cos \ left (3x \ right) — \ cos x} = — \ cot \ left (2x \ right) \ детская кроватка x [/ латекс]
[латекс] \ frac {\ cos \ left (3x \ right) + \ cos x} {\ cos \ left (3x \ right) — \ cos x} = — \ cot \ left (2x \ right) \ детская кроватка x [/ латекс]
58.{2} \ left (3x \ right) [/ латекс]
63. [латекс] \ tan \ left (\ frac {\ pi} {4} -t \ right) = \ frac {1- \ tan t} {1+ \ tan t} [/ latex]
Регулятор транскрипции Sin3A способствует онкогенному потенциалу STAT3
Графический реферат
Резюме
Эпигенетическое молчание промоторных и энхансерных областей — обычное явление в злокачественных клетках. Фактор транскрипции STAT3 аберрантно активируется в нескольких опухолях, где его конститутивное ацетилирование объясняет репрессию транскрипции ряда генов-супрессоров опухолей (TSG) с помощью молекулярных механизмов, которые еще предстоит понять.Используя нуклеофозмин-анапластическую киназу-положительную (NPM-ALK + ) анапластическую крупноклеточную лимфому (ALCL) в качестве модельной системы, мы обнаружили в клетках и ксенотрансплантатах опухолей, полученных от пациентов, что STAT3 конститутивно ацетилируется в результате активности ALK. Ацетилирование STAT3 зависело от интактной ALK-индуцированной PI3K- и mTORC1-зависимой передачи сигналов и было чувствительно к ресвератролу. Ресвератрол снижал ацетилирование STAT3, спасал экспрессию TSG и индуцировал апоптотическую гибель клеток ALCL. STAT3 конститутивно связывает комплекс транскрипционного репрессора Sin3A, а STAT3 и Sin3A связывают промоторную область молчащего TSG посредством механизма, чувствительного к ресвератролу.Подавление SIN3A вызывало повторную экспрессию TSG, индуцировало апоптотическую гибель клеток ALCL in vitro и препятствовало канцерогенному потенциалу ALCL in vivo . Конститутивное взаимодействие STAT3-Sin3A было также обнаружено в клетках аденокарциномы груди и оказалось критическим для подавления TSG и выживания клеток. В совокупности эти результаты предполагают, что ацетилирование STAT3, управляемое онкогенами, и его конститутивная ассоциация с Sin3A представляют собой новые и сопутствующие события, вносящие вклад в онкогенный потенциал STAT3.
Ацетилирование STAT3 зависело от интактной ALK-индуцированной PI3K- и mTORC1-зависимой передачи сигналов и было чувствительно к ресвератролу. Ресвератрол снижал ацетилирование STAT3, спасал экспрессию TSG и индуцировал апоптотическую гибель клеток ALCL. STAT3 конститутивно связывает комплекс транскрипционного репрессора Sin3A, а STAT3 и Sin3A связывают промоторную область молчащего TSG посредством механизма, чувствительного к ресвератролу.Подавление SIN3A вызывало повторную экспрессию TSG, индуцировало апоптотическую гибель клеток ALCL in vitro и препятствовало канцерогенному потенциалу ALCL in vivo . Конститутивное взаимодействие STAT3-Sin3A было также обнаружено в клетках аденокарциномы груди и оказалось критическим для подавления TSG и выживания клеток. В совокупности эти результаты предполагают, что ацетилирование STAT3, управляемое онкогенами, и его конститутивная ассоциация с Sin3A представляют собой новые и сопутствующие события, вносящие вклад в онкогенный потенциал STAT3.
Значение: Это исследование определяет транскрипционный регуляторный комплекс Sin3A как медиатор активности репрессора транскрипции STAT3 и идентифицирует ось STAT3 / Sin3A как лекарственную мишень для противодействия зависимым от STAT3 опухолям.
Введение
STAT3 представляет собой фактор транскрипции, обнаруживаемый в конститутивно активной форме при большом количестве злокачественных новообразований, включая рак груди, яичников, поджелудочной железы, желудка и лейкоз, после аберрантной активации онкопротеинов и растворимых факторов (1– 4).Он также играет центральную роль в онкогенном потенциале химерного белка нуклеофозмин (NPM) -анапластическая киназа лимфомы (ALK) (NPM-ALK), который является результатом хромосомной транслокации, обнаруженной в подмножестве CD30 + неходжкинских T -клеточные анапластические крупноклеточные лимфомы (ALCL; ссылки 5, 6). В ALK + ALCL химерный белок NPM-ALK конститутивно активируется посредством аутофосфорилирования и оказался онкогенным как in vitro , так и in vivo (7, 8). Клеточные линии ALK + и образцы пациентов обнаруживают конститутивную активацию STAT3 (9-11), который вносит вклад в NPM-ALK-зависимую трансформацию, действуя одновременно как активатор транскрипции и как репрессор транскрипции.Действительно, хотя конститутивное фосфорилирование STAT3 на Tyr705 поддерживает каноническую онкогенную роль STAT3 как активатора генов, участвующих в пролиферации, выживании, инвазии и иммуносупрессии клеток (12, 13), дерегуляция STAT3 также приводит к аберрантному эпигенетическому молчанию нескольких генов-супрессоров опухолей. (TSG), включая гены, участвующие в идентичности Т-клеток и апоптозе (14–16). Было показано, что вмешательство в экспрессию STAT3, а также лечение деметилирующими агентами или ингибиторами деацетилаз восстанавливают экспрессию TSG и индуцируют апоптоз клеток ALCL ALK + , что лежит в основе важного вклада STAT3-опосредованного эпигенетического молчания в трансформацию клеток (14, 15, 17, 18).
Клеточные линии ALK + и образцы пациентов обнаруживают конститутивную активацию STAT3 (9-11), который вносит вклад в NPM-ALK-зависимую трансформацию, действуя одновременно как активатор транскрипции и как репрессор транскрипции.Действительно, хотя конститутивное фосфорилирование STAT3 на Tyr705 поддерживает каноническую онкогенную роль STAT3 как активатора генов, участвующих в пролиферации, выживании, инвазии и иммуносупрессии клеток (12, 13), дерегуляция STAT3 также приводит к аберрантному эпигенетическому молчанию нескольких генов-супрессоров опухолей. (TSG), включая гены, участвующие в идентичности Т-клеток и апоптозе (14–16). Было показано, что вмешательство в экспрессию STAT3, а также лечение деметилирующими агентами или ингибиторами деацетилаз восстанавливают экспрессию TSG и индуцируют апоптоз клеток ALCL ALK + , что лежит в основе важного вклада STAT3-опосредованного эпигенетического молчания в трансформацию клеток (14, 15, 17, 18).
Взаимодействие STAT3 с эпигенетическими регуляторами изучается с целью выявления новых терапевтических мишеней. Недавние сообщения подчеркнули роль ацетилирования в репрессии транскрипции, опосредованной STAT3. В самом деле, помимо фосфорилирования по тирозиновым и сериновым остаткам, STAT3 обнаруживается гиперацетилированным при ряде злокачественных новообразований, а ацетилированный STAT3, как было показано, обеспечивает эпигенетическое молчание TSG (19-25). Следует отметить, что ацетилирование STAT3 способствует связыванию с Sin3A (26), членом комплекса регуляторов транскрипции Sin3A, который включает гистоновые деацетилазы (HDAC) и ДНК-метилтрансферазы (DNMT).На сегодняшний день вопрос о том, играет ли Sin3A роль в опосредованном STAT3 подавлении гена-супрессора опухоли при раке, остается неисследованным.
Недавние сообщения подчеркнули роль ацетилирования в репрессии транскрипции, опосредованной STAT3. В самом деле, помимо фосфорилирования по тирозиновым и сериновым остаткам, STAT3 обнаруживается гиперацетилированным при ряде злокачественных новообразований, а ацетилированный STAT3, как было показано, обеспечивает эпигенетическое молчание TSG (19-25). Следует отметить, что ацетилирование STAT3 способствует связыванию с Sin3A (26), членом комплекса регуляторов транскрипции Sin3A, который включает гистоновые деацетилазы (HDAC) и ДНК-метилтрансферазы (DNMT).На сегодняшний день вопрос о том, играет ли Sin3A роль в опосредованном STAT3 подавлении гена-супрессора опухоли при раке, остается неисследованным.
Здесь, используя NPM-ALK + ALCL в качестве модельной системы, мы показываем, что STAT3 гиперацетилирован в клетках ALCL и полученном от пациента ксенотрансплантате опухоли и что индуцирование деацетилирования STAT3 с помощью ресвератрола восстанавливает транскрипцию TSG. Кроме того, мы идентифицировали комплекс Sin3A в качестве конститутивного партнера по связыванию STAT3 и ключевого медиатора репрессии транскрипции и онкогенного потенциала STAT3-зависимых TSG как в клетках NPM-ALK + ALCL, так и в клетках аденокарциномы молочной железы.Таким образом, мы предполагаем, что Sin3A вносит вклад в управляемое STAT3 подавление TSG и онкогенный потенциал.
Кроме того, мы идентифицировали комплекс Sin3A в качестве конститутивного партнера по связыванию STAT3 и ключевого медиатора репрессии транскрипции и онкогенного потенциала STAT3-зависимых TSG как в клетках NPM-ALK + ALCL, так и в клетках аденокарциномы молочной железы.Таким образом, мы предполагаем, что Sin3A вносит вклад в управляемое STAT3 подавление TSG и онкогенный потенциал.
Материалы и методы
Клеточные линии и лекарственные препараты
Клетки ALCL человека Клетки SU-DHL-1, Sup-M2, JB6 и OCI-Ly12 были любезно предоставлены Роберто Кьярле и Роберто Пива (Университет Турина, Турин, США). Италия). Клетки рака молочной железы человека MDA-MB-231, MCF7 и HEK-293 были любезно предоставлены Розой Бернарди (Научный институт Сан-Раффаэле, Милан, Италия). Идентичность клеток была окончательно проанализирована в июне и июле 2018 года с помощью анализа коротких тандемных повторов (GenePrint 10 System, Promega и Fragment Length Analysuis; Eurofins genomics) и подтверждена для всех, за исключением клеток JB6 и OCI-Ly12, для которых существует нет ссылки в принятой базе данных (https: // www. dsmz.de). Образцы ALCL культивировали в среде RPMI 1640 с добавлением антибиотиков, глутамина и 10% FBS. Клетки MDA-MB-231, MCF7 и HEK-293 культивировали в среде DMEM с добавлением антибиотиков, глутамина и 10% FBS. Клетки обычно тестировали на загрязнение Mycoplasma и пассировали не более чем за 1 месяц до экспериментов. Там, где указано, клетки обрабатывали кризотинибом (Sigma Aldrich, номер в каталоге PZ0191), LY294002 (Promega, номер в каталоге V1201), рапамицином (Calbiochem, номер в каталоге.553210), ресвератрол (Sigma Aldrich, каталожный номер R5010), U0126 (Promega, каталожный номер V1121). Рост и жизнеспособность клеток определяли по исключению трипанового синего (Gibco, номер в каталоге 15250-061).
dsmz.de). Образцы ALCL культивировали в среде RPMI 1640 с добавлением антибиотиков, глутамина и 10% FBS. Клетки MDA-MB-231, MCF7 и HEK-293 культивировали в среде DMEM с добавлением антибиотиков, глутамина и 10% FBS. Клетки обычно тестировали на загрязнение Mycoplasma и пассировали не более чем за 1 месяц до экспериментов. Там, где указано, клетки обрабатывали кризотинибом (Sigma Aldrich, номер в каталоге PZ0191), LY294002 (Promega, номер в каталоге V1201), рапамицином (Calbiochem, номер в каталоге.553210), ресвератрол (Sigma Aldrich, каталожный номер R5010), U0126 (Promega, каталожный номер V1121). Рост и жизнеспособность клеток определяли по исключению трипанового синего (Gibco, номер в каталоге 15250-061).
Вестерн-блоттинг и иммунопреципитация
Общие лизаты выделяли в 2% SDS Tris-HCl 65 ммоль / л буфера для лизиса pH 6,8 и обрабатывали ультразвуком. Цитозольные и ядерные экстракты получали последовательным гипотоническим методом [HEPES 20 ммоль / л pH 8, NaCl 10 ммоль / л, MgCl 2 1,5 ммоль / л, EDTA 0,2 ммоль / л, Triton 0.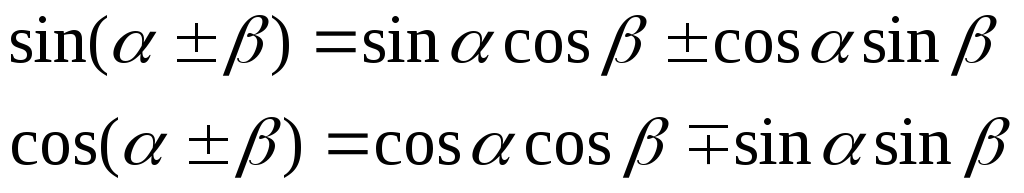 1%, глицерин 20%, NaV 3 O 4 , NaF, TSA 1 мкмоль / л, набор ингибиторов протеаз I (Calbiochem, каталожный номер 539131)] и гипертонический (гипотонический буфер + NaCl 400 ммоль / л и ДНКаза I) экстракция. Концентрацию белка оценивали с помощью модифицированного анализа белка Лоури (DC Protein Assay Reagents, Bio-Rad, каталожный номер 500-0116). Равные количества лизата разделяли с помощью SDS-PAGE, переносили на нитроцеллюлозную мембрану, блокировали 5% молоком в TBS и подвергали иммуноблоттингу.
1%, глицерин 20%, NaV 3 O 4 , NaF, TSA 1 мкмоль / л, набор ингибиторов протеаз I (Calbiochem, каталожный номер 539131)] и гипертонический (гипотонический буфер + NaCl 400 ммоль / л и ДНКаза I) экстракция. Концентрацию белка оценивали с помощью модифицированного анализа белка Лоури (DC Protein Assay Reagents, Bio-Rad, каталожный номер 500-0116). Равные количества лизата разделяли с помощью SDS-PAGE, переносили на нитроцеллюлозную мембрану, блокировали 5% молоком в TBS и подвергали иммуноблоттингу.
Для иммунопреципитации эндогенных белков ядерные лизаты разбавляли до изотонического состояния и иммунопреципитировали с использованием 1 мкг антител (анти-Sin3A sc-994 / sc-767, нормальный кроличий IgG sc-2027 были от Santa Cruz Biotechnology).Иммунокомплексы восстанавливали путем добавления белка A Dynabeads (Invitrogen, номер по каталогу 10002D) или белка G Sepharose 4 Fast Flow (GE Healthcare, номер по каталогу 71-7083-00) и анализировали с помощью иммуноблоттинга. Для иммунопреципитации мутантов Sin3A и STAT3 клетки Hek293 лизировали в модифицированном буфере RIPA через 48 часов после трансфекции и иммунопреципитировали 1 мкг антител против Sin3A (анти-Sin3A sc-994 / sc-767 и D9D6). Иммунокомплексы восстанавливали путем добавления Protein G Sepharose 4 Fast Flow (GE Healthcare, каталог №71-7083-00) и проанализировали иммуноблоттингом. Были использованы следующие первичные антитела: анти-STAT3 (124H6), анти-Ac-Lys 685 -STAT3 (# 2523), анти-P-Tyr 705 STAT3 (# 9131), анти-P-Ser 727 STAT3 (# 9134), anti-S6 (# 2317), anti-PS 235/236 S6 (# 2211), anti-Sin3A (# D1B7), anti-PY 1606 NPM-ALK (# 3341) и anti-Blimp1 (# 9115) от Cell Signaling Technology; антитела против Sin3A (sc-994, sc-767) и против актина (sc-1616) были от Santa Cruz Biotechnology; и антитело против тубулина (T6074) было от Sigma.
Для иммунопреципитации мутантов Sin3A и STAT3 клетки Hek293 лизировали в модифицированном буфере RIPA через 48 часов после трансфекции и иммунопреципитировали 1 мкг антител против Sin3A (анти-Sin3A sc-994 / sc-767 и D9D6). Иммунокомплексы восстанавливали путем добавления Protein G Sepharose 4 Fast Flow (GE Healthcare, каталог №71-7083-00) и проанализировали иммуноблоттингом. Были использованы следующие первичные антитела: анти-STAT3 (124H6), анти-Ac-Lys 685 -STAT3 (# 2523), анти-P-Tyr 705 STAT3 (# 9131), анти-P-Ser 727 STAT3 (# 9134), anti-S6 (# 2317), anti-PS 235/236 S6 (# 2211), anti-Sin3A (# D1B7), anti-PY 1606 NPM-ALK (# 3341) и anti-Blimp1 (# 9115) от Cell Signaling Technology; антитела против Sin3A (sc-994, sc-767) и против актина (sc-1616) были от Santa Cruz Biotechnology; и антитело против тубулина (T6074) было от Sigma.
ChIP, ChIP-re-ChIP и ChIP-seq
Для экспериментов по иммунопреципитации хроматина (ChIP) клетки фиксировали не содержащим метанола формальдегидом (Thermo Scientific, каталожный номер 28906) и лизировали в буфере для лизиса 1 (LB1, 50 ммоль / л HEPES-KOH pH7,5, 140 ммоль / л NaCl, 1 ммоль / л EDTA, 10% глицерин, 0,5% NP40, 0,25% TritonX100), LB2 (10 ммоль / л TrisHCl pH 8, 200 ммоль / л NaCl, 1 ммоль / л EDTA, 0,5 ммоль / л EGTA) и LB3 (10 ммоль / л TrisHCl pH 8, 100 ммоль / л NaCl, 1 ммоль / л EGTA, 0,1% Na-дезоксихолат, 0. 5% N-лауроилсаркозин) с добавлением коктейля ингибиторов протеазы. Образцы обрабатывали ультразвуком с использованием ультразвукового устройства Diagenode Bioruptor. Обработанные ультразвуком лизаты инкубировали с антителами (анти-STAT3 # 124H6, анти-Sin3A # sc-994 / sc-767 или нормальный кроличий IgG # sc-2027, Cell Signaling Technology) при 4 ° C при вращении в течение ночи. Иммунокомплексы восстанавливали добавлением магнитных шариков с протеином А (Invitrogen, номер по каталогу 10002D), ресуспендировали в 1% SDS NaHCO 3 и обрабатывали протеиназой K (Promega, номер по каталогу.V3021), а затем с помощью РНКазы A. ДНК очищали с использованием набора MiniElute Reaction Cleanup Kit (Qiagen, номер в каталоге 28204). Один процент обработанного ультразвуком хроматина был использован в качестве входных данных. Иммунопреципитированная ДНК и ввод были проанализированы с помощью qRT-PCR (список праймеров доступен в дополнительной таблице S1). Данные были выражены в соответствии с формулой скорректированного ввода [100 × 2 (Скорректированный ввод — C t (IP) ]).
5% N-лауроилсаркозин) с добавлением коктейля ингибиторов протеазы. Образцы обрабатывали ультразвуком с использованием ультразвукового устройства Diagenode Bioruptor. Обработанные ультразвуком лизаты инкубировали с антителами (анти-STAT3 # 124H6, анти-Sin3A # sc-994 / sc-767 или нормальный кроличий IgG # sc-2027, Cell Signaling Technology) при 4 ° C при вращении в течение ночи. Иммунокомплексы восстанавливали добавлением магнитных шариков с протеином А (Invitrogen, номер по каталогу 10002D), ресуспендировали в 1% SDS NaHCO 3 и обрабатывали протеиназой K (Promega, номер по каталогу.V3021), а затем с помощью РНКазы A. ДНК очищали с использованием набора MiniElute Reaction Cleanup Kit (Qiagen, номер в каталоге 28204). Один процент обработанного ультразвуком хроматина был использован в качестве входных данных. Иммунопреципитированная ДНК и ввод были проанализированы с помощью qRT-PCR (список праймеров доступен в дополнительной таблице S1). Данные были выражены в соответствии с формулой скорректированного ввода [100 × 2 (Скорректированный ввод — C t (IP) ]). В ChIP-re-ChIP 3 × 10 7 клеток обрабатывали ультразвуком (Covaris) в LB3 без NaCl.К растворимой хроматической фракции добавляли NaCl и SDS и инкубировали с кроличьими mAb против SIN3A [SIN3A (D9D6), Cell Signaling Technology; или STAT3)] антитело. Мышиный IgG1 (M5284, Sigma) и кроличий E-Tag (13419s, Cell Signaling Technology) использовали в качестве контроля изотипа. Иммунокомплексы выделяли на шариках с протеином А, последовательно промывали в WB1 (20 ммоль / л трис-HCl pH 8, 150 ммоль / л NaCl, 2 ммоль / л EDTA, 1% тритон, 0,1% SDS) и WB2 (20 ммоль / л). ммоль / л Tris-HCl pH 8, 150 ммоль / л NaCl, 2 ммоль / л EDTA, 1% тритон, 0,1% SDS) и элюируется буфером TE (10 ммоль / л Tris-HCl pH 8,0.25 ммоль / л ЭДТА, pH 8). Затем элюированную фракцию разбавляли 20 ммоль / л Трис-HCl pH 8, 2 ммоль / л EDTA pH 8, 1% TRITON X-100, 150 ммоль / л NaCl и инкубировали с анти-STAT-3 (или анти-Sin3A. ) Ag или контрольный IgG, затем бусинки с протеином A и обработанные, как описано выше. Для эксперимента ChIP-seq всего 10 7 клеток фиксировали 1% формальдегидом, лизировали и обрабатывали ультразвуком (Branson Sonicator; Branson), в результате чего средний размер ДНК составлял 200 п.
В ChIP-re-ChIP 3 × 10 7 клеток обрабатывали ультразвуком (Covaris) в LB3 без NaCl.К растворимой хроматической фракции добавляли NaCl и SDS и инкубировали с кроличьими mAb против SIN3A [SIN3A (D9D6), Cell Signaling Technology; или STAT3)] антитело. Мышиный IgG1 (M5284, Sigma) и кроличий E-Tag (13419s, Cell Signaling Technology) использовали в качестве контроля изотипа. Иммунокомплексы выделяли на шариках с протеином А, последовательно промывали в WB1 (20 ммоль / л трис-HCl pH 8, 150 ммоль / л NaCl, 2 ммоль / л EDTA, 1% тритон, 0,1% SDS) и WB2 (20 ммоль / л). ммоль / л Tris-HCl pH 8, 150 ммоль / л NaCl, 2 ммоль / л EDTA, 1% тритон, 0,1% SDS) и элюируется буфером TE (10 ммоль / л Tris-HCl pH 8,0.25 ммоль / л ЭДТА, pH 8). Затем элюированную фракцию разбавляли 20 ммоль / л Трис-HCl pH 8, 2 ммоль / л EDTA pH 8, 1% TRITON X-100, 150 ммоль / л NaCl и инкубировали с анти-STAT-3 (или анти-Sin3A. ) Ag или контрольный IgG, затем бусинки с протеином A и обработанные, как описано выше. Для эксперимента ChIP-seq всего 10 7 клеток фиксировали 1% формальдегидом, лизировали и обрабатывали ультразвуком (Branson Sonicator; Branson), в результате чего средний размер ДНК составлял 200 п. н. К предварительно очищенному образцу добавляли антитела Anti-STAT3 (Cell Signaling Technology, 9139; 5 мкг) или контрольные IgG (Millipore 12-370, 12-371) и инкубировали в течение ночи при 4 ° C.Комплексы очищали с использованием гранул протеина А (Roche) с последующим элюированием с гранул и декросс-сшиванием. ДНК очищали с использованием колонок для очистки ПЦР (QIAGEN) и амплифицировали с помощью qRT-PCR с использованием SYBR Green (Applied Biosystems) на 7900HT Fast Real-Time PCR System (Applied Biosystems). Необработанные образцы ChIP-seq выравнивали с помощью выравнивателя bwa. Определение пиков выполнялось с использованием MACS2 (версия 2.1.1) для идентификации сайтов связывания факторов транскрипции. Только пики, названные с FDR <0,05, были названы значительно обогащенными.Для создания сигнальных дорожек использовалась команда macs2 bdgcmp, чтобы рассчитать изменение кратности в формате графа, а затем преобразовать в bigwig с помощью инструментария UCSC.
н. К предварительно очищенному образцу добавляли антитела Anti-STAT3 (Cell Signaling Technology, 9139; 5 мкг) или контрольные IgG (Millipore 12-370, 12-371) и инкубировали в течение ночи при 4 ° C.Комплексы очищали с использованием гранул протеина А (Roche) с последующим элюированием с гранул и декросс-сшиванием. ДНК очищали с использованием колонок для очистки ПЦР (QIAGEN) и амплифицировали с помощью qRT-PCR с использованием SYBR Green (Applied Biosystems) на 7900HT Fast Real-Time PCR System (Applied Biosystems). Необработанные образцы ChIP-seq выравнивали с помощью выравнивателя bwa. Определение пиков выполнялось с использованием MACS2 (версия 2.1.1) для идентификации сайтов связывания факторов транскрипции. Только пики, названные с FDR <0,05, были названы значительно обогащенными.Для создания сигнальных дорожек использовалась команда macs2 bdgcmp, чтобы рассчитать изменение кратности в формате графа, а затем преобразовать в bigwig с помощью инструментария UCSC.
RNA-seq
RNA-seq выполняли, как описано ранее (27).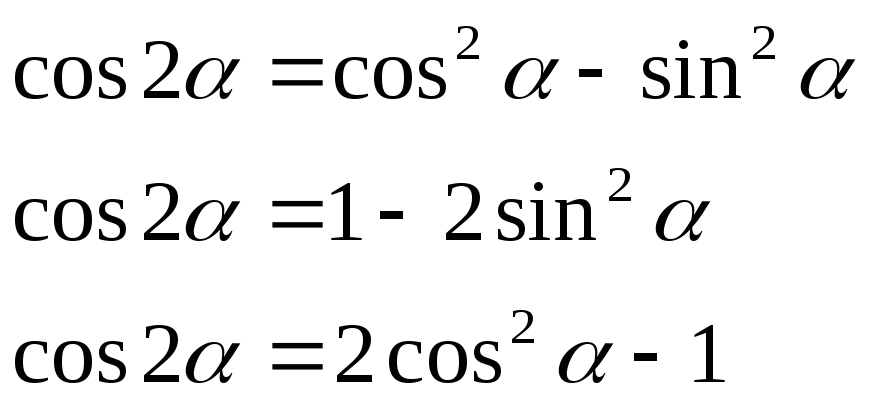 Для всех наборов TruSeq Stranded Total RNA используется один и тот же рабочий процесс. Вкратце, удаление рибосомной РНК (рРНК) достигалось с использованием биотинилированных, специфичных для мишени олигонуклеотидов в сочетании с гранулами для удаления рРНК Ribo-Zero. Набор Ribo-Zero Человек / Мышь / Крыса истощает образцы цитоплазматической рРНК, а набор Ribo-Zero Gold истощает образцы как цитоплазматической, так и митохондриальной рРНК.После очистки РНК была фрагментирована на мелкие кусочки с использованием двухвалентных катионов при повышенной температуре. Затем расщепленные фрагменты РНК копировали в кДНК первой цепи с использованием обратной транскриптазы и случайных праймеров с последующим синтезом кДНК второй цепи с использованием ДНК-полимеразы I и РНКазы H. Затем к этим фрагментам кДНК добавляли одно основание «A» и затем перевязка адаптера. Продукты очищают и обогащают с помощью ПЦР для создания конечной библиотеки кДНК. Секвенирование РНК по парным концам при длине считывания 100 п.
Для всех наборов TruSeq Stranded Total RNA используется один и тот же рабочий процесс. Вкратце, удаление рибосомной РНК (рРНК) достигалось с использованием биотинилированных, специфичных для мишени олигонуклеотидов в сочетании с гранулами для удаления рРНК Ribo-Zero. Набор Ribo-Zero Человек / Мышь / Крыса истощает образцы цитоплазматической рРНК, а набор Ribo-Zero Gold истощает образцы как цитоплазматической, так и митохондриальной рРНК.После очистки РНК была фрагментирована на мелкие кусочки с использованием двухвалентных катионов при повышенной температуре. Затем расщепленные фрагменты РНК копировали в кДНК первой цепи с использованием обратной транскриптазы и случайных праймеров с последующим синтезом кДНК второй цепи с использованием ДНК-полимеразы I и РНКазы H. Затем к этим фрагментам кДНК добавляли одно основание «A» и затем перевязка адаптера. Продукты очищают и обогащают с помощью ПЦР для создания конечной библиотеки кДНК. Секвенирование РНК по парным концам при длине считывания 100 п.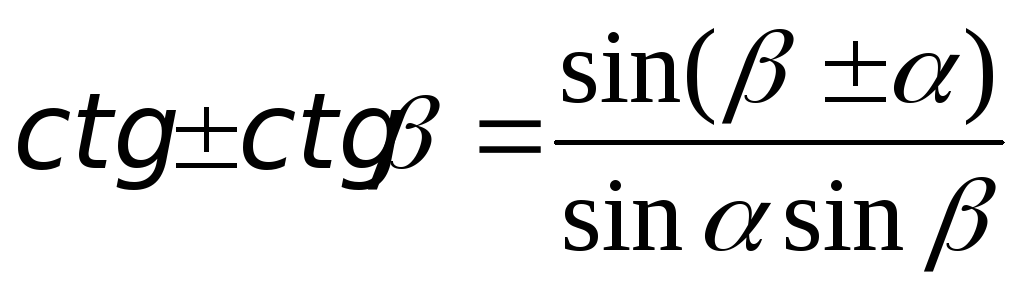 н. выполняли с помощью HiSeq2500 (Illumina).Необработанные секвенированные чтения были сопоставлены с эталонным геномом человека (версия hg19 от UCSC) с использованием выравнивателя STAR (версия 2.4.2). Выровненные чтения были количественно сопоставлены со справочной аннотацией (hg19 из UCSC) для получения FPKM (фрагментов на килобазу на миллион) и необработанных подсчетов с использованием CuffLinks (v 2.2.1) и HTSeq , соответственно.
н. выполняли с помощью HiSeq2500 (Illumina).Необработанные секвенированные чтения были сопоставлены с эталонным геномом человека (версия hg19 от UCSC) с использованием выравнивателя STAR (версия 2.4.2). Выровненные чтения были количественно сопоставлены со справочной аннотацией (hg19 из UCSC) для получения FPKM (фрагментов на килобазу на миллион) и необработанных подсчетов с использованием CuffLinks (v 2.2.1) и HTSeq , соответственно.
Трансфекция плазмиды и siRNA, продуцирование лентивируса shRNAmir и трансдукция
Клетки Hek293 и MDA-231 были временно трансфицированы с использованием реагента для трансфекции PolyFect (Qiagen) в соответствии с инструкциями производителя.PMet7-etag-STAT3WT, pMet7-etag-STAT3K685Q и pMet7-etag-STAT3K685R были любезно предоставлены доктором Яном Тавернье (VIB, Гент, Бельгия). Лентивирусные векторы pGIPZ-GFP-SIN3A-shRNAmir (V2LHS_96677 и V2LHS_96678) и pGIPZ-GFP-control-shRNAmir (RHS4346) были приобретены в Open Biosystems. Использовали лентивирусную упаковку pCMV-dR8.74 и псевдотип VSV-G / pMD2.G (любезно предоставленные доктором Винченцо Калаутти, Dulbecco Telethon Institute, c / o Центр молекулярной биотехнологии, Туринский университет, Турин, Италия).Контрольная миРНК siGENOME и миРНК 3′-UTR STAT3 были приобретены у Thermo Fisher Scientific (D-001210-03 и D-003544-19), а глушитель миРНК SIN3A был приобретен у Ambion (s24800).
Использовали лентивирусную упаковку pCMV-dR8.74 и псевдотип VSV-G / pMD2.G (любезно предоставленные доктором Винченцо Калаутти, Dulbecco Telethon Institute, c / o Центр молекулярной биотехнологии, Туринский университет, Турин, Италия).Контрольная миРНК siGENOME и миРНК 3′-UTR STAT3 были приобретены у Thermo Fisher Scientific (D-001210-03 и D-003544-19), а глушитель миРНК SIN3A был приобретен у Ambion (s24800).
Для индивидуальных экспериментов по сайленсингу, 50 нмоль / л siGENOME, не нацеливающая siRNA Control или STAT3 siRNA (Thermo Fisher Scientific), или SIN3A siRNA Silencer (Ambion) трансфицировали в клетки MDA-MB-231 с использованием Dharmafect The Scientific Transfection reagent ( ) следуя инструкциям производителя.Если указано, трансфекцию ДНК-плазмиды проводили через 24 часа. Вестерн-блоттинг и анализ qRT-PCR проводили через 5 дней после трансфекции миРНК. Лентивирусные стоки получали в клетках Hek293, трансфицированных pGIPZ-shSIN3A, pGIPZ shSIN3A # 2 или pGIPZshControl (Open Biosystems) вместе с векторами pCMV-dR8. 74 и VSV-G / pMD2.G. Вирус титровали на клеточной линии Hek293. Клетки NPM-ALK + инфицировали в присутствии полибрена, собирали через 1 день после трансдукции и культивировали в свежей среде с добавлением пуромицина.После 48 часов отбора жизнеспособные клетки выделяли центрифугированием плотности на градиенте фиколла (GE Healthcare, номер в каталоге 17-1440-02).
74 и VSV-G / pMD2.G. Вирус титровали на клеточной линии Hek293. Клетки NPM-ALK + инфицировали в присутствии полибрена, собирали через 1 день после трансдукции и культивировали в свежей среде с добавлением пуромицина.После 48 часов отбора жизнеспособные клетки выделяли центрифугированием плотности на градиенте фиколла (GE Healthcare, номер в каталоге 17-1440-02).
qRT-PCR
РНК очищали с помощью набора RNeasy Mini Kit (QIAGEN, номер в каталоге 74104) в соответствии с инструкциями производителя. Один микрограмм общей РНК ретротранскрибировали в течение 1 часа при 42 ° C с помощью ретротранскриптазы M-MLV (Invitrogen, номер в каталоге 28025-013) в присутствии праймера oligo (dT) 15 (Promega, номер в каталоге C1101), dNTP (евроклон) и ингибитор РНКзин-рибонуклеазы (Promega, каталожный номер.N2111). кДНК разводили в 10 раз для проведения qRT-PCR с SYBR Green Master Mix (Applied Biosystems, номер по каталогу 4309155) с ген-специфическими праймерами (суммированными в дополнительной таблице S1). Значения C t были нормализованы к экспрессии генов домашнего хозяйства с использованием метода ΔΔ C t . Список пар праймеров, используемых в этой работе, указан в дополнительной таблице S1.
Значения C t были нормализованы к экспрессии генов домашнего хозяйства с использованием метода ΔΔ C t . Список пар праймеров, используемых в этой работе, указан в дополнительной таблице S1.
Анализ проточной цитометрии
Апоптотическую гибель клеток измеряли с помощью окрашивания аннексином V-APC и 7AAD (BD Biosciences, каталожные номера.550474 и 559925) в соответствии с инструкциями производителя, где указанные клетки окрашивали на предмет экспрессии поверхностного IL2Rγ анти-IL2Rγ-APC (каталожный номер 563682, клон TUGh5) или соответствующим изотипическим контролем. Образцы были взяты с помощью анализатора BD Accuri C6. Синглеты определяли путем построения графика зависимости площади FSC от высоты FSC и анализировали с помощью программного обеспечения FlowJo.
Иммунофлуоресценция
Клетки NPM-ALK + высевали центрифугированием цитоспина на предметные стекла Thermo Fisher Scientific Superfrost Plus, фиксировали в 4% формальдегиде, промывали PBS и проницали в ледяном 100% метаноле при -20 ° C. в течение 10 минут.Слайды блокировали в PBS + 5% нормальной козьей сыворотке + 0,3% TritonX100 в течение 1 часа и окрашивали первичными антителами (анти-STAT3 # 9139 от Cell Signaling Technology; анти-Sin3A # sc-767 от Santa Cruz Biotechnology) в PBS + BSA. 1% + 0,3% TritonX100) в течение ночи при 4 ° C. Затем слайды окрашивали вторичными антителами и DAPI. Изображения получали с помощью конфокального микроскопа (Leica DMI6000) с объективом 40x и анализировали с помощью ImageJ (NIH).
в течение 10 минут.Слайды блокировали в PBS + 5% нормальной козьей сыворотке + 0,3% TritonX100 в течение 1 часа и окрашивали первичными антителами (анти-STAT3 # 9139 от Cell Signaling Technology; анти-Sin3A # sc-767 от Santa Cruz Biotechnology) в PBS + BSA. 1% + 0,3% TritonX100) в течение ночи при 4 ° C. Затем слайды окрашивали вторичными антителами и DAPI. Изображения получали с помощью конфокального микроскопа (Leica DMI6000) с объективом 40x и анализировали с помощью ImageJ (NIH).
Исследования проводились в соответствии с руководящими принципами Европейского Союза и с одобрения Института Сан-Раффаэле (Милан, Италия; IACUC-814) и Медицинского колледжа Вейл Корнелл (Нью-Йорк, Нью-Йорк; IACUC). 2014-0024) Институциональные этические комитеты.Животных содержали и разводили в специальных помещениях для животных, свободных от патогенов. Ксенотрансплантаты опухоли, полученные от пациентов (PDTX), были созданы следующим образом: из хирургического театра свежие фрагменты ткани (ткани перед трансплантатом) хранились в PBS и / или в полной среде (RPMI 1640 с добавлением 10% FCS и антибиотиками) и быстро доставлялись в палату сортировки хирургической патологии. Выделенные фрагменты ткани были выбраны для имплантатов трансплантата опухоли только тогда, когда было доступно достаточно материала для рутинной диагностики и молекулярных анализов.Все образцы обрабатывались в стерильных условиях. Образцы трансплантата опухоли разрезали на несколько частей 3 × 3 × 1 мм (несколько частей / образец) в полной среде и имплантировали свежую и / или криоконсервированную в 10% замороженную среду DMSO-RPMI 1640 с добавлением 20% FCS. Сначала анестезировали NSG в возрасте 6-8 недель (Ромпун 0,05 мкл / г и Золетил 1,6 мкг / г внутримышечно). Затем, когда животные лежали на вентральной части, спинную область стерилизовали (70% этанол). Впоследствии был сделан кожный разрез толщиной 0,3 см вдоль срединной дорсальной области ретро-затылочной кости и небольшой карман был создан тупым рассечением.Множественные фрагменты ткани трансплантата опухоли (2–4) были перенесены в подкожно в каждом кармане с помощью тупоконечных щипцов с матригелем или без него. Срезанные края заклеивались одним металлическим зажимом.
Выделенные фрагменты ткани были выбраны для имплантатов трансплантата опухоли только тогда, когда было доступно достаточно материала для рутинной диагностики и молекулярных анализов.Все образцы обрабатывались в стерильных условиях. Образцы трансплантата опухоли разрезали на несколько частей 3 × 3 × 1 мм (несколько частей / образец) в полной среде и имплантировали свежую и / или криоконсервированную в 10% замороженную среду DMSO-RPMI 1640 с добавлением 20% FCS. Сначала анестезировали NSG в возрасте 6-8 недель (Ромпун 0,05 мкл / г и Золетил 1,6 мкг / г внутримышечно). Затем, когда животные лежали на вентральной части, спинную область стерилизовали (70% этанол). Впоследствии был сделан кожный разрез толщиной 0,3 см вдоль срединной дорсальной области ретро-затылочной кости и небольшой карман был создан тупым рассечением.Множественные фрагменты ткани трансплантата опухоли (2–4) были перенесены в подкожно в каждом кармане с помощью тупоконечных щипцов с матригелем или без него. Срезанные края заклеивались одним металлическим зажимом. После процедуры мышей регулярно проверяли, пока они не становились бдительными. Имплантированных животных содержали в однополых группах. Аналогичные частоты наблюдались как у самцов, так и у самок мышей. Рост имплантата оценивали путем пальпации и / или с помощью сканирования МРТ и собирали, когда требовались опухолевые массы. Животных-реципиентов регулярно проверяли и умерщвляли при первых признаках бедствия.При сборе мышей умерщвляли в камере CO 2 и собирали трансплантаты для гистологической оценки, повторной трансплантации или мгновенного замораживания в жидком азоте. При повторной трансплантации фрагменты лимфомы трансплантировали мышам NSG, и мышей умерщвляли, когда опухоли достигали приблизительно 1,5 см в диаметре. Опухоли вырезали, разрезали на 5-миллиметровые кубики и замораживали для дополнительных трансплантатов или переваривали коллагеназой I и ДНКазой I в течение 1 часа при 37 ° C. Жизнеспособные клетки выделяли центрифугированием плотности на градиенте фиколла (GE Healthcare, каталог №17-1440-02) и непосредственно использовали для экстракции РНК и общего белка или культивировали в течение 48 часов в присутствии ресвератрола или носителя.
После процедуры мышей регулярно проверяли, пока они не становились бдительными. Имплантированных животных содержали в однополых группах. Аналогичные частоты наблюдались как у самцов, так и у самок мышей. Рост имплантата оценивали путем пальпации и / или с помощью сканирования МРТ и собирали, когда требовались опухолевые массы. Животных-реципиентов регулярно проверяли и умерщвляли при первых признаках бедствия.При сборе мышей умерщвляли в камере CO 2 и собирали трансплантаты для гистологической оценки, повторной трансплантации или мгновенного замораживания в жидком азоте. При повторной трансплантации фрагменты лимфомы трансплантировали мышам NSG, и мышей умерщвляли, когда опухоли достигали приблизительно 1,5 см в диаметре. Опухоли вырезали, разрезали на 5-миллиметровые кубики и замораживали для дополнительных трансплантатов или переваривали коллагеназой I и ДНКазой I в течение 1 часа при 37 ° C. Жизнеспособные клетки выделяли центрифугированием плотности на градиенте фиколла (GE Healthcare, каталог №17-1440-02) и непосредственно использовали для экстракции РНК и общего белка или культивировали в течение 48 часов в присутствии ресвератрола или носителя. Чтобы исключить контаминацию стромальных и эритроидных клеток мыши, образцы окрашивали поверхность антимышиным H-2K [d] (клон SF1-1.1, номер в каталоге 562004), антимышиным TER-119 (клон TER-119, каталог № 561032) и антитела против CD45 человека (номер в каталоге 555485, клон HI30) или соответствующие контроли изотипа, полученные с помощью анализатора BD Accuri C6.
Чтобы исключить контаминацию стромальных и эритроидных клеток мыши, образцы окрашивали поверхность антимышиным H-2K [d] (клон SF1-1.1, номер в каталоге 562004), антимышиным TER-119 (клон TER-119, каталог № 561032) и антитела против CD45 человека (номер в каталоге 555485, клон HI30) или соответствующие контроли изотипа, полученные с помощью анализатора BD Accuri C6.
В выбранных экспериментах использовали клетки NPM-ALK + .Всего 10 5 клеток трансдуцировали лентивирусом pGIPZ shSIN3A или pGIPZ-shControl, суспендировали в BD Matrigel Matrix Growth Factor Reduced (номер по каталогу 356230) и вводили подкожно в задний бок мышей NSG. Матригель применяли для повышения эффективности приживления и роста злокачественных клеток. Рост опухоли контролировали штангенциркулем, и мышей умерщвляли, когда опухоли достигали приблизительно 1,5 см в диаметре. Опухолевые массы собирали, взвешивали и превращали в суспензию отдельных клеток для дальнейшего анализа.
Результаты
STAT3 конститутивно ацетилируется в ALK
+ ALCL STAT3 поддерживает трансформацию, управляемую NPM-ALK, способствуя подавлению транскрипции субпопуляции TSG посредством молекулярных механизмов, которые остаются в значительной степени неизвестными (14–16, 18, 28). , 29). Поскольку ацетилирование STAT3 было связано с репрессией транскрипции в нескольких моделях рака (23, 24), мы исследовали посттрансляционные модификации STAT3 в клетках NPM-ALK + и PDTX. Как сообщалось ранее (10), мы обнаружили, что STAT3 конститутивно фосфорилируется как по остаткам Tyr705, так и по Ser727 в клетках, экспрессирующих NPM-ALK (Sup-M2, JB6 и SU-DHL-1), а не в NPM-ALK — контрольные клетки ALCL (OCI-Ly12; рис.1А; Дополнительный рис. S1A). STAT3 также был конститутивно ацетилирован в клетках NPM-ALK + (фиг. 1A; дополнительные фиг. S1A и S1B) и PDTX ALK + (фиг. 1B), но не в контроле ALK —. Следует отметить, что в то время как фосфорилирование STAT3 Tyr705 однозначно зависело от ALK, фосфорилирование и ацетилирование STAT3 Ser727 также зависело от киназ Ser / Thr mTOR, PI3K и MAPK, ранее описанных мишеней для ALK (30, 31). Действительно, лечение кризотинибом, мощным и селективным ингибитором ALK, подавляло фосфорилирование Tyr и Ser и ацетилирование Lys (рис.
, 29). Поскольку ацетилирование STAT3 было связано с репрессией транскрипции в нескольких моделях рака (23, 24), мы исследовали посттрансляционные модификации STAT3 в клетках NPM-ALK + и PDTX. Как сообщалось ранее (10), мы обнаружили, что STAT3 конститутивно фосфорилируется как по остаткам Tyr705, так и по Ser727 в клетках, экспрессирующих NPM-ALK (Sup-M2, JB6 и SU-DHL-1), а не в NPM-ALK — контрольные клетки ALCL (OCI-Ly12; рис.1А; Дополнительный рис. S1A). STAT3 также был конститутивно ацетилирован в клетках NPM-ALK + (фиг. 1A; дополнительные фиг. S1A и S1B) и PDTX ALK + (фиг. 1B), но не в контроле ALK —. Следует отметить, что в то время как фосфорилирование STAT3 Tyr705 однозначно зависело от ALK, фосфорилирование и ацетилирование STAT3 Ser727 также зависело от киназ Ser / Thr mTOR, PI3K и MAPK, ранее описанных мишеней для ALK (30, 31). Действительно, лечение кризотинибом, мощным и селективным ингибитором ALK, подавляло фосфорилирование Tyr и Ser и ацетилирование Lys (рис. 1С; Дополнительный рис. S1C). Напротив, рапамицин (нацеленный на mTOR), LY294009 (нацеленный на PI3K) и U0126 (нацеленный на MAPK) ингибировал фосфорилирование STAT3 Ser727 и ацетилирование Lys685, не влияя на фосфорилирование Tyr705 (дополнительный рисунок S1D). Таким образом, STAT3 постоянно фосфорилируется и ацетилируется в клетках ALK + .
1С; Дополнительный рис. S1C). Напротив, рапамицин (нацеленный на mTOR), LY294009 (нацеленный на PI3K) и U0126 (нацеленный на MAPK) ингибировал фосфорилирование STAT3 Ser727 и ацетилирование Lys685, не влияя на фосфорилирование Tyr705 (дополнительный рисунок S1D). Таким образом, STAT3 постоянно фосфорилируется и ацетилируется в клетках ALK + .
Конститутивное фосфорилирование и ацетилирование STAT3 в NPM-ALK + ALCL коррелирует с подавлением онкосупрессорных генов. A – C, NPM-ALK + (Sup-M2, JB6, SU-DHL-1), ALK — (OCI-Ly12) ячейки ALCL и NPM-ALK + PDTX (PDTX # 1 , PDTX # 2) лизировали в буфере для образцов SDS и анализировали вестерн-блоттингом с указанными антителами. C, Клетки обрабатывали кризотинибом 100 нмоль / л в течение 24 часов. Данные в A – C представляют как минимум три независимых эксперимента. D, Экспрессию гена оценивали с помощью qRT-PCR. Результаты указывают на относительные уровни мРНК, рассчитанные для контрольных клеток OCI-Ly12.Планки погрешностей, стандартное отклонение ( n = 2).
Результаты указывают на относительные уровни мРНК, рассчитанные для контрольных клеток OCI-Ly12.Планки погрешностей, стандартное отклонение ( n = 2).
Затем мы сравнили экспрессию ряда TSG, репрессированных STAT3, в клетках ALK + ( IL2Rγ, LAT и LEF1 ; ссылки 14, 15, 32) или при другом раке. модели ( DDIT3, ATF3, PHLDA1 и DUSP4 ; каталожный номер 33). Мы наблюдали, что уровни экспрессии TSG были ниже в клетках ALK + по сравнению с контрольными ALK — (фиг. 1D). Напротив, клетки ALK + показали более высокую экспрессию SOCS3 , канонического транскрибируемого гена STAT3, по сравнению с контрольными ALK — (дополнительный рис.S1E), подтверждая представление о том, что в NPM-ALK + ALCL, STAT3 транскрипционно активен. С помощью анализа ChIP-seq мы обнаружили, что STAT3 связан с промотором ряда TSG, среди которых PRDM1 , кодирующий белок Blimp1, часто обнаруживаемый с подавлением регуляции как в B-, так и в T-клеточных лимфомах (дополнительный рисунок S2A). ; ссылка 34). Кризотиниб ингибировал связывание STAT3 с областями промотора PRDM1 (дополнительный рис. S2A) и, хотя он снижал экспрессию SOCS3, он увеличивал экспрессию некоторых из STAT3-репрессированных TSG ( DDIT3, PRDM1 и LAT ; дополнительный рис.S2B), поддерживая их ALK-зависимую репрессию транскрипции.
; ссылка 34). Кризотиниб ингибировал связывание STAT3 с областями промотора PRDM1 (дополнительный рис. S2A) и, хотя он снижал экспрессию SOCS3, он увеличивал экспрессию некоторых из STAT3-репрессированных TSG ( DDIT3, PRDM1 и LAT ; дополнительный рис.S2B), поддерживая их ALK-зависимую репрессию транскрипции.
Таким образом, в NPM-ALK + ALCL, STAT3 конститутивно фосфорилируется и ацетилируется, и это коррелирует с репрессией ряда TSG.
STAT3 и Sin3A конститутивно связываются в клетках ALK
+ и связывают промоторные области TSG Поскольку цитокин-управляемое ацетилирование STAT3 индуцирует временную ассоциацию STAT3 с комплексом транскрипционного регулятора Sin3A (26), мы спросили, существует ли конститутивное ацетилирование STAT3 в NPM. Клетки -ALK + могут способствовать его связыванию с Sin3A.Сначала мы оценили субклеточную локализацию Sin3A и ацетилированного STAT3 и анализ вестерн-блоттинга и обнаружили, что оба они представлены почти исключительно в ядре (рис. 2A). Конфокальный анализ иммунофлуоресценции выявил, что STAT3 и Sin3A колокализуются в ядре клеток NPM-ALK + (фиг. 2B). Более того, с помощью коиммунопреципитации мы обнаружили, что эндогенный STAT3 взаимодействует с эндогенным Sin3A конститутивным, независимым от стимула образом (Fig. 2C).
2A). Конфокальный анализ иммунофлуоресценции выявил, что STAT3 и Sin3A колокализуются в ядре клеток NPM-ALK + (фиг. 2B). Более того, с помощью коиммунопреципитации мы обнаружили, что эндогенный STAT3 взаимодействует с эндогенным Sin3A конститутивным, независимым от стимула образом (Fig. 2C).
Репрессор транскрипции Sin3A связывается с STAT3 и с промоторными областями STAT3-репрессированных генов онкосупрессоров в NPM-ALK + ALCL.Субклеточную локализацию A и B, Sin3A, ac-STAT3 (Lys685) и STAT3 оценивали в цитозольной и ядерной фракциях с помощью вестерн-блот-анализа ( A ) и иммунофлуоресценции ( B ) в NPM-ALK . + сот. ДНК B, окрашивали DAPI, и изображения получали с помощью конфокального микроскопа (увеличение × 40). C, Ядерные лизаты подвергали иммунопреципитации с помощью антител против Sin3A или нормального кроличьего IgG и анализировали с указанными антителами. Результаты являются репрезентативными для трех независимых экспериментов. D, Экстракты сшитого хроматина иммунопреципитировали антителами против Sin3A, анти-STAT3 или поликлональным иммуноглобулином (IgG). Очищенную ДНК анализировали с помощью qRT-PCR. Результаты показывают процент иммунопреципитированной ДНК над входом; планки погрешностей, стандартное отклонение ( n = 4). Односторонний парный тест t , *, P <0,05. E, Экстракты сшитого хроматина подвергали последовательной ChIP-re-ChIP с антителами против Sin3A и анти-STAT3 (слева) или наоборот (справа).Соответствующие контрольные антитела изотипа использовали для контроля конкретных обогащений. Показан один эксперимент, представляющий два независимых определения.
Результаты являются репрезентативными для трех независимых экспериментов. D, Экстракты сшитого хроматина иммунопреципитировали антителами против Sin3A, анти-STAT3 или поликлональным иммуноглобулином (IgG). Очищенную ДНК анализировали с помощью qRT-PCR. Результаты показывают процент иммунопреципитированной ДНК над входом; планки погрешностей, стандартное отклонение ( n = 4). Односторонний парный тест t , *, P <0,05. E, Экстракты сшитого хроматина подвергали последовательной ChIP-re-ChIP с антителами против Sin3A и анти-STAT3 (слева) или наоборот (справа).Соответствующие контрольные антитела изотипа использовали для контроля конкретных обогащений. Показан один эксперимент, представляющий два независимых определения.
Чтобы исследовать предполагаемые эффекты комплекса STAT3-Sin3A, мы проанализировали способность этих факторов связывать промоторы генов, репрессированных STAT3, в анализах ChIP. Мы выбрали три репрезентативных ALK-репрессированных гена ( PRDM1, IL2R , , LAT) и обнаружили, что и STAT3, и Sin3A были конститутивно связаны с одними и теми же участками промотора (рис. 2D). Чтобы более прямо продемонстрировать, что STAT3 и Sin3A одновременно связываются с одними и теми же геномными сайтами, мы провели последовательные эксперименты с ChIP-re-ChIP. В двух из трех независимых определений мы обнаружили, что STAT3 и Sin3A специфически обогащены промоторной областью PRDM1 (рис. 2E). Так было в последовательных микросхемах STAT3 / Sin3A и Sin3A / STAT3. Хотя аналогичные тенденции были обнаружены при опросе связывания с IL2Rg , результаты не были показательными для LAT .Мы полагаем, что некоторая вариабельность может быть связана с природой комплекса STAT3-Sin3A, вероятно, включающего несколько белков и динамически регулируемого в асинхронно делящихся трансформированных клетках. Т.о., учитывая способность Sin3A связывать HDACs и DNMTs и регулировать транскрипцию эпигенетическими средствами, эти данные предполагают роль Sin3A в репрессии транскрипции TSG, опосредованной STAT3.
2D). Чтобы более прямо продемонстрировать, что STAT3 и Sin3A одновременно связываются с одними и теми же геномными сайтами, мы провели последовательные эксперименты с ChIP-re-ChIP. В двух из трех независимых определений мы обнаружили, что STAT3 и Sin3A специфически обогащены промоторной областью PRDM1 (рис. 2E). Так было в последовательных микросхемах STAT3 / Sin3A и Sin3A / STAT3. Хотя аналогичные тенденции были обнаружены при опросе связывания с IL2Rg , результаты не были показательными для LAT .Мы полагаем, что некоторая вариабельность может быть связана с природой комплекса STAT3-Sin3A, вероятно, включающего несколько белков и динамически регулируемого в асинхронно делящихся трансформированных клетках. Т.о., учитывая способность Sin3A связывать HDACs и DNMTs и регулировать транскрипцию эпигенетическими средствами, эти данные предполагают роль Sin3A в репрессии транскрипции TSG, опосредованной STAT3.
Ресвератрол ингибирует ацетилирование STAT3, связывание Sin3A с промоторами TSG и восстанавливает экспрессию TSG
Чтобы выяснить, требуется ли ацетилирование STAT3 для рекрутирования Sin3A на промоторы TSG и для их репрессии транскрипции, мы обработали клетки NPM-ALK + ресвератролом. , полифенол, ранее показано, что он ингибирует ацетилирование STAT3 (35, 36).Мы обнаружили, что ресвератрол значительно снижает ацетилирование STAT3, что подтверждается вестерн-блоттингом с антителом, специфичным для ацетил-Lys685. Ресвератрол также снижает фосфорилирование Ser727 без значительного влияния на фосфорилирование STAT3 Tyr705 (фиг. 3A; дополнительный фиг. S3A), что еще больше подчеркивает перекрестную регуляцию между ацетилированием и фосфорилированием Ser727. Одновременно ресвератрол уменьшал рекрутирование Sin3A и STAT3 в промоторные области PRDM1 и IL2Rγ (рис.3B) и вызвали повторную экспрессию этих и нескольких других STAT3-репрессированных TSG в клетках NPM-ALK + (фиг. 3C; дополнительные фиг. S3B и S3C). Полученная экспрессия IL2Rγ, PRDM1, / Blimp-1 и DDIT3, / CHOP была подтверждена на уровне белка либо с помощью анализа FACS (фиг. 3D), либо с помощью вестерн-блоттинга (фиг. 3E и F).
, полифенол, ранее показано, что он ингибирует ацетилирование STAT3 (35, 36).Мы обнаружили, что ресвератрол значительно снижает ацетилирование STAT3, что подтверждается вестерн-блоттингом с антителом, специфичным для ацетил-Lys685. Ресвератрол также снижает фосфорилирование Ser727 без значительного влияния на фосфорилирование STAT3 Tyr705 (фиг. 3A; дополнительный фиг. S3A), что еще больше подчеркивает перекрестную регуляцию между ацетилированием и фосфорилированием Ser727. Одновременно ресвератрол уменьшал рекрутирование Sin3A и STAT3 в промоторные области PRDM1 и IL2Rγ (рис.3B) и вызвали повторную экспрессию этих и нескольких других STAT3-репрессированных TSG в клетках NPM-ALK + (фиг. 3C; дополнительные фиг. S3B и S3C). Полученная экспрессия IL2Rγ, PRDM1, / Blimp-1 и DDIT3, / CHOP была подтверждена на уровне белка либо с помощью анализа FACS (фиг. 3D), либо с помощью вестерн-блоттинга (фиг. 3E и F).
Ресвератрол ингибирует ацетилирование STAT3 и фосфорилирование Ser 727 и связывание Sin3A с промоторами онкосупрессорных генов, способствуя их экспрессии и апоптотической гибели клеток. Клетки NPM-ALK + культивировали в отсутствие (NT) или в присутствии ресвератрола (20 мкмоль / л) в течение 24 часов, а затем анализировали вестерн-блоттингом ( A , E и F ). ChIP ( B ) или qPCR ( C ). Результаты B указывают на кратное увеличение (% введенной ДНК) по сравнению с необработанным образцом; планки погрешностей — это стандартное отклонение по крайней мере от двух независимых экспериментов. Результаты в C указывают на относительные уровни мРНК в необработанном образце (пунктирная линия).Планки погрешностей, стандартное отклонение ( n > 3). Экспрессию D, IL2Rγ измеряли с помощью FACS. Необработанные клетки и окрашенные изотипическим контролем обработанные клетки показаны как контроли. Экспрессию E, и F, CHOP и BLIMP исследовали с помощью Вестерн-блоттинга. E, Представлен репрезентативный анализ, а в F показана экспрессия относительно уровней актина в независимых исследованиях ( n = 3).
Клетки NPM-ALK + культивировали в отсутствие (NT) или в присутствии ресвератрола (20 мкмоль / л) в течение 24 часов, а затем анализировали вестерн-блоттингом ( A , E и F ). ChIP ( B ) или qPCR ( C ). Результаты B указывают на кратное увеличение (% введенной ДНК) по сравнению с необработанным образцом; планки погрешностей — это стандартное отклонение по крайней мере от двух независимых экспериментов. Результаты в C указывают на относительные уровни мРНК в необработанном образце (пунктирная линия).Планки погрешностей, стандартное отклонение ( n > 3). Экспрессию D, IL2Rγ измеряли с помощью FACS. Необработанные клетки и окрашенные изотипическим контролем обработанные клетки показаны как контроли. Экспрессию E, и F, CHOP и BLIMP исследовали с помощью Вестерн-блоттинга. E, Представлен репрезентативный анализ, а в F показана экспрессия относительно уровней актина в независимых исследованиях ( n = 3). Двусторонний парный t тест, *, P <0.05; **, P <0,01; ***, P <0,005.
Двусторонний парный t тест, *, P <0.05; **, P <0,01; ***, P <0,005.
Обработка клеток ресвератролом улучшила экспрессию TSG также в обработанных ex vivo ALK + PDTX (дополнительная фигура S3D). Среди других генов экспрессия STAT3 оказалась нечувствительной к лекарству как в клетках ALK + , так и в клетках ALK — (дополнительный рисунок S3E). Одновременно с индукцией реэкспрессии TSG ресвератрол индуцировал клетки NPM-ALK + , чтобы они претерпели апоптотическую гибель клеток (дополнительный рис.S3F и S3G). Напротив, клетки ALK — OCI-Ly12 оказались нечувствительными к лекарству (дополнительные рисунки S3F и S3G).
Затем мы спросили, подавляет ли ресвератрол связь STAT3 с Sin3A. Мы исследовали эту проблему на клетках Hek293, стимулированных LIF, которые, как ранее было показано, быстро индуцируют ацетилирование STAT3 и связывание Sin3A (26). Как показано на дополнительном рисунке S4, ресвератрол препятствовал LIF-индуцированному ацетилированию STAT3 (дополнительный рисунок S4A), лишь частично снижая ядерную локализацию STAT3 (дополнительный рисунок). S4B) и полностью аннулировали связывание STAT3 с Sin3A (дополнительный рисунок S4C). Важно отметить, что хотя ресвератрол препятствовал ацетилированию STAT3 Lys685, уникальная мутация STAT3 Lys685, имитирующая ацетил (STAT3K685Q) или ацетил-дефицитный (STAT3K685R), не влияла на связывание STAT3 с Sin3A (дополнительные рисунки S4D и S4E), что убедительно свидетельствует о том, что другие. Остатки лизина STAT3 рядом с Lys685 регулируют взаимодействие STAT3-Sin3A.
S4B) и полностью аннулировали связывание STAT3 с Sin3A (дополнительный рисунок S4C). Важно отметить, что хотя ресвератрол препятствовал ацетилированию STAT3 Lys685, уникальная мутация STAT3 Lys685, имитирующая ацетил (STAT3K685Q) или ацетил-дефицитный (STAT3K685R), не влияла на связывание STAT3 с Sin3A (дополнительные рисунки S4D и S4E), что убедительно свидетельствует о том, что другие. Остатки лизина STAT3 рядом с Lys685 регулируют взаимодействие STAT3-Sin3A.
Вместе эти результаты показывают, что ресвератрол вызывает снижение ацетилирования STAT3 и фосфорилирования S727, высвобождение Sin3A и STAT3 из промоторов TSG, усиление экспрессии TSG и апоптотическую гибель клеток NPM-ALK + .
SIN3A сайленсинг вызывает экспрессию TSG, индуцирует апоптотическую гибель клеток и препятствует канцерогенному потенциалу ALK + ALCL Чтобы более точно проверить, зависит ли транскрипционный тормоз TSG от Sin3A, мы трансдуцировали клетки NPM-ALK + ALCL с лентивирусным вектором, кодирующим SIN3A -специфическую короткую шпилечную РНК (shSIN3A). Была использована несиленная контрольная кшРНК (shControl), тогда как устойчивость к GFP и пуромицину была адаптирована для обеспечения возможности отслеживания и отбора трансдуцированных клеток.К пяти дням отбора клетки shSIN3A экспрессировали значительно более низкие уровни Sin3A по сравнению с клетками, трансдуцированными shControl, при сохранении сопоставимой экспрессии STAT3 (фиг. 4A). Кроме того, нокдаун SIN3A индуцировал повторную экспрессию ресвератрол-чувствительных STAT3-контролируемых TSG как на уровне РНК (фиг. 4B), так и на уровне белка (фиг. 4C и D). При сравнении поведения клеток в культуре мы обнаружили, что клетки shSIN3A показали более медленную скорость роста по сравнению с клетками shControl, и после 5-го дня, одновременно с повторной экспрессией TSG, их количество больше не увеличивалось (рис.4E) и были обогащены апоптотическими клетками (фиг. 4F). Аналогичные результаты были получены со вторым несвязанным shSIN3A (shSIN3A # 2), таким образом исключая возможные нецелевые эффекты.
Была использована несиленная контрольная кшРНК (shControl), тогда как устойчивость к GFP и пуромицину была адаптирована для обеспечения возможности отслеживания и отбора трансдуцированных клеток.К пяти дням отбора клетки shSIN3A экспрессировали значительно более низкие уровни Sin3A по сравнению с клетками, трансдуцированными shControl, при сохранении сопоставимой экспрессии STAT3 (фиг. 4A). Кроме того, нокдаун SIN3A индуцировал повторную экспрессию ресвератрол-чувствительных STAT3-контролируемых TSG как на уровне РНК (фиг. 4B), так и на уровне белка (фиг. 4C и D). При сравнении поведения клеток в культуре мы обнаружили, что клетки shSIN3A показали более медленную скорость роста по сравнению с клетками shControl, и после 5-го дня, одновременно с повторной экспрессией TSG, их количество больше не увеличивалось (рис.4E) и были обогащены апоптотическими клетками (фиг. 4F). Аналогичные результаты были получены со вторым несвязанным shSIN3A (shSIN3A # 2), таким образом исключая возможные нецелевые эффекты.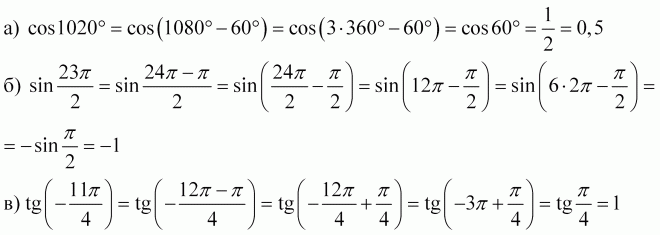 Кроме того, в этом случае молчание SIN3A (дополнительный рисунок S5A) вызвало экспрессию PRDM1, LAT (дополнительный рисунок S5B) и IL2Rγ (дополнительный рисунок S5C) и апоптоз благоприятных клеток (дополнительный рисунок S5D). .
Кроме того, в этом случае молчание SIN3A (дополнительный рисунок S5A) вызвало экспрессию PRDM1, LAT (дополнительный рисунок S5B) и IL2Rγ (дополнительный рисунок S5C) и апоптоз благоприятных клеток (дополнительный рисунок S5D). .
SIN3A вызывает экспрессию онкосупрессорного гена и индуцирует апоптоз клеток NPM-ALK + .Клетки NPM-ALK + трансдуцировали shControl или shSIN3A и анализировали вестерн-блоттингом ( A и D ) или qRT-PCR ( B ) через 5 и 8 дней после трансдукции соответственно. B, Результаты указывают на относительные уровни мРНК, рассчитанные для образца shControl (пунктирная линия). Планки погрешностей, стандартное отклонение ( n > 4). Двусторонний парный тест t , *, P <0,05; **, P <0,01; ***, P <0,005. C, Точечные диаграммы отображают анализ FACS через 8 дней после трансдукции. D, Показано относительное выражение. Данные представляют два независимых эксперимента. E, Рост клеток NPM-ALK + , трансдуцированных shControl или shSIN3A, в указанные моменты времени оценивали с помощью трипанового синего. Результаты указывают на количество клеток. Через день после подавления активности клетки высевали из расчета 10 5 клеток / мл. На 3 и 5 день клетки подсчитывали и повторно высевали (10 5 клеток / мл), чтобы избежать слияния. Данные представляют собой клетки / мл. Планки погрешностей, стандартное отклонение независимых экспериментов ( n = 2–4). F, Апоптоз клеток shControl или shSIN3A NPM-ALK + оценивали через 8 дней после трансдукции проточной цитометрией через окрашивание аннексином V-FITC и 7AAD. Показаны процентные значения ± стандартное отклонение аннексина V + клеток репрезентативного эксперимента ( n = 3). Статистическая значимость была проанализирована с помощью двустороннего парного теста t .
D, Показано относительное выражение. Данные представляют два независимых эксперимента. E, Рост клеток NPM-ALK + , трансдуцированных shControl или shSIN3A, в указанные моменты времени оценивали с помощью трипанового синего. Результаты указывают на количество клеток. Через день после подавления активности клетки высевали из расчета 10 5 клеток / мл. На 3 и 5 день клетки подсчитывали и повторно высевали (10 5 клеток / мл), чтобы избежать слияния. Данные представляют собой клетки / мл. Планки погрешностей, стандартное отклонение независимых экспериментов ( n = 2–4). F, Апоптоз клеток shControl или shSIN3A NPM-ALK + оценивали через 8 дней после трансдукции проточной цитометрией через окрашивание аннексином V-FITC и 7AAD. Показаны процентные значения ± стандартное отклонение аннексина V + клеток репрезентативного эксперимента ( n = 3). Статистическая значимость была проанализирована с помощью двустороннего парного теста t . *, P <0,05; **, P <0,01.
*, P <0,05; **, P <0,01.
Затем мы спросили, будет ли подавление Sin3A также влиять на канцерогенный потенциал клеток NPM-ALK + in vivo .С этой целью клетки shControl и shSIN3A вводили подкожно мышам с ослабленным иммунитетом NSG-3GS и наблюдали за развитием опухоли с течением времени. Мы обнаружили, что у мышей, зараженных опухолевыми клетками ALK + , лишенными SIN3A , развились опухоли в более поздние сроки (фиг. 5A) и продемонстрировали значительно увеличенную выживаемость (фиг. 5B) по сравнению с мышами, зараженными клетками shControl. Следует отметить, что во время умерщвления клетки, полученные из опухолей shSIN3A, показали более низкую экспрессию GFP (рис.5C) и более высокие уровни SIN3A по сравнению с уровнями, измеренными во время инъекции (фиг. 5D), в то время как уровни GFP оставались сопоставимыми в клетках из опухолей shControl во время инъекции и умерщвления. Это свидетельствует о росте in vivo клеток с субоптимальным подавлением SIN3A .
SIN3A сайленсинг препятствует ALK + ALCL in vivo канцерогенным потенциалом. A и B, shControl или shSIN3A-трансдуцированные клетки NPM-ALK + вводили подкожно в бок мышей NSG ( n = 6).Объемы опухоли (± стандартное отклонение; двусторонний непарный тест t , *, P <0,05; A ) и общая выживаемость (логарифм, тест Мантела-Кокса, **, P <0,01; n = 6; B ). Во время умерщвления опухоли диссоциировали на отдельные клетки и анализировали с помощью проточной цитометрии на экспрессию GFP ( C ) или с помощью qRT-PCR ( D ) по сравнению с клетками во время инъекции или с нетрансдуцированными клетками. C, Результаты репрезентативны для 6 мышей в группе. D, Экспрессия SIN3A (± стандартное отклонение) у отдельных мышей.
Вместе эти данные показывают, что Sin3A участвует в репрессии TSG в клетках NPM-ALK + и что его ингибирование способствует экспрессии TSG и апоптозу, препятствуя росту опухолевых клеток in vitro и in vivo . Таким образом, эти данные подчеркивают роль Sin3A в канцерогенном потенциале ALK и предполагают, что подавление / ингибирование Sin3A является новой стратегией ингибирования трансформации, управляемой STAT3.
Таким образом, эти данные подчеркивают роль Sin3A в канцерогенном потенциале ALK и предполагают, что подавление / ингибирование Sin3A является новой стратегией ингибирования трансформации, управляемой STAT3.
Sin3A способствует онкогенному потенциалу STAT3 также в клетках рака молочной железы.
STAT3 конститутивно активируется при многих типах рака, и это коррелирует с более тяжелым прогнозом (37). При раке молочной железы аберрантная передача сигналов STAT3 обнаруживается более чем в 40% случаев, в которых он способствует прогрессированию опухоли за счет дерегуляции экспрессии ряда нижестоящих генов-мишеней, участвующих в пролиферации, ангиогенезе, переходе эпителия в мезенхиму и инвазии (38).Чтобы выяснить, можно ли наблюдать вклад комплекса Sin3A в управляемую STAT3 репрессию транскрипции TSG в опухолях, отличных от ALK + ALCL, мы выбрали опухолевые клетки молочной железы MCF7 и MDA-MB-231, из которых только последние несут конститутивный STAT3. активация. Как показано на фиг. 6A, было обнаружено, что STAT3 ацетилирован в клетках MDA-MB-231, а не в контрольных клетках MCF7. Кроме того, как наблюдалось в клетках ALK + , STAT3 и Sin3A соосаждены в ядерных лизатах MDA-MB-231 (рис.6B), тогда как в клетках MCF7 STAT3 и Sin3A образовывали комплекс только при стимуляции цитокином LIF, активирующим STAT3 (дополнительный рисунок S6A).
Как показано на фиг. 6A, было обнаружено, что STAT3 ацетилирован в клетках MDA-MB-231, а не в контрольных клетках MCF7. Кроме того, как наблюдалось в клетках ALK + , STAT3 и Sin3A соосаждены в ядерных лизатах MDA-MB-231 (рис.6B), тогда как в клетках MCF7 STAT3 и Sin3A образовывали комплекс только при стимуляции цитокином LIF, активирующим STAT3 (дополнительный рисунок S6A).
Sin3A взаимодействует с STAT3 и контролирует экспрессию генов в клетках рака груди. A, Вестерн-блот анализ ядерных лизатов клеток аденокарциномы молочной железы человека MDA-MB-231 и MCF7. Данные представляют три независимых определения. B, Ядерные лизаты клеток MDA-MB-231 иммунопреципитировали антителами против Sin3A или нормальным кроличьим IgG и анализировали с указанными антителами.Изображен один репрезентативный эксперимент из трех. Клетки MDA-MB-231 трансфицировали siControl или siSIN3A и анализировали с помощью qRT-PCR ( C ) или вестерн-блоттинга ( D ). C, Уровни мРНК DDIT3 , рассчитанные для образца siControl. Планки погрешностей, стандартное отклонение ( n = 4). Двусторонний парный тест t , *** P <0,005. E и F, Рост клеток и жизнеспособность клеток MDA-MB-231, трансфицированных siControl и siSIN3A, оценивали через 5 дней после трансфекции подсчетом трипанового синего ( E ) и анализом FACS экспрессии аннексина V ( F ; n > 3).
C, Уровни мРНК DDIT3 , рассчитанные для образца siControl. Планки погрешностей, стандартное отклонение ( n = 4). Двусторонний парный тест t , *** P <0,005. E и F, Рост клеток и жизнеспособность клеток MDA-MB-231, трансфицированных siControl и siSIN3A, оценивали через 5 дней после трансфекции подсчетом трипанового синего ( E ) и анализом FACS экспрессии аннексина V ( F ; n > 3).
Чтобы оценить вклад Sin3A в опосредованную STAT3 репрессию транскрипции, клетки MDA-MB-231 трансфицировали контрольной миРНК (siControl) или SIN3A миРНК (siSIN3A). Интересно, что мы обнаружили, что молчание SIN3A увеличивало экспрессию ряда генов, среди которых ген DDIT3 / CHOP (фиг. 6C), посредством механизма, чувствительного к ресвератролу (дополнительный рисунок S6B). Кроме того, подавление Sin3A также увеличивает уровни белка CHOP (рис.6D), уменьшали рост клеток MDA-MB-231 (фиг. 6E) и способствовали апоптозу клеток (фиг. 6F). Кроме того, в этом случае мутация STAT3 Lys685 не повлияла на экспрессию DDIT3 / CHOP (дополнительный рисунок S6C и S6D), что дополнительно подтверждает, что другие лизины, помимо Lys685, играют роль в Sin3A-зависимом STAT3-управляемом репрессия транскрипции.
Взятые вместе, эти результаты предполагают, что комплекс STAT3 / Sin3A также действует в клетках рака молочной железы в качестве репрессора транскрипции, подтверждая идею о том, что Sin3A, способствующий онкогенному потенциалу STAT3, может представлять собой общую характеристику рака с конститутивной активацией STAT3.
Обсуждение
Здесь мы показываем, что STAT3 конститутивно фосфорилируется и ацетилируется в клетках ALK + и ALCL PDTX, и он связан с репрессорным комплексом транскрипции Sin3A, и что эти события имеют решающее значение для репрессии ряда TSG. ранее сообщалось, что он подавляется STAT3 и имеет решающее значение для канцерогенного потенциала NPM-ALK.
Роль STAT3 в трансформированном фенотипе ALK + ALCL и в контроле роста опухоли in vitro и in vivo давно признана (9).Хотя онкогенный потенциал STAT3 изначально был связан с его функцией активатора транскрипции, позже было сообщено, что после подавления активности STAT3 количество генов с усиленной регуляцией превысило число генов с пониженной регуляцией в ALK + ALCL (16). Было показано, что в этих клетках STAT3-зависимое молчание TSG включает метилирование TSG-регуляторных областей (14) посредством привлечения эпигенетических модификаторов, таких как DNMT1, HDAC1 и MeCP2 (15, 28, 29). Поскольку они являются хорошо известными интеракторами репрессорного комплекса Sin3A, наши данные показывают, что STAT3 конститутивно связывается с профилем Sin3A и представляет собой более подробный ландшафт онкогенного потенциала STAT3 благодаря его способности действовать как активатор транскрипции и репрессор (рис.7).
Рисунок 7.Схематическая модель сотрудничества между Sin3A и STAT3 в репрессии транскрипции TSG. Аберрантная экспрессия химерной киназы ALK приводит к конститутивному фосфорилированию STAT3 Y705 и транскрипционной активности, способствуя экспрессии онкогена. Кроме того, ALK активирует несколько киназ Ser / Thr, которые, в свою очередь, приводят к фосфорилированию STAT3 Ser727 и ацетилированию лизина. Ацетилированный STAT3 связывается с комплексом Sin3A, вероятно, способствуя его привлечению к регуляторным элементам нескольких генов-супрессоров опухолей ( PRDM1 на схеме), что совместно приводит к эпигенетическому молчанию.
Предыдущие исследования описали взаимодействие между STAT3 и Sin3A как временное и цитокин-зависимое событие, посредством которого ацетилирование STAT3 будет способствовать связыванию с Sin3A, которое, в свою очередь, опосредует его деацетилирование, подавляя его транскрипционную активность (26). В ALCL NPM-ALK + мы обнаружили, что STAT3 был конститутивно фосфорилирован и ацетилирован, а также конститутивно связан с Sin3A независимым от стимула образом. Мы предполагаем, что гиперфосфорилирование и ацетилирование STAT3 отвечает за длительное связывание с Sin3A и подавление критических TSG эпигенетическими средствами, и что это способствует трансформированному фенотипу.Соответственно, ресвератрол, который, как ранее было показано, способствует деацетилированию STAT3 и препятствует его активности в качестве репрессора транскрипции (23, 24), также ингибирует фосфорилирование и ацетилирование STAT3 Ser727 в клетках NPM-ALK + , образование комплекса STAT3 / Sin3A и связывание Sin3A со STAT3. -контролируемые гены PRDM1 и IL2Rg , вызывали повторную экспрессию субнабора STAT3-репрессированных генов и способствовали апоптотической гибели клеток NPM-ALK + ALCL. Хотя ресвератрол может контролировать множество субстратов, он не влияет на экспрессию TSG в клетках ALK —.
Механизм, с помощью которого ресвератрол контролирует ацетилирование STAT3 ниже NPM-ALK, еще предстоит определить и может включать активацию деацетилаз или ингибирование ацетилтрансфераз. Хотя ресвератрол является известным активатором деацетилазы сиртуина 1 (39, 40), он, по-видимому, не является единственной причиной деацетилирования STAT3. Действительно, нокдаун Sirtuin1 вызвал усиление ацетилирования Lys685 [дополнительный рис. S7A, но не отменял способность ресвератрола повышать экспрессию TSG (DDIT3 изображен на дополнительном рис.S7B]. Т.о., др. Деацетилазы, такие как HDACs, др. Sirtuins или Lysyl Oxidase 3, все ранее описанные для деацетилирования STAT3 (41-43), также могут играть роль.
Ацетилирование STAT3 обычно катализируется ацетилтрансферазами p300 / CBP (19, 41). Хотя p300 / CBP ранее не был связан с NPM-ALK, Ser / Thr киназы MAPK, PI3K и mTOR, активированные ниже NPM-ALK (30, 31), могут представлять собой предполагаемые недостающие звенья. Действительно, фосфорилирование Ser727 действует как сайт стыковки для p300 / CBP (44).Мы обнаружили, что ингибирование MAPK, PI3K и mTOR снижает фосфорилирование Ser727, а также ацетилирование Lys685. Поскольку ресвератрол также влияет на активность mTOR, это может представлять собой дополнительный механизм контроля ацетилирования STAT3 (45, 46). С этой точки зрения, явная активность Ser / Thr киназ, общее событие в ряде раковых заболеваний (41, 47-50), может быть ответственной за конститутивное фосфорилирование STAT3 Ser727 и ацетилирование Lys и в конечном итоге за его активность как репрессора транскрипции.
Вмешательство в экспрессию Sin3A вызывает нарушение транскрипции, наложенное на экспрессию TSG.Это коррелировало с индукцией гибели опухолевых клеток in vitro и со снижением канцерогенного потенциала ALCL in vivo . Механизм, с помощью которого Sin3A способствует репрессии TSG, еще предстоит установить. Разумно предположить, что через STAT3 Sin3A присоединяет эпигенетические модификаторы к критическим промоторам и / или энхансерным областям, подавляя экспрессию TSG. В соответствии с этим представлением, хотя уровни Sin3A были снижены уже через четыре дня после замалчивания, реэкспрессия TSG и апоптотическая гибель клеток наблюдались только через дополнительные 24–72 часа.Остается определить, играет ли роль активное или пассивное (посредством клеточного деления) деметилирование.
Сотрудничество между STAT3 и Sin3A в репрессии транскрипции TSG не было характерным для NPM-ALK-трансформированных клеток ALCL, но также наблюдалось в клетках аденокарциномы молочной железы, предполагая, что ось STAT3 / Sin3A может работать всякий раз, когда STAT3 конститутивно активируется, а в в частности, когда он ацетилирован. Поскольку несколько событий могут привести к явной активации STAT3, включая аберрантную или хроническую стимуляцию цитокинами и факторами роста, конститутивное включение дикого типа и мутированных рецепторов RTK и дерегулированную активацию рецепторов, связанных с G-белком (51), вполне вероятно, что ось STAT3 – Sin3A, описанная здесь, активна в большом количестве опухолей, зависимых от STAT3.Мы предполагаем, что могут иметь место эффекты, специфичные для опухолей или онкогенов, и приводить к разнообразному и, возможно, эпигенетическому ремоделированию, специфичному для клеточного типа. Действительно, мы обнаружили, что только подмножество корегулируемых генов STAT3 и Sin3A, идентифицированных в клетках ALK + , также было чувствительно к подавлению сигнала SIN3A в клетках MDA-MB-231. Кроме того, мы обнаружили, что гены, репрессированные STAT3, не были одинаково чувствительны к ингибированию PI3K или к эпигенетическим препаратам 5′-аза-2′-дезоксицитидин и трихостатин A (дополнительный рис.S7C). Т.о., возможно, что специфические для клеточного типа сигнатуры развиваются вторично по отношению к посттрансляционным модификациям STAT3, а также корегуляции с помощью др. Путей.
Ресвератрол повысил уровни Blimp-1 и Chop. Хотя изменения были очень небольшими, они достигли статистической значимости по сравнению с независимыми определениями. Вопрос о том, будут ли такие небольшие изменения per se биологически значимыми, может быть спорным, и еще предстоит определить. Однократная сверхэкспрессия некоторых реэкспрессированных генов (i.e., DDIT3 / CHOP, Blimp1, FOS ) было достаточно для индукции апоптоза раковых клеток в предыдущих исследованиях (32, 33). Тем не менее, отключение только одного белка за раз не спасало клетки от апоптоза, вызванного ингибированием STAT3, что позволяет предположить, что несколько факторов вносят вклад в гибель опухолевых клеток в результате блокирования STAT3. Мы предполагаем, что сопутствующая активация нескольких STAT3-репрессированных TSG способствует задержке роста опухолевых клеток и наблюдаемому апоптотическому фенотипу.
Идентичность ацетилированных лизинов STAT3 и их влияние на другие посттрансляционные модификации также могут формировать интерактом STAT3.Мы обнаружили, что Lys685 конститутивно ацетилирован. Тем не менее, наши результаты вместе с предыдущими исследованиями (26) не подтверждают, что Lys685 однозначно ответственен за взаимодействие STAT3-Sin3A. Действительно, мутация STAT3 Lys685, имитирующая ацетил (STAT3K685Q) или ацетил-дефицитную (STAT3K685R), не влияла на связывание STAT3 с Sin3A. Остается определить, могут ли дополнительные остатки Lys быть ацетилированы и контролировать взаимодействие с Sin3A, обеспечивая клеточно-специфические события. Поскольку гомолог STAT3 человека содержит несколько чрезвычайно консервативных остатков лизина (≥ 47), вполне вероятно, что могут существовать разные паттерны ацетилирования STAT3, которые объясняют разные биологические функции.Для решения этой проблемы потребуется идентификация критических остатков. Учитывая представления о том, что (i) N-концевые домены STAT3 и STAT5 необходимы для репрессии транскрипции TSG (33, 52), и (ii) ацетилирование двух остатков лизина, расположенных в N-концевом домене STAT3 (т. Е. on Lys49 и Lys87) способствует взаимодействию STAT3-Sin3A (26), есть соблазн предположить роль N-концевого домена STAT3 в Sin3A-опосредованной репрессии транскрипции. В подтверждение этой возможности было обнаружено, что проницаемые для клеток аналоги этой области специфически связываются со STAT3 и ингибируют STAT3-зависимые выживание и рост раковых клеток (53).
В заключение, наши данные подтверждают ранее неизвестную роль Sin3A в онкогенном потенциале STAT3. Поскольку связывание STAT3 с Sin3A контролируется внеклеточными сигналами в физиологических условиях (26), их конститутивное взаимодействие в раковых клетках может представлять собой многообещающую мишень для лекарств. Генерация молекул, способных превзойти или нарушить связывание с выбранными интеракторами, как описано ранее для Sin3A-MAD1 (54) и Sin3A-Foxo1 (55), при сохранении дополнительных специфических функций должно оказаться более селективным и менее токсичным, чем протестированные. на сегодняшний день.
Раскрытие информации о потенциальных конфликтах интересов
О потенциальных конфликтах интересов не сообщалось.
Вклад авторов
Концепция и дизайн: Г. Гамби, Г. Инхирами, Л. Икарди, А. Мондино
Разработка методологии: Г. Гамби, Л. Риччи, Р. Ван, Л. Icardi
Сбор данных (предоставленные животные, приобретенные и обслуживаемые пациенты, предоставленные помещения и т. Д.): G. Gambi, M. Ponzoni, G. Inghirami
Анализ и интерпретация данных (e.g., статистический анализ, биостатистика, вычислительный анализ): G. Gambi, L. Ricci, A. Verma, O. Elemento, G. Inghirami, L. Icardi, A. Mondino
Написание, обзор и / или редакция рукописи: Г. Гамби, М. Понзони, Г. Ингирами, Л. Икарди, А. Мондино
Руководитель: Л. Икарди, А. Мондино
Прочие (проведенные эксперименты): E .Di Simone
Прочее (проведенные эксперименты и полученные образцы): В.Бассо
Благодарности
Авторы благодарны доктору Кьярле и доктору Пиве (Туринский университет, Турин, Италия), доктору Бернарди и доктору Бонданце (Научный институт Сан-Рафаэле, Милан, Италия), доктору Тавернье ( VIB, Гент, Бельгия) и доктору Калаутти (Институт телемарафона Дульбекко, Центр молекулярной биотехнологии Туринского университета) за полезные реагенты. Эта работа была поддержана щедрым даром анонимного спонсора и грантами Associazione Italiana Ricerca sul Cancro (AIRC IG15883; A.Мондино), а также из AIRC 5 × 1000 (№ 10007) и Общества лейкозных лимфом (SCOR 2015; Дж. Ингирами). Л. Икарди был поддержан стипендиями, финансируемыми Международной постдокторской программой Сан-Раффаэле (INVEST) и Итальянской ассоциацией per la Ricerca sul Cancro (AIRC-iCare) при частичной финансовой поддержке Европейской комиссии (FP7 – Marie Curie Actions – People – COFUND. ). L. Ricci была поддержана очным конкурсом «Seed Grant», финансируемым из средств Министерства здравоохранения Италии в 2014 финансовом году в размере 5 × 1000.
Расходы на публикацию этой статьи были частично покрыты за счет оплаты страницы. Таким образом, данная статья должна быть помечена как реклама в соответствии с 18 U.S.C. Раздел 1734 исключительно для указания этого факта.
Сноски
Примечание: Дополнительные данные для этой статьи доступны на сайте Cancer Research Online (http://cancerres.aacrjournals.org/).
Cancer Res 2019; 79: 3076–87
- Поступила 2 февраля 2018 г.
- Редакция получена 14 июня 2018 г.
- Принята 23 января 2019 г.
- Опубликована впервые 28 января 2019 г.
- © Американская ассоциация исследований рака, 2019 г.
Функция в кубе синуса — Исчисление
Эта статья посвящена конкретной функции от подмножества действительных чисел до действительных чисел. Информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференциации и интеграции, представлена в статье.
Посмотреть полный список конкретных функций в этой вики
Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. Д.), Мы следуем соглашению, согласно которому все углы измеряются в радианах. Так, например, угол измеряется как.
Определение
Эта функция, обозначенная, определяется как комбинация функции куба и функции синуса. Явно это карта:
Для краткости пишем или.
Основные данные
| Арт. | Стоимость |
|---|---|
| Домен по умолчанию | все действительные числа, т.е. все |
| диапазон | закрытый интервал, т.е. абсолютное максимальное значение: 1, абсолютное минимальное значение: -1 |
| период | , т.е. |
| локальные максимальные значения и точки достижения | Все локальные максимальные значения равны 1, и они достигаются во всех точках формы, где изменяется по целым числам. |
| локальные минимальные значения и точки достижения | Все локальные минимальные значения равны -1, и они достигаются во всех точках формы, где варьируется по целым числам. |
| точек перегиба (обе координаты) | Все точки формы, а также точки формы и where варьируются в зависимости от целых чисел. |
| производная | |
| вторая производная | |
| первообразное | |
| важные симметрии | нечетная функция (следует из того, что композиция нечетных функций является нечетной, и того факта, что функция куба и синусоидальная функция являются нечетными) полуоборотная симметрия относительно всех точек формы зеркальная симметрия относительно всех линий. |
Личности
Имеем удостоверение:
График
Вот основной график, построенный на интервале:
Вот более крупный график, нарисованный на интервале. Толстые черные точки соответствуют локальным экстремальным значениям, а толстые красные точки соответствуют точкам перегиба.
Дифференциация
Первая производная
Чтобы дифференцировать один раз, мы используем цепное правило дифференциации.Явно мы рассматриваем функцию как составную часть функции куба и функции синуса, поэтому функция куба — это внешняя функция , а функция синуса — это внутренняя функция .
Получаем:
[ПОКАЗАТЬ БОЛЬШЕ]Интеграция
Первая первообразная: стандартный метод
Переписываем, а затем интегрируем u-заменой где. Ясно:
Сейчас ставлю. У нас есть, поэтому мы можем заменить на, и мы получаем:
Путем полиномиального интегрирования получаем:
Вставляя обратно, получаем:
. 3 и sin.Таким образом, мы можем антидифференцировать (то есть интегрировать) функцию любое количество раз, при этом первообразное выражение чередуется между кубической функцией синуса и кубической функцией косинуса.
СерияPower и серия Тейлора
Расчет степенного ряда
Мы можем использовать удостоверение личности:
У нас есть силовая серия:
Таким образом, получаем степенной ряд:
Подставляя в формулу, получаем:
Первые несколько терминов следующие:
таблиц математических формул
таблиц математических формул1.Десятичные множители
| 10 1 | дека (да) | 10 -1 | деци (d) |
| 10 2 | гекто (ч) | 10 -2 | санти (с) |
| 10 3 | килограмм (k) | 10 -3 | милли (м) |
| 10 6 | мега (М) | 10 -6 | микро (u) |
| 10 9 | гига (G) | 10 -9 | нано (п) |
| 10 12 | тера (т) | 10 -12 | пико (п) |
| 10 15 | пета (P) | 10 -15 | фемто (ж) |
| 10 18 | exa (E) | 10 -18 | атто (а) |
2.Серия
Серия Маклорена.
1. e x = 1 + x + x 2 /2! + … + x n / n! + … для всех x2. грех х = х — х 3 /3! + x 5 /5! — х 7 /7! + … для всех x
3. cos x = 1 — x 2 /2! + х 4 /4! — х 6 /6! + … для всех x
4. ln (1 + x) = x — x 2 /2 + x 3 /3 -… + (-1) n + 1 x n / n +… для (-1
9. cosh x = x + x 2 /2! + х 4 /4! + x 6 /6! + … для всех x
10. arcsinh x = x — (1/2) x 3 /3 + (1.3 / 2.4) x 5 /5 — (1.3.5 / 2.4.6) x 7 /7 + .. . для (-1
Геометрическая серия.
13. Sn = a + a r + a r 2 + a r 3 + … + a r n-1 = a (1 — r n ) / (1 — r)Целочисленная серия.
14. 1 + 2 + 3 + … + n = (1/2) n (n + 1)15. 1 2 + 2 2 + 3 2 + … + n 2 = (1/6) n (n + 1) (2n + 1)
15. 1 3 + 2 3 + 3 3 + … + n 3 = [(1/2) n (n + 1)] 2
3.Факториал, перестановки и комбинации.
1. n факториал = n! = п. (п — 1). (п — 2) … 2.12. Перестановки n объектов, взятых r в момент времени:
п П р = п! / [(п — г)! ]
3. Комбинации n объектов, взятых r в данный момент:
п С г = п! / [ р ! (п — р)! ]
4. Биномиальное разложение (формула).
1. Если n является положительным целым числом, мы можем разложить (x + y) n следующим образом(x + y) n = n C 0 x n + n C 1 x n — 1 y + n C 2 x n — 2 y 2 +… + n C n y n
Общий член n C r определяется как
п С г = п! / [ р ! (п — р)! ]
5. Тригонометрические формулы.
Формулы суммы / разности углов.
1. cos (A + B) = cos A cos B — sin A sin B2. cos (A — B) = cos A cos B + sin A sin B
3. sin (A + B) = sin A cos B + cos A sin B
4. sin (A — B) = sin A cos B — cos A sin B
5. загар (A + B) = [загар A + загар B] / [1 — загар A загар B]
6. загар (A — B) = [загар A — загар B] / [1 + загар A загар B]
Сумма / разность формул тригонометрических функций.
7. sin A + sin B = 2 sin [(A + B) / 2] cos [(A — B) / 2]8. грех A — грех B = 2 cos [(A + B) / 2] sin [(A — B) / 2]
9. cos A + cos B = 2 cos [(A + B) / 2] cos [(A — B) / 2]
10. cos A — cos B = — 2 sin [(A + B) / 2] sin [(A — B) / 2]
Произведение формул тригонометрических функций.
11. 2 sin A cos B = sin (A + B) + sin (A — B)12. 2 cos A sin B = sin (A + B) — sin (A — B)
13. 2 cos A cos B = cos (A + B) + cos (A — B)
14.2 sin A sin B = — cos (A + B) + cos (A — B)
Формулы множественных углов.
15. sin 2A = 2 sin A cos A16. cos 2A = cos 2 A — sin 2 A = 2 cos 2 A — 1 = 1-2 sin 2 A
17. sin 3A = 3 sin A — 4 sin 3 A
18. cos 3A = 4 cos 3 A — 3 cos A
Формулы снижения мощности.
19. sin 2 A = (1/2) [1 — cos 2A]19. cos 2 A = (1/2) [1 + cos 2A]
Другие таблицы формул
Таблица производных.Таблица интегралов.

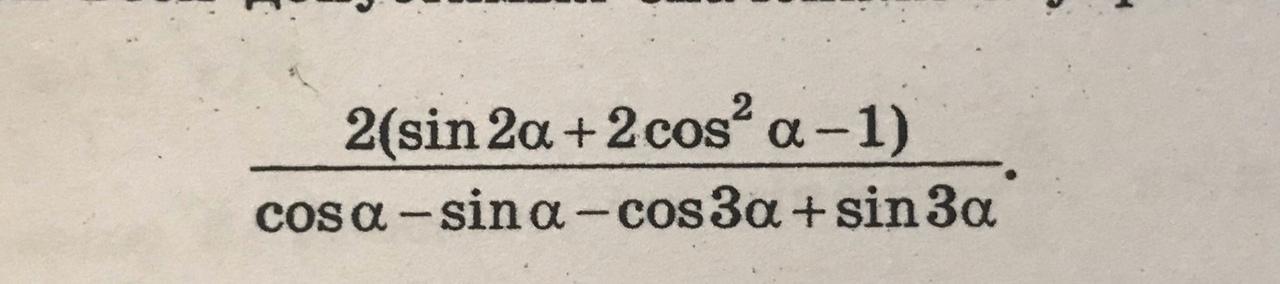
 ctg(a) = 1
ctg(a) = 1 r, S = p.r2
r, S = p.r2


