Формулы квадрата суммы и квадрата разности двух выражений – методическая разработка для учителей, Андреева Вероника Юрьевна
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу): |
|
|
7.2.1.10 знать и применять формулы сокращённого умножения: |
|
|
Цели урока: |
Все учащиеся знают формулы сокращенного умножения. Большинство учащихся знают и могут применить ту или иную формулу сокращенного умножения. Некоторые учащиеся знают, применяют и могут проанализировать применение формул сокращенного умножения. |
|
Критерии успеха: |
|
|
Привитие ценностей: |
ценности, основанные на национальной идее «Мәңгілік ел»: — казахстанский патриотизм и гражданская ответственность; — уважение; — сотрудничество; — труд и творчество; — открытость; — образование в течение всей жизни. |
|
Межпредметные связи: |
взаимосвязь с предметами самопознание и информатика. |
|
Навыки использования ИКТ: |
на данном уроке учащиеся используют ноутбуки, умеют пользоваться интернет ресурсом BilimLand. |
|
Предварительные знания: |
умение выполнять действия с одночленами и многочленами. |
|
План |
||||||
|
Запланированная деятельность |
Ресурсы |
|||||
|
Действия учителя |
Действия ученика |
оценивание |
|
|||
|
НАЧАЛО УРОКА |
Мотивация к учебной деятельности |
|||||
|
1. Приветствует учеников, проверяет готовность к уроку. Психологический настрой. Дерево достижений Обратите внимание на наше одинокое дерево. У каждого из вас есть листочки разного цвета. Я попрошу вас взять один из них (любого цвета) и помочь нашему дереву покрыться разноцветной листвой. Тех, кто выбрал зеленый лист, ожидает успех на сегодняшнем занятии. Те, кто выбрал: красный – желают общаться; желтый – проявят активность. Помните, что красота дерева зависит от вас, ваших стремлений и ожиданий. |
Учащиеся поочередно подходят и прикрепляют листочки к дереву. |
СО «Словесная оценка» |
Листочки разного цвета
|
|||
Актуализация знаний учащихся
(Создание необходимой образовательной среды)
|
Ещё в глубокой древности было подмечено, что некоторые многочлены можно умножить короче и быстрее, чем все остальные. — Начать наше занятие мне бы хотелось со слов замечательной женщины, великого математика – Софьи Васильевны Ковалевской: «У математиков существует свой язык – это формулы». Для определения темы и целей урока предлагаю учащимся просмотреть видео из сайта BilimLand. |
Формулы сокращенного умножения. https://bilimland.kz/ru/courses/math-ru/algebra/preobrazovanie-algebraicheskix-vyrazhenij/formuly-sokrashennogo-umnozheniya/lesson/kvadrat-summy-i-kvadrat-raznosti-dvux-vyrazhenii |
||
|
Учащимся предлагаются задания из сайта BilimLand |
Учащиеся за компьютерами выполняют упражнение из ресурса BilimLand |
ФО «Сигналы рукой» Если вы заполнили все пропуски верно, то поднимите пальчик вверх. Если вы допустили не более двух ошибок – отведите его в сторону. Если же совсем не справились с заданием, то опустите палец вниз. Молодцы! Продолжаем дальше наш урок. |
https://bilimland.kz/ru/courses/math-ru/algebra/preobrazovanie-algebraicheskix-vyrazhenij/formuly-sokrashennogo-umnozheniya/lesson/kvadrat-summy-i-kvadrat-raznosti-dvux-vyrazhenii |
СЕРЕДИНА УРОКА
|
Изучение нового материала. «Исследование» — Выполните, пожалуйста, задание, перемножив пары двучленов. Результаты запишите в стандартном виде. Работа по группам. Работаю с таблицами (у каждой группы в таблице свои 3 примера)
— Ребята, посмотрите. — Итак, мы открыли формулу квадрат суммы двух выражений: (а + b)2 = а2 + 2аb + b2. — Продолжаем исследование. Изменится ли результат, если будем возводить в квадрат не (а + b), а выражение (а – b)? Предлагаю вам проверить это на практике. Замените в своих таблицах сумму в левом столбце на разность и выполните вычисления. Совместное обсуждение. В чем отличие от результатов первых вычислений? — Итак, мы открыли вторую формулу сокращенного умножения — формулу квадрат разности двух выражений: (а — b)2 = а2 — 2аb + b2. Обобщение учителя: Равенство (1) – квадрат сумы, равенство (2) – квадрат разности, они называются формулами сокращенного умножения. Применяются для упрощения вычислений. Эти формулы можно читать как слева направо, так и справа налево. |
Формулы сокращенного умножения. Квадрат суммы и квадрат разности двух выражений
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
• Самостоятельная работа
• «Умножение многочленов»»
№1. Умножить многочлены:
а) (а + 2)(в – 3),
б) (х – 4)(х + 5),
в) (2х + 5)(3х – 1).
№2. Упростить выражение:
а) (х + 2)(х – 5) -3х(1 – 2х),
б) (а + 3)(а – 2) + (а – 3)(а + 6),
в) (х – 7)(3х – 2) – (5х + 1)(2х – 4).
№3. Решить уравнение:
а) (х + 3)(х – 2) — (х + 4)(х – 1) = 3х,
б) (2х + 6)(7 – 4х) = (2 – х)(8х + 1) + 15.
2. История создания страны формул:
ДиофантАлександрийский
(III век н. э.) —
древнегреческий
математик.
Еще в глубокой древности
было замечено, что некоторые
многочлены можно умножать
быстрее, чем все остальные.
Так, древнегреческими
математиками еще до нашей
эры (более 2000 лет назад)
геометрическим способом
были выведены некоторые
формулы, которые получили
название формулы
сокращенного умножения.
3. Формулы сокращенного умножения
квадрат суммыи
квадрат разности
двух выражений
4. ЭПИГРАФ К УРОКУ:
«У МАТЕМАТИКОВ СУЩЕСТВУЕТСВОЙ ЯЗЫК –
ЭТО
ФОРМУЛЫ»
С. В. Ковалевская
(1850-1891)
5. Устная работа
• Найти квадраты выражений y; 4; -2/7; 3m; 8xy; 5a2b.Как можно назвать эти выражения?
• Найти произведение одночленов 6x и 9h.
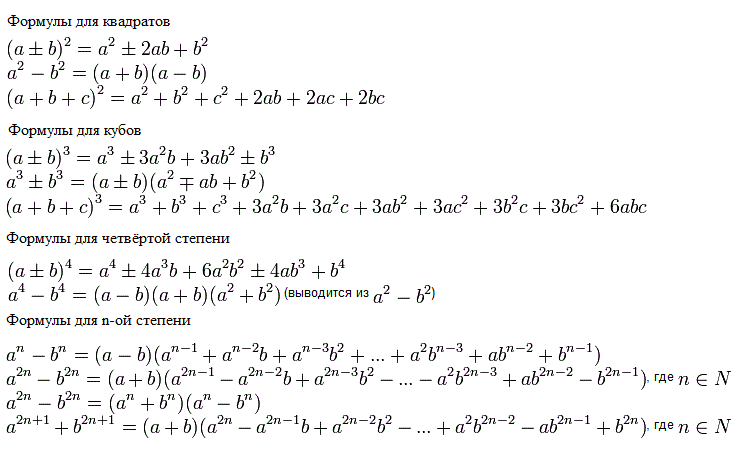
Чему равно их удвоенное произведение?
• Прочитать выражение:
a) m + n
б) (m+n)2
в) m2+n2
г) 2mn
д) (m-n)2
е) m2 — n2
• Выполнить умножение многочленов (c-5)(r+2).
Как можно назвать полученное выражение?
6. Остров исследований №1
Результат умножения1) (m + n) (m + n) =
=
2) (c + d) (c + d) =
=
3) (p + q) (p + q) =
=
4) (k + 3) (k + 3) =
=
5) ( 5 + m)( 5 + m) =
=
7. Остров исследований №1
Результат умножения1) (m + n) (m + n) =
= m2 + 2 m n + n 2
2) (c + d) (c + d) =
= c2 + 2 c d + d 2
3) (p + q) (p + q) =
= p2 + 2qp + q2
4) (k + 3) (k + 3) =
= k2 + 6 k + 9
5) ( 5 + m)( 5 + m) =
= n2 + 10 n + 25
8. Остров исследований №1
1) (m + n) (m + n) =(m + n)2
= m2 + 2 m n + n 2
2) (c + d) (c + d) =
(c + d) 2
= c2 + 2 c d + d 2
3) (p + q) (p + q) =
(p + q)2
= p2 + 2qp + q2
4) (k + 3) (k + 3) =
(k + 9)2
= k2 + 6 k + 9
5) ( 5 + m)( 5 + m) =
( 5 + m)2
= n2 + 10 n + 25
9.
 ОТКРЫТИЕ № 1ФОРМУЛА
ОТКРЫТИЕ № 1ФОРМУЛАКВАДРАТ СУММЫ ДВУХ
ВЫРАЖЕНИЙ:
(а +
2
b) =
2
а
+ 2аb +
2
b
10. ПРИМЕНЕНИЕ ФОРМУЛЫ КВАДРАТА СУММЫ (а + b)2 = а2 + 2аb + b2
Вместо a и b в эту формулу можно подставить любыевыражения
ШИФРОГРАММЫ:
11. Остров исследований №2
Результат умножения1) (m — n) (m — n) =
=
2) (c — d) (c — d) =
=
3) (p — q) (p — q) =
=
4) (k — 3) (k — 3) =
=
5) ( 5 — m)( 5 — m) =
=
12. Остров исследований №2
Результат умножения1) (m — n) (m — n) =
= m2 — 2 m n + n 2
2) (c — d) (c — d) =
= c2 — 2 c d + d 2
3) (p — q) (p — q) =
= p2 — 2qp + q2
4) (k — 3) (k — 3) =
= k2 — 6 k + 9
5) ( 5 — m)( 5 — m) =
= n2 — 10 n + 25
13. Остров исследований №2
1) (m — n) (m — n) =(m — n)2
= m2 — 2 m n + n 2
2) (c — d) (c — d) =
(c — d) 2
= c2 — 2 c d + d 2
3) (p — q) (p — q) =
(p — q)2
= p2 — 2qp + q2
4) (k — 3) (k — 3) =
(k — 9)2
= k2 — 6 k + 9
5) ( 5 — m)( 5 — m) =
( 5 — m)2
= n2 — 10 n + 25
14.
 ОТКРЫТИЕ № 2ФОРМУЛА
ОТКРЫТИЕ № 2ФОРМУЛАКВАДРАТ РАЗНОСТИ ДВУХ
ВЫРАЖЕНИЙ:
(а —
2
b) =
2
а
— 2аb +
2
b
15. ПРИМЕНЕНИЕ ФОРМУЛЫ КВАДРАТА РАЗНОСТИ (а — b)2 = а2 — 2аb + b2
ШИФРОГРАММЫ:16. Найдите ошибки:
НАЙДИТЕ ОШИБКИ:2
у)
2
2
у
(b = b – 2bу +
2
2
(6 + с) = 36 +- 12с + с
2
2
(р — 10) = р — 20р + 100
2
2
(2а + 1) = 4а + 42а + 1
17. Геометрическое обоснование формул сокращенного умножения
ГЕОМЕТРИЧЕСКОЕ ОБОСНОВАНИЕФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ
(a+b)2= a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
Представить в виде многочлена:
1) f d
f 2 fd d
2) m 1
m 2m 1
3) 3k 4
9k 24k 16
2
2
2
2
2
2
4) 2 x 7 y
2
4 x 28 xy 49 y
6) b d
7) 5 p 4q
5) c k
2 2
3 2
2
3
4 2
2
4
c 2ck k
2
2
4
b 2b d d
4
2
3
2
6
25 p 40 p q 16q
6
3
4
8
Представить в виде многочлена:
1) s z
s 2 sz z
2) m 1
m 2m 1
3) 4 3k
16 24k 9k
4) 5 x 2 y
25 x 20 xy 4 y
2
2
2
2
2
6) t c
7) 3m 4n
2
5) k p
2
7 2
4
6
3 2
2
2
2
2
k 2k p p
4
2
2
2
t 2t c c
8
4 7
14
9m 24m n 16n
12
6
3
6
Мало иметь
хороший ум,
главное –
уметь его
применять
Рене Декарт — (1596-1650)
— французский философ,
математик, физик и
физиолог
English Русский Правила
Формула полного квадрата A минус B — Примеры
Формула (a — b) 2 используется для нахождения квадрата двучлена. Формула (a — b) 2 также широко известна как квадрат разницы между двумя терминами. Эта формула иногда используется для разложения бинома на множители. Чтобы найти формулу (a — b) 2 , мы просто умножим (a — b) (a — b). (а — б) 2 = (а — б)(а — б) = а 2 — аб — ба + б 2 = а 4 2 Следовательно, (a — b) 2 формула: (a — b) 2 = a 2 — 2ab + b 2 Рассмотрим площадь 9 (0a — 0 4) квадрата длиной (a — b). Чтобы доказать, что (a — b) 2 = a 2 — 2ab + b 2 , уменьшите длину всех сторон на коэффициент b, и получится a — b. На рисунке выше (а — б) 2 отображается синей областью. Теперь вычтите вертикальные и горизонтальные полосы, имеющие площадь a×b. Удаление a × b дважды также удалит перекрывающийся квадрат в правом нижнем углу дважды, поэтому добавьте b 2 . При перестановке данных мы имеем (a − b) 2 = a 2 — ab — ab + b 2 . Следовательно, это доказывает алгебраическое тождество (a − b) 2 = a 2 − 2ab + b 2 Хотите находить сложные математические решения за считанные секунды? 92 формулы в этом разделе решенных примеров. Пример 1: Найдите значение (x – 2y) 2 , используя формулу (a – b) 2 . Решение: Найти: Значение (x — 2y) 2 . Ответ: (x — 2y) 2 = x 2 — 4xy + 4y 909004 2 . Пример 2: Разложить на множители x 2 — 6xy + 9y 2 , используя формулу полного квадрата a минус b. Решение: Разложить на множители: x 2 — 6xy + 9y 2 . — 3 года) 2 . Пример 3: Упростите следующее, используя формулу (a — b) 2 . (7x — 4y) 2 Решение: a = 7x и b = 4y Ответ: (7x — 4y) 2 = 49x 2 — 56xy + 16y 2 . (a — b) 2 формула читается как минус b целого квадрата. Его разложение выражается как (a — b) 2 = a 2 — 2ab + b 2 Формула (a — b) 2 также известна как одно из важных алгебраических тождеств. Давайте разберемся в использовании формулы (a — b) 2 с помощью следующего примера. Следующие шаги выполняются при использовании (a — b) 2 92}}
\end{выравнивание}
$$ Вы должны (в конце концов) быть в состоянии умножить
такие выражения
не написав
любые промежуточные результаты. Эта формула полного квадрата a минус b является одним из наиболее часто используемых алгебраических тождеств. Эта формула также известна как формула квадрата разности двух членов. Формула (a — b) 2 используется для факторизации некоторых специальных типов трехчленов. В этой формуле мы находим квадрат разницы между двумя терминами, а затем решаем его с помощью алгебраического тождества. Давайте узнаем больше о целом квадрате a минус b вместе с решенными примерами в следующем разделе. 92 Формула?
Эта формула полного квадрата a минус b является одним из наиболее часто используемых алгебраических тождеств. Эта формула также известна как формула квадрата разности двух членов. Формула (a — b) 2 используется для факторизации некоторых специальных типов трехчленов. В этой формуле мы находим квадрат разницы между двумя терминами, а затем решаем его с помощью алгебраического тождества. Давайте узнаем больше о целом квадрате a минус b вместе с решенными примерами в следующем разделе. 92 Формула?5
Доказательство A минус B Формула целого квадрата
 На приведенном выше рисунке показан самый большой квадрат с площадью 2 .
На приведенном выше рисунке показан самый большой квадрат с площадью 2 .
Предположим, что a = x и b = 2y.
Подставим эти значения в (a — b) 2 формулу:
(a — b) 2 = a 2 — 2ab + b 2
(x-2y) 2 = (x) 2 — 2(x)(2y) + (2y) 2
= x 2 — 4xy + 4y 2
Мы можем записать данное выражение как:
х 2 — 6xy + 9y 2 = (x) 2 — 2 (x) (3y) + (3y) 2 .
Используя (a — b) 2 формулу:
а 2 — 2аб + б 2 = (а — б) 2
Подставьте a = x и b = 3y в эту формулу:
(x) 2 — 2 (x) (3y) + (3y) 2 = (x — 3y) 2 
Используя формулу (a — b) 2 = a 2 — 2ab + b 2
(7x) 2 — 2(7x)(4y) + (4y) 2
49x 2 — 56xy + 16y 2 Часто задаваемые вопросы о формуле полного квадрата A минус B
Что такое расширение (a — b)
2 формулы? Что такое (a — b)
2 Формула в алгебре?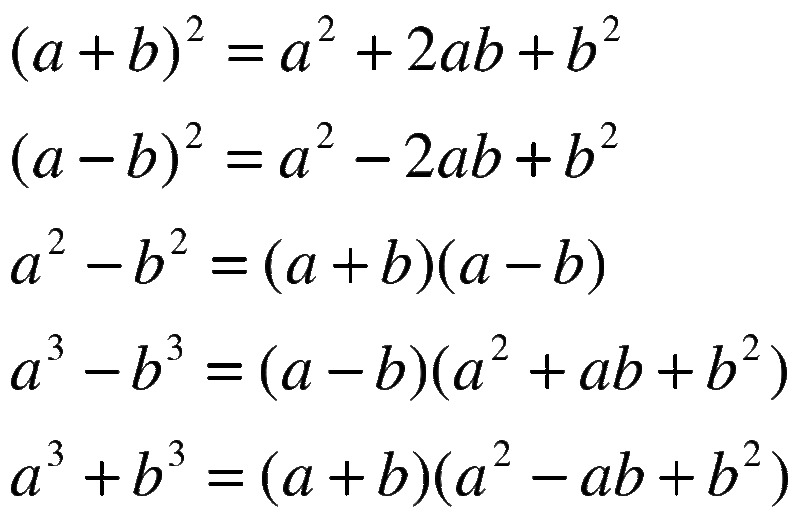 Читается как минус b целого квадрата. Его (а — б) 2 формула выражается как (a — b) 2 = a 2 — 2ab + b 2
Читается как минус b целого квадрата. Его (а — б) 2 формула выражается как (a — b) 2 = a 2 — 2ab + b 2 Как упростить числа с помощью формулы A минус B целого квадрата?
Пример: Найдите значение (20 – 5) 2 по формуле (a – b) 2 .
Чтобы найти: (20- 5) 2
Предположим, что a = 20 и b = 5,
Мы подставим их в формулу (a — b) 2 .
(a — b) 2 = a 2 — 2ab + b 2
(20-5) 2 = 20 2 — 2(20)(5) + 5 2
= 400 — 200 + 25 90 113
= 225
Ответ: (20 — 5) 2 = 225. Как использовать (a — b)
2 формула Дать шаги?



 Организационный момент
Организационный момент Так появились формулы сокращенного умножения. Их несколько. Сегодня мы с вами в роли исследователей «откроем» ещё две из этих формул.
Так появились формулы сокращенного умножения. Их несколько. Сегодня мы с вами в роли исследователей «откроем» ещё две из этих формул.
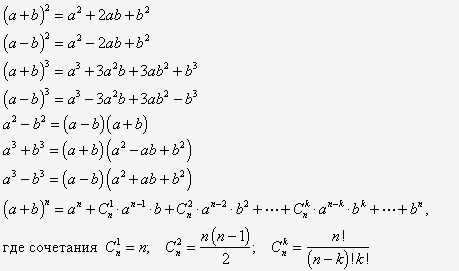 Есть ли что-то общее в условиях и ответах предложенных упражнений?
Есть ли что-то общее в условиях и ответах предложенных упражнений? При чтении справа налево многочлены а
При чтении справа налево многочлены а