Тригонометрические таблицы.
Тригонометрические таблицы.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тригонометрические функции острого угла | Справочник по математике
Решение всяких треугольников в конечном счете сводится к решению прямоугольных треугольников. В прямоугольном же треугольнике АВС отношение двух его сторон, например катета а к гипотенузе с, всецело зависит от величины одного из острых углов, например А (рис. 1).
рис.1
Отношения различных пар сторон прямоугольного треугольника и называются тригонометрическими функциями его острого угла. По отношению к углу А эти функции получают следующие названия и обозначения:
1. Синус: sin А = a/c (отношение противолежащего катета к гипотенузе).
2. Косинус: cos А = b/c (отношение прилежащего катета к гипотенузе).
3. Тангенс: tg A = a/b (отношение противолежащего катета к прилежащему).
4. Котангенс: ctg А = b/a (отношение прилежащего катета к противолежащему).
5. Секанс: sec А = c/b (отношение гипотенузы к прилежащему катету).
6. Косеканс: cosec А = c/a (отношение гипотенузы к противолежащему катету).
По отношению к углу В («дополнительному» углу но отношению к А) названия соответственно меняются:
sin В = b/c ; cos В = a/c ; tg В = b/a ;
ctg В = a/b ; sec В = c/a ; cosec В = c/b .
Для некоторых углов можно написать точные выражения их тригонометрических величин. Важнейшие случаи даны в таблице ниже*.
Важнейшие случаи даны в таблице ниже*.
Эта таблица имеет больше теоретическое, чем практическое значение, так как содержит неизвлекаемые точно корни. Для большинства же углов даже и с помощью корней нельзя записать точные числовые значения тригонометрических функций. Но приближенные их значения можно вычислить с любой желаемой степенью точности (см. §26).
| A | sin A | cos A | tg A | ctg A | sec A | cosec A |
| 0° | 0 | 1 | 0 | ∞ | 1 | ∞ |
| 30° | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45° | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 90° | 1 | 0 | ∞ | 0 | ∞ | 1 |
*Углы 0° и 90°, строго говоря, не могут входить в прямоугольный треугольник в качестве его острых углов. Однако при расширении понятия тригонометрической функции (см. §6) рассматриваются значения тригонометрических функций и для этих углов. С другой стороны, один из острых углов треугольника может сколь угодно приблизиться к 90°, другой будет тогда приближаться к нулю; тогда соответствующие тригонометрические величины будут приближаться к значениям, указанным в таблице.
Однако при расширении понятия тригонометрической функции (см. §6) рассматриваются значения тригонометрических функций и для этих углов. С другой стороны, один из острых углов треугольника может сколь угодно приблизиться к 90°, другой будет тогда приближаться к нулю; тогда соответствующие тригонометрические величины будут приближаться к значениям, указанным в таблице.
Знак ∞, встречающийся в этой таблице, указывает на то, что абсолютное значение данной величины неограниченно возрастает, когда угол приближается к тому значению, которое указано в таблице. Это и имеют в виду, когда говорят, что величина «равняется бесконечности» или «обращается в бесконечность» (см. Арифметика, §23 и Функции и графики, §12).
Таблица тригонометрии — Изучите CBSE
Таблица тригонометрии : Тригонометрия — это раздел математики, занимающийся изучением длины, углов и их взаимосвязей в треугольнике. Тригонометрические соотношения применимы только для прямоугольных треугольников, один из углов которых равен 90 o
Тригонометрическая таблица состоит из следующих взаимосвязанных между собой тригонометрических соотношений – sin, cos, tan, cos , сек, койка.
- sin (обратная величина косеканса) = напротив гипотенузы
- cos (обратное значение секанса) = соседний по гипотенузе
- тангенс (обратное значение котангенса) = напротив соседнего
- cot (обратное касательной) = смежное над противоположным
- косек (обратная величина к синусу) = гипотенуза относительно противоположной
- сек (обратная величина косинуса) = гипотенуза относительно соседнего сек.
В вычислениях можно легко разобраться, если запомнить таблицу функций, наиболее известную как Тригонометрическая таблица . Это находит применение в нескольких областях. Некоторые из них включают навигационные видеоигры, авиацию, науку, географию, инженерию, геометрию и т. д. Тригонометрическая таблица помогла во многих разработках и в области машиностроения для первых инноваций.
В таблице тригонометрических соотношений приведены значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 90°. Эти значения имеют повышенный приоритет по сравнению с другими, поскольку наиболее важные проблемы используют эти соотношения. Поэтому очень важно знать и помнить соотношения этих стандартных углов.
Эти значения имеют повышенный приоритет по сравнению с другими, поскольку наиболее важные проблемы используют эти соотношения. Поэтому очень важно знать и помнить соотношения этих стандартных углов.
Советы по запоминанию тригонометрической таблицы
Тригонометрическая таблицаЗапоминание таблицы тригонометрии будет полезно, так как она находит много применений, и существует много способов запомнить таблицу. Автоматическое знание формул, соотношений и тождеств тригонометрии приведет к выяснению таблицы и значений. Таблица тригонометрических соотношений зависит от формул тригонометрии точно так же, как все функции тригонометрии взаимосвязаны друг с другом.
Прежде чем начать, лучше попытаться запомнить эти значения и знать следующие тригонометрические отношения дополнительных углов.
- sin x = cos (90∘−x)
- потому что х = грех (90∘−х)
- загар x = детская кроватка (90∘−x)
- кроватка х = загар (90∘−x)
- сек х = детская кроватка (90∘−x)
- раскладушка x = сек (90∘−x)
Взаимные соотношения тригонометрических отношений
- 1 / sin x = cosec x
- 1 / cos х= сек х
- 1/сек х= cos х
- 1 / коричневая x= детская кроватка x
- 1 / детская кроватка x= коричневый x
- 1/ cosec x = sin x
Шаги по созданию тригонометрической таблицы:
Шаг 1 : Нарисуйте табличную колонку с необходимыми углами, такими как 0, 30 O , 45 O , 60 O , 90 O , 180 O. , 270 o , 360 o в верхнем ряду и все 6 тригонометрических функций, таких как синус, косинус, тангенс, косеканс, секанс и котангенс в первом столбце.
, 270 o , 360 o в верхнем ряду и все 6 тригонометрических функций, таких как синус, косинус, тангенс, косеканс, секанс и котангенс в первом столбце.
Шаг 2 :
Шаг 3 :
.
Подробное руководство по тригонометрии Таблица
Тригонометрия — это раздел математики, изучающий стороны и углы треугольников. Синус, косинус и тангенс кривой внутри треугольника являются наиболее часто используемыми тригонометрическими отношениями для вычисления в тригонометрии. Вы можете быстро определить основные тригонометрические числа наиболее часто встречающихся углов, используя тригонометрическую таблицу.
Что такое тригонометрическая таблица? Тригонометрическая таблица по существу представляет собой табличную компиляцию значений тригонометрических отношений для различных обычных углов, таких как 0°, 30°, 45°, 60° и 90°, часто с дополнительными углами, такими как 180°, 270° и 360° включены. Из-за существования шаблонов в тригонометрических соотношениях и даже между углами легко прогнозировать значения таблицы тригонометрии и использовать таблицу в качестве справочной информации для вычисления тригонометрических значений для многих других углов. Функция синуса, функция косинуса, функция tan, функция кроватки, функция sec и функция cosec являются тригонометрическими функциями.
Из-за существования шаблонов в тригонометрических соотношениях и даже между углами легко прогнозировать значения таблицы тригонометрии и использовать таблицу в качестве справочной информации для вычисления тригонометрических значений для многих других углов. Функция синуса, функция косинуса, функция tan, функция кроватки, функция sec и функция cosec являются тригонометрическими функциями.
Тригонометрическая таблица полезна в различных ситуациях. Он необходим для навигации, исследований и архитектуры. Эта таблица широко использовалась в доцифровую эпоху, даже до появления карманных калькуляторов. Стол также помог в создании первых механических вычислительных машин. Алгоритмы быстрого преобразования Фурье (БПФ) — еще одно известное применение тригонометрических таблиц.
Таблицы тригонометрииЗдесь представлены таблицы тригонометрии в радианах и отношениях.
Таблица тригонометрии в радианах| Таблица тригонометрии в радианах | ||||||||
| Углы (в радианах) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| грех | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| потому что | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| желтовато-коричневый | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| детская кроватка | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| косек | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| сек | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| Тригонометрическая таблица отношений | ||||||||
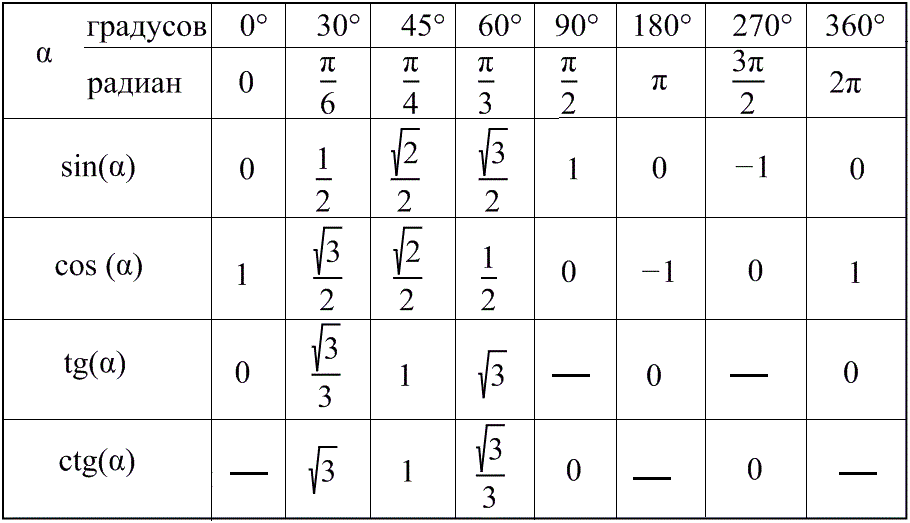
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| грех | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| потому что | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| желтовато-коричневый | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| детская кроватка | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| косек | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| с | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Значения тригонометрических соотношений для углов 0°, 30°, 45°, 60° и 90° широко используются для решения задач тригонометрии. Эти значения связаны с измерением длин и углов прямоугольного треугольника. Следовательно, стандартные углы в тригонометрии равны 0°, 30°, 45°, 60° и 90°.
Эти значения связаны с измерением длин и углов прямоугольного треугольника. Следовательно, стандартные углы в тригонометрии равны 0°, 30°, 45°, 60° и 90°.
Шаг 1:
Составьте таблицу, в верхней строке которой указаны углы, такие как 0°, 30°, 45°, 60° и 90°, а в первой колонке перечислены тригонометрические функции, такие как sin, cos, tan, cosec, sec. , кроватка.
Шаг 2. Определите значение sin
Чтобы найти значения sin, разделите 0, 1, 2, 3, 4 на 4 под корнем в указанном порядке. Рассмотрим следующий пример.
Чтобы найти значение sin 0°
√0/4 = 0
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| грех | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
Шаг 3. Определите значение cos
Определите значение cos
Значение cos является обратной величиной угла sin. Чтобы найти значение cos, разделите его на 4 в порядке, обратном порядку sin. Например, чтобы найти cos 0°, разделите 4 на 4 под корнем. Рассмотрим следующий пример.
Чтобы найти значение cos 0°
√4/4 = 1
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| потому что | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
Шаг 4. Определите значение тангенса
Определите значение тангенса
Tan определяется делением sin на cos. Тан равен sin/cos. Разделите значение sin при 0° на значение cos при 0°, чтобы получить значение tan при 0°. Рассмотрим следующий пример.
tan 0°= 0/1 = 0
Точно так же будет и таблица.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| желтовато-коричневый | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
Шаг 5. Определите значение cot
Определите значение cot
Обратная величина tan является значением cot. Разделите 1 на значение tan при 0°, чтобы получить значение cot при 0°. В результате значение будет таким: кроватка 0° = 1/0 = не ограничена или не определена
Аналогично таблица для детской кроватки показана ниже.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| детская кроватка | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
Шаг 6. Определите значение cosec
Определите значение cosec
Обратная величина sin при 0° равна значению cosec при 0°.
cosec 0° = 1/0 = не ограничено или не определено
Аналогичным образом таблица для cosec приведена ниже.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| косек | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
Шаг 7: Определите значение sec
Любые распространенные значения cos могут быть использованы для расчета sec. Значение sec при 0° является обратным значением cos при 0°. В результате значение будет таким:
Значение sec при 0° является обратным значением cos при 0°. В результате значение будет таким:
Секунда 0° = 1/1 = 1
Таблица для сек показана ниже.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| с | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Знание таблицы тригонометрии может помочь вам решить задачи по тригонометрии, а запомнить таблицу тригонометрии для нормальных углов в диапазоне от 0° до 90° довольно просто.

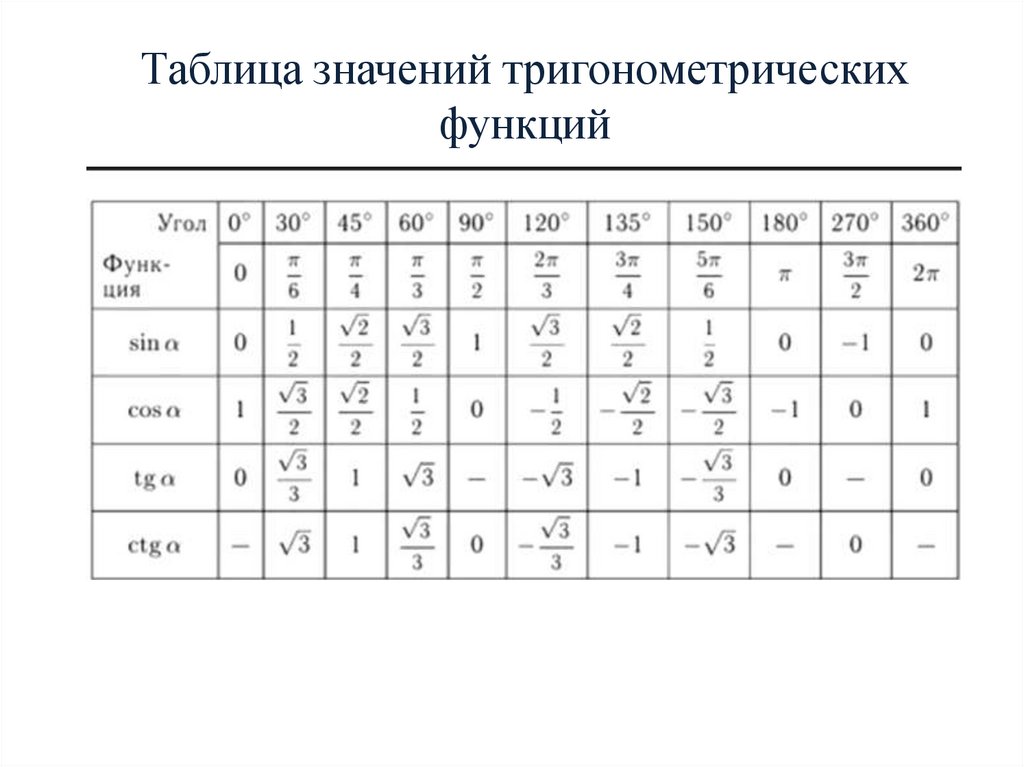 Можно каждый раз создавать эти
таблицы самостоятельно. Проще взять готовую
таблицу, например, со страницы Википедии, и
использовать ее в своей работе.
Можно каждый раз создавать эти
таблицы самостоятельно. Проще взять готовую
таблицу, например, со страницы Википедии, и
использовать ее в своей работе.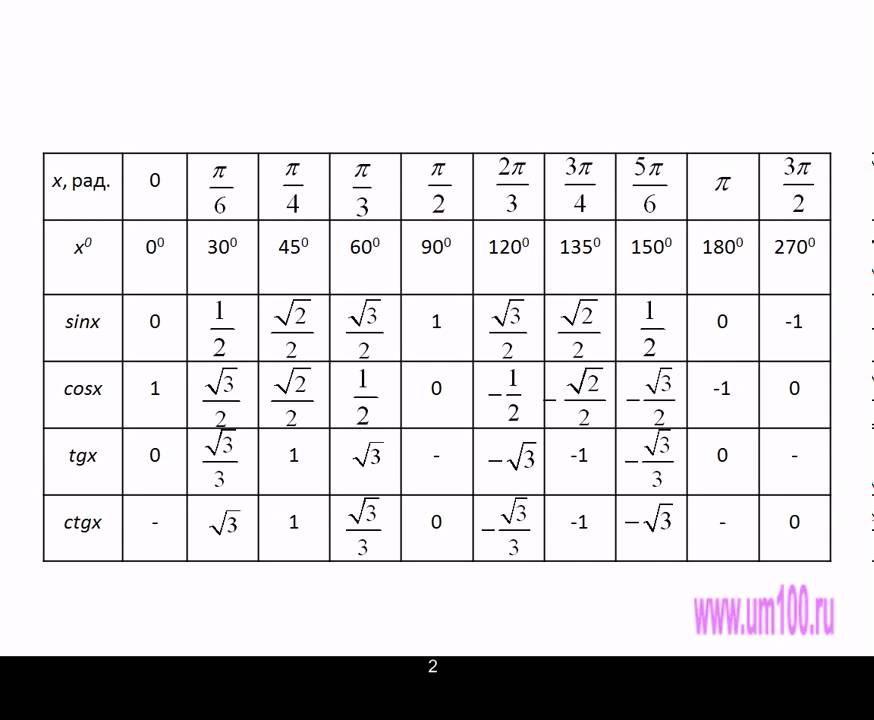 Возможно они окажутся полезными в
практической деятельности.
Возможно они окажутся полезными в
практической деятельности.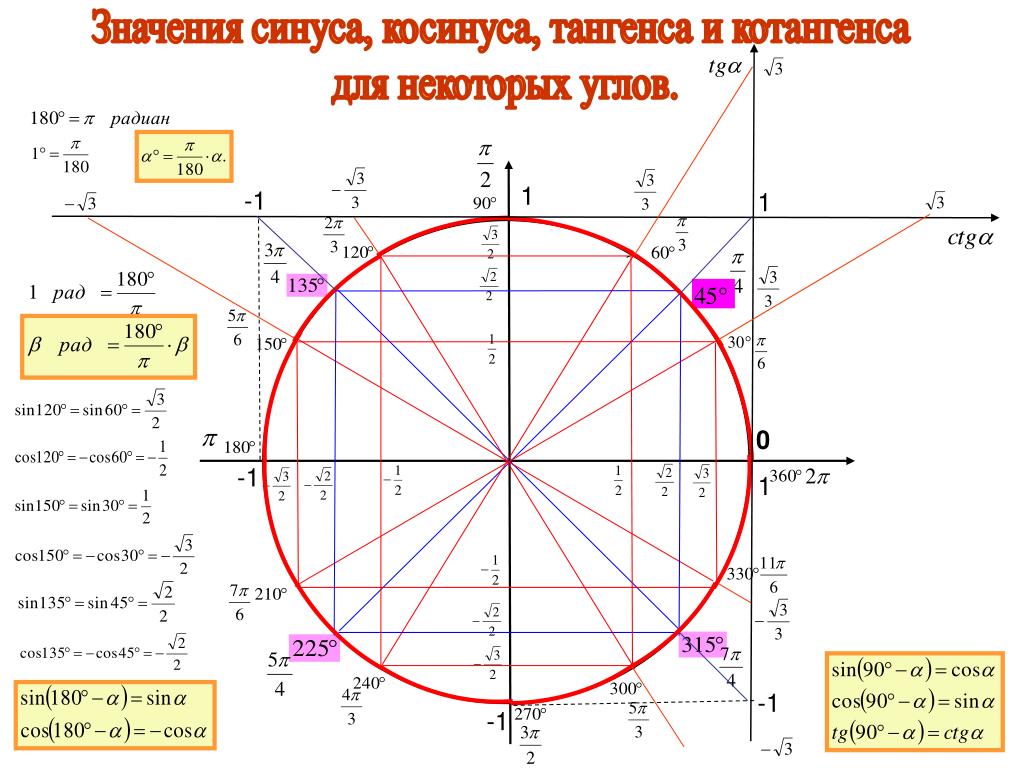
 ..
.. 
 Г., Сенина
Г.Н., МБОУ «СОШ № 4», г. Корсаков
Г., Сенина
Г.Н., МБОУ «СОШ № 4», г. Корсаков