9 класс, следствие, особенности вычисления через синус
Нахождение площади треугольника
Существует несколько формул для нахождения площади треугольника. В зависимости от известных данных нужно выбрать одну из них.
Площадь треугольника через высоту и основание
Этот способ нахождения площади треугольника изучают на уроках геометрии в 8 классе и используют чаще всего.
Теорема 1Площадь треугольника равна половине произведения высоты на основание, к которой проведена эта высота.
Формула 1S=½ah
где S — площадь треугольника,
а — длина основания,
h — высота, проведенная к а.
Следствия теоремы:
- У прямоугольного треугольника один катет можно принять за основание, а второй — за высоту.
- Если у двух треугольников высоты равны, то отношение между их площадями равно отношению между основаниями.
Нахождение площади треугольника по двум сторонам и углу между ними
В вычислении используется синус угла. Данный способ применяют после знакомства с этим понятием в 9 классе.
Данный способ применяют после знакомства с этим понятием в 9 классе.
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Формула 2S=½ab·sin γ
где S — площадь треугольника,
a и b — его стороны,
γ — угол между a и b.
Формула Герона
Если у треугольника известны длины трех сторон, то его площадь можно найти по формуле Герона.
Формула 3S=pp-ap-bp-c
где S — площадь треугольника,
a, b, с — его стороны,
р — полупериметр, р=a+b+c2.
Площадь треугольника по радиусу описанной окружности
Площадь треугольника можно вычислить, зная три его стороны и радиус описанной окружности.
Формула 4S=abc4R
где S — площадь треугольника,
R — радиус окружности, описанной около данного треугольника,
a, b, c — стороны треугольника.
Также площадь треугольника можно найти, если известны радиус описанной окружности и величины трех углов треугольника.
Формула 5S= 2R2·sin∠A·sin∠B·sin∠C
где S — площадь треугольника,
∠A, ∠B, ∠С — углы треугольника,
R — радиус описанной окружности.
Площадь треугольника по радиусу вписанной окружности
Теорема 3Площадь треугольника равна произведению полупериметра на радиус вписанной окружности.
Формула 5S=p·r
где S — площадь треугольника,
r — радиус вписанной окружности,
р — полупериметр, вычисляем по формуле р=a+b+c2.
Понятие подобия треугольников
Определение 1Подобные треугольники — это такие треугольники, у которых углы попарно равны, а лежащие напротив равных углов стороны пропорциональны. Эти стороны называются сходственными.
У подобных треугольников соответственно пропорциональны также медианы, высоты, биссектрисы, периметры. Соотношение между этими величинами равно коэффициенту подобия.
Соотношение между этими величинами равно коэффициенту подобия.
Коэффициент подобия — это отношение между периметрами двух подобных треугольников.
Теорема 4Отношение между площадями подобных треугольников равно коэффициенту подобия в квадрате.
Доказательство:
Пусть ΔDEF подобен ΔKMN, записывают ΔDEF∼ΔKMN.
Следовательно, DE:KM=EF:MN=DF:KN=k, где k — коэффициент подобия ΔDEF и ΔKMN.
Если у двух треугольников равны углы, то их площади соотносятся как произведение сторон, заключающих данные углы.
Так как ∠D=∠K, то
SDEFSKMN=DE×DFKM××N=DEKM×DFKN=k·k=k2.
Теорема доказана.
Задачи на применение теоремы для 9 класса
Рассмотрим решения задач, которые помогут в самостоятельном выполнении заданий.
Задача 1Дано: два подобных треугольника. Коэффициент подобия между ними равен 2.
Найти: отношение между площадями этих треугольников.
Решение: в соответствии с изученной теоремой о соотношении площадей подобных треугольников
S1S2=k2=22=2.
Ответ: S1S2=2.
Задача 2Дано: Два треугольника подобны. ΔDEF∼ΔKMN. Их площади равны 500см2и125см2.SΔDEF=500см2, SΔKMN=125см2. Сторона DE равна 18 см.
Найти: сходственную ей сторону КМ.
Решение:
Вычислим отношение между SDEF и SKMN:
SDEFSKMN=500125=4.
Согласно теореме о соотношении площадей подобных треугольников k2=4,аk=2.
Из подобия треугольников следует, что DEKM=2⇒KM=DE:2=18:2=9(см).
Ответ: КМ=9 см.
Задача 3Дано: треугольник ΔOPQ,SΔOPQ равна 12см2. Параллельно стороне OQ в ΔOPQ проведена средняя линия KM.
Найти: S треугольника, образованного средней линией KM и сторонами OP и PQ треугольника OPQ, то есть площадь ΔKPM.
Решение:
ΔOPQ и ΔKPM подобны, так как равны их углы.
∠P — общий, ∠POQ=∠PKM и ∠PQO=∠PMK как соответственные углы при параллельных прямых и секущей.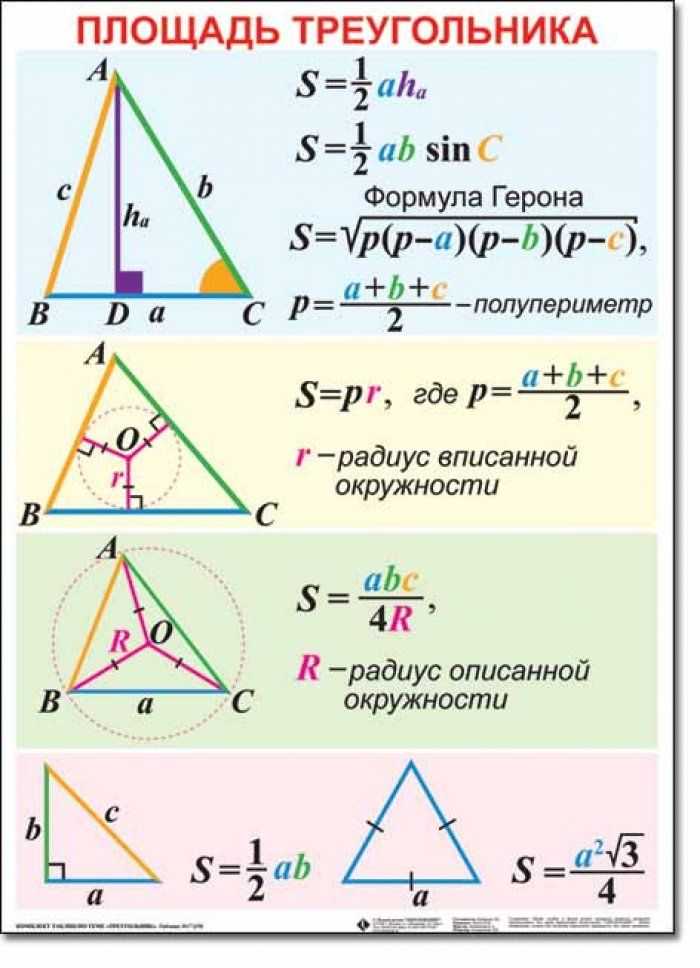
Сходственные стороны ΔOPQ и ΔKPM пропорциональны, коэффициент пропорциональности равен 2, так как согласно теореме о средней линии треугольника KM=OQ2.
Применим теорему об отношении площадей подобных треугольников: SΔOPQSΔKPM=22=4,
SΔKPM=SΔOPQ4=12:4=3(см2).
Ответ: 3см2.
План-конспект урока геометрии для 9 класса Тема «Теорема о площади треугольника» | План-конспект урока по геометрии (9 класс):
МБОУ СОШ №14 им.Г.К.Жукова , с.Кривековское
Задание 2.
Класс: 9
УМК: Геометрия, 7 — 9: учебник для общеобразовательных учреждений/ Л. С. Атанасян и др., — 17 — е изд., — М.: Просвещение, 2016 г.
Тема: «Теорема о площади треугольника»
Цели урока:
I.Содержательная цель: формирование умений и навыков в решение задач различными геометрические преобразованиями; умений переносить свои знания в новую нестандартную ситуацию.
Деятельностная цель: создать условия для формирования умений структурировать и систематизировать информацию; для самостоятельного получения новых знаний о нахождении площади треугольников
II. Задачи урока:
Задачи урока:
1) систематизация и обобщение ранее полученных знаний, умений и навыков;
2) отработка навыков решения задач.
Развивающие:
1) развивать умение работать с электронными образовательными ресурсами, анализировать, делать выводы;
2) развивать творческие, коммуникативные способности, воображение учащихся;
3) развивать монологическую речь учащихся, поддерживать интерес к уроку математики через межпредметные связи,
4) развивать логическое мышление.
Воспитательные:
1) воспитывать умение высказывать свою точку зрения, слушать других, принимать участие в диалоге;
2) формировать способности к позитивному сотрудничеству, повышение ответственности не только за собственные знания, но и за успехи команды.
III. Планируемые результаты:
Предметные: знать теорему о площади треугольника ,уметь записывать разными способами и применять при решении задач на нахождение площади треугольников.
Метапредметные: уметь находить нужную информацию, обрабатывать, делать выводы, выдавать готовый продукт.
Личностные: уметь работать в коллективе, отстаивать свою точку зрения.
IV. Формы работы учащихся: фронтальная, групповая, индивидуальная.
V. Технологии: технология развивающего обучения, исследовательская деятельность.
VI.Методы обучения
1) Проблемный 2) частично-поисковый 3) репродуктивный
VII. Средства обучения : компьютер учителя, проектор, доска, чертежи, раздаточный материал, презентация.
VIII. Учебно-методический комплекс: учебник «Геометрия», 7-9 класс, Л.С. Атанасян. В.Ф. Бутузов, С.Б.Кадомцев и др., М.: Просвещение, 2017.
IX. План урока:
- Мотивация учебной деятельности учащихся (5 мин.).
1. Проверка готовности учащихся к уроку. Настрой учащихся на урок.(3 мин.)
2. Проверка домашнего задания. (те же 3 мин.)
3. Дифференцированное деление на III группы (2 мин.).
- Этап актуализации знаний учащихся. (10 мин.). 1. Фронтальная работа (повторение теоретического материала) по теме , начальная (подготавливающая) работа с понятиями, определениями
- Этап постановки цели и задач урока (2 мин.
 ).
). - Этап приобретения и систематизация ранее полученных знаний (8 мин.). 1. Работа в малых группах (командах). 2. Последующая проверка выполненных заданий.
- Этап применение знаний и умений в новой ситуации (10 мин.).
1. Работа в дифференцированных группах
«Исследовательская работа»
- Этап постановки домашнего задания (2мин.).
- Этап рефлексии учебной деятельности на уроке (3 мин.)
Ход урока:
I. Мотивация учебной деятельности учащихся (2 мин.).
1. Проверка готовности учащихся к уроку. Настрой учащихся на урок.
Проверка домашнего задания.
Цель: включение в учебную деятельность на личностно значимом уровне «хочу» + «могу» + «надо» — (организационный момент, положительная самоорганизация).Дифференцированное деление на III группы (2 мин.).
II. Этап актуализации знаний учащихся. (6 мин.)
Геометрический диктант :
- Письменно ответить на вопросы учителя:
- Сумма длин всех сторон многоугольника (периметр)
- Плоскость, заключенная внутри многоугольника (площадь)
- Геометрическая фигура, состоящая из трех точек, соединенных между собой отрезками.
 (треугольник)
(треугольник) - Геометрическая фигура, состоящая из четырех вершин, четырех сторон и имеющая две диагонали. (четырехугольник)
- Сторона прямоугольного треугольника, лежащая напротив прямого угла.
(гипотенуза)
- Чему равен sin30° (0,5 от гипотенузы)
- Это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. (высота треугольника).
В тетрадях присутствует запись основных понятий темы:
- периметр, 2) площадь, 3) треугольник, 4) четырехугольник,
5) гипотенуза, 6) 0,5 , 7) высота.
- Выполните построение , используя классификацию треугольников по углам. (Учащиеся выполняют построение)
(Сравнивая со слайдом презентации). Дается задание группам, вспомнить правило нахождения площади треугольника (достраиваем до четырехугольника, через высоту). Вспоминаем известные формулы площади треугольника:
Для прямоугольного треугольника: SΔ=
Для разностороннего треугольника: SΔ=aha= bhb=chc
Какую известную формулу вы не указали ( формулу Герона, для нахождения площади треугольника). Запишите её.
Запишите её.
Теперь давайте поработаем с определениями, и вы заодно проверите правильно ли вы запомнили некоторые понятия и определения: (устный мини-опрос)
Прямоугольный треугольник-это…
Катет, лежащий против угла в 30° равен…
Для какого треугольника сформулирована теорема Пифагора? Сформулируйте её.
Синусом острого угла прямоугольного треугольника называется…
Косинусом…
Тангенсом…
Что общего между суммой углов треугольника и суммой смежных углов?
IiI. Этап постановки цели и задач урока (2 мин.).
Цель: помочь учащимся сформулировать цели и задачи урока. Формулирование темы урока.
Обратите внимание на последнюю формулу площади треугольника, что общего и что отличает части это формулы друг от друга и от формулы площади прямоугольного треугольника. Правильно: Множитель ½ и произведение основания на высоту(катетов). Каким образом вы находили площадь треугольника ? Правильно: Используя способ геометрического преобразования, вы построили высоту на выбранную вами сторону треугольника и через вершины этой стороны провели параллельные прямые. Через площадь четырехугольника нашли площадь треугольника.
Через площадь четырехугольника нашли площадь треугольника.
Учащиеся высказывают свое мнение. Выслушав всех, учитель обобщает сказанное и озвучивает цели и задачи урока.
Цель урока:
Задачи урока:
IV. Этап приобретения и усвоения новых знаний (8 мин.).
- Объясним решение задач для ваших треугольников.
Вызываются учащиеся к доске с объяснением решения. Вызвал ли поиск решения некоторые затруднения? Какая задача не поддавалась решению, исходя из тех знаний, какими вы владеете? Последняя. Какую формулу нам необходимо придумать, чтобы можно было решать последнюю задачу? Наверное, такую, чтобы там присутствовал угол. Действительно, есть такая теорема, которая решит вашу проблему.
Название теоремы и является темой нашего урока. Запишем в тетрадях «Теорема о площади треугольника». Как вы думаете, какую цель нам надо достичь на уроке? (познакомиться с новой теоремой, научиться её доказывать и применять её в решении задач)
Теорема: площадь треугольника равна половине произведения двух его сторон на синус угла между ними.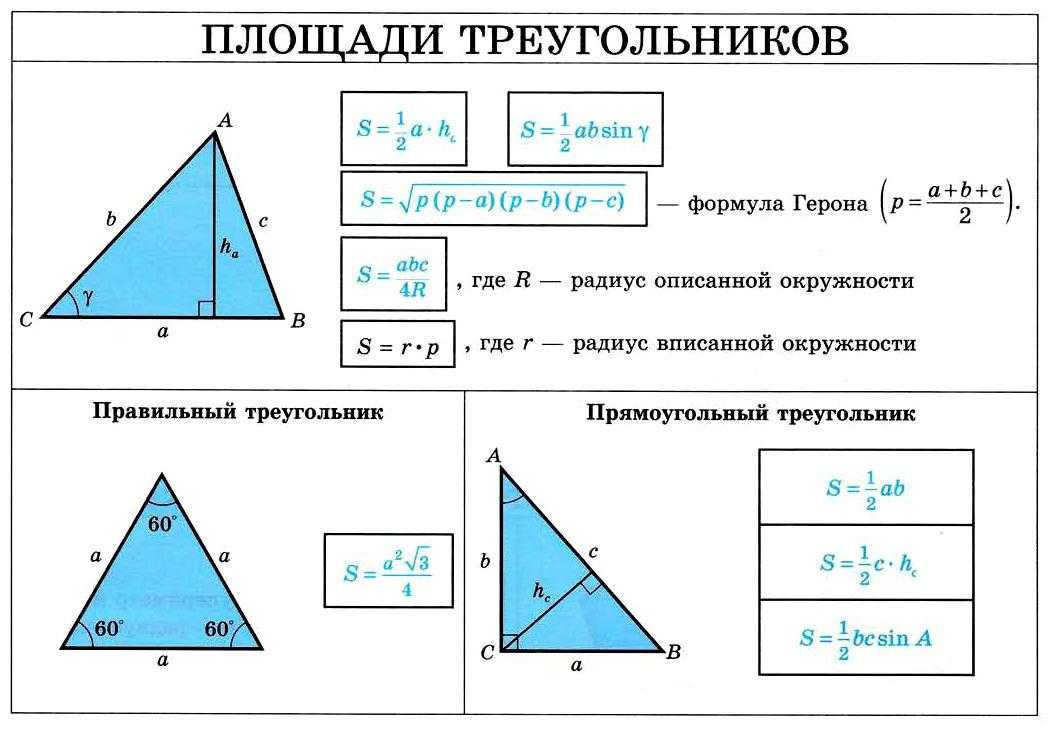 Давайте её докажем.
Давайте её докажем.
Итак, что нам дано. Треугольник, две стороны и угол между ними. Что надо доказать? Что площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Все это изобразим на чертеже.
Далее учитель с помощью учащихся доказывает теорему. В учебнике на странице 256 тоже приведено доказательство теоремы. Вы с ним познакомитесь, когда будете готовиться к следующему уроку.
Эту теорему можно применить для нахождения площади любого треугольника? Да.
V. Этап применения знаний и умений в новой ситуации:
1) Решим по вариантам задачи. Перед выполнением задания получите опорный конспект с порядком выполнения задания и условием задачи.
Вспомним: Формулы приведения для синуса α и табличные значения :
sin(180°-30°) = sin150°=sin30°=0,5
sin 60° = , sin 45° = и sin 90° =
Формулы приведения и значения синусов углов записываем на доске и в тетрадях. Дано, чертеж , решение и ответ вносим в тетради.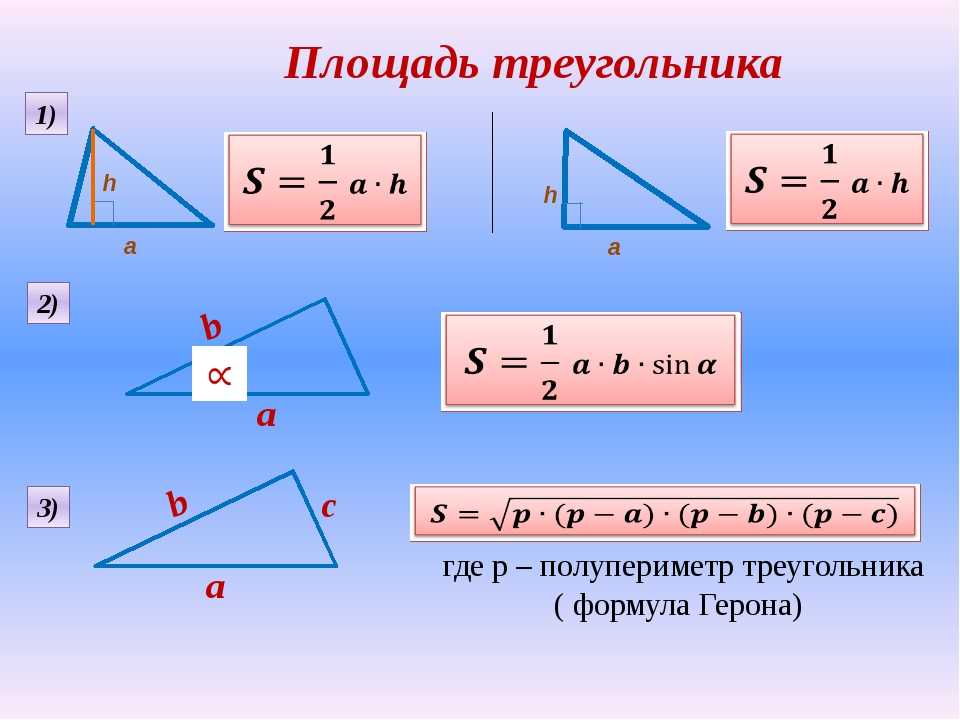
Карточки с задачами и алгоритм выполнения задания можно представить на уроке на слайде презентации и/или в качестве раздаточного материала.
Группа I. Найти площадь треугольника , если известно, что стороны треугольника равны 15 и 12 см, а угол между ними равен 150°.
Группа II. Найти площадь треугольника , если известно, что стороны треугольника равны 5 и 4 см, а угол между ними равен 60°
Группа III. Найти площадь треугольника , если известно, что стороны треугольника равны 3 и 6 см, а угол между ними равен 45°
3) Последующая проверка выполненных заданий. Обмен тетрадями. Взаимопроверка.
Карточка для проверки: Группа I.
Решение: По теореме о площади треугольника, имеем:
SΔАВС= АВ·АС· = ·12·15·= ·12·15·0,5=45 см2
Ответ: 45 см2
Карточка для проверки: Группа II.
ДАНО:
ΔАВС .
АВ=4
АС=5
=60°
НАЙТИ : SΔАВС-?
Решение: По теореме о площади треугольника, имеем:
SΔАВС= АВ·АС· = ·4·5·= ·4·5·=15 см2
Ответ: 15 см2
Карточка для проверки: Группа III.
ДАНО:
ΔАВС .
АВ=6
АС=3
=45°
НАЙТИ : SΔАВС-?
Решение: По теореме о площади треугольника, имеем:
SΔАВС= АВ·АС· = ·6·3·= ·6·3·= 9 см2
Ответ: 9 см2
VI. Этап постановки домашнего задания:.
С какой новой теоремой мы познакомились? Сформулируйте её. Достигли вы своей цели на уроке? А теперь посмотрите на задачу на экране. Сможете вы найти площадь этого треугольника? Какое тождество здесь необходимо использовать? Основное тригонометрическое. Подробнее эту задачу мы решим на следующем уроке.
Домашнее задание: п. 96, №1020(а, б), №1021, №1022
VII. Этап рефлексии учебной деятельности на уроке.
Цель: соотнести полученный результат с поставленной целью и провести самоанализ и самооценку собственной деятельности.
- 1. Организация совместной рефлексии. Какую цель поставили на уроке? Удалось ли ее достичь? Каким способом? Где можно применить полученные знания? Что на уроке хорошо получилось? Над чем еще нужно поработать? Подведение итогов урока: учитель объявляет оценки за работу на уроке, комментирует их, отвечает на возникшие вопросы.
 Благодарит учащихся за урок.
Благодарит учащихся за урок.
В это время учащиеся заполняют небольшую анкету, которая позволяет осуществить самоанализ, дать качественную и количественную оценку уроку.
Выберите вариант ответа и подчеркните
1 | На уроке я работал: | активно | пассивно |
2 | Своей работой на уроке | я доволен | не доволен |
3 | Урок мне показался | коротким | длинным |
4 | За урок я: | не устал | устал |
5 | Мое настроение: | стало лучше | стало хуже |
6 | Материал урока мне был: | понятен | не понятен |
7 | Материал урока мне был: | полезен | бесполезен |
8 | Материал урока мне был: | интересен | скучен |
МБОУ СОШ № 14 им. Г.К.Жукова, с. Кривенковское
Г.К.Жукова, с. Кривенковское
Урок по геометрии 9 класс
Тема : «Теорема о площади треугольника»
Урок подготовила учитель математики Н.А.Данилова.
2019-2020 учебный год Данилова Н.А.
Площадь треугольников — простые для понимания примеры и решения
Этот урок покажет вам различные способы нахождения площади треугольников. По определению, площадь треугольника — это пространство, занимаемое треугольником в двумерной плоскости.
Формула площади треугольника
Наиболее распространенным способом нахождения площади треугольника является использование базовой формулы, показанной ниже синим цветом.
Площадь треугольника = (основание × высота)/2
Красная линия представляет длину основания (назовите ее b, если хотите), а синяя линия представляет длину высоты.
Как видите, чтобы найти площадь, просто умножьте основание треугольника на высоту треугольника и разделите результат на 2.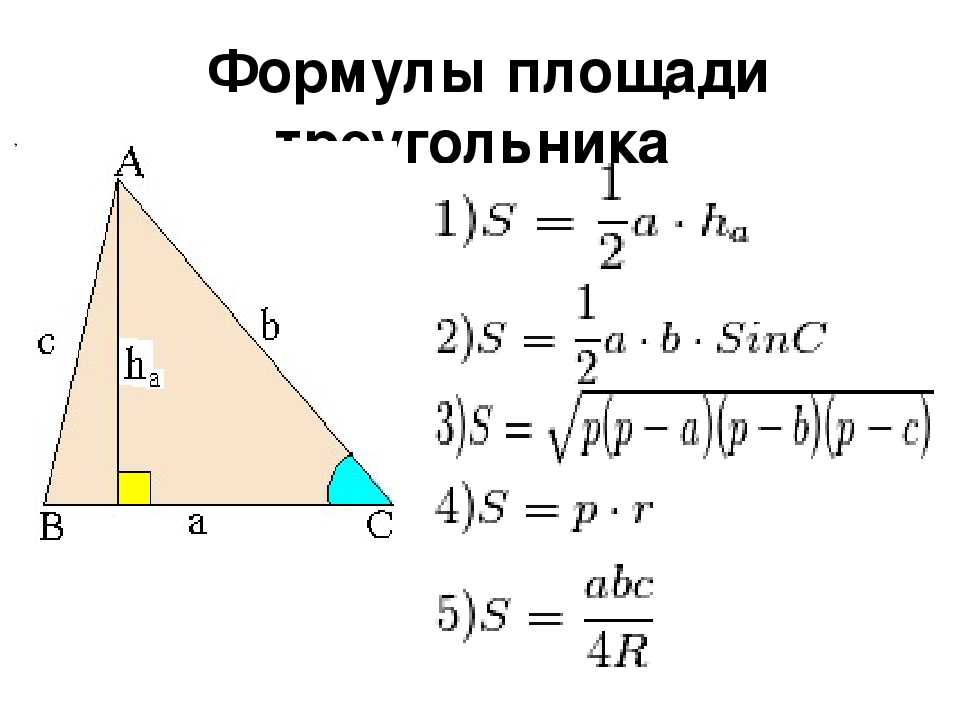
Площадь треугольника
Однако вы также можете найти площадь треугольника на основе следующих двух случаев:
- Известны три стороны треугольников (треугольник SSS)
- Известны две стороны и угол между ними (треугольник SAS)
Площадь выражена в квадратных единицах.
- Если основание и высота измеряются в метрах, то площадь измеряется в квадратных метрах или м 2 .
- Если основание и высота измеряются в сантиметрах, то площадь измеряется в квадратных сантиметрах или см 2 . Пример № 10003
Площадь = (основание × высота)/2
Площадь = (9 × 4)/2
Площадь = 36/2
Площадь = 18
Площадь 18 квадратных дюймов или 18 дюймов
Пример №2
Найдите площадь тупоугольного треугольника, показанного на рисунке ниже, с основанием 4 дюйма и высотой 3 дюйма:
Площадь = (основание × высота)/2
Площадь = (4 × 3)/ 2
Площадь = 12/2
Площадь = 6
Площадь 6 квадратных дюймов или 6 дюймов 2
Пример №3
Найдите площадь прямоугольного треугольника, показанного на рисунке ниже, с основанием 5 дюймов и высотой 6 дюймов:
Площадь = (основание × высота)/2
Площадь = (5 × 6)/2
Площадь = 30/2
Площадь = 15
Площадь равна 15 квадратных дюймов или 15 дюймов треугольника известны (SSS)
Древнегреческий математик Герон наиболее известен своей формулой площади треугольника, когда известны длины его сторон a, b и c.

Площадь представляет собой квадратный корень из произведения s(s-a)(s-b)(s-c).
A =√[s(s-a)(s-b)(s-c)], где s — полупериметр треугольника.
s = (a + b + c)/2
Пример #4
Длины сторон треугольника равны 15 футам, 9 футам и 12 футам. Воспользуйтесь формулой Герона, чтобы найти площадь треугольника.
s = (a + b + c)/2
s = (15 + 9 + 12)/2
s = (36)/2
s = 18
A =√[s(s-a) (с-б)(с-с)]
А =√[18(18-15)(18-9)(18-12)]
А =√[18(3)(9)(6)]
А =√[(54)( 54)]
A =√(2916)
A = 54 квадратных фута
Изучите формулу Герона, чтобы увидеть больше примеров.
Площадь треугольника, когда известны две стороны и угол между ними (SAS)
Когда известны две стороны и угол между двумя сторонами (SAS), площадь равна половине произведения смежных сторон на синус прилежащего треугольника угол.
Следовательно, используйте приведенную ниже формулу, чтобы найти площадь:
Площадь = [bc(sinA)]/2
Пример #5
Длины двух смежных сторон треугольника равны 8 см и 12 см.
 Угол между сторонами 60 градусов. Найдите площадь треугольника.
Угол между сторонами 60 градусов. Найдите площадь треугольника.Пусть b = 8 см, c = 12 см и A = 60 градусов
Площадь = [bc(sin A)]/2
Площадь = [8×12(sin 60 градусов)]/2
Площадь = [96(sin 60 градусов)]/2
Площадь = [96(0,866)]/2
Площадь = (83,136)/2
Площадь = 41,568 см 2
Настоящий урок о площади треугольника, данный sas, чтобы увидеть, как была получена формула, и еще 1 пример, показывающий, как использовать формулу.
Пройди тест ниже и узнай, насколько хорошо ты можешь найти площадь треугольника.
Квадратичная формула: простые шаги
26, 23 января 11:44
Узнайте о квадратной формуле, дискриминанте, важных определениях, связанных с формулой, и приложениях.
Подробнее
Формула площади — Список важных формул
25, 23 января 05:54
Что такое формула площади для двумерной фигуры? Вот список тех, которые вы должны знать!
Читать далее
Лаборатория математики с заданием — Вывести формулу для нахождения площади треугольника
by Prasanna треугольник
Материалы Требуются
- Три листа белой бумаги
- Аст листа глазированной бумаги
- Геометрическая коробка
- А Трубка с клетом
- Ага ножницы
Процедура
Шаг 1: Сначала рассмотрим остроугольный треугольник.
Шаг 2: Постройте остроугольный треугольник на листе белой бумаги, как показано на рис. 27.1(а).
Шаг 3: Сделайте точную копию этого треугольника на глянцевой бумаге. Из верхней вершины опустите перпендикуляр на противоположную сторону, как показано на рис. 27.1(b). Разрежьте треугольник по его границе. Также разрезаем его на две части по перпендикуляру.
Шаг 4: Наклейте эти два треугольника рядом с ΔABC на белую бумагу так, чтобы получился прямоугольник, как показано на рис. 27.1(c).
27.1(c).
Шаг 5: Запишите свои наблюдения (см. Наблюдение 1).
Шаг 6: Теперь рассмотрим прямоугольный треугольник.
Шаг 7: Постройте прямоугольный треугольник на другом листе белой бумаги, как показано на рис. 27.2(а).
Шаг 8: Сделайте точную копию этого треугольника на глянцевой бумаге. Вырежьте этот треугольник по границе и приклейте его рядом с треугольником на белую бумагу так, чтобы получился прямоугольник, как показано на рис. 27.2(b).
Шаг 9: Запишите свои наблюдения (см. Наблюдение 2).
Шаг 10: Теперь рассмотрим тупоугольный треугольник.
Шаг 11: Постройте треугольник с тупым углом на третьем листе белой бумаги, как показано на рис. 27.3(а).
Шаг 12: Сделайте точную копию этого треугольника на глянцевой бумаге. Вырежьте этот треугольник по границе и приклейте его рядом с треугольником на белую бумагу так, чтобы получился параллелограмм, как показано на рис.

 ).
). (треугольник)
(треугольник)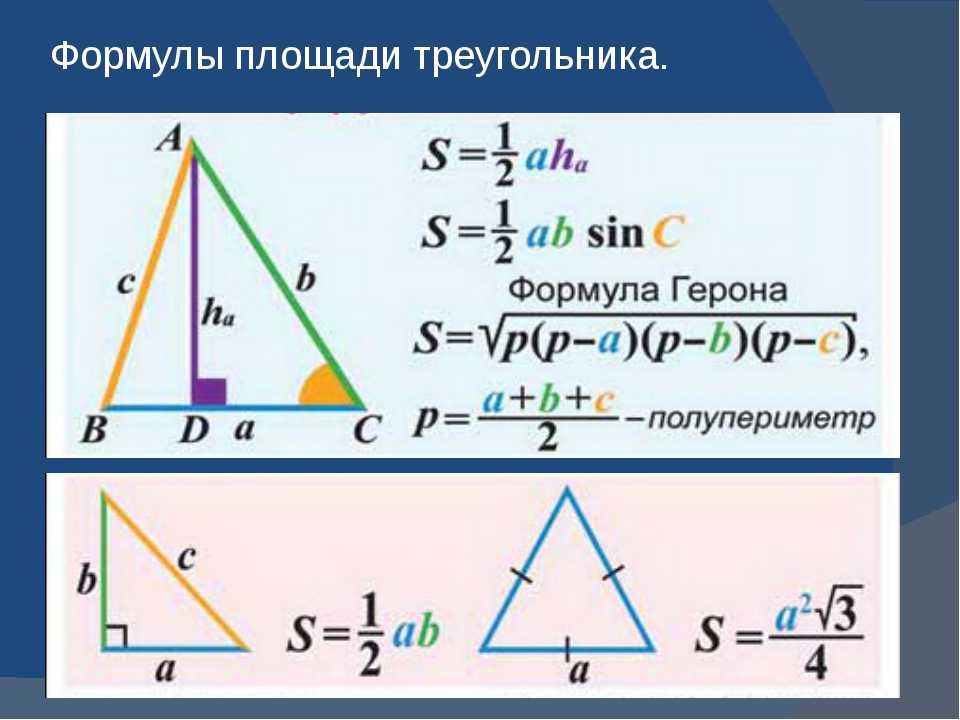 Благодарит учащихся за урок.
Благодарит учащихся за урок.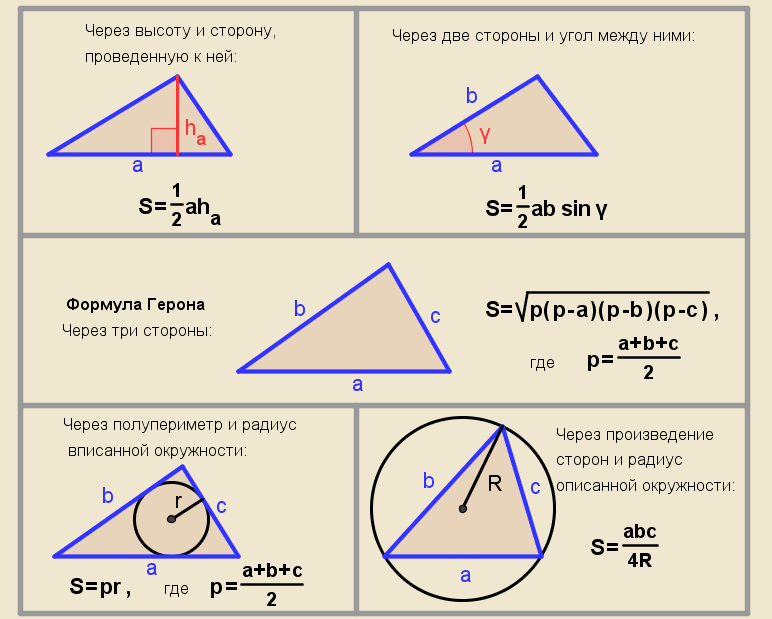
 Угол между сторонами 60 градусов. Найдите площадь треугольника.
Угол между сторонами 60 градусов. Найдите площадь треугольника. 27.1(c).
27.1(c). 