Метод гаусса математика: Как решить методом Гаусса СЛАУ (систему линейных уравнений). Правила, примеры

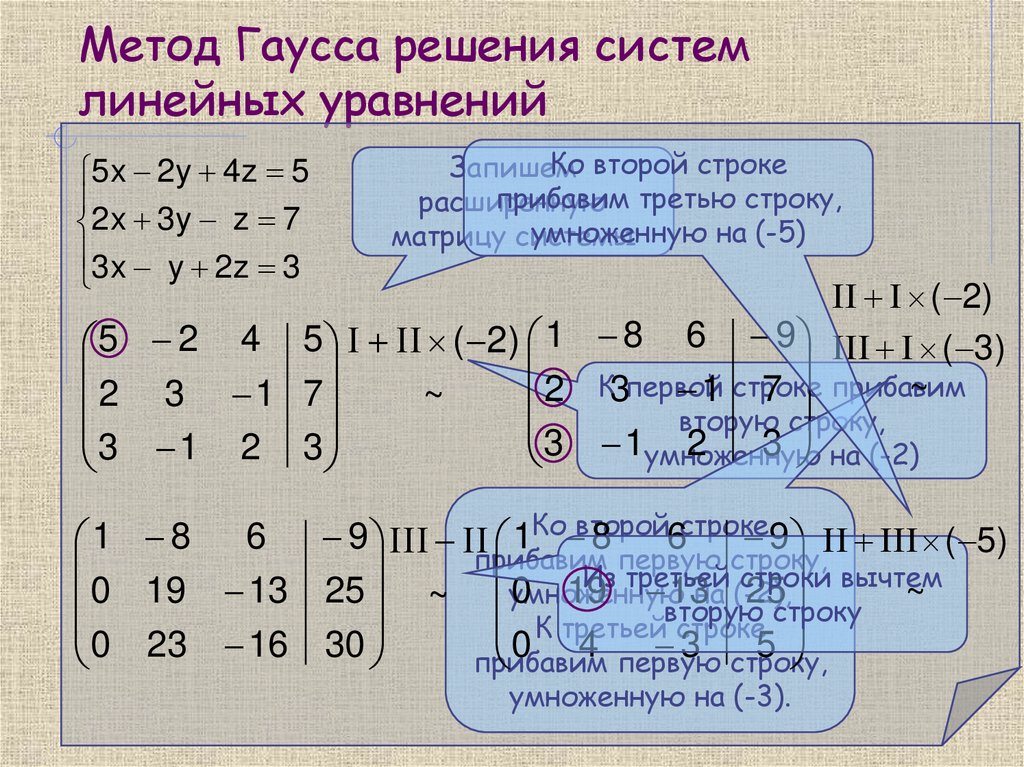
А теперь рассмотрим тот же пример системы линейных алгебраических уравнений, что рассматривали ранее, только теперь с помощью матрицы.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Пример №3:

Запишем матрицу.

Теперь так же само, как и в предыдущем варианте, надо 3 во втором ряду первом столбце превратить в 0. Каждое число первого ряда надо умножаем на -3, а затем сложить с числами второго.

Так же само 4 в третьем ряду первом столбце превращаем в 0. Каждое число первого ряда умножаем на -4, а затем сложить с числами третьего ряда.

Чтобы привести к ступенчатому виду, или как в научной и учебной литературе называется трапециевидный или треугольный вид. Нужно сделать так чтобы во второй строке во втором столбце место -4 стала 1. Умножаем на \[-\frac{1}{4}\]

В третьем ряду надо – 5 превратить в 0. Множим вторую строку на 5 и слаживаем её с третьей.

\[-\frac{7}{2}\] превращаем в 1. Третий ряд умножаем на \[-\frac{7}{2}\].

Теперь возвращаемся от матрицы к системе уравнений.

Конечный вариант выходит тот же.

\[ \left\{\begin{array}{l} x_{1}=1 \\ x_{2}=2 \\ x_{3}=3 \end{array}\right. \]

Ответ: \[x_{1}=1, x_{2}=2, x_{3}=3\].

Пример №4.

Записываем расширенную матрицу для данного СЛАУ.

\[ \left(\begin{array}{llrr} 3 & 2 & -5 \mid & -1 \\ 2 & -1 & 3 \mid & 13 \\ 1 & 2 & -1 & 9 \end{array}\right) \]

Переставляем третью строку на первое место.

\[ \left(\begin{array}{rrrr} 1 & 2 & -1 & 9 \\ 3 & 2 & -5 & -1 \\ 2 & -1 & 3 \mid & 13 \end{array}\right) \]

Убираем 3 с первого столбца второй строки. Первый ряд умножаем на -3 и складываем с вторым.

\[ \left(\begin{array}{cccc} 1 & 2 & -1 & 9 \\ 0 & -4 & -2 \mid & -28 \\ 2 & -1 & 3 \mid & 13 \end{array}\right) \]

Убираем 2 с первого столбца второй строки. Первый ряд умножаем на -2 и складываем с третьим.

\[ \left(\begin{array}{cccc} 1 & 2 & -1 & 9 \\ 0 & -4 & -2 \mid & -28 \\ 0 & -5 & 5 \mid & -5 \end{array}\right) \]

Превращаем -4 во втором столбце второй строки в 1. Умножаем второй ряд на -\[\frac{1}{4}\].

\[ \left(\begin{array}{cccc} 1 & 2 & -1 \mid & 9 \\ 0 & 1 & \frac{1}{2} \mid & 7 \\ 0 & -5 & 5 \mid & -5 \end{array}\right) \]

Убираем -5 с второго столбца третьей строки. Второй ряд умножаем на 5 и складываем с третьим.

\[ \left(\begin{array}{cccc} 1 & 2 & -1 \mid & 9 \\ 0 & 1 & \frac{1}{2} \mid & 7 \\ 0 & 0 & \frac{15}{2} \mid & 30 \end{array}\right) \]

Превращаем \[\frac{15}{2}\] с третьего столбце третьей строки в 1. Умножаем третий ряд на \[\frac{2}{15}\]

\[ \left(\begin{array}{cccc} 1 & 2 & -1 & 9 \\ 0 & 1 & \frac{1}{2} \mid & 7 \\ 0 & 0 & 1 \mid & 4 \end{array}\right) \]

А теперь возвращаемся к системе линейных алгебраических уравнений.

\[ \left\{\begin{array}{c} x+2 y-z=9 \\ y+\frac{1}{2} z=7 \\ z=4 \end{array}\right. \]

Приступаем к обратному ходу методу Гаусса.

\[ \left\{\begin{array}{c} x+2 y-z=9 \\ y=5 \\ z=4 \end{array}\right. \]

\[ \left\{\begin{array}{l} x=3 \\ y=5 \\ z=4 \end{array}\right. \]

Ответ: х=3, у=5, z=4.

Пример №5.

Переводим в матричную систему и проводим элементарные преобразование.

В конечном результате исходная система свелась к ступенчатой.

\[\left\{\begin{array}{c} x_{1}-x_{2}-5 x_{3}=2 \\ x_{2}+13 x_{3}-5 x_{4}=-3 \end{array}\right.\]

Ответ: \[x_{2}=5 x_{4}-13 x_{3}-3 ; \quad x_{1}=5 x_{4}-8 x_{3}-1\]

Применение метода Гаусса в электротехнике Текст научной статьи по специальности «Математика»

128 ИНТЕЛЛЕКТУАЛЬНЫЙ ПОТЕНЦИАЛ XXI ВЕКА: СТУПЕНИ ПОЗНАНИЯ

ПРИМЕНЕНИЕ МЕТОДА ГАУССА В ЭЛЕКТРОТЕХНИКЕ

© Ерёмкин Д.С.*, Лисицын Н.С.*

Дальневосточный федеральный университет, г. Владивосток

В данной статье рассматривается тема прикладного значения метода Гаусса в электротехнике. Представлена теория, охватывающая данную тему. Проведен анализ основных вопросов. Приведены примеры, демонстрирующие практическое использование метода Гаусса при расчетах электротехнических величин.

Ключевые слова метод Гаусса, электротехника.

В современном мире математика и технические науки развиваются в тесном взаимодействии и сотрудничестве друг с другом. Сегодня трудно представить научно-техническую деятельность, где бы не использовались фундаментальные исследования в области математики. Все технические инновации, которые окружают нас в повседневной жизни, есть результат плодотворного сотрудничества техники с математикой. Взаимодействие математических и прикладных дисциплин приводит к их двустороннему обогащению. С одной стороны мы наблюдаем это в применении математического аппарата для решения технических задач. С другой стороны, инженерная практика в существенной мере определяет и стимулирует развитие самой математики. Такой симбиоз математики и технических наук уже весьма высоко зарекомендовал себя и открывает далекие перспективы в будущем.

Математика является фундаментом в инженерном деле. Инженерное дело, в ходе своего развития постоянно расширяет сферу своего приложения, и, тем самым, отвечает все более обширным и сложным техническим задачам. Также, стоит отметить, что вместе с расширением прикладной сферы инженерного дела происходит усиление его специализации. Вследствие развития науки и техники происходит расщепление основных специальностей, появляются новые, ориентированные на более узкий круг практических задач. Таким образом, инженер, являясь специалистом в узкой области, должен базировать свои знания на прочном фундаменте математических и естественных наук. Благодаря различным методам решения технических задач, математический аппарат инженера легко приспосабливается к решению задач в конкретной области.

* Кафедра Электроэнергетики и электротехники. Научный руководитель: Дмух Г.Ю., доцент кафедры Алгебры, геометрии и анализа ШЕН ДВФУ, кандидат педагогических наук.

Важнейшую роль играет умение инженера выбрать соответствующий его задаче математический аппарат и наиболее эффективно использовать его для получения требуемого результата.

В данной статье мы рассмотрим прикладное значение одного из важнейших разделов математики, а именно метода Гаусса в электротехнике. X—

ак1Х1 + ак 2 х2 + … + а кпхп = Ьк

Преобразуем систему, исключив неизвестное х во всех уравнениях системы, кроме первого. Для этого умножим обе части первого уравнения

на —— и сложим со вторым уравнением системы. Затем умножим обе час-

ти первого уравнения на

и сложим с третьим уравнением системы.

Продолжаем этот процесс, пока система не примет вид:

а11х1 + а12х2 + … + а1п Хп = Ь1

а*2х2 + … + а2п Хп = Ь2

а*2 х2 + … + а*пХп = Ьк

Затем процесс повторяется уже делением второй строки на а 22, столбец за столбцом, в итоге, матрица приводится к верхнетреугольному виду.

Второй этап решения заключается в решении ступенчатой системы, просто находя неизвестные х:

а

31

а

130 ИНТЕЛЛЕКТУАЛЬНЫЙ ПОТЕНЦИАЛ XXI ВЕКА: СТУПЕНИ ПОЗНАНИЯ

= й*

Хп-1 = Ьп-1 ап-1пХп

Хп-2 = Ьп-2 — ап-2пХп — ап-2п-1Хп-1

Рассмотрим на примере применение метода Гаусса в электротехнике. Для этого решим задачу по нахождению тока. Пример 1:

Схема постоянного тока содержит три замкнутых контура. Используя известный многим закон Кирхгофа для данной задачи, а именно для замкнутых контуров, получаем систему уравнений для тока в миллиамперах:

I + 212 + 313 = 20 41 — 6/2 + 8/3 =-52 -91 + 2/2 — 4/3 = 12

(1) (2) (3)

1. Вычтем из уравнения (2) уравнение (1), умножая его на 4:

0 -14/2 — 4/3 =-132

(4)

Из уравнения (3) вычтем уравнение (1), домноженное на -9:

0 + 20/2 + 23/3 = 192

2. Вычтем из уравнения (5) уравнение (4), умноженное на

0 + 0 + 17.3/3 = 4

20 -14 ‘

(5)

(6)

3. Из уравнения (6) находим /3 = = 0.2 мА, затем последовательно , -132 + 0.8

вычисляем 12 =-—-= 9.37 мА из уравнения (4), откуда находим

11 = 0,66 мА, подставляя известные нам переменные 12 и 13 в уравнение (1). Пример 2:

Схема электрической цепи содержит три замкнутых контура. Используя закон Кирхгофа, найдем сопротивления на участках цепи с помощью системы уравнений:

^ + 5Д2 + 2Д3 = 25 8^ + Я2 — 2Д3 = 16 6^ — 4Д2 — 5Д3 =-15

(7)

(8) (9)

1. Вычтем из уравнения (8) уравнение (7), умножая его на 8:

0 — 39Л2 -18Я3 =-184 (10)

Из уравнения (9) вычтем уравнение (7), домноженное на 6:

0 — 34Д2-17Я3 =-165 (11)

-34

2. Вычтем из уравнения (11) уравнение (10), умноженное на -—:

0 — 0-1.308Д3 =-4.59 (12)

-4.59

3. Из уравнения (12) находим Л3 =—= 351 Ом, затем последовательно вычисляем Л2 =-— = 3.098 « 3.1 Ом из уравнения (10), откуда находим Я-[ = 2,49 Ом, подставляя известные нам переменные Я2 и Я3 в уравнение (7).

Список литературы:

1. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. -изд. 5-е. — М.: Айрис-пресс, 2005. — 279 с.

2. Сигорский В.П. Математический аппарат инженера. — изд. 2-е, стереотип. — «Техтка», 1977. — 753 с.

АНАЛИЗ СУЩЕСТВУЮЩИХ ПРОЦЕССНЫХ ПОДХОДОВ К УПРАВЛЕНИЮ ИНЦИДЕНТАМИ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ

© Костомаров В.А.*

Московский государственный университет экономики, статистики и информатики (МЭСИ), г. Москва

Рассматриваются процессные подходы, принятые в международных и национальных стандартах в области информационной безопасности и проводится сравнительный анализ представленных процессных подходов.

Ключевые слова: управление информационной безопасностью, процессный подход, менеджмент инцидентов ИБ.

* Магистрант кафедры Автоматизированных систем обработки информации и управления. Научный руководитель: Микрюков А.А. заведующий кафедрой Автоматизированных систем обработки информации и управления МЭСИ, кандидат технических наук, доцент.

Академия математического образования Гаусса

Добро пожаловать в Академию математического образования Гаусса!

Gauss Math предлагает внешкольную программу повышения квалификации по математике , предназначенную для того, чтобы помочь детям улучшить свое логическое и абстрактное мышление, добиться успеха в многочисленных конкурсах  стандартизированных тестов и приобрести интерес к математике и естественным наукам на всю жизнь.

• Регистрация на Летнюю онлайн-программу Gauss 2023 начнется 1 марта. См. Лето 2023 года. Ознакомьтесь с информацией о классе и заполните регистрационную форму: https://forms.gle/dpQxMw9xX1521y4K6
• Gauss запустит исследовательскую программу квантовых вычислений летом и в течение всего года. Пожалуйста, обратитесь к исследовательским программам. Крайний срок подачи заявок 31 мая .
• Математический турнир Gauss 2023 пройдет онлайн 10 июня . Пожалуйста, обратитесь к Математическому турниру Гаусса. Крайний срок регистрации 8 июня.
• Конкурс Logistem Science Challenger 2023 будет проходить онлайн 17 июня . См. Logistem Science Challenger 2023 года. Крайний срок регистрации – 15 июня. Пожалуйста, обратитесь к конкурсу письма Гаусса 2023 года

Почему математика Гаусса?

Школьное математическое образование теперь ежедневно обсуждается в редакционных статьях, на радио и телевидении и даже в залах Конгресса.
Вероятно, этому есть много причин, но наиболее очевидными являются:

• Школьная программа США описывается как «ширина в милю и глубина в дюйм»;
• В начальной школе не уделяется особого внимания созданию прочной основы базовых математических и естественных понятий;
• Отсутствует многоуровневый подход к преподаванию сложной математики или физики в средней школе
• Лишь ограниченное число учащихся (менее 20%) достигают продвинутого уровня математики и изучают физику в средней школе
• Между учебными программами по математике и естественным наукам и учебниками начальной, средней и старшей школы существует небольшая корреляция и преемственность.

Что мы (родители и педагоги) можем сделать, чтобы помочь нашим детям добиться успехов в математике и физике? И почему мы должны делать упор на математику и физику из всех школьных предметов? Ответ очень простой. Потому что математику считают «экономикой информации», а физику всегда называют «логикой технологической революции». Все мы понимаем, что нашим детям предстоит жить и работать в 21 веке, и наш долг помочь им не только добиться успеха во всем, чем они хотят заниматься в жизни, но и помочь им быть счастливыми и гордиться собой. и их достижений. И что может быть лучше для родителей, чтобы помочь своим детям добиться успеха, чем познакомить их с хорошей, структурированной, веселой и свободной от стресса, но сложной программой по математике и физике на самой ранней стадии. И в этом вся суть ИГРЫ.

• Наша учебная программа дополняет стандартную школьную программу, но также предлагает более сложные задачи и задания, чем обычно ожидается в классе. Наша учебная программа разработана таким образом, чтобы соответствовать и превосходить требования по математике на экзаменах SAT, ACT и AP. Наша олимпиадная учебная программа по математике имеет собственную систему, направленную на достижение наивысших стандартов математического мастерства.
• Математические рассуждения и их применение являются важным компонентом нашей учебной программы. Мы фокусируемся на уникальных темах для каждого уровня, в которых ранее изученные навыки и методы будут укрепляться и развиваться на каждом этапе. Особое внимание уделяется аргументации и применению.
• Строгие против интуитивных:  Математика – довольно строгая и строгая дисциплина, и, хотя мы не можем переоценить важность строгих математических рассуждений, чрезвычайно важно научить учащихся использовать правдоподобные рассуждения для решения сложных задач. В конечном счете, для студентов крайне важно развивать математическую интуицию, которая станет жизненно важной, когда они будут работать над сложными математическими сценариями в будущем.
• Понимание против запоминания : Само собой разумеется, чтобы освоить математику, нужно запомнить определенные факты, формулы и теоремы. Однако, что действительно важно для успеха детей в математике, так это понимание значения математических задач и их решений. Таким образом, дети могут интуитивно получить много замечательных, но простых ответов.
• Повторение против творчества:  Повторение является неотъемлемой частью процесса обучения для маленьких детей, следовательно, «практика делает совершенным». Однако не менее важно поощрять детей к поиску творческих решений. Например, детей следует с самого раннего возраста учить думать о том, как изменить данную математическую задачу, чтобы получить новое (или другое) решение.
• Геометрический и алгебраический методы: Алгебраические и геометрические методы во многом дополняют друг друга. Наша учебная программа предназначена для развития у учащихся способности решать задачи с помощью наиболее эффективных инструментов, имеющихся в их распоряжении.
  

Академия математического образования им. экспертом в районе Нью-Джерси за ее энтузиазм и преданность обучению и наставничеству учащихся всех классов. Она является очень опытным учителем и подготовила много молодых математических талантов, завоевавших множество наград и медалей на национальных и международных математических соревнованиях. Как основатель Академии Гаусса, она инициировала систематическую математическую программу для Академии Гаусса с 2012 года. В частности, она разработала и внедрила очень успешную программу решения задач с целью повышения способности студентов к логическому мышлению, навыков решения задач. и всесторонняя научная зрелость. Многие выпускники Академии Гаусса были приняты в лучшие национальные учебные заведения США, включая Гарвард, Массачусетский технологический институт, Принстон, Колумбию и многие другие.

• Ф.Ю. Доктор философии в области физики, всемирно известный исследователь, его обширный исследовательский опыт является гарантией успеха исследовательских программ Гаусса. Он будет курировать исследовательские программы Гаусса, гарантируя, что участвующие студенты смогут реализовать свой потенциал в проведении своих передовых исследований в области математики и естественных наук. Студенты-исследователи Gauss отличились на конкурсе Intel.

• Доктор Ю.С. Доктор философии по физике, опытный научный сотрудник и преподаватель, он будет руководить широким спектром тем исследований, начиная от квантовой физики, исследования операций и заканчивая численным моделированием.

• Доктор Ф.Л. доктор философии по физике, опытный исследователь и тренер соревнований по физике в районе Нью-Джерси. За последние три года он обучил многих студентов-физиков выигрывать олимпиады по физике. Он будет курировать программы Гаусса по физике, начиная с уровня чести до уровня олимпиады по физике.

• Доктор Дж.С. доктор математики, получил образование в Массачусетском технологическом институте и Мичигане. Он преподает соревновательную математику и решение математических задач по Гауссу.

• Доктор Э. В., доктор педагогических наук и магистр математики. Он является экспертом в преподавании математических секций SAT и ACT. Он преподает решение математических задач, программирование и курсы SAT/ACT в Gauss.

• Доктор В.С., кандидат физической химии. Постоянный преподавательский опыт в колледже по общей химии и общей физике. Постоянный опыт преподавания в государственных средних школах по предметам Honor Physics, AP Physics 1, Honor Chemistry и AP Chemistry. Высококвалифицированный преподаватель из Нью-Джерси со стандартным сертификатом физики и химии. Он преподает математические соревнования, физику и химию по Гауссу.

• Доктор Г.П., доктор философии в области физики, получивший образование в Массачусетском технологическом институте и Колумбийском университете. Бывший профессор университета, посвятивший себя обучению. Он преподает соревновательную математику и физику по Гауссу.

• Доктор М. Б., кандидат математических наук. Он преподавал математику и физику в течение последних 15 лет на всех уровнях и последние несколько лет работал адъюнкт-профессором по этим предметам. Он преподает решение математических задач и физику по Гауссу.

• Г-н Р. А., магистр математики, опыт работы более 40 лет, хорошо разбирается в математике, физике и химии. Он преподает математические соревнования, решение математических задач, уроки AP по химии и AP по физике по Гауссу.

• Г-жа L.Q., магистр компьютерных наук. Она преподает решение математических задач и компьютерное программирование в Gauss.

• Мистер А.С., магистр математики. Он преподавал предварительную алгебру, алгебру I и II, геометрию, предварительный анализ, исчисление, физику для старших классов, вероятность и статистику на уровне колледжа, элементарное компьютерное программирование на уровне колледжа, математику ACT и математику SAT за последние три года. Он преподает решение математических задач и программу программирования в Gauss.

  No related posts.