Формулы для шара: Сфера, шар, сегмент и сектор. Формулы и свойства

Содержание

Сфера, шар, сегмент и сектор. Формулы и свойства

Навигация по странице: Определение сферы Определение шара Объём шара Площадь поверхности сферы Уравнение сферы Основные свойства сферы и шара Секущая, хорда, секущая плоскость и их свойства Касательная, касательная плоскость и их свойства Сегмент шара Срез шара Сектор шара Касательные сферы Концентрические сферы

Определение.

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой

центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара:

V =	4	πR³ =	1	πD³
	3		6

Формула. Площадь поверхности сферы

через радиус или диаметр:

S = 4πR² = πD²

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x — x₀)² + (y — y₀)² + (z — z₀)² = R²

3. Параметрическое уравнение сферы с центром в точке (x₀, y₀, z₀):

x = x₀ + R · sin θ · cos φy = y₀ + R · sin θ · sin φz = z₀ + R · cos θ

где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара).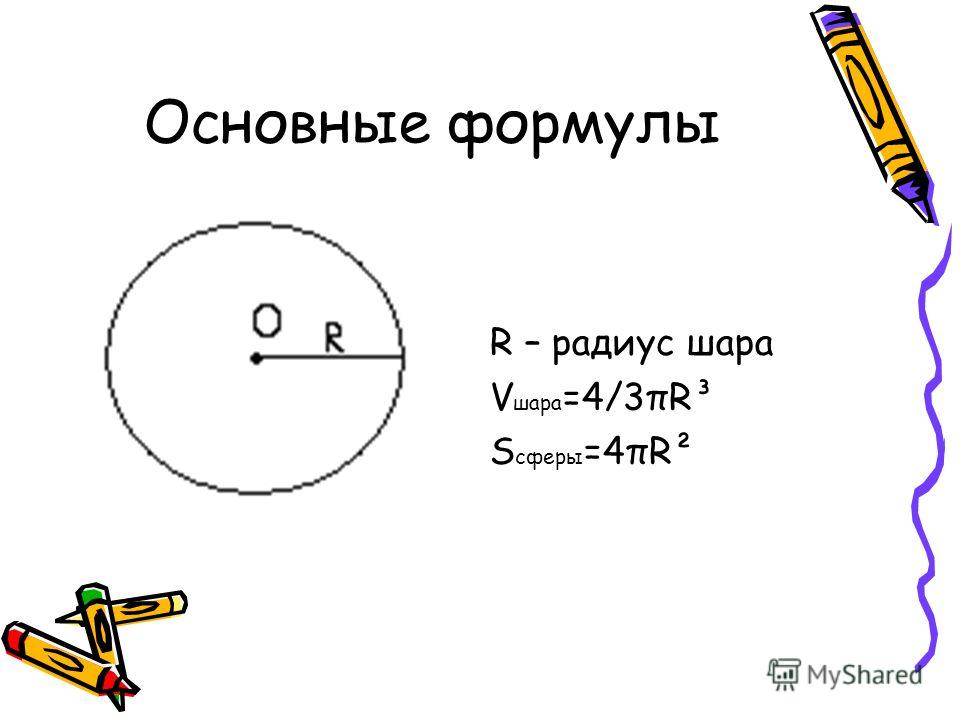 Радиус r такого круга можно найти по формуле:

r = √R² — m²,

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью.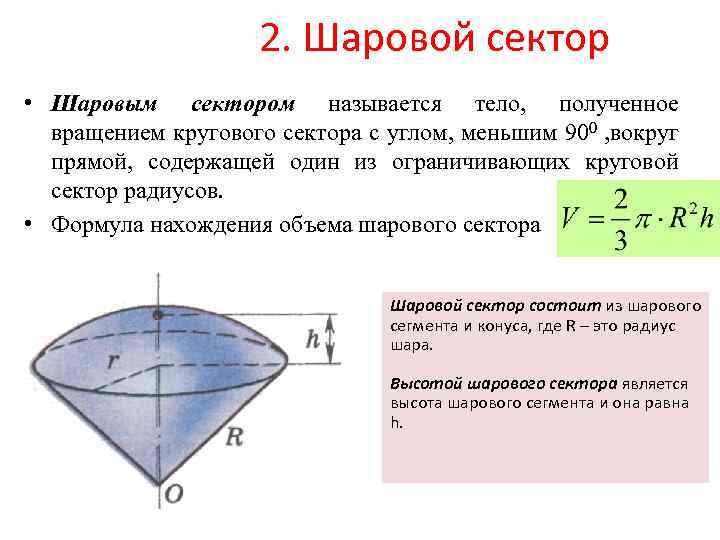 Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула. Объём сегмента сферы с высотой h через радиус сферы R:

V =	h²π	(3R — h)
	3

Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.

Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Формула. Площадь поверхности сектора S с высотой O

1H (h) через радиус шара OH (R):

S = πR(2h + √2hR — h²)

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

V =	2πR²h
	3

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

Все таблицы и формулы

Центр шара определение. Шар и сфера, объем шара, площадь сферы, формулы

Сфера и шар

Слово «сфера» произошло от греческого слова «сфайра», которое переводится на русский язык как «мяч».

ШАР-символ будущего.

Символ шара-глобальность шара Земли. Символ будущего, он отличается от креста тем, что последний олицетворяет собой страдание и человеческую смерть. В Древнем Египте впервые пришли к заключению, что земля шарообразна. Это предположение послужило основой для многочисленных размышлений о бессмертии земли и возможности бессмертия населяющих ее живых организмах.

Человек, держащий шар в руках, символизирует субъекта, несущего тяготы мира Не случайно подобными скульптурами украшены некоторые вокзалы Западной Европы, например в Хельсинки: здесь запечатлены тяготы, выпадающие на плечи путешественника.

Таким образом, шар и глобус — это знаки промысла, проведения, вечности, власти и могущество коронованных особ

Каменное полушарие сферы воплощается в религиозных храмах — куполах православных церквей в России; ступах, связанных с местом пребывания бодхисаттв в Индии. В Индонезии ступы приобрели форму колокола с каменным шпилем наверху и называются дагобы.

В греко-римской мифологии шар символизировал удачу, судьбу, ассоциируясь с Тихэ (Фортуной), стоящей на шаре. Знаменитая картина Пикассо «Девочка на шаре» — танцующая Фортуна.

Форма шара в природе Многие ягоды имеют форму шара.

Планеты имеют форму шара.

Некоторые деревья имеют сферическую форму.

Определение сферы Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки

Сфера –это поверхность, полученная вращением полуокружности вокруг диаметра

Данная точка (О) называется центром сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы, называется радиусом сферы (R-радиус сферы). Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Очевидно, что диаметр сферы равен 2R.

Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.

Шаровой сегмент Шаровым сегментом называется часть шара, отсекаемая от него какой — нибудь плоскостью.

Шаровой слой Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями.

Шаровой сектор Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 900, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.

Плоскость,проходящая через центр шара,называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом,а сечение сферы — большой окружностью. Сечение шара

Закрепляем Решите задачу № 573, №574 (а)

Уравнение сферы в прямоугольной системе координат M(x;y;z)-произвольная точка, принадлежащая сфере. /MC/= v(x-x0)2+(y-y0)2+(z-z0)2 т.к. MC=R, то (x-x0)2+(y-y0)2+(z-z0)2=R2

Задание 1.Найдите координаты центра и радиуса сферы, заданной уравнением: x?+y?+z?=49 (X-3)?+(y+2)?+z?=2 2. Напишите уравнение сферы радиуса R с центром А, если A(2;-4;7) R=3 A(0;0;0) R=v2 A(2;0;0) R=4 3. Решите задачу №577(а)

Взаимное расположение сферы и плоскости Обозначим радиус сферы буквой R, а расстояние от ее центра до плоскости?-буквой d. Введем систему координат так, чтобы плоскость Oxy совпадала с плоскостью?, а центр С сферы лежал на положительной полуоси Oz.

В этой системе координат точка C (о;о;d), поэтому сфера имеет уравнение x2+y2+(z-d)2=R? Плоскость совпадает с координатной плоскостью Oxy, и поэтому ее уравнение имеет вид z=0

Таким образом вопрос о взаимном расположении сферы и плоскости сводится к исследованию системы уравнений. Подставив z=0 во второе уравнение, получим x?+y?=R?-d? Возможны 3 случая:

x?+y?=R?-d? Если d>R, то сфера и плоскость не имеют общих точек.

x?+y?=R?-d? Если d=R, то сфера и плоскость именуют только одну общую точку. В этом случае? называют касательной плоскостью к сфере

x?+y?=R?-d? Если d

Закрепляем Решите задачу №580, №581

Касательная плоскость к сфере Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания А плоскости и сферы.

Теорема:Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. Доказательство: Рассмотрим плоскость?, касающуюся сферы с центром О в точке А. Докажем, что ОА перпендикулярен?. Предположим, что это не так. Тогда радиус ОА является наклонной к плоскости?, и, следовательно расстояние от центра сферы до плоскости меньше радиуса сферы. Поэтому сфера и плоскость пересекаются по окружности. Это противоречит тому, что-касательная, т.е. сфера и плоскость имеют только одну общую точку. Полученное противоречие доказывает, что ОА перпендикулярен?.

Обратная теорема:Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Закрепляем Решите задачу № 592

Площадь сферы Сферу нельзя развернуть на плоскость! Описанным около сферы многогранником называется многогранник, всех граней которого которого касается сфера. Сфера называется вписанной в многогранник

Задание: Площадь сечения сферы, проходящего через её центр, равна 9м2. Найдите площадь сферы. Решение: Сечение, проходящее через центр сферы есть окружность. Sсеч =?r2, 9= ?R2, R=v9/? . Sсферы=4 ?r2 , Sсферы=4? · 9/? =36м2

Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.

Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.

Шар

Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.

Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.

Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.

В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.

Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.

Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.

Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.

Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.

Объем шара

Формула для вычисления объема шара имеет вид:

где R — радиус шара.

Если нужно найти объем шарового сегмента — воспользуйтесь формулой:

V сег =πh 2 (R-h/3), h — высота шарового сегмента.

Площадь поверхности шара или сферы

Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):

где R — радиус сферы.

Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»

M(x;y;z)-произвольная точка, принадлежащая сфере, след.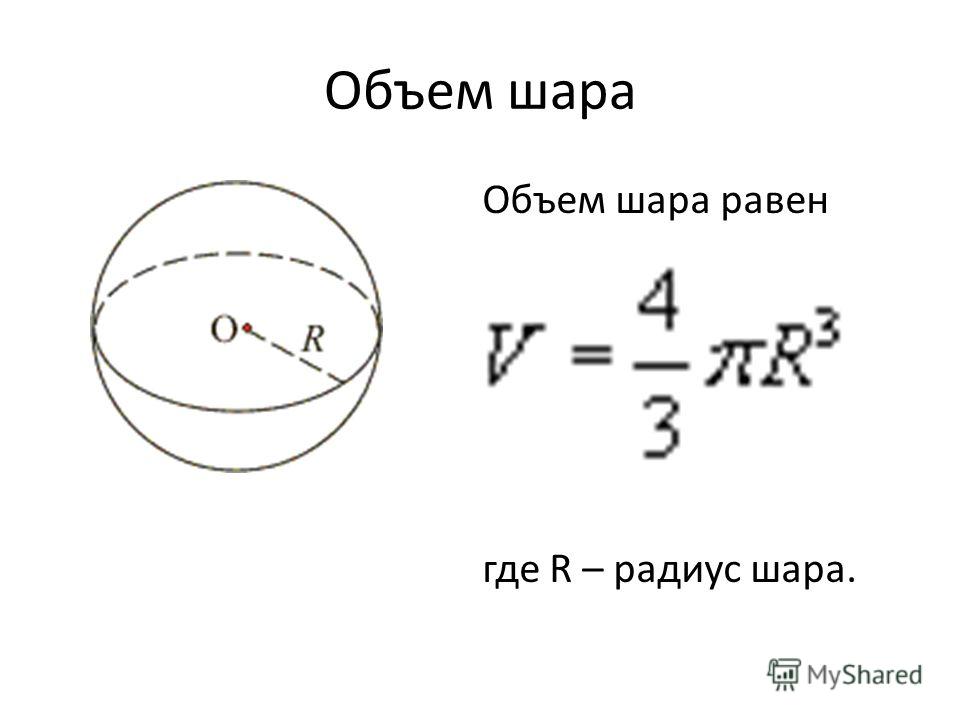 2 не имеет решений

Касательная плоскость к сфере

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.

Теорема:

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Доказательство:

Предположим, что ОА не перпендикулярен плоскости, след. ОА-наклонная к плоскости, след. ОА > R , но т.А принадлежит сфере, то получаем противоречие, след. ОА перпендикулярен плоскости.

Теорема:

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Доказательство:

Из условия теоремы следует, что данный радиус является перпендикуляром, проведённым из центра сферы к данной плоскости. Поэтому расстояние от центра сферы до плоскости равно радиусу сферы, и, следовательно, сфера и плоскость имеют только одну общую точку.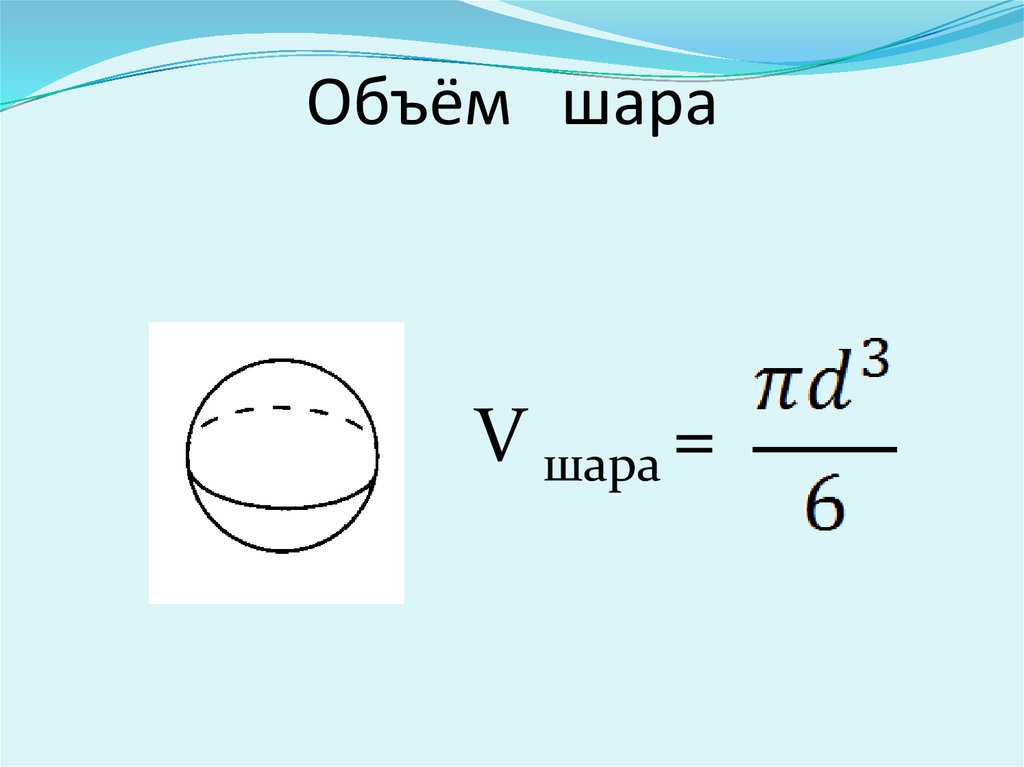 Это означает, что данная плоскость является касательной к сфере.

Площадь сферы:

Для определения площади сферы воспользуемся понятием описанного многогранника. Многогранник называется описанным около сферы (шара) , если сфера касается всех его граней. При этом сфера называется вписанной в многогранник.

Пусть описанный около сферы многогранник имеет n-граней. Будем неограниченно увеличивать n таким образом, чтобы наибольший размер каждой грани стремился к нулю. За площадь сферы примем предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани. Можно доказать, что этот предел существует, и получить формулу для вычисления площади сферы радиуса R: S=4ПR:2

‌‌‌V‌ районная научно-практическая конференция исследовательских, проектных и творческих работ учащихся «Первые шаги в науке»

Исследовательская работа по теме:

«Сфера и шар – обычные геометрические тела».

Выполнил: ученик 9 класса МБОУ

«Кочетовская средняя общеобразовательная школа» Романов Дима.

Руководитель: учитель математики и физики Тремаскина В.С.

Введение ___________________________________________________________3

1. История изучения геометрических тел: шар, сфера_______________________3

2. Сфера и шар.

2.1. Понятие сферы и шара___________________________________________3-4

2.2. Уравнение сферы________________________________________________4

2.3. Взаимное расположение сферы и плоскости_________________________4-6

2.4. Касательная плоскость к сфере____________________________________6-7

2.5. Площадь сферы и объём шара____________________________________ 7

2.6. Получение сферы_______________________________________________ 7-8

2.7. Нахождение сферы и шара в природе______________________________ 9-13

2.8.Сфера и шар в повседневной жизни _________________________________14-15

2.9.Применение сферы и шара в архитектуре____________________________16-22

2.10. Применение сферы и шара в геодезии______________________________23

2. 11Применение сферы и шара в астрономии и географии_________________24

2.12. Сфера и шар в искусстве_________________________________________25

Заключение___________________________________________________________25

Литература___________________________________________________________26

Актуальность выбранной темы.

На протяжении веков человечество не переставало пополнять свои научные знания в той или иной области наук. Множество ученых геометров, да и простых людей, интересовались такой фигурой как шар и его “оболочкой”, носящей название сфера. Многие реальные объекты в физике, астрономии, биологии и других естественных науках имеют форму шара. Поэтому вопросам изучения свойств шара отводилась в различные исторические эпохи и отводится в наше время значительная роль.

Цель исследования: изучить геометрические тела шар и сферу, рассмотреть их применение в разных областях науки, в повседневной жизни, в природе, создать презентацию «Сфера и шар – обычные геометрические тела».

Задачи:

1. Собрать материал о шаре и сфере используя различные источники информации, в том числе Интернет-ресурсы.

2. Систематизировать материал о шаре и сфере.

4. Создать презентацию«Сфера и шар – обычные геометрические тела ».

5. Представить работу на уроке геометрии при изучении темы «Сфера и шар».

Объект исследования : сфера и шар

Предмет исследования : элементы и свойства сферы и шара

Гипотеза: Шары нам нужны для того что бы делать наш мир более разнообразным и объёмным.

Методы: частично-поисковый, исследовательский, сравнительный анализ, синтез, практический.

Результат исследования: полученные знания нужны не только астрономам, штурманам морских кораблей, самолетов, космических кораблей, которые по звездам определяют свои координаты, но и строителям шахт, метрополитенов, тоннелей, архитекторам, а также при геодезических съёмках больших территорий поверхности Земли, когда становится необходимым учитывать её шарообразность, в повседневной жизни.

Научная новизна: теоретический материал представлен в форме доступной для понимания учащимися старших классов.

Практическая значимость: данный материал может использоваться в качестве основы для элективного курса в классах физико-математического профиля, на уроках при изучении тем «Сфера и шар».

Введение

На протяжении многих веков человечество не переставало пополнять свои научные знания в той или иной области науки. Стереометрия, как наука о фигурах в пространстве, неотъемлемо связана со многими из научных дисциплин. К таким дисциплинам относятся: математика, физика, информатика и программирование, а также химия и биология. В последних стоит проблема изучения микромира, который представляет собой сложнейшую комбинацию различных частиц в пространстве относительно друг друга. В архитектуре постоянно используются теоремы и следствия из стереометрии.

Множество учёных геометров, да и простых людей, интересовались такой фигурой как шар и его «оболочкой», носящей название сфера. Удивительно, но шар является единственным телом, обладающим большей площадью поверхности при объёме, равном объёму других сравниваемых тел, таких как куб, призма или прочие всевозможные многогранники. С шарами мы имеем дело ежедневно. К примеру, почти каждый человек пользуется шариковый ручкой в конец стержня которой вмонтирован металлический шар, вращающийся под действием сил трения между ним и бумагой и в процессе поворота на своей поверхности шар «выносит» очередную порцию чернил. В автомобильной промышленности изготавливаются шаровые опоры, являющиеся очень важной деталью в автомобиле и обеспечивающей правильный поворот колёс и устойчивость машины на дороге. Элементы машин, самолётов, ракет, мотоциклов, снарядов, плавательных судов, подвергающиеся постоянным воздействиям воды или воздуха, преимущественно имеют какие либо сферические поверхности, называемые обтекателями.

История изучения геометрических тел: шар, сфера

Шаром принято называть тело, ограниченное сферой, т. е. шар и сфера – это разные геометрические тела. Однако оба слова « шар» и « сфера» происходят от одного и того же греческого слова « сфайра» — мяч. При этом слово « шар» образовалось от перехода согласных сф в ш.

В XI книге «Начал» Евклид определяет шар как фигуру, описанную вращающимся около неподвижного диаметра полукругом. В древности сфера была в большом почёте. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы.

Сфера всегда широко применялась в различных областях науки и техники.

2.1. Понятие сферы и шара

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

Тело, ограниченное сферой, называется шаром.

Данная точка называется центром сферы, а данное расстояние – радиусом сферы.

Отрезок, соединяющий две точки сферы и проходящий

через ее центр, называется диаметром сферы.

Центр, радиус, диаметр сферы называется также центром, радиусом и диаметром шара.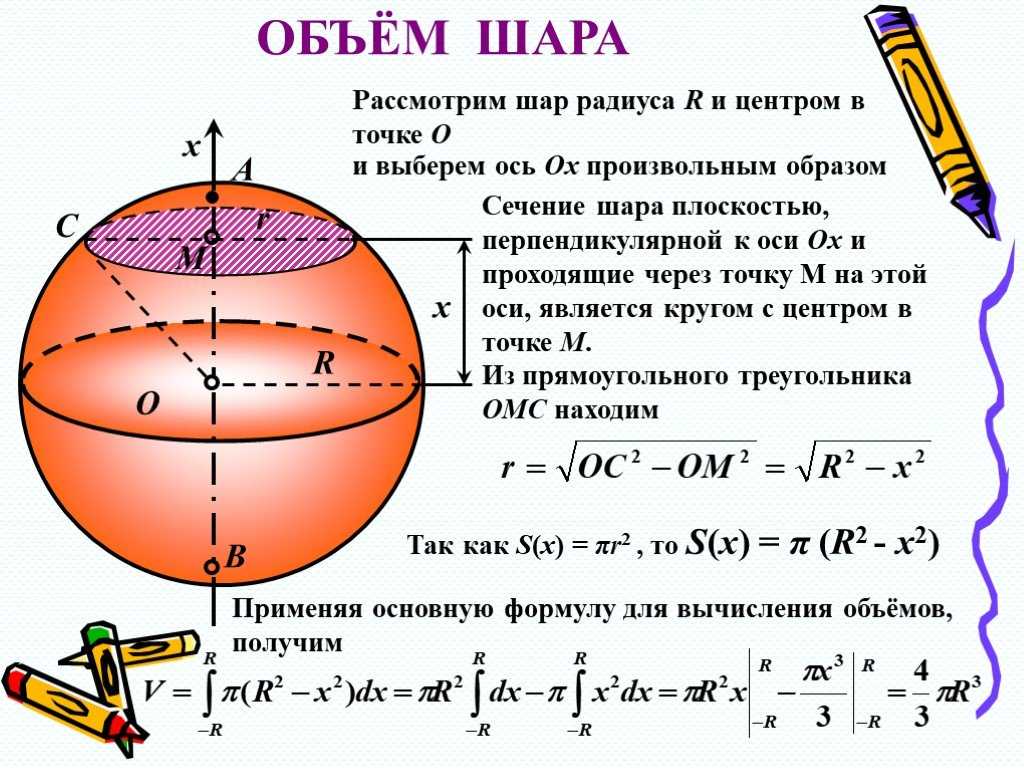

2.2. Уравнение сферы

Зададим прямоугольную систему координат О xyz

Построим сферу c центром в точке C (x 0;y 0;z 0)

и радиусом R

МС = (x – x 0 ) 2 + (y – y 0 ) 2 + (z – z 0 ) 2

МС = R , или МС2 = R2

следовательно уравнение

сферы имеет вид:

(x — x 0 ) 2 + (y — y 0 ) 2 + (z — z 0 ) 2 = R 2

2.3. Взаимное расположение сферы и плоскости

Дано:

Сфера радиуса R с центром С (х 0 ; у 0 ; z 0), точка М (х; у; z ) лежит на сфере.

Чему равно расстояние МС?

Т. к. МС = R , то

С С СС

Дано: плоскость α , сфера (С; R ),

d — расстояние от центра С до плоскости α .

Введем систему координат, где точка С (x 0 ;y 0 ;z 0). Составим уравнения сферы и плоскости α .

П
усть точка С лежит на оси z . Тогда ее координаты (0; 0; d ).

Уравнение сферы:

Уравнение плоскости α : z = 0

Исследуем систему уравнений:

z = 0

Тогда

1
) d

Тогда

уравнение окружности (О; r )

Сечение сферы плоскостью – окружность

2
) d = R .

Тогда

Верно при

х = 0 и у = 0

Сфера и плоскость имеют одну общую точку.

3
) d > R .

Тогда

не имеет решений.

Сфера и плоскость не имеют общих точек.

2.4. Касательная плоскость к сфере

Теорема. Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Дано: сфера с центром О и радиусом R , α — касательная к сфере в точке А плоскость.

Доказать: OA а .

Доказательство: Пусть OA не перпендикулярна плоскости а , тогда OA является наклонной к плоскости, значит, расстояние от центра до плоскости d R . Т.е. сфера должна пересекаться с плоскостью по окружности, но это не удовлетворяет условию теоремы. Значит, OA а .

Докажем обратную теорему.

Дано: сфера с центром О и радиусом OA , а, OA а .

Доказать: а – касательная плоскость.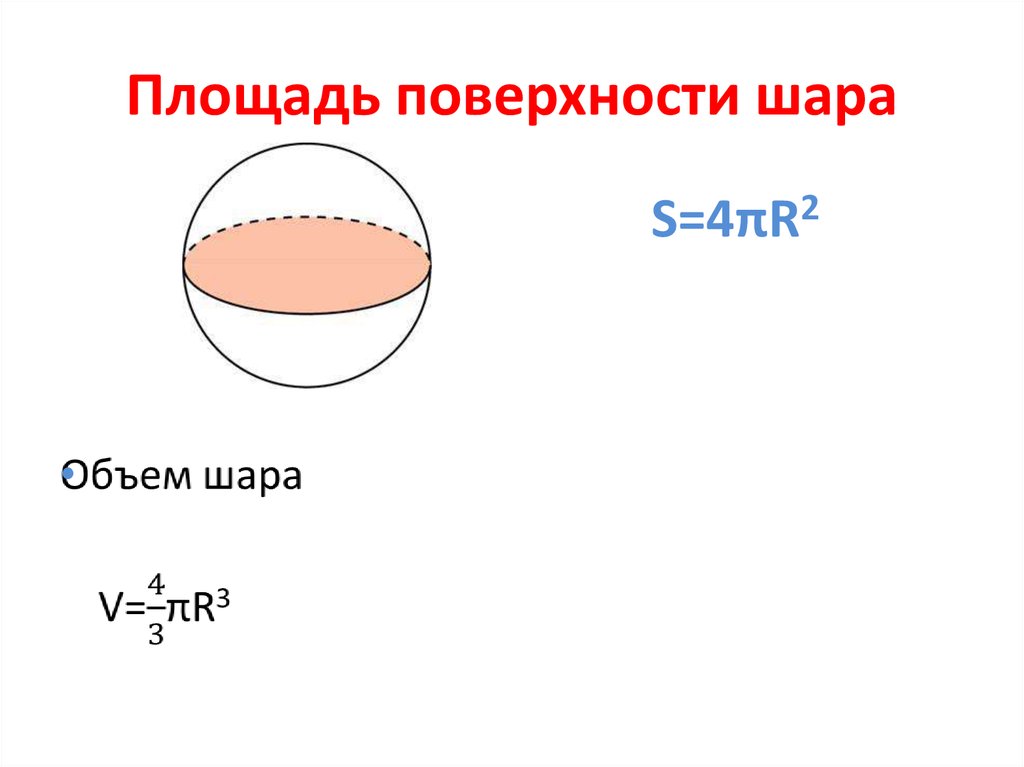

Доказательство: Т.к. OA а , то расстояние от центра сферы до плоскости равно радиусу. Значит, сфера и плоскость имеют одну общую точку. По определению, плоскость является касательной к сфере.

2.5. Площадь сферы и объём шара

и шара радиуса определяются формулами:

Доказательство

Возьмём четверть круга радиуса R с центром в точке . Уравнение окружности этого круга: , откуда .

Функция непрерывная, возрастающая, неотрицательная. При вращении четверти круга вокруг оси Ox образуется полушар, следовательно:

Откуда Ч. т. д.

Доказательство

Ч. т. д.

Часть шара, [ ] осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом. Основанием шарового сегмента называется кругABCD . Высотой шарового сегмента называется отрезок NM , т.е. длина перпендикуляра, восстановленного из центраN основания до пересечения с поверхностью шара. ТочкаM называется вершиной шарового сегмента.

Объем шарового сегмента выражается формулой:

V = π h 2 ( R − 1/3 h)

Шаровой слой — это часть шара [ ], заключенная между двумя секущими параллельными плоскостями. Шаровой пояс или Шаровая зона — это кривая поверхность шарового слоя. Круги ABC и DEF это основания шарового пояса. Расстояние между основаниямиON — это высота шарового слоя.

Объем шарового слоя выражается формулой:

V = 1/6 π h 3 + 1/2 π( r 1 2 + r 2 2 ) h

Шаровой сектор — это часть шара [ ], ограниченная кривой поверхностью шарового сегмента и конической поверхностью основанием которой служит основание сегмента, а вершиной — центр шара.

Объем шарового сектора равен , основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу

V = 1/3 R S = 2/3 π R 2 h

2.6. Получение сферы

Сферу можно получить вращением полуокружности АСВ вокруг диаметра АВ

2.7. Нахождение сферы и шара в природе

Загадки природы — Шары-послания. Эти загадочные каменные образования идеально круглой формы были обнаружены в конце 1940-х годов в джунглях центрально американской Республики Коста-Рика. Шары имеют размеры от 10 см до 3-4 метров в диаметре. При аэросъемке выяснилось, что они разбросаны по поверхности земли не случайно, а составляют геометрические фигуры. Возможно даже, что шары не разбросаны, а разложены в виде огромной звездной карты; каждый шар — это звезда с соответствующим описанием.

Среди гипотез происхождения шаров есть только экзотические версии: от пришельцев до скульпторов Атлантиды. Есть версия и о том, что шары вырезали (в расчете на будущие дивиденды от туризма) скучающие нацистские мигранты, наводнившие Латинскую Америку после краха «третьего рейха». Естественными причинами объяснить обилие шаров и странные рисунки на них не удалось. В Казахстане при разработке песчаного карьера на достаточно большой глубине также были обнаружены несколько крупных экземпляров таких валунов… Об этой находке сообщала комиссия «Феномен»; увы, фотографий находок не сохранилось.

Хрустальный шарик. Макросъёмка. На ветке какого-то дерева лежит шар из стекла, в нём отражается окружающая его природа. Очень симпатичные жёлтые цветочки и зелёная сочная трава.

Светящиеся шары

на фото в местах силы — результат распада урана или плазмоидная форма жизни?

Храм Гроба Господня и другие места Израиля

И
нтересное природное явление на берегу мичиганского озера сформировались тысячи правильных ледяных шаров

Морские водоросли в виде необычных шаров

Странные шары появились на побережье Хэмптона, что на восточном побережье США, в июне 2002 года. Приливная волна стала выносить несметное число таких зеленоватых шаров — мягких, отдаленно напоминающих губку и размером с мячик для тенниса или гольфа. На расстоянии примерно 300 метров или больше весь песчаный пляж буквально был усеян такими шарами. Тут же начались споры- что это и откуда? В дебаты оказались вовлеченными и биологи маринисты, и отдыхающие на пляже, и случайные прохожие. Прежде никто не видел здесь ничего подобного.

Природа боится симметрии, природа не знает идеальных геометрических фигур. Зато человек может заставить природу приобрести эти чуждые ей формы. Наглядный пример тому — творчество корейского художника Lee Jae-Hyo, который создает из стволов деревьев идеальные сферы

Т

ысячи небольших фиолетовых шариков странным образом оказались в центре пустыни в штате Аризона, США. Жители города Тусон Джеральдина Варгас и ее муж обнаружили необъяснимое скопление непонятных шаров пару недель назад во время прогулки по окрестностям. «Мы фотографировали природу пустыни, когда натолкнулись на это странное место… не понимаю, как мы сразу его не заметили? — рассказала Джеральдина журналистам. – Оно просто искрилось на солнце». Фотографы отправили фото со странными объектами своей знакомой зоологу, но она не смогла сказать, что же это такое, у нее даже не было никаких предположений на этот счет.

2.8 Сфера и шар в повседневной жизни

Н
а геометрический шар похожи глобус, футбольный мяч, новогодние игрушки.

Шар из пенопласта своими руками

Зорбинг (zorbing) – это один из самых модных экстремальных развлечений на сегодняшний день. Зорбинг позволит вам испытать новые, необычно яркие и мощные ощущения и встряхнуться от обыденности повседневной жизни.

Что такое шар Зорб

Зорб (ZORB) представляет из себя прозрачную сферу (шар) диаметром 3,2 метра внутри которой находится сфера диаметром 1,8 метра, в которой находится зорбонавт (пассажир зорба ). Пространство между этими сферами наполняется воздухом, давлением которого сферы распираются между собой, а стропами, наоборот, удерживаются. Такая система очень хорошо амортизирует, сглаживает неровности трассы и делает катание безопасным.

2.9.Применение сферы и шара в архитектуре

Такой дом называется ВИГВАМ . Такие дома строят ИНДЕЙЦЫ .

Шары и полусферы из нержавеющей стали

Фонтан «Вращающийся шар » в Санкт-

Петербурге —

Современные дома

А если дом не просто на дереве, а ещё и в форме шара.

Это поселок из самых настоящих круглых домов .

С
овременные круглые дома

Монреальская Биосфера — выставочный павильон США на Экспо-67 в Канаде,

созданная архитектором Ричардом Фуллером.

Отель в виде прозрачных шаров

В
о французском городе Рубе (Roubaix) в одном из парков открыли портативные гостиничные номера Hotel Bolha. Сделали это специально для людей, которые даже в центре городских джунглей желают побыть ближе к природе. Концепцию пузыря придумал дизайнер Пьер Стефан Дюма. Такая продвинутая конструкция была создана с целью временного присоединения постояльцев к неизведанному. Ведь не многие могут себе позволить поспать под круглым потолком.

Платье из шаров.

Дачный офис Скоро весна (а там и лето) и многие начнут ездить на дачу отдыхать.
Но иногда на даче нужно поработать (чтоб тебя!). Нет места где уединится?
Можно вот в таком вот небольшом шарообразном сооружение «Archipod»:

ЭНЕРГОЭФФЕКТИВНОСТЬ в архитектуре . Умный Дом — молекула.

В парке науки и техники La Vilette, построенном на месте скотобойни на восточной окраине Парижа, бросается в глаза гигантский шар, в зеркальной поверхности которого отражается парижское небо и окружающий пейзаж. На сегодняшний день это здание считается самым совершенным в мире сооружением сферической формы. Парижане называют его «Жеод» (Gеode). Это – панорамный

кинотеатр с самым большим в Европе экраном . дом-шар зеркало

Такие шары из ниток можно просто подвесить к веткам дерева, если ваш праздник проходит на природе, или к потолку. А также ими можно оформить банкетный стол, дополнив композицию свечами и цветами.

2.10. Применение сферы и шара в геодезии.

Картографические проекции

отображения всей поверхности земного эллипсоида (См. ) или какую-либо её части на плоскость, получаемые в основном с целью построения карты.

Масштаб. К. п. строятся в определённом масштабе. Уменьшая мысленно земной эллипсоид в М раз, например в 10 000 000 раз, получают его геометрическую модель — , изображение которого уже в натуральную величину на плоскости даёт карту поверхности этого эллипсоида. Величина 1: М (в примере 1: 10 000 000) определяет главный, или общий, масштаб карты. Т. к. поверхности эллипсоида и шара не могут быть развёрнуты на плоскость без разрывов и складок (они не принадлежат к классу развёртывающихся поверхностей (См. )), любой К. п. присущи искажения длин линий, углов и т.п., свойственные всякой карте. Основной характеристикой К. п. в любой её точке является частный масштаб μ. Это — величина, обратная отношению бесконечно малого отрезка ds на земном эллипсоиде к его изображению dσ на плоскости: μ min ≤ μ ≤ μ max , и равенство здесь возможно лишь в отдельных точках или вдоль некоторых линий на карте. Т. о., главный масштаб карты характеризует её только в общих чертах, в некотором осреднённом виде. Отношение μ/М называют относительным масштабом, или увеличением длины, разность М = 1.

1. Сети сферических координатных линий.

2.11. Применение сферы и шара в астрономии и географии.

Сфера и шар, так же как окружность и круг, рассматривали еще в глубокой древности. Открытие шарообразности Земли, появление представлений о небесной сфере дали толчок к развитию специальной науки – СФЕРИКИ, изучающей расположенные на сфере фигуры.

Осуществляя кругосветные путешествия, мореплаватели заметили, что при возвращении в то же место наблюдается потеря или выигрыш целых суток, что было бы совершенно невозможно, если бы Земля имела форму диска.

Итак, доказательствами шарообразности Земли в настоящее время служат:

Всегда кругообразная фигура горизонта в океане и в открытых низменностях или плоскогорьях;

Кругосветные путешествия.

Постепенное приближение или удаление предметов;

И
зучая различные географические карты, мы обнаружили, что в географии есть географические названия, связанные с шаром. Например, между Северным и Южными островами Новой Земли есть пролив, который соединяет Баренцево и Карское моря, который называется Маточкин Шар, или пролив между берегами острова Вайгач и материком Евразии – Югорский Шар. Мы думаем, что эти проливы названы шарами в силу того, что их размеры, форма дна напоминают шаровую поверхность.

2.12. Сфера и шар в искусстве

Математика Эшера

Кроме того, «игрой» с логикой пространства являются картины Эшера, на которых изображены различные «невозможные фигуры»; Эшер изображал их как отдельно, так и в сюжетных литографиях и гравюрах

Три сферы. 1946

Рука с отражающей сферой. 1935

Заключение

Думаю, что собранный мной материал и знания, полученные в ходе проделанной работы можно использовать на уроках геометрии, труда, в повседневной жизни, в качестве основы для элективного курса в классах физико-математического профиля, а так же на внеклассных занятиях для расширения кругозора учеников.

Адамар Ж. Элементарная геометрия. Ч.2. М. Учпедгиз, 1958. Андреев

Атанасян Л.С. Геометрия. Ч.2. – М: Просвещение, 1987. – 352с.

Базылев В.Т. Геометрия. М: Просвещение, 1975.

Базылев В.Т. Сборник задач по геометрии. М: Просвещение, 1980. -240с.

Егоров И.П. Геометрия. – М: Просвещение, 1979. – 256с.

Егоров И.П. Основания геометрии. – М: Просвещение, 1984. – 144с.

Задачник «Кванта»: Математика. Часть 1. / Под ред. Н.Б. Васильева. М: 1997.

Розенфельд Б.А. История неевклидовой геометрии. Развитие понятия о геометрическом пространстве. М. Наука., 1976. – 408с.

Энциклопедия элементарной математики. Кн.4 – Геометрия. М., 1963.

10.Интернет-ресурсы.

Определение шара Шар – это тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки (или фигура, ограниченная сферой). Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Шар

Плоскость,проходящая через центр шара,называется диаметральной плоскостью.Плоскость,проходящая через центр шара,называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом,а сечение сферы — большой окружностью.Сечение шара диаметральной плоскостью называется большим кругом,а сечение сферы — большой окружностью.

X²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек. R, то сфера и плоскость не имеют общих точек.»> R, то сфера и плоскость не имеют общих точек.»> R, то сфера и плоскость не имеют общих точек.» title=»x²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.»> title=»x²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.»>

Касательная плоскость к сфере касательной плоскостью к сфереПлоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, точкой касания А плоскости и сферы.а их общая точка называется точкой касания А плоскости и сферы.

Теорема: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. Доказательство: Рассмотрим плоскость α, касающуюся сферы с центром О в точке А. Докажем, что ОА перпендикулярен α. Предположим, что это не так. Тогда радиус ОА является наклонной к плоскости α, и, следовательно расстояние от центра сферы до плоскости меньше радиуса сферы. Поэтому сфера и плоскость пересекаются по окружности. Это противоречит тому, что-касательная, т.е. сфера и плоскость имеют только одну общую точку. Полученное противоречие доказывает, что ОА перпендикулярен α.

Основные элементы шара. Сфера, шар, сегмент и сектор

В главе 2 мы продолжим “строительную геометрию» и расскажем о строении и свойствах важнейших пространственных фигур — шара и сферы, цилиндров и конусов, призм и пирамид. Большинство предметов, созданных руками человека, — здания, машины, мебель, посуда и т.д., и т.п., состоит из частей, имеющих форму этих фигур.

§ 4. СФЕРА И ШАР

После прямых и плоскостей сфера и шар — самые простые, но очень важные и богатые разнообразными свойствами пространственные фигуры. О геометрических свойствах шара и его поверхности — сферы — написаны целые книги. Некоторые из этих свойств были известны еще древнегреческим геометрам, а некоторые найдены совсем недавно, в последние годы. Эти свойства (вместе с законами естествознания) объясняют, почему, например, форму шара имеют небесные тела и икринки рыб, почему в форме шара делают батискафы и футбольные мячи, почему так распространены в технике шарикоподшипники и т.д. Мы можем доказать лишь самые простые свойства шара. Доказательства других, хотя и очень важных свойств, часто требуют применения совсем не элементарных методов, хотя формулировки таких свойств могут быть очень простыми: например, среди всех тел, имеющих данную площадь поверхности, наибольший объем у шара.

4.1. Определения сферы и шара.

Определяются сфера и шар в пространстве совершенно так же, как окружность и круг на плоскости. Сферой называется фигура, состоящая из всех точек пространства, удаленных от данной

ной точки на одно и то же (положительное) расстояние.

Эта точка называется центром сферы, а расстояние — ее радиусом (рис. 4.1).

Итак, сфера с центром О и радиусом R — это фигура, образованная всеми точками X пространства, для которых

Шаром называется фигура, образованная всеми точками пространства, находящимися на расстоянии не большем данного (положительного) расстояния от данной точки. Эта точка называется центром шара, а данное расстояние — его радиусом.

Итак, шар с центром О и радиусом R — это фигура, образованная всеми точками X пространства, для которых

Те точки X шара с центром О и радиусом R, для которых образуют сферу. Говорят, что эта сфера ограничивает данный шар или что она является его поверхностью.

О тех же точках X шара, для которых говорят, что они лежат внутри шара.

Радиусом сферы (и шара) называют не только расстояние , но и любой отрезок, соединяющий центр с точкой сферы.

Шар

Объем шара

Формула для вычисления объема шара имеет вид:

где R — радиус шара.

Если нужно найти объем шарового сегмента — воспользуйтесь формулой:

V сег =πh 2 (R-h/3), h — высота шарового сегмента.

Площадь поверхности шара или сферы

Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):

где R — радиус сферы.

Шар ( сфера )

Сферическая поверхность. Шар (сфера). Сечения шара: круги.

Теорема Архимеда. Части шара:шаровой (сферический) сегмент,

шаровой слой, шаровой пояс, шаровой сектор.

Сферическая поверхность – это геометрическое место точек ( т.е. множе ство всех точек ) в пространстве, равноудалённых от одной точки O, которая называется центром сферической поверхности ( рис. 90 ). Радиус AOи диаметр AB определяются так же, как и в окружности.

Шар (сфера ) — это тело, ограниченное сферической поверхностью. Можно получить шар, вращая полукруг (или круг ) вокруг диаметра. Все плоские сечения шара – круги (рис.90 ). Наибольший круг лежит в сечении, проходящем через центр шара, и называется большим кругом . Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара (AB, рис.91 ).Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (A и B , рис.91 ), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.

Объём шара в полтора раза меньше объёма описанного вокруг него цилиндра (рис.92 ), а поверхность шара в полтора раза меньше полной поверхности того же цилиндра ( теорема Архимеда ):

Здесь S шара и V шара — соответственно поверхность и объём шара;

S цил и V цил — полная поверхность и объём описанного цилиндра.

Части шара. Часть шара (сферы ), отсекаемая от него какой-либо плоскостью (ABC, рис.93 ), называется шаровым (сферическим ) сегментом . Круг ABC называется основанием шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, называется высотой шарового сегмента. Точка M называется вершиной шарового сегмента.

Часть сферы, заключённая между двумя параллельными плоскостями ABC и DEF, пересекающими сферическую поверхность ( рис.93 ), называется шаровым слоем ; кривая поверхность шарового слоя называется шаровым поясом ( зоной ). Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота . Часть шара, ограниченная кривой поверхностью сферического сегмента (AMCB, рис.93) и конической поверхностью OABC, основанием которой служит основание сегмента (ABC), а вершиной – центр шара O, называется шаровым сектором .

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью). Действительно, все ли из нас хорошо знают из школьной программы геометрию и могут сходу ответить на данный вопрос? Сфера имеет некоторые отличия от шара, которые нужно знать не только школьникам, чтобы получить хорошую оценку за свои продемонстрированные знания, но и многим другим людям, например, чья работа непосредственно связана с чертежами.

Определение

Шар – совокупность всех точек пространства. Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. Шар, как геометрическое тело, образуется следующим образом: происходит вращение полукруга возле его диаметра. Что касается сферы, то это и есть поверхность шара (например, замкнутый шар включает ее, открытый – нет). Вычисление площади или объема шара – это целые геометрические формулы, которые очень сложны, несмотря на кажущуюся простоту самой геометрической фигуры.

Сфера , как было отмечено выше, представляет собой поверхность шара, его оболочку. От центра сферы все точки в пространстве равноудалены. Что касается радиуса геометрического тела, то им называют любой отрезок, одна точка которого – непосредственно центр сферы, а другая может находиться в любой точке на поверхности. Можно сказать, что сфера является оболочкой шара без какого-либо содержимого (более конкретные примеры будут приведены ниже). Также как и шар, сфера является телом вращения. Кстати, многие также задаются вопросом, чем же отличаются круг и окружность от сферы и шара. Здесь все просто: в первом случае это фигуры на плоскости, во втором – в пространстве.

Сравнение

Уже было сказано о том, что сфера является поверхностью шара, что уже дает возможность говорить об одном весомом признаке отличия. Разница между двумя геометрическими телами наблюдается и в некоторых других аспектах:

Все точки шара находятся на одинаковом расстоянии от центра, при этом тело ограничено поверхностью (сферой, которая является пустой внутри). Иными словами, сфера полая. Обычно для простоты понимания приводят простой пример с воздушным и бильярдным шаром. Оба этих предмета называют шарами, однако в первом случае мы имеем дело со сферой, а во втором с полноценным шаром со своим содержимым внутри.
Сфера имеет свою площадь, но при этом у нее нет объема. Шар же наоборот: его объем можно вычислить, в то время как у него нет площади. Кто-то может сказать, что это главный признак отличия, но он проявляется только в том случае, если необходимо производить какие-то расчеты (сложные геометрические формулы). Поэтому главным отличием является то, что сфера полая, а шар – тело с содержимым внутри.
Еще одно отличие кроется в радиусе. Например, радиусом сферы называется не только расстояние точек до центра. Радиусом может называться любой отрезок, соединяющий точку на сфере с ее центром. Все эти отрезки равны между собой. Что касается шара, то лежащие внутри него точки удалены от центра меньше, чем на радиус (как раз из-за ограничивающей его сферы).

Выводы сайт

Сфера полая, в то время как шар является заполненным внутри телом. Например, воздушный шар – это сфера, бильярдный шар – это полноценный шар.
Сфера имеет площадь и не имеет объем, шар же наоборот.
Третье отличие – это измерение радиуса двух геометрических тел.

Определение.

Сфера (поверхность шара ) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Формула. Объём шара :

V =	4	π R 3 =	1	π D 3
	3		6

Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4π R 2 = π D 2

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :

x 2 + y 2 + z 2 = R 2

2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0) в декартовой системе координат :

(x — x 0) 2 + (y — y 0) 2 + (z — z 0) 2 = R 2

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются , а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

Местом сечения секущей плоскости на сфере всегда будет малая окружность , а на шаре местом сечения будет малый круг . Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R 2 — m 2 ,

Где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Касательная, касательная плоскость к сфере и их свойства

Определение. Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение. Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2π Rh

Шар стереометрия. Шар и сфера, объем шара, площадь сферы, формулы

Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг его диаметра как оси.

Площадь поверхности шара можно найти по формулам:

где r – радиус шара, d – диаметр шара.

Объём шара находится по формуле:

V = 4 / 3 πr 3 ,

где r – радиус шара.

Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле

Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большим кругом, а сечение сферы – большой окружностью.

Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

Плоскость, которая и проходит через точку А шаровой поверхности и перпендикулярна радиусу, проведённому в точку А, называется касательной плоскостью. Точка А называется точкой касания.

Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.

Прямая, которая проходит через точку А шаровой поверхности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.

Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причём все они лежат в касательной плоскости шара.

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Круг ABC – основание шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, – высота шарового сегмента. Точка M – вершина шарового сегмента.

Площадь поверхности шарового сегмента можно вычислить по формуле:

Объём шарового сегмента можно найти по формуле:

V = πh 2 (R – 1/3h),

где R – радиус большого круга, h – высота шарового сегмента.

Шаровой сектор получается из шарового сегмента и конуса, следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.

Шаровой сектор – это часть шара, ограниченная кривой поверхностью сферического сегмента (на нашем рисунке – это AMCB) и конической поверхностью (на рисунке – это OABC), основанием которой служит основание сегмента (ABC), а вершиной – центр шара O.

Объем шарового сектора находится по формуле:

V = 2/3 πR 2 H.

Шаровый слой – это часть шара, заключённая между двумя параллельными плоскостями (на рисунке плоскостями ABC и DEF), пересекающими сферическую поверхность. Кривая поверхность шарового слоя называется шаровым поясом (зоной). Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Шар ( сфера )

Сферическая поверхность. Шар (сфера). Сечения шара: круги.

Теорема Архимеда. Части шара:шаровой (сферический) сегмент,

шаровой слой, шаровой пояс, шаровой сектор.

Сферическая поверхность – это геометрическое место точек ( т.е. множе ство всех точек ) в пространстве, равноудалённых от одной точки O, которая называется центром сферической поверхности ( рис.90 ). Радиус AOи диаметр AB определяются так же, как и в окружности.

Шар (сфера ) — это тело, ограниченное сферической поверхностью. Можно получить шар, вращая полукруг (или круг ) вокруг диаметра. Все плоские сечения шара – круги (рис.90 ). Наибольший круг лежит в сечении, проходящем через центр шара, и называется большим кругом . Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара ( AB, рис.91 ).Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (A и B , рис.91 ), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.

Здесь S шара и V шара — соответственно поверхность и объём шара;

S цил и V цил — полная поверхность и объём описанного цилиндра.

Части шара. Часть шара (сферы ), отсекаемая от него какой-либо плоскостью ( ABC, рис. 93 ), называется шаровым (сферическим ) сегментом . Круг ABC называется основанием шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, называется высотой шарового сегмента. Точка M называется вершиной шарового сегмента.

Часть сферы, заключённая между двумя параллельными плоскостями ABC и DEF, пересекающими сферическую поверхность ( рис.93 ), называется шаровым слоем ; кривая поверхность шарового слоя называется шаровым поясом ( зоной ). Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота . Часть шара, ограниченная кривой поверхностью сферического сегмента ( AMCB, рис.93) и конической поверхностью OABC, основанием которой служит основание сегмента ( ABC), а вершиной – центр шара O, называется шаровым сектором .

§ 4. СФЕРА И ШАР

4.1. Определения сферы и шара.

ной точки на одно и то же (положительное) расстояние.

Эта точка называется центром сферы, а расстояние — ее радиусом (рис. 4.1).

Итак, сфера с центром О и радиусом R — это фигура, образованная всеми точками X пространства, для которых

Итак, шар с центром О и радиусом R — это фигура, образованная всеми точками X пространства, для которых

О тех же точках X шара, для которых говорят, что они лежат внутри шара.

Радиусом сферы (и шара) называют не только расстояние , но и любой отрезок, соединяющий центр с точкой сферы.

Обьем сферы. Шар и сфера, объем шара, площадь сферы, формулы

Многие тела, которые мы встречаем в жизни или о которых слышали, имеют шарообразную форму, например футбольный мяч, падающая капля воды во время дождя или наша планета. В связи с этим является актуальным рассмотрение вопроса, как находить объем шара.

Фигура шар в геометрии

Перед тем как ответить на вопрос, шара, рассмотрим подробнее это тело. Некоторые люди путают его со сферой. Внешне они действительно похожи, однако шар — это заполненный внутри объект, сфера же представляет собой лишь внешнюю оболочку шара бесконечно малой толщины.

С точки зрения геометрии шар можно представить совокупностью точек, причем те из них, которые лежат на его поверхности (они образуют сферу), находятся на одинаковом расстоянии от центра фигуры. Это расстояние называют радиусом. По сути, радиус — это единственный параметр, с помощью которого можно описать любые свойства шара, такие как площадь его поверхности или объем.

На рисунке ниже приведен пример шара.

Если внимательно посмотреть на этот идеальный круглый объект, то можно догадаться, как его получить из обычного круга. Для этого достаточно вращать эту плоскую фигуру вокруг оси, совпадающей с его диаметром.

Одним из известных древних литературных источников, в котором достаточно подробно рассматриваются свойства этой объемной фигуры, является труд греческого философа Евклида — «Элементы».

Площадь поверхности и объем

Рассматривая вопрос, как находить объем шара, помимо этой величины, следует привести формулу для его площади, поскольку оба выражения можно связать друг с другом, как будет показано ниже.

Итак, чтобы вычислить объем шара, следует применить одну из следующих двух формул:

V = 4/3 *pi * R3;
V = 67/16 * R3.

Здесь R — радиус фигуры. Первая из приведенных формул является точной, однако, чтобы воспользоваться этим преимуществом, необходимо использовать соответствующее число знаков после запятой для числа pi. Второе выражение дает вполне хороший результат, отличаясь от первого всего на 0,03 %. Для ряда практических задач этой точности более чем достаточно.

Равна этой величине для сферы, то есть выражается формулой S = 4 * pi * R2. Если отсюда выразить радиус, а затем подставить его в первую формулу для объема, тогда получим: R = √ (S / (4 * pi)) = > V = S / 3 * √ (S / (4 * pi)).

Таким образом, мы рассмотрели вопросы, как найти объем шара через радиус и через площадь его поверхности. Эти выражения можно с успехом применять на практике. Далее в статье приведем пример их использования.

Задача с каплей дождя

Вода, когда находится в невесомости, приобретает форму шарообразной капли. Связано это с наличием сил поверхностного натяжения, которые стремятся минимизировать площадь поверхности. Шар, в свою очередь, обладает наименьшим ее значением среди всех геометрических фигур с одинаковой массой.

Во время дождя падающая капля воды находится в невесомости, поэтому ее формой является шар (здесь пренебрегаем силой сопротивления воздуха). Необходимо определить объем, площадь поверхности и радиус этой капли, если известно, что ее масса составляет 0,05 грамма.

Объем определить просто, для этого следует поделить известную массу на плотность H 2 O (ρ = 1 г/см 3). Тогда V = 0,05 / 1 = 0,05 см 3 .

Зная, как найти объем шара, следует выразить из формулы радиус и подставить полученное значение, имеем: R = ∛ (3 * V / (4 * pi)) = ∛ (3 * 0,05 / (4 * 3,1416)) = 0,2285 см.

Теперь значение радиуса подставляем в выражение для площади поверхности фигуры, получаем: S = 4 * 3,1416 * 0,22852 = 0,6561 см 2 .

Таким образом, зная, как находить объем шара, мы получили ответы на все вопросы задачи: R = 2,285 мм, S = 0,6561 см 2 и V = 0,05 см 3 .

Радиус шара (обозначается как r или R) – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Как и в случае круга, радиус шара является важной величиной, которая необходима для нахождения диаметра шара, длины окружности, площади поверхности и/или объема. Но радиус шара можно найти и по данному значению диаметра, длины окружности и другой величины. Используйте формулу, в которую можно подставить данные значения.

Шаги

Формулы для вычисления радиуса

Вычислите радиус по диаметру. Радиус равен половине диаметра, поэтому используйте формулу г = D/2 . Эта такая же формула, которая используется при вычислении радиуса и диаметра круга.

Например, дан шар с диаметром 16 см. Радиус этого шара: r = 16/2 = 8 см . Если диаметр равен 42 см, то радиус равен 21 см (42/2=21).

Вычислите радиус по длине окружности. Используйте формулу: r = C/2π . Так как длина окружности C = πD = 2πr, то разделите формулу для вычисления длины окружности на 2π и получите формулу для нахождения радиуса.

Например, дан шар с длиной окружности 20 см. Радиус этого шара: r = 20/2π = 3,183 см .
Такая же формула используется при вычислении радиуса и длины окружности круга.

Вычислите радиус по объему шара. Используйте формулу: r = ((V/π)(3/4)) 1/3 . Объем шара вычисляется по формуле V = (4/3)πr 3 . Обособив r на одной стороне уравнения, вы получите формулу ((V/π)(3/4)) 3 = г, то есть для вычисления радиуса объем шара делим на π, результат умножаем на 3/4, а полученный результат возводим в степень 1/3 (или извлекаем кубический корень).

Например, дан шар с объемом 100 см 3 . Радиус этого шара вычисляется так:
- ((V/π)(3/4)) 1/3 = r
- ((100/π)(3/4)) 1/3 = r
- ((31,83)(3/4)) 1/3 = r
- (23,87) 1/3 = r
- 2,88 см = r

Вычислите радиус по площади поверхности. Используйте формулу: г = √(A/(4 π)) . Площадь поверхности шара вычисляется по формуле А = 4πr 2 . Обособив r на одной стороне уравнения, вы получите формулу √(A/(4π)) = r, то есть, чтобы вычислить радиус, нужно извлечь квадратный корень из площади поверхности, деленной на 4π. Вместо того чтобы извлекать корень, выражение (A/(4π)) можно возвести в степень 1/2.

Например, дан шар с площадью поверхности 1200 см 3 . Радиус этого шара вычисляется так:
- √(A/(4π)) = r
- √(1200/(4π)) = r
- √(300/(π)) = r
- √(95,49) = r
- 9,77 см = r

Определение основных величин

Запомните основные величины, которые имеют отношение к вычислению радиуса шара. Радиус шара – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Радиус шара можно вычислить по данным значениям диаметра, длины окружности, объема или площади поверхности.
Воспользуйтесь значениями данных величин, чтобы найти радиус. Радиус можно вычислить по данным значениям диаметра, длины окружности, объема и площади поверхности. Более того, указанные величины можно найти по данному значению радиуса. Чтобы вычислить радиус, просто преобразуйте формулы для нахождения указанных величин. Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности.

Нахождение радиуса по расстоянию между двумя точками

Найдите координаты (х,у,z) центра шара. Радиус шара равен расстоянию между его центром и любой точкой, лежащей на поверхности шара. Если известны координаты центра шара и любой точки, лежащей на его поверхности, можно найти радиус шара по специальной формуле, вычислив расстояние между двумя точками. Сначала найдите координаты центра шара. Имейте в виду, что так как шар является трехмерной фигурой, то точка будет иметь три координаты (х,у,z), а не две (х,у).
- Рассмотрим пример. Дан шар с центром с координатами (4,-1,12) . Воспользуйтесь этими координатами, чтобы найти радиус шара.
Найдите координаты точки, лежащей на поверхности шара. Теперь нужно найти координаты (х,у,z) любой точки, лежащей на поверхности шара. Так как все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара, для вычисления радиуса шара можно выбрать любую точку.
- В нашем примере допустим, что некоторая точка, лежащая на поверхности шара, имеет координаты (3,3,0) . Вычислив расстояние между этой точкой и центром шара, вы найдете радиус.
Вычислите радиус по формуле d = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2). Узнав координаты центра шара и точки, лежащей на его поверхности, вы можете найти расстояние между ними, которое равно радиусу шара. Расстояние между двумя точками вычисляется по формуле d = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2), где d – расстояние между точками, (x 1 ,y 1 ,z 1) – координаты центра шара, (x 2 ,y 2 ,z 2) – координаты точки, лежащей на поверхности шара.
- В рассматриваемом примере вместо (x 1 ,y 1 ,z 1) подставьте (4,-1,12), а вместо (x 2 ,y 2 ,z 2) подставьте (3,3,0):
  - d = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2)
  - d = √((3 — 4) 2 + (3 — -1) 2 + (0 — 12) 2)
  - d = √((-1) 2 + (4) 2 + (-12) 2)
  - d = √(1 + 16 + 144)
  - d = √(161)
  - d = 12,69 . Это искомый радиус шара.
Имейте в виду, что в общих случаях r = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2). Все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара. Если в формуле для нахождения расстояния между двумя точками «d» заменить на «r», получится формула для вычисления радиуса шара по известным координатам (x 1 ,y 1 ,z 1) центра шара и координатам (x 2 ,y 2 ,z 2) любой точки, лежащей на поверхности шара.
- Возведите обе стороны этого уравнения в квадрат, и получите r 2 = (x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2 . Отметьте, что это уравнение соответствует уравнению сферы r 2 = x 2 + y 2 + z 2 с центром с координатами (0,0,0).

Не забывайте про порядок выполнения математических операций. Если вы не помните этот порядок, а ваш калькулятор умеет работать с круглыми скобками, пользуйтесь ими.
В этой статье рассказывается о вычислении радиуса шара. Но если вы испытываете затруднения с изучением геометрии, лучше начать с вычисления величин, связанных с шаром, через известное значение радиуса.
π (Пи) – это буква греческого алфавита, которая обозначает постоянную, равную отношению диаметра круга к длине его окружности. Число Пи является иррациональным числом, которое не записывается как отношение действительных чисел. Существует множество приближений, например, отношение 333/106 позволит найти число Пи с точностью до четырех цифр после десятичной запятой. Как правило, пользуются приблизительным значением числа Пи, которое равно 3,14.

где V – искомый объем шара , π – 3,14 , R – радиус.

Таким образом, при радиусе 10 сантиметров объем шара равен:

3,14 × 10 3

= 4186,7

кубических сантиметров.

В геометрии шар определяется как некое тело, представляющее собой совокупность всех точек пространства, которые располагаются от центра на расстоянии, не более заданного, называемого радиусом шара. Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.

С этим геометрическим телом очень часто сталкиваются инженеры-конструкторы и архитекторы, которым часто приходится вычислять объем шара . Скажем, в конструкции передней подвески подавляющего большинства современных автомобилей используются так называемые шаровые опоры, в которых, как нетрудно догадаться из самого названия, одними из основных элементов являются именно шары. С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет вычислен их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.

В технике широчайшее распространение получили такие детали, как шариковые подшипники, с помощью которых происходит крепление осей в неподвижных частях различных узлов и агрегатов и обеспечивается их вращение. Следует заметить, что при их расчете конструкторам требуется найти объем шара (а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки. Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.

Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений. В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда. Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.

Без шаров немыслима такая интересная и популярная игра, как бильярд. Для их производства используются различные материалы (кость, камень, металл, пластмассы) и используются различные технологические процессы. Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные). Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.

Наконец, без таких геометрических тел, как шары, не обходится ни одна новогодняя или рождественская елка. Изготавливаются эти украшения в большинстве случаев из стекла методом выдувания, и при их производстве наибольшее внимание уделяется не точности размеров, а эстетичности изделий. Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются.

Шар — это геометрическое тело вращения, образованное путем вращения круга или полукруга вокруг его диаметра. Также шар — это пространство, ограниченное сферической поверхностью. Существует множество реальных сферических объектов и связанных с ними задач, для решения которых требуется определить объем шара.

Шар и сфера

Круг — самая древняя геометрическая фигура, и античные ученые придавали ей сакральное значение. Круг — это символ нескончаемого времени и пространства, символ Вселенной и бытия. По мнению Пифагора, круг — прекраснейшая из фигур. В трехмерном пространстве окружность превращается в сферу, такую же идеальную, космическую и прекрасную, как и круг.

Сфера по-древнегречески означает «мяч». Сфера представляет собой поверхность, образованную бесконечным множеством точек, равноудаленных от центра фигуры. Пространство, ограниченное сферой, и есть шар. Шар — идеальная геометрическая фигура, форму которой принимают многие реальные объекты. К примеру, в реальной жизни форму шара имеют пушечные ядра, подшипники или мячи, в природе — капли воды, кроны деревьев или ягоды, в космосе — звезды, метеоры или планеты.

Объем шара

Определение объема сферической фигуры — сложная задача, ведь такое геометрическое тело нельзя разбить на кубы или треугольные призмы, формулы объемов которых уже известны. Современная наука позволяет вычислить объем шара при помощи определенного интеграла, однако каким образом была выведена формула объема в Древней Греции, когда об интегралах еще никто не слышал? Архимед вычислил объем шара при помощи конуса и цилиндра, так как формулы объемов этих фигур были уже определены древнегреческим философом и математиком Демокритом.

Архимед представил половину шара при помощи одинаковых конуса и цилиндра, при этом радиус каждой фигуры был равен ее высоте R = h. Античный ученый представил конус и цилиндр разбитыми на бесконечное количество маленьких цилиндров. Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:

0,5 Vsh = Vc − Vk

Объем конуса вычисляется по простой формуле:

Vk = 1/3 × So × h,

но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:

Vk = 1/3 × pi × R × R 2 = 1/3 pi × R 3

Объем цилиндра вычисляется по формуле:

Vc = pi × R 2 × h,

но считая, что высота цилиндра равна его радиусу, мы получаем:

Vc = pi × R 3 .

Используя эти формулы, Архимед получил:

0,5 Vsh = pi × R 3 — 1/3 pi × R 3 или Vsh = 4/3 pi × R 3

Современное определение формулы объема шара выводится из интеграла от площади сферической поверхности, однако результат остается все тем же

Vsh = 4/3 pi × R 3

Расчет объема шара может понадобиться как в реальной жизни, так и при решении абстрактных задач. Для вычисления объема шара при помощи онлайн-калькулятора вам понадобится узнать всего один параметр на выбор: диаметр или радиус сферы. Рассмотрим пару примеров.

Примеры из жизни

Пушечные ядра

Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде

Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.

Воздушные шары

Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат

Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.

Заключение

Необходимость определения объема шара может возникнуть в самых разных ситуациях: от абстрактных школьных задач до научных изысканий и производственных вопросов. Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.

основные формулы и пример их использования

Шар это геометрическое тело, образованное в результате вращения полукруга на оси своего диаметра.

Вычислить объем шара

Объем шара можно вычислить по формуле:

R – радиус шара

V – объем шара

Найти объем шара радиусом сантиметров.

Для того чтобы вычислить объем шара формула используется следующая:

где – искомый объем шара, – , – радиус.

Таким образом, при радиусе сантиметров объем шара равен:

3,14 × 103

= 4186,7

кубических сантиметров.

Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.

С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет вычислен их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.

Следует заметить, что при их расчете конструкторам требуется найти объем шара (а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки.

Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.

Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений.

В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда. Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.

Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные). Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.

Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются.

Сфера — одно из простейших геометрических тел, в котором все точки ее поверхности находятся на одном и том же расстоянии от центра изображения. Расстояние от центра сферы до любой точки на ее поверхности называется радиусом.

Объем мяча

Диаметр шара называется удвоенным радиусом.

Как найти объем шара вокруг его радиуса

Если мы знаем радиус сферы, мы можем легко вычислить ее величину. Для этого умножьте куб на радиус и четверное число Pi, после чего результат будет разделен на три. Формула для определения объема шара по его радиусу выглядит следующим образом: .
Для тех, кто забыл, мы помним, что число Pi является фиксированным значением и равно 3.14.

Как найти объем сферы на диаметр

Если диаметр сферы известен из условий задачи, ее объем вычисляется по следующей формуле: , то есть.

число Pi следует умножить на диаметр диаметра, то полученный результат делится на 6.

Как определить массу шара

Масса тела — это физическая величина, указывающая степень ее инертности. Масса физического тела зависит от объема занимаемого пространства и плотности материала, из которого он собирается. Объем тела правильной формы (скажем, бить ) нетрудно рассчитать, и если материал, из которого он изготовлен, также известен, навалом это разрешено быть очень примитивным.

инструкции

первый Укажите сумму бить .

Как рассчитать объем шара

Для этого достаточно знать один из ваших параметров — радиус, диаметр, поверхность и т. Д. Скажите, знаете ли вы диаметр бить (d), его объем (V) разрешается определять, как одна шестая часть продукта с диаметром поднимается в кубе с числом Pi: V = π * d? / 6. Через радиус бить (r) объем выражается как одна треть произведения числа Pi, который в четыре раза увеличивается с радиусом, помещенным в куб: V = 4 * π * r? / 3.

второй подсчитывать навалом бить (m), умножьте его объем с великолепной плотностью вещества (p): m = p * V.

Если это материал бить не однородный, то мы должны взять среднюю плотность. В этой формуле мы заменяем объем бить через его известные параметры, допускается принимать по известному диаметру бить формула m = p * π * d? / 6 и для главного радиуса m = p * 4 * π * r? / 3.

третий Используйте для расчетов, например, типичный калькулятор программного обеспечения, который входит в базовую операционную систему Windows, любую сильную версию, используемую сегодня.

Самый простой способ начать — нажатием win + r, чтобы открыть типичный диалог для запуска программы, затем введите команду calc и нажмите кнопку OK. 1/3 — извлечение кубического корня.

Источники:

диаметр это

Окружностью называется геометрическая фигура на плоскости, которая состоит из всех точек этой плоскости находящихся на одинаковом расстоянии от заданной точки. Заданная точка при этом называется центром окружности , а расстояние, на котором точки окружности находятся от её центра – радиусом окружности . Область плоскости ограниченная окружностью называется кругом.Существует несколько методов расчёта диаметра окружности , выбор конкретного зависти от имеющихся первоначальных данных.

Инструкция

Видео по теме

При проведении построений различных геометрических фигур иногда требуется определить их характеристики: длину, ширину, высоту и так далее. Если речь идет о круге или окружности, то часто приходится определять их диаметр. Диаметр представляет собой отрезок прямой, который соединяет две наиболее удаленных друг от друга точки, расположенные на окружности.

Вам понадобится

— измерительная линейка;
— циркуль;
— калькулятор.

Инструкция

В самом простом случае определите диаметр по формуле D = 2R, где R – радиус окружности с центром в точке О. Такая удобна, если вы вычерчиваете круг с заранее оговоренным . Например, если при построении фигуры вы установите раствор ножек циркуля равным 50 мм, то диаметр круга, полученного в результате, будет равен удвоенному радиусу, то есть 100 мм.

Если вам известна длина окружности, составляющей внешнюю границу круга, то используйте для определения диаметра формулу:

D = L / p, где
L – длина окружности;
p – число «пи», равное приблизительно 3,14.

Например, если длина 180 мм, то диаметр будет равняться приблизительно: D = 180 / 3,14 = 57,3 мм.

Если вы имеете предварительно вычерченный круг с радиусом, диаметром и длиной окружности, то для приблизительного диаметра используйте и измерительную линейку . Сложность заключается в том, чтобы найти на

Определение.

Сфера (поверхность шара ) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Определение.

Формула. Объём шара :

V =	4	π R 3 =	1	π D 3
	3		6

Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4π R 2 = π D 2

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :

x 2 + y 2 + z 2 = R 2

2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0) в декартовой системе координат :

(x — x 0) 2 + (y — y 0) 2 + (z — z 0) 2 = R 2

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются , а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

Местом сечения секущей плоскости на сфере всегда будет малая окружность , а на шаре местом сечения будет малый круг . Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R 2 — m 2 ,

Где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Касательная, касательная плоскость к сфере и их свойства

Определение. Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2π Rh

Сферические фигуры окружают нас практически везде, однако, мы настолько к ним привыкли, что не придаем этому внимания. Тем временем, случается так, что нам необходимо узнать объем какой-нибудь из них. Но все ли знают, как найти объем шара ? Углубляться в школьные воспоминания, чтобы восстановить в голове курс геометрии? Не затрудняйте себе задачу. Давайте лучше включим логику, и разберемся с этим вопросом.

Инструкция:

Начнем с примера, когда формула объема шара нам не понадобится — представим, что у нас есть возможность произвести вычисления практическим путем . Один из наиболее простых способов это сделать — последовать по стопам Архимеда, определив объем не самого шара непосредственно, а вытесненной им воды . Для этого нужно положить его в емкость, подходящую по размерам, предварительно отметив уровень воды. Погрузив сферу целиком в жидкость, сделайте повторные измерения. Теперь осталось найти разницу между получившимися цифрами. Конечно, лучше всего будет поместить шар в емкость с делениями, к примеру, в мерный стакан — если позволяет размер. Таким образом, мы сразу получим нужную характеристику — обычно деления показаны в миллилитрах. В ином случае, просто переведите число в кубические метры.
Если вы уверены в том, из какого именно материала сделана сфера, постарайтесь определить ее плотность — эта информация наверняка найдется на просторах всемирной сети. В этой ситуации от вас потребуется лишь взвесить данную фигуру, после чего воспользоваться простой формулой объема шара, разделив вес предмета на его плотность: V=m/p .
Может случиться, что предыдущие варианты вам недоступны. Не отчаивайтесь — если есть возможность узнать радиус шара, к нам на помощь придет нужная формула, более сложная, чем предыдущая, но доступная. Нам необходимо умножить число Пи на 4, после чего перемножить получившееся число на значение радиуса в кубе. В итоге разделите все это на 3, и получите объем шара: V=4*π*r³/3 . Разберем простой пример: радиус сферы — 30 см ., тогда объем фигуры будет составлять: 4*3,14*30³/3 = 11340см³ ≈ 0,113м³.
Бывает и так, что гораздо легче найти диаметр фигуры , нежели его радиус. Этот вариант даже лучше — можно не производить таких сложных вычислений, формула становится значительно проще. Нам нужно будет лишь умножить диаметр в кубе на число Пи, после чего разделить получившееся число на шесть: V=π*d³/6 . К примеру, вы узнали, что диаметр вашей сферы составляет 25 см., тогда ее объем будет равняться: 3,14*25³/6 = 8177,08333см³ ≈ 0,818м³.

Шар и сфера

Объем шара

0,5 Vsh = Vc − Vk

Объем конуса вычисляется по простой формуле:

Vk = 1/3 × So × h,

но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:

Vk = 1/3 × pi × R × R 2 = 1/3 pi × R 3

Объем цилиндра вычисляется по формуле:

Vc = pi × R 2 × h,

но считая, что высота цилиндра равна его радиусу, мы получаем:

Vc = pi × R 3 .

Используя эти формулы, Архимед получил:

0,5 Vsh = pi × R 3 — 1/3 pi × R 3 или Vsh = 4/3 pi × R 3

Vsh = 4/3 pi × R 3

Примеры из жизни

Пушечные ядра

Воздушные шары

Заключение

Варенье из бузины: польза и вред

Узнать встретимся ли мы. Сонник дома солнца. Как правильно сформулировать вопрос в процессе гадания

Сфера – значение, формулы, свойства, примеры

Сфера – это трехмерный объект круглой формы. В отличие от других трехмерных фигур, сфера не имеет ни вершин, ни ребер. Все точки на его поверхности равноудалены от его центра. Другими словами, расстояние от центра сферы до любой точки поверхности равно. Мы видим вокруг себя много объектов реального мира, которые имеют сферическую форму. Наша планета Земля не имеет идеальной формы сферы, но ее называют сфероидом. Причина, по которой его называют сфероидом, заключается в том, что он почти похож на шар.

1.	Что такое сфера?
2.	Формула сферы
3.	Свойства сферы
4.	Окружность сферы
5.	Разница между кругом и сферой
6.	FAQ по Sphere

Что такое сфера?

В геометрии сфера представляет собой трехмерную твердую фигуру круглой формы. С математической точки зрения это комбинация набора точек, соединенных одной общей точкой на равных расстояниях в трех измерениях. Некоторые примеры сферы включают баскетбольный мяч, мыльный пузырь, теннисный мяч и т. д. Важными элементами сферы являются следующие:

Радиус : длина отрезка, проведенного между центром сферы и любую точку на его поверхности. Если «O» — это центр сферы, а A — любая точка на ее поверхности, то расстояние OA — это ее радиус (посмотрите на изображение ниже для справки).
Диаметр : Длина отрезка от одной точки на поверхности сферы до другой точки, прямо противоположной ей, проходящей через центр, называется диаметром сферы. Длина диаметра ровно в два раза больше длины радиуса.
Окружность : Длина большого круга сферы называется ее окружностью. На приведенном ниже рисунке граница пунктирного круга или поперечное сечение сферы, содержащей ее центр, называется ее окружностью.
Volume : Как и любой другой трехмерный объект, сфера также занимает некоторое пространство. Это количество пространства, которое он занимает, называется его объемом. Выражается в кубических единицах.
Площадь поверхности : Площадь, занимаемая поверхностью сферы, является площадью ее поверхности. Измеряется в квадратных единицах.

Формулы сфер

Как мы обсуждали в предыдущем разделе, сфера имеет радиус, диаметр, длину окружности, площадь поверхности и объем. Учитывая, что сфера имеет радиус «r», в следующей таблице перечислены важные формулы сферы.

Имя	Формула
Диаметр	2 × радиус сферы
Окружность	2πr, где π — константа, принимающая значение 22/7 или 3,14 (приблизительно)
Площадь поверхности	4πr ²
Том	(4/3)πr ³

Площадь поверхности сферы

Площадь, покрытая внешней поверхностью сферы, называется площадью поверхности сферы. Измеряется в квадратных единицах. Следовательно, формула для нахождения площади поверхности сферы:

Площадь поверхности сферы, S = 4πr ²

С точки зрения диаметра, площадь поверхности сферы определяется как S = 4π(d/2 ) ² , где d — диаметр. Ознакомьтесь с площадью поверхности сферы для получения более подробной информации.

Объем сферы

Объем сферы — это мера пространства, которое она может занять. Измеряется в кубических единицах. Формула объема сферы приведена ниже:

Объем сферы, V = (4/3)πr ³

где

V — это объем
r — это радиус, а
π (пи) составляет прибл. 3.14 или 22/7.

Подробнее читайте в статье об объеме сферы.

Свойства сферы

Сфера — это трехмерный объект, все точки внешней поверхности которого равноудалены от центра. Следующие свойства сферы помогут вам легко идентифицировать сферу. Они следующие:

Симметричен во всех направлениях.
Имеет только изогнутую поверхность.
У него нет ни ребер, ни вершин.
Любая точка на поверхности находится на постоянном расстоянии от центра, известном как радиус.
Сфера не является многогранником, потому что у нее нет вершин, ребер и плоских граней. Многогранник — это объект, у которого обязательно должна быть плоская грань.
Пузырьки воздуха принимают форму сферы, потому что площадь поверхности сферы наименьшая.
Среди всех фигур с одинаковой площадью поверхности сфера будет иметь наибольший объем. Формула объема сферы: 4/3 × πr ³ кубических единиц.

Окружность сферы

Окружность сферы определяется как длина большого круга сферы. Это общая граница большого круга. Большой круг — это тот, который содержит центр и диаметр сферы. Это максимально возможный круг, который можно нарисовать внутри сферы. Его также можно определить как поперечное сечение сферы, когда она разрезана по диаметру. Окружность сферы можно рассчитать, если ее радиус известен по формуле 2πr единиц , что совпадает с формулой длины окружности.

Разница между кругом и сферой

Круг и сфера — две разные формы. Важные различия между кругом и сферой следующие:

Круг	Сфера
Круг — это двумерная фигура.	Сфера — это трехмерная форма.
Окружность простирается в двух направлениях: по оси X и по оси Y.	Он простирается в трех направлениях: по оси x, по оси y и по оси z.
Не имеет объема.	Имеет объем, так как занимает некоторое пространство.
Имеет одну плоскую поверхность.	Имеет одну изогнутую поверхность.
Площадь круга πr ² квадратных единиц.	Площадь поверхности сферы составляет 4πr ² квадратных единиц.

Важные примечания:

Площадь поверхности сферы 4πr ² .
Объем сферы равен 4/3πr ³ .
В геометрии половина сферы известна как «полусфера».
Общая площадь поверхности и объем по формуле полушария составляют ровно половину формулы площади и объема сферы.

► Похожие темы

Ознакомьтесь с интересными статьями, посвященными форме сферы. Нажмите, чтобы узнать больше!

Прямоугольный
Цилиндр
Конус
Призмы

Примеры сфер

Пример 1: Найдите диаметр и длину окружности сферы с радиусом 7 единиц.
Решение:
Дано, радиус = 7 единиц.
Диаметр = 2 × радиус.
Следовательно, диаметр = 2 × 7
= 14 ед.
Окружность сферы = 2πr
= 2 × (22/7) × 7
= 44 единицы
Следовательно, диаметр и длина окружности сферы радиусом 7 единиц составляют 14 единиц и 44 единицы соответственно.
Пример 2: Найдите объем сферы, радиус которой равен 8 единицам.
Решение:
Формула объема сферы: (4/3) πr ³ кубических единиц. Примите значение π как 22/7. Дано, радиус = 8 единиц. Подставляя значение радиуса в формулу, получаем,
Объем = (4/3) π × 8 ³
= (4/3) × (22/7) × 8 × 8 × 8
= 2145,52 куб.ед.
Следовательно, объем сферы = 2145,52 кубических единиц.
Пример 3: Найдите площадь поверхности сферы, радиус которой равен 5 единицам. Примите значение π как 22/7.
Решение:
Как мы знаем, площадь поверхности сферы = 4πr ² квадратных единиц. Подставляя значение радиуса в формулу, получаем,
Площадь поверхности = 4 × (22/7) × 5 ²
= 4 × (22/7) × 25
= 314,28 квадратных единиц
Следовательно, требуемая площадь поверхности составляет 314,28 квадратных единиц.

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по форме сферы

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о Сфере

Что такое форма сферы?

Сфера — это трехмерная фигура без вершин и краев. Все точки на его поверхности равноудалены от его центра. Некоторые реальные примеры сферы включают футбольный мяч, баскетбольный мяч, модель земного шара и т. д. Поскольку сфера является трехмерным объектом, она имеет площадь поверхности и объем.

Каков диаметр сферы?

Длина отрезка, соединяющего две противоположные точки на поверхности сферы, проходящей через ее центр, называется диаметром сферы. Его можно рассчитать, умножив радиус на 2.

Как найти площадь поверхности сферы?

Площадь поверхности сферы – это площадь, занимаемая ее внешней поверхностью или границей. Проще говоря, количество материала, используемого для покрытия внешней части сферы, дает площадь ее поверхности. Формула для нахождения площади поверхности сферы: 4πr ² кв.ед.

Как найти объем шара?

Объем сферы — это объем пространства, занимаемый сферой. Например, представьте себе сферический воздушный шар. Количество воздуха внутри шара и есть его объем. Формула объема сферы: (4/3) π r ³ кубических единиц.

Есть ли у сферы лицо?

Лицом называется плоская или изогнутая поверхность трехмерного объекта. Например, у куба 6 граней. Таким образом, сфера имеет только одну грань, которая является криволинейной поверхностью. У него нет плоских граней.

В чем разница между кругом и сферой?

Круг и сфера — разные объекты. Поскольку они оба имеют круглую форму, это создает путаницу, как будто эти две формы похожи. Различия, которые подчеркивают, что оба являются разными объектами, следующие:

Круг — это двумерная фигура, тогда как сфера — это трехмерный объект.
Окружность вытянута по оси x и оси y, тогда как сфера вытянута в трех направлениях (ось x, ось y и ось z).
Круг имеет только площадь, а сфера имеет площадь поверхности и объем.

Трехмерна ли сфера?

Да, сфера — это трехмерный объект, занимающий три оси: ось X, ось Y и ось Z. У него есть площадь поверхности и объем, как и у любого другого трехмерного объекта.

В чем разница между сферой и сфероидом?

Сфера — это трехмерный объект идеальной сферической формы. Радиус сферы одинаков во всех точках сферы от ее центра, тогда как сфероид похож на сферу, но радиус не одинаков во всех точках от центра сфероида. Планета Земля считается сфероидом по своей природе.

Как найти длину окружности сферы?

Окружность сферы – это длина границы большого круга сферы. Это поперечное сечение, которое содержит центр сферы. Его можно рассчитать по формуле 2πr единиц.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по форме сферы [PDF]

Калькулятор объема сферы

Создано Ханной Памула, кандидатом наук

Рецензировано Богной Шик и Аденой Бенн

Последнее обновление: 10 сентября 2022 г.

Содержание:

Формула объема сферы
Как найти объем сферы?
Расчет объема сферической крышки
Расчет объема полушария
Хотите узнать больше?
Часто задаваемые вопросы

Если вы когда-нибудь задавались вопросом, каков объем Земли, футбольного мяча или гелиевого шара, наш калькулятор объема сферы здесь для вас. Это может помочь рассчитать объем сферы, учитывая радиус или длину окружности. Также благодаря этому калькулятору можно определить объем сферической шапки или объем полушария.

Формула объема сферы

Сфера — это идеально круглый геометрический трехмерный объект. Формула для его объема равна:

объем = (4/3) × π × r³

Обычно вы не знаете радиус, но вместо этого вы можете измерить длину окружности сферы, например, с помощью веревки. или веревка. Окружность сферы — это одномерное расстояние вокруг сферы в ее самом широком месте.

длина окружности = 2 × π × r , поэтому r = длина окружности / (2 × π)

Как найти объем шара?

Знаете ли вы, каков объем официального футбольного мяча чемпионата мира по футболу под названием размера 5 ? Или баскетбольный мяч размер 7 ? Давай проверим!

Введите радиус сферы . Для размера 5 радиус футбольного мяча должен быть равен 4,3-4,5 дюйма. Возьмем 4,4 на .
Объем сферы появился как окружность. Он равен 357 у.е. в и 27,6 в .
Предположим, что нам неизвестен радиус баскетбольного мяча. Введите окружность вместо . Для баскетбольного мяча размера 7 типичным является 29,5 в .
Отображается объем сферы и радиус, 433,5 у.е. в и 4,7 в соответственно.

А теперь попробуй посчитать что-нибудь другое, возьми что-нибудь побольше… Может, хочешь узнать объем Земли? Средний радиус составляет примерно 6,37 × 10 ⁶ м. Тогда объем равен:

объем = (4/3) × π × (6370000 м)³ = 1 082 696 932 430 002 306 149 м³

Расчет объема сферической крышки

сфера, отрезанная плоскостью. Формула его объема:

объем = ((π × h²) / 3) × (3r - h) или
объем = (1/6) × π × h × (3a² + h²) , где радиус сферы r , высота шапочки (синяя) h , а a — это радиус основания колпачка.

Мы также можем использовать эти формулы, чтобы найти объем противоположного купола (оранжевого), как показано на рисунке. Однако обязательно используйте правильное измерение для h , которое всегда должно быть высотой сферического колпака или купола , которые мы хотим найти.

Одним из примеров сферического купола является аквариум. Подсчитаем, сколько воды нам нужно, чтобы его наполнить:

Найдите высоту кепки . Например, 7 в .
Определить радиус основания колпачка . Это также то же самое, что и радиус открытия аквариума. Допустим, он равен 3.1305 в .
Введите эти значения в наш калькулятор . После этого наш калькулятор покажет, что объем сферической крышки равен 287,35 у.е. в , а соответствующий радиус сферы равен 4.2 в .
Чтобы рассчитать объем полной сферы, используйте базовый калькулятор. Введите радиус 4.2 в .
Теперь вы знаете, что в нашем примере аквариум имеет объем 287,35 у.е. в , по сравнению с 310,3 у.е. в для объема полной сферы с тем же радиусом.

Расчет объема полушария

Как его рассчитать? Просто используйте формулу объема сферической шапки с параметрами, равными друг другу: радиус сферы = высота шапки = радиус основания кепки . Кроме того, вы можете разделить результат полной сферы на 2.

Хотите больше?

Калькулятор объема сферы — это только один из наших потрясающих инструментов для измерения объема. Ознакомьтесь с другими:

Калькулятор объема цилиндра;
Калькулятор объема конуса;
Калькулятор объема – для всех основных твердых тел; и
Конвертер объема – преобразование единиц измерения объема.

Часто задаваемые вопросы

Как рассчитать объем сферы с диаметром?

объем = (1/6) × π × d³

Чтобы получить это из стандартной формулы объема сферы объем = (4/3) × π × r³ , замените r на d/2 . Таким образом, мы используем тот факт, что радиус равен половине диаметра.

Каков объем сферы радиусом 2?

объем = (4/3) × π × 8 ≈ 33,5

0455 и вставляем r = 2 .

Каков объем сферы с окружностью 10?

Чтобы получить объем сферы из ее окружности c = 10 :

Вычислите радиус из окружности: r = c / (2 × π) ≈ 1,59 .
Примените формулу объем = (4/3) × π × r³ с r = 2 .
Получаем объем = (4/3) × π × 1,59³ ≈ 16,89 .

Как найти радиус сферы по объему?

Нам нужно решить формулу объем = (4/3) × π × радиус³ для радиуса:

Разделить обе части на (4/3) × π . Получаем 3/(4π) × объем = радиус³ .
Возьмем кубический корень ∛ с обеих сторон: ∛(3/(4π) × объем) = радиус .
Вот оно! Теперь вам просто нужно подставить значение объема для вычисления радиуса.

Ханна Памула, кандидат наук

Сфера

Радиус (r)

Окружность

Том

Сферическая крышка / полушария

Высота крышки (H)

Радиус сферы (R)

Радиус базы крышки (A)

Объем

Проверьте 20 аналогичные 3D Geometry Calculators 📦

. полусферыCubeCube Рассчитать: найти v, a, d… Еще 17

Формулы сферы — GeeksforGeeks

Сфера представляет собой круглый трехмерный объект. В отличие от других трехмерных фигур, сфера не имеет вершин и краев. Расстояние от центра сферы до любой точки поверхности одинаково. В геометрии сфера – это объемная фигура круглой формы. С математической точки зрения это комбинация множества точек, соединенных общими точками, равноудаленными в трех измерениях. Примеры сфер включают баскетбол, мыльные пузыри и теннисные мячи.

Формулы сферы

Существуют три основные формулы для сферы, включая формулы для диаметра сферы, площади поверхности сферы и объема сферы. Все эти формулы перечислены в таблице ниже.
Диаметр сферы D = 2R
Площадь поверхности сферы A = 4πr ²
Объем сферы (4/3).0113

Какова площадь поверхности сферы?

Площадь, покрытая внешней поверхностью сферы, называется площадью поверхности сферы. Сфера представляет собой трехмерную форму круга. Основное различие между сферой и кругом заключается в том, что круг имеет двумерную (2D) форму, тогда как сфера имеет трехмерную форму.

Вывод площади поверхности сферы

Поскольку сфера круглая, мы связываем ее с изогнутой формой, такой как цилиндр, чтобы найти площадь поверхности. Цилиндр имеет криволинейную поверхность, а также плоскую поверхность. Теперь, если радиус цилиндра равен радиусу сферы, это означает, что сфера может идеально вписаться в цилиндр. Это приводит нас к выводу, что высота цилиндра равна высоте сферы. Так что эту высоту можно назвать диаметром сферы.

Мы знаем, что если радиус цилиндра и сферы одинаково, то площадь поверхности сферы

, а высоту цилиндра также можно назвать диаметром сферы, потому что мы предполагаем, что эта сфера безупречно помещается в цилиндре.
Следовательно, высота цилиндра = диаметру сферы = 2r.
SO, Площадь поверхности сферы составляет 2πrh = 2πr (2r) = 4πr ² (Потому что H = 2r)
Также негрированная площадь сфера равна 4πr ². , так как в сфере нет плоской поверхности.
Пример : Если радиус сферы равен 14 см, найдите площадь ее поверхности. (вы можете использовать π = 3,14 для вашего удобства).
Решение:
Известно, что радиус сферы равен 14см.
Площадь поверхности сферы = 4πr ² = 4 * π *(14) ² = 24 см ²
Каков объем сферы?
Объем сферы – это пространство, занимаемое внутренней частью сферы. Нарисуйте полукруг на листе бумаги и поверните его на 360 градусов, чтобы получилась сфера. Есть два типа сфер: твердые сферы и полые сферы. Объемы двух типов сфер различны. В следующем разделе мы узнаем о томах.
Вычисление объема сферы
Как уже доказал Архимед, если цилиндр, конус или сфера имеют радиус «r» и одинаковую площадь поперечного сечения, то их объемы связаны как 1:2:3.
Следовательно, мы можем сказать, что
Объем цилиндра = объем конуса + объем сферы
Объем сферы = объем цилиндра – объем конуса
Теперь из предыдущего знания мы должны знать, что объем цилиндра = πr ² ч и объем конуса = (1/3)πr ² ч
подставив значения в вышеприведенное выражение, получим
Объем шара = πr ² ч – (1/3)πr ² h = (2/3)πr ² h
мы предполагаем, что высота цилиндра = диаметру сферы = 2r
Следовательно, объем сферы равен (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³
Кроме того, если у нас есть полая сфера, то
Пусть R = радиус внешней сферы, r = радиус внутренней сферы, тогда
объем полой сферы = объем внешней сферы – объем внутренней сферы
⇒ объем полой сферы = (4/3 )πR ³ – (4/3)πr ³ = (4/3)π(R ³ – r ³ )
радиус 6 см.
Решение :
Дано, что радиус сферы равен 6см.
Объем шара = (4/3)πr ³ = ((4/3) × π × (6 см) ³ ) = 904,779 см ³
Пример 2. Найдите объем шара, внутренний радиус которого равен 5 см, а внешний радиус равен 8 см.
Решение :
Внешний радиус сферы R = 8 см.
и Внутренний радиус сферы r = 5 см.
Теперь объем полой сферы = (4/3)π(R ³ – r ³ ) = (4/3)π((8 см) ³ – (5 см) ³ ) = 1621,062 см ³ .
Полушарие
Полушарие является половиной сферы. Другими словами, если сфера разрезается на две симметричные части через центр, то она называется полусферой. Поскольку это половина сферы, то объем и площадь поверхности равны половине объема и площади поверхности сферы.
Объем полусферы = (1/2)(4/3)πr ³
Площадь поверхности сферы = (1/2)(4πr ² )
Полушарие
Свойства сферы
Ниже приведены свойства сферы:
У нее нет ни вершины, ни края.
Это не многогранник.
Все точки сферы находятся на одинаковом расстоянии от центра.
У него изогнутая грань, а не плоская.
Он идеально симметричен.
Сравнение круга и сферы
Круг Сфера
Круг существует в двумерной форме. Сфера представляет собой трехмерную форму.
Окружность может проходить только в двух направлениях: по оси X и по оси Y. Он простирается во всех трех направлениях: по оси X, оси Y и оси Z.
У него нет тома. Имеет объем, поскольку занимает некоторое пространство.
Площадь круга πr ² квадратных единиц. Площадь поверхности сферы составляет 4πr ² квадратных единиц.
Примеры вопросов
Вопрос 1. Диаметр бейсбольного мяча составляет 80 мм. Найдите объем бейсбольного мяча. (π = 3,14)
Решение:
нам дано, что диаметр d = 2R
D = 80 мм.
r = 40 мм
Теперь объем сферы = (4/3) πr ³ = (4/3) π (40 мм) ³ = 268082.573 мм ³
Вопрос 2: Хоулоли расплавиться в такую же маленькую полую сферу. Внутренний и внешний радиусы большей сферы равны 5 см и 7 см соответственно. Если внутренний и внешний радиусы маленьких сфер равны 3 см и 4 см соответственно, сколько маленьких сфер можно составить? (π=3,14)
Решение:
Мы знаем, что объем сферы = (4/3)πr ³
Теперь объем большей сферы = объем сферы с внешним радиусом – объем сферы с внутренний радиус
⇒ Объем большей сферы = (4/3) * π * (7см) ³ – (4/3)π(5см) ³
⇒ Объем большей сферы = (4/ 3) * π * (343-125) = (4/3) * π * (218) см ³
Таким же образом объем меньшего шара = (4/3) * π * (4см) ³ – (4/3) * π * (3см) ³
⇒ Объем меньшей сферы = (4/3) * π *(64-27) = (4/3) * π * ( 37) см ³
следовательно, количество сфер, которые можно сформировать = объем большей сферы/объем меньшей сферы
следовательно, количество сфер, которые можно сформировать = (4/3) * π * (218) см ³ / (4/3) * π * (37) см ³
⇒ количество сфер, которые можно сформировать = 5,92 ≈ 6 сфер.
Вопрос 3: Когда вы меняете форму объекта со сферы на цилиндр, объем цилиндра увеличивается, уменьшается или остается неизменным. (π=3,14)
Решение:
Объем — это скалярная величина, описывающая объем трехмерного пространства, окруженного близлежащими поверхностями.
При трансформации тела в другое тело количество материала остается прежним, поэтому объем тела не меняется.
Следовательно, том остается без изменений .
Вопрос 4: Поверхность сферы 500 см ² . Если вы измените радиус, чтобы уменьшить площадь на 50%, то найдите радиус. (π=3,14)
Решение:
Поскольку площадь уменьшилась на 50 %, мы можем сказать, что
Новая площадь поверхности = 50 % исходной площади
⇒ 4/r 3 2 ⇒ 2 * 500
⇒ r ² = (1/2 * 500) / 4π
⇒ R ² = 250/12,56
⇒ R ² = 19,8945
⇒ R = 4,46 см

A Formula для сравнения выбранного Sport Compressibobite
9001
A Formula.
1991 март; 25(1):34-7.
дои: 10.1136/bjsm.25.1.34.
Л.Дж. Доуэлл ¹ , Г. Кребс
принадлежность
¹ Департамент здравоохранения и физического воспитания Техасского университета A&M, College Station 77843-4243.
PMID: 19
PMCID: PMC1478814
DOI: 10.1136/бжсм.25.1.34
Бесплатная статья ЧВК
Сравнительное исследование
L J Dowell et al. Бр Дж Спорт Мед. 1991 март
Бесплатная статья ЧВК
. 1991 март; 25(1):34-7.
дои: 10.1136/bjsm.25.1.34.
Авторы
Л.Дж. Доуэлл ¹ , Г. Кребс
принадлежность
¹ Департамент здравоохранения и физического воспитания Техасского университета A&M, College Station 77843-4243.
PMID: 19
PMCID: PMC1478814
DOI: 10. 1136/бжсм.25.1.34
Абстрактный
Целью данного исследования было разработать формулу для определения и сравнения сжимаемости выбранных спортивных мячей. Шесть мячей (баскетбольный, волейбольный, футбольный, бейсбольный, гандбольный, мяч для гольфа) бросали по десять раз с каждой из четырех разных высот на гладкую твердую поверхность, покрытую белым листом печатной бумаги, покрытым листом копировальной бумаги. Диаметр области контакта каждого шарика, отпечатанного на бумаге для печати, измеряли штангенциркулем в миллиметрах. Из данных было рассчитано расстояние (d), на которое сжимался каждый шар для каждой скорости (v). Было обнаружено, что существует линейная зависимость между скоростью при ударе и расстоянием для каждого исследуемого шара. Был рассчитан коэффициент сжимаемости (с) для каждого шара и разработана формула для определения расстояния, на которое каждый шар будет сжиматься при заданной скорости. Когда скорость измеряется в метрах в секунду, а расстояние, на которое сжимается мяч, измеряется в миллиметрах, формула для определения d для выбранных мячей в порядке сжимаемости: баскетбольный мяч d = 3,07v, волейбольный мяч d = 2,90v, футбольный мяч d = 2,80v, бейсбольный мяч d = 0,77v, гандбольный мяч d = 0,53v и мяч для гольфа d = 0,17v.
Похожие статьи
«Травмы волейбольной спортивной школы».
Кноблох К., Росснер Д., Гесслинг Т., Рихтер М., Креттек С. Кноблох К. и соавт. Спортверлетц Спортшаден. 2004 г.; 18 (4): 185-9. doi: 10.1055/s-2004-813481. Спортверлетц Спортшаден. 2004. PMID: 15592981 Немецкий.
Игровые характеристики сотрясений мозга, связанных со спортом.
Гельмич И. Гельмич И. J Sports Med Phys Fitness. 2018 янв-февраль;58(1-2):172-179. doi: 10.23736/S0022-4707.16.06677-9. Epub 2016 14 сентября. J Sports Med Phys Fitness. 2018. PMID: 27636403
Контактные травмы с мячом в 11 видах спорта Национальной студенческой спортивной ассоциации: программа наблюдения за травмами, 2009 г.-2010 г. По 2014-2015 гг.
Фрейзер М.А., Грумс Д.Р., Гускевич К.М., Керр З.Ю. Фрейзер М.А. и соавт. Джей Атл Трейн. 2017 июль; 52 (7): 698-707. дои: 10.4085/1062-6050-52.3.10. Эпаб 2017 23 мая. Джей Атл Трейн. 2017. PMID: 28535098 Бесплатная статья ЧВК.
Исследование эффекта наклбола в футболе с использованием умного мяча и тренажера.
Игер Д., Исхак К., Чжоу С., Хоссейн И. Игер Д. и соавт. Датчики (Базель). 2022 24 мая; 22(11):3984. doi: 10.3390/s22113984. Датчики (Базель). 2022. PMID: 35684605 Бесплатная статья ЧВК. Обзор.
Травмы головы и головы в футболе.
Kirkendall DT, Jordan SE, Garrett WE. Киркендалл Д.Т. и соавт. Спорт Мед. 2001;31(5):369-86. doi: 10.2165/00007256-200131050-00006. Спорт Мед. 2001. PMID: 11347686 Обзор.
Посмотреть все похожие статьи
Цитируется
Обзор Британского журнала спортивной медицины за 1991–1995 гг.
Томпсон Б. Томпсон Б. Бр Дж Спорт Мед. 1996 декабрь; 30 (4): 354-5. дои: 10.1136/bjsm.30.4.354. Бр Дж Спорт Мед. 1996. PMID:
02 Бесплатная статья ЧВК.
использованная литература
Может ли J Appl Sport Sci. 1984 июнь; 9 (2): 94-101 — пабмед
ДЖАМА. 1983 20 мая; 249(19):2682-5 — пабмед
S Afr Med J. 1983 19 марта; 63 (12): 434 — пабмед
Am J Офтальмол. 1982 г., февраль; 93 (2): 145–56. — пабмед
Бр Дж Спорт Мед. 1985 март; 19 (1): 43-4 — пабмед
Типы публикаций
термины MeSH
Формула сферы – Вывод, Доказательство, Объяснение площади
Содержание
Формулы сферы
В геометрии сфера описывается как геометрический круглый объект в трехмерной плоскости, имеющий абсолютно симметричную форму. В детстве все мы привыкли играть мячами для крикета. Итак, хорошим примером сферы является мяч для крикета. В геометрии сфера — это круглая форма в трехмерной плоскости. В этой статье мы узнаем о формулах сферы для определения ее объема и общей площади поверхности.
Формула сферы: Что такое сфера?
Сфера описывается как геометрический круглый объект в трехмерной плоскости, имеющий абсолютно симметричную форму. Все точки на поверхности находятся на одинаковом расстоянии от центра (радиус)
Пример — футбольный мяч, теннисный мяч, глобус и т. д.
Формула сферы: свойства общей площади поверхности (TSA)
Центр сферы — В сфере все точки на поверхности находятся на одинаковом расстоянии от фиксированной точки, эта точка считается центром сферы.
Радиус сферы- Прямая линия, соединяющая центр сферы и любую точку на поверхности. называется радиусом. Обычно Радиус обозначается буквой r.
Диаметр сферы- Диаметр — это самая длинная прямая линия, проходящая через центр сферы и пересекающая любые две точки на поверхности сферы. Таким образом. Эти две точки и центр сферы лежат в диаметре, обозначаемом D.
В сфере Диаметр всегда удваивается по радиусу по длине.
Свойства сферы
Формула сферы Площадь, Диаметр, Объем
Диаметр сферы Д = 2 р
Площадь сферы А =4 π r²
Объем Сферы В = 4/3 π r³
Формула сферы Диаметр
Диаметр – это самая длинная прямая, проходящая через центр сферы и пересекающаяся с любыми двумя точками на поверхности сферы. Диаметр сферы всегда удваивается из-за радиуса длины этой конкретной сферы.
D = 2 r
Формула сферы Площадь
Общая площадь поверхности сферы считается ее полной криволинейной поверхностью. Сфера не имеет ни ребер, ни боковых поверхностей. Итак, мы считаем, что общая площадь поверхности сферы равна общей площади криволинейной поверхности.
Формула для определения общей площади поверхности сферы:
Общая площадь поверхности = 4 π r² квадратных единиц.
{ Выше π является постоянной величиной, равной 3,14 или 22/7 }
Общая площадь поверхности шара
Формула шара Объем
Объем шара определяется как вмещающая способность шара в нем. Формула для определения объема сферы: –
Предположим, что V – это объем сферы,
Тогда Объем = 4/3 π r³ кубических единиц, , где π – постоянная, равная 3,14 или 22/7. , r — радиус сферы.
Объем сферы
Формула сферы: Разница между кругом и сферой Объяснение
Хотя форма обеих фигур круглая, основное различие между Кругом и сферой заключается в том, что Круг — это двухмерная фигура, а сфера — это трехмерный объект. Сфера имеет площадь и объем. Но у круга есть только площадь и длина окружности.
Разница между кругом и сферой
Формула сферы Доказательство на примере
В. Диаметр сферы 12 см . Найдите радиус и площадь полной поверхности шара.
а) 6 см и 270 π см² b) 6 см и 144 π см² c) 12 см и 144 π см² d) Ни одно из этих значений.
Ответ- Предположим, что радиус сферы равен r
Диаметр данной сферы равен -D= 12 см.
Все мы знаем, что диаметр в два раза больше радиуса длины.
Итак, D= 2r
или 12 = 2r
или r = 6 см
Формула общей площади поверхности сферы: –
4 π r² квадратных единиц.
Общая площадь поверхности = 4 π (6)²
= 4× π × 36
= 144 π или 452,16 см²
Q. Найдите объем сферы, радиус которой равен 3 см.
а) 27π см³ б) 36π см³ в) 36 см³ г) Ни один из этих
Ответ-
Формула для определения объема шара:
V = 4/3 π r³ кубических единиц.
Объем- V= 4/3 π ( 3) ³ см³
V= 36 π см³
Итак, вариант (б) правильный.
Q. Если площадь поверхности шара 616 см². Найдите радиус сферы.
(a) 4 см (b) 7 см (c) 49 см (d) Ничего из перечисленного.
Ответ- мы знаем, что формула площади поверхности сферы – 4πr²
Здесь площадь поверхности сферы равна 616 см².
4πr² = 616
r² = 616 /(4 × 22/7) [ π =22/7]
r² = 616 × 7 / 22×4
r² = 49
или, r = 7 см
Радиус сферы составляет 7 см.
Значит, вариант (б) правильный.
Q. Если радиус сферы увеличить в 2 раза. Каков его объем? (Радиус = r)
(a) 4/3 πr³ (b) 43/3πr³ (c) 32/3 r³ (d) Ничего из перечисленного.
Ответ – Предыдущий радиус сферы r
После увеличения в 2 раза радиус равен 2r
Объем сферы равен – 4/3 π(r)³
= 4/3 π(2r) ³ = 4/3 π(8r³) = 32/3 r³ кубических единиц.
Следовательно, вариант (с) правильный.
Сфера на основе формул Практические вопросы
Если радиус сферы увеличить в 2 раза. Какова его общая поверхность? (Радиус = r)
Диаметр шара 6 см. Найдите радиус и площадь полной поверхности шара.
Найдите объем шара радиусом 5 см.
Если площадь поверхности шара 343 см³ . Рассчитайте диаметр сферы.
Связанный пост:
Заявление о приеме на работу – образец письма, формат, пример для класса 12
Типы углов в математике с определением, градусами и примерами
Название 118 элементов, их символы и атомные номера
Формат написания уведомления для класса 12, темы 10 с примерами
Тригонометрическая таблица: формула, значение, диаграмма, отношение, PDF для класса 10
Формула площади равностороннего треугольника с высотой
Формат письма редактору, примеры вопросов, пример класса 10, 12
Что такое удобрения? — определение, значение, типы, примеры
Полная форма доктора медицины в школе, медицине, образовании в Индии
Коллоидный раствор — определение, свойства, примеры, размер частиц для класса 12
Формула сферы: часто задаваемые вопросы
Q. Является ли сфера трехмерной?
Ответ- Да. Сфера представляет собой трехмерную круглую фигуру.
Q. Что такое сфера?
Ответ- Сфера описывается как геометрическая круглая фигура в трехмерной плоскости, имеющая абсолютно симметричную форму.
Пример-футбол, мяч для крикета, глобус и т. д.
Q. Как рассчитать объем шара?
Ответ- Формула для вычисления объема сферы:
V = 4/3 π r³ кубических единиц, где π — константа, равная 3,14 или 22/7,r — радиус сферы
Q. Как найти площадь поверхности сферы?
Ответ- Общая площадь поверхности сферы считается ее полной криволинейной поверхностью.
Формула для определения общей площади поверхности сферы: – = 4 π r² квадратных единиц.
Q. В чем разница между Кругом и сферой?
Ответ- Хотя форма обеих фигур похожа, основное различие между Кругом и сферой заключается в том, что Круг двумерный, а сфера — трехмерная фигура.
Делиться заботой!
15
акции
Ньютоновская механика. Модель/формула для прыгающего мяча
Задавать вопрос
Спросил 6 лет, 4 месяца назад
Изменено 6 месяцев назад
Просмотрено 44k раз
$\begingroup$
Я программирую анимацию прыгающего мяча и хочу, чтобы она была максимально реалистичной.
Я полностью понимаю физику, когда мяч поднимается и падает: он ускоряется вниз со скоростью 9,8 метра в секунду в секунду.
Но как только он упадет на землю, я пропал. Я знаю, что он испытывает некоторое сжатие, которое снова переводит его скорость вверх, и в этот момент гравитация снова становится единственной силой, действующей на него. Но я не знаю, как смоделировать сжатие и отклонение мяча, падающего на землю.
(Кроме того, я имею дело только со строго вертикальной линейной скоростью и ускорением. Мяч не движется горизонтально и вообще не вращается. И я предполагаю, что потери на сопротивление воздуха незначительны.)
Я знаю, что существуют константы для иметь дело с: насколько мяч сопротивляется сжатию и сколько энергии теряется при отскоке, но я не знаю, как они связаны.
Может ли кто-нибудь дать мне объяснение из одного или двух абзацев и/или (а) формулу (е) и/или указать мне ресурс, где я могу прочитать больше? (да, я уже потратил час или около того на гугление)
Я буду рад продолжать читать об этом, пока не пойму, я просто не знаю, куда обратиться в этот момент.
Заранее спасибо!
ньютоновская механика
силы
энергия
моделирование
$\endgroup$
4
$\begingroup$
Вы говорите, что игнорируете трение воздуха, но предполагаете частично неупругое столкновение. Это означает, что мы можем разбить задачу на две части: 92$$, где $v_0$ — скорость сразу после отскока. Эта скорость будет меняться от одного отскока к другому.
Во время удара мяч деформируется и возникает трение. Точную форму мяча во время удара трудно описать простым уравнением, поскольку она зависит от состава мяча и пола. В качестве упрощения предположим, что мяч представляет собой «массу на пружине с небольшими потерями с жесткостью пружины $ k $»; тогда мяч будет совершать (приблизительно) затухающие простые гармонические движения во время удара: это означает, что время удара будет 92$ для удобства) он приземлится через 1 секунду со скоростью 10 м/с, а после отскока (какое-то короткое время $\Delta t$) снова всплывет с меньшей скоростью $v_1 = 7,5 м/с $. Время, проведенное в воздухе до следующего отскока, определяется как $$t_1 = 2\frac{v_1}{g} = 2\rho \frac{v_0}{g}$$
Пока мяч находится в контакте с земли, мы можем считать, что его центр движется примерно по синусоиде — как я уже сказал, важно то, что время контакта не зависит от высоты падения (в предположении линейной жесткости пружины). В действительности, чем больше деформируется мяч, тем больше будет увеличиваться жесткость пружины, что на самом деле сократит время контакта, поскольку скорость удара выше. Но для вашей симуляции это вряд ли имеет значение.
Чтобы перейти от вышесказанного к «математической модели», вы можете изменить этот код Python в соответствии с вашими потребностями:
 из math import sqrt
импортировать matplotlib.pyplot как plt
h0 = 5 # м/с
v = 0 # м/с, скорость течения
g = 10 # м/с/с
t = 0 # время начала
dt = 0,001 # временной шаг
rho = 0,75 # коэффициент восстановления
tau = 0,10 # время контакта для отскока
hmax = h0 # отслеживать максимальную высоту
ч = ч0
hstop = 0.01 # остановка при отскоке менее 1 см
свободное падение = истинное # состояние: свободное падение или контакт
t_last = -sqrt(2*h0/g) # время, которое мы должны были запустить, чтобы добраться до h0 в момент t=0
vmax = sqrt(2 * hmax * g)
Н = []
Т = []
в то время как (hmax > hstop):
  если (свободное падение):
    hnew = h + v*dt - 0,5*g*dt*dt
    если (hновый <0):
      t = t_last + 2*sqrt(2*hmax/g)
      свободное падение = ложь
      t_last = t + тау
      ч = 0
    еще:
      т = т + дт
      v = v - g*dt
      ч = чновое
  еще:
    т = т + тау
    vmax = vmax * ро
    v = vмакс. 
    свободное падение = правда
    ч = 0
  hmax = 0,5*vmax*vmax/г
  H. добавить (h)
  Т.добавить(т)
print("остановлено подпрыгивание в t=%.3f\n"%(t))
plt.figure()
plt.plot(T, H)
plt.xlabel('время')
plt.ylabel('высота')
plt.title('прыгающий мяч')
 
Этот код создает следующий график:
$\endgroup$
3
$\begingroup$
Visual Solutions (теперь Altair) производит программное обеспечение VisSim. Вот демонстрационная блок-схема, которую они использовали для имитации прыгающего мяча:
Блоки $1/s$ — это блоки-интеграторы из библиотеки VisSim.
График прыгающего мяча с этими параметрами показан ниже.
Если вы заинтересованы в этом, демо-версия поставляется вместе с установкой, и вы можете загрузить бесплатную 60-дневную пробную версию здесь
$\endgroup$
2
$\begingroup$
Ну, сложность в том, что мяч касается стены.
No related posts.