Решение лоду: Линейные однородные дифференциальные уравнения второго порядка

Содержание

Линейные однородные дифференциальные уравнения второго порядка

Основные понятия о линейных дифференциальных уравнениях второго порядка и их решениях
Линейное однородное дифференциальное уравнения второго порядка и его решение
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: теория и практика

Линейным дифференциальным уравнением второго порядка называется уравнение вида

y» + p(x)y‘ + q(x)y = f(x),

где y — функция, которую требуется найти, а p(x), q(x) и f(x) — непрерывные функции на некотором интервале (a, b).

Если правая часть уравнения равна нулю (f(x) = 0), то уравнение называется линейным однородным уравнением. Таким уравнениям и будет в основном посвящена практическая часть этого урока. Если же правая часть уравнения не равна нулю (

f(x) ≠ 0), то уравнение называется линейным неоднородным уравнением (смотрите отдельный урок).

В задачах от нас требуется разрешить уравнение относительно y»:

y» = −p(x)y‘ − q(x)y + f(x).

Линейные дифференциальные уравнения второго порядка имеют единственное решение задачи Коши.

Рассмотрим линейное однородное дифференциальное уравнение второго порядка:

y» + p(x)y‘ + q(x)y = 0.

Если y1(x) и y2(x) — частные решения этого уравнения, то верны следующие высказывания:

1) y1(x) + y

2(x) — также является решением этого уравнения;

2) Cy1(x), где C — произвольная постоянная (константа), также является решением этого уравнения.

Из этих двух высказываний следует, что функция

C1y1(x) + C2y2(x)

также является решением этого уравнения.

Возникает справедливый вопрос: не является ли это решение общим решением линейного однородного дифференциального уравнения второго порядка, то есть таким решением, в котором при различных значениях C1 и C2 можно получить все возможные решения уравнения?

Ответ на этот вопрос следуюший: может, но при некотором условии. Это условие о том, какими свойствами должны обладать частные решения

y1(x) и y2(x).

И это условие называется условием линейной независимости частных решений.

Теорема. Функция C1y1(x) + C2y2(x) является общим решением линейного однородного дифференциального уравнения второго порядка, если функции y1(x) и y2(x) линейно независимы.

Определение. Функции y1(x) и y2(x) называются линейно независимыми, если их отношение является константой, отличной от нуля:

y1(x)/y2(x) = k; k = const; k ≠ 0.

Однако установить по определению, являются ли эти функции линейно независимыми, часто очень трудоёмко.

Существует способ установления линейной независимости с помощью определителя Вронского W(x):

Если определитель Вронского не равен нулю, то решения — линейно независимые. Если определитель Вронского равен нулю, то решения — линейно зависимымые.

Пример 1. Найти общее решение линейного однородного дифференциального уравнения .

Решение. Интегрируем дважды и, как легко заметить, чтобы разность второй производной функции и самой функции была равна нулю, решения должны быть связаны с экспонентой, производная которой равна ей самой. То есть частными решениями являются и .

Так как определитель Вронского

не равен нулю, то эти решения линейно независимы. Следовательно, общее решение данного уравнения можно записать в виде

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

y» + py‘ + qy = 0,

где p и q — постоянные величины.

На то, что это уравнение второго порядка, указывает наличие второй производной от искомой функции, а на его однородность — нуль в правой части. Постоянными коэффициентами называются уже упомянутые выше величины.

Чтобы решить линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, нужно сначала решить так называемое характеристическое уравнение вида

k² + pq + q = 0,

которое, как видно, является обычным квадратным уравнением.

В зависимости от решения характеристического уравнения возможны три различных варианта решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, которые сейчас разберём. Для полной определённости будем считать, что все частные решения прошли проверку определителем Вронского и он во всех случаях не равен нулю. Сомневающиеся, впрочем, могут проверить это самостоятельно.

Корни характеристического уравнения — действительные и различные

Иными словами, . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

Пример 2. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение имеет вид , его корни и — вещественные и различные. Соответствующие частные решения уравнения: и . Общее решение данного дифференциального уравения имеет вид

Пример 3. Решить линейное однородное дифференциальное уравнение

Корни характеристического уравения — вещественные и равные

То есть, . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

Пример 4. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение имеет равные корни . Соответствующие частные решения уравнения: и . Общее решение данного дифференциального уравения имеет вид

Нет времени вникать в решение? Можно заказать работу!

Пример 5. Решить линейное однородное дифференциальное уравнение

Корни характеристического уравнения — комплексные

То есть, , , . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

Пример 6. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение имеет комплексные корни и . Соответственно и . Общее решение данного дифференциального уравения имеет вид

Пример 7. Решить линейное однородное дифференциальное уравнение

Решить линейное однородное дифференциальное уравнение с постоянными коэффициентами самостоятельно, а затем посмотреть решение

Пример 8. Решить линейное однородное дифференциальное уравнение

Пример 9. Решить линейное однородное дифференциальное уравнение

Посмотреть правильные решения и ответы примеров 8 и 9.

Назад

Листать

Вперёд>>>

К началу страницы

Пройти тест по теме Дифференциальные уравнения

Всё по теме «Дифференциальные уравнения»

Порядок дифференциального уравнения и его решения, задача Коши

Дифференциальные уравнения с разделяющимися переменными

Однородные дифференциальные уравнения первого порядка

Линейные дифференциальные уравнения первого порядка

Дифференциальные уравнения Бернулли

Дифференциальные уравнения в полных дифференциалах

Дифференциальные уравнения второго порядка, допускающие понижение порядка

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Поделиться с друзьями

3.

4. Линейные однородные дифференциальные уравнения

Линейные однородные дифференциальные уравнения (ЛОДУ) имеют самостоятельное значение, а также – вспомогательное значение в качестве первого этапа в процессе решения линейных неоднородных дифференциальных уравнений.

Теорема (о линейных свойствах решений ЛОДУ).

Если функции , заданные на некотором интервале , являются решениями линейного однородного дифференциального уравнения, то их линейная комбинация Также является решением.

Доказательство. Если линейное однородное дифференциальное уравнение записать с помощью линейного дифференциального оператора, то это уравнение будет иметь вид . Так как дифференциальный оператор обладает свойством линейности, то

, что и доказывает теорему.

Определение. Система решений ОЛДУ, заданных на некотором интервале , называется фундаментальной, если эти решения линейно независимы на интервале , а число этих решений равно порядку дифференциального уравнения.

Теорема (критерий фундаментальности решений).

Для того чтобы система решений ОЛДУ порядка с непрерывными на некотором интервале коэффициентами Была фундаментальной, необходимо и достаточно, чтобы Вронскиан системы был отличен от нуля во всех точках интервала .

Доказательство. Докажем достаточность условия теоремы. Если у системы решений ОЛДУ порядка , заданных на некотором интервале , Вронскиан не равен нулю во всех точках интервала , то по признаку независимости функций данная система является фундаментальной, что и доказывает достаточность условия теоремы.

Для доказательства необходимости условия теоремы, предположим обратное. Положим, что существует точка , где Вронскиан равен нулю, а система решений ОЛДУ порядка является линейно независимой.

Выберем числа , не все равные нулю, и такие, что они являются решениями однородной линейной системы уравнений

Это возможно по теореме о существовании нетривиального решения, так как определителем этой системы является Вронскиан , который по предположению равен нулю. Линейная комбинация решений Также является решением. Из вида построенной системы следует, что числа Есть коэффициенты решения задачи Коши с начальными условиями вида .

Но таким же начальным условиям удовлетворяет и нулевое решение . Так как по условию доказываемой теоремы коэффициенты ОЛДУ непрерывны на интервале , то справедлива теорема о существовании и единственности решения на интервале . Отсюда следует, что построенное решение и нулевое решение совпадают, т. е. , причем не все числа Одновременно равны нулю. Это означает, что решения линейно зависимы, хотя предполагалось обратное. Полученное противоречие завершает доказательство необходимости условия теоремы. Таким образом, теорема полностью доказана.

Теорема (о структуре общего решения ЛОДУ).

Если ОЛДУ порядка с непрерывными на некотором интервале коэффициентами имеет фундаментальную систему из решений, то линейная комбинация произвольных постоянных И Решений , является общим решением ОЛДУ.

Доказательство. В теореме о линейных свойствах ОЛДУ утверждается, что линейная комбинация Является решением. Докажем далее, что эта линейная комбинация является общим решением, т. е. в любой точке для допустимых начальных условий существует решение задачи Коши, которое получается из общего решения при некоторых значениях произвольных постоянных. Подставляя начальные условия в общее решение и его производные до — го порядка, получим систему линейных уравнений

Определителем этой системы является Вронскиан , который не равен нулю, поскольку по условию теоремы решения образуют фундаментальную систему. При условии данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных , которое обозначим как . Линейная комбинация вида является решением, получена из общего решения при некоторых значениях Произвольных постоянных и по построению удовлетворяет начальным условиям. Таким образом, теорема полностью доказана.

Если начальные значения Удовлетворяют условиям теоремы Коши, то функция Является единственным решением задачи Коши.

Частным случаем линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами вида ,

Где – некоторые числа.

Так как постоянные функции непрерывны на любом промежутке, то по теореме о структуре общего решения ОЛДУ для того, чтобы найти общее решение данного уравнения достаточно построить фундаментальную систему решений .

Как было предложено Л. Эйлером, будем искать частное решение ОЛДУ с постоянными коэффициентами в виде экспоненциальной функции , где – некоторое число. Дифференцируя эту функцию раз и подставляя полученные функции в решаемое дифференциальное уравнение получим следующие равенства:

Так как экспоненциальная функция строго положительна, то обязательно равен нулю полином -ой степени, т. е. . Полученное алгебраическое уравнением называют Характеристическим уравнением ОЛДУ.

Формально характеристическое уравнение ОЛДУ находят, подставляя в дифференциальное уравнение вместо Соответственно .

Таким образом, если некоторое число является решением данного характеристического уравнения ОЛДУ, то экспоненциальная функция является решением ОЛДУ.

Из основной теоремы алгебры следует, что характеристическое уравнение ОЛДУ имеет корней с учетом их кратности. Рассмотрим следующие варианты.

1. Все корней вещественные и различные.

Если ОЛДУ с постоянными коэффициентами имеет второй порядок, то характеристическое уравнение является квадратным уравнением вида . Каждому корню Соответствуют частные решения ,. Как было показано ранее в примере, эти функции являются линейно независимыми. Для уравнения второго порядка это означает, что система функций , образует фундаментальную систему решений ОЛДУ. Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация Является общим решением ОЛДУ второго порядка с постоянными коэффициентами.

Пример. Решить ОЛДУ второго порядка .

Характеристическое уравнение данного ОЛДУ имеет вид . Оно имеет вещественные различные корни , . Каждому корню Соответствуют частные решения , , которые образуют фундаментальную систему решений.

Отсюда, есть общее решение ОЛДУ.

Доказано, что ОЛДУ с постоянными коэффициентами порядка в том случае, когда все корни характеристического уравнения вещественные и различные, имеет общее решение аналогичного вида .

Пример. Найти общее решение ОЛДУ третьего порядка .

Характеристическое уравнение данного ОЛДУ имеет вид .

Оно имеет вещественные различные корни , , .

Отсюда, есть общее решение данного ОЛДУ третьего порядка с постоянными коэффициентами.

2. Все корней вещественные, но среди них есть кратные.

Рассмотрим вначале и более подробно ОЛДУ с постоянными коэффициентами второго порядка. Его характеристическое уравнение является квадратным уравнением вида , которое может иметь один корень кратности два. Этому корню соответствует частное решение . Второе частное решение ищем в виде .

Подставим функцию в исходное дифференциальное уравнение. Тогда

В правой части последнего равенства первая скобка равна нулю, так как Есть корень характеристического уравнения, а вторая скобка равна нулю, так как в данном случае дискриминант квадратного уравнения равен нулю и, следовательно, .

Таким образом, показано, что предлагаемая функция есть решение.

Ранее в примере было показано, что функции , являются линейно независимыми. Для уравнения второго порядка это означает, что система функций , образует фундаментальную систему решений ОЛДУ.

Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация

Является общим решением ОЛДУ второго порядка с постоянными коэффициентами.

Пример. Решить ОЛДУ второго порядка .

Характеристическое уравнение данного ОЛДУ имеет вид . Оно имеет один вещественный корень кратности два. Для уравнения второго порядка это означает, что система функций , образует фундаментальную систему решений ОЛДУ. Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация Является общим решением ОЛДУ второго порядка с постоянными коэффициентами.

В общем случае дифференциального уравнения порядка каждому простому корню соответствует одно частное решение вида , а каждому корню кратности соответствует частных решений вида .

Доказано, что общее решение ОЛДУ с постоянными коэффициентами порядка в данном случае представляет собой линейную комбинацию произвольных постоянных И частных фундаментальных решений указанных выше видов.

Пример. Найти общее решение ОЛДУ с постоянными коэффициентами четвертого порядка .

Характеристическое уравнение имеет один простой корень и корень кратности три.

Общее решение данного уравнения в соответствии с изложенной теорией имеет вид

3. Среди корней могут быть как вещественные, так и комплексные корни.

Если характеристическое уравнение имеет вещественные коэффициенты, то, как было доказано ранее в теории алгебраических уравнений, каждому комплексному корню обязательно соответствует сопряженный корень .

Рассмотрим вначале ОЛДУ с постоянными вещественными коэффициентами второго порядка. Если его характеристическое уравнение содержит комплексный корень вида , то второй корень обязательно имеет вид . Частными решениями такого ОЛДУ являются функции , .

Так как исходное ОЛДУ имеет вещественные коэффициенты, то полезно наряду с решениями, представленными в комплексной форме, иметь вещественные решения.

Воспользуемся формулами Эйлера, и представим решения в тригонометрическом виде

Далее, построим линейные комбинации этих решений следующего вида:

, .

По теореме о линейных свойствах решений данные функции также являются решениями исходного ОЛДУ. Составим Вронскиан для этих решений

Так как экспоненциальная функция строго положительна, а характеристическое уравнение имеет комплексные корни (, то Вронскиан всегда отличен от нуля. В соответствии с критерием фундаментальности, решения , являются линейно независимыми, и для уравнения второго порядка образует фундаментальную систему решений.

Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация

Является общим решением ОЛДУ второго порядка с постоянными коэффициентами, если его характеристическое уравнение имеет два комплексных корня.

Пример. Решить ОЛДУ второго порядка .

Характеристическое уравнение данного ОЛДУ имеет вид . Уравнение имеет пару комплексно-сопряженных корней и . Из общей теории следует, что решения , являются линейно независимыми и для уравнения второго порядка образует фундаментальную систему решений. Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация является общим решением данного ОЛДУ второго порядка с вещественными коэффициентами.

В общем случае каждой паре простых комплексно-сопряженных корней соответствует два частных решения вида , , а каждой паре корней кратности соответствует частных решений следующего вида:

Доказано, что общее решение ОЛДУ порядка с постоянными вещественными коэффициентами в общем случае представляет собой линейную комбинацию произвольных постоянных И фундаментальных решений всех указанных выше видов.

Пример. Решить ОЛДУ пятого порядка .

Характеристическое уравнение данного ОЛДУ имеет вид . Оно имеет один вещественный корень и пару комплексно-сопряженных корней , Кратности два.

В соответствии с общей теорией система функций , , Является фундаментальной системой решений, а линейная комбинация есть общее решение данного ОЛДУ пятого порядка с вещественными коэффициентами.

< Предыдущая		Следующая >

31.Свойства решений лоду

ДУ вида называется линейным однородным дифференциальным уравнением с постоянным коэффициентами.Где a,b,c-постоянные вещественные числа.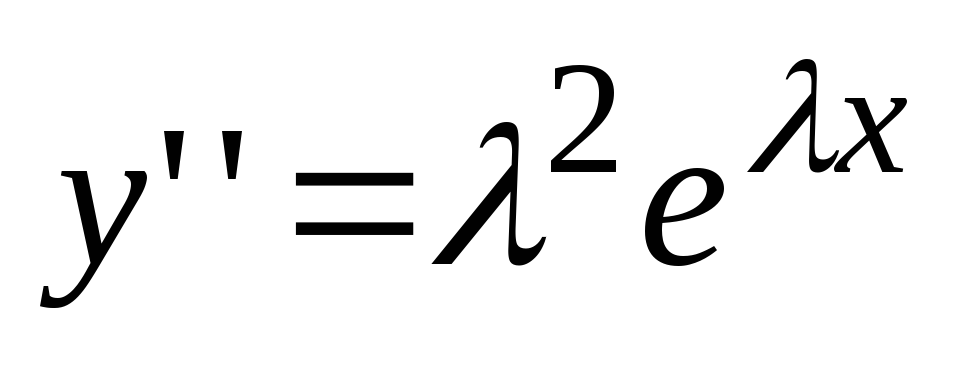

Будем искать частные решения ДУ в виде , где , тогда .

Подставляя значения в ДУ, находим

Так как то получим следующее алгебраическое выражение

которое называется характеристическим уравнением для ЛОДУ

Совокупность частных линейно независимых решений составляет фундаментальную систему решений ЛОДУ.

Определение : Компоненты общего решения дифференциального уравнения определяются в зависимости от характера корней характеристического уравнения следующим образом:

1) каждому действительному простому (т.е. не кратному) корню в общем решении соответствует слагаемое вида ;

2) каждому действительному корню кратности в общем решении соответствует слагаемое вида

;

3) каждой паре комплексных сопряженных простых корней и в общем решении соответствует слагаемое вида ;

каждой паре комплексных сопряженных корней и кратности в общем решении соответствует слагаемое вида

32. Определитель Вронского

Определение. Система функций называется линейно независимой на некотором промежутке, если ни одна из этих функций не представляется в виде линейной комбинации всех остальных.

В случае двух функций это означает, что , т.е. . Последнее условие можно переписать в виде или . Стоящий в числителе этого выражения определитель называется определителем Вронского для функций и . Таким образом, определитель Вронского для двух линейно независимых функций не может быть тождественно равен нулю.

Пусть – определитель Вронского для линейно независимых решений и уравнения (2.3). Убедимся подстановкой, что функция удовлетворяет уравнению . (3.1)

Действительно, . Поскольку функции и удовлетворяют уравнению (2.3), то , т.е. – решение уравнения (3.1). Найдем это решение: ; . Откуда , . , , .

В правой части этой формулы надо взять знак плюс, так как только в этом случае при получается тождество. Таким образом,

(3.2)

Это формула называется формулой Лиувилля. Выше было показано, что определитель Вронского для линейно независимых функций не может быть тождественно равен нулю. Следовательно, существует такая точка , в которой определитель для линейно независимых решений уравнения (2.3) отличен от нуля. Тогда из формулы Лиувилля следует, что функция будет отлична от нуля при всех значениях из рассматриваемого промежутка, поскольку при любом значении оба множителя в правой части формулы (3.2) отличны от нуля.

33. Структура общего решения лоду

Теорема. Если и – линейно независимые решения уравнения (2.3), то их линейная комбинация , где и – произвольные постоянные, будет общим решением этого уравнения.

Доказательство.

То, что есть решение уравнения (2.3), следует из теоремы о свойствах решений лоду 2-го порядка. Надо только еще показать, что решение будет общим, т. е. надо показать, что при любых начальных условиях , можно выбрать произвольные постоянные и так, чтобы удовлетворить этим условиям. Запишем начальные условия в виде:

Постоянные и из этой системы линейных алгебраических уравнений определяются однозначно, так как определитель этой системы есть значение определителя Вронского для линейно независимых решений лоду при :

а такой определитель, как мы видели в предыдущем параграфе, отличен от нуля. Теорема доказана.

34-35Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.

Рассмотрим случай линейного неоднородного дифференциального уравнения с постоянными коэффициентами ЛНДУ

(2),

где a, b, c — действительные постоянные, а непрерывная на некотором интервале функция.

Теорема 7.2. (о структуре общего решения ЛНДУ):

Общее решение y ЛНДУ (2) есть сумма общего решения y₀ соответствующего однородного уравнения ЛОДУ и любого частного решения неоднородного уравнения:

Таким образом, чтобы найти общее решение ЛНДУ, нужно найти общее решение соответствующего ЛОДУ и какое-нибудь частное решение ЛНДУ. В общем случае задача отыскания частного решения является сложной.

Частное решение ЛНДУ можно найти методом вариации произвольных постоянных или методом подбора (метод неопределенных коэффициентов

по виду правой части уравнении.)

Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами

Ниже разберем способы, как решить линейные однородные и неоднородные дифференциальные уравнения порядка выше второго, имеющих постоянные коэффициенты. Подобные уравнения представлены записями y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0 и y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=f(x), в которых f0, f1,…, fn-1 — являются действительными числами, а функция f(x) является непрерывной на интервале интегрирования X.

Оговоримся, что аналитическое решение подобных уравнений иногда неосуществимо, тогда используются приближенные методы. Но, конечно, некоторые случаи дают возможность определить общее решение.

Общее решение ЛОДУ и ЛДНУ

Мы зададим формулировку двух теорем, показывающих, какого вида общих решений ЛОДУ и ЛНДУ n-ого порядка следует искать.

Теорема 1

Общим решением y0 ЛОДУ y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0 на интервале
X (коэффициенты f0(x), f1(x),…, fn-1(x) непрерывны на X) будет линейная комбинация
n линейно независимых частных решений ЛОДУ yj, j=1, 2,…, n, содержащая произвольные постоянные коэффициенты Cj, j=1, 2,…, n, то есть y0=∑j=1nCj·yj.

Теорема 2

Общим решением y ЛНДУ y(n)+fn-1·y(n-1)+. ..+f1·y’+f0·y=f(x) на интервале X(коэффициенты f0(x), f1(x),…, fn-1(x) непрерывны на X ) и функцией f(x) будет являться сумма y=y0+y~, где y0 — общее решение соответствующего ЛОДУ y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0, а y~ — некоторое частное решение исходного ЛНДУ.

Итак, общее решение линейного неоднородного дифференциального уравнения, содержащего постоянные коэффициенты y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=f(x), нужно искать, как y=y0+y~, где y~ — некоторое его частное решение, а y0=∑j=1nCj·yj – общее решение соответствующего однородного дифференциального уравнения y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0.

В первую очередь рассмотрим, как осуществлять нахождение y0=∑j=1nCj·yj — общее решение ЛОДУ n-ого порядка с постоянными коэффициентами, а потом научимся определять частное решение y~ линейного неоднородного дифференциального уравнения n-ого порядка при постоянных коэффициентах.

Определение 1

Алгебраическое уравнение n-ого порядка kn+fn-1·kn-1+. ..+f1·k+f0=0 носит название характеристического уравнения линейного однородного дифференциального уравнения n-ого порядка, содержащего постоянные коэффициенты, записи y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0.

Возможно определить n частных линейно независимых решений y1, y2,…, yn исходного ЛОДУ, исходя из значений найденных n корней характеристического уравнения k1, k2,…, kn.

Методы решения ЛОДУ и ЛНДУ

Укажем все существующие варианты и приведем примеры на каждый.

Когда все решения k1, k2,…, kn характеристического уравнения kn+fn-1·kn-1+…+f1·k+f0=0 действительны и различны, линейно независимые частные решения будут выглядеть так:
y1=ek1·x, y2=ek2·x,…, yn=ekn·x. Общее же решение ЛОДУ n-ого порядка при постоянных коэффициентах запишем как: y0=C1·ek1·x+C2·ek2·x+…+Cn·ekn·x.

Пример 1

Задано ЛОДУ третьего порядка, содержащее постоянные коэффициенты y»’-3y»-y’+3y=0. Определите его общее решение.

Решение

Cоставим характеристическое уравнение и найдем его корни, разложив предварительно многочлен из левой части равенства на множители, используя метод группировки:
k3-3k2-k+3=0k2(k-3)-(k-3)=0(k2-1)(k-3)=0k1=-1, k2=1, k3=3

Ответ: найденные корни являются действительными и различными, значит общее решение ЛОДУ третьего порядка с постоянными коэффициентами запишем как: y0=C1·e-x+C2ex+C3·e3x.

Когда решения характеристического уравнения являются действительными и одинаковыми ( k1=k2=…=kn=k0), линейно независимые частные решения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами буду иметь вид: y1=ek0·x, y2=x·ek0·x,…, yn=xn-1·ek0·x.

Общее же решение ЛОДУ будет выглядеть так:
y0=C1·ek0·x+C2·ek0·x+…+Cn·xn-1·ek0·x==ek0·x·C1+C2·x+…+Cn·xn-1

Пример 2

Задано дифференциальное уравнение: y(4)-8k(3)+24y»-32y’+16y=0. Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k4-8k3+24k2-32k+16=0.

Преобразуем данное характеристическое уравнение, используя формулу бинома Ньютона, оно примет вид: k-24=0. Отсюда мы выделим его четырехкратный корень k0 = 2.

Ответ: общим решением заданного ЛОДУ станет: y0=e2x·C1+C2·x+C3·x2+C4·x3

Когда решения характеристического уравнения линейного однородного дифференциального уравнения n-ого порядка при постоянных коэффициентах — различные комплексно сопряженные пары α1±i·β1, α2±i·β2,. .., αm±i·βm, n=2m, линейно независимые частные решения такого ЛОДУ будут иметь вид:
y1=eα1x·cos β1x, y2=eα1x·sin β1x,y3=eα2x·cos β2x, y4=eα2x·sin β2x,…yn-1=eαmx·cos βmx, yn=eαmx·sin βmx

Общее же решение запишем так:

y0=eα1x·C1·cosβ1x+C2·sinβ1x++eα2x·C3·cosβ2x+C4·sinβ2x+…++eαmx·Cn-1·cosβmx+Cn·sinβmx

Пример 3

Задано ЛОДУ четвертого порядка при постоянных коэффициентах y(4)-6y(3)+14y»-6y’+13y=0. Необходимо его проинтегрировать.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k4-6k3+14k2-6k+13=0. Осуществим преобразования и группировки:

k4-6k3+14k2-6k+13=0k4+k2-6k3+k+13k2+1=0k2+1k2-6k+13=0

Из полученного результата несложно записать две пары комплексно сопряженных корней k1,2=±i и k3,4=3±2·i.

Ответ: общее решение заданного линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами запишется как:
y0=e0·C1·cos x+C2·sin x+e3x·C3·cos 2x+C4·sin 2x==C1·cos x+C2·sin x+e3x·C3·cos 2x+C4·sin 2x

Когда решения характеристического уравнения — это совпадающие комплексно сопряженные пары α±i·β, линейно независимыми частными решениями линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами будут записи:
y1=eα·x·cos β x, y2=eα·x·sin β x,y3=eα·x·x·cos β x, y4=eα·x·x·sin β x,…yn-1=eα·x·xm-1·cos β x, yn=eα·x·xm-1·sin β x

Общим решением ЛОДУ будет:

y0=eα·x·C1·cosβ x+C2·sinβ x++eα·x·x·C4·cosβ x+C3·sinβ x+. ..++eα·x·xm-1·Cn-1·cosβ x+Cn·sinβ x==eα·x·cosβ x·C1+C3·x+…+Cn-1·xm-1++eα·x·sin β x·C2+C4·x+…+Cn·xm-1

Пример 4

Задано линейное однородное дифференциальное уравнение с постоянными коэффициентами y(4)-4y(3)+14y»-20y’+25y=0. Необходимо определить его общее решение.

Решение

Составим запись характеристического уравнения, заданного ЛОДУ, и определим его корни:

k4-4k3+14k2-20k+25=0k4-4k3+4k2+10k2-20k+25=0(k2-2k)2+10(k2-2k)+25=0(k2-2k+5)2=0D=-22-4·1·5=-16k1, 2=k3, 4=2±-162=1±2·i

Таким образом, решением характеристического уравнения будет двукратная комплексно сопряженная пара α±β·i=1±2·i.

Ответ: общее решение заданного ЛОДУ: y0=ex·cos 2x·(C1+C3·x)+ex·sin 2x·(C2+C4·x)

Встречаются различные комбинации указанных случаев: некоторые корни характеристического уравнения ЛОДУ n-ого порядка с постоянными коэффициентами являются действительными и различными, некоторые — действительными и совпадающими, а какие-то — комплексно сопряженными парами или совпадающими комплексно сопряженными парами.

Пример 5

Задано дифференциальное уравнение y(5)-9y(4)+41(3)+35y»-424y’+492y=0. Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k5-9k4+41k3+35k2-424k+492=0.

Левая часть содержит многочлен, который возможно разложить на множители. В числе делителей свободного члена определяем двукратный корень k1=k2=2 и корень k3=-3.

На основе схемы Горнера получим разложение: k5-9k4+41k3+35k2-424k+492=k+3k-22k2-8k+41.

Квадратное уравнение k2-8k+41=0 дает нам оставшиеся корни k4, 5=4±5·i.

Ответ: общим решением заданного ЛОДУ с постоянными коэффициентами будет: y0=e2x·C1+C2x+C3·e-3x+e4x·C4·cos 5x+C5·sin 5x

Таким образом, мы рассмотрели основные случаи, когда возможно определить y0 — общее решение ЛОДУ n-ого порядка с постоянными коэффициентами.

Следующее, что мы разберем – это ответ на вопрос, как решить линейное неоднородное дифференциальное уравнение n-ого порядка с постоянными коэффициентами записи y(n)+fn-1·y(n-1)+. ..+f1·y’+f0·y=f(x).

Общее решение в таком случае составляется как сумма общего решения соответствующего ЛОДУ и частного решения исходного ЛНДУ: y=y0+y~. Поскольку мы уже умеем определять y0, остается разобраться с нахождением y~, т.е. частного решения ЛНДУ порядка n с постоянными коэффициентами.

Приведем все способы нахождения y~ согласно тому, какой вид имеет функция f(x), находящаяся в правой части рассматриваемого ЛНДУ.

Когда f(x) представлена в виде многочлена n-ой степени f(x) = Pn(x), частным решением ЛНДУ станет: y~=Qn(x)·xγ. Здесь Qn(x) является многочленом степени n, а r – указывает, сколько корней характеристического уравнения равно нулю.
Когда функция f(x) представлена в виде произведения многочлена степени n и экспоненты f(x)=Pn(x)·eα·x, частным решением ЛНДУ второго порядка станет: y~=eα·x·Qn(x)·xγ. Здесь Qn(x) является многочленом n-ой степени, r указывает, сколько корней характеристического уравнения равно α.
Когда функция f(x) записана как f(x)=A1cos(βx)+B1sin(βx), где А1 и В1 – числа, частным решением ЛНДУ станет запись y~=Acosβx+Bsinβx·xγ. Здесь где А и В являются неопределенными коэффициентами, r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно ±iβ.
Когда f(x)=eαx·Pn(x)sinβx+Qkxcosβx, то y~=eαx·Lmxsinβx+Nmxcosβx·xγ, где r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно α±iβ, Pn(x), Qk(x), Lm(x) и Nm(x) являются многочленами степени n, k, m и m соответственно, m=max(n,k).

Коэффициенты, которые неизвестны, определяются из равенства y~(n)+fn-1·y~(n-1)+…+f1y~’+f0·y~=f(x)

Подробности нахождения решений уравнений в каждом из указанных случаев можно изучить в статье линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, поскольку схемы решения ЛНДУ степени выше второй полностью совпадают.

Когда функция f(x) имеет любой иной вид, общее решение ЛНДУ возможно определить, используя метод вариации произвольных постоянных. Его разберем подробнее.

Пусть нам заданы yj, j=1,2,…, n — n линейно независимые частные решения соответствующего ЛОДУ, тогда, используя различные вариации произвольных постоянных, общим решением ЛНДУ
n-ого порядка с постоянными коэффициентами будет запись: н=∑j=1nCj(x)·yj. В нахождении производных функций Cj(x), j=1, 2,…, n поможет система уравнений:

∑j=1nCj'(x)·yj=0∑j=1nCj'(x)·y’j=0∑j=1nCj'(x)·y»j=0…∑j=1nCj'(x)·yj(n-2)=0∑j=1nCj'(x)·yj(n-1)=0

а собственно функции Cj(x), j=1, 2,…, n найдем при последующем интегрировании.

Разберем пример.

Пример 6

Задано ЛНДУ с постоянными коэффициентами: y»’-5y»+6y’=2x. Необходимо найти его общее решение.

Решение

Составим характеристическое уравнение: k3-5k2+6k=0. Корни данного уравнения: k1=0, k2=2 и k3=3. Таким образом, общим решением ЛОДУ будет запись: y0=C1+C2·e2x+C3·e3x, а частные линейно независимые решения это: y1=1, y2=e2x, y3=e3x.

Варьируем произвольные постоянные: y=C1(x)+C2(x)·e2x+C3(x)·e3x.

Чтобы определить C1(x), C2(x) и C3(x), составим систему уравнений:

C’1(x)·y1+C’2(x)·y2+C’3(x)·y3=0C’1(x)·y’1+C’2(x)·y’2+C’3(x)·y’3=0C’1(x)·y»1+C’2(x)·y»2+C’3(x)·y»3=2x⇔C’1(x)·1+C’2x·e2x’+C’3(x)·y3=0C’1(x)·1’+C’2x·e2x’+C’3(x)·e3x’=0C’1(x)·1»+C’2x·e2x»+C’3(x)·e3x»=2x⇔C’1(x)·1+C’2x·e2x+C’3(x)·e3x=0C’1(x)·0+C’2(x)·2e2x+C’3(x)·3e3x=0C’1(x)·0+C’2(x)·4e2x+C’3(x)·9e3x=2x

Решаем, используя метод Крамера:

∆=1e2xe3x02e2x3e3x04e2x9e3x=18e2x·e3x-12e2x·e3x=6e5x∆C1′(x)=0e2xe3x02e2x3e3x2x4e2x9e3x=e5x·2x⇒C’1(x)=∆C1′(x)∆=e5x·2x6e5x=16·2x∆C2′(x)=10e3x003e3x02x9e3x=-3ex·2x⇒C’2(x)=∆C2′(x)∆=-3e3x·2x6e5x=-12·e-2x·2x∆C3′(x)=1e2x002e2x004e2x2x=2e2x·2x⇒C’3(x)=∆C3′(x)∆=2e2x·2x6e5x=13·e-3x·2x

Интегрируем C’1(x)=16·2x с помощью таблицы первообразных, а
C’2(x)=-12·e-2x·2x и C’3(x)=13·e-3x·2x при помощи метода интегрирования по частям, получим:
C1(x)=16·∫2xdx=16·2xln 2+C4C2(x)=-12·∫e-2x·2xdx=-12·e-2x·2xln 2-2+C5C3(x)=13·∫e-3x·2xdx=13·e-3x·2xln 2-3+C6

Ответ: искомым общим решением заданного ЛОДУ с постоянными коэффициентами будет:

y=C1(x)+C2(x)·e2x+C3(x)·e3x==16·2xln 2+C4+-12·e-2x·2xln 2-2+C5·e2x++13·e-3x·2xln 2-3+C6·e3x

где C4, C5 и C6 – произвольные постоянные.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р. {2\cdot 0} =C_{1} +C_{2} +4\cdot C_{3} $.

Решаем систему $\left\{\begin{array}{c} {C_{1} +C_{2} +C_{3} =4} \\ {-C_{1} +C_{2} +2\cdot C_{3} =1} \\ {C_{1} +C_{2} +4\cdot C_{3} =1} \end{array}\right. $ по формулам Крамера:

\[\Delta =\left|\begin{array}{ccc} {1} & {1} & {1} \\ {-1} & {1} & {2} \\ {1} & {1} & {4} \end{array}\right|=6, \Delta _{1} =\left|\begin{array}{ccc} {4} & {1} & {1} \\ {1} & {1} & {2} \\ {1} & {1} & {4} \end{array}\right|=6,\] \[\Delta _{2} =\left|\begin{array}{ccc} {1} & {4} & {1} \\ {-1} & {1} & {2} \\ {1} & {1} & {4} \end{array}\right|=24, \Delta _{3} =\left|\begin{array}{ccc} {1} & {1} & {4} \\ {-1} & {1} & {1} \\ {1} & {1} & {1} \end{array}\right|=-6,\] \[C_{1} =\frac{\Delta _{1} }{\Delta } =\frac{6}{6} =1, C_{2} =\frac{\Delta _{2} }{\Delta } =\frac{24}{6} =4, C_{3} =\frac{\Delta _{3} }{\Delta } =\frac{-6}{6} =-1.\]

Таким образом, ЧР имеет вид: $y=e^{-x} +4\cdot e^{x} -e^{2\cdot x} $.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 19.01.2022

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

определение и пример с решением

Оглавление:

Основные определения

Дифференциальное уравнение — го порядка, вида

называется линейным. Коэффициенты — функции независимой переменной , или постоянные числа. Функция независимой переменной называется правой частью уравнения (9.8).

Если правая часть , то уравнение (9.8) называется линейным неоднородным дифференциальным уравнением, сокращенно ЛНДУ. Если, то уравнение

называется линейным однородным дифференциальным уравнением, сокращенно ЛОДУ.

Если в уравнениях (9.8) и (9.9) левые части совпадают, то уравнение (9.9) называется ЛОДУ, соответствующим ЛНДУ (9.8).

Для линейного уравнения — го порядка (однородного или неоднородного) задача Коши формулируется следующим образом: определить частное решение уравнения , удовлетворяющее заданным начальным условиям , .

Свойства решений ПОДУ

Свойства решений ЛОДУ сформулируем в виде теорем.

Теорема 1. Если и — решения однородного уравнения (9.9), то сумма также решение этого уравнения.

Теорема 2. Если — решение уравнения (8.10), , то также решение этого уравнения.

Линейно независимые функции

Система функций , определенных в интервале , называется линейно независимой в этом интервале, если ни одну из этих функций нельзя представить в виде линейной комбинации остальных для всех значений .

С другой стороны, функции линейно зависимы, если существуют постоянные , не все равные нулю, такие, что для всех значений в интервале выполняется тождественно соотношение .

(Если не существуют не равные нулю постоянные , такие, что выполняется последнее тождество, то функции линейно независимы).

Структура общего решения линейного однородного уравнения

Любая система линейно независимых частных решений линейного однородного уравнения — го порядка называется фундаментальной системой.

Для всякого линейного однородного дифференциального уравнения существует фундаментальная система решений.

Теорема. Если образуют фундаментальную систему решений однородного линейного уравнения (8. 10), то общее решение уравнения определяется формулой

Примечание — теорема справедлива для произвольных ПОДУ, как с постоянными, так и с переменными коэффициентами.

Пример 9.4

Уравнение имеет два частных решения и , что легко проверить подстановкой. Такие решения линейно независимы. Они образуют фундаментальную систему заданного дифференциального уравнения. Согласно теореме, общее решение уравнения: .

ЛОДУ с постоянными коэффициентами. Характеристическое уравнение

Если ЛОДУ имеет переменные коэффициенты, фундаментальную систему решений найти чрезвычайно сложно. Но если коэффициенты уравнения все постоянные числа, имеется единый метод определения фундаментальной системы, независимый от порядка дифференциального уравнения.

В технических приложениях чаще всего используются линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейное однородное уравнение второго порядка имеет вид:

Чтобы найти частные решения линейного однородного уравнения с постоянными коэффициентами, нужно составить для него характеристическое уравнение и решить его.

Характеристическое уравнение составляется по следующему правилу: сохраняя коэффициенты , ЛОДУ, нужно заменить функцию единицей, а её производные — соответствующими степенями .

Для уравнения (9.11) характеристическое уравнение является квадратным алгебраическим уравнением вида

Напомним, что решение квадратного уравнения

определяется по формулам:

где дискриминант .

Если , то уравнение имеет два действительных различных корня.

Если , то уравнение имеет два одинаковых корня.

Если , то уравнение не имеет действительных корней, но корни уравнения, все таки, есть.

Предположим, дискриминант квадратного уравнения . Тогда корень квадратный из -16 можно записать в виде:

Обозначим и назовем мнимой единицей. Подставим значение корня из дискриминанта в формулы (9.12). Корни и будут содержать мнимую единицу . Числа, содержащие мнимую единицу, называют комплексными.

Таким образом, если , то квадратное уравнение имеет два комплексных корня вида .

При этом — действительная часть комплексного числа, — мнимая часть комплексного числа. Комплексные корни квадратного уравнения отличаются друг от друга знаком мнимой части. Такие комплексные числа называются сопряженными.

В зависимости от вида корней характеристического уравнения общее решение ЛОДУ второго порядка можно определить с помощью следующей таблицы 5 общих решений ЛОДУ второго порядка.

Таблица 5 — Общее решение ЛОДУ второго порядка

Пример выполнения задания

Пример:

Найти частное решение уравнения, удовлетворяющее указанным начальным условиям:

В задании требуется найти частное решение однородного линейного уравнения с постоянными коэффициентами (ЛОДУ), удовлетворяющее указанным начальным условиям, то есть решить задачу Коши.

Задача решается в следующей последовательности:

Для заданного уравнения записывается характеристическое уравнение, и определяются его корни.
По таблице 5 общих решений ЛОДУ в зависимости от найденных корней записывается общее решение.
Определяется производная от общего решения.
Подставляя в решение и его производную начальные условия, находим значения произвольных постоянных .
Записывается частное решение с найденными значениями произвольных постоянных .

Ход выполнения задания иллюстрируется в следующих примерах. В примере 9.5 выполнены два первых пункта задания; в примере 9.6 выполнены все пункты задания.

Пример 9.5

Найти общие решения уравнений:

Решение:

а) Записываем характеристическое уравнение: .

Вычисляем дискриминант . Находим корень квадратный из дискриминанта: . По формулам (9.12) вычисляем корни.

. Корни уравнения комплексные и сопряжённые. Согласно пункту 3 таблицы 5 общее решение уравнения

б) Записываем характеристическое уравнение: . В неполном квадратном уравнении дискриминант вычислять не надо; , отсюда . Действительные части корней равны нулю. Согласно пункту 4 таблицы 5 общее решение ЛОДУ имеет вид:

в) Составляем характеристическое уравнение . Корни характеристического уравнения , что соответствует пункту 1 таблицы 5 общих решений ЛОДУ. Общее решение .

Пример 9.6

Найти частное решение уравнения , удовлетворяющее начальным условиям .

Решение:

Корни характеристического уравнения действительные, кратные . Согласно пункту 2 таблицы 5 общее решение . Производная общего решения имеет вид: . Согласно начальным условиям, при функция , её производная равна -1. Подставим в общее решение и его производную значения, заданные начальными условиями, получим систему уравнений относительно неизвестных :

Запишем частное решение, удовлетворяющее начальным условиям:

Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:

Высшая математика для 1 курса

Возможно вам будут полезны эти страницы:

Андреа Лоди — Мила

2021-12

Обучение эвристике планирования в методах ветвей и границ

Антония Чмиела, Элиас Б. Халил, Амброс М. Глейкснер, Андреа Лоди и Себастьян Покутта и Алгоритмы второго порядка для крупномасштабного машинного обучения.

Санаэ Лотфи, Тифен Боннио де Рюсселе, Доминик Орбан и Андреа Лоди

НОЛЬ: Игра в игры по математическому программированию.

Габриэле Драготто, Шрирам Санкаранараянан, Маргарида Карвалью и Андреа Лоди

Алгоритм Cut and Play: вычисление равновесия Нэша с помощью внешних приближений.

Маргарида Карвальо, Габриэле Драготто, Андреа Лоди и Срирам Санкаранараянан

Управление в режиме реального времени планом маршрутов транспортных средств с зависящим от времени временем в пути по дорожной сети

Маха Гмира, Мишель Жендро, Андреа Лоди и Жан-Ив Потвин

2021-10

Сокращения с измененной формулой решетки

Карен Аардал, Андреа Лоди, Андреа Трамонтани, Фредерик фон Хейманн и Лоуренс А. Вулси

Расширение вместимости в задаче приема в колледж.

Федерико Боббио, Маргарида Карвальо, Андреа Лоди и Альфредо Торрико

2021-09

Руководство по вычислительному тестированию подходов машинного обучения к задачам маршрутизации транспортных средств.

Лука Аккорси, Андреа Лоди и Даниэле Виго

JANOS: интегрированная структура прогнозного и предписывающего моделирования

Дэвид Бергман, Тенг Хуанг, Филип Брукс, Андреа Лоди и Арвинд У. Рагунатан

Предсказание тактических решений задач оперативного планирования в условиях несовершенной информации

Эрик Ларсен, Себастьен Лашапель, Йошуа Бенжио, Эмма Фреджингер, Саймон Лакост-Жюльен и Андреа Лоди

Точный метод для (ограниченных) задач оптимизации ассортимента с учетом себестоимости продукции

Маркус Лейтнер, Андреа Лоди, Роберто Роберти и Клаудио Соле

Об оценке моделей дискретного выбора для выявления иррационального поведения клиентов

Санджай Доминик Йена, Андреа Лоди и Клаудио Соле

2021-08

Комбинаторная оптимизация и рассуждения с графовыми нейронными сетями

Квентин Каппарт, Дидье Шетела, Элиас Б. Халил, Андреа Лоди, Кристофер Моррис и Петар Величкович целочисленное нелинейное программирование

Бенджамин Мюллер, Гонсало Муньос, Максим Гассе, Амброс Глейкснер, Андреа Лоди и Фелипе Серрано

Об обобщенной суррогатной двойственности в смешанно-целочисленном нелинейном программировании

Бенджамин Мюллер, Гонсало Муньос, Максим Гассе, Амброс М. Глейкснер, Андреа Лоди и Фелипе Серрано

Квадратичная задача о нескольких рюкзаках с конфликтами и балансовыми ограничениями

Филипп Оливье, Андреа Лоди и Жиль Пезан

Машина

602 202 — Выбор столбцов на основе обучения для генерации столбцов

Муад Морабит, Ги Десолнье и Андреа Лоди

Меры баланса в комбинаторной оптимизации

Филипп Оливье, Андреа Лоди и Жиль Пезан

Минимизация мощности, ограничения и регуляризация: обзор.

Андреас М. Тильманн, Даниэль Бинсток, Андреа Лоди и Александра Шварц

2021-05

Изучение метрики Вассерштейна для анализа времени до события Йошуа Бенжио

Проблема назначения покрытия для одноранговых облаков на базе Swarm: пример использования распределенного трехмерного отображения

Леандро Р. Коста, Даниэль Алоиз, Лука Дж. Джаноли и Андреа Лоди

2021-04

Машинное обучение для комбинаторной оптимизации: методологический обзор горизонта

Йошуа Бенжио, Андреа Лоди и Антуан Пруво

Школа: библиотека для обучения внутри MILP Solvers.

Antoine Prouvost, Justin Dumouchelle, Maxime Gasse, Didier Chételat и Andrea Lodi

2021-03

Эвристика для оптимизации трехмерных картографических миссий по роевым специальным облакам

Leandro R. Costa, Daniel Aloise, Luca G. Джаноли и Андреа Лоди

2021-02

Алгоритмы ветвей «цена-и-отсечение» для задачи маршрутизации транспортных средств со стохастическим и коррелированным временем в пути

Борзу Ростами, Гай Десолнье, Фаусто Эррико и Андреа Лоди решатель для линейной оптимизации

Матье Танно, Мигель Ф. Аньос и Андреа Лоди

Прогнозирование распределения вероятностей времени в пути автобуса для перехода к надежному планированию услуг общественного транспорта.

Леа Рикар, Ги Десолнье, Андреа Лоди и Луи-Мартен Руссо

2021-01

Может ли машинное обучение помочь в решении проблем контроля за бронированием при управлении грузоподъемностью

Джастин Дюмушель, Эмма Фрежингер и Андреа Лоди Тестирование алгоритма управления микросетью

Кристофер Нил, Ханане Дагдуги, Андреа Лоди и Хосе М. Фернандес

Точная алгоритмическая структура для класса смешанных целочисленных программ с ограничениями равновесия

Теодора Дэн, Андреа Лоди и Патрис Маркотт

Многоуровневые подходы к проблеме критических узлов

Андреа Баджо, Маргарида Карвалью, Андреа Лоди и Андреа Трамонтани

Оценка влияния усовершенствования на систему управления доходами: приложение авиакомпании.

Грета Лааге, Эмма Фреджингер, Уильям Л. Гамильтон, Андреа Лоди и Гийом Рабюссо

Справедливость во времени при динамическом распределении ресурсов с помощью приложения в здравоохранении

Андреа Лоди, Филипп Оливье, Жиль Пезан и Срирам Санкаранараянан

Планирование работы насосов в распределительных сетях питьевой воды с ответвлениями на основе LP/NLP

Гратьен Бонвин, Софи Демасси и Андреа Лоди

Изучение хордовых расширений

05 Defeng 9 Лю, Андреа Лоди и Матье Танно

Обучение в местных отделениях (приглашенная лекция).

Дефен Лю и Андреа Лоди

Оценка воздействия: приводит ли улучшение системы управления доходами к увеличению доходов?

Грета Лааге, Эмма Фрежингер, Андреа Лоди и Гийом Рабюссо

Замечание об иерархии Лассера для различных формулировок задачи о максимальном независимом множестве

Мигель Ф. Анжос, Юсуф Эмине, Андреа Лоди и Чжао Сун задача маршрутизации транспортных средств с временными окнами в сети дорог

Маха Гмира, Мишель Жандро, Андреа Лоди и Жан-Ив Потвин

2020-12

Стохастический демпфированный L-BFGS с контролируемой нормой приближения Гессе

Санаэ Лотфи, Тифан Боннио де Рюсселе, Доминик Орбан и Андреа Лоди

Обучение работе с возмущениями параметров в комбинаторной оптимизации: приложение для определения местоположения объекта для доставки на дом

Маха Гмира, Мишель Жендро, Андреа Лоди и Жан-Ив Потвен

2020-11

Параметризация деревьев поиска ветвей и границ для изучения политик ветвления

Джулия Зарпеллон, Джейсон Джо, Андреа Лоди и Йошуа Бенжио

2020-10

Ecole: спортивная библиотека для машинного обучения в комбинаторных решателях оптимизации

Антуан Пруво, Джастин Дюмушель, Лара Скавуззо, Максим Шатель и Андреа Лоди

Стохастическая адаптивная регуляризация с динамической выборкой для машинного обучения

Санаэ Лотфи, Доминик Орбан и Андреа Лоди

Стохастическая демпфированная L-BFGS с контролируемой нормой приближения Гессе

Санаэ Лотфи, Тифан Бонниот, Доминик Орбан и Андреа Лоди

2020-09

Модель частично ранжированного выбора для крупномасштабной оптимизации ассортимента на основе данных

Санджай Доминик Йена, Андреа Лоди, Хьюго Палмер и Клаудио Соле 9004 9004 Алгоритм, основанный на обучении, для быстрого вычисления хороших первичных решений для стохастических целочисленных программ

Йошуа Бенжио, Эмма Фреджингер, Андреа Лоди, Рахул Патель и Шрирам Санкаранараянан

Обнаружение точки изменения путем кросс-энтропийной максимизации.

Орельен Серр, Дидье Шетела и Андреа Лоди

2020-08

Анализ устойчивости алгоритмов управления микросетями против вредоносных входных данных

Кристофер Нил, Ранва Аль Малла, Хосе Фернандес и Андреа Лоди оптимизация для четырехъядерного BDD

4 задача об устойчивом множестве

Хайме Э. Гонсалес, Андре А. Сире, Андреа Лоди и Луи-Мартен Руссо

Метод внешней аппроксимации с несколькими разрезами для конкурентного размещения предприятий при случайных полезностях

Тиен Май и Андреа Лоди

2020-06

Гибридные модели для обучения разветвлению

Пратик Гупта, Максим Гассе, Элиас Б. Халил, М. Паван Кумар, Андреа Лоди и Йошуа Бенжио

Разработка и внедрение модульный решатель внутренних точек для линейной оптимизации

Мигель Ф. Анжос, Андреа Лоди и Матье Танно

Многоагентная оптимизация ассортимента на рынках последовательного сопоставления

Альфредо Торрико, Маргарида Карвальо и Андреа Лоди

Доказуемые гарантии для общих рынков двустороннего последовательного сопоставления

Альфредо Торрико, Маргарида Карвалью и Андреа Лоди

2020-05

Модель ILP для MRF с несколькими метками и ограничениями связности , Андреа Трамонтани и Исмаил Бен Айед

2020-04

Предисловие к специальному выпуску INFOR «Непрерывная оптимизация и приложения в машинном обучении и анализе данных»

Мигель Ф. Анжос, Фабиан Бастин, Себастьен Ле Дигабель и Андреа Лоди

Proceedings of the Edge Intelligence Workshop, Монреаль, Канада, 2–3 марта 2020 г.

Charles Audet, Sébastien Le Digabel, Andrea Lodi, Dominique Orban и Vahid Partovi Nia

Проблема назначения покрытия для рекламы на основе роя -hoc облака: пример использования распределенного трехмерного картографирования

Леандро Р. Коста, Даниэль Алоизе, Лука Г. Джаноли и Андреа Лоди

Интегрированное целочисленное программирование и дерево поиска диаграмм решений с приложением к задаче о максимальном независимом множестве

Хайме Э. Гонсалес, Андре Аугусто Сире, Андреа Лоди и Луи-Мартен Руссо

2020-03

Совместное местоположение и цены в среде, оптимизированной для пользователей

Теодора Дэн, Андреа Лоди и Патрис Маркотт

1020002

2

Математическая оптимизация для эффективных и надежных энергетических сетей. Лоди и Йошуа Бенжио

Адаптация активации в нейронных сетях.

Farnoush Farhadi, Vahid Partovi Nia и Andrea Lodi

2019-12

Дизъюнктивные сокращения в конической оптимизации смешанного интеллекта

Diescuntive Cuts For Sixedteger-integer integere-integer integrea integer integer integer integer integer.

. Лоди, Матье Танно и Хуан Пабло Вьельма

2019-11

Теоретико-игровой анализ программ обмена почек.

Маргарида Карвалью и Андреа Лоди

Нелинейные задачи с ограничением шансов в приложениях к планированию гидроэлектростанций

Андреа Лоди, Энрико Малагути, Джакомо Нанничини и Димитри Томопулос

2019-10

Игры Нэша среди лидеров Штакельберга.

Маргарида Карвалью, Габриэле Драготто, Фелипе Фейжу, Андреа Лоди и Шрирам Санкаранараянан

Когда Нэш встречает Штакельберга

Маргарида Карвалью, Габриэле Драготто, Фелипе Фейжу, Андреа Лоди и Шрирам Санкаранараянан

2019-09

Интерактивные аннотации с ограничением подключения для паноптической сегментации

Рубинг Шен, Бо Танг, Исмаил Бен Айед, Андреа Лоди и Томас Гутье

Точная комбинаторная оптимизация с использованием графовых сверточных нейронных сетей Ferroni, Laurent Charlin and Andrea Lodi

2019-06

Использование плотностей решений на основе стоимости из релаксаций TSP для решения задач маршрутизации

Pierre Coste, Andrea Lodi и Gilles Pesant

Изучение результатов разрешения MILP до достижения предела времени

Мартина Фишетти, Андреа Лоди и Джулия Зарпеллон

Tulip: решатель линейной оптимизации внутренних точек с открытым исходным кодом и абстрактной линейной алгеброй

Мигель Ф. Анжос, Андреа Лоди и Матье Танно

QPLIB: библиотека экземпляров квадратичного программирования

Фабио Фурини, Эмилиано Траверси, Пьетро Белотти, Антонио Франджиони, Амброс М. Глейкснер, Ник Гулд, Лео Либерти, Андреа Лоди, Рут Мизенер, Ханс Д. Миттельманн, Николаос В. Сахинидис, Стефан Вигерске и Анжелика Вигеле

2019-05

Прогнозирование нежелательных явлений с помощью телемониторинга и глубокого обучения

Antoine Prouvost, Andrea Lodi, Louis-Martin Rousseau and Jonathan Vallee , Йонас Швайгер и Андреа Трамонтани

Алгоритм оптимизации ассортимента в рамках параметрических моделей дискретного выбора

Тьен Май и Андреа Лоди

2019-03

Десять лет накачки осуществимости, и это продолжается

Тимо Бертольд, Андреа Лоди и Доменико Сальванин

2019-01

Децентрализованная структура для оптимальной координации распределенных энергетических ресурсов

Мигель Ф. Анжос, Андреа Лоди5

и Матье

2018-12

Планирование трафика M2M по восходящему каналу LTE плотной сети малых сот

Мельхиорре Данило Абриньяни, Лоренца Джуппони, Андреа Лоди и Роберто Вердоне

2018-10

Вычисление равновесия Нэша для игр целочисленного программирования

Margarida Carvalho, Andrea Lodi и João Pedro Pedroso

2018-08

Схема аппроксимации на основе PCA для комбинаторной оптимизации с неопределенными и коррелированными данными Эррико и Андреа Лоди

2018-07

Прогнозирование итогов решения целочисленных линейных программ при несовершенной информации с помощью машинного обучения.

Эрик Ларсен, Себастьян Лашапель, Йошуа Бенжио, Эмма Фреджингер, Симон Лакост-Жюльен и Андреа Лоди

2018-06

Сравнение методов оптимизации для многокритериальных задач упаковки в контейнеры с ограничениями

Филипп Оливье, Андреа Лоди и Жиль Пезан

Изучение классификации задач смешанно-целочисленного квадратичного программирования

Пьер Лоди и Андреа Бонами, Андреа Бонами Джулия Зарпеллон

Учимся ранжировать цензурированные данные о выживании.

Марго Лак, Тристан Сильвен, Джозеф Пол Коэн, Элоиза Кардинал, Андреа Лоди и Йошуа Бенжио

2018-04

Эксперименты по проектированию виртуальной частной сети с вогнутой емкостью

Андреа Лоди и Ахмад Моради

2018-03

Полиномиальный алгоритм для непрерывной двухуровневой задачи о рюкзаке

2018-01

Точные и приближенные методы решения задачи маршрутизации транспортных средств со стохастическим и коррелированным временем в пути

Фаусто Эррико, Гай Десолнье, Андреа Лоди и Борзу Ростам

Выпуклая переформулировка и внешняя аппроксимация для класса бинарных квадратичных программ

Борзу Ростами, Фаусто Эррико и Андреа Лоди

Публикации, собранные и отформатированные с помощью Paperoni

Mazzera’s | Кухня Реконструировать | Реконструкция ванны | Лоди, Калифорния

«Мы с женой очень довольны нашей новой кухней и окнами. Качество исполнения было на самом высоком уровне. Установка Дэйвом множества окон и обеих раздвижных дверей прошла превосходно! Мы очень довольны окнами с двойным остеклением. На внутренней стороне стекла не скапливается вода, нет сквозняков, они также снижают количество постороннего шума, проникающего в дом. В результате дом станет более комфортным, а счета за коммунальные услуги меньше. Я отапливаю весь дом дровяной печью, и легко поддерживать температуру 70 градусов. Со старыми окнами это было бы невозможно.

Великолепная новая кухня! Я никогда не ремонтировал кухню и не знал, чего ожидать. После разговора с вами мы поняли, что нашли подходящего человека для нашего проекта. Вы нашли время, чтобы спланировать кухню к нашему удовлетворению, включив некоторые из наших идей в дизайн. Ваша смета расходов была отправлена оперативно, и мы никогда не чувствовали давления, что облегчало принятие решений. Вы позволили мне и моей жене выполнить часть работы самостоятельно, это не только снизило некоторые расходы, но и заставило нас чувствовать себя более частью опыта. Непростая задача — перестроить кухню. Стив проделал замечательную работу, каким активом он должен быть. Красиво оформленный шкаф, установленный мастерски вплоть до лепнины. Освещение идеальное, именно там, где оно необходимо, и не подавляющее. Производственный график соблюдался буквально. Ваша оценка от четырех до шести недель была идеальной, и мы приготовили ужин на День Благодарения на нашей новой кухне.

Гэри, с тобой было приятно работать. Трудно найти человека или компанию, которые заставляют своих клиентов чувствовать себя важными, вы, конечно, чувствуете. Вы честный человек, и мы считаем, что вы скорее друг семьи, чем деловой знакомый. Желаем вам успешного 2001 года! Если мы можем быть вам чем-то полезны, смело звоните нам. Мы будем рады ответить на любые вопросы потенциальных клиентов или позволить им лично увидеть вашу работу. У меня есть фотографии всего процесса».

— Пол и Дебби Кокола

«Я хочу, чтобы вы знали, как мы с Дебби довольны новой кухней, которую вы спроектировали и установили. В результате нашего обширного изучения и исследования различных строителей мы знаем, что сделали лучший выбор, выбрав Mazzera. Установка прошла в установленные сроки и по сметной стоимости, и я ценю профессионализм и тщательность, которые ваша фирма привнесла в этот проект.

Вы проделали выдающуюся работу по выполнению наших основных задач по сохранению архитектурного колорита нашего 1927 Дом в колониальном стиле, но с современной техникой, которую мы хотели. Ни один другой строитель не приблизился к вашей концепции. Ваша цена, безусловно, была справедливой и учитывала возможности нашего бюджета.

Мы также хотели бы, чтобы вы передали нашу самую искреннюю благодарность всем людям, которые были вовлечены в этот проект. Слишком часто в ходе проекта, подобного этому, мы часто не можем сказать спасибо достаточно громко, чтобы все это услышали. Мы знаем, что все эти люди настаивали на превосходной работе, и мы оба благодарны за высокие стандарты качества, которые все они привнесли в проект.

Опять же, мы в восторге от кухни. Здесь не только приятно готовить еду, но и эта комната стала местом семейных встреч. Спасибо за все, что вы сделали, чтобы сделать этот проект таким замечательным!»

— Michael Hohn

«Мы просто хотели написать и поблагодарить вас за нашу прекрасную новую кухню. Мы это любим! Как вы знаете, мы много ходили по магазинам, прежде чем выбрать Mazzera для нашего проекта реконструкции. Вопреки распространенному мнению, ваша цитата была не самой дорогой; на самом деле, вы были в центре внимания, и после личного разговора с несколькими вашими довольными клиентами мы были уверены, что работа будет выполнена хорошо. Mazzera более чем оправдал наши ожидания. Ваши люди были умелыми и вежливыми, и работа продвигалась гладко. Качество вашей мебели говорит само за себя, и оно соответствует качеству вашей работы. Особая благодарность Роджеру, который прекрасно справился с установкой. Также спасибо тебе, Гэри, за то, что позаботился обо всех деталях отделки и помог мне собрать воедино мои идеи.

Новая кухня неизмеримо увеличила ценность нашего дома и, что более важно, удовольствие, которое мы получаем от него. Мы будем рады показать его потенциальным клиентам. Спасибо еще раз.»

— Стив и Лори Игер

«Мы с Донной хотим поблагодарить вас за прекрасную работу, которую Mazzera проделала по реконструкции нашего нижнего этажа. Это долгожданное улучшение по сравнению с предыдущим планом этажа. Пространство используется гораздо лучше.

Шкафы тоже великолепны. Нам нравится отделка, а интерьеры просто великолепны. Мы часто просто сидим и смотрим на них, не очень веря, что когда-то у нас были шкафы, которые сейчас стоят в гараже.

Больше всего мы хотим сказать вам, как мы были впечатлены всеми мастерами, которых вы нам прислали. Все они были очень компетентны и явно заботились о том, что делали. В частности, Стив и Уэйн прекрасно все совместили. Я бы хотел, чтобы они работали на нас в любое время.
Наконец, спасибо за ваше видение и организацию. Вы сделали все так гладко. Пожалуйста, примите это вино в знак нашей благодарности за хорошо выполненную работу.

P.S.: Я рад, что не зарабатываю на жизнь сносом. Это игра молодых».

— Дэйв и Донна Флетчер

Дерево Лоди | Charity Navigator Profile

Миссия: Недоступно

Tree Lodi является организацией 501(c)(3) с 2006 годом, установленным Налоговым управлением США, и пожертвования не облагаются налогом.

Это ваша некоммерческая организация? Получите доступ к некоммерческому порталу, чтобы отправить данные и загрузить набор инструментов для оценки.

Контактная информация

URL недоступен

2316 PORTSMOUTH DR
Woodbridge CA 95242-4721

Encompass Rating System By Charity Navigator

Общая оценка

В настоящее время не набирают

. В настоящее время нам требуется маяк «Финансы и подотчетность» или «Маяк воздействия и результатов», чтобы иметь право на оценку Encompass. См. ниже, чтобы узнать, почему эта организация не соответствует требованиям.

Узнайте о рейтинговой системе Encompass: Обзор | Часто задаваемые вопросы | Примечания к выпуску

Далее: Воздействие и результаты

Финансы и подотчетность

Этот балл дает оценку финансового состояния некоммерческой организации (стабильность, эффективность и устойчивость) и ее приверженности методам и политикам управления.

Баллы по финансам и подотчетности

В настоящее время баллы отсутствуют

Эта организация не может быть оценена с помощью нашей методологии Encompass Rating, поскольку она подает форму 990-N, разрешенную IRS для благотворительных организаций с годовым доходом менее 50 000 долларов США.

Примечание: Отсутствие балла не говорит о положительной или отрицательной оценке, это лишь говорит о том, что мы еще не оценивали эту организацию.

Back to Overall

Additional Information

Unscored

Total Revenue

and Expenses
No Data Available
Salary of

Key Persons
No Data Available
IRS Опубликованные данные

(Business Master File)
Доступные данные
Источники данных

(Формы IRS 990)

Эта бета-функция в настоящее время доступна только на экранах настольных компьютеров или планшетов. Загляните позже, чтобы узнать об обновлениях.

Общие доходы и расходы

Данные отсутствуют

Данные о доходах и расходах недоступны для этой организации. Эти данные доступны только в том случае, если эта благотворительная организация по крайней мере за один год подала электронную форму 9.90 данных, поданных за последние шесть лет.

Заработная плата ключевых лиц

Нет данных

Данные ключевых лиц в настоящее время недоступны для этой организации. Эти данные доступны только в том случае, если эта благотворительная организация имеет по крайней мере один год электронных данных формы 990, поданных в течение последних шести лет.

Данные основного бизнес-файла

Ниже приведены некоторые ключевые данные из основного бизнес-файла IRS для освобожденной организации (BMF) для этой организации. Узнайте больше о BMF на веб-сайте IRS

Виды деятельности:

Данные о деятельности, не предоставленные IRS

Статус фонда:

Организация, которая получает значительную часть своей поддержки от государственного подразделения или широкой общественности 170(b)(1)(A)( vi) (Код фонда BMF: 15)

Принадлежность:

Независимая — организация является независимой организацией или независимой вспомогательной организацией (т. е. не связанной с национальной, региональной или географической группой организаций). (Код принадлежности BMF: 3)

Источники данных: Формы IRS 990

Форма 990 — это документ, который некоммерческие организации ежегодно подают в IRS. Мы используем данные о финансах и отчетности для формирования рейтингов Encompass. Щелкните здесь, чтобы просмотреть формы 990 этой организации на веб-сайте IRS (если таковые имеются).

Предыдущий: Финансы и подотчетность / Следующий: Лидерство и адаптивность

Воздействие и результаты

Эта оценка оценивает фактическое влияние некоммерческой организации на жизнь тех, кому она служит, и определяет, насколько эффективно она использует донорские ресурсы. для достижения этого воздействия.

Оценка воздействия и результатов

В настоящее время не оценивается

Tree Lodi в настоящее время не может быть оценено с помощью нашей методологии Encompass Rating Impact & Results, потому что либо (A) оно соответствует критериям, но мы еще не получили данные; (B) мы еще не разработали алгоритм для оценки его программного воздействия; (C) его программы не являются прямыми услугами; или (D) он не сильно зависит от взносов отдельных доноров.

Примечание: Отсутствие балла не указывает на положительную или отрицательную оценку, это лишь указывает на то, что мы еще не оценивали организацию.

Узнайте больше о воздействии и результатах.

Вы работаете в Tree Lodi? Присоединяйтесь к списку ожидания для получения обновленной оценки воздействия и результатов.

Вернуться к общей оценке

Предыдущая: Воздействие и результаты / Далее: Культура и сообщество

Лидерство и способность к адаптации

реагировать на изменения составляющих спроса/потребностей или других соответствующих социальных и экономических условий для достижения миссии организации.

Оценка Лидерства и Адаптивности

В настоящее время не оценивается

В настоящее время Tree Lodi не имеет права на получение оценки Лидерства и Адаптивности, поскольку мы не получили ее ответы на опрос L&A.

Примечание: Отсутствие балла не говорит о положительной или отрицательной оценке, это лишь говорит о том, что организация еще не представила данные для оценки.

Вернуться к разделу Общие

Предыдущий: Лидерство и адаптивность

Культура и сообщество

Этот балл дает оценку культуры организации и ее связи с сообществом, которому она служит. Узнайте больше о том, как и почему мы оцениваем культуру и сообщество.

Оценка по культуре и сообществу

В настоящее время не оценивается

Tree Lodi в настоящее время не имеет права на получение оценки по культуре и сообществу, поскольку мы не получили данные об отзывах участников или разнообразии, равенстве и включении. Некоммерческим организациям рекомендуется заполнять разделы «Как мы слушаем» и «Практика справедливости» в своем профиле Candid.

Примечание: Отсутствие балла не указывает на положительную или отрицательную оценку, это указывает только на то, что мы еще не оценивали организацию.

Back to Overall

Culture & Community Report

Unscored

Constituent Feedback
No Data Available
Diversity, Equity, & Inclusion
No Data Available
Анализ и исследования

Эта бета-функция в настоящее время доступна только на экранах компьютеров и планшетов. Загляните позже, чтобы узнать об обновлениях.

Отзывы постоянных участников

Разнообразие, справедливость и инклюзивность

Эта организация не предоставила информацию о методах разнообразия, справедливости и инклюзивности (DEI), которые она внедряет в настоящее время. Таким образом, организация не получила оценку по этому показателю. Charity Navigator считает, что некоммерческие организации, реализующие эффективную политику и практику DEI, могут улучшить процесс принятия решений некоммерческой организацией, мотивацию персонала, инновации и эффективность.

Методология

Мы используем данные, собранные Candid, для документирования и оценки методов DEI, применяемых организацией. Некоммерческим организациям рекомендуется заполнить раздел «Стратегии акционерного капитала» в своих профилях Candid, чтобы получить рейтинг.

Узнайте больше о методике.

Отзывы постоянных клиентов

Данные обратной связи постоянных клиентов и Практики прослушивания недоступны для этой организации. Charity Navigator считает, что некоммерческие организации, которые используют инклюзивные методы, такие как сбор отзывов от людей и сообществ, которым они служат, могут быть более эффективными.

Методология

Мы сотрудничаем с Candid, чтобы опросить организации об их методах обратной связи. Некоммерческие организации могут заполнить раздел «Как мы слушаем» своего профиля Candid, чтобы получить рейтинг.

Узнайте больше о методике.

Анализ и исследования

Как и общая рейтинговая система Encompass, маяк культуры и сообщества развивается по мере разработки показателей и готовности к интеграции. Ниже вы можете найти дополнительную информацию о показателях, которые мы в настоящее время оцениваем в этом маяке, и их значимости для некоммерческой деятельности.

Отзывы постоянных клиентов

Разнообразие, равенство и инклюзивность

У корзины подарков возникли некоторые проблемы. Если вы хотите сделать пожертвование, пожалуйста, обновите страницу. Если проблема не устранена, свяжитесь с нами.
Идентификатор корзины: не присвоено

Что означает Lodu? Лоду Значение Имени

Сущность имени Лоду означает серьезность, мысль, интуицию, намерение и мудрость.

❶ Что означает Лоду?

Очень духовный человек, который часто полагается на интуицию при принятии решений.

Ваш ум богат и глубок, но часто закрыт для других людей. Иногда вам нужно уединение, чтобы прояснить, что происходит в вашей жизни.

Это, однако, не делает вас человеком, с которым трудно ладить.

Напротив, у вас много талантов, и вы всегда можете сказать, что чувствуют другие. В любви и отношениях вы, как правило, очень страстны. Личность Лоду

❷ Что означает Lodu?

Сильная интуиция — одно из ваших величайших оружий. Может быть, поэтому у вас хороший нюх на тренды. Часто обнаруживает их раньше всех.

Это большое преимущество. Мало кто любит перемены, а вот те, кого зовут Лоду, на самом деле их любят.

Все, что является новым или может вас удивить, приветствуется с распростертыми объятиями. Рутина так называемой нормальной жизни безмерно утомляла. Желая летать высоко и испытать приключения, вы можете лучше всего подходить для несколько необычной работы.
Работа, в которой точность и внимание к деталям не так важны, позволит раскрыть ваши таланты.

Примеры могут быть связаны с рекламой или письмом. Пробудить интерес или выбрать правильное направление — это то, что у вас получается лучше всего. Быстрая адаптация к новым обстоятельствам делает вас потрясающими в путешествиях.

Если бы кто-то заболел и не пришел на работу, вы могли бы с легкостью справиться с новым вызовом. Будучи талантливым во многих областях, у вас есть свои специфические интересы, которые вдохновляют.

Ваш жизнерадостный характер делает вас популярным повсюду. Настоящий лучик солнца. Интуиция может помочь вам читать и понимать людей до определенной степени. Однако, если вы тщательно разовьете этот навык, он может стать очень полезным. Легко отвлекаться — одна из ваших слабостей. Вот почему вы должны записывать все свои блестящие идеи, чтобы не забыть их.

❸ Имя Лоду Значение

Вы стремитесь к более глубокому пониманию себя и своих близких. Люди, которым дали это имя, хотят открывать, исследовать и постигать.

Разгадывать загадки и узнавать секреты — один из ваших любимых способов времяпрепровождения.

Способность заглянуть за кулисы — это талант, с которым вы родились. Научиться следовать своей интуиции будет очень полезно.

Ваши инстинкты обычно очень остры. Время от времени вы склонны быть довольно сдержанным. Это может быть признаком глубокой мысли. В такие моменты по-настоящему понять вас могут только те, кто обращает внимание на каждую деталь.

Независимо от того, где вы находитесь, люди склонны уважать вас. Вас окружает некая атмосфера авторитета. Одна часть, в которой вы должны попытаться стать лучше, — это эмоциональная открытость. В социальных ситуациях вы склонны уходить в свой собственный мир, чтобы размышлять над старыми проблемами.

❹ Список 4 Удивительных Значений Имен

L Буква L Значение Лоду
Люди, в имени которых есть буква L, никогда не соглашаются просто слушать и верить. Вместо этого они на самом деле ищут доказательства, которые доказывают то, что было сказано.
Такое поведение справедливо во всех сферах их жизни! Вот почему, если вы хотите показать им свою признательность или любовь, вы должны продемонстрировать это действиями. Например, объятия, совместный просмотр фильма, совместный ужин или что-то еще реальное, что можно увидеть или почувствовать. Это люди глубокой мысли и новых идей, всегда способные открыто выражать себя. Обычно все, что они делают, имеет некоторую ценность. Для них чрезвычайно важны романтические отношения. Их идеальный партнер способен стимулировать их интеллектуально.
Их сильный характер позволяет им идти на жертвы, если что-то идет вразрез с их убеждениями. Предан своему делу. Всегда отдаюсь на сто процентов.
O Буква O Значение Лоду
Любовь важнее всего, и к ней очень серьезно относятся люди, в имени которых есть буква О. Это люди отношений, которые хотят поделиться своей жизнью и ценят лояльность. Редко можно встретить их одинокими.
Хотя они кажутся застенчивыми и сдержанными в своих желаниях. В глубине души им просто нравится заниматься веселыми делами с партнером. Сострадательные любовники, которые прежде всего стремятся к обязательствам и усилиям для поддержания отношений. Однако последнее иногда приводит их к излишней притяжательности. Одним из уникальных навыков, которыми они обладают, является способность эффективно справляться с различными объемами энергии, времени или денег. Что позволяет им оставаться на высоте в самых сложных ситуациях.
Творческие люди, обладающие потрясающим воображением. Для них очень важно быть частью семьи. Это делает их цельными, давая им чувство цели.
D Буква D Значение Lodu
Люди, чьи имена имеют букву D, как правило, чрезвычайно страстны, верны и сильны в своих эмоциях и обязательствах. Как только они решат что-то сделать для кого-то, они отдадут все, что у них есть от себя, чтобы это произошло.
Вот почему очень редко можно увидеть, как они терпят неудачу или сдаются! Такая же настойчивость справедлива и в отношении сердечных дел. Любовь и забота дарятся людям, которые становятся объектами их желания. В большинстве своем это не очень поверхностные люди. Довольно талантливые по своей природе, они имеют сильную поддерживающую личность, которая довольно лояльна. Некоторые из самых больших недостатков — это ревность и недостаток терпения. Эти черты трудно изменить, потому что ими движет эго. Исключительный опыт может дать им большую стимуляцию. Занятия экстремальными видами спорта могут привести их в опасные ситуации.
Тот, кто дарит безусловную любовь и нуждается в эмоциональном равновесии. Если вы не найдете эмоциональной стабильности, это может очень негативно на вас повлиять. У вас есть художественный талант, и вы можете добиться больших успехов, если будете готовы приложить усилия. В мире полно талантливых людей, которые потерпели неудачу, потому что стали ленивыми.
U Буква U Значение слова Lodu
Любовь и романтика — это то, что приносит наибольшее счастье в вашу жизнь, когда ваше имя содержит букву U. Если вы не влюблены, обычно вы постоянно ищете кого-то особенного.
Тем не менее, эти романы также имеют тенденцию принимать форму вызова. Как правило, очень предприимчивые, вы получаете волнение от ощущения свободы. Способность понимать чувства других — одна из ваших величайших способностей. Дарение подарков приносит вам большую радость и чувство удовлетворения. Это из-за твоего великодушия
Способен очень свободно выражать себя. Жить так, как если бы это была комедия или трагедия. В результате много эмоциональных взлетов и падений. Они не конформисты. Всегда стремится к совершенству, которого трудно достичь.

Find Your Own Name

Different Ways To Spell Lodu

Lodygina
Lodyjensky
Lodylyn
Lodymar
Lodymer
Lodyn
Lodyr
Lodyrenza
Lodysheeno
Lodyver
Lodyx
Лодзь
Лодзя
Лоджик
Лодзи
Лодзя
Лодзьинский
Лоэай
Лоеандро
0 Лоеб

570

Имя Lodu Произношение

Хотите знать, как произносится это имя? Просто нажмите на кнопку и слушайте:

Имена, начинающиеся с L

❝ Слишком часто мы недооцениваем силу прикосновения, улыбки, доброго слова, внимательного слушателя, честного комплимента или малейшего проявления заботы , все из которых могут изменить жизнь. ❞

Бывший капитан Майк Фишер выходит из отставки в Nashville Predators

Эл.

распечатать

Майк Фишер решил завершить карьеру в НХЛ и вернуться в «Нэшвилл Предаторз», с которым он играл в финале Кубка Стэнли в прошлом сезоне.

Фишер подписал контракт на профессиональные пробы, чтобы начать работать с командой, и он рассчитывает подписать контракт на оставшуюся часть сезона до крайнего срока обмена 26 февраля, когда должны быть определены составы после окончания сезона. Он тренировался в полной экипировке «Хищников» в среду утром на «Бриджстоун Арене».

«Потерпите меня, я все еще немного запыхался после катания сегодня утром», — пошутил Фишер. «Здорово вернуться».

37-летний Фишер сказал, что обдумывал это решение несколько недель.

«Меня всегда немного раздражало, когда парни выходили из отставки. Я действительно не думал, что это возможно», — сказал он. «Я просто подумал о возможности. Насколько хороша эта команда. О пробеге в прошлом году и о том, что может быть. Я получил благословение от семьи и моей жены».

Майк Фишер вернется в желто-черную форму после того, как решил завершить карьеру и вернуться в «Хищники». Кристофер Ханевинкель-США СЕГОДНЯ Спорт

Фишер сказал, что его жена, звезда кантри-музыки Кэрри Андервуд, поощряла его возвращение в НХЛ.

«Кэрри каждые несколько дней спрашивала меня, собираюсь ли я это сделать. Она хотела, чтобы я это сделал. И обычно она была права», — сказал Фишер, пятый бомбардир в истории «Хищников» (109).

Это происходит! Рыба вернулась! Так горжусь тобой, детка! Хотим кубок!!! https://t.co/ohP7zPtT1s
— Кэрри Андервуд (@carrieunderwood) 31 января 2018 г.

Генеральный менеджер «Хищников» Дэвид Пойл сказал, что Фишер больше не станет капитаном команды, и эта честь была оказана защитнику Роману Джози. Пойл сказал, что внутри команды обсуждалось, захочет ли Фишер вернуться в НХЛ. Тренер Питер Лавиолетт поговорил с Фишером, и встреча с Джози завершила сделку. Лавиолетт сказал, что руководители команды рады возвращению Фишера.

«[Мы] вернем в нашу раздевалку потрясающего человека и потрясающего игрока», — сказал Лавиолетт.

Фишер сказал, что он «немного» потренировался на пенсии, но потребуется некоторое время, чтобы войти в игровую форму.

Фишер объявил об окончании своей 17-летней карьеры в НХЛ 3 августа на пресс-конференции и в письме болельщикам. «Знание того, что мы были так близки к победе в июне, только усложняет процесс расставания, но я делаю это с надеждой. тоже есть чему порадоваться», — написал он.

Фишер сказал в начале сезона, что он все еще живет в жизни после НХЛ. «Я хочу взять отпуск, чтобы понять, каково это не играть, просто понять, какой будет повседневная жизнь», — сказал он The Tennessean.

Пойл сказал, что у Фишера нет расписания игр.

«Он принял решение. У него есть огонь и желание вернуться. Каждый раз, когда он ставит перед собой задачу, он ее выполняет», — сказал Пойл.

Возвращение Фишера укрепляет и без того сильную группу центровых «Хищников», включая Райана Йохансена, Кайла Терриса и Ника Бонино, который заменил Фишера в межсезонье. Фишер также поможет решить проблемы Predators (29-12-7) имеют одинаковую силу среди своих шести худших нападающих, поскольку Бонино (минус-92), Остин Уотсон (минус-82) и Калле Ярнкрок (минус-73) являются одними из худших Хищников в дифференциале попыток броска.

Фишер забил 18 голов и отдал 24 передачи в 72 матчах за «Хищников» в прошлом сезоне, показывая 16:37 за игру. У него было четыре передачи в 20 играх плей-офф. Фишер сказал, что потенциал команды выиграть Кубок Стэнли, проиграв «Питтсбург Пингвинз» в шести играх в июне прошлого года, был одним из факторов, повлиявших на возвращение в НХЛ.

«Я считаю, что эта команда создана для победы и имеет очень хорошие шансы. Это одна из причин, по которой я хочу вернуться», — сказал Фишер. «Но мы не выиграли в прошлом году, и это была лучшая часть моей карьеры».

Электронная почта

Условия использования
Политика конфиденциальности
Реклама на основе интересов
Права ЕС на конфиденциальность
Политика использования файлов cookie
Управление настройками конфиденциальности

Суды Непала на скамье подсудимых за мягкие приговоры за преступления против тигров

Законы Непала о преступлениях против дикой природы относительно строги, но правонарушителям, как правило, выносятся мягкие приговоры суда. Туфан Неупане анализирует несколько вердиктов, чтобы понять, связана ли проблема с законом или судебным разбирательством.

4 мая 2015 года полиция Непала арестовала Рамджаса Банджару с тигриной шкурой и 47 костями тигра.

Дальнейшее расследование показало, что Банджара, гражданин Индии, был причастен к торговле частями тела тигра. в Непале и что его разыскивали в Индии за преступления против дикой природы.

Прокуроры добились вынесения ему обвинительного приговора в соответствии с Законом о национальных парках и охране дикой природы от 1973 года и потребовали в районном суде Бардии максимальное наказание и меры наказания, предусмотренные законом — от пяти до 15 лет лишения свободы, штраф в размере от 500 рупий, 000 до 1 миллиона рупий (4 293–8 586 долларов США) или и то, и другое.

Банджара признался, что купил шкуру тигра за 15 000 рупий (128 долларов США) у неизвестного лица. Судебно-медицинская экспертиза кожи и костей показала, что они принадлежали бенгальскому тигру, исчезающему виду, обитающему только на Индийском субконтиненте.

В 2016 году Бардийский районный суд приговорил его к пяти годам лишения свободы — минимальному наказанию за преступление. Затем прокуратура обжаловала приговор, но Высокий суд Непалгунджа оставил приговор в силе в 2017 году. Закон Непала не допускает дальнейшего обжалования, если оба суда вынесли один и тот же приговор по делу о лишении свободы на срок менее 10 лет.

К маю 2020 года Банджара был освобожден после отбытия полного тюремного срока, недавно подтвердил информационный сотрудник Высокого суда Мунна Сингх Четри. С тех пор у полиции нет информации о его местонахождении.

«Не было смысла снова арестовывать Банджару после того, как он отбыл свой срок в тюрьме, потому что у нас не было других дел против него», — сказал Бирендра Джохари, офицер отдела охраны дикой природы Центрального бюро расследований (CIB) полиции Непала.

«Однако мы знаем, что против него возбуждено несколько дел в Индии», — добавил Джохари, опасавшийся, что Банджара может возобновить торговлю дикими животными в Непале, если его не арестуют в Индии.

Мягкое наказание

Дело Банджары является лишь одним из примеров того, как преступники, совершившие преступления против дикой природы, обычно получают мягкие пощечины, говорят защитники природы, несмотря на то, что законы Непала более строгие по сравнению с законами соседних стран.

Эта схема побудила преступников возобновить торговлю людьми после освобождения из тюрьмы, – сказал Рамприт Ядав, бывший директор по охране природы национального парка Читван.

«Законы суровы, но вора в законе ухитрилась пройти через суды на свободе, а бедняки, которые работали перевозчиками и не могут позволить себе защищаться в судах, попадают под удар. Они остаются в тюрьме, в то время как вора в законе, как правило, формирует новые преступные группы и возобновляет торговлю дикими животными», — сказал Ядав.

Оценка текущих преступлений против дикой природы показывает, что методы действий браконьеров и оружие, которое они используют для убийства диких животных, остаются неизменными, и что они возобновили свои преступления, добавил Ядав.

После отсутствия случаев браконьерства с участием носорогов в течение трех с половиной лет, например, с октября 2020 года по меньшей мере 16 однорогих носорогов были найдены мертвыми. Правительственное расследование подтвердило, что четверо из них были убиты браконьерами.

Кришна Прасад Бхуртел, член парламента провинции Багмати и бывший председатель комитета по управлению буферной зоной национального парка Читван, обвинил судей в том, что они несерьезно относятся к охране дикой природы при вынесении приговоров по преступлениям против дикой природы.

«Строгие правовые нормы бессмысленны, если правонарушителям даются минимальные наказания независимо от тяжести совершенных ими преступлений», — сказал Бхуртел.

«Известные браконьеры и меткие стрелки в последние несколько лет отбывали срок в тюрьме, но, возможно, их снова использовали в торговле дикими животными после того, как они были освобождены с минимальными приговорами», — сказал Бхуртел.

Кумар Паудел, научный исследователь преступлений против дикой природы, сказал, что крупные торговцы людьми могут влиять на политиков и суды, чтобы смягчить наказание или выйти на свободу.

В рамках исследовательского проекта под названием Охрана природы: мнения людей, заключенных в тюрьму за преступления против дикой природы в Непале, Паудел посетил несколько тюрем по всей стране и взял интервью у заключенных. Он обнаружил, что 75% осужденных были выходцами из коренных общин.

«В законах есть лазейки. Воров в законе редко арестовывают, а в тех случаях, когда их арестовывают, им удается выйти на свободу», — отметил Паудель.

Лоду Дайм: печально известный контрабандист дикой природы был экстрадирован в Непал индийской полицией в 2018 году, но был освобожден под залог судами Непала и скрылся / Фото предоставлено CIB

Лоду Дайм

Так было с Лоду Даймом, жителем Катманду и известным торговцем людьми, осужденным за незаконную торговлю частями тигра.

12 января 2013 г. автомобиль, направлявшийся из Катманду на границу с Китаем Расува, был остановлен с пятью целыми тигровыми шкурами, 512 кусками тигровых костей и 122 тигровыми челюстями. Полиция арестовала владельца автомобиля Сук Бахадура Таманга и водителя Накула Таманга.

Широко сообщалось, что в деле фигурирует вор в законе о преступлениях против дикой природы.

Сук Бахадур Таманг признал, что он был курьером и что товары принадлежали Лоду Дайму, который заплатил ему 100 000 рупий (858 долларов США) за транспортировку.

Полиция провела обыск в доме Дайма в Катманду и конфисковала части диких животных, товары из частей животных, восемь паспортов и наличные деньги в нескольких международных валютах. К тому времени Дайм скрылся.

Затем прокуратура возбудила дело против трех мужчин в Управлении лесного хозяйства округа Нувакот. 27 июня 2013 г. окружной инспектор лесного хозяйства приговорил Дайма к штрафу в размере 100 000 рупий (858 долларов США) 9. 1061 заочно после того, как выяснилось, что он не был причастен к торговле частями диких животных в автомобиле, но был виновен в хранении их у себя дома в Катманду.

Водителю было приказано заплатить штраф в размере 100 000 рупий (858 долларов США), а владелец автомобиля был приговорен к девяти годам лишения свободы и штрафу в размере 60 000 рупий (515 долларов США) — намного больше, чем приговор, вынесенный Дайму.

Государственная прокуратура подала апелляцию в Высокий суд Патана, оспаривая приговор. 24 февраля 2018 г. Верховный суд приговорил Дайма заочно к пяти годам лишения свободы, сославшись на тяжесть преступления и роль, которую Дайм сыграл в преступлении.

Все это время Дайм оставался на свободе, пока в мае 2018 года его не вернули в Непал после ареста в Индии с помощью индийской полиции.

В июле 2018 года он получил постановление Верховного суда, позволяющее ему обжаловать приговор высшего суда и не выходить из тюрьмы под залог до вынесения решения. На момент публикации этой истории Верховный суд еще не приступил к рассмотрению апелляции Дайма.

Однако, по словам офицера полиции отдела дикой природы CIB, Дайм сбежал обратно в Индию, так как условия залога не ограничивали его передвижения. Напротив, владелец автомобиля, который признался в перевозке контрабанды диких животных, все еще находится в тюрьме, отбывая свой девятилетний срок.

Граждане Индии Рамдаял Бабариа и Шраван Бабариа. Осужденные за поездку в Непал из района Панчкула в Индии для продажи тигровой шкуры и частей тела, они были приговорены 3 января 2017 года к пяти годам тюремного заключения и штрафу в размере 50 000 рупий. По данным районного суда, оба уже освобождены / Фото предоставлено ЦИБ

Тяжесть преступления

В то время как Закон о национальных парках и охране дикой природы Непала 1973 года предусматривает тюремное заключение на срок до 15 лет, в зависимости от тяжести преступления, Закон Индии о защите дикой природы 1972 года устанавливает максимальное наказание в размере семь лет или штраф в размере 25 000 рупий (343 доллара США), или и то, и другое.

Закон Бутана об охране лесов и природы 1995 года предписывает лишение свободы сроком до пяти лет, а Бангладеш допускает тюремное заключение на срок от двух до семи лет для первых правонарушителей со штрафом в размере от 100 000 (1179 долларов США)) до 1 миллиона (11795 долларов) бангладешских така.

Заместитель суперинтенданта полиции Радж Кумар Рай, начальник отдела дикой природы CIB, сказал, что освобождение торговцев дикой природой после отбытия коротких тюремных сроков в Непале в последние годы представляет собой проблему.

«Выявлено, что многие другие преступники продолжают ту же преступную деятельность после отбытия тюремного срока», — сказал он.

Главный специалист по охране природы национального парка Читван Ананат Барал сказал, что судьи, похоже, не понимают серьезности преступлений против дикой природы и важности защиты исчезающих видов.

«Некоторые судьи, по-видимому, считают, что убийство детеныша буйвола и однорогого носорога влечет за собой аналогичные правонарушения. Они считают, что не должны никого отправлять в тюрьму просто за убийство животного», — сказал Бараль.

«Сами национальные парки рассматривали дела о правонарушениях в отношении дикой природы и назначали виновным максимальные наказания, — сказал он. — Но в настоящее время суды рассматривают дела о правонарушениях в дикой природе и назначают более низкие наказания. Это отрицательно сказалось на природоохранном секторе».

Квазисудебные органы, такие как национальные парки, охотничьи заповедники, управления охраняемых территорий и районные управления лесного хозяйства, которые использовались для расследования, судебного преследования и проведения судебных процессов, связанных с преступлениями против дикой природы, до того, как новая Конституция, принятая в сентябре 2015 года, поручала дела, связанные с преступлениями, наказуемыми более одного года лишения свободы в районные суды.

Окружные суды применяли минимальные меры наказания, а позже их примеру последовали высокие суды и Верховный суд. По словам Барала, это стало новой тенденцией в судебных делах, связанных с дикой природой.

Окружной суд Читвана, где судьи слушали большинство дел о преступлениях против дикой природы, отверг этот аргумент. Один из судей этого суда, попросивший не называть его имени, сказал: «Почти все обвиняемые [обвиняемые] ранее были осуждены и заключены в тюрьму, но теперь мы выносим приговоры по этим преступлениям с учетом того, что права человека обвиняемых не нарушаются.

«Мы рассматриваем вопрос о том, был ли преступник вовлечен в запланированное, а также оцениваем его / ее роль в преступлении при вынесении приговора», — сказал судья.

Туфан Неупане, специальный корреспондент журнала Himalkhabar, пишет о правосудии переходного периода, правах человека, судебной системе, преступлениях против дикой природы и окружающей среде. Это расследование спонсировали #WildEye Asia и Internews ’ Earth Journalism Network. Первоначально он был опубликован на Oxpeckers и был отредактирован здесь для увеличения длины и ясности.

Линейные однородные дифференциальные уравнения второго порядка

Решить линейное однородное дифференциальное уравнение с постоянными коэффициентами самостоятельно, а затем посмотреть решение

3.

31.Свойства решений лоду

32. Определитель Вронского

33. Структура общего решения лоду

Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами

Общее решение ЛОДУ и ЛДНУ

Методы решения ЛОДУ и ЛНДУ

определение и пример с решением

Андреа Лоди — Мила

2021-12

2021-10

2021-09

2021-08

2021-05

2021-04

2021-03

2021-02

2021-01

2020-12

2020-11

2020-10

2020-09

2020-08

4 задача об устойчивом множестве

2020-06

2020-05

2020-04

2020-03

1020002

2

2019-12

2019-11

2019-10

2019-09

2019-06

2019-05

2019-03

2019-01

и Матье

2018-12

2018-10

2018-08

2018-07

2018-06

2018-04

2018-03

2018-01

Mazzera’s | Кухня Реконструировать | Реконструкция ванны | Лоди, Калифорния

Дерево Лоди | Charity Navigator Profile

Encompass Rating System By Charity Navigator

Общая оценка

В настоящее время не набирают

Финансы и подотчетность

Баллы по финансам и подотчетности

В настоящее время баллы отсутствуют

Additional Information

Unscored

Total Revenue

Salary of

IRS Опубликованные данные

Источники данных

Общие доходы и расходы

Данные отсутствуют

Заработная плата ключевых лиц

Нет данных

Данные основного бизнес-файла

Виды деятельности:

Статус фонда:

Принадлежность:

Источники данных: Формы IRS 990

Воздействие и результаты

Оценка воздействия и результатов

В настоящее время не оценивается

Лидерство и способность к адаптации

Оценка Лидерства и Адаптивности

В настоящее время не оценивается

Культура и сообщество

Оценка по культуре и сообществу