Логарифм 100: Как быстро найти любой логарифм с помощью обычного цикла

Содержание

Как быстро найти любой логарифм с помощью обычного цикла

На прошлой неделе мы рассказали, что такое логарифм и зачем он нужен. Сегодня найдём логарифм с помощью программирования.

Вот короткая версия теории:

Логарифм — это в какую степень нужно возвести одно число, чтобы получить другое число.
То, число, которое возводят в степень, называется основанием логарифма.
Логарифм обозначается словом log.
Например, log(10) 100 = 2, потому что 10² = 100.
Есть ещё обозначение lg — это то же самое, что log(10). И есть ln — это то же самое, что log(e), где e — это число Эйлера, важная математическая константа.
Логарифмы используются в каждой значимой области нашей жизни, от биологии до физики.

Теперь, когда мы знаем достаточно про логарифм, то можем написать программу, которая нам найдёт любой логарифм по любому основанию.

В чём идея

Мы уже выяснили, что логарифм — это степень, в которую нужно возвести основание логарифма, чтобы получить нужное число. Получается, что нам нужно подобрать такую степень, чтобы при возведении она давала такое же число — это и будет ответом к решению логарифма.

Алгоритм поиска будет таким:

Найдём минимальное значение степени, возведение в которую ещё не превысит наше число.
Это значит, что следующее за ним целое число — уже перебор, и основание в этой степени точно превысит наше число.
Будем делить этот промежуток пополам нужное количество раз, пока не получим нужную точность ответа после запятой.
Когда цикл закончится, середина оставшегося промежутка и будет ответом.

Мы так уже делили границы пополам в задаче про то, как угадать число за 7 попыток, поэтому, если алгоритм показался немного непонятным, — перечитайте то решение и возвращайтесь сюда.

Готовим переменные

Для работы программы пользователь должен будет указать три вещи:

Основание логарифма.
Число, от которого мы берём этот логарифм.
Точность решения. Точность указываем в количестве точно вычисленных знаков после запятой.

Выделим переменные для этого:

# на старте границы поиска значения логарифма все равны нулю
start = 0
end = 0
middle = 0
# логарифм какого числа мы ищем
num = 600
# основание логарифма
base = 10
# сколько нужно знаков после запятой
accuracy = 4

Вычисляем границы

Поиск делаем так: начинаем считать от нуля и на каждом шаге увеличиваем это значение на единицу. Как только мы превысили аргумент (то, от чего берём логарифм) — это наша конечная граница. Соответственно, предыдущее значение, которое на единицу меньше, будет стартовой границей.

# пока основание в очередной степени не превысило само число — 
while base**end <= num:
    # увеличиваем конечную границу поиска на единицу
    end += 1
# откатываемся на один шаг назад от конечной границы, чтобы найти начальную границу
start = end - 1

Проверяем, вдруг мы сразу нашли решение

На всякий случай перед тем, как идти дальше, проверим, будет ли решением наша стартовая граница — это сразу может сэкономить нам много сил в дальнейшем:

Проверяем, вдруг мы сразу нашли решение
На всякий случай перед тем, как идти дальше, проверим, будет ли решением наша стартовая граница — это сразу может сэкономить нам много сил в дальнейшем:
# если сразу нашли целое значение степени
if base**start == num:
    # выводим решение
    print('log(' + str(base) + ')' + str(num) + ' = ' + str(start))
    # останавливаем программу
    exit(0)

Считаем логарифм

Мы будем считать логарифм не классическим способом из высшей математики, а простым приближением — найдём ответ с приемлемой точностью.

За точность отвечает переменная accuracy, но в цикле мы её умножим на 4. Это неочевидный ход, поэтому сейчас объясним, в чём тут дело.

На каждом шаге цикла мы делим границу пополам, но если деление выпадает на чётную значимую цифру, то при делении у нас не увеличится количество знаков после запятой. Например, если нам нужна точность 2 знака после запятой, то если вторым шагом цикла мы разделим 0,4 на 2, то у нас останется один знак после запятой (0,2). Таких делений может быть 4 подряд, прежде чем мы доберёмся до следующего знака: 8 → 4 → 2 → 1, поэтому мы и умножаем требуемую точность на 4 — чтобы гарантированно получить нужную точность.

Теперь запишем этот цикл на языке программирования. Его можно было сделать изящнее, например, вложив условные операторы друг в друга или используя оператор множественного выбора, но так получается нагляднее:

# организуем цикл, чтобы получить нужную точность после запятой
for i in range(accuracy*4):
    # увеличиваем счётчик цикла
    i += 1
    # находим серединное значение
    middle = (start + end) / 2
    # если основание в этой степени больше нашего числа, то сдвигаем к середине конечную границу
    if base**middle > num:
        end = middle
    # если основание в этой степени больше нашего числа, то сдвигаем к середине начальную границу
    if base**middle < num:
        start = middle
    # если основание в этой степени равно нашему числу
    if base**middle == num:
        # выводим ответ и выходим из цикла
        print('log(' + base + ')' + num + ' = ' + start)
        break

Выводим ответ

Это самая простая часть алгоритма:

# когда цикл закончился — выводим ответ
print('log(' + str(base) + ')' + str(num) + ' = ' + str(middle))

Проверяем работу

Для проверки посчитаем log(10) 600 с помощью нашей программы:

Ответ программы — 2,77815 с точностью 5 знаков после запятой

Теперь запустим калькулятор и проверим наше решение:

Первые 5 знаков после запятой — те же самые, значит? Алгоритм работает верно

# на старте границы поиска значения логарифма все равны нулю
start = 0
end = 0
middle = 0
# логарифм какого числа мы ищем
num = 600
# основание логарифма
base = 10
# сколько нужно знаков после запятой
accuracy = 5
# пока основание в очередной степени не превысило само число — 
while base**end <= num:
    # увеличиваем конечную границу поиска на единицу
    end += 1
# откатываемся на один шаг назад от конечной границы, чтобы найти начальную границу
start = end - 1
# если сразу нашли целое значение степени
if base**start == num:
    # выводим решение
    print('log(' + str(base) + ')' + str(num) + ' = ' + str(start))
    # останавливаем программу
    exit(0)
# организуем цикл, чтобы получить нужную точность после запятой
for i in range(accuracy*4):
    # увеличиваем счётчик цикла
    i += 1
    # находим серединное значение
    middle = (start + end) / 2
    # если основание в этой степени больше нашего числа, то сдвигаем к середине конечную границу
    if base**middle > num:
        end = middle
    # если основание в этой степени больше нашего числа, то сдвигаем к середине начальную границу
    if base**middle < num:
        start = middle
    # если основание в этой степени равно нашему числу
    if base**middle == num:
        # выводим ответ и выходим из цикла
        print('log(' + base + ')' + num + ' = ' + start)
        break
# когда цикл закончился — выводим ответ
print('log(' + str(base) + ')' + str(num) + ' = ' + str(middle))

Текст:

Михаил Полянин

Редактор:

Максим Ильяхов

Художник:

Даня Берковский

Корректор:

Ирина Михеева

Вёрстка:

Кирилл Климентьев

Соцсети:

Алина Грызлова

Mathway | Популярные задачи

1	Множитель	x^2-4
2	Множитель	4x^2+20x+16
3	График	y=-x^2
4	Вычислить	2+2
5	Множитель	x^2-25
6	Множитель	x^2+5x+6
7	Множитель	x^2-9
8	Множитель	x^3-8
9	Вычислить	квадратный корень из 12
10	Вычислить	квадратный корень из 20
11	Вычислить	квадратный корень из 50
12	Множитель	x^2-16
13	Вычислить	квадратный корень из 75
14	Множитель	x^2-1
15	Множитель	x^3+8
16	Вычислить	-2^2
17	Вычислить	квадратный корень из (-3)^4
18	Вычислить	квадратный корень из 45
19	Вычислить	квадратный корень из 32
20	Вычислить	квадратный корень из 18
21	Множитель	x^4-16
22	Вычислить	квадратный корень из 48
23	Вычислить	квадратный корень из 72
24	Вычислить	квадратный корень из (-2)^4
25	Множитель	x^3-27
26	Вычислить	-3^2
27	Множитель	x^4-1
28	Множитель	x^2+x-6
29	Множитель	x^3+27
30	Множитель	x^2-5x+6
31	Вычислить	квадратный корень из 24
32	Множитель	x^2-36
33	Множитель	x^2-4x+4
34	Вычислить	-4^2
35	Множитель	x^2-x-6
36	Множитель	x^4-81
37	Множитель	x^3-64
38	Вычислить	4^3
39	Множитель	x^3-1
40	График	y=x^2
41	Вычислить	2^3
42	Вычислить	(-12+ квадратный корень из -18)/60
43	Множитель	x^2-6x+9
44	Множитель	x^2-64
45	График	y=2x
46	Множитель	x^3+64
47	Вычислить	(-8+ квадратный корень из -12)/40
48	Множитель	x^2-8x+16
49	Вычислить	3^4
50	Вычислить	-5^2
51	Множитель	x^2-49
52	Вычислить	(-20+ квадратный корень из -75)/40
53	Множитель	x^2+6x+9
54	Множитель	4x^2-25
55	Вычислить	квадратный корень из 28
56	Множитель	x^2-81
57	Вычислить	2^5
58	Вычислить	-8^2
59	Вычислить	2^4
60	Множитель	4x^2-9
61	Вычислить	(-20+ квадратный корень из -50)/60
62	Вычислить	(-8+ квадратный корень из -20)/24
63	Множитель	x^2+4x+4
64	Множитель	x^2-10x+25
65	Вычислить	квадратный корень из -16
66	Множитель	x^2-2x+1
67	Вычислить	-7^2
68	График	f(x)=2^x
69	Вычислить	2^-2
70	Вычислить	квадратный корень из 27
71	Вычислить	квадратный корень из 80
72	Множитель	x^3+125
73	Вычислить	-9^2
74	Множитель	2x^2-5x-3
75	Вычислить	квадратный корень из 40
76	Множитель	x^2+2x+1
77	Множитель	x^2+8x+16
78	График	y=3x
79	Множитель	x^2+10x+25
80	Вычислить	3^3
81	Вычислить	5^-2
82	График	f(x)=x^2
83	Вычислить	квадратный корень из 54
84	Вычислить	(-12+ квадратный корень из -45)/24
85	Множитель	x^2+x-2
86	Вычислить	(-3)^3
87	Множитель	x^2-12x+36
88	Множитель	x^2+4
89	Вычислить	квадратный корень из (-8)^2
90	Множитель	x^2+7x+12
91	Вычислить	квадратный корень из -25
92	Множитель	x^2-x-20
93	Вычислить	5^3
94	Множитель	x^2+8x+15
95	Множитель	x^2+7x+10
96	Множитель	2x^2+5x-3
97	Вычислить квадратный корень	квадратный корень из 116
98	Множитель	x^2-x-12
99	Множитель	x^2-x-2
100	Вычислить	2^2

Mathway | Популярные задачи

1	Множитель	x^2-4
2	Множитель	4x^2+20x+16
3	График	y=-x^2
4	Вычислить	2+2
5	Множитель	x^2-25
6	Множитель	x^2+5x+6
7	Множитель	x^2-9
8	Множитель	x^3-8
9	Вычислить	квадратный корень из 12
10	Вычислить	квадратный корень из 20
11	Вычислить	квадратный корень из 50
12	Множитель	x^2-16
13	Вычислить	квадратный корень из 75
14	Множитель	x^2-1
15	Множитель	x^3+8
16	Вычислить	-2^2
17	Вычислить	квадратный корень из (-3)^4
18	Вычислить	квадратный корень из 45
19	Вычислить	квадратный корень из 32
20	Вычислить	квадратный корень из 18
21	Множитель	x^4-16
22	Вычислить	квадратный корень из 48
23	Вычислить	квадратный корень из 72
24	Вычислить	квадратный корень из (-2)^4
25	Множитель	x^3-27
26	Вычислить	-3^2
27	Множитель	x^4-1
28	Множитель	x^2+x-6
29	Множитель	x^3+27
30	Множитель	x^2-5x+6
31	Вычислить	квадратный корень из 24
32	Множитель	x^2-36
33	Множитель	x^2-4x+4
34	Вычислить	-4^2
35	Множитель	x^2-x-6
36	Множитель	x^4-81
37	Множитель	x^3-64
38	Вычислить	4^3
39	Множитель	x^3-1
40	График	y=x^2
41	Вычислить	2^3
42	Вычислить	(-12+ квадратный корень из -18)/60
43	Множитель	x^2-6x+9
44	Множитель	x^2-64
45	График	y=2x
46	Множитель	x^3+64
47	Вычислить	(-8+ квадратный корень из -12)/40
48	Множитель	x^2-8x+16
49	Вычислить	3^4
50	Вычислить	-5^2
51	Множитель	x^2-49
52	Вычислить	(-20+ квадратный корень из -75)/40
53	Множитель	x^2+6x+9
54	Множитель	4x^2-25
55	Вычислить	квадратный корень из 28
56	Множитель	x^2-81
57	Вычислить	2^5
58	Вычислить	-8^2
59	Вычислить	2^4
60	Множитель	4x^2-9
61	Вычислить	(-20+ квадратный корень из -50)/60
62	Вычислить	(-8+ квадратный корень из -20)/24
63	Множитель	x^2+4x+4
64	Множитель	x^2-10x+25
65	Вычислить	квадратный корень из -16
66	Множитель	x^2-2x+1
67	Вычислить	-7^2
68	График	f(x)=2^x
69	Вычислить	2^-2
70	Вычислить	квадратный корень из 27
71	Вычислить	квадратный корень из 80
72	Множитель	x^3+125
73	Вычислить	-9^2
74	Множитель	2x^2-5x-3
75	Вычислить	квадратный корень из 40
76	Множитель	x^2+2x+1
77	Множитель	x^2+8x+16
78	График	y=3x
79	Множитель	x^2+10x+25
80	Вычислить	3^3
81	Вычислить	5^-2
82	График	f(x)=x^2
83	Вычислить	квадратный корень из 54
84	Вычислить	(-12+ квадратный корень из -45)/24
85	Множитель	x^2+x-2
86	Вычислить	(-3)^3
87	Множитель	x^2-12x+36
88	Множитель	x^2+4
89	Вычислить	квадратный корень из (-8)^2
90	Множитель	x^2+7x+12
91	Вычислить	квадратный корень из -25
92	Множитель	x^2-x-20
93	Вычислить	5^3
94	Множитель	x^2+8x+15
95	Множитель	x^2+7x+10
96	Множитель	2x^2+5x-3
97	Вычислить квадратный корень	квадратный корень из 116
98	Множитель	x^2-x-12
99	Множитель	x^2-x-2
100	Вычислить	2^2

Zero To Hero

Содержание:

1.	Число e означает рост
2.	Натуральный логарифм означает время
3.	Этот нестандартный логарифмический счёт
4.	Логарифмическое умножение — просто умора
5.	Использование натурального логарифма при произвольном росте
6.	Отпадный пример: Правило 72
7.	Дополнение: Натуральный логарифм от e

Мы уже разобрались с экспоненциальной функцией в посвящённой ей статье, и нашей следующей целью становится натуральный логарифм.

В учебниках математики определение натурального логарифма такое, что ничего «натурального», естественного в нём нет: он определяется как действие, обратное функции e^x, странной уже самой по себе.

Так что вот вам новое, упрощённое объяснение: Натуральный логарифм — это время, необходимое, чтобы вырасти до определённого уровня.

Представьте, что вы сделали инвестицию мишками Гамми (а кто так не делает?) с непрерывной доходностью 100% годовых. Если вы преследуете цель достичь десятикратного роста вклада, при условии «сложных процентов», вам пришлось бы ждать всего-то ln(10) = 2.3 года. Не можете понять, почему необходимо только пару лет, чтобы достичь 10х роста? Не понимаете, почему последовательность не 1, 2, 4, 8? Почитайте про число e.

Число e и натуральный логарифм — братья-близнецы:

e^x — уровень, достигнутый при непрерывном росте за определённый промежуток времени.
натуральный логарифм (ln) — промежуток времени, необходимый для роста до определённого уровня.

Совсем неплохо, правда? Пока математики подбирают слова, чтобы дать вам длинное путанное определение, давайте поближе посмотрим на это простое и ясное.

Число e означает рост

Число e означает непрерывный рост. Как мы видели в прошлом примере, e^x позволяет нам увязать процент и время: 3 года при росте 100% есть то же самое, что и 1 год при 300%, при условии «сложных процентов».

Можно подставлять любые значения процента и времени (50% на протяжении 4 лет), но лучше задать процент как 100% для удобства (получается 100% на протяжении 2 лет). За счёт перехода к 100% мы можем сфокусироваться исключительно на компоненте времени:

e^x = e^{процент * время} = e^{1.0 * время} = e^время

Очевидно, что e^x означает:

насколько вырастет мой вклад через x единиц времени (при условии 100%-го непрерывного роста).
например, через 3 промежутка времени я получу в e³ = 20.08 раз больше «штуковин».

e^x — это масштабирующий коэффициент, показывающий, до какого уровня мы вырастем за x отрезков времени.

Натуральный логарифм означает время

Натуральный логарифм — это инверсия числа e, такой причудливый термин для обозначения противоположности. Кстати, о причудах; по латыни он называется logarithmus naturali, отсюда и появилась аббревиатура ln.

И что эта инверсия или противоположность означает?

e^x позволяет нам подставить время и получить рост.
ln(x) позволяет нам взять рост или доход и узнать время, необходимое для его получения.

Например:

e³ равняется 20.08. Через три отрезка времени у нас будет в 20.08 раз больше того, с чего мы начали.
ln(20.08) будет примерно 3. Если вас интересует рост в 20.08 раз, вам понадобится 3 промежутка времени (опять же, при условии стопроцентного непрерывного роста).

Всё ещё читаете? Натуральный логарифм показывает время, нужное, чтобы достичь желаемого уровня.

Этот нестандартный логарифмический счёт

Вы проходили логарифмы — это странные существа. Как им удалось превратить умножение в сложение? А деление в вычитание? Давайте посмотрим.

Чему равняется ln(1)? Интуитивно понятно, что вопрос стоит так: сколько нужно ждать, чтобы получить в 1 раз больше того, что у меня есть?

Ноль. Нуль. Нисколько. У вас уже это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.

ln(1) = 0

Хорошо, что насчёт дробного значения? Через сколько у нас останется 1/2 от имеющегося количества? Мы знаем, что при стопроцентном непрерывном росте ln(2) означает время, необходимое для удвоения. Если мы обратим время вспять (т.е. подождём отрицательное количество времени), то получим половину от того, что имеем.

ln(1/2) = —ln(2) = —0.693

Логично, правда? Если мы вернёмся назад (время вспять) на 0.693 секунды, то обнаружим половину имеющегося количества. Вообще можно переворачивать дробь и брать отрицательное значение: ln(1/3) = —ln(3) = —1.09. Это означает, что, если мы вернёмся в прошлое на 1.09 отрезков времени, то обнаружим только треть от нынешнего числа.

Ладно, а как насчёт логарифма отрицательного числа? Сколько времени нужно, чтобы «вырастить» колонию бактерий от 1 до —3?

Это невозможно! Нельзя получить отрицательное число бактерий, не так ли? Вы можете получить максимум (эээ… минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.

ln(отрицательное число) = неопределено

«Неопределено» означает, что нет такого промежутка времени, который надо было бы прождать, чтобы получить отрицательное значение.

Логарифмическое умножение — просто умора

Сколько времени займёт четырёхкратный рост? Конечно, можно просто взять ln(4). Но это слишком просто, мы пойдём другим путём.

Можно представить четырёхкратный рост как удвоение (требующее ln(2) единиц времени) и затем снова удвоение (требующее ещё ln(2) единиц времени):

Время на 4х рост = ln(4) = Время на удвоится и затем ещё раз удвоится = ln(2) + ln(2)

Интересно. Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?

ln(a*b) = ln(a) + ln(b)

Логарифм от A, умноженного на B, есть log(A) + log(B). Это отношение сразу обретает смысл, если оперировать в терминах роста.

Если вас интересует 30-кратный рост, вы можете подождать ln(30) за один присест, либо же подождать ln(3) Для утроения, и затем ещё ln(10) для удесятирения. Конечный результат тот же самый, так что конечно время должно оставаться постоянным (и остаётся).

Что на счёт деления? В частности, ln(5/3) означает: сколько времени понадобится для того, чтобы вырасти в 5 раз, и затем получить 1/3 от этого?

Отлично, рост в 5 раз есть ln(5). Рост в 1/3 раза займёт -ln(3) единиц времени. Итак,

ln(5/3) = ln(5) – ln(3)

Сие означает: дайте вырасти в 5 раз, и затем «вернитесь во времени» к той отметке, где останется всего треть от того количества, так что у вас получится 5/3 рост. В общем получается

ln(a/b) = ln(a) – ln(b)

Я надеюсь, что странная арифметика логарифмов начинает обретать для вас смысл: умножение показателей роста становится сложением единиц времени роста, а деление превращается в вычитание единиц времени. Не надо запоминать правила, попробуйте осознать их.

Использование натурального логарифма при произвольном росте

— Ну конечно, — скажете вы, — это всё хорошо, если рост 100%-ный, а что в случае 5%, которые я получаю?»

Нет проблем.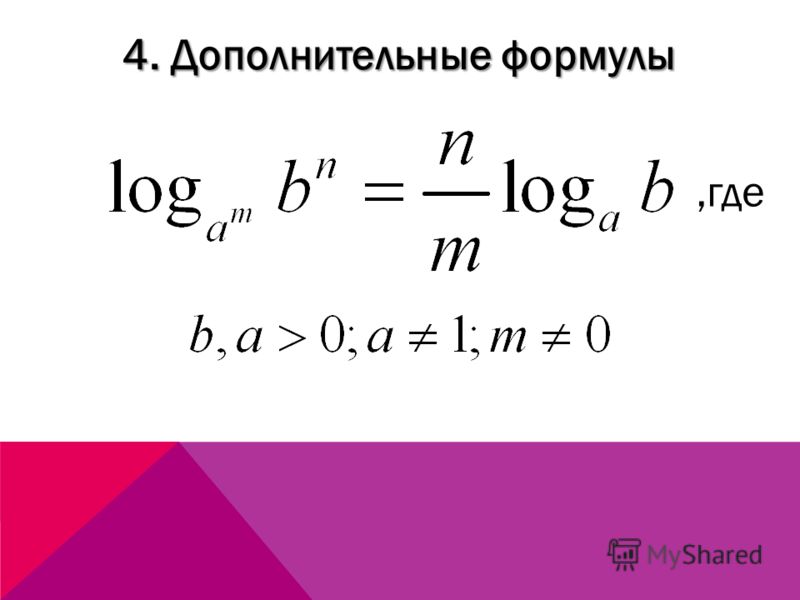 «Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения e^x. Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.

Допустим, мы хотим достичь 30-кратного роста: берём ln(30) и получаем 3.4 Это означает:

e^x = рост
e^3.4 = 30

Очевидно, это уравнение означает «100%-ная доходность на протяжении 3.4 лет даёт рост в 30 раз». Мы можем записать это уравнение в таком виде:

e^x = e^{ставка*время}
e^{100% * 3.4 года} = 30

Мы можем менять значения «ставки» и «времени», лишь бы ставка * время оставалось 3.4. Например, если нас интересует 30-кратный рост — сколько нам придётся ждать при процентной ставке 5%?

ln(30) = 3.4
ставка * время = 3.4
0.05 * время = 3.4
время = 3.4 / 0.05 = 68 лет

Я рассуждаю так: «ln(30) = 3. 4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».

100% за 3.4 года = 1.0 * 3.4 = 3.4
200% за 1.7 года = 2.0 * 1.7 = 3.4 [200%-ный рост означает уменьшение времени вдвое]
50% за 6.8 года = 0.5 * 6.8 = 3.4 [50%-ный рост означает, что понадобится в 2 раза больше времени]
5% за 68 года = .05 * 68 = 3.4 [5%-ный рост означает, что понадобится в 20 раз больше времени].

Здорово, правда? Натуральный логарифм может использоваться с любыми значениями процентной ставки и времени, поскольку их произведение остаётся постоянным. Можете перемещать значения переменных сколько душе угодно.

Отпадный пример: Правило семидесяти двух

Правило семидесяти двух — математический приём, позволяющий оценить, сколько времени понадобится, чтобы ваши деньги удвоились. Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.

Сколько времени понадобится, чтобы удвоить ваши деньги при 100% ставке, нарастающей ежегодно?

Оп-па. Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.

Теперь вопрос прост: Как быстро можно удвоиться при 100%-ном росте? ln(2) = 0.693. Нужно 0.693 единиц времени (лет — в нашем случае), чтобы удвоить нашу сумму с непрерывным ростом 100%.

Так, а что если процентная ставка — не 100%, а скажем, 5% или 10%?

Легко! Поскольку ставка * время = 0.693, мы удвоим сумму:

ставка * время = 0.693
время = 0.693 / ставка

Получается, если рост 10%-ный, это займёт 0.693 / 0.10 = 6.93 лет на удвоение.

Чтобы упростить вычисления, давайте домножим обе части на 100, тогда можно будет говорить «10», а не «0. 10″:

время на удвоение = 69.3 / ставка, где ставка выражена в процентах.

Теперь черёд удваиваться при ставке 5%, 69.3 / 5 = 13.86 лет. Однако 69.3 — не самое удобное делимое. Давайте выберем близкое число, 72, которое удобно делить на 2, 3, 4, 6, 8 и другие числа.

время на удвоение = 72 / ставка

что и является правилом семидесяти двух. Всё шито-крыто.

Если вам нужно найти время для утроения, можете использовать ln(3) ~ 109.8 и получить

время на утроение = 110 / ставка

Что является ещё одним полезным правилом. «Правило 72» применимо росту по процентным ставкам, росту населения, культур бактерий, и всего, что растёт экспоненциально.

Что дальше?

Надеюсь, натуральный логарифм теперь приобрёл для вас смысл — он показывает время, необходимое для роста любого числа при экспоненциальном росте. Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.

Каждый раз, когда вы видите ln(x), вспоминайте «время, нужное, чтобы вырасти в Х раз». В предстоящей статье я опишу e и ln в связке, так что свежий аромат математики заполнит воздух.

Дополнение: Натуральный логарифм от e

Быстрая викторина: сколько будет ln(e)?

математический робот скажет: поскольку они определены как инверсия одна другой, очевидно, что ln(e) = 1.
понимающий человек: ln(e) это число времени, чтобы вырасти в «е» раз (около 2.718). Однако число e само по себе является мерой роста в 1 раз, так что ln(e) = 1.

Мыслите ясно.

Перевод статьи «Demystifying the Natural Logarithm (ln)»

Число e основание натурального логарифма. Логарифм

Число e означает рост

Число e означает непрерывный рост. Как мы видели в прошлом примере, e x позволяет нам увязать процент и время: 3 года при росте 100% есть то же самое, что и 1 год при 300%, при условии «сложных процентов».

e x = e процент * время = e 1.0 * время = e время

Очевидно, что e x означает:

насколько вырастет мой вклад через x единиц времени (при условии 100%-го непрерывного роста).
например, через 3 промежутка времени я получу в e 3 = 20.08 раз больше «штуковин».

e x — это масштабирующий коэффициент, показывающий, до какого уровня мы вырастем за x отрезков времени.

Натуральный логарифм означает время

Натуральный логарифм — это инверсия числа e, такой причудливый термин для обозначения противоположности. Кстати, о причудах; по латыни он называется logarithmus naturali , отсюда и появилась аббревиатура ln.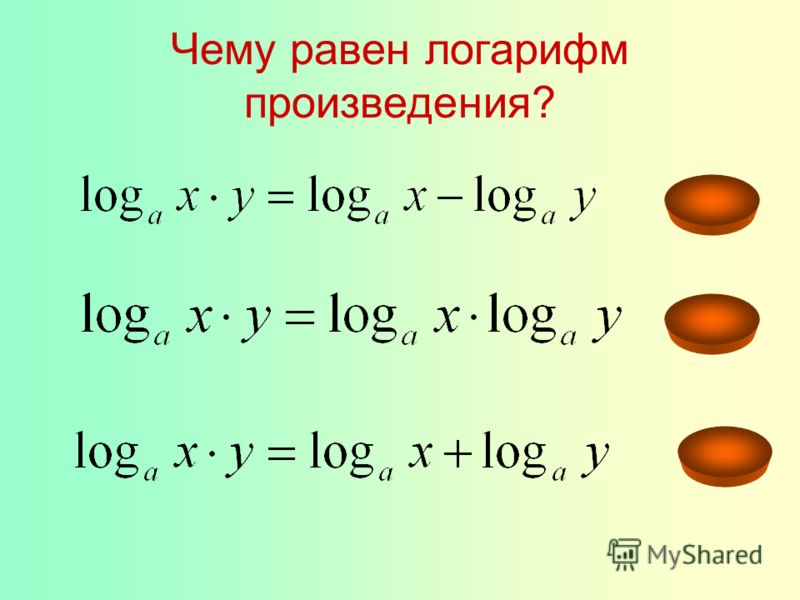

И что эта инверсия или противоположность означает?

e x позволяет нам подставить время и получить рост.
ln(x) позволяет нам взять рост или доход и узнать время, необходимое для его получения.

Например:

e 3 равняется 20.08. Через три отрезка времени у нас будет в 20.08 раз больше того, с чего мы начали.
ln(20.08) будет примерно 3. Если вас интересует рост в 20.08 раз, вам понадобится 3 промежутка времени (опять же, при условии стопроцентного непрерывного роста).

Всё ещё читаете? Натуральный логарифм показывает время, нужное, чтобы достичь желаемого уровня.

Этот нестандартный логарифмический счёт

ln(1) = 0

ln(1/2) = -ln(2) = -0.693

Логично, правда? Если мы вернёмся назад (время вспять) на 0.693 секунды, то обнаружим половину имеющегося количества. Вообще можно переворачивать дробь и брать отрицательное значение: ln(1/3) = -ln(3) = -1.09. Это означает, что, если мы вернёмся в прошлое на 1.09 отрезков времени, то обнаружим только треть от нынешнего числа.

Ладно, а как насчёт логарифма отрицательного числа? Сколько времени нужно, чтобы «вырастить» колонию бактерий от 1 до -3?

Это невозможно! Нельзя получить отрицательное число бактерий, не так ли? Вы можете получить максимум (эээ. .. минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.

ln(отрицательное число) = неопределено

Логарифмическое умножение — просто умора

Время на 4х рост = ln(4) = Время на удвоится и затем ещё раз удвоится = ln(2) + ln(2)

ln(a*b) = ln(a) + ln(b)

Отлично, рост в 5 раз есть ln(5). Рост в 1/3 раза займёт -ln(3) единиц времени. Итак,

ln(5/3) = ln(5) – ln(3)

ln(a/b) = ln(a) – ln(b)

Использование натурального логарифма при произвольном росте

Ну конечно, — скажете вы, — это всё хорошо, если рост 100%-ный, а что в случае 5%, которые я получаю?»

Нет проблем. «Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения e x . Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.

Допустим, мы хотим достичь 30-кратного роста: берём ln(30) и получаем 3.4 Это означает:

e x = рост
e 3.4 = 30

e x = e ставка*время
e 100% * 3.4 года = 30

ln(30) = 3.

4
ставка * время = 3.4
0.05 * время = 3.4
время = 3.4 / 0.05 = 68 лет

Я рассуждаю так: «ln(30) = 3.4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».

100% за 3.4 года = 1.0 * 3.4 = 3.4
200% за 1.7 года = 2.0 * 1.7 = 3.4
50% за 6.8 года = 0.5 * 6.8 = 3.4
5% за 68 года = .05 * 68 = 3.4 .

Отпадный пример: Правило семидесяти двух

Сколько времени понадобится, чтобы удвоить ваши деньги при 100% ставке, нарастающей ежегодно?

Оп-па.

Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.

Так, а что если процентная ставка — не 100%, а скажем, 5% или 10%?

Легко! Поскольку ставка * время = 0.693, мы удвоим сумму:

ставка * время = 0.693
время = 0.693 / ставка

Получается, если рост 10%-ный, это займёт 0.693 / 0.10 = 6.93 лет на удвоение.

Чтобы упростить вычисления, давайте домножим обе части на 100, тогда можно будет говорить «10», а не «0. 10″:

время на удвоение = 69.3 / ставка, где ставка выражена в процентах.

время на удвоение = 72 / ставка

что и является правилом семидесяти двух. Всё шито-крыто.

Если вам нужно найти время для утроения, можете использовать ln(3) ~ 109.8 и получить

время на утроение = 110 / ставка

Что дальше?

Дополнение: Натуральный логарифм от e

Быстрая викторина: сколько будет ln(e)?

математический робот скажет: поскольку они определены как инверсия одна другой, очевидно, что ln(e) = 1.
понимающий человек: ln(e) это число времени, чтобы вырасти в «е» раз (около 2.718). Однако число e само по себе является мерой роста в 1 раз, так что ln(e) = 1.

Мыслите ясно.

9 сентября 2013

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
Десятичный a, где основанием служит число 10.
Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.

Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;

но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.

Определение

Натуральный логарифм — это функция y = ln x , обратная к экспоненте , x = e y , и являющаяся логарифмом по основанию числа е : ln x = log e x .

Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/ x .

Исходя из определения , основанием натурального логарифма является число е :
е ≅ 2,718281828459045… ;
.

График функции y = ln x .

График натурального логарифма (функции y = ln x ) получается из графика экспоненты зеркальным отражением относительно прямой y = x .

Натуральный логарифм определен при положительных значениях переменной x . Он монотонно возрастает на своей области определения.

При x → 0 пределом натурального логарифма является минус бесконечность ( — ∞ ).

При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a растет быстрее логарифма.

Свойства натурального логарифма

Область определения, множество значений, экстремумы, возрастание, убывание

Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.

Значения ln x

ln 1 = 0

Основные формулы натуральных логарифмов

Формулы, вытекающие из определения обратной функции:

Основное свойство логарифмов и его следствия

Формула замены основания

Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:

Доказательства этих формул представлены в разделе «Логарифм» .

Обратная функция

Обратной для натурального логарифма является экспонента .

Если , то

Если , то .

Производная ln x

Производная натурального логарифма:
.
Производная натурального логарифма от модуля x :
.
Производная n-го порядка:
.
Вывод формул > > >

Интеграл

Интеграл вычисляется интегрированием по частям :
.
Итак,

Выражения через комплексные числа

Рассмотрим функцию комплексной переменной z :
.
Выразим комплексную переменную z через модуль r и аргумент φ :
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ определен не однозначно. Если положить
, где n — целое,
то будет одним и тем же числом при различных n .

Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.

Разложение в степенной ряд

При имеет место разложение:

Использованная литература:
И. Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что a c = b: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b > 0) &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp

Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.

Основное логарифмическое тождество

a log a b = b (a > 0, a ≠ 1) (2)

Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.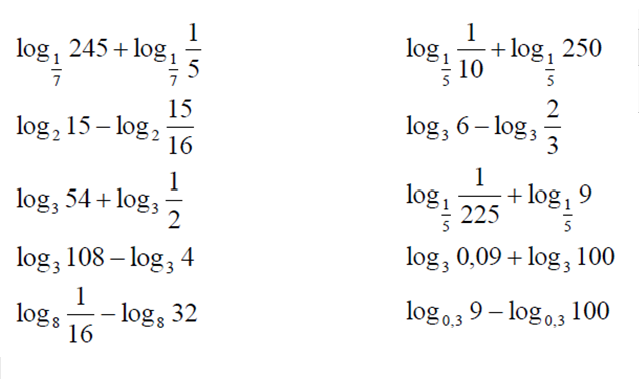

Два очевидных следствия определения логарифма

log a a = 1 (a > 0, a ≠ 1) (3)
log a 1 = 0 (a > 0, a ≠ 1) (4)

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.

Логарифм произведения и логарифм частного

log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)

Log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) (6)

Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.

Действительно, выражение log a (f (x) g (x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.

Преобразуя данное выражение в сумму log a f (x) + log a g (x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).

Степень можно выносить за знак логарифма

log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

Log a (f (x) 2 = 2 log a f (x)

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Формула перехода к новому основанию

log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) (8)

Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.

Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):

Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)

Несколько простых примеров с логарифмами

Пример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.

Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log 5 125 = 3. Мы использовали формулу перехода к новому основанию (8).

Таблица формул, связанных с логарифмами

a log a b = b (a > 0, a ≠ 1)

log a a = 1 (a > 0, a ≠ 1)

log a 1 = 0 (a > 0, a ≠ 1)

log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b p = p log a b (a > 0, a ≠ 1, b > 0)

log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1)

log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1)

Логарифмом числа b по основанию а называется показатель степени, в который нужно возвести число а чтобы получить число b.

Если , то .

Логарифм — крайне важная математическая величина , поскольку логарифмическое исчисление позволяет не только решать показательные уравнения, но и оперировать с показателями, дифференцировать показательные и логарифмические функции, интегрировать их и приводить к более приемлемому виду, подлежащему расчету.

Вконтакте

Все свойства логарифмов связаны напрямую со свойствами показательных функций. Например, тот факт, что означает, что:

Следует заметить, что при решении конкретных задач, свойства логарифмов могут оказаться более важными и полезными, чем правила работы со степенями.

Приведем некоторые тождества:

Приведем основные алгебраические выражения:

;

Внимание! может существовать только при x>0, x≠1, y>0.

Постараемся разобраться с вопросом, что такое натуральные логарифмы. Отдельный интерес в математике представляют два вида — первый имеет в основании число «10», и носит название «десятичный логарифм». Второй называется натуральным. Основание натурального логарифма — число «е». Именно о нем мы и будем детально говорить в этой статье.

Обозначения:

lg x — десятичный;
ln x — натуральный.

Используя тождество можно увидеть, что ln e = 1, как и то, что lg 10=1.

График натурального логарифма

Построим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его «вручную», чтобы знать, как правильно посчитать логарифм.

Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:

Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве: . Для натурального логарифма это тождество будет выглядеть таким образом:

Для удобства мы можем взять пять опорных точек:

;

Таким образом, подсчет натуральных логарифмов — довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.

Построив по точкам график, получаем приблизительный график:

Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) — все числа больше нуля.

Внимание! В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма .

Область значений (т.е. все допустимые значения функции y = ln x) — все числа в интервале .

Предел натурального log

Изучая график, возникает вопрос — как ведет себя функция при y

Очевидно, что график функции стремится пересечь ось у, но не сможет этого сделать, поскольку натуральный логарифм при х

Предел натурального log можно записать таким образом:

Формула замены основания логарифма

Иметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.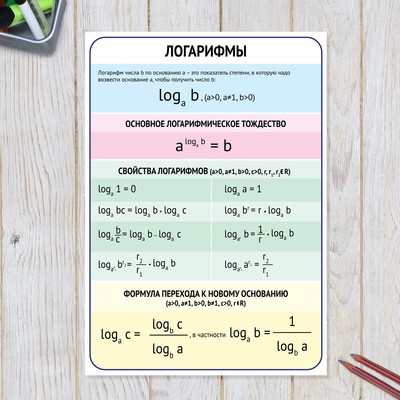

Начнем с логарифмического тождества:

Тогда любое число, либо переменную у можно представить в виде:

где х — любое число (положительное согласно свойствам логарифма).

Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:

Воспользуемся свойством (только вместо «с» у нас выражение):

Отсюда получаем универсальную формулу:

В частности, если z=e, то тогда:

Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.

Решаем задачи

Для того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.

Задача 1 . Необходимо решить уравнение ln x = 3.

Решение: Используя определение логарифма: если , то , получаем:

Задача 2 . Решите уравнение (5 + 3 * ln (x — 3)) = 3.

Решение: Используя определение логарифма: если , то , получаем:

Еще раз применим определение логарифма:

Таким образом:

Можно приближенно вычислить ответ, а можно оставить его и в таком виде.

Задача 3. Решите уравнение .

Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:

Перед нами квадратное уравнение. Найдем его дискриминант:

Первый корень уравнения:

Второй корень уравнения:

Вспоминая о том, что мы производили подстановку t = ln x, получаем:

В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е — зачастую отражает темп роста экспоненциальных величин.

В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти N понадобится битов.

В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.

В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее — процессы, которые математически можно описать только при помощи логарифмирования.

В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.

Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.

Натуральный логарифм Функция y=ln x ее свойства

Доказательство основного свойства натурального логарифма

Десятичный логарифм и его свойства. Свойства логарифмов и примеры их решений. Исчерпывающий гид (2020) Lg натуральный логарифм

Область допустимых значений (ОДЗ) логарифма

Теперь поговорим об ограничениях (ОДЗ — область допустимых значений переменных).

Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:

То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться.

Почему так?

Начнем с простого: допустим, что. Тогда, например, число не существует, так как в какую бы степень мы не возводили, всегда получается. Более того, не существует ни для какого. Но при этом может равняться чему угодно (по той же причине — в любой степени равно). Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.

Похожая проблема у нас и в случае: в любой положительной степени — это, а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что).

При мы столкнемся с проблемой возведения в дробную степень (которая представляется в виде корня: . Например, (то есть), а вот не существует.

Поэтому и отрицательные основания проще выбросить, чем возиться с ними.

Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).

В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:

Решим уравнение.

Вспомним определение: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. И по условию, эта степень равна: .

Получаем обычное квадратное уравнение: . Решим его с помощью теоремы Виета: сумма корней равна, а произведение. Легко подобрать, это числа и.

Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?

Это явно неверно, так как основание не может быть отрицательным, то есть корень — «сторонний».

Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:

Тогда, получив корни и, сразу отбросим корень, и напишем правильный ответ.

Пример 1 (попробуй решить самостоятельно):

Найдите корень уравнения. Если корней несколько, в ответе укажите меньший из них.

Решение:

В первую очередь напишем ОДЗ:

Теперь вспоминаем, что такое логарифм: в какую степень нужно возвести основание, чтобы получить аргумент? Во вторую. То есть:

Казалось бы, меньший корень равен. Но это не так: согласно ОДЗ корень — сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: .

Ответ: .

Основное логарифмическое тождество

Вспомним определение логарифма в общем виде:

Подставим во второе равенство вместо логарифм:

Это равенство называется основным логарифмическим тождеством . Хотя по сути это равенство — просто по-другому записанное определение логарифма :

Это степень, в которую нужно возвести, чтобы получить.

Например:

Реши еще следующие примеры:

Пример 2.

Найдите значение выражения.

Решение:

Вспомним правило из раздела : , то есть, при возведении степени в степень показатели перемножаются. Применим его:

Пример 3.

Докажите, что.

Решение:

Свойства логарифмов

К сожалению, задачи не всегда такие простые — зачастую сперва нужно упростить выражение, привести его к привычному виду, и только потом будет возможно посчитать значение. Это проще всего сделать, зная свойства логарифмов . Так что давай выучим основные свойства логарифмов. Каждое из них я буду доказывать, ведь любое правило проще запомнить, если знать, откуда оно берется.

Все эти свойства нужно обязательно запомнить, без них большинство задач с логарифмами решить не получится.

А теперь обо всех свойствах логарифмов подробнее.

Свойство 1:

Доказательство:

Пусть, тогда.

Имеем: , ч.т.д.

Свойство 2: Сумма логарифмов

Сумма логарифмов с одинаковыми основаниями равна логарифму произведения: .

Доказательство:

Пусть, тогда. Пусть, тогда.

Пример: Найдите значение выражения: .

Решение: .

Только что выученная формула помогает упростить сумму логарифмов, а не разность, так что сразу эти логарифмы не объединить. Но можно сделать наоборот — «разбить» первый логарифм на два:А вот обещанное упрощение:
.
Зачем это нужно? Ну например: чему равно?

Теперь очевидно, что.

Теперь упрости сам:

Задачи:

Ответы:

Свойство 3: Разность логарифмов:

Доказательство:

Все точно так же, как и в пункте 2:

Пусть, тогда.

Пусть, тогда. Имеем:

Пример из прошлого пункта теперь становится еще проще:

Пример посложнее: . Догадаешься сам, как решить?

Здесь нужно заметить, что у нас нету ни одной формулы про логарифмы в квадрате. Это что-то сродни выражению — такое сразу не упростить.

Поэтому отвлечемся от формул про логарифмы, и подумаем, какие вообще формулы мы используем в математике чаще всего? Еще начиная с 7 класса!

Это — . Нужно привыкнуть к тому, что они везде! И в показательных, и в тригонометрических, и в иррациональных задачах они встречаются. Поэтому их нужно обязательно помнить.

Если присмотреться к первым двум слагаемым, становится ясно, что это разность квадратов :

Ответ для проверки:

Упрости сам.

Примеры

Ответы.

Свойство 4: Вынесение показателя степени из аргумента логарифма:
Доказательство: И здесь тоже используем определение логарифма:пусть, тогда. Имеем: , ч.т.д.
Можно понять это правило так:
То есть степень аргумента выносится вперед логарифма, как коэффициент.
Пример: Найдите значение выражения.
Решение: .
Реши сам:
Примеры:
Ответы:
Свойство 5: Вынесение показателя степени из основания логарифма:
Доказательство: Пусть, тогда.
Имеем: , ч.т.д.
Запоминаем: из основания степень выносится как обратное число, в отличии от предыдущего случая!
Свойство 6: Вынесение показателя степени из основания и аргумента логарифма:
Или если степени одинаковые: .
Свойство 7: Переход к новому основанию:
Доказательство: Пусть, тогда.
Имеем: , ч.т.д.
Свойство 8: Замена местами основания и аргумента логарифма:
Доказательство: Это частный случай формулы 7: если подставить, получим: , ч.т.д.
Рассмотрим еще несколько примеров.
Пример 4.
Найдите значение выражения.
Используем свойство логарифмов № 2 — сумма логарифмов с одинаковым основанием равна логарифму произведения:
Пример 5.
Найдите значение выражения.
Решение:
Используем свойство логарифмов № 3 и № 4:
Пример 6.
Найдите значение выражения.
Решение:
Используем свойство № 7 — перейдем к основанию 2:
Пример 7.
Найдите значение выражения.
Решение:
Как тебе статья?
Если ты читаешь эти строки, значит ты прочитал всю статью.
И это круто!
А теперь расскажи нам как тебе статья?
Научился ты решать логарифмы? Если нет, то в чем проблема?
Пиши нам в комментах ниже.
И, да, удачи на экзаменах.
На ЕГЭ и ОГЭ и вообще в жизни
Нередко берут цифру десять. Логарифмы чисел по основанию десять именуют десятичными . При проведении вычислений с десятичным логарифмом общепринято оперировать знаком lg , а не log ; при этом число десять, определяющие основание, не указывают. Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .
Для десятичных логарифмов типичны те же особенности, которые есть у логарифмов при основании, большем единицы. А именно, десятичные логарифмы характеризуются исключительно для положительных чисел. Десятичные логарифмы чисел, больших единицы, положительны, а чисел, меньших единицы, отрицательны; из двух не отрицательных чисел большему эквивалентен и больший десятичный логарифм и т. д. Дополнительно, десятичные логарифмы имеют отличительные черты и своеобразные признаки, которыми и поясняется, зачем в качестве основания логарифмов комфортно предпочитать именно цифру десять.
Перед тем как разобрать эти свойства, ознакомимся с нижеследующими формулировками.
Целая часть десятичного логарифма числа а именуется характеристикой , а дробная — мантиссой этого логарифма.
Характеристика десятичного логарифма числа а указывается как , а мантисса как {lg а }.
Возьмем, скажем, lg 2 ≈ 0,3010.Соответственно = 0, {lg 2} ≈ 0,3010.
Подобно и для lg 543,1 ≈2,7349. Соответственно, = 2, {lg 543,1}≈ 0,7349.
Достаточно повсеместно употребляется вычисление десятичных логарифмов положительных чисел по таблицам.
Характерные признаки десятичных логарифмов.
Первый признак десятичного логарифма. целого не отрицательного числа, представленного единицей со следующими нулями, есть целое положительное число, равное численности нулей в записи выбранного числа.
Возьмем, lg 100 = 2, lg 1 00000 = 5.
Обобщенно, если
То а = 10 n , из чего получаем
lg a = lg 10 n = n lg 10 = п .
Второй признак. Десятичный логарифм положительной десятичной дроби , показанный единицей с предыдущими нулями, равен — п , где п — численность нулей в представлении этого числа, учитывая и нуль целых.
Рассмотрим, lg 0,001 = — 3, lg 0,000001 =-6.
Обобщенно, если
,
То a = 10 -n и получается
lga= lg 10 n =-n lg 10 =-п
Третий признак. Характеристика десятичного логарифма не отрицательного числа, большего единицы, равна численности цифр в целой части этого числа исключая одну.
Разберем данный признак 1) Характеристика логарифма lg 75,631 приравнена к 1.
И правда, 10
lg 10
1 .
Отсюда следует,
lg 75,631 = 1 +б,
Смещение запятой в десятичной дроби вправо или влево равнозначно операции перемножения этой дроби на степень числа десять с целым показателем п (положительным или отрицательным). И следовательно, при смещении запятой в положительной десятичной дроби влево или вправо мантисса десятичного логарифма этой дроби не меняется.
Так, {lg 0,0053} = {lg 0,53} = {lg 0,0000053}.
Из программы средней школы известно, что
любое положительное число можно представить как число 10 в какой-то степени.
Однако это просто в том случае, когда число кратно 10.
Пример :
число 100 − это 10х10 или 102
число 1000 −это 10х10х10 или 103
и т.д.
Как же быть в том случае, если, например, надо выразить число 8299 как число 10 в какой-то степени? Как найти это число с определённой степенью точности, которое в данном случае равно 3,919…?
Выход — это логарифм и логарифмические таблицы
Знание логарифмов и умение пользоваться логарифмическими таблицами позволяет значительно упростить многие сложные арифметические операции.Для практического применения удобны десятичные логарифмы.
Историческая справка .
Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен вглубь истории вплоть до древневавилонской математики (около 2000 года до н. э.). Однако первые таблицы логарифмов составили независимо друг от друга шотландский математик HUДж. Непер (1550—1617) U Hи швейцарец И. Бюрги (1552—1632). Первые таблицы десятичных логарифмов были составлены и опубликованы английским математиком Г. Бриггсом (1561 —1630).
Предлагаем читателю, не вдаваясь глубоко в математическую суть вопроса, запомнить или восстановить в памяти несколько простейших определений, выводов и формул:
Определение логарифм а.
Логарифмом данного числа называется показатель степени, в которую нужно возвести другое число, называемое основанием логарифма (а ), чтобы получить данное число.
При всяком основании, логарифм единицы есть нуль:
а0 = 1
Отрицательные числа не имеют логарифмов
Всякое положительное число имеет логарифм
При основании, большем 1, логарифмы чисел, меньших 1, отрицательны, а логарифмы чисел, больших 1, положительны
Логарифм основания равен 1
Большему числу соответствует больший логарифм
С возрастанием числа от 0 до 1 логарифм его возрастает от —∞ до 0; с возрастанием числа от 1 до +∞ логарифм его возрастает от 1 до +∞ (где, ± ∞ − знак, принятый в математике для обозначения отрицательной или положительной бесконечности чисел)
Для практического применения удобны логарифмы, основанием которых является число10
Эти логарифмы называются десятичными и обозначаются lg . Например:
логарифм числа 10 по основанию 10 равен 1. Иначе говоря, число 10 нужно возвести в первую степень, чтобы получить число 10 (101 = 10), т.е. lg10 = 1
логарифм числа 100 по основанию 10 равен 2. Иначе говоря, число 10 нужно возвести в квадрат, чтобы получить число 100 (102 = 100),т.е. lg100 = 2
UВывод №1 U: логарифм целого числа, изображаемого единицей с нулями, есть целое положительное число, содержащее столько единиц, сколько нулей в изображении числа
логарифма числа 0,1 по основанию 10 равен -1. Иначе говоря, число 10 нужно возвести в минус первую степень, чтобы получить число 0,1 (10-1 = 0,1), т.е. lg0,1 = -1
логарифма числа 0,01 по основанию 10 равен -2. Иначе говоря, число 10 нужно возвести в минус вторую степень, чтобы получить число 0,1 (10-2 = 0,01), т.е. lg0,01 = -2
UВывод №2 U: логарифм десятичной дроби, изображаемой единицею с предшествующими нулями, есть целое отрицательное число содержащее столько отрицательных единиц, сколько нулей в изображении дроби, считая, в том числе, и 0 целых
в соответствии с определением №1 (см. выше):
lg1 = 0
логарифм числа 8300 по основанию 10 равен 3,9191… Иначе говоря, число 10 нужно возвести в степень 3,9191… , чтобы получить число 8300 (103,9191…= 8300), т.е. lg8300 =3,9191…
UВывод №3 U: логарифма числа, не выраженного единицей с нулями, есть число иррациональное и, следовательно, не может быть выражен точно посредством цифр.
Обыкновенно иррациональные логарифмы выражают приближенно в виде десятичной дроби с несколькими десятичными знаками. Целое число этой дроби (хотя бы это было „0 целых») называется характеристикой , а дробная часть — мантиссой логарифма. Если, например, логарифм есть 1,5441 , то характеристика его равна 1 , а мантисса есть 0,5441 .
Основные свойства логарифмов, в т.ч. десятичных:
логарифм произведения равен сумме логарифмов сомножителей: lg( a. b)= lgа + lgb
логарифм частного равен логарифму делимого без логарифма делителя, т.е. логарифм дроби равен логарифму числителя без логарифма знаменателя:
логарифмы двух взаимообратных чисел по одному и тому же основанию отличаются друг от друга только знаком
логарифм степени равен произведению показателя степени на логарифм её основания, т.е. логарифм степени равен показателю этой степени, умноженному на логарифм возводимого в степень числа:
lg( bk)= k. lg b
Чтобы окончательно понять, что такое десятичный логарифм произвольного числа, детально рассмотрим несколько примеров.
UПример №2.1.1 U.
Возьмем какое-нибудь целое, например 623 и смешанное число, например 623,57.
Мы знаем, что логарифм числа состоит из характеристики и мантиссы.
Сосчитаем, сколько цифр в данном целом числе, или в целой части смешанного числа. В наших примерах этих цифр 3.
Поэтому каждое из чисел 623 и 623,57 больше 100, но меньше 1000.
Таким образом можно сделать вывод, что логарифм каждого из этих чисел будет больше lg 100, т. е. больше 2, но меньше lg 1000, т. е. меньше 3 (вспомним, что большее число имеет и больший логарифм).
Следовательно:
lg 623 = 2,…
lg 623,57 = 2,…
(точки заменяют собою неизвестные мантиссы).
UВывод №4 U: десятичные логарифмы обладают тем удобством, что их характеристику всегда можно найти по одному виду числа .
Пусть вообще в данном целом числе, или в целой части данного смешанного числа, содержится m цифр. Так как самое малое целое число, содержащее m цифр, есть единица с m-1 нулями на конце, то (обозначая данное число N) можем написать неравенство:

следовательно,
m-1 поэтому
lg N = (m-1) + положительная дробь.
значит
характеристика lgN = m-1
UВывод №5 U: характеристика десятичного логарифма целого или смешанного числа содержит столько положительных единиц, сколько цифр в целой части числа без одной.
UПример №2.1.2.
Теперь возьмём несколько десятичных дробей, т.е. чисел меньших 1 (другими словами имеющих 0 целых):
0,35; 0,07; 0,0056; 0,0008 и т. п.
Логарифмы каждого из этих чисел будут находиться в промежутке между двумя целыми отрицательными числами, различающимися на одну единицу. Причём каждый из них равен меньшему из этих отрицательных чисел, увеличенному на некоторую положительную дробь.
Например,
lg0,0056= -3 + положительная дробь
В данном случае положительная дробь будет равна 0,7482.
Тогда:
lg 0,0056 = -3 + 0,7482
UПримечания U:
Такие суммы, как -3 + 0,7482, состоящие из целого отрицательного числа и положительной десятичной дроби, условились при логарифмических вычислениях писать сокращенно так:
,7482
(такое число читается: с минусом, 7482 десятитысячных), т. е. ставят знак минус над характеристикой с целью показать, что он относится только к этой характеристике, а не к мантиссе, которая остается положительной.
Таким образом, приведенные выше числа можно записать в виде десятичных логарифмов
lg 0,35 =, …
lg 0,07 =, …
lg 0,00008 =, …
Пусть вообще число A есть десятичная дробь, у которой перед первой значащей цифрой α стоит m нулей, считая, в том числе, и 0 целых:

тогда, очевидно, что

Следовательно:

т. е.
-m Так как из двух целых чисел:
-m и -(m-1) меньшее есть -m
то
lg А = -m + положительная дробь
UВывод №6 U: характеристика логарифма десятичной дроби, т.е. числа меньшего 1, содержит в себе столько отрицательных единиц, сколько нулей в изображении десятичной дроби перед первой значащей цифрой, считая, в том числе, и нуль целых; мантисса же такого логарифма положительна
Пример №2.1.3.
Умножим какое-нибудь число N (целое или дробное — всe равно) на 10, на 100 на 1000…, вообще на 1 c нулями, и посмотрим, как от этого изменится lg N.
Так как логарифм произведения равен сумме логарифмов сомножителей, то
lg (N.10) = lg N + lg 10 = lg N + 1;
lg (N.100) = lg N + lg 100 = lg N + 2;
lg (N.1000) = lg N + lg 1000 = lg N + 3 и т. д.
Когда к lg N мы прибавляем какое-нибудь целое число, то это число всегда прибавляется к характеристике; при этом мантисса всегда остаётся в этих случаях неизменной.
Пример
если lg N = 2,7804, то 2,7804 + 1 =3,7804; 2,7804 + 2 = 4,7801 и т. п.;
или если lg N = 3,5649, то 3,5649 + 1 = 2,5649; 3,5649 — 2 = 1,5649, и т. п.
Вывод №7 : от умножения числа на 10, 100, 1000,.., вообще на 1 с нулями, мантисса логарифма не изменяется, а характеристика увеличивается на столько единиц, сколько нулей во множителе.
Подобно этому, приняв во внимание, что логарифм частного равен логарифму делимого без логарифма делителя, мы получим:
lg N/10 = lg N — lg 10 = lg N — 1;
lg N/100 = log N — log 100 = log N — 2;
log N/1000 = log N — log 1000 = log N — 3 и т. п.
Когда из lg N вычитается целое число из логарифма вычитать это целое число всегда следует из характеристики, а мантиссу оставлять без изменения. то можно сказать:
Вывод №8 : От деления числа на 1 с нулями мантисса логарифма не изменяется, а характеристика уменьшается на столько единиц, сколько нулей в делителе.
Вывод №9 : мантисса логарифма десятичного числа не изменяется от перенесения в числе запятой, потому что перенесение запятой равносильно умножению или делению на 10, 100, 1000 и т. д.
Таким образом, логарифмы чисел:
0,00423, 0,0423, 4,23, 423
отличаются только характеристиками, но не мантиссами (при условии, что все мантиссы положительны).
Вывод №9 : мантиссы чисел, имеющих одну и ту же значащую часть, но отличающихся только нулями на конце, одинаковы: так, логарифмы чисел: 23, 230, 2300, 23 000 отличаются только характеристиками.
Степень отдельно взятого числа называется математическим термином, придуманным несколько столетий назад. В геометрии и алгебре встречается два варианта — десятичные и натуральные логарифмы. Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.
Особенности и важные признаки
На данный момент различают десять известных математических качеств. Самыми распространенными и востребованными из них являются:
Подкоренной log, разделенный на величину корня, всегда такой же, как и десятичный логарифм √.
Произведение log всегда равно сумме производителя.
Lg = величине степени, перемноженной на число, которое в нее возводится.
Если от log делимого отнять делитель, получится lg частного.
Кроме того, есть уравнение, основанное на главном тождестве (считается ключевым), переход к обновленному основанию и несколько второстепенных формул.
Вычисление десятичного логарифма — довольно специфическая задача, поэтому к интегрированию свойств в решение необходимо подходить осторожно и регулярно проверять свои действия и последовательность. Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.
Разновидности математического термина
Главные отличия математического числа «спрятаны» в основании (a). Если оно имеет показатель 10, то это десятичный log. В обратном случае «a» преобразуется в «у» и обладает трансцендентными и иррациональными признаками. Также стоит отметить, что натуральная величина рассчитывается специальным уравнением, где доказательством становится теория, изучаемая за пределами школьной программы старших классов.
Логарифмы десятичного типа получили широкое применение при вычислении сложных формул. Составлены целые таблицы, облегчающие расчеты и наглядно показывающие процесс решения задачи. При этом перед непосредственным переходом к делу нужно возвести log в К тому же в каждом магазине школьных принадлежностей можно найти специальную линейку с нанесенной шкалой, помогающей решить уравнение любой сложности.
Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.
Два вида формулы
Все типы и разновидности задач на вычисление ответа, имеющие в условии термин log, обладают отдельным названием и строгим математическим устройством. Показательное уравнение является практически точной копией логарифмических расчетов, если смотреть со стороны правильности решения. Просто первый вариант включает в себя специализированное число, помогающее быстрее разобраться в условии, а второй заменяет log на обыкновенную степень. При этом вычисления с применением последней формулы должны включать в себя переменное значение.
Разница и терминология
Оба главных показателя обладают собственными особенностями, отличающими числа друг от друга:
Десятичный логарифм. Важная деталь числа — обязательное наличие основания. Стандартный вариант величины равен 10. Маркируется последовательностью — log x или lg x.
Натуральный. Если его основанием является знак «e», представляющий собой константу, идентичную строго рассчитанному уравнению, где n стремительно движется к бесконечности, то приблизительный размер числа в цифровом эквиваленте составляет 2.72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x.
Разные. Кроме основных логарифмов встречаются шестнадцатиричные и двоичные виды (основание 16 и 2 соответственно). Есть еще сложнейший вариант с базовым показателем 64, подпадающий под систематизированное управление адаптивного типа, с геометрической точностью производящее расчет итогового результата.
Терминология включает в себя следующие величины, входящие в алгебраическую задачу:
значение;
аргумент;
основание.
Вычисление log числа
Есть три способа быстро и в устной форме сделать все необходимые расчеты по нахождению интересующего результата с обязательным правильным итогом решения.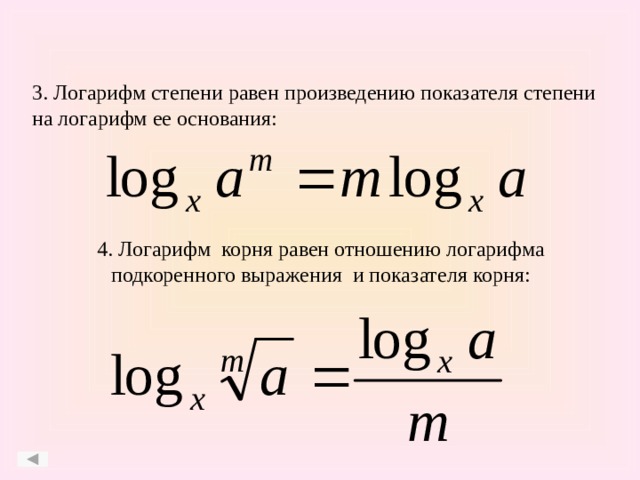 Изначально приближаем десятичный логарифм к своему порядку (научная запись числа в степени). Каждую положительную величину можно задать уравнением, где она будет равен мантиссе (цифра от 1 до 9), перемноженной на десятку в n-й степени. Такой вариант подсчета создан на основе двух математических фактов:
произведение и сумма log всегда имеют одинаковый показатель;
логарифм, взятый из числа от одного до десяти, не может превышать величину в 1 пункт.
Если ошибка в вычислении все-таки происходит, то она никогда не бывает меньше одного в сторону вычитания.
Точность повышается, если учесть, что lg с основанием три имеет итоговый результат — пять десятых от единицы. Поэтому любое математическое значение больше 3 автоматически добавляет к ответу один пункт.
Практически идеальная точность достигается, если под рукой есть специализированная таблица, которую можно легко применять в своих оценочных действиях. С ее помощью можно выяснить, чему равен десятичный логарифм до десятых процентов от оригинального числа.
История вещественного log
Шестнадцатый век остро испытывал потребности в более сложных исчислениях, чем было известно науке того времени. Особенно это касалось деления и умножения многозначных цифр с большой последовательностью, в том числе дробей.
В конце второй половины эпохи сразу несколько умов пришли к выводу о сложении чисел с помощью таблицы, которая сопоставляла две и геометрическую. При этом все базовые расчеты должны были упираться в последнюю величину. Таким же образом ученые интегрировали и вычитание.
Первое упоминание об lg состоялось в 1614 году. Это сделал любитель-математик по фамилии Непер. Стоит отметить, что, несмотря на огромную популяризацию полученных результатов, в формуле была сделана ошибка из-за незнаний некоторых определений, появившихся позже. Она начиналась с шестого знака показателя. Наиболее близки к пониманию логарифма были братья Бернулли, а дебютное узаконивание произошло в восемнадцатом столетии Эйлером. Он же и распространил функцию в область образования.
История комплексного log
Дебютные попытки интегрировать lg в широкие массы делали на заре 18-го века Бернулли и Лейбниц. Но целостных теоретических выкладок они так и не сумели составить. По этому поводу велась целая дискуссия, но точного определения числу не присваивали. Позже диалог возобновился, но уже между Эйлером и Даламбером.
Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.
Таблицы
Свойства числа указывают на то, что многозначные цифры можно не перемножать, а найти их log и сложить посредством специализированных таблиц.
Особенно ценным этот показатель стал для астрономов, которые вынуждены работать с большим набором последовательностей. В советское время десятичный логарифм искали в сборнике Брадиса, выпущенного в 1921 году. Позже, в 1971 году, появилось издание Веги.
Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Содержание
Область определения, множество значений, возрастание, убывание
Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.
Область определения 0 0
Область значений — ∞ — ∞
Монотонность монотонно возрастает монотонно убывает
Нули, y = 0 x = 1 x = 1
Точки пересечения с осью ординат, x = 0 нет нет
+ ∞ — ∞
— ∞ + ∞
Частные значения

Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:
Логарифм по основанию e называется натуральным логарифмом :
Основные формулы логарифмов
Свойства логарифма, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Логарифмирование — это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей преобразуются в суммы членов.
Потенцирование — это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов преобразуются в произведения сомножителей.
Доказательство основных формул логарифмов
Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.
Рассмотрим свойство показательной функции
.
Тогда
.
Применим свойство показательной функции
:
.
Докажем формулу замены основания.
;
.
Полагая c = b , имеем:
Обратная функция
Обратной для логарифма по основанию a является показательная функция с показателем степени a .
Если , то
Если , то
Производная логарифма
Производная логарифма от модуля x :
.
Производная n-го порядка:
.
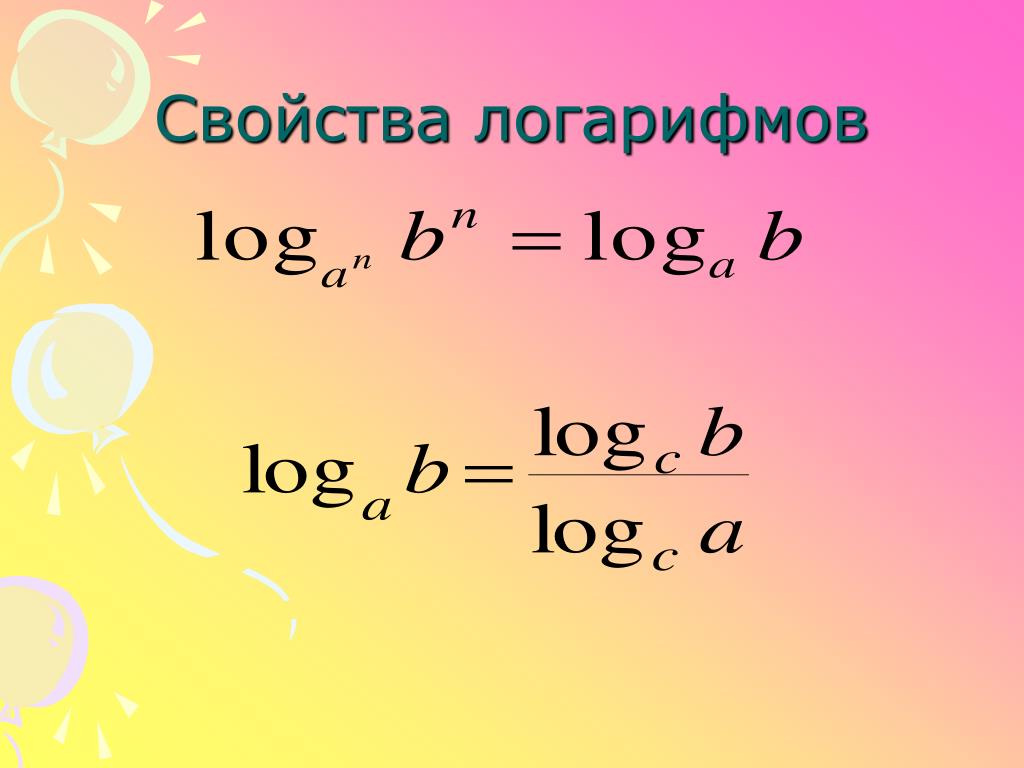
Вывод формул > > >
Для нахождения производной логарифма, его нужно привести к основанию e .
;
.
Интеграл
Интеграл от логарифма вычисляется интегрированием по частям : .
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексного числа z :
.
Выразим комплексное число z через модуль r и аргумент φ :
.
Тогда, используя свойства логарифма, имеем:
.
Или
Однако, аргумент φ определен не однозначно. Если положить
, где n — целое,
то будет одним и тем же числом при различных n .
Поэтому логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
См. также: 3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92
Использование логарифмического преобразования в регрессии и прогнозировании
Концепции данных

Принципы и риски прогнозирования (pdf)
Известное прогнозирование цитаты
Как перемещать данные вокруг
Узнай свои данные
Поправка на инфляцию (дефляция)
Поправка на сезонность
Стационарность и разность
Логарифм трансформация

преобразование логарифмов
Введение в логарифмы : Логарифмы являются одним из наиболее важные математические инструменты в наборе инструментов статистического моделирования, так что вы должны быть хорошо знакомы с их свойствами и использованием. А логарифмическая функция определяется по «основанию», т.е. положительное число: , если b обозначает базовое число, то Логарифм по основанию b числа X — это, по определению, число Y такое, что b ^Д = Х . Например, основание-2 логарифм 8 равен 3, потому что 2 ³ = 8, а по основанию-10 логарифм 100 равен 2, потому что 10 ² = 100.   Существует три вида логарифмов. в стандартном использовании: логарифм по основанию 2 (преимущественно используется в информатике и теория музыки), логарифм по основанию 10 (преимущественно используется в технике), и натуральный логарифм (преимущественно используемый в математике и физика и по экономике и бизнесу ). В натуральной логарифмической функции основание число — трансцендентное число « e» десятичное расширение которого равно 2,718282…, поэтому натуральная логарифмическая функция и экспоненциальная функция ( e ^x ) являются инверсиями друг друга. только различия между этими тремя логарифмическими функциями являются мультипликативными коэффициенты масштабирования, поэтому логически они эквивалентны для целей моделирования, но выбор базы важен из соображений удобства и условности, согласно настройке.
В стандартной математической записи, а также в Excel и большинстве других аналитических программ, выражение LN(X) является натуральным логарифмом X, и EXP(X) — экспоненциальная функция X, поэтому EXP(LN(X)) = X и LN(EXP(X)) = X.   Это означает, что функцию EXP можно использовать для преобразования естественные прогнозы (и их соответствующие нижняя и верхняя достоверность пределы) обратно в реальные единицы. Вы не можете использовать функцию EXP, чтобы напрямую удалить статистику ошибок модели, приспособленной к естественно-логарифмические данные. Тебе следует сначала конвертируйте прогнозы обратно в реальные единицы, а затем пересчитайте ошибки и статистика ошибок в реальных единицах, если важно иметь те числа. Однако ошибка статистику модели, приспособленной к данным естественного каротажа, часто можно интерпретировать как приблизительные меры процентов ошибка, как описано ниже, и в ситуациях, когда ведение журнала уместно в Во-первых, часто бывает интересно измерить и сравнить ошибки в процентное соотношение.

В общем, выражение LOG _b (.) используется для обозначения логарифмической функции по основанию b, и LN используется для особого случая естественного журнала, в то время как LOG часто используется для особого случая журнала базы 10. В частности, LOG означает вход в систему с основанием 10. Эксель. В Statgraphics, увы, функция, которая называется LOG — это натуральный журнал , в то время как функция логарифма по основанию 10 — LOG10. В оставшейся части этого раздела (и в другом месте на сайте), как LOG, так и LN будут использоваться для ссылки на натуральная функция журнала , для совместимости с Статграфическое обозначение. Также, символ «≈» означает приблизительно равных , с аппроксимация более точна в относительном выражении для меньшего абсолютного значения, как показано в таблице ниже.

Изменение в натуральный логарифм ≈ изменение в процентах : натуральный логарифм и его основание e обладают некоторыми магическими свойствами, которые вы может вспомнить из исчисления (и который вы, возможно, надеялись, что никогда не встретите опять таки). Например, функция e ^X является собственной производной, а производная LN(X) равна 1/X. Но в целях бизнес-анализа, его большим преимуществом является то, что небольших изменений в естественном log переменной напрямую интерпретируются как процентные изменения, в очень близком приближении . Причина этого в том, что график Y = LN(X) проходит через точку (1, 0) и имеет там наклон 1, поэтому он касается прямая линия, уравнение которой Y = X-1 (пунктирная линия на графике ниже):

Это свойство естественной логарифмической функции означает, что

LN(1+r) ≈ r

, когда r намного меньше 1 по величине. Почему это важно? Предположим, что X увеличивается на небольшую процент, например 5%. Это означает что он меняется с X на X(1+r), где г = 0,05. Теперь обратите внимание:

LN(X (1+r)) = LN(X) + LN(1+r) ≈ LN(X) + r

Таким образом, при увеличении X на 5%, т. е. умножении на коэффициент 1,05, натуральный log изменения X от LN(X) до LN(X) + 0,05, до очень близкого приближение. Увеличение X на 5% поэтому (почти) эквивалентно добавлению 0,05 к LN(X).

От теперь я буду называть изменения натуральных логарифмов «diff-журналы». (В Statgraphics, логарифмическое преобразование X буквально выглядит как DIFF(LOG(X)).) В следующей таблице показано точное соответствие для процентов в диапазоне от -50% до +100%:

Как видите, процентные изменения и diff-логи почти точно такие же в пределах +/- 5%, и они остаются очень близко к +/- 20%. Для больших при процентном изменении они начинают расходиться асимметричным образом. Обратите внимание, что журнал различий, соответствующий к уменьшению на 50% составляет -0,693, в то время как логарифм дифференциала увеличения на 100% составляет +0,693, ровно противоположное число. Это отражает тот факт, что за 50-процентным снижением следует 100-процентное увеличение. (или наоборот) возвращает вас в то же место.

процентное изменение Y в период t определяется как (Y _t -Y _t-1 )/Y _t-1 , что всего лишь приблизительно равно LN(Y _t ) — LN(Y _t-1 ), но приближение почти точное , если процентное изменение невелико, как показано в таблице выше. В Статграфические термины означают, что DIFF(Y)/LAG(Y,1) практически идентичен РАЗН(ЛОГ(Г)). Если вы не верите я, вот график процентного изменения продаж автомобилей по сравнению с первым разность его логарифма с увеличением за последние 5 лет. Синий и красные линии практически неразличимы, за исключением самых высоких и самых низких точки. (Опять же, LOG означает LN в Statgraphics.)
Если ситуация это тот, в котором процентные изменения потенциально достаточно велики для этого приближение будет неточным, лучше использовать логарифмические единицы, а не процентные единицы, потому что это учитывает начисление сложных процентов в систематическом образом, и он симметричен с точки зрения последовательностей прибылей и убытков . Журнал различий -0,5, за которым следует журнал различий +0,5, возвращает вас к вашей исходной позиции, тогда как 50%-й убыток сменяется 50%-м приростом (или наоборот). наоборот) оставляет вас в худшем положении.
(Вернуться к началу страницы.)
Линеаризация экспоненциального роста и инфляции: T Логарифм произведения равен сумма логарифмов, т. е. LOG(XY) = LOG(X) + LOG(Y), независимо от основание логарифма. Таким образом, ведение журнала преобразует мультипликативных отношений. в аддитивных отношений, и тем самым он преобразует экспоненциальных (составной рост) трендов до линейных трендов . Логарифмируя переменные, которые мультипликативно связаны и/или экспоненциально растут со временем, мы можем часто объясняют их поведение линейными моделями. Например, вот график LOG(АВТОПРОДАЖА). Обратите внимание, что преобразование журнала преобразует экспоненциальный рост до линейного модель роста, и она одновременно преобразует мультипликативную (пропорциональную дисперсию) сезонную модель в аддитивную (постоянную дисперсию) сезонную модель. шаблон. (Сравните это с исходным графиком AUTOSALE.) Эти преобразования делают преобразованные данные гораздо более подходящими для линейные/аддитивные модели.

Запись ряда часто имеет эффект, очень похожий на сдувание: он выпрямляет экспоненциальные модели роста и уменьшает гетероскедастичность (т.е. стабилизирует дисперсия). Таким образом, ведение журнала — это «бедных мужской дефлятор» , который не требует никаких внешних данных (или каких-либо ломать голову над тем, какой индекс цен использовать). Логирование не а именно то же самое, что и дефлятирование — оно не устраняет восходящего тренда в данные, но он может выпрямить тренд, чтобы его можно было лучше подогнать линейная модель. Дефляция сама по себе не выпрямит кривую экспоненциального роста, если рост частично реальным и лишь частично обусловленным инфляцией.
Если вы собираемся регистрировать данные, а затем подгонять модель, которая явно или неявно использует разностных (например, случайное блуждание, экспоненциальное сглаживание или модель ARIMA), то обычно излишне дефлировать с помощью индекса цен, если уровень инфляции изменяется очень медленно: процентное изменение, измеренное в номинальных долларах, будет почти так же, как процентное изменение постоянных долларов. В Статграфике обозначения, это означает, что DIFF(LOG(Y/CPI)) почти идентичен DIFF(LOG(Y)): единственная разница между ними — очень слабый шум из-за колебаний в уровне инфляции. Чтобы продемонстрировать это, вот график первого разница зарегистрированных продаж автомобилей с дефляцией и без нее:
По регистрации , а не , а не сдувание, вы избегаете необходимости включать явный прогноз будущей инфляции в модель: вы просто складываете инфляцию в одну кучу с любыми другими источниками устойчивого составного роста в исходных данных. логирование данные до подбора модели случайного блуждания дают так называемое геометрическое случайное блуждание, т. е. случайное блуждание с геометрическим, а не линейным ростом. Геометрическое случайное блуждание — это модель прогнозирования по умолчанию, которая обычно используется для данных о ценах на акции. (Вернуться к началу страницы.)
Тренд измеряется в натуральных логарифмических единицах ≈ рост в процентах:   Поскольку изменения натурального логарифма (почти) равны до процентов изменений в исходном ряду, отсюда следует, что наклон линии тренда, подогнанной к зарегистрированным данным, равна среднему процентам рост в исходной серии. Например, на графике LOG(AUTOSALE), показанном выше, если вы «на глазок» линии тренда, вы увидите, что величина зарегистрированных продаж автомобилей увеличивается на около 2,5 (с 1,5 до 4,0) за 25 лет, что в среднем составляет около 0,1 в год, т. е. 10% в год. Гораздо проще оценить эту тенденцию по зарегистрированному графику, чем по исходному незарегистрированному один! Полученная здесь цифра 10% равна 9. 0947 номинальный рост, в т.ч. инфляция. Если бы вместо этого мы увидели линию тренда на графике зарегистрированных дефлятированных продаж, т. е. LOG(AUTOSALE/CPI), его наклон будет равен среднему реальному процентам. рост.
Обычно тенденция оценивается более точно путем подгонки статистической модели который явно включает локальный или глобальный параметр тренда, такой как линейный модель тренда или случайного блуждания с дрейфом или модель линейного экспоненциального сглаживания. Когда модель такого типа подгоняется в сочетании с логарифмическим преобразованием, его трендовый параметр можно интерпретировать как процентный темп роста.

(Вернуться к началу страница.)
Ошибки измеряется в натуральных логарифмических единицах ≈ ошибки в процентах: Еще одно интересное свойство логарифма заключается в том, что ошибки в предсказании регистрируемого ряда можно интерпретировать как приблизительные процентные ошибки в предсказании исходного ряда, хотя проценты относительно прогнозируемых значений, а не фактических значений. (обычно один интерпретирует «процентную ошибку» как ошибку, выраженную как процент от фактического значения, а не прогнозируемого значения, хотя статистические свойства процентных ошибок обычно очень похожи независимо от от того, рассчитываются ли проценты относительно фактических значений или прогнозы.)
Таким образом, если вы используете оценку методом наименьших квадратов, чтобы подогнать модель линейного прогнозирования к зарегистрированным данных, вы неявно минимизируете среднеквадратичную процентную ошибку , а не среднеквадратичная ошибка в исходных единицах, что, вероятно, хорошо вещь, если преобразование журнала было уместным в первую очередь. И если вы посмотрите статистику ошибок в зарегистрированных единицах, вы можете интерпретировать их как проценты, если они не слишком велики, например, если их стандартное отклонение равно 0,1. или менее. В пределах этого диапазона стандартное отклонение ошибок в прогнозировании зарегистрированного ряда составляет приблизительно стандартное отклонение процентных ошибок при предсказании исходного серии, а средняя абсолютная ошибка (MAE) в прогнозировании зарегистрированной серии равна примерно средняя абсолютная процентная ошибка (MAPE) в прогнозировании оригинальный сериал. (я использую эталон 0,1 здесь, потому что в этот момент вариация стандартного отклонения 2, критическое значение для 95% доверительный интервал будет равен 0,2, а соответствие между дифф-логами и процентами начинает изрядно отваливаться быстро превышает это значение, как показано в таблице выше. Если стандартное отклонение ошибки в зарегистрированных единиц больше 0,1, вам следует рассчитать доверительные интервалы в зарегистрированных единиц, а затем отдельно отменить регистрацию их нижних и верхних значений с помощью функцию EXP.)
(Вернуться к началу страница.)
Коэффициенты в логарифмических регрессиях ≈ пропорциональные процентные изменения : Во многих экономических ситуациях (особенно отношения цены и спроса), предельное влияние одной переменной на ожидаемое значение другого является линейным с точки зрения процентов изменений, а не абсолютных изменения. В таких случаях применение преобразование натурального логарифма или diff-log как в зависимый, так и в независимый переменные могут подойти. Этот этот вопрос будет обсуждаться более подробно в главе о регрессии этих заметки. В частности, часть 3 продажи пива Пример регрессии иллюстрирует применение преобразования журнала в моделирование влияния цены на спрос, в том числе как использовать EXP (экспоненциальная) функция для «нерегистрации» прогнозов и доверительных интервалов преобразовать их обратно в единицы исходных данных. 9N} = M}
Цель эквивалентных уравнений, как показано выше, состоит в том, чтобы обеспечить прямую связь между логарифмической формой и экспоненциальной формой. Понимание этой базовой концепции может помочь нам решить некоторые алгебраические задачи, требующие переключения с одной формы на другую.
Рассмотрим далее, как переставляются переменные M, N и b, когда логарифмическая форма выражается как экспоненциальная форма и наоборот.
Наблюдения за «переключателем» в позициях переменных:
Нижний индекс b в логарифмической форме становится основанием в экспоненциальной форме.
Основание N в логарифмической форме становится показателем степени или надстрочным индексом b в экспоненциальной форме.
Переменная M изолирована в одной части уравнения.
Вот несколько быстрых иллюстраций того, как преобразовать логарифмическую форму в экспоненциальную и наоборот.
Логарифмическая форма ⟷ Экспоненциальная форма 9{{1 \over 4}}} = 3
Теперь мы собираемся обсудить «особых случаев» , которые естественным образом возникают из основного определения логарифма в терминах показательного уравнения. Мы будем использовать приведенное выше определение, чтобы ответить на некоторые из этих вопросов. Лучший способ обозначить концепцию — использовать примеры.
Примеры решения основных логарифмических уравнений
Пример 1: Решить y в логарифмическом уравнении log ₃ 3 = y .
Переписав логарифмическое уравнение log ₃ 3 = y в экспоненциальную форму, мы получим 3 = 3 ^y . Как вы думаете, какое значение y может сделать экспоненциальное уравнение верным? Другими словами, мы хотим найти показатель степени, в который нужно возвести 3, чтобы получить 3. Похоже, что единственный ответ — 1, потому что, когда y = 1, мы имеем 3=3 ¹ .
Фактически, мы можем обобщить эту идею в простое правило…
Логарифм ненулевое и неотрицательное число , в котором основанием является само число ВСЕГДА равно 1 .
Пример 2: Найдите x в логарифмическом уравнении log ₈ 1 = x .
Это логарифмическое уравнение в экспоненциальной форме записывается как 1 = 8 ^x . Каким может быть значение показателя степени x, чтобы сделать его истинным утверждением? Используя нулевое свойство экспоненты, b ⁰ = 1 , мы знаем, что любое число (за исключением нуля) при возведении в ноль всегда равно 1. Вполне логично, что в 1 = 8 ^x значение должно быть x = 0 , потому что 8 ⁰ = 1 .
Также есть правило, которое обрабатывает такие случаи, когда мы пытаемся получить логарифм 1 по любому основанию.
Логарифм числа 1 с любым значением b (b — положительное число, но b ≠1) равен ВСЕГДА равен ноль (0).
Пример 3: Найти k в логарифмическом уравнении log ₄ (−1) = k .
Преобразуя в экспоненциальное уравнение, мы имеем −1 = 4 ^k . Это похоже на вопрос с подвохом, верно? Нам нужно найти показатель степени k, чтобы сделать показательное уравнение верным утверждением.
Действительно ли есть такое значение? Я не думаю, что есть один! На самом деле, мы не можем найти ни одного числа, на которое можно возвести 4, чтобы получить −1. Поэтому мы говорим, что решения нет или оно неопределенно.
Логарифм отрицательного числа равен undefined .
Пример 4: Найти w в логарифмическом уравнении log ₂ (0) = w .
Последний «особый случай» возникает, когда мы пытаемся найти логарифм нуля. Снова преобразуя это логарифмическое уравнение в экспоненциальное, мы получаем 0 = 2 ^w . Мы снова столкнулись со странной ситуацией, потому что мы хотим поднять основание 2 на некоторый показатель, чтобы в результате получился ноль. Есть ли такая ценность? Можешь попробовать. Но согласитесь, что такой ценности не существует! Следовательно, это еще один случай, когда наш ответ равен 9.1206 не определено или нет решения .
Логарифм нуля равен undefined .
You might also be interested in:
Condensing Logarithms
Expanding Logarithms
Logarithm Rules
Solving Logarithmic Equations
Exponential and Logarithmic Models
Exponential and Logarithmic Models
Графер
Калькулятор
Возврат
Справка
Точечная диаграмма
Содержание: Эта страница соответствует § 4,5 (стр. 359) текста.
Предлагаемые проблемы из текста:
р. 366 #7,9,15,17,25,33,35,69
Экспоненциальный рост и спад
Другие модели
Экспоненциальный рост и упадок

Двумя распространенными типами математических моделей являются

Экспоненциальный рост: y = a e ^бх, б > 0,
Экспоненциальное затухание: y = a e ^-bx , b > 0,

Пример 1.

В течение 1980-х годов население одного города увеличилось со 100 000 до 205 000 человек. Население по годам указано в таблице ниже.
Год
1980
1981
1982 г.
1983
1984
1985
1986
1987
1988 г.
1989 г.
Население в тысячах
100
108
117
127
138
149
162
175
190
205
Эти данные хорошо аппроксимируются моделью экспоненциального роста P = 100 e ^0,08t , где t — число лет, начиная с 1980 г. Другими словами, 1980 г. соответствует t = 0, 1981 г. соответствует t = 1 и т. д. Данные точки и модель представлены на графике ниже.
Точки данных о населении и модель P = 100 e ^{0,08 т}
, где t — количество лет с 1980 года.
Задача 1. Используйте модель для прогнозирования численности населения города в 1994 г.
1991 соответствует t = 11, поэтому наша модель предсказывает, что население составит
человек.
P = 100 e ^0,08*11 = 241 тысяча.
Задача 2: Согласно нашей модели, когда численность населения достигнет 300 тысяч?
Чтобы решить эту задачу, приравняем 100 e ^0,08t к 300 и найдем t.
100 е ^0,08т = 300
e ^0,08t = 3 Возьмем натуральный логарифм обеих частей.
ln e ^{0,08 т} = ln 3
0,08t = ln 3
t = (ln 3)/0,08 = 13,73, приблизительно.
Таким образом, население, как ожидается, достигнет 300 тысяч примерно на три четверти пути в течение года. 1993.
Важно понимать ограничения этой модели. Хотя из графика видно, что для t между 0 и 9 значения модели очень близки к фактическим значениям населения, мы не должны предполагать, что наша модель будет дать точный прогноз численности населения для значений t, намного превышающих 9. Например, модель предсказывает что в 2080 году (t = 100) население города будет почти 300 миллионов человек! Это маловероятно.

Предположим, мы знаем, что переменная y может быть выражена в форме ae ^bx , но мы не знаем значения а и б. Если нам даны любые две точки на графике y, то можно найти числа a и b. простейший случай, который часто встречается в приложениях, когда мы знаем значение y, когда x = 0 и еще одна точка на графике y.

Пример 2.

Предположим, что население P растет экспоненциально, поэтому P = ae ^bt , где t измеряется в годах.
Если P = 15000 в 1990 г., а P выросло до 17000 в 1993 г., найдите формулу для P.
Пусть t будет количеством лет с 1990 года. Тогда a = 15000 , значение P при t = 0,
Обратите внимание, что t можно было выбрать по-другому. Например, мы можем позволить t быть количеством лет с 1900 года. Но тогда мы не знали бы значения P при t = 0, поэтому мы не знали бы значения a сразу.
Нам еще нужно найти б. Все, что мы знаем о b, это то, что оно положительно, поскольку население растет. С использованием значение, которое мы нашли для a, у нас есть
P = 15000 e ^bt .
1993 год соответствует t = 3, поэтому мы подставляем P = 17000 и t = 3 в приведенное выше уравнение и находим б.
17000 = 15000 е ^3b
Мы несколько раз решали уравнения такого вида. Первым шагом является выделение экспоненциального члена. затем возьмем натуральный логарифм обеих частей.
17/15 = е ^3б
пер. (17/15) = пер. е ^3b
лн (17/15) = 3б
б = (ln(17/15))/3 = 0,0417 (приблизительно)
Следовательно, P = 15000 e ^{0,0417 t}
Основываясь на этой модели, когда численность населения достигнет 20 000 человек?
Примите P равным 20000 и найдите t.
20000 = 15000 е ^{0,0417 т}
4/3 = е ^{0,0417 т}
ln (4/3) = ln e ^{0,0417 т}
ln (4/3) = 0,0417 т
t = (ln (4/3))/0,0417 = 6,9 года
Таким образом, мы ожидаем, что к концу 1996 года численность населения достигнет 20 000 человек.

Упражнение 1 :

Найдите модель типа P = ae ^bt , где t — количество лет с 1970, если P = 30000 в 1970 г. и P = 36000 в 1977 г. Используйте эту модель, чтобы предсказать значение P в 1980 г.
Ответить

Когда коэффициент x (или как там называется независимая переменная) равен отрицательному , тогда мы моделируем убывающая переменная . Это называется экспоненциальным распадом. Мы проиллюстрируем экспоненциальное затухание, рассматривая радиоактивное вещество. Образец радиоактивного вещества со временем распадается.

Пример 3.

Масса (в граммах) радиоактивного материала в образце определяется выражением N = 100e ^-0,0017t , где t равно измеряется годами.
Найдите период полураспада этого радиоактивного вещества.
Период полураспада радиоактивного вещества – это время, необходимое для распада половины данного образца. Обратите внимание, что период полураспада не зависит от размера образца. Если период полураспада определенного радиоактивного материала составляет 700 лет, то если начальная масса образца 1000 грамм, то через 700 лет будет 500 грамм. Если начальная масса образца всего 8 грамм, через 700 лет будет 4 грамма.
В этом примере масса радиоактивного материала составляет 100 граммов в момент времени t = 0. Следовательно, период полураспада равен количество времени, необходимое для распада образца до 50 граммов. Таким образом, мы можем найти период полураспада, приравняв N до 50 и решение для t.
100e ^-0,0017t = 50
e ^-0,0017t = 0,5
Примечание. Если бы начальное количество было 800 граммов, то нам пришлось бы решить уравнение 800e ^-0,0017t =400, и после деления обеих частей на 800 мы получим e ^-0,0017t = 0,5, что совпадает с уравнением выше. Вот почему период полураспада не зависит от исходного количества.
ln e ^-0,0017t = ln 0,5
-0,0017t = ln 0,5
t = (ln 0,5)/-0,0017 = 408 лет (приблизительно)
Вопрос : Почему (ln 0,5)/-0,0017 равно (ln 2)/0,0017?

В предыдущем разделе мы обсуждали важный пример экспоненциального роста, а именно непрерывный начисление процентов. Вычисление периода полураспада радиоактивного вещества очень похоже на вычисление удвоение времени для инвестиций.

Пример 4.

Если 1000 долларов инвестируются под 9% годовых с постоянным начислением сложных процентов, сколько времени потребуется для инвестирования? удвоить? Используя формулу сложных процентов A = Pe ^рт , у нас
А = 1000e ^0,09t
Мы хотим найти время, за которое инвестиции удвоятся, то есть до 2000 долларов, поэтому устанавливаем А равно 2000 и найти t.
1000e ^0,09t = 2000 Разделите обе части на 1000.
е ^{0,09 т} = 2
Примечание : Как и период полураспада, время удвоения не зависит от первоначальных инвестиций P. Если бы мы начали с 50 долларами и спросили, сколько времени пройдет, прежде чем у нас будет 100 долларов, тогда мы бы решили уравнение
50e ^0,09t = 100, и после деления обеих частей на 50 мы снова получим e ^0,09t = 2,
.
ln e ^{0,09 т} = ln 2
0,09 т = ln 2
t = (ln 2)/0,09 = 7,7 года (приблизительно).
Вопрос: Если вы инвестируете 3000 долларов под 9% годовых, сколько вы будете иметь через 15 с половиной лет?
Ответ: Около 12000 долларов. Это легко аппроксимировать, потому что время удвоения составляет 7,7 года, поэтому 15,5 лет соответствует до чуть более двух удвоений. 3000 -> 6000 -> 12000.

Упражнение 2 :

Сколько времени требуется инвестициям, чтобы утроили при непрерывном начислении процентов 11? Ответ

Вернуться к содержанию

Другие модели

Пример 5.

Рассмотрим следующие точки данных.
х
1
2
3
4
5
6
7
г.
0,5
2,6
3,6
4,5
4,9
5,4
5,7
Когда мы наносим эти точки, мы видим, что они не лежат ни на какой экспоненциальной кривой, но форма очень очень похоже на логарифмический график. Это говорит о том, что логарифмическая модель является разумной. На приведенном ниже графике показано точки данных и функция y = 0,63 + 2,7 ln x, которая достаточно хорошо соответствует точкам данных.

Вернуться к содержанию

Графер	Калькулятор	Возврат
Справка	Точечная диаграмма	Возврат

Логарифмические функции | Алгебра и тригонометрия

Цели обучения

В этом разделе вы:

Преобразуете логарифмическую форму в экспоненциальную.
Преобразование экспоненциальной формы в логарифмическую.
Вычисление логарифмов.
Используйте десятичные логарифмы.
Используйте натуральные логарифмы.

Рис. 1. Разрушения после землетрясения 11 марта 2011 г. в Хонсю, Япония. (кредит: Дэниел Пирс)

В 2010 году на Гаити произошло сильное землетрясение, разрушившее или повредившее более 285 000 домов ^[1] . Год спустя другое, более сильное землетрясение разрушило Хонсю, Япония, разрушив или повредив более 332 000 зданий, 90 940 [2] 90 941 таких, как показано на (Рисунок). Несмотря на то, что оба нанесли значительный ущерб, землетрясение 2011 года было в 100 раз сильнее, чем землетрясение на Гаити. Откуда нам знать? Магнитуда землетрясений измеряется по шкале, известной как шкала Рихтера. Землетрясение на Гаити зарегистрировало 7 баллов по шкале Рихтера 9 баллов.{4}=10 000[/latex] раз лучше! На этом уроке мы исследуем природу шкалы Рихтера и функцию десятичного счисления, от которой она зависит.

Преобразование логарифмической формы в экспоненциальную

Чтобы проанализировать магнитуду землетрясений или сравнить магнитуды двух разных землетрясений, нам необходимо иметь возможность преобразовывать логарифмическую форму в экспоненциальную. {х}=500,[/латекс], где [латекс]\,х\,[/латекс] представляет собой разницу величин по шкале Рихтера. Как бы мы решили для[латекс]\,х?[/латекс] 9{y}\,[/latex] также является функцией. Как и в случае со всеми обратными функциями, мы просто меняем местами [латекс]\,x\,[/латекс] и [латекс]\,у\,[/латекс] и находим [латекс]\,у\,[/ латекс], чтобы найти обратную функцию. Чтобы представить [латекс]\,у\,[/латекс] как функцию [латекс]\,х,[/латекс], мы используем логарифмическую функцию вида [латекс]\,у={\mathrm{log} }_{b}\left(x\right).\,[/latex]Основание[latex]\,b\,[/latex] логарифм числа — это показатель степени, на который мы должны возвести[latex] \,b\,[/latex], чтобы получить это число. 9{y}=x,\text{}b>0,b\ne 1[/latex]

Обратите внимание, что основание[latex]\,b\,[/latex] всегда положительно.

Поскольку логарифм — это функция, его правильнее всего записывать как [латекс]\,{\mathrm{log}}_{b}\left(x\right),[/latex], используя круглые скобки для обозначения вычисления функции , точно так же, как и в случае [latex]\,f\left(x\right). \,[/latex]Однако, когда ввод представляет собой одну переменную или число, обычно можно увидеть, что скобки опущены, а выражение написано без круглых скобок, как[latex]\,{\mathrm{log}}_{b}x.\,[/latex]Обратите внимание, что многие калькуляторы требуют круглых скобок вокруг[latex]\,x.[/latex] 9{y}=x[/latex]

, где

мы читаем [латекс]\,{\mathrm{log}}_{b}\left(x\right)\,[/latex]как, » логарифм по основанию[латекс]\,b\,[/латекс]из[латекс]\,х[/латекс]» или «логарифм по основанию[латекс]\,b\,[/латекс]из[латекс]\ ,х.»[/латекс]
логарифм[latex]\,y\,[/latex] — это показатель степени, в которую [latex]\,b\,[/latex] нужно возвести, чтобы получить [latex]\,x.[/latex]

Кроме того, поскольку логарифмическая и экспоненциальная функции меняют местами значения [latex]\,x\,[/latex] и [latex]\,y\,[/latex], домен и диапазон экспоненциальной функции меняются местами для логарифмическая функция. Следовательно,

область определения логарифмической функции с основанием[latex]\,b \text{is} \left(0,\infty \right). [/latex]
диапазон логарифмической функции с основанием [латекс]\,b \text{is} \left(-\infty ,\infty \right).[/latex]

Можем ли мы взять логарифм отрицательного числа?

Нет. Поскольку основание экспоненциальной функции всегда положительно, никакая степень этого основания не может быть отрицательной. Мы никогда не можем логарифмировать отрицательное число. Кроме того, мы не можем логарифмировать ноль. Калькуляторы могут выводить логарифм отрицательного числа в сложном режиме, но логарифм отрицательного числа не является действительным числом. 9{у}=х.[/латекс]

Преобразование логарифмической формы в экспоненциальную

Напишите следующие логарифмические уравнения в экспоненциальной форме.

[латекс] {\ mathrm {log}} _ {6} \ влево (\ sqrt {6} \ вправо) = \ гидроразрыва {1} {2} [/ латекс]
[латекс] {\ mathrm {log}} _ {3} \ влево (9 \ вправо) = 2 [/латекс]

Показать раствор

Попробуйте

Напишите следующие логарифмические уравнения в экспоненциальной форме.

[латекс] {\ mathrm {log}} _ {10} \ влево (1 000 000 \ вправо) = 6 [/ латекс]
[латекс] {\ mathrm {log}} _ {5} \ влево (25 \ вправо) = 2 [/латекс]

Показать раствор

Преобразование экспоненциальной формы в логарифмическую

Чтобы преобразовать экспоненциальную форму в логарифмическую, мы выполняем те же действия в обратном порядке. Мы идентифицируем базовый [латекс]\,b,[/латекс]показатель[латекс]\,х,[/латекс] и выходной[латекс]\,у.\,[/латекс]. Затем мы пишем[латекс]\, x={\mathrm{log}}_{b}\left(y\right).[/latex]

Преобразование экспоненциальной формы в логарифмическую

Напишите следующие экспоненциальные уравнения в логарифмической форме. 9{у}=х.\,[/латекс]

Используйте предыдущее знание степеней [латекс]\,b\,[/латекс]идентифицируйте[латекс]\,у\,[/латекс], задав вопрос: «В каком показателе следует [латекс]\,b\,[/ латекс] быть поднятым, чтобы получить [латекс]\,х?[/латекс]»

Решаем логарифмы в уме

Решаем [латекс]\,y={\mathrm{log}}_{4}\left(64\right)\,[/latex] без использования калькулятора.

Показать решение

Попробуйте

Решите [латекс]\,y={\mathrm{log}}_{121}\left(11\right)\,[/latex] без использования калькулятора.

Показать решение

Вычисление логарифма обратной величины

с помощью калькулятора.

Показать решение

Попробуйте

Оцените [латекс]\,y={\mathrm{log}}_{2}\left(\frac{1}{32}\right)\,[/latex] без использования калькулятора.

Показать решение

Использование десятичных логарифмов

Иногда мы можем увидеть логарифм, записанный без основания. В этом случае мы предполагаем, что основание равно 10. Другими словами, выражение [латекс]\,\mathrm{log}\left(x\right)\,[/latex]означает[латекс]\,{\mathrm {log}}_{10}\left(x\right).\,[/latex]Мы называем логарифм по основанию 10 числом десятичный логарифм . Для измерения шкалы Рихтера, упомянутой в начале раздела, используются десятичные логарифмы. Шкалы для измерения яркости звезд и pH кислот и оснований также используют десятичные логарифмы.

Определение десятичного логарифма

Десятичный логарифм — это логарифм с основанием [латекс]\,10.\,[/латекс] Мы пишем [латекс]\,{\mathrm{log}}_{10}\left (x\right)\,[/latex]просто как[latex]\,\mathrm{log}\left(x\right).\,[/latex]Десятичный логарифм положительного числа[latex]\,x \,[/latex] удовлетворяет следующему определению. 9{y}=x[/latex]

Читаем[latex]\,\mathrm{log}\left(x\right)\,[/latex]как «логарифм по основанию[latex]\,10\ ,[/latex]of[latex]\,x\,[/latex]» или «логарифм по основанию 10 of[latex]\,x.[/latex]»

Логарифм[latex]\,y\,[ /latex] — это показатель степени, в которую [latex]\,10\,[/latex] нужно возвести, чтобы получить [latex]\,x.[/latex]

How To

Учитывая десятичный логарифм вида [latex]\,y=\mathrm{log}\left(x\right),[/latex] мысленно оцените его.

Перепишите аргумент [латекс]\,х\,[/латекс] как степень [латекс]\,10:\,[/латекс][латекс]{10}^{у}=х. [ /латекс]
Используйте предыдущие знания о степенях [латекс]\,10\,[/латекс], чтобы идентифицировать [латекс]\,у\,[/латекс], задав вопрос: «В какой степени должен [латекс]\,10\,[ /latex]быть поднятым, чтобы получить[latex]\,x?[/latex]»

Нахождение значения десятичного логарифма в уме

Вычисление[латекс]\,у=\mathrm{лог}\влево(1000\вправо)\,[/латекс] без использования калькулятора.

Показать решение

Попробуйте

Вычислите[латекс]\,y=\mathrm{log}\left(1,000,000\right).[/latex]

Показать решение

Как

Учитывая десятичный логарифм в форме [латекс]\,у=\mathrm{log}\left(x\right),[/latex]оцените его с помощью калькулятора.

Нажмите [ЖУРНАЛ] .
Введите значение, данное для [латекс]\,x,[/латекс], а затем [ ) ] .
Нажмите [ВВОД] .

Нахождение значения десятичного логарифма с помощью калькулятора

Вычислить [латекс]\,y=\mathrm{log}\left(321\right)\,[/latex]до четырех знаков после запятой с помощью калькулятора. 9{3}=1000.\,[/latex]Поскольку 321 находится между 100 и 1000, мы знаем, что [latex]\,\mathrm{log}\left(321\right)\,[/latex]должен быть между[ латекс]\,\mathrm{log}\left(100\right)\,[/latex]and[latex]\,\mathrm{log}\left(1000\right).\,[/latex]Это дает нам следующее:

[латекс]\begin{array}{ccccc}100& <& 321& <& 1000\\ 2& <& 2.5065& <& 3\end{массив}[/latex]

Попробуйте

Оценить[ латекс]\,y=\mathrm{log}\left(123\right)\,[/latex]до четырех знаков после запятой с помощью калькулятора. 9{x}=8500\,[/latex] представляет эту ситуацию, где [latex]\,x\,[/latex] — разница величин по шкале Рихтера. Какова была разница в величинах с точностью до тысячных?

Показать решение

Использование натуральных логарифмов

Наиболее часто используемым основанием для логарифмов является[латекс]\,е. \,[/латекс]Основание[латекс]\,е\,[/латекс]логарифмы важны в вычислениях и некоторых научных приложениях ; они называются натуральных логарифмов . Основание [латекс] \, е \, [/ латекс] логарифм, [латекс] \, {\ mathrm {log}} _ {е} \ влево (х \ вправо), [/ латекс] имеет свои собственные обозначения, [ латекс]\,\mathrm{ln}\left(x\right).[/latex]

Большинство значений [латекс]\,\mathrm{ln}\left(x\right)\,[/латекс] можно найти только с помощью калькулятора. Основное исключение состоит в том, что, поскольку логарифм 1 всегда равен 0 по любому основанию, [латекс]\,\mathrm{ln}1=0.\,[/латекс]Для других натуральных логарифмов мы можем использовать [латекс] \,\mathrm{ln}\,[/latex], который можно найти в большинстве научных калькуляторов. Мы также можем найти натуральный логарифм любой степени [латекс]\,е\,[/латекс], используя обратное свойство логарифмов.

Определение натурального логарифма 9{\mathrm{ln}\left(x\right)}=x\,[/latex]for[latex]\,x>0.[/latex]

How To

Дан натуральный логарифм в форме [латекс]\,y=\mathrm{ln}\left(x\right),[/latex] оцените его с помощью калькулятора.

Нажмите [LN] .
Введите значение, данное для [латекс]\,х,[/латекс], а затем [ ) ] .
Нажмите [ВВОД] .

Вычисление натурального логарифма с помощью калькулятора

Вычислить [латекс]\,y=\mathrm{ln}\left(500\right)\,[/latex]до четырех знаков после запятой с помощью калькулятора.

Показать решение

Попробовать

Вычислить[латекс]\,\mathrm{ln}\left(-500\right).[/латекс]

Показать решение

Доступ к этому онлайн-ресурсу для получения дополнительных инструкций и практики с логарифмами.

Введение в логарифмы

Ключевые уравнения

9{у}=х.[/латекс]

Определение логарифмической функции

Для [латекс]\текст{ } x>0,b>0,b\ne 1,[/latex]<[latex]y={\mathrm{log}}_{b}\left(x\right) \text{ }[/latex] тогда и только тогда, когда[latex]\text{ }{b}^{y}=x.

[/latex]

Ключевые понятия

Обратная экспоненциальная функция является логарифмической функцией, а обратная логарифмическая функция является экспоненциальной функцией.
Логарифмические уравнения можно записать в эквивалентной экспоненциальной форме, используя определение логарифма. См. (Рисунок).
Экспоненциальные уравнения могут быть записаны в их эквивалентной логарифмической форме, используя определение логарифма См. (Рисунок).
Логарифмические функции с основанием [латекс]\,b\,[/латекс] можно вычислить в уме, используя предварительное знание степеней [латекс]\,b.\,[/латекс] См. (Рисунок) и (Рисунок).
Десятичные логарифмы можно вычислить в уме, используя предварительное знание степеней [latex]\,10.\,[/latex] См. (Рисунок) .
Когда десятичные логарифмы невозможно вычислить в уме, можно использовать калькулятор. См. (Рисунок) .

Реальные экспоненциальные задачи с основанием[latex]\,10\,[/latex] можно переписать в виде десятичного логарифма, а затем вычислить с помощью калькулятора. См. (Рисунок) 9{x}?\,[/latex]Каков результат составления этих двух функций?
Как можно решить логарифмическое уравнение [латекс]\,{\mathrm{log}}_{b}x=y\,[/latex]для[латекс]\,х\,[/латекс], используя свойства экспонентов?
Показать решение
Обсудите значение десятичного логарифма. Каково его отношение к логарифму с основанием [латекс]\,b,[/латекс] и чем отличается обозначение?
Обсудите значение натурального логарифма. Каково его отношение к логарифму с основанием [латекс]\,b,[/латекс] и чем отличается обозначение?
Показать решение
Алгебраический
Для следующих упражнений перепишите каждое уравнение в экспоненциальной форме.
[латекс] {\ текст {журнал}} _ {4} \ влево (q \ вправо) = м [/ латекс]
[латекс] {\ текст {лог}} _ {а} \ влево (б \ right)=c[/latex]
Показать решение
[латекс] {\ mathrm {лог}} _ {16} \ влево (у \ вправо) = х [/латекс]
[латекс] {\ mathrm {лог}} _ {х} \ влево (64 \ right)=y[/latex]
Показать решение
[латекс] {\ mathrm {log}} _ {у} \ влево (х \ вправо) = -11 [/латекс] 9{k}=h[/latex]
Показать решение
В следующих упражнениях найдите [латекс]\,х\,[/латекс] путем преобразования логарифмического уравнения в экспоненциальную форму.
[латекс] {\ текст {журнал}} _ {3} \ влево (х \ вправо) = 2 [/ латекс]
[латекс] {\ текст {лог}} _ {2} \ влево (х \ right)=-3[/latex]
Показать решение
[латекс] {\ текст {журнал}} _ {5} \ влево (х \ вправо) = 2 [/ латекс]
[латекс] {\ mathrm {лог}} _ {3} \ влево (х \ right)=3[/latex]
Показать решение
[латекс] {\ текст {журнал}} _ {2} \ влево (х \ вправо) = 6 [/ латекс]
[латекс] {\ текст {лог}} _ {9} \ влево (х \ вправо) = \ гидроразрыва {1} {2} [/латекс]
Показать решение
[латекс] {\ текст {журнал}} _ {18} \ влево (х \ вправо) = 2 [/ латекс]
[латекс] {\ mathrm {лог}} _ {6} \ влево (х \ right)=-3[/latex]
Показать решение
[латекс]\текст{журнал}\влево(х\вправо)=3[/латекс]
[латекс]\текст{ln}\влево(х\вправо)=2[/латекс]
Показать решение
В следующих упражнениях для упрощения используйте определение десятичного и натурального логарифмов.
{\mathrm{ln}\left(10.125\right)}+4[/latex]
Показать решение
Числовое
В следующих упражнениях вычислите базовое[латекс]\,b\,[/латекс]логарифмическое выражение без использования калькулятора.
[латекс] {\ текст {журнал}} _ {3} \ влево (\ гидроразрыва {1} {27} \ вправо) [/ латекс]
[латекс] {\ текст {лог}} _ {6} \left(\sqrt{6}\right)[/latex]
Показать решение
[латекс] {\ текст {журнал}} _ {2} \ влево (\ гидроразрыва {1} {8} \ вправо) + 4 [/латекс]
[латекс] 6 {\ текст {лог}} _ {8}\влево(4\вправо)[/латекс] 9{\frac{2}{5}}\right)[/latex]
Показать решение
Технология
В следующих упражнениях оцените каждое выражение с помощью калькулятора. Округлить до тысячных.
[латекс]\текст{журнал}\влево(0,04\вправо)[/латекс]
[латекс]\текст{ln}\влево(15\вправо)[/латекс]
Показать решение
[латекс]\текст{ln}\left(\frac{4}{5}\right)[/latex]
[латекс]\text{log}\left(\sqrt{2}\right)[ /латекс]
Показать решение
[латекс]\текст{ln}\влево(\sqrt{2}\вправо)[/латекс]
Расширения
Находится [латекс]\,х=0\,[/латекс]в области определения функции[латекс]\,f\left(x\right)=\mathrm{log}\left(x\ right)?\,[/latex]Если да, то каково значение функции, когда[latex]\,x=0?\,[/latex]Проверьте результат.
Показать решение
Is[latex]\,f\left(x\right)=0\,[/latex]в диапазоне функции[latex]\,f\left(x\right)=\mathrm{log}\ left(x\right)?\,[/latex]Если да, то для какого значения [latex]\,x?\,[/latex]Проверьте результат.
Существует ли число[латекс]\,х\,[/латекс]такое, что[латекс]\,\mathrm{ln}х=2?\,[/латекс]Если да, то какое это число? Проверьте результат. 9{2}}{t}\right),[/latex], где[latex]\,f\,[/latex] – это настройка «f-stop» камеры, а [latex]t[/latex] – время экспозиции в секундах. Предположим, что значение диафрагмы равно [латекс]\,8\,[/латекс], а желаемое время экспозиции равно [латекс]\,2\,[/латекс]секунд. Каким будет результирующий индекс экспозиции?
См. предыдущее упражнение. Предположим, экспонометр на камере показывает [латекс]\,EI\,[/латекс][латекс]\,-2,[/латекс], а желаемое время экспозиции составляет 16 секунд. Какой должна быть настройка f-stop?
Показать решение
Уровни интенсивности I двух землетрясений, измеренные на сейсмографе, можно сравнить по формуле[latex]\,\mathrm{log}\frac{{I}_{1}}{{I}_{2} }={M}_{1}-{M}_{2}\,[/latex], где [latex]\,M\,[/latex] — величина, определяемая по шкале Рихтера. В августе 2009 года на острове Хонсю в Японии произошло землетрясение магнитудой 6,1. В марте 2011 года в том же регионе произошло еще одно, более разрушительное землетрясение, на этот раз магнитудой 9,0. ^[5] Во сколько раз было сильнее землетрясение 2011 года? Округлить до ближайшего целого числа.
Глоссарий
десятичный логарифм
показатель степени, в которую нужно возвести 10, чтобы получить [латекс]\,х;\,[/латекс][латекс]\,{\mathrm{log}}_{10}\left(x\right)\,[ /латекс] записывается просто как [латекс]\,\mathrm{log}\left(x\right).[/latex]
логарифм
показатель степени, в которую [латекс]\,b\,[/латекс] нужно возвести, чтобы получить [латекс]\,х;\,[/латекс]запись[латекс]\,у={\mathrm{log}} _{b}\влево(х\вправо)[/латекс]
натуральный логарифм
показатель степени, в которую нужно возвести число[латекс]\,е\,[/латекс], чтобы получить[латекс]\,х;[/латекс][латекс]\,{\mathrm{log}}_{е }\left(x\right)\,[/latex] записывается как [латекс]\,\mathrm{ln}\left(x\right). [/latex]
http://earthquake.usgs.gov/earthquakes/eqinthenews/2010/us2010rja6/#summary. По состоянию на 04.03.2013. ↵
http://earthquake.usgs.gov/earthquakes/eqinthenews/2011/usc0001xgp/#summary. По состоянию на 04.03.2013. ↵
http://earthquake.usgs.gov/earthquakes/eqinthenews/2010/us2010rja6/. По состоянию на 04.03.2013. ↵
http://earthquake.usgs.gov/earthquakes/eqinthenews/2010/us2010rja6/. По состоянию на 04.03.2013. ↵
http://earthquake.usgs.gov/earthquakes/world/historical.php. По состоянию на 04.03.2014. ↵
Математические слова: десятичный логарифм
Математические слова: десятичный логарифм
индекс: нажмите на букву
индекс: предметные области

Общий Логарифм
Логарифм по основанию 10 числа. То есть мощность 10 необходима равняться заданному числу. Десятичный логарифм x равен записанный журнал x . Например, log 100 равен 2, поскольку 10 ² = 100.

См. также
Натуральный логарифм, правила логарифмирования

эта страница обновлена 19 июля 17
Математические слова: термины и формулы от алгебры I до исчисления
написано, проиллюстрировано и создано веб-мастером Брюсом Симмонсом
Авторское право © Брюс Симмонс, 2000 г.
No related posts.
Навигация по записям
Предыдущая статьяРешение лоду: Линейные однородные дифференциальные уравнения второго порядка
Следующая статья4 х график: Mathway | Популярные задачи
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта