Уравнение прямой онлайн по двум точкам: Онлайн калькулятор. Уравнение прямой проходящей через две точки

Уравнение прямой.

Навигация по странице: Определение прямой Уравнение прямой на плоскости Уравнение прямой с угловым коэффициентом Уравнение прямой в отрезках на осях Уравнение прямой, проходящей через две различные точки на плоскости Параметрическое уравнение прямой на плоскости Каноническое уравнение прямой на плоскости Уравнение прямой в пространстве Уравнение прямой, проходящей через две различные точки в пространстве Параметрическое уравнение прямой в пространстве Каноническое уравнение прямой в пространстве Прямая как линия пересечения двух плоскостей Онлайн калькулятор. Уравнение прямой по координатам двух точек. Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками. Уравнение прямой на плоскости Любую прямую на плоскости можно задать уравнением прямой первой степени вида A x + B y + C = 0 где A и B не могут быть одновременно равны нулю. Уравнение прямой с угловым коэффициентом Общее уравнение прямой при B≠0 можно привести к виду y = k x + b где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ. Уравнение прямой в отрезках на осях Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках x  +  y  = 1 a b Уравнение прямой, проходящей через две различные точки на плоскости Если прямая проходит через две точки A(x1, y1) и B(x2, y2), такие что x1 ≠ x2 и y1 ≠ y2, то уравнение прямой можно найти, используя следующую формулу x — x1  =  y — y1 x2 — x1 y2 — y1 Параметрическое уравнение прямой на плоскости Параметрические уравнения прямой могут быть записаны следующим образом x = l t + x0 y = m t + y0 где (x0, y0) — координаты точки лежащей на прямой, {l, m} — координаты направляющего вектора прямой. Каноническое уравнение прямой на плоскости Если известны координаты точки A(x0, y0) лежащей на прямой и направляющего вектора n = {l; m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу x — x0  =  y — y0 l m Пример. Найти уравнение прямой проходящей через две точки A(1, 7) и B(2,3). Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки x — 1  =  y — 7 2 — 1 3 — 7 Из этого уравнения выразим y через x x — 1  =  y — 7 1 -4 y — 7 = -4(x — 1) y = -4x + 11 Уравнение прямой в пространстве Уравнение прямой, проходящей через две различные точки в пространстве Если прямая проходит через две точки A(x1, y1, z1) и B(x2, y2, z2), такие что x1 ≠ x2, y1 ≠ y2 и z1 ≠ z2, то уравнение прямой можно найти используя следующую формулу x — x1  =  y — y1  =  z — z1 x2 — x1 y2 — y1 z2 — z 1 Параметрическое уравнение прямой в пространстве Параметрические уравнения прямой могут быть записаны следующим образом x = l t + x0 y = m t + y0 z = n t + z0 где (x0, y0, z0) — координаты точки лежащей на прямой, {l; m; n} — координаты направляющего вектора прямой. Каноническое уравнение прямой в пространстве Если известны координаты точки A(x0, y0, z0) лежащей на прямой и направляющего вектора n = {l; m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу x — x0  =  y — y0  =  z — z0 l m n Прямая как линия пересечения двух плоскостей Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений A1x + B1y + C1z + D1 = 0 A2x + B2y + C2z + D2 = 0 при условии, что не имеет место равенство A1  =  B1  =  C1 . A2 B2 C2 Аналитическая геометрия: Вступление и оглавлениеРасстояние между двумя точками.Середина отрезка. Координаты середины отрезка.Уравнение прямой.Уравнение плоскости.Расстояние от точки до плоскости.Расстояние между плоскостями.Расстояние от точки до прямой на плоскости.Расстояние от точки до прямой в пространстве.Угол между плоскостями.Угол между прямой и плоскостью. Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Уравнение прямой как результат пересечения плоскостей

Египетские дроби. Часть вторая Египетские (аликвотные) дроби По сегменту определить радиус окружности Круг и площадь, отсекаемая перпендикулярами Деление треугольника на равные площади параллельными Определение основных параметров целого числа Свойства обратных тригонометрических функций Разделить шар на равные объемы параллельными плоскостями Взаимосвязь между организмами с различными типами обмена веществ Аутотрофные и миксотрофные организмы Рассечение круга прямыми на равные площади Период нечетной дроби онлайн. Первые полторы тысяч разложений. Представить дробь, как сумму её множителей Решение системы из двух однородных диофантовых уравнений Расчет основных параметров четырехполюсника Цепочка остатков от деления в кольце целого числа Система счисления на базе ряда Фибоначчи онлайн Уравнение пятой степени. Частное решение. Рассчитать площадь треугольника по трем сторонам онлайн Общее решение линейного диофантового неоднородного уравнения Частное решение диофантового уравнения с несколькими неизвестными Онлайн разложение дробно рациональной функции Корни характеристического уравнения Имя пользователя при работе с Excel Распределение частот появления букв русского алфавита в текстах

Коэффициенты первой плоскости Коэффициенты второй плоскости Уравнение первой плоскости Уравнение второй плоскости Уравнение прямой как пересечение двух плоскостей Определяем  уравнение прямой в пространстве если нам известны  общие уравнения двух плоскостей. Обновление  от 13 октября 2019 года: Используется алгоритм описанный в статье ФРС. Фундаментальное решение системы уравнений Если  первая  плоскость задана уравнением вида а другая плоскость  уравнением вида и они перескаются, то  уравнение полученной прямой можно найти по двум точкам, принадлежащих одновременно этим плоскостям. Прямая в пространстве, проходящая через две точки  и   может быть представлена в виде канонического уравнения   \(\cfrac{x-x_0}{x_1-x_0}=\cfrac{y-y_0}{y_1-y_0}=\cfrac{z-z_0}{z_1-z_0}\)   B принципе этого достаточно  что бы решить уравнение. Положим что z=0  ( можно брать любое число, но с нулем оно как то удобнее) тогда уравнения плоскости приобретают вид     Получили систему линейных уравнений которая легко решается. Определили таким образом точку    Теперь пусть z=1 и решаем систему    и получаем вторую точку     Эти две точки принадлежат обеим плоскостям и значит уравнение прямой имеет вид   \(\cfrac{x-x_0}{x_1-x_0}=\cfrac{y-y_0}{y_1-y_0}=\cfrac{z}{1}\)   Есть еще второй способ, использующий вектора. Рассмотрим и его.   Если известна точка в пространстве   и направляющий вектор  то уравнение прямой имеет вид  \(\cfrac{x-x_0}{m}=\cfrac{y-y_0}{n}=\cfrac{z-z_0}{p}\)  Узнав координаты точки    ( например по выше приведенному решению)  нам осталось  узнать направляющий вектор. Для этого вычислим векторное произведение \(\begin{pmatrix}i&j&k\\A_1&B_1&C_1\\A_2&B_2&C_2\end{pmatrix}=im+jn+kp\)   и подставив вычисленные значения в  уравнение   \(\cfrac{x-x_0}{m}=\cfrac{y-y_0}{n}=\cfrac{z-z_0}{p}\)   мы узнаем уравнение прямой в пространстве, как пресечение двух плоскостей.   Созданный онлайн калькулятор позволяет автоматически находить  уравнение прямой по двум заданным  общим уравнениям плоскостей.     Две плоскости заданные уравнениями вида лишь тогда параллельны, когда верным  становится соотношение \(\cfrac{A_1}{A_2}=\cfrac{B_1}{B_2}=\cfrac{C_1}{C_2}\)     Эллипсоид. Построение по точкам >> Поиск по сайту

Русский и английский алфавит в одну строку Часовая и минутная стрелка онлайн.Угол между ними. Универсальный калькулятор комплексных чисел онлайн Перемешать буквы в тексте онлайн Массовая доля химического вещества онлайн Декoдировать текст \u0xxx онлайн Частотный анализ текста онлайн Поворот точек на произвольный угол онлайн Площадь многоугольника по координатам онлайн Обратный и дополнительный код числа онлайн Остаток числа в степени по модулю Расчет процентов онлайн Как перевести градусы в минуты и секунды Поиск объекта по географическим координатам Расчет пропорций и соотношений Время восхода и захода Солнца и Луны для местности DameWare Mini Control. Настройка. Растворимость металлов в различных жидкостях Калькулятор географических координат Расчет значения функции Эйлера Теория графов. Матрица смежности онлайн Географические координаты любых городов мира Перевод числа в код Грея и обратно Онлайн определение эквивалентного сопротивления Произвольный треугольник по заданным параметрам НОД двух многочленов. Greatest Common Factor (GCF) Площадь пересечения окружностей на плоскости Непрерывные, цепные дроби онлайн Калькулятор онлайн расчета количества рабочих дней Построить ненаправленный граф по матрице Расчет заряда и разряда конденсатора через сопротивление Месторождения золота и его спутники Сообщество животных. Кто как называется? Расчет понижающего конденсатора Система комплексных линейных уравнений Из показательной в алгебраическую. Подробно Проекция точки на плоскость онлайн Дата выхода на работу из отпуска, декрета онлайн Определение формулы касательной к окружности Расчет параметров конденсатора онлайн Онлайн расчеты Подписаться письмом

Общее уравнение прямой на плоскости

• Уравнение прямой по точке и вектору нормали
• Уравнение прямой по точке и направляющему вектору
• Уравнение прямой, проходящей через две точки на плоскости
• Преобразование уравнения прямой с угловым коэффициентом в общее уравнение прямой
• Неполные уравнения прямой

Уравнение вида называется общим уравнением прямой на плоскости. При различных численных значениях A, B и C, в том числе нулевых, оно может определять всевозможные прямые без исключения.

Одна из фундаментальных задач аналитической геометрии — составление общего уравнения прямой по точке, ей принадлежащей, и вектору нормали.

Вектор нормали — это вектор, перпендикулярный искомой прямой. Вектор нормали чаще всего записывается так: . Координаты точки — и .

Общее уравнение прямой на плоскости по точке и вектору нормали составляется по формуле:

  (1).

Пример 1. Составить общее уравнение прямой на плоскости, если она проходит через точку и вектор нормали к ней .

Решение. Используя формулу (1), получаем:

Из примера 1 видно, что координаты вектора нормали пропорциональны числам A и B из общего уравнения прямой на плоскости. Это не совпадение, а закономерность! Поэтому в общем случае, если известно общее уравнение прямой на плоскости, то вектор нормали к прямой можно записать так: .

Пример 2. Задано общее уравнение прямой на плоскости: . Записать вектор нормали к этой прямой.

Решение. В заданном уравнении , . Поэтому вектор нормали запишется:

.

Если вектор нормали перпендикулярен искомой прямой, то направляющий вектор параллелен ей. Направляющий вектор обычно записывается так: . Имеет место следующая зависимость координат направляющего вектора от чисел A и B общего уравнения прямой: .

Общее уравнение прямой по точке и направляющему вектору можно составить по формуле

,   (2)

известной как каноническое уравнение прямой на плоскости.

Пример 3. Составить общее уравнение прямой на плоскости, если она проходит через точку и её направляющий вектор .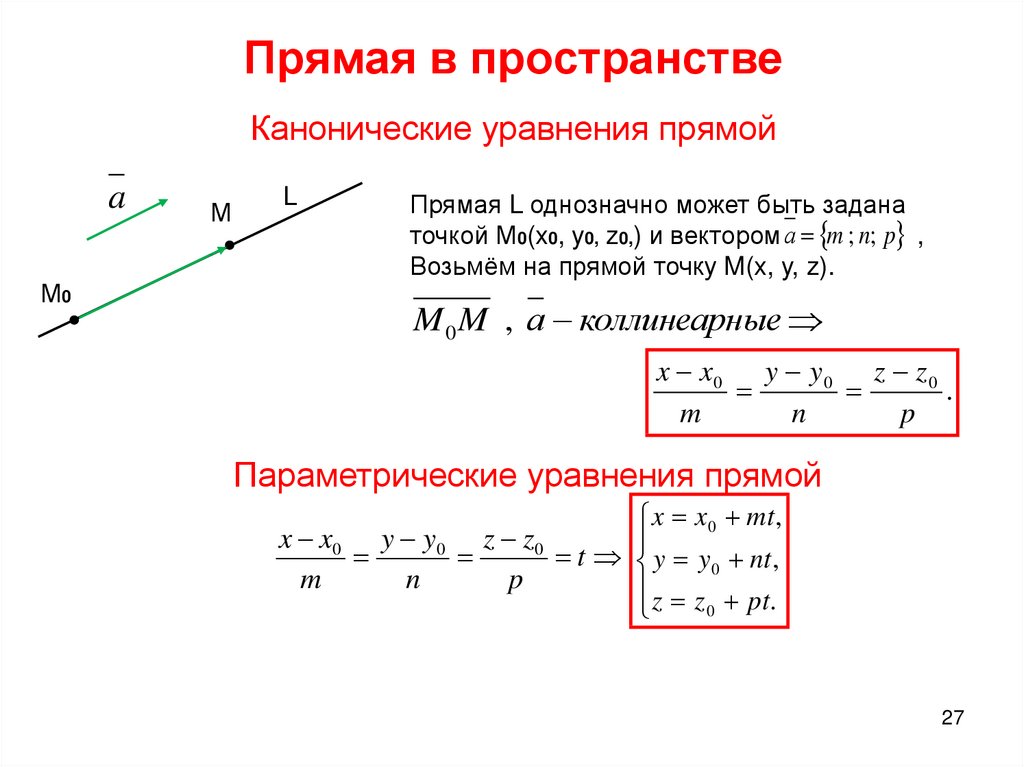

Решение. Используя формулу (2), имеем:

.

Далее путём преобразований получаем:

На всякий случай сделаем проверку — подставим в полученное общее уравнение прямой координаты точки, которая должна ей принадлежать:

.

Получили верное равенство. А координаты вектора связаны с числами A и B уравнения закономерностью . Значит, задание выполнено корректно.

---

Пример 4. Задано общее уравнение прямой на плоскости: . Записать направляющий вектор к этой прямой.

Решение. В заданном уравнении , . Поэтому направляющий вектор запишется:

.

Решая задачи контрольных работ, особенно, если задач много и к концу контрольной студент стремится наверстать упущенное за время обдумывания заданий, можно запутаться в знаках, записывая вектор нормали и направляющий вектор. Будьте внимательны!

Если заданы две точки и , то уравнение прямой, проходящей через эти точки, можно составить по формуле

.   (3)

Полученное выражение следует преобразовать к виду общего уравнения прямой.

Пример 5. Составить общее уравнение прямой на плоскости, если она проходит через точки и .

Решение. Используя формулу (3), имеем:

.

Далее путём преобразований получаем:

Получили общее уравнение плоскости.

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Прямая и плоскость

Пример 6. Построить в прямоугольной системе координат на плоскости прямую, заданную общим уравнением .

Решение. Для построения прямой достаточно знать координаты каких-либо двух точек, например, точек пересечения прямой с координатными осями. Полагая в данном уравнении , получим , т.е. — точка пересечения прямой с осью Oy.

При получим , т.е. — точка пересечения прямой с осью Ox.

По двум точкам и строим прямую (рисунок слева.)

Вектором нормали этой прямой служит вектор .

Во многих задачах аналитической геометрии возникает необходимость преобразовать уравнения одного вида к уравнению другого вида. Преобразование уравнения прямой с угловым коэффициентом в общее уравнение прямой делается достаточно просто: в уравнении вида всё переносим в левую часть, а в правой остаётся нуль. Получается уравнение вида .

Пример 7. Дано уравнение прямой с угловым коэффициентом . Записать уравнение этой прямой в общем виде и направляющий вектор этой прямой.

Решение. Всё переносим в левую часть, а в правой оставляем нуль:

.

Получили общее уравнение прямой.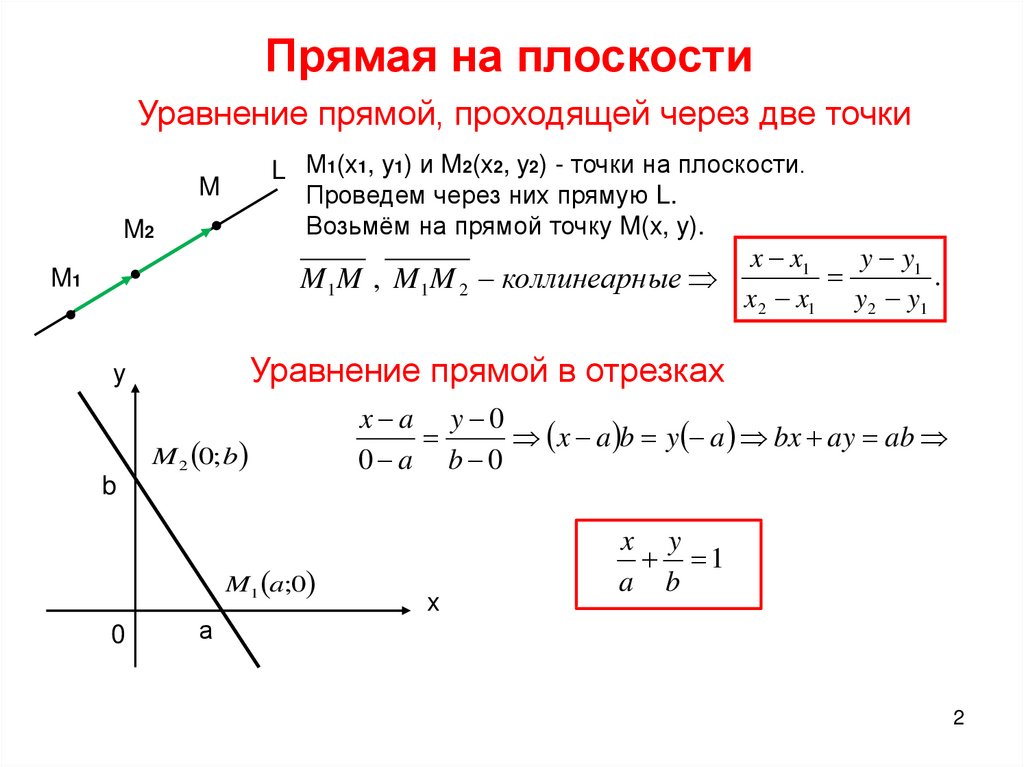 В нём . Поэтому направляющий вектор запишется так:

.

Рассмотрим особенности расположения прямой на плоскости в тех случаях, когда те или иные коэффициенты общего уравнения прямой равны нулю.

1. При уравнение определяет прямую, проходящую через начало координат, так как кординаты точки удовлетворяют этому уравнению.

2. При уравнение определяет прямую, параллельную оси Ox, поскольку вектор нормали этой прямой перпендикулярен оси Ox. Аналогично при уравнение определяет прямую, параллельную оси Oy.

3. При уравнение определяет ось Ox, так как эта прямая одновременно параллельна оси Ox и проходит через начало координат. Аналогично, при уравнение определяет ось Oy.

Пример 8. Построить в прямоугольной системе координат на плоскости прямую, заданную общим уравнением .

Решение. В данном уравнении свободный член равен нулю, поэтому оно определяет прямую, проходящую через начало координат. Следовательно, в точке прямая пересекает обе координатные оси. Для построения прямой нужно знать ещё какую-либо её точку. Для этого дадим одной из переменных в заданном уравнении произвольное значение, например, , и найдём соответствующее значение x: . Теперь строим прямую, проходящую через начало координат и точку (рисунок слева).

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Прямая и плоскость

Всё по теме «Прямая на плоскости

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой на плоскости

Уравнение прямой в отрезках

Каноническое уравнение прямой на плоскости

Параметрические уравнения прямой на плоскости

Нормальное уравнение прямой на плоскости, расстояние от точки до прямой

Уравнение прямой по двум точкам формула

Данный онлайн-сервис поможет составить уравнение прямой в двухмерном или трехмерном пространстве.

Прямая – линия, путь которой равен расстоянию между двумя точками.
Через любые две несовпадающие точки можно провести прямую, притом только одну.
Две несовпадающие прямые на плоскости являются параллельными или пересекаются в одной точке.

Уравнение прямой по двум точкам (на плоскости):

Уравнение прямой в пространстве:

1. Составьте уравнение прямой на плоскости, проходящей через точки А(3;-4) и В(-6;12).
   Посмотреть решение

Запишем общее уравнение прямой на плоскости:

По условию задачи получим значения:

Ответ:

Сначала записываем уравнение для прямой в пространстве в общем виде:

Запишем значения координат:

Ответ:

Для того, чтобы составить уравнение прямой, необходимо найти координаты двух точек, через которые она проходит. Первая точка С(0;-4). Вторая точка М лежит на середине стороны АВ треугольника. Ее координаты находим по формуле:

Координаты точки М(3;1).

Запишем уравнение прямой на плоскости в общем виде:

По введенным пользователем координатам двух точек вывести уравнение прямой, проходящей через эти точки.

Общее уравнение прямой имеет вид y = kx + b . Для какой-то конкретной прямой в уравнении коэффициенты k и b заменяются на числа, например, y = 4x — 2 . Задача сводится именно к нахождению этих коэффициентов.

Так как координаты точки это значения x и y , то мы имеем два уравнения. Пусть, например, координаты точки А(3;2), а координаты B(-1;-1). Получаем уравнения:
2 = k*3 + b,
-1 = k*(-1) + b.
Решая полученную систему уравнений находим значения k и b :
b = 2 — 3k
-1 = -k + 2 — 3k
4k = 3
k = 3/4 = 0.75
b = 2 — 3 * 0.75 = 2 — 2.25 = -0.25
Таким образом, получается уравнение конкретной прямой, проходящей через указанные точки: y = 0.75x — 0.25.

Алгоритм решения данной задаче на языке программирования будет таков:

1. Получить значения координат первой точки и присвоить их переменным, например x1 и y1 .
2. Получить значения координат ( x2, y2 ) второй точки.
3. Вычислить значение k по формуле k = (y1 — y2) / (x1 — x2) .
4. Вычислить значение b по формуле b = y2 — k * x2 .
5. Вывести на экран полученное уравнение.

var
x1 , y1 , x2 , y2 : real ;
k , b : real ;

begin
write ( ‘A(x1;y1): ‘ ) ; readln ( x1 , y1 ) ;
write ( ‘B(x2;y2): ‘ ) ; readln ( x2 , y2 ) ;

k : = ( y1 — y2 ) / ( x1 — x2 ) ;
b : = y2 — k * x2 ;

writeln ( ‘y = ‘ , k : 0 : 2 , ‘x + ‘ , b : 0 : 2 ) ;
end .

Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.

Уравнение прямой, проходящей через две заданные точки на плоскости

Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.

Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.

Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.

В каноническом уравнении прямой на плоскости, имеющего вид x — x 1 a x = y — y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .

Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .

Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 — x 1 , y 2 — y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 .

Рассмотрим рисунок, приведенный ниже.

Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ .

Рассмотрим подробней на решении нескольких примеров.

Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 — 5 , 2 3 , M 2 1 , — 1 6 .

Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . По условию задачи имеем, что x 1 = — 5 , y 1 = 2 3 , x 2 = 1 , y 2 = — 1 6 . Необходимо подставить числовые значения в уравнение x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . Отсюда получим, что каноническое уравнение примет вид x — ( — 5 ) 1 — ( — 5 ) = y — 2 3 — 1 6 — 2 3 ⇔ x + 5 6 = y — 2 3 — 5 6 .

Ответ: x + 5 6 = y — 2 3 — 5 6 .

При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.

Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .

Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки.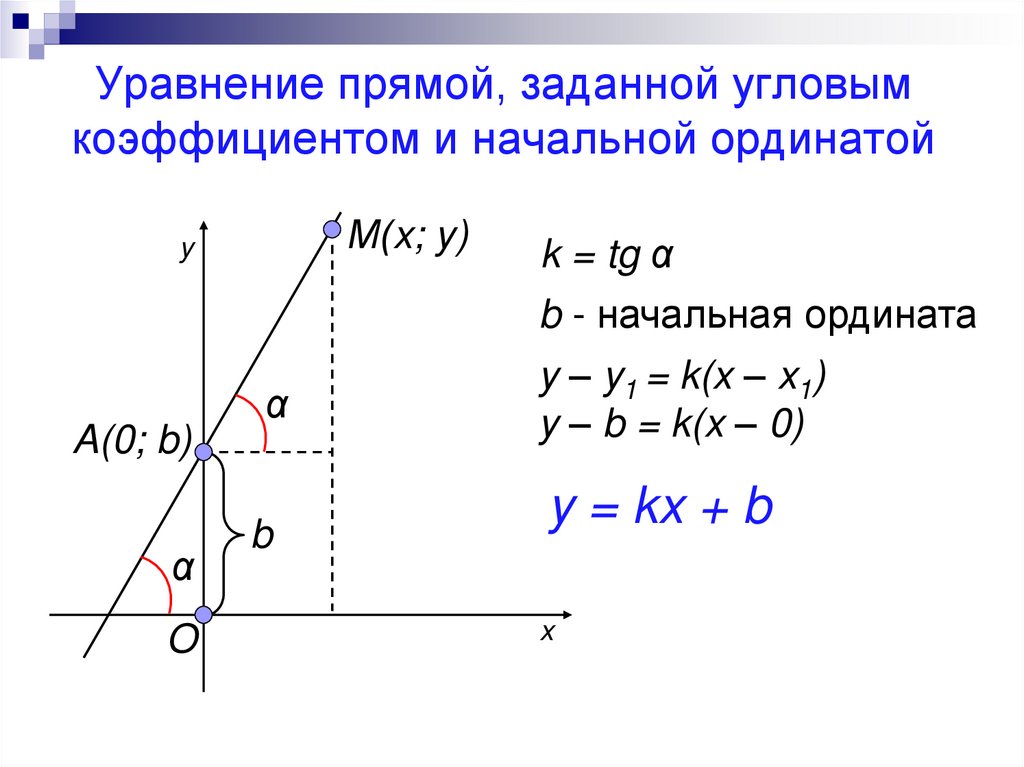 Получим уравнение вида x — 1 4 — 1 = y — 1 2 — 1 ⇔ x — 1 3 = y — 1 1 .

Приведем каноническое уравнение к искомому виду, тогда получим:

x — 1 3 = y — 1 1 ⇔ 1 · x — 1 = 3 · y — 1 ⇔ x — 3 y + 2 = 0

Ответ: x — 3 y + 2 = 0 .

Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x — x 1 = 0 .

Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .

Для этого найдем k = y 2 — y 1 x 2 — x 1 b = y 1 — y 2 — y 1 x 2 — x 1 · x 1 или k = y 2 — y 1 x 2 — x 1 b = y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 1 или y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.

Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .

Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( — 7 , — 5 ) и M 2 ( 2 , 1 ) .

Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что — 5 = k · ( — 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему — 5 = k · — 7 + b 1 = k · 2 + b и решим.

При подстановке получаем, что

— 5 = k · — 7 + b 1 = k · 2 + b ⇔ b = — 5 + 7 k 2 k + b = 1 ⇔ b = — 5 + 7 k 2 k — 5 + 7 k = 1 ⇔ ⇔ b = — 5 + 7 k k = 2 3 ⇔ b = — 5 + 7 · 2 3 k = 2 3 ⇔ b = — 1 3 k = 2 3

Теперь значения k = 2 3 и b = — 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x — 1 3 .

Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.

Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( — 7 , — 5 ) , имеющее вид x — ( — 7 ) 2 — ( — 7 ) = y — ( — 5 ) 1 — ( — 5 ) ⇔ x + 7 9 = y + 5 6 .

Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x — 1 3 .

Ответ: y = 2 3 x — 1 3 .

Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве

Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.

Имеем, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .

Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , в свою очередь параметрические x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ z = z 1 + ( z 2 — z 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ z = z 2 + ( z 2 — z 1 ) · λ .

Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.

Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , — 3 , 0 ) и M 2 ( 1 , — 3 , — 5 ) .

Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 .

По условию имеем, что x 1 = 2 , y 1 = — 3 , z 1 = 0 , x 2 = 1 , y 2 = — 3 , z 2 = — 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:

x — 2 1 — 2 = y — ( — 3 ) — 3 — ( — 3 ) = z — 0 — 5 — 0 ⇔ x — 2 — 1 = y + 3 0 = z — 5

Ответ: x — 2 — 1 = y + 3 0 = z — 5 .

Что такое направляющий вектор прямой?

Содержание

• — Как вычислить направляющий вектор прямой?
• — Как называется вектор параллельный прямой?
• — Что такое уравнение прямой?
• — Как найти нормальный вектор к прямой?
• — Как перейти к общему уравнению прямой?
• — Как найти нормальное уравнение прямой?
• — Как найти вектор по двум точкам?
• — Как записать уравнение прямой в каноническом виде?
• — Чем задается прямая?
• — Как составить уравнение прямой вида Ax By C 0?
• — Какие есть уравнения прямой?
• — Как найти нормальный вектор к плоскости?
• — Как найти вектор перпендикулярный вектору?
• — Как определяется уравнение прямой в пространстве?

Канонические уравнения прямой. Параметрические уравнения прямой Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.

Как вычислить направляющий вектор прямой?

Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой. 3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой →n=(A, B)

Как называется вектор параллельный прямой?

Направляющим вектором прямой называется вектор, параллельный прямой, которую он определяет или совпадающий с ней. Рассмотрим прямую , заданную точкой , лежащей на ней, и направляющим вектором с координатами , при этом вектор — ненулевой.

Что такое уравнение прямой?

Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе Oxy O x y , называется уравнением прямой на плоскости. Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y .

Как найти нормальный вектор к прямой?

Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения Ax+By+C=0 A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.

Как перейти к общему уравнению прямой?

Уравнение, имеющее вид Ax+By+C=0 A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат Oxy O x y .

Как найти нормальное уравнение прямой?

Уравнение вида cos α⋅x+cos β⋅y−p=0 cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой.

Как найти вектор по двум точкам?

Определеие. Чтобы найти координаты вектора AB, зная координаты его начальной точки А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

Как записать уравнение прямой в каноническом виде?

Запись вида x−x1ax=y−y1ay x — x 1 a x = y — y 1 a y также называют уравнением прямой в каноническом виде.

Чем задается прямая?

Общее уравнение прямой.

Теорема. … задает прямую, параллельную оси абсцисс Ox, а при В=0 – параллельную оси ординат Oy. Таким образом, любую прямую на плоскости в заданной прямоугольной системе координат Oxy можно описать с помощью общего уравнения прямой при некотором наборе значений чисел А, В и С.

Как составить уравнение прямой вида Ax By C 0?

уравнение прямой имеет вид Ax+C = 0 или By+C = 0. Эти уравнения можно записать в виде x = a и y = b . Таким образом, прямая в уравнении которой отсутствует одна из координат, параллельна оси отсутствующей координаты Page 8 4) Пусть в общем уравнении прямой C = 0 и один из коэф- фициентов A или B тоже нулевой, т. е.

Какие есть уравнения прямой?

Уравнения прямой на плоскости

• Общее уравнение прямой
• Уравнение прямой с угловым коэффициентом
• Уравнение прямой в отрезках
• Нормальное уравнение прямой
• Уравнение прямой, проходящей через две заданные несовпадающие точки
• Векторное параметрическое уравнение прямой
• Параметрические уравнения прямой

Как найти нормальный вектор к плоскости?

Для определения нормального вектора →n=(A, B, C) n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид Ax+By+Cz+D=0 A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Как найти вектор перпендикулярный вектору?

Условие перпендикулярности векторов

1. Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
2. Даны два вектора ⃗a(xa;ya) a → ( x a ; y a ) и ⃗b(xb;yb) b → ( x b ; y b ) . Эти векторы будут перпендикулярны, если выражение xaxb + yayb = 0.

Как определяется уравнение прямой в пространстве?

Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей. Напомним одну аксиому: если две плоскости в пространстве имеют общую точку, то они имеют общую прямую, на которой находятся все общие точки этих плоскостей. … определяет координаты каждой точки прямой a, то есть, определяет прямую a.

Интересные материалы:

Какой корень у слова удалось?
Какой корень у слова урок?
Какой корень у слова выразить?
Какой корень в слове аппетит?
Какой корень в слове бассейн?
Какой корень в слове белка?
Какой корень в слове белый?
Какой корень в слове берёзки?
Какой корень в слове Березняк?
Какой корень в слове бежать?

Составить уравнение прямой онлайн с решением.

Общее уравнение прямой. Частные случаи общего уравнения прямой

Общее уравнение прямой:

Частные случаи общего уравнения прямой:

а) Если C = 0, уравнение (2) будет иметь вид

Ax + By = 0,

и прямая, определяемая этим уравнением, проходит через начало координат, так как координаты начала координат x = 0, y = 0 удовлетворяют этому уравнению.

б) Если в общем уравнении прямой (2) B = 0, то уравнение примет вид

Ax + С = 0, или .

Уравнение не содержит переменной y , а определяемая этим уравнением прямая параллельна оси Oy .

в) Если в общем уравнении прямой (2) A = 0, то это уравнение примет вид

By + С = 0, или ;

уравнение не содержит переменной x , а определяемая им прямая параллельна оси Ox .

Следует запомнить: если прямая параллельна какой-нибудь координатной оси, то в ее уравнении отсутствует член, содержащий координату, одноименную с этой осью.

г) При C = 0 и A = 0 уравнение (2) принимает вид By = 0, или y = 0.

Это уравнение оси Ox .

д) При C = 0 и B = 0 уравнение (2) запишется в виде Ax = 0 или x = 0.

Это уравнение оси Oy .

Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Условие параллельности прямых. Условие перпендикулярности прямых.

l 1 l 2 l 1: A 1 x + B 1 y + C 1 = 0
l 2: A 2 x + B 2 y + C 2 = 0

S 2 S 1 Вектора S 1 и S 2 называются направляющими для своих прямых.

Угол между прямыми l 1 и l 2 определяется углом между направляющими векторами.
Теорема 1: cos угла между l 1 и l 2 = cos(l 1 ; l 2) =

Теорема 2: Для того, чтобы 2 прямые были равны необходимо и достаточно:

Теорема 3: чтобы 2 прямые были перпендикулярны необходимо и достаточно:

L 1 l 2 ó A 1 A 2 + B 1 B 2 = 0

Общее уравнение плоскости и его частные случаи. Уравнение плоскости в отрезках.

Общее уравнение плоскости:

Ax + By + Cz + D = 0

Частные случаи:

1. D=0 Ax+By+Cz = 0 – плоскость проходит через начало координат

2. С=0 Ax+By+D = 0 – плоскость || OZ

3. В=0 Ax+Cz+d = 0 – плоскость || OY

4. A=0 By+Cz+D = 0 – плоскость || OX

5. A=0 и D=0 By+Cz = 0 – плоскость проходит через OX

6. В=0 и D=0 Ax+Cz = 0 – плоскость проходит через OY

7. C=0 и D=0 Ax+By = 0 – плоскость проходит через OZ

Взаимное расположение плоскостей и прямых линий в пространстве:

1. Углом между прямыми в пространстве называется угол между их направляющими векторами.

Cos (l 1 ; l 2) = cos(S 1 ; S 2) = =

2. Углом между плоскостями определяется через угол между их нормальными векторами.

Cos (l 1 ; l 2) = cos(N 1 ; N 2) = =

3. Косинус угла между прямой и плоскостью можно найти через sin угла между направляющим вектором прямой и нормальным вектором плоскости.

4. 2 прямые || в пространстве, когда их || направляющие вектора

5. 2 плоскости || когда || нормальные вектора

6. Аналогично вводятся понятия перпендикулярности прямых и плоскостей.

Вопрос №14

Различные виды уравнения прямой линии на плоскости(уравнение прямой в отрезках, с угловым коэффициентом и др.)

Уравнение прямой в отрезках:
Допустим, что в общем уравнении прямой:

1. С = 0 Ах + Ву = 0 – прямая проходит через начало координат.

2. а = 0 Ву + С = 0 у =

3. в = 0 Ах + С = 0 х =

4. в=С=0 Ах = 0 х = 0

5. а=С=0 Ву = 0 у = 0

Уравнение прямой с угловым коэффициентом:

Любая прямая, не равная оси ОУ (В не=0), может быть записана в след. виде:

k = tgα α – угол между прямой и положительно направленной линией ОХ

b – точка пересечения прямой с осью ОУ

Док-во:

Ах+Ву+С = 0

Ву= -Ах-С |:В

Уравнение прямой по двум точкам:

Вопрос №16

Конечный предел функции в точке и при x→∞

Конечный предел в точке х 0:

Число А называется пределом функции y = f(x) при x→х­ 0­ , если для любого Е > 0 существует б > 0 такое, что при х ≠x 0 , удовлетворяющее неравенству |х – х 0 |

Предел обозначается: = A

Конечный предел в точке +∞:

Число А называется пределом функции y = f(x) при x→ + ∞ , если для любого Е > 0 существует С > 0, такое что при x > C выполняется неравенство |f(x) — A|

Предел обозначается: = A

Конечный предел в точке -∞:

Число А называется пределом функции y = f(x) при x→-∞, если для любого Е

Каноническими уравнениями прямой в пространстве называются уравнения, определяющие прямую, проходящую через заданную точку коллинеарно направляющему вектору.

Пусть дана точка и направляющий вектор . Произвольная точка лежит на прямой l только в том случае, если векторы и коллинеарны, т. е. для них выполняется условие:

.

Приведённые выше уравнения и есть канонические уравнения прямой.

Числа m , n и p являются проекциями направляющего вектора на координатные оси. Так как вектор ненулевой, то все числа m , n и p не могут одновременно равняться нулю. Но одно или два из них могут оказаться равными нулю. В аналитической геометрии допускается, например, такая запись:

,

которая означает, что проекции вектора на оси Oy и Oz равны нулю. Поэтому и вектор , и прямая, заданная каноническими уравнениями, перпендикулярны осям Oy и Oz , т. е. плоскости yOz .

Пример 1. Составить уравнения прямой в пространстве, перпендикулярной плоскости и проходящей через точку пересечения этой плоскости с осью Oz .

Решение. Найдём точку пересечения данной плоскости с осью Oz . Так как любая точка, лежащая на оси Oz , имеет координаты , то, полагая в заданном уравнении плоскости x = y = 0 , получим 4z — 8 = 0 или z = 2 . Следовательно, точка пересечения данной плоскости с осью Oz имеет координаты (0; 0; 2) . Поскольку искомая прямая перпендикулярна плоскости, она параллельна вектору её нормали . Поэтому направляющим вектором прямой может служить вектор нормали заданной плоскости.

Теперь запишем искомые уравнения прямой, проходящей через точку A = (0; 0; 2) в направлении вектора :

Уравнения прямой, проходящей через две данные точки

Прямая может быть задана двумя лежащими на ней точками и В этом случае направляющим вектором прямой может служить вектор . Тогда канонические уравнения прямой примут вид

.

Приведённые выше уравнения и определяют прямую, проходящую через две заданные точки.

Пример 2. Составить уравнение прямой в пространстве, проходящей через точки и .

Решение. Запишем искомые уравнения прямой в виде, приведённом выше в теоретической справке:

.

Так как , то искомая прямая перпендикулярна оси Oy .

Прямая как линия пересечения плоскостей

Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей и , т. е. как множество точек, удовлетворяющих системе двух линейных уравнений

Уравнения системы называются также общими уравнениями прямой в пространстве.

Пример 3. Составить канонические уравнения прямой в пространстве, заданной общими уравнениями

Решение. Чтобы написать канонические уравнения прямой или, что то же самое, уравнения прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой. Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например yOz и xOz .

Точка пересечения прямой с плоскостью yOz имеет абсциссу x = 0 . Поэтому, полагая в данной системе уравнений x = 0 , получим систему с двумя переменными:

Её решение y = 2 , z = 6 вместе с x = 0 определяет точку A (0; 2; 6) искомой прямой. Полагая затем в заданной системе уравнений y = 0 , получим систему

Её решение x = -2 , z = 0 вместе с y = 0 определяет точку B (-2; 0; 0) пересечения прямой с плоскостью xOz .

Теперь запишем уравнения прямой, проходящей через точки A (0; 2; 6) и B (-2; 0; 0) :

,

или после деления знаменателей на -2:

,

Уравнение прямой проходящей через две точки. В статье » » я обещал вам разобрать второй способ решения представленных задач на нахождение производной, при данном графике функции и касательной к этому графику. Этот способ мы разберём в , не пропустите! Почему в следующей?

Дело в том, что там будет использоваться формула уравнения прямой. Конечно, можно было бы просто показать данную формулу и посоветовать вам её выучить. Но лучше объяснить – от куда она исходит (как выводится). Это необходимо! Если вы её забудете, то быстро восстановить её не представит труда. Ниже подробно всё изложено. Итак, у нас на координатной плоскости имеется две точки А (х 1 ;у 1) и В(х 2 ;у 2), через указанные точки проведена прямая:

Вот сама формула прямой:

*То есть при подстановке конкретных координат точек мы получим уравнение вида y=kx+b.

**Если данную формулу просто «зазубрить», то имеется большая вероятность запутаться с индексами при х . Кроме того, индексы могут обозначаться по разному, например:

Поэтому-то и важно понимать смысл.

Теперь вывод этой формулы. Всё очень просто!

Треугольники АВЕ и ACF подобны по острому углу (первый признак подобия прямоугольных треугольников). Из этого следует, что отношения соответственных элементов равны, то есть:

Теперь просто выражаем данные отрезки через разность координат точек:

Конечно, не будет никакой ошибки если вы запишите отношения элементов в другом порядке (главное соблюдать соответствие):

В результате получится одно и тоже уравнение прямой. Это всё!

То есть, как бы не были обозначены сами точки (и их координаты), понимая данную формулу вы всегда найдёте уравнение прямой.

Формулу можно вывести используя свойства векторов, но принцип вывода будет тот же, так как речь будет идти о пропорциональности их координат. В этом случае работает всё то же подобие прямоугольных треугольников. На мой взгляд описанный выше вывод более понятнее)).

Посмотреть вывод через координаты векторов >>>

Пусть на координатной плоскости построена прямая, проходящая через две заданные точки А(х 1 ;у 1) и В(х 2 ;у 2). Отметим на прямой произвольную точку С с координатами (x ; y ). Также обозначим два вектора:

Известно, что у векторов лежащих на параллельных прямых (либо на одной прямой), их соответствующие координаты пропорциональны, то есть:

— записываем равенство отношений соответствующих координат:

Рассмотрим пример:

Найти уравнение прямой, проходящей через две точки с координатами (2;5) и (7:3).

Можно даже не строить саму прямую. Применяем формулу:

Важно, чтобы вы уловили соответствие, при составлении соотношения. Вы не ошибётесь, если запишите:

Ответ: у=-2/5x+29/5 иди у=-0,4x+5,8

Для того, чтобы убедится, что полученное уравнение найдено верно, обязательно делайте проверку — подставьте в него координаты данных в условии точек. Должны получится верные равенства.

На этом всё. Надеюсь, материал был вам полезен.

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.

Yandex.RTB R-A-339285-1

Пусть на плоскости задана прямоугольная система координат O x y .

Теорема 1

Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А, В, С.

Доказательство

указанная теорема состоит из двух пунктов, докажем каждый из них.

1. Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.

Пусть существует некоторая точка М 0 (x 0 , y 0) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A (x — x 0) + B (y — y 0) = 0 . Оно эквивалентно A x + B y + C = 0 .

Полученное уравнение A (x — x 0) + B (y — y 0) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = (A , B) и M 0 M → = (x — x 0 , y — y 0) . Таким образом, множество точек M (x , y) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = (A , B) . Можем предположить, что это не так, но тогда бы векторы n → = (A , B) и M 0 M → = (x — x 0 , y — y 0) не являлись бы перпендикулярными, и равенство A (x — x 0) + B (y — y 0) = 0 не было бы верным.

Следовательно, уравнение A (x — x 0) + B (y — y 0) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.

1. Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .

Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 (x 0 , y 0) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = (A , B) .

Пусть также существует некоторая точка M (x , y) – плавающая точка прямой. В таком случае, векторы n → = (A , B) и M 0 M → = (x — x 0 , y — y 0) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:

n → , M 0 M → = A (x — x 0) + B (y — y 0) = 0

Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C: C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .

Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.

Определение 1

Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .

Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.

Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .

Рассмотрим конкретный пример общего уравнения прямой.

Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = (2 , 3) . Изобразим заданную прямую линию на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.

Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.

Определение 2

Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А, В, С отличны от нуля. В ином случае уравнение является неполным .

Разберем все вариации неполного общего уравнения прямой.

1. Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек (x , y) , координаты которых равны одному и тому же числу — C B .
2. Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
3. Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
4. Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
5. Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел (0 , 0) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .

Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Пример 1

Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.

Решение

Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:

A · 2 7 + C = 0

Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0

Ответ: 7 x — 2 = 0

Пример 2

На чертеже изображена прямая, необходимо записать ее уравнение.

Решение

Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку (0 , 3) .

Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки (0 , 3) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С: С = — 3 . Используем известные значения В и С, получаем требуемое уравнение прямой: y — 3 = 0 .

Ответ: y — 3 = 0 .

Общее уравнение прямой, проходящей через заданную точку плоскости

Пусть заданная прямая проходит через точку М 0 (x 0 , y 0) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A (x — x 0) + B (y — y 0) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 (x 0 , y 0) и имеет нормальный вектор n → = (A , B) .

Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.

Пример 3

Даны точка М 0 (- 3 , 4) , через которую проходит прямая, и нормальный вектор этой прямой n → = (1 , — 2) . Необходимо записать уравнение заданной прямой.

Решение

Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:

A (x — x 0) + B (y — y 0) = 0 ⇔ 1 · (x — (- 3)) — 2 · y (y — 4) = 0 ⇔ ⇔ x — 2 y + 22 = 0

Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:

A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0

Теперь найдем значение С, используя заданную условием задачи точку М 0 (- 3 , 4) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .

Ответ: x — 2 · y + 11 = 0 .

Пример 4

Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.

Решение

Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:

2 3 x 0 — y 0 — 1 2 = 0

Определяем y 0: 2 3 · (- 3) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2

Ответ: — 5 2

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.

Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .

Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .

Это равенство возможно записать как пропорцию: x + C A — B = y A .

В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .

Перепишем равенство в виде пропорции: x — B = y + C B A .

Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.

Пример 5

Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.

Решение

Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .

Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.

Ответ: x — 3 = y — 4 3 0 .

Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.

Пример 6

Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.

Решение

Осуществим переход от общего уравнения к каноническому:

2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

Теперь примем обе части полученного канонического уравнения равными λ , тогда:

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .

Пример 7

Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.

Решение

Произведем нужные действия по алгоритму:

2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x

Ответ: y = — 2 7 x .

Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y:

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Пример 8

Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.

Решение

Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Ответ: x — 1 2 + y 1 14 = 1 .

В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.

Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:

x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0

Каноническое уравнение преобразуется к общему по следующей схеме:

x — x 1 a x = y — y 1 a y ⇔ a y · (x — x 1) = a x (y — y 1) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0

Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0

Пример 9

Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.

Решение

Осуществим переход от параметрических уравнений к каноническому:

x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0

Перейдем от канонического к общему:

x + 1 2 = y — 4 0 ⇔ 0 · (x + 1) = 2 (y — 4) ⇔ y — 4 = 0

Ответ: y — 4 = 0

Пример 10

Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.

Решение:

Просто перепишем уравнение в необходимом виде:

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0

Ответ: 1 3 x + 2 y — 1 = 0 .

Составление общего уравнения прямой

Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A (x — x 0) + B (y — y 0) = 0 . Там же мы разобрали соответствующий пример.

Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.

Пример 11

Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 (4 , 1) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.

Решение

Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = (2 , — 3) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:

A (x — x 0) + B (y — y 0) = 0 ⇔ 2 (x — 4) — 3 (y — 1) = 0 ⇔ 2 x — 3 y — 5 = 0

Ответ: 2 x — 3 y — 5 = 0 .

Пример 12

Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.

Решение

Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .

Тогда n → = (3 , 5) . Прямая проходит через начало координат, т.е. через точку О (0 , 0) . Составим общее уравнение заданной прямой:

A (x — x 0) + B (y — y 0) = 0 ⇔ 3 (x — 0) + 5 (y — 0) = 0 ⇔ 3 x + 5 y = 0

Ответ : 3 x + 5 y = 0 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

В данной статье мы рассмотрим общее уравнение прямой на плоскости. Приведем примеры построения общего уравнения прямой, если известны две точки этой прямой или если известна одна точка и нормальный вектор этой прямой. Представим методы преобразования уравнения в общем виде в канонический и параметрический виды.

Пусть задана произвольная декартова прямоугольная система координат Oxy . Рассмотрим уравнение первой степени или линейное уравнение:

Ax+By+C =0,

(1)

где A, B, C − некоторые постоянные, причем хотя бы один из элементов A и B отлично от нуля.

Мы покажем, что линейное уравнение на плоскости определяет прямую. Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат на плоскости каждая прямая линия может быть задана линейным уравнением. Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат на плоскости определяет прямую линию.

Доказательство. Достаточно доказать, что прямая L определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть на плоскости задана прямая L . Выберем систему координат так, чтобы ось Ox совпадал с прямой L , а ось Oy был перпендикулярной к ней. Тогда уравнение прямой L примет следующий вид:

y=0.

(2)

Все точки на прямой L будут удовлетворять линейному уравнению (2), а все точки вне этой прямой, не будут удовлетворять уравнению (2). Первая часть теоремы доказана.

Пусть задана декартова прямоугольная система координат и пусть задана линейное уравнение (1), где хотя бы один из элементов A и B отличен от нуля. Найдем геометрическое место точек, координаты которых удовлетворяют уравнению (1). Так как хотя бы один из коэффициентов A и B отличен от нуля, то уравнение (1) имеет хотя бы одно решение M (x 0 ,y 0). (Например, при A ≠0, точка M 0 (−C/A , 0) принадлежит данному геометрическому месту точек). Подставляя эти координаты в (1) получим тождество

Ax 0 +By 0 +C =0.

(3)

Вычтем из (1) тождество (3):

A (x −x 0)+B (y −y 0)=0.

(4)

Очевидно, что уравнение (4) эквивалентно уравнению (1). Поэтому достаточно доказать, что (4) определяет некоторую прямую.

Поскольку мы рассматриваем декартову прямоугольную систему координат, то из равенства (4) следует, что вектор с компонентами {x−x 0 , y−y 0 } ортогонален вектору n с координатами {A,B }.

Рассмотрим некоторую прямую L , проходящую через точку M 0 (x 0 , y 0) и перпендикулярной вектору n (Рис.1). Пусть точка M (x ,y) принадлежит прямой L . Тогда вектор с координатами x−x 0 , y−y 0 перпендикулярен n и уравнение (4) удовлетворено (скалярное произведение векторов n и равно нулю). Обратно, если точка M (x ,y) не лежит на прямой L , то вектор с координатами x−x 0 , y−y 0 не ортогонален вектору n и уравнение (4) не удовлетворено. Теорема доказана.

Доказательство. Так как прямые (5) и (6) определяют одну и ту же прямую, то нормальные векторы n 1 ={A 1 ,B 1 } и n 2 ={A 2 ,B 2 } коллинеарны. Так как векторы n 1 ≠0, n 2 ≠0, то существует такое число λ , что n 2 =n 1 λ . Отсюда имеем: A 2 =A 1 λ , B 2 =B 1 λ . Докажем, что C 2 =C 1 λ . Очевидно, что совпадающие прямые имеют общую точку M 0 (x 0 , y 0). Умножая уравнение (5) на λ и вычитая из него уравнение (6) получим:

Так как выполнены первые два равенства из выражений (7), то C 1 λ −C 2 =0. Т.е. C 2 =C 1 λ . Замечание доказано.

Заметим, что уравнение (4) определяет уравнение прямой, проходящей через точку M 0 (x 0 , y 0) и имеющий нормальный вектор n ={A,B }. Поэтому, если известен нормальный вектор прямой и точка, принадлежащая этой прямой, то можно построить общее уравнение прямой с помощью уравнения (4).

Пример 1. Прямая проходит через точку M =(4,−1) и имеет нормальный вектор n ={3, 5}. Построить общее уравнение прямой.

Решение. Имеем: x 0 =4, y 0 =−1, A =3, B =5. Для построения общего уравнения прямой, подставим эти значения в уравнение (4):

Ответ:

Вектор параллелен прямой L и, следовательно, перпердикулярен нормальному вектору прямой L . Построим нормальный вектор прямой L , учитывая, что скалярное произведение векторов n и равно нулю. Можем записать, например, n ={1,−3}.

Для построения общего уравнения прямой воспользуемся формулой (4). Подставим в (4) координаты точки M 1 (можем взять также координаты точки M 2) и нормального вектора n :

Подставляя координаты точек M 1 и M 2 в (9) можем убедится, что прямая заданная уравнением (9) проходит через эти точки.

Ответ:

Вычтем (10) из (1):

Мы получили каноническое уравнение прямой. Вектор q ={−B , A } является направляющим вектором прямой (12).

Обратное преобразование смотрите .

Пример 3. Прямая на плоскости представлена следующим общим уравнением:

Переместим на право вторую слагаемую и разделим обе части уравнения на 2·5.

Найти уравнение прямой из двух точек — y=ax+b

Уравнение прямой, расчет онлайн

Сводка :

Калькулятор уравнения прямой позволяет рассчитать уравнение прямой по координатам двух точек с пошаговым расчетом.

уравнение_прямая_линия онлайн

---

Описание :

На плане есть одна и только одна прямая линия, проходящая через две точки. В системе (O,`vec(i)`,`vec(j)`) плана возможно по координатам двух точек найти уравнение прямой из координаты двух точек найти уравнение прямой .

Калькулятор позволяет найти уравнение прямой (вида y=ax+b) по координатам двух точек, задав шаги расчета.

Этот калькулятор умеет определять уравнение прямой через две точки с разными абсциссами, но и уравнение прямой через две точки с одинаковой абсциссой.

Уравнение прямой из двух точек с разными абсциссами

Этот пример показывает как рассчитать уравнение прямой, проходящей через точки с координатами A[3;0] и B[2;5] , после вычисления возвращается результат `[y=15-5*x]`.

Уравнение прямой из двух точек с одинаковой абсциссой

Например, для вычислить уравнение прямой линии через точки A[3;2] и B[3;3] введите уравнение_прямая_линия(`[3;2];[3;4]`), после вычисления возвращается результат `[x=3]`.

Построить прямую из двух точек

В некоторых случаях калькулятор после определения уравнения прямой из двух точек предложит провести прямую связанные с этим уравнением. Для этого, когда это возможно, достаточно нажать на ссылку, которая появляется в области подробных расчетов.

Синтаксис:

уравнение_прямая_линия(точка1;точка2)

---

Примеры:

equation_straight_line(`[3;1];[2;5]`) возвращает [y=13-4*x]

Расчет онлайн с помощью уравнения_прямой_линии (найти уравнение прямой из двух точек)

См. также

Список связанных калькуляторов:

• Решение квадратного уравнения с комплексным числом : complexe_solve. Калькулятор уравнений комплексных чисел возвращает комплексные значения, для которых квадратное уравнение равно нулю.
• Расчет дискриминанта онлайн: дискриминант. Калькулятор, который позволяет вычислить дискриминант квадратного уравнения онлайн.
• Найти уравнение прямой линии из двух точек: уравнение_прямой_линии. Калькулятор уравнения прямой позволяет рассчитать уравнение прямой по координатам двух точек с пошаговым расчетом.
• Найдите уравнение касательной линии: уравнение_касательной_линии. Калькулятор уравнения касательной используется для расчета уравнения касательной к кривой в заданной точке абсцисс с поэтапным вычислением.
• Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
• Калькулятор решения для x: уравнение_решателя. Решатель уравнений позволяет решать уравнения с неизвестным с шагами расчета: линейное уравнение, квадратное уравнение, логарифмическое уравнение, дифференциальное уравнение.
• Калькулятор неравенства: неравенство_решатель. Решатель неравенств, который решает неравенство с деталями расчета: линейное неравенство, квадратное неравенство.
• Решение системы линейных уравнений :solve_equations. Решатель систем линейных уравнений позволяет решать уравнения с несколькими неизвестными: система уравнений с 2 ​​неизвестными, система уравнений с 3 неизвестными, система с n неизвестными.
• Решатель обратного отсчета: arithmetic_solver. Этот решатель обратного отсчета позволяет найти целевое число из набора целых чисел с помощью арифметических операций.

---

Список связанных упражнений:

• Рассчитать по координатам точки уравнение прямой, проходящей через начало координат. Цель этого упражнения — найти уравнение прямой, представляющей линейную функцию, проходящую через заданную точку.
• Вычисление уравнения прямой по координатам двух точек : Цель этого упражнения — найти уравнение прямой по двум точкам.

---

Напоминания о курсах, калькуляторы, упражнения и игры: Уравнения, Геометрия

 

Уравнения прямых

В этом разделе вы узнаете об уравнениях прямых.

Эти уравнения могут принимать различные формы в зависимости от фактов, которые мы знаем о линиях. Итак, для начала предположим, что у нас есть прямая линия, содержащая точки из следующего списка.

На линии еще много точек, но их достаточно, чтобы увидеть закономерность. Если вы возьмете любое значение x и добавите 2, мы получим соответствующее значение y.

То есть

0 + 2 = 2

1 + 2 = 3

2 + 2 = 4

3 + 2 = 5

Здесь мы можем видеть фиксированную связь между x и y co- ординаты любой точки на прямой, и уравнение

y  =  x + 2

всегда верно для точек на прямой. Мы можем пометить линию, используя это уравнение.

Предположим, у нас есть график прямой линии, и мы хотим найти ее уравнение.

Для любой прямой, если мы хотим найти уравнение, мы должны иметь следующую информацию об этой прямой.

(i) Наклон и точка пересечения по оси Y

(ii)  Одна точка и точка пересечения

(iii) Две точки

(iv) Две точки пересечения (по оси X и по оси Y)

Если есть одна из пяти данных, приведенных выше, мы сможем найти уравнение прямой линии, используя формулы, приведенные ниже.

Теперь давайте посмотрим на различные формы уравнения прямой линии.

Различные формы уравнений прямых линий

1. Уравнение прямой с пересечением наклона:

y = mx + b

m —> наклон

b —-> пересечение с осью

2. Уравнение формы точки-наклона линии:

y — y ₁  = m(x — x ₁ )

м —> уклон

(x ₁ , y _{1) —-> точка}

3. Двухточечное уравнение прямой:

(y — y ₁ )/(y ₂  — y ₁ ) = (x — x ₁ )/(x _{3 -90 x 1 )}

Две точки —-> (x ₁ , y ₁ ) и (x ₂ , y ₂ )

4. Форма пересечения

x/a + y/b = 1

a —-> x-точка

b —-> y-точка

Помимо приведенных выше форм уравнения прямой, существуют и другие способы чтобы получить уравнение прямой.

1. Если прямая проходит через точку (0, k) на оси y и параллельно оси x, то уравнение прямой имеет вид

y = k

2. Если прямая проходит через точку (c, 0) на оси x и параллельно оси y, то уравнение прямой имеет вид

x = c

3. Уравнение оси x имеет вид

y  = 0

(поскольку значение y во всех точках оси x равно нулю)

4. Уравнение оси y равно

x = 0

(Поскольку значение ‘x’ во всех точках оси Y равно нулю)

5. Общая форма уравнения прямой:

ax + by + c  = 0

Решенные задачи

Задача 1 :

Найдите общий вид уравнения прямой линии, наклон которой равен 3, а точка пересечения с осью y -2.

Решение:

Дано: Наклон m = 3 и точка пересечения с осью b = -2.

Уравнение прямой линии в форме пересечения наклона: 

y  =  mx + b

Подставьте m = 3 вместо m и b = -2.

y  =  3x — 2

Вычтите y с каждой стороны.

0 = 3x — y — 2

или

3x — y — 2 = 0

Задача 2 :

Найдите общий вид уравнения прямой, проходящей через точки (-1, 1) и (2, -4).

Решение:

Дано: Две точки на прямой: (-1, 1) и (2, -4).

Уравнение прямой в двухточечной форме равно 

(Y — Y ₁ ) / (Y ₂ — Y ₁ ) = (x — x ₁ ) / (x ₂ — x ₁ )
9000

. 1 , y ₁ )  =  (-1, 1) и (x ₂ , y ₂ )  =  (2, -4).

(y — 1) / (-4 — 1)  =  (x + 1) / (2 + 1)

Упростить.

(y — 1) / (-5)  =  (x + 1) / 3

Перекрестное умножение.

3(y — 1)  = -5(x + 1)

3y — 3  = -5x — 5

5x + 3y + 2  =  0

Задача 3 :

Найдите общее уравнение прямой, проходящей через точку (-2, 3) с наклоном 1/3.

Решение:

Дано: Точка = (-2, 3) и наклон m = 1/3

Уравнение прямой линии в форме точки-наклона: )  

Замена (x ₁ , y ₁ ) = (-2 , 3) ​​и m = 1/3.

г — 3  =  1/3 ⋅ (x + 2)

Умножить каждую сторону на 3.

3(y — 3)  =  x + 2

Упростить.

3y — 9  =  x + 2

Вычтите 3y с каждой стороны.

-9  =  x — 3y + 2

Добавьте 9 с каждой стороны.

0  =  x — 3y + 11

или

x — 3y + 11 = 0

Задача 4 :

Найдите общее уравнение прямой линии, точка пересечения по оси x -2 и точка пересечения по оси y равна 3.

Решение:

Дано: точка пересечения по оси x равна -2, а точка пересечения по оси y равна 3,9.0005

Уравнение прямой линии в форме пересечения: 

x/a + y/b  =  1

Подставьте a = -2 и b = 3. 

x/(-2) + y/3  =  1 — —-(1)

Наименьшее общее кратное (2, 3) равно 6.

Итак, умножьте каждую сторону (1) на 6. 

-3x + 2y  =  6

Умножьте каждую сторону на — 1.

3x — 2y  =  -6

Добавьте 6 с каждой стороны.

3x — 2y + 6  =  0

Задача 5 :

Найдите уравнение прямой, параллельной оси y и проходящей через (-5, 0).

Решение:

Уравнение прямой, параллельной оси Y:

x = c

заданная линия

х = -5

или

х + 5 = 0

Задача 6 :

Найдите уравнение прямой, параллельной оси абсцисс и проходящей через (0, 6).

Решение :

Уравнение прямой, параллельной оси X, равно 9.0005

y = k

Проходит через точку (0, 6)

Тогда

6 = k

Итак, уравнение данной прямой равно

y = 6

или 5  =  0

Пожалуйста, отправьте свой отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

Как узнать, находится ли точка на прямой с помощью уравнения

Вся алгебра 1 Ресурсы

10 диагностических тестов 557 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

Алгебра 1 Помощь » Функции и линии » Уравнения прямых » Формула точек и расстояний » Как узнать, находится ли точка на прямой с уравнением

Какая из следующих точек не находится на прямой y = 7x + 2?

Возможные ответы:

(–2, –12)

(0, 2)

(1, 10)

(–1, –5)

(2, 16)

7 (7) Правильный ответ:5 1, 10)

Объяснение:

Чтобы узнать, находится ли точка (x, y) на графике линии, мы подставляем значения и смотрим, получается ли верное утверждение, например, 10 = 10. Если мы получаем что-то другое, например 6 = 4, мы знаем, что точка не лежит на прямой, потому что она не удовлетворяет уравнению. В данных вариантах, когда мы подставляем (1, 10), мы получаем 10 = 7 + 2, что неверно, что делает этот ответ искомым.

y = 7x + 2

(2, 16) дает 16 = 7(2) + 2 = 14 + 2 = 16

(–1, –5) дает –5 = 7(–1) + 2 = –7 + 2 = –5

(0, 2) дает 2 = 7(0) + 2 = 0 + 2 = 2

(–2, –12) дает –12 = 7(–2) + 2 = –14 + 2 = –12

Все это верно.

(1, 10) дает 10 = 7(1) + 2 = 7 + 2 = 9

10 = 9 — ложное утверждение.

Сообщить об ошибке

Какая точка находится на линии ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы определить, находится ли точка на прямой, просто подставьте точки обратно в уравнение. Когда мы подставляем (2,7) в уравнение as и соответственно, уравнение получается, что указывает на то, что точка расположена на прямой.

Сообщить об ошибке

Какое из следующих утверждений неверно?

Возможные ответы:

 перпендикулярно .

Точки и лежат на прямой .

Прямые  и  параллельны.

 и оба выпадают на строчку .

Правильный ответ:

 и оба падают на линию .

Объяснение:

Линии с одинаковым наклоном параллельны (если только две линии не идентичны), а линии с противоположно обратными наклонами перпендикулярны. Таким образом, осталось оценить только те два оператора, которые содержат набор точек.

Рассмотрим  и .

Таким образом, наклон или  равен 2.

Подстановка точки  в наполовину законченное уравнение дает нам значение . Таким образом, это утверждение верно, и единственным ответом может быть утверждение, содержащее  и .

На всякий случай проверим.

  дает нам значение наклона 6, поэтому мы уже можем сказать, что уравнение для линии не будет . Мы нашли свой ответ.

Сообщить об ошибке

Какие из этих прямых проходят через точку (6,5) на координатной плоскости xy?

Возможные ответы:

Ни один из других ответов

Правильный ответ:

9

5

5 Объяснение:

Чтобы узнать, находится ли точка на прямой, вы можете снова подставить точки в уравнение. Если значения равны друг другу, то точка должна быть на прямой. В этом случае единственное уравнение, где (6,5) правильно подходит в качестве значения, — это .

Сообщить об ошибке

Какие из следующих точек находятся на линии, описываемой уравнением?

 

Возможные ответы:

Два из этих вариантов ответа верны.

Правильный ответ:

Два из этих вариантов ответа верны.

Объяснение:

Самый простой способ узнать, попадает ли точка на определенную линию, — это подставить первое значение точки для  и второе значение для .

Если мы сделаем это для , мы обнаружим, что

 

, что верно.

Уравнение также верно для , но неверно для других значений. Итак, два варианта ответа верны.

Сообщить об ошибке

Какая из следующих упорядоченных пар лежит на линии, заданной уравнением ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы определить, какая упорядоченная пара удовлетворяет уравнению, было бы полезно преобразовать уравнение в форму пересечения наклона.

Затем подставьте каждую заказанную пару и посмотрите, удовлетворяет ли она уравнению. Мы ищем значение, которое дает желаемый ответ.

удовлетворяет уравнению. Все остальные пункты нет.

(Примечание: вы также можете использовать исходное уравнение в стандартной форме).

Сообщить об ошибке

На какой из этих прямых расположена точка (3,2)?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы определить, находится ли точка на линии, вы можете включить ее в уравнение, чтобы увидеть, остается ли уравнение действительным/равным точке.

Подстановка точки (3,2) в уравнение дает

, что работает. Ни одно из других уравнений не останется равным после включения в (3,2).

Сообщить об ошибке

На какой из этих прямых лежит точка (2,7)?

Возможные ответы:

Ни один из этих ответов

Правильный ответ:9

5

5 Объяснение:

Чтобы определить, находится ли точка на заданной линии, просто вставьте координаты точки в линию. В этом случае вставка координат в единственную строку, где вы можете вставить координаты и получить правильное уравнение, это . Подстановка (2,7) даст вам уравнение , которое соответствует .

Сообщить об ошибке

Какие из этих точек попадают на график прямой

Возможные ответы:

Две из этих точек попадают на график этого уравнения.

Все три эти точки попадают на график этого уравнения.

Правильный ответ:

Все три эти точки попадают на график этого уравнения.

Объяснение:

Чтобы узнать, находится ли точка на линии с уравнением, нам просто нужно подставить значения точки и и посмотреть, верно ли уравнение. Например, давайте посмотрим на точку . Подстановка в уравнение дает нам

или

, что верно.

Итак, эта точка попадает на прямую. Проделав то же самое с двумя другими точками, мы увидим, что да, все три точки попадают на линию, выраженную этим уравнением.

Сообщить об ошибке

Какая точка находится на прямой

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы определить, находится ли точка на прямой, вы можете просто подставить координаты x и y в уравнение. Другой способ решить эту проблему — построить график линии и посмотреть, попадает ли она на линию. Подключение даст верное утверждение, так что оно на линии.

Сообщить об ошибке

← Назад 1 2 3 Далее →

Уведомление об авторских правах

Все ресурсы по алгебре 1

10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept

Уравнение линии из двух точек

Уравнение калькулятора линии иллюстрирует вертикальное изменение, деленное на горизонтальное изменение, а также графические иллюстрации. Мы также описываем его как рост над изменением пробега в декартовых координатах.

Итак, давайте перейдем к более подробному изучению уравнения линии и сценария его определения!

Сосредоточься!

Что такое уравнение линии?

Уравнение прямой в алгебраической форме представляет собой набор точек, которые вместе образуют линию в системе координат. Многие точки соединяются вместе, представленные в виде полной линии, и мы находим только две точки, чтобы нарисовать линию в декартовых координатах.

Типы линейных уравнений:

Существует 3 распространенных типа уравнения линии с наклоном. Мы можем найти уравнение линии в его общей форме и их соответствующую связь с этими уравнениями линии, как указано ниже:

• Форма наклона точки
• Форма пересечения уклонов
• Стандартная форма

Форма наклона точки:

Общее уравнение в форме наклона точки может быть записано как:
y – y1 = m(x – x1)
строка
«m» — это наклон линии

Точечная форма наклона: В точечно-наклонной форме нам нужна только одна точка (x1,y1), чтобы найти уравнение линии в точечно-наклонной форме.
Когда у нас есть только одна точка ( x1,y1) и значения наклона «m».
Может быть удобно ввести значения одной точки и наклона (м) в уравнение линейного калькулятора.

Нас можно определить в уравнении прямой, проходящей через две точки в вышеупомянутых калькуляторах. Калькулятор точки-наклона лучше всего раскрывать и рисовать уравнение линии.

Форма пересечения наклона:

Форма пересечения наклона может быть записана в виде:
y = mx + c
Где
«m» — наклон линии
«c» is10 y-пересечение уравнения прямой

 Калькуляторы пересечения наклона слишком полезны для нахождения формы пересечения наклона.

Стандартная форма:

Стандартная форма уравнения для линии может быть записана как:

Ax + By = C

Мы также можем записать стандарт так:

 Ax + By + C = 0

Где

A, а B — коэффициенты переменных x, y 8 C» — точка пересечения линии по оси Y.

Стандартную форму уравнения можно хорошо проиллюстрировать с помощью Калькулятора стандартной формы.

Примеры всех форм уравнения линии:

Мы раскрываем всю концепцию уравнения линии, изображая практические примеры формы точечного наклона, формы пересечения наклона и формы эталонов соответственно.

Пример Форма наклона точки :

Рассмотрим по одной точке вдоль оси x и оси y (3,5), а наклон «m» равен 6. Мы можем написать уравнение прямой, проходящей через точки (3,5) и имеющей наклон «6». Мы знаем, как найти уравнение линии Point Slope Form, поэтому может быть просто, как найти уравнение линии с одной точкой и наклоном?

                                       y – y1 = M (x — x1)

Установка значений в уравнение линии в точечной форме:

Y — 5 = 6 (x — 3) Y — 5 = 6 (x — 3) Y — 5 = 6 (x — 3) Y — 5 = 6 (x — 3) . представляет собой уравнение линии в форме «точка-наклон»:

Пример в форме «наклон-пересечение»:

Теперь рассмотрим, что наклон линии «m» равен 6, а точка пересечения с осью y «c» равна 8. , Тогда уравнение линии в форме наклона-пересечения:

y = M x + c

Помещение значений в уравнение с наклоном-перевод найти по уравнению линейного калькулятора 

Пример стандартной формы:

Вы можете использовать форму точки-наклона или формулу пересечения наклона, чтобы преобразовать ее в стандартную форму:

Вы должны знать, что мы не можем использовать дроби или десятичные дроби в качестве коэффициента «x». Это означает, что коэффициент «x» должен быть просто положительным:

Возьмите форму перехвата наклона:

y = 6x+8

Теперь мы применяем операцию:

⇒ 6x+8-й = 0

                                                   ⇒    6x-y+8 = 0

Стандартная форма следующая:

6x-y = -8

Как найти y-Intercept линейного уравнения:

2 We может найти точку пересечения y, когда x = 0, это точка, в которой линия пересекает ось y. Теперь подставляем значения в уравнение линейного калькулятора, находим значения:

y = 3x -7

Используя уравнение y = 3x -6, сохраните x = 0, чтобы найти y -intercept:

y = 3 (0) -7

y = — 7

Точка пересечения с ординатой равна «-7».

Как найти пересечение линии по оси X Уравнение:

Пересечение линии по оси X равно значению x при y=0. Это точка пересечения прямой с осью x декартовых координат. Мы можем написать уравнение прямой, проходящей через точки y=0, следующим образом:

Используя уравнение: 

                                           y = 3x – 6, поставьте y=0

Чтобы найти точку пересечения по оси x.

0 = 3x-6

3x = 6

X-Intercept-2 из формы перехвата наклона линейного уравнения:

x = 2

Наклон параллельных линий:

Когда мы находим наклон одной линии, тогда будут те же значения параллельной линии, поскольку они имеют одинаковые значения «m». Поэтому они никогда не пересекаются друг с другом.

Наклон перпендикулярных линий:

Наклон перпендикулярных линий будет равен отрицательной обратной величине известного наклона.

Мы можем найти уравнение прямой, перпендикулярной другой. Эти строки из 9Угол 0° при их пересечении. Мы можем найти наклоны, перпендикулярные друг другу, с помощью уравнения линейного калькулятора.

Как найти уравнение прямой, перпендикулярной другим?

Рассмотрим линию с наклоном -5.
Тогда каков наклон линии, перпендикулярной ей?

• Сначала возьмите отрицательное значение наклона вашей линии
  -(-5) = 5
• Во-вторых, возьмите обратное число.
• 5 — целое число, его знаменатель равен 1.
• Обратное 5/1 равно 1/5.
• Отрицательная инверсия -5 представляет собой наклон 1/5.
• Наклон перпендикулярной линии равен 1/5.

Уравнение прямой, проходящей через две точки и перпендикулярной друг к другу, имеет наклон «5» и ⅕ соответственно.

Работа над уравнением линии Калькулятор:

Вы можете найти уравнение формы точка-наклон линии, форма наклона-пересечения и стандартная форма, дополнительно мы можем найти уравнение линии с двумя точками на декартовой координаты.

Ввод:

• Вставьте значения, выбрав раскрывающееся меню.
• Выберите «Две точки», «Одна точка» или «Y-пересечение» из списка 
• Вставить значения
• Нажмите кнопку расчета

Результат:

Уравнение прямой из двух точек Калькулятор раскрывает через некоторое решение всех форм уравнения прямой. Графическое представление позволяет нам легко понять всю концепцию.

• Отображается подробное решение.
• Также представлено графическое представление

Часто задаваемые вопросы:

Как построить график уравнения прямой?

Вы можете построить уравнение, найдя точку пересечения y = c уравнения y = mx + b и наклон линии.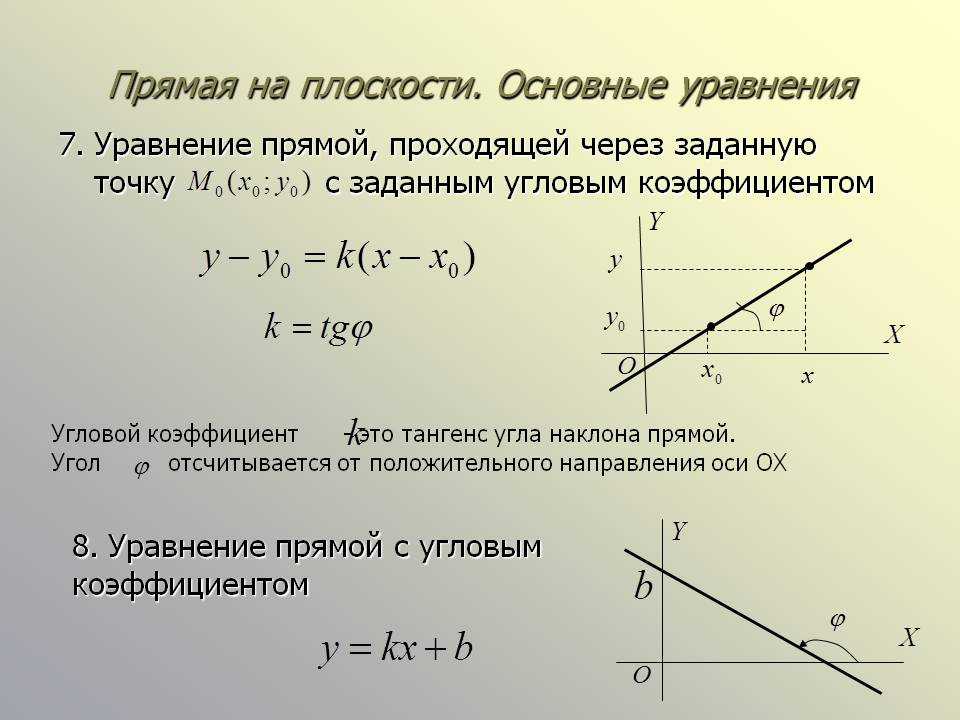

Что такое точка пересечения Y прямой?

Это точка, в которой прямая пересекает ось y, и x=0, когда y=mx+c. Тогда c является точкой пересечения уравнения по оси y.

Вывод:

Линейные уравнения очень важны в математических и повседневных приложениях. Мы можем описать взаимосвязь между двумя переменными, чтобы предсказать, рассчитать скорость и определить взаимосвязь между двумя величинами. Калькулятор уравнения линии изображает весь процесс построения уравнения линии.

Ссылки:

Из источника content.byui.edu: Форма точки-наклона линии, Дополнительные ресурсы

Из источника Википедии: Линия, Определения и описания, В декартовых координатах

Из источника chilimath.com: Пути построения графика, Координаты X, Y

Рисование графика прямой линии

Содержание | Дом

Назад к Разделу 1

x — и y -пересечения графа

Рисование графика

Форма   y = x .

Вертикальные и горизонтальные линии

x — и y -пересечения графа

Пересечение x графика — это значение x , при котором график пересекает ось x . Точка пересечения y — это значение y , где оно пересекает ось y .

Чтобы найти x -перехват, мы должны найти значение x , где y = 0 — потому что при каждые точки на оси x , y = 0,

Пример 1.   Вычислить значение x , когда y = 0, то есть найти точку пересечения x   y  = 2 x  + 10,

Решение . Положив y = 0, мы должны решить уравнение

	2 x + 10	=	0.
	У нас есть:
	2 x	=	−10
	х	=	−5.

Пересечение x равно −5.

Задача 10.   Вычислить значение x , когда y = 0,

а)	г	=	2 x + 4		б)	г	=	3 х — 12
	2 x + 4	=	0			3 x − 12	=	0
	2 x	=	−4			3 x	=	12
	х	=	−2			х	=	4

в)	г	=	4 x + 1
	4 x + 1	=	0
	4 x	=	−1
	х	=	— ¼

Чтобы найти точку пересечения y графика, мы должны найти значение y , когда x  = 0 — потому что в каждой точке на оси y x = 0. Но когда уравнение имеет вид

y  =  ax + b ,

y -intercept просто b . Когда х = 0,

y  =  0 + b  =  b .

Рисование графика

Две точки определяют прямую линию. И два самых важных момента это х — и и -перехваты. Поэтому всякий раз, когда мы рисуем график, мы всегда отмечаем эти точки.

Задача 11.

а)	Когда у нас есть уравнение прямой линии, как нам найти точку пересечения x ?

Положи y = 0 и найди х .

b) Как найти y −перехват?

Положите x = 0 и найдите y .

Задача 12. Отметьте точки пересечения x и y и нарисуйте график

.

у = 2 х + 6.

Точка пересечения x -3 является решением уравнения 2 x + 6 = 0. Точка пересечения y — это постоянный член, 6. График представляет собой прямую линию, проходящую через эти две точки пересечения.

Пример 2. Отметьте точки пересечения x и y и нарисуйте график

5 x − 2 y  = 10,

Решение . Хотя это не имеет формы y = x + b , стратегия та же. Найдите точки пересечения, поставив x , затем y , равное 0,

.

Когда мы ставим х = 0, у нас

	−2 г	=	10.
	Отсюда следует
	г	=	−5.

Когда мы кладем y = 0, мы имеем

	5 x	=	10.
	Отсюда следует
	х	=	2.

Вот график:

Задача 13.

а)	В уравнении   y = a x + b , где на графике мы находим b ?

Как и — перехват.

б)	Где мы находим решение для   a x  +  b  = 0 ?

Как перехват x .

Задача 14.   Отметьте x − и y − пересекаются, и рисуем график.

а)	у = 2 х — 6		б)	y = −3 x + 3
в)	у = 4 х + 2		г)	х — у = 3
				См. пример 2.
д)	х — 2 у + 2 = 0		е)	2 х — 3 у — 6 = 0
г)	у = — х + 1		ч)	у = 6 х — 3

Задача 15. Форма y = x .

а)	Когда уравнение имеет форму   y = x  (например,   y  = 2 x ), что номер б ? 0

б)	Следовательно, какой номер и -перехват? 0

c) Через какую точку проходит линия?

Происхождение. Другими словами, точки пересечения x и y совпадают.

d)  Как найти другую точку на прямой?

Выберите любое значение для x . Затем уравнение определит значение y .

(В следующем уроке мы увидим, что и — это наклон линии.

Пример 3.   Нарисуйте график   y = 2 x .

Решение . Поскольку b = 0, график проходит через начало координат. Чтобы найти другую точку, пусть, например, x = 1. Затем y = 2 ·  1 = 2. Точка (1, 2) находится на графике:

Пример 4.    Нарисуйте график   y  =

2 3

х .

Решение . Опять же, поскольку b = 0, график проходит через начало координат. Чтобы найти другую точку, выберите целое число x таким образом, чтобы и также будут целыми числами. Выберите x , равное знаменателю, 3. Тогда точка (3, 2) находится на графике.

Задача 16.   Нарисуйте каждый график.

а)	у = 4 х		б)	y = − x

в)

y =

3 5

х

г)

y = −

2 5

х

Пример 6. Вертикальные и горизонтальные линии.

Уравнение вида

x  =  Число

— уравнение вертикальной линии. Например,

x = 3,

x = 3 — координата x равна 3 — верно для каждой точки на этой линии.

Уравнение вида

y  =  Число

— уравнение горизонтальной линии. Например,

y  = −4.

y -координата равна −4 в каждой точке этой линии.

Задача 17.   Нарисуйте каждый график.

а)	х = 5		б)	х = −2
в)	у = 3		г)	г = -1

Задача 18.

а)  Что такое уравнение оси x ?

г = 0

b)  Каково уравнение оси y ?

х = 0

Назад к Разделу 1

Следующий урок:  Наклон прямой линии

Содержание | Главная

---

Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.

---

Copyright © 2021 Лоуренс Спектор

Вопросы или комментарии?

Электронная почта: [email protected]

3.3 Нахождение уравнения прямой — Алгебра среднего уровня 2e

Цели обучения

К концу этого раздела вы сможете:

• Находить уравнение прямой с учетом наклона и точки пересечения по оси Y
• Найдите уравнение прямой по заданному наклону и точке
• Найдите уравнение прямой по двум точкам
• Найти уравнение прямой, параллельной заданной прямой
• Найти уравнение прямой, перпендикулярной заданной прямой

Приготовься 3,7

Прежде чем приступить к работе, пройдите этот тест на готовность.

Решить: 25(х+15).25(х+15).
Если вы пропустили эту проблему, просмотрите пример 1.50.

Приготовься 3,8

Упрощение: −3(x−(−2)).−3(x−(−2)).
Если вы пропустили эту проблему, просмотрите пример 1.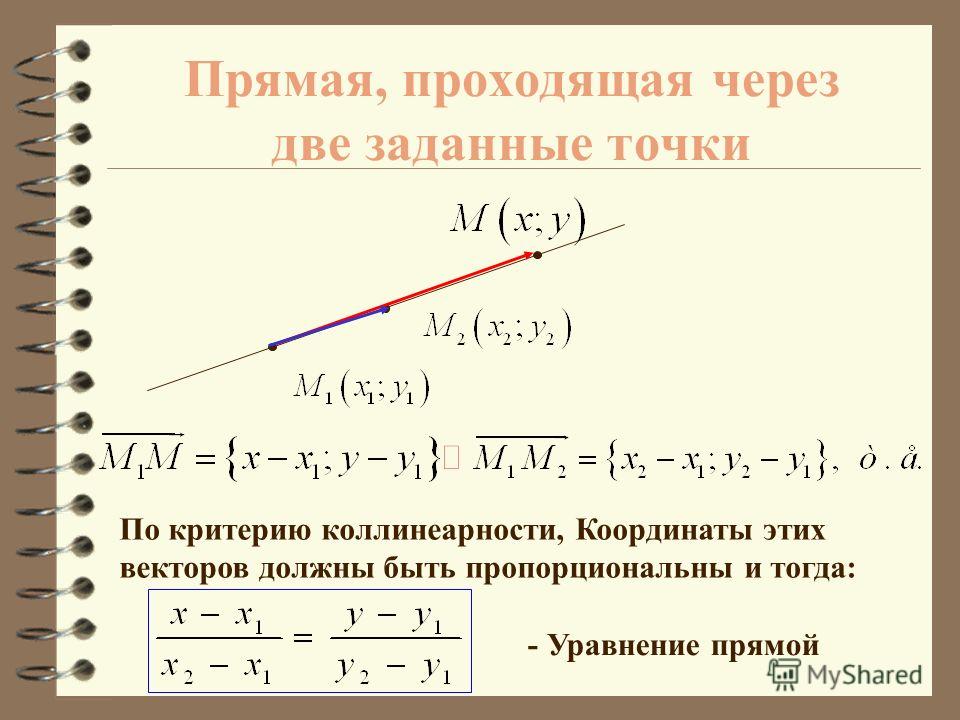 53.

Приготовься 3,9

Найдите y : y−3=−2(x+1).y−3=−2(x+1).
Если вы пропустили эту проблему, просмотрите пример 2.31.

Как интернет-компании узнают, что «вам также может понравиться» конкретный товар, основанный на том, что вы только что заказали? Откуда экономисты могут знать, как повышение минимальной заработной платы повлияет на уровень безработицы? Как медицинские исследователи создают лекарства для воздействия на раковые клетки? Как дорожные инженеры могут предсказать влияние повышения или снижения цен на бензин на ваше время в пути? Это все математика.

Физические науки, социальные науки и деловой мир полны ситуаций, которые можно смоделировать с помощью линейных уравнений, связывающих две переменные. Чтобы создать математическую модель линейной зависимости между двумя переменными, мы должны уметь найти уравнение прямой. В этом разделе мы рассмотрим несколько способов записи уравнения прямой. Конкретный метод, который мы используем, будет определяться тем, какая информация нам предоставляется.

Найдите уравнение прямой, зная наклон и

г -Перехват

Мы можем легко определить наклон и пересечение линии, если уравнение будет записано в форме наклона и пересечения, y=mx+b.y=mx+b. Теперь сделаем обратное — начнем с наклона и y — точки пересечения и используем их для нахождения уравнения прямой.

Пример 3,24

Найдите уравнение прямой с наклоном −9−9 и y -перехватом (0,−4).(0,−4).

Решение

Так как нам дан наклон и y -пересечение линии, мы можем подставить нужные значения в форму наклона-пересечения, y=mx+b.y=mx+b.

Назовите склон.
Имя y -перехват.
Подставьте значения в y=mx+b.y=mx+b.

Попытайся 3,47

Найти уравнение прямой с наклоном 2525 и y -пересечение (0,4).(0,4).

Попытайся 3,48

Найдите уравнение прямой с наклоном −1−1 и точкой пересечения y (0,−3).(0,−3).

Иногда наклон и точку пересечения необходимо определить по графику.

Пример 3,25

Найдите уравнение линии, показанной на графике.

Решение

Нам нужно найти наклон и y -пересечение линии с графика, чтобы мы могли подставить нужные значения в форму наклона-пересечения, y=mx+b. y=mx+b.

Чтобы найти наклон, мы выбираем две точки на графике.

y -отрезок равен (0,−4)(0,−4), и граф проходит через (3,−2).(3,−2).

Найдите наклон, посчитав подъем и пробег.
Найдите и -перехват.
Подставьте значения в y=mx+b.y=mx+b.

Попытайся 3,49

Найдите уравнение линии, показанной на графике.

Попытайся 3,50

Найдите уравнение линии, показанной на графике.

Найдите уравнение линии по заданному наклону и точке

Нахождение уравнения прямой с использованием формы уравнения с пересечением наклона работает хорошо, когда вам известен наклон и y — перехват или когда вы читаете их с графика. Но что происходит, когда у вас есть другая точка вместо точки пересечения и ?

Мы собираемся использовать формулу наклона для получения другой формы уравнения прямой.

Предположим, у нас есть линия с уклоном м , которая содержит определенную точку (x1,y1)(x1,y1) и некоторую другую точку, которую мы будем называть просто (x,y).(x,y). Мы можем записать наклон этой линии, а затем изменить его форму.

	м=у-у1х-х1м=у-у1х-х1
Умножьте обе части уравнения на x−x1. x−x1.	m(x−x1)=(y−y1x−x1)(x−x1)m(x−x1)=(y−y1x−x1)(x−x1)
Упрощение.	m(x−x1)=y−y1m(x−x1)=y−y1
Перепишите уравнение с элементами yy слева.	y−y1=m(x−x1)y−y1=m(x−x1)

Этот формат называется точечно-наклонной формой уравнения прямой.

Точечно-наклонная форма уравнения линии

Форма точка-наклон уравнения линии с наклоном м и содержащей точку (x1,y1)(x1,y1):

y−y1=m(x−x1)y− у1=м(х-х1)

Мы можем использовать форму уравнения точка-наклон, чтобы найти уравнение линии, когда мы знаем наклон и по крайней мере одну точку. Затем мы перепишем уравнение в форме пересечения наклона. В большинстве приложений линейных уравнений используется форма пересечения наклона.

Пример 3,26

Как найти уравнение прямой по заданной точке и наклону

Найдите уравнение прямой с наклоном m=−13m=−13, содержащей точку (6,−4).(6,−4) . Запишите уравнение в форме пересечения наклона.

Решение

Попытайся 3,51

Найдите уравнение прямой с наклоном m=−25m=−25 и содержащей точку (10,−5).(10,−5).

Попытайся 3,52

Найдите уравнение прямой с наклоном m=−34,m=−34 и содержащей точку (4,−7).(4,−7).

Мы перечисляем шаги для удобства.

Как

Найти уравнение прямой по наклону и точке.

1. Шаг 1. Определите уклон.
2. Шаг 2. Определите точку.
3. Шаг 3. Подставьте значения в форму точка-наклон, y−y1=m(x−x1).y−y1=m(x−x1).
4. Шаг 4. Запишите уравнение в форме пересечения наклона.

Пример 3,27

Найдите уравнение горизонтальной прямой, содержащей точку (−2,−6).(−2,−6). Запишите уравнение в форме пересечения наклона.

Решение

Каждая горизонтальная линия имеет наклон 0. Мы можем подставить наклон и точки в форму точка-наклон, y−y1=m(x−x1).y−y1=m(x−x1).

Определите уклон.
Определите точку.
Подставьте значения в y−y1=m(x−x1).y−y1=m(x−x1).
Упрощение.
Пишите в форме пересечения наклона.	Это форма y , но ее можно записать как y=0x−6.y=0x−6.

Получилась ли у нас форма горизонтальной линии y=b?y=b?

Попытайся 3,53

Найдите уравнение горизонтальной прямой, содержащей точку (−3,8).(−3,8).

Попытайся 3,54

Найдите уравнение горизонтальной прямой, содержащей точку (−1,4).(−1,4).

Найдите уравнение прямой по двум точкам

При сборе реальных данных линейная модель может быть создана из двух точек данных. В следующем примере мы увидим, как найти уравнение прямой, когда заданы только две точки.

Пока у нас есть два варианта нахождения уравнения прямой: наклон-пересечение или точка-наклон. Когда мы начинаем с двух точек, имеет смысл использовать форму точка-наклон.

Но тогда нам нужен наклон. Можем ли мы найти наклон всего по двум точкам? Да. Затем, когда у нас есть наклон, мы можем использовать его и одну из заданных точек, чтобы найти уравнение.

Пример 3,28

Как найти уравнение прямой по двум точкам

Найдите уравнение прямой, содержащей точки (−3,−1)(−3,−1) и (2,−2)(2,− 2) Запишите уравнение в форме пересечения наклона.

Решение

Попытайся 3,55

Найдите уравнение прямой, содержащей точки (−2,−4)(−2,−4) и (1,−3).(1,−3).

Попытайся 3,56

Найдите уравнение прямой, содержащей точки (−4,−3)(−4,−3) и (1,−5).(1,−5).

Здесь приведены шаги.

Как

Найти уравнение прямой по двум точкам.

1. Шаг 1. Найдите наклон по заданным точкам. м=у2-у1х2-х1м=у2-у1х2-х1
2. Шаг 2. Выберите одну точку.
3. Шаг 3. Подставьте значения в форму точка-наклон: y−y1=m(x−x1).y−y1=m(x−x1).
4. Шаг 4. Запишите уравнение в форме пересечения наклона.

Пример 3,29

Найдите уравнение прямой, содержащей точки (−3,5)(−3,5) и (−3,4). (−3,4). Запишите уравнение в форме пересечения наклона.

Решение

Опять же, первым шагом будет определение уклона.

Найдите наклон прямой, проходящей через (−3,5)(−3,5) и (−3,4).(−3,4).	м=у2-у1х2-х1м=у2-у1х2-х1
	м=4-5-3-(-3)м=4-5-3-(-3)
	м=-10м=-10
	Наклон не определен.

Это говорит нам о том, что это вертикальная линия. Оба наших пункта имеют x -координата 3. 3. Таким образом, наше уравнение прямой имеет вид x=−3.x=−3. Поскольку y не существует, мы не можем записать его в форме пересечения наклона.

Вы можете нарисовать график, используя две заданные точки. Согласуется ли ваш график с нашим выводом о том, что это вертикальная линия?

Попытайся 3,57

Найдите уравнение прямой, содержащей точки (5,1)(5,1) и (5,−4).(5,−4).

Попытайся 3,58

Найдите уравнение прямой, содержащей точки (−4,4)(−4,4) и (−4,3).(−4,3).

Мы видели, что мы можем использовать либо форму пересечения наклона, либо форму точка-наклон, чтобы найти уравнение прямой. Какую форму мы будем использовать, будет зависеть от информации, которую мы получим.

Написать уравнение прямой
Если указано:	Использование:	Форма:
Наклон и у -пересечение	наклон-пересечение	y=mx+by=mx+b
Уклон и вершина	точка-наклон	y−y1=m(x−x1)y−y1=m(x−x1)
Две точки	точка-наклон	y−y1=m(x−x1)y−y1=m(x−x1)

Найти уравнение прямой, параллельной заданной прямой

Предположим, нам нужно найти уравнение прямой, проходящей через определенную точку и параллельной заданной прямой. Мы можем использовать тот факт, что параллельные прямые имеют одинаковый наклон. Итак, у нас будет точка и наклон — как раз то, что нам нужно, чтобы использовать уравнение точка-наклон.

Во-первых, давайте посмотрим на это графически.

На этом графике показано y=2x−3.y=2x−3. Мы хотим построить линию, параллельную этой линии и проходящую через точку (−2,1).(−2,1).

Мы знаем, что параллельные прямые имеют одинаковый наклон. Таким образом, вторая линия будет иметь тот же наклон, что и y=2x−3.y=2x−3. Этот наклон равен m∥=2.m∥=2. Мы будем использовать обозначение m∥m∥ для представления наклона линии, параллельной линии с наклоном м . (Обратите внимание, что нижний индекс || выглядит как две параллельные линии.)

Вторая линия проходит через (−2,1)(−2,1) и имеет m=2.m=2.

Чтобы построить линию, мы начинаем с (−2,1)(−2,1) и считаем подъем и бег.

При m=2m=2 (или m=21m=21) отсчитываем подъем 2 и разбег 1. Рисуем линию, как показано на графике.

Линии кажутся параллельными? Проходит ли вторая строка через (−2,1)?(−2,1)?

Нас попросили нарисовать линию, теперь давайте посмотрим, как это сделать алгебраически.

Мы можем использовать либо форму наклона-отрезка, либо форму точки-наклона, чтобы найти уравнение прямой. Здесь мы знаем одну точку и можем найти наклон. Поэтому мы будем использовать форму точка-наклон.

Пример 3.30

Как найти уравнение прямой, параллельной заданной прямой и точке

Найдите уравнение прямой, параллельной y=2x−3y=2x−3, содержащей точку (−2,1).(− 2,1). Запишите уравнение в форме пересечения наклона.

Решение

Посмотрите на график с параллельными линиями, показанными ранее. Имеет ли это уравнение смысл? Что такое и -пересечение линии? Что такое наклон?

Попытайся 3,59

Найдите уравнение прямой, параллельной прямой y=3x+1y=3x+1, содержащей точку (4,2). (4,2). Запишите уравнение в форме пересечения наклона.

Попытайся 3,60

Найдите уравнение прямой, параллельной прямой y=12x−3y=12x−3, содержащей точку (6,4).(6,4).

Запишите уравнение в форме пересечения наклона.

Как

Найдите уравнение прямой, параллельной данной прямой.

1. Шаг 1. Найдите наклон данной прямой.
2. Шаг 2. Найдите наклон параллельной прямой.
3. Шаг 3. Определите точку.
4. Шаг 4. Подставьте значения в форму точка-наклон: y−y1=m(x−x1).y−y1=m(x−x1).
5. Шаг 5. Запишите уравнение в форме пересечения наклона.

Найти уравнение прямой, перпендикулярной заданной прямой

Теперь рассмотрим перпендикулярные линии. Допустим, нам нужно найти прямую, проходящую через определенную точку и перпендикулярную данной прямой. Мы можем использовать тот факт, что перпендикулярные прямые имеют отрицательные обратные наклоны. Мы снова будем использовать уравнение точка-наклон, как мы делали с параллельными линиями.

На этом графике показано y=2x−3.y=2x−3. Теперь мы хотим построить линию, перпендикулярную этой линии и проходящую через (−2,1).(−2,1).

Мы знаем, что перпендикулярные прямые имеют отрицательные обратные наклоны.

Мы будем использовать обозначение m⊥m⊥ для представления наклона линии, перпендикулярной линии с наклоном м . (Обратите внимание, что нижний индекс ⊥⊥ выглядит как прямые углы, образованные двумя перпендикулярными линиями.)

y=2x−3перпендикулярная линия m=2m⊥=−12y=2x−3перпендикулярная линия m=2m⊥=−12

Теперь мы знаем, что перпендикуляр проходит через (−2,1)(−2,1) с m⊥=−12.m⊥=−12.

Чтобы построить линию, мы начнем с (−2,1)(−2,1) и посчитаем подъем −1−1 и пробег 2. Затем нарисуем линию.

Линии кажутся перпендикулярными? Проходит ли вторая строка через (−2,1)?(−2,1)?

Нас попросили нарисовать линию, теперь давайте посмотрим, как это сделать алгебраически.

Мы можем использовать либо форму наклона-отрезка, либо форму точки-наклона, чтобы найти уравнение прямой. В этом примере мы знаем одну точку и можем найти наклон, поэтому будем использовать форму точка-наклон.

Пример 3.31

Как найти уравнение прямой, перпендикулярной заданной прямой и точке

Найдите уравнение прямой, перпендикулярной y=2x−3y=2x−3, содержащей точку (−2,1).(− 2,1). Запишите уравнение в форме пересечения наклона.

Решение

Попытайся 3,61

Найдите уравнение прямой, перпендикулярной прямой y=3x+1y=3x+1, содержащей точку (4,2).(4,2). Запишите уравнение в форме пересечения наклона.

Попытайся 3,62

Найдите уравнение прямой, перпендикулярной прямой y=12x−3y=12x−3, содержащей точку (6,4).(6,4). Запишите уравнение в форме пересечения наклона.

Как

Найдите уравнение прямой, перпендикулярной данной прямой.

1. Шаг 1. Найдите наклон данной прямой.
2. Шаг 2. Найдите наклон перпендикулярной линии.
3. Шаг 3. Определите точку.
4. Шаг 4. Подставьте значения в форму точка-наклон, y−y1=m(x−x1).y−y1=m(x−x1).
5. Шаг 5. Запишите уравнение в форме пересечения наклона.

Пример 3,32

Найдите уравнение прямой, перпендикулярной x=5x=5, содержащей точку (3,−2).(3,−2). Запишите уравнение в форме пересечения наклона.

Решение

Опять же, поскольку мы знаем одну точку, вариант «точка-наклон» кажется более многообещающим, чем вариант «наклон-пересечение». Нам нужен наклон, чтобы использовать эту форму, и мы знаем, что новая линия будет перпендикулярна x=5.x=5. Эта линия вертикальна, поэтому ее перпендикуляр будет горизонтальным. Это говорит нам, что m⊥=0.m⊥=0.

Определите точку.	(3,−2)(3,−2)
Определите наклон перпендикулярной линии.	м⊥=0м⊥=0
Подставьте значения в y−y1=m(x−x1).y−y1=m(x−x1).	y−y1=m(x−x1)y−y1=m(x−x1)
	у-(-2)=0(х-3)у-(-2)=0(х-3)
Упрощение.	у+2=0у+2=0
	у=-2у=-2

Нарисуйте график обеих линий. На вашем графике линии кажутся перпендикулярными?

Попытайся 3,63

Найдите уравнение прямой, перпендикулярной прямой x=4x=4, содержащей точку (4,−5). (4,−5).. Запишите уравнение в виде точки пересечения.

Попытайся 3,64

Найдите уравнение прямой, перпендикулярной прямой x=2x=2, содержащей точку (2,−1).(2,−1). Запишите уравнение в форме пересечения наклона.

В примере 3.32 мы использовали форму точка-наклон, чтобы найти уравнение. Мы могли бы посмотреть на это по-другому.

Мы хотим найти прямую, перпендикулярную x=5x=5, содержащую точку (3,−2).(3,−2). Этот график показывает нам линию x=5x=5 и точку (3,−2).(3,−2).

Мы знаем, что каждая линия, перпендикулярная вертикальной линии, горизонтальна, поэтому мы нарисуем горизонтальную линию через (3,−2).(3,−2).

Линии кажутся перпендикулярными?

Если мы посмотрим на несколько точек на этой горизонтальной линии, мы заметим, что все они имеют y -координаты −2.−2. Итак, уравнение линии, перпендикулярной вертикальной линии x=5x=5, равно y=−2.y=−2.

Пример 3,33

Найдите уравнение прямой, перпендикулярной y=−3y=−3, содержащей точку (−3,5). (−3,5). Запишите уравнение в форме пересечения наклона.

Решение

Линия y=−3y=−3 является горизонтальной линией. Любая линия, перпендикулярная к ней, должна быть вертикальной в виде x=a.x=a. Поскольку перпендикулярная линия вертикальна и проходит через (−3,5),(−3,5), каждая точка на ней имеет x -координата −3.−3. Уравнение перпендикулярной линии: x=−3x=−3

Вы можете зарисовать линии. Они кажутся перпендикулярными?

Попытайся 3,65

Найдите уравнение прямой, перпендикулярной прямой y=1y=1, содержащей точку (−5,1).(−5,1). Запишите уравнение в форме пересечения наклона.

Попытайся 3,66

Найдите уравнение прямой, перпендикулярной прямой y=−5y=−5, содержащей точку (−4,−5).(−4,−5). Запишите уравнение в форме пересечения наклона.

Раздел 3.3 Упражнения

Практика делает совершенным

Найдите уравнение прямой с учетом наклона и y -Intercept

В следующих упражнениях найдите уравнение прямой с заданным наклоном и y -точкой пересечения. Запишите уравнение в форме пересечения наклона.

155.

наклон 3 и
yy-точка (0,5)(0,5)

156.

наклон 8 и
y — точка пересечения (0,−6)(0,−6)

157.

наклон −3−3 и
точка пересечения yy (0,−1)(0,−1)

158.

наклон −1−1 и
точка пересечения yy (0,3)(0,3)

159.

наклон 1515 и
yy-отрезок (0,−5)(0,−5)

160.

наклон −34−34 и
точка пересечения yy (0,−2)(0,−2)

161.

наклон 0 и
yy-intercept (0,−1)(0,−1)

162.

наклон −4−4 и
точка пересечения yy (0,0)(0,0)

В следующих упражнениях найдите уравнение линии, показанной на каждом графике. Запишите уравнение в форме пересечения наклона.

163.

164.

165.

166.

167.

168.

169.

170.

Найти уравнение прямой по наклону и точке

В следующих упражнениях найдите уравнение прямой с заданным наклоном, содержащей заданную точку. Запишите уравнение в форме пересечения наклона.

171.

м=58,м=58, точка (8,3)(8,3)

172.

м=56,м=56, точка (6,7)(6,7)

173.

м=-35,м=-35, точка (10,-5)(10,-5)

174.

м=-34,м=-34, точка (8,-5)(8,-5)

175.

м=-32, м=-32, точка (-4,-3)(-4,-3)

176.

m=-52,m=-52, точка (-8,-2)(-8,-2)

177.

m=-7,m=-7, точка (-1,-3)(-1,-3)

178.

m=−4,m=−4, точка (−2,−3)(−2,−3)

179.

Горизонтальная линия, содержащая (−2,5)(−2,5)

180.

Горизонтальная линия, содержащая (−2,−3)(−2,−3)

181.

Горизонтальная линия, содержащая (−1,−7)(−1,−7)

182.

Горизонтальная линия, содержащая (4,−8)(4,−8)

Найти уравнение прямой по двум точкам

В следующих упражнениях найдите уравнение прямой, содержащей заданные точки. Запишите уравнение в форме пересечения наклона.

183.

(2,6)(2,6) и (5,3)(5,3)

184.

(4,3)(4,3) и (8,1)(8,1)

185.

(−3,−4)(−3,−4) и (5,−2)(5,−2)

186.

(-5,-3)(-5,-3) и (4,-6)(4,-6)

187.

(-1,3)(-1,3) и (-6,-7)(-6,-7)

188.

(−2,8)(−2,8) и (−4,−6)(−4,−6)

189.

(0,4)(0,4) и (2,−3)(2,−3)

190.

(0,−2)(0,−2) и (−5,−3)(−5,−3)

191.

(7,2)(7,2) и (7,−2)(7,−2)

192.

(-2,1)(-2,1) и (-2,-4)(-2,-4)

193.

(3,−4)(3,−4) и (5,−4)(5,−4)

194.

(-6,-3)(-6,-3) и (-1,-3)(-1,-3)

Найти уравнение прямой, параллельной заданной прямой

В следующих упражнениях найдите уравнение прямой, параллельной данной прямой и содержащей заданную точку. Запишите уравнение в форме пересечения наклона.

195.

строка у=4х+2,у=4х+2,
точка (1,2)(1,2)

196.

линия y=−3x−1,y=−3x−1,
точка (2,−3).(2,−3).

197.

строка 2x−y=6,2x−y=6,
точка (3,0).(3,0).

198.

линия 2x+3y=6,2x+3y=6,
точка (0,5).(0,5).

199.

линия x=-4,x=-4,
точка (-3,-5).(-3,-5).

200.

линия x−2=0,x−2=0,
точка (1,−2)(1,−2)

201.

линия y=5,y=5,
точка (2,−2)(2,−2)

202.

линия y+2=0,y+2=0,
точка (3,−3)(3,−3)

Найти уравнение прямой, перпендикулярной заданной прямой

В следующих упражнениях найдите уравнение прямой, перпендикулярной данной прямой и содержащей заданную точку. Запишите уравнение в форме пересечения наклона.

203.

линия y=−2x+3,y=−2x+3,
точка (2,2)(2,2)

204.

линия y=−x+5,y=−x+5,
точка (3,3)(3,3)

205.

линия y=34x−2,y=34x−2,
точка (−3,4)(−3,4)

206.

линия y=23x−4,y=23x−4,
точка (2,−4)(2,−4)

207.

линия 2x−3y=8,2x−3y=8,
точка (4,−1)(4,−1)

208.

строка 4x−3y=5,4x−3y=5,
точка (−3,2)(−3,2)

209.

линия 2x+5y=6,2x+5y=6,
точка (0,0)(0,0)

210.

линия 4x+5y=−3,4x+5y=−3,
точка (0,0)(0,0)

211.

линия x=3,x=3,
точка (3,4)(3,4)

212.

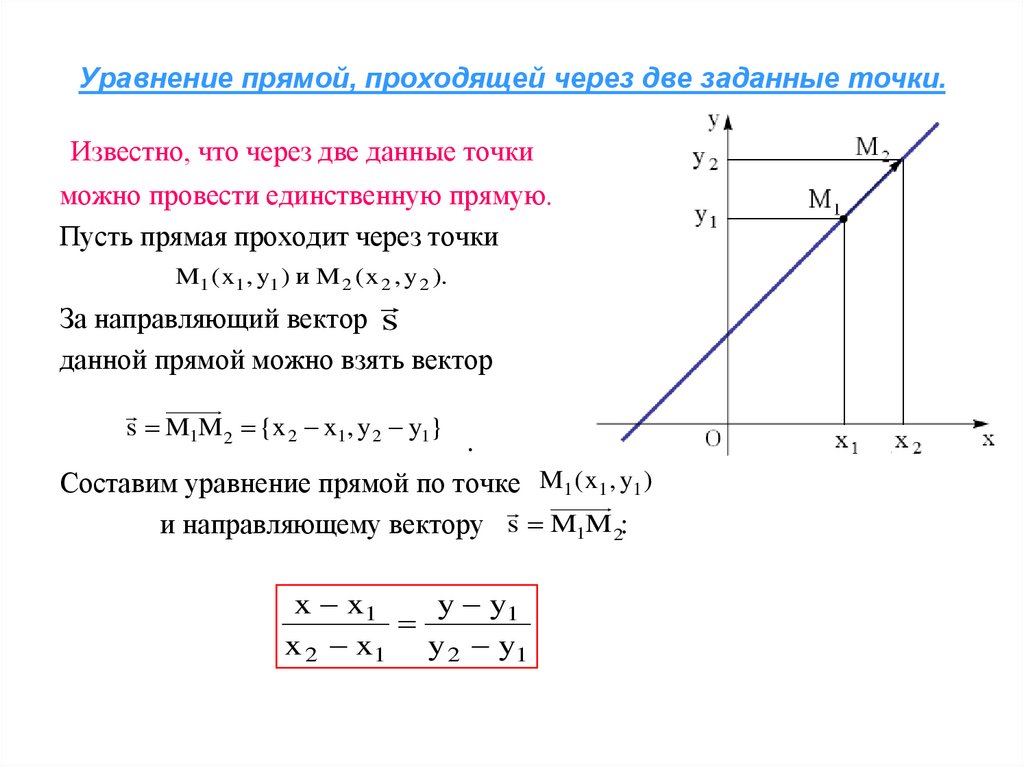
линия x=−5,x=−5,
точка (1,−2)(1,−2)

213.

линия x=7,x=7,
точка (−3,−4)(−3,−4)

214.

линия x=−1,x=−1,
точка (−4,0)(−4,0)

215.

линия y-3=0,y-3=0,
точка (-2,-4)(-2,-4)

216.

линия y-6=0,y-6=0,
точка (-5,-3)(-5,-3)

217.

линия у -ось,
точка (3,4)(3,4)

218.

линия у — ось,
точка (2,1)(2,1)

Смешанная практика

В следующих упражнениях найдите уравнение каждой линии. Запишите уравнение в форме пересечения наклона.

219.

Содержит точки (4,3)(4,3) и (8,1)(8,1)

220.

Содержит точки (−2,0)(−2,0) и (−3,−2)(−3,−2)

221.

m=16,m=16, содержащий точку (6,1)(6,1)

222.

m=56,m=56, содержащий точку (6,7)(6,7)

223.

Параллельно прямой 4x+3y=6,4x+3y=6, содержащей точку (0,−3)(0,−3)

224.

Параллельно прямой 2x+3y=6,2x+3y=6, содержащей точку (0,5)(0,5)

225.

m=−34,m=−34, содержащий точку (8,−5)(8,−5)

226.

m=−35,m=−35, содержащий точку (10,−5)(10,−5)

227.

Перпендикулярно прямой y-1=0,y-1=0, точка (-2,6)(-2,6)

228.

Перпендикулярно линии y -ось, точка (−6,2)(−6,2)

229.

Параллельно линии x=−3,x=−3, содержащей точку (−2,−1)(−2,−1)

230.

Параллельно линии x=−4,x=−4, содержащей точку (−3,−5)(−3,−5)

231.

Содержит точки (−3,−4)(−3,−4) и (2,−5)(2,−5)

232.

Содержит точки (−5,−3)(−5,−3) и (4,−6)(4,−6)

233.

Перпендикулярно линии x−2y=5,x−2y=5, точка (−2,2)(−2,2)

234.

Перпендикулярно линии 4x+3y=1,4x+3y=1, точка (0,0)(0,0)

Письменные упражнения

235.

Почему все горизонтальные линии параллельны?

236.

Объясните своими словами, почему наклоны двух перпендикулярных прямых должны иметь противоположные знаки.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.

No related posts.