Примеры с параметрами и методы их решения
В последние годы на вступительных экзаменах, на итоговом тестировании в форме ЕГЭ предлагаются задачи с параметрами. Эти задачи позволяют диагностировать уровень математического и, главное, логического мышления абитуриентов, способность осуществлять исследовательскую деятельность, а также просто знание основных разделов школьного курса математики.
Взгляд на параметр как на равноправную
переменную находит своё отражение в графических
методах. В самом деле, поскольку параметр “равен
в правах” с переменной, то ему, естественно,
можно “выделить” и свою координатную ось. Таким
образом, возникает координатная плоскость . Отказ
от традиционного выбора букв и для обозначения
осей, определяет один из эффективнейших методов
решения задач с параметрами – “метод
областей”. Наряду с другими методами,
применяемыми при решении задач с параметрами, я
знакомлю своих учеников и с графическими
приёмами, обращая внимание на то, как распознать
“такие” задачи и как выглядит процесс решения
задачи.
Самые общие признаки, которые помогут узнавать задачи, подходящие под рассматриваемый метод:
- в задаче фигурирует лишь один параметр и одна переменная ; они конструируют некоторые аналитические выражения , и т.д.;
- графики уравнений , и т.д. в системе координат строятся несложно.
- Процесс решения задач схематично выглядит так:
- строится графический образ;
- пересекается полученный график прямыми, перпендикулярными параметрической оси;
- “снимается” нужная информация.
- Переходим к решению задач, к которым рекомендации более конкретны:
- получить равенство вида , выражая параметр через переменную;
- на плоскости строить график функции .
Задача 1. “При каких значениях параметра неравенство выполняется при всех ?”
Решение.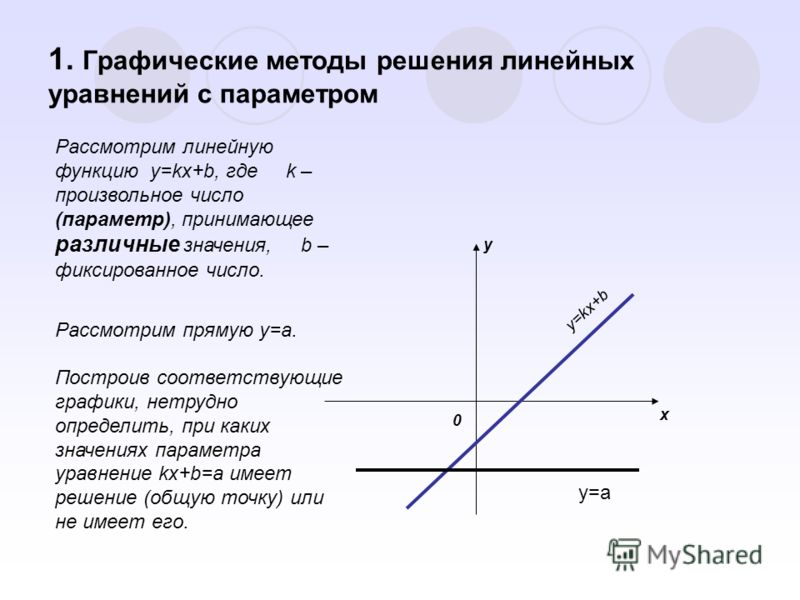 1). Раскроем модули с учётом знака
подмодульного выражения:
1). Раскроем модули с учётом знака
подмодульного выражения:
2). Запишем все системы получившихся неравенств:
а)
б) в)
г)
3). Покажем множество точек, удовлетворяющих каждой системе неравенств (рис.1а).
4). Объединяя все области, показанные на рисунке штриховкой, можно заметить, что неравенству не удовлетворяют точки , лежащие внутри парабол.
На рисунке видно, что при любом значении параметра можно найти область, где лежат точки, координаты которых удовлетворяют исходному неравенству. Неравенство выполняется при всех , если . Ответ: при .
Рассмотренный пример представляет собой “открытую задачу” — можно рассмотреть решение целого класса задач, не изменяя рассмотренное в примере выражение,
Задача. При каких значениях параметра уравнение не
имеет решений? Ответ: при .
При каких значениях параметра уравнение не
имеет решений? Ответ: при .
Задача. При каких значениях параметра уравнение имеет два решения? Запишите оба найденных решения.
Ответ: , тогда , ;
, тогда ;
, тогда ; , тогда , .
Задача. При каких значениях параметра уравнение имеет один корень? Найдите этот корень. Ответ: при при .
Задача. Решите неравенство .
(“Работают” точки, лежащие внутри парабол).
Ответ: , ;
, ; , решений нет;
, ; , .
Задача 2.Найдите все значения параметра а, при каждом из которых система неравенств образует на числовой прямой отрезок длины 1.
Решение. Перепишем исходную систему в таком виде
Все решения этой системы (пары вида )
образуют некоторую область, ограниченную
параболами и (рис 1).
Очевидно, решением системы неравенств будет отрезок длины 1 при и при . Ответ: ; .
Задача 3.Найдите все значения параметра , при которых множество решений неравенства содержит число , а так же содержит два отрезка длиной , не имеющие общих точек.
Решение. По смыслу неравенства ; перепишем неравенство, умножив обе его части на (), получаем неравенство:
, ,
, ,
(1)
Неравенство (1) равносильно совокупности двух систем:
1) 2)
Покажем области, которые соответствуют этим системам (рис. 2).
Очевидно, интервал не может содержать отрезка длины . Значит, два непересекающихся отрезка длины содержатся в интервале Это возможно при , т.е. при . Ответ: .
Задача 4.Найдите все значения параметра , при каждом из
которых множество решений неравенства
содержит отрезок длиной 4 и при этом содержится в
некотором отрезке длиной 7.
Решение. Проведём равносильные преобразования, учитывая, что и .
, ,
, ,
; последнее неравенство равносильно совокупности двух систем:
1) 2)
Покажем области, которые соответствуют этим системам (рис. 3).
1) При множество решений – это интервал длиной, меньшей 4. При множество решений – это объединение двух интервалов .Содержать отрезок длиной 4 может только интервал . Но тогда , и объединение уже не содержится ни в каком отрезке длиной 7. Значит, такие не удовлетворяют условию.
2) множество решений – это интервал . Он содержит отрезок длиной 4, только если его длина больше 4, т.е. при . Он содержится в отрезке длиной 7, только если его длина не больше 7, т. е. при , тогда . Ответ: .
Задача 5. Найдите все значения параметра , при
которых множество решений неравенства
содержит число 4, а также содержит два
непересекающихся отрезка длиной 4 каждый.
Решение. По условия . Домножим обе части неравенства на (). Получим равносильное неравенство, в котором сгруппируем все члены в левой части и преобразуем её в произведение:
, ,
, .
Из последнего неравенства следует:
1) 2)
Покажем области, которые соответствуют этим системам (рис. 4).
а) При получаем интервал , не содержащий числа 4. При получаем интервал , также не содержащий числа 4.
б) При получаем объединение двух интервалов. Непересекающиеся отрезки длиной 4 могут располагаться только в интервале . Это возможно только в том случае, если длина интервала больше 8, т. е. если . При таких выполнено и другое условие: . Ответ: .
Задача 6. Найдите все значения параметра , при которых
множество решений неравенства
содержит какой-нибудь отрезок длиной 2, но не
содержит никакого отрезка длиной 3.
Решение. По смыслу задания , умножим обе части неравенства на , сгруппируем все члены в левой части неравенства и преобразуем её в произведение:
, ,
, . Из последнего неравенства следует:
1) 2)
Покажем область, которая соответствует первой системе (рис. 5).
Очевидно, что условие задачи выполняется, если . Ответ: .
Задача 7. Найдите все значения параметра , при которых множество решений неравенства 1+ содержится в некотором отрезке длиной 1 и при этом содержит какой-нибудь отрезок длиной 0,5.
Решение. 1). Укажем ОДЗ переменной и параметра:
2). Перепишем неравенство в виде
, ,
, ,
(1). Неравенство (1) равносильно совокупности двух систем:
1)
2)
С учётом ОДЗ решения систем выглядят так:
1)
а) б)
Покажем область, соответствующую системе а) (рис. 6).
6).
2)
а) б)
Покажем область, соответствующую системе а) (рис. 7). Ответ: .
Задача 8. Шесть чисел образуют возрастающую арифметическую прогрессию. Первый, второй и четвертый члены этой прогрессии являются решениями неравенства , а остальные
не являются решениями этого неравенства. Найдите множество всех возможных значений первого члена таких прогрессий.
Решение. I. Найдём все решения неравенства
а). ОДЗ: , т.е.
(учли в решении, что функция возрастает на ).
б). На ОДЗ неравенство равносильно неравенству , т.е. , что даёт:
1).
2).
Очевидно, решением неравенства служит множество значений .
II. Проиллюстрируем вторую часть задачи о
членах возрастающей арифметической прогрессии
рисунком (рис.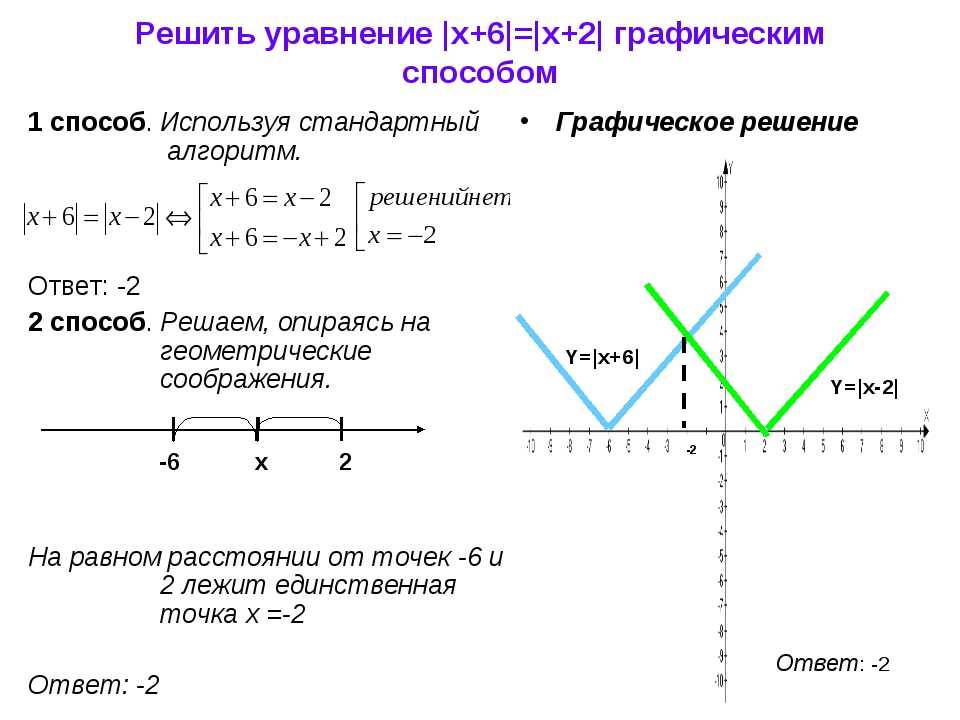 8, где -
первый член, — второй и т.д.). Заметим, что:
8, где -
первый член, — второй и т.д.). Заметим, что:
или имеем систему линейных неравенств:
решим её графическим способом. Строим прямые и , а также прямые
, , , , , , .
Все решения этой системы образуют область, показанную штриховкой на рисунке (рис.9).
Ответ: возможные значения первого члена .
Задача 9. Найдите все значения при которых в области определения функции столько же целых чисел, сколько их в области определения функции
Решение. I. Покажем, что в области определения второй функции имеется ровно три целых числа. Целые значения из области определения функции удовлетворяют условию , тогда это числа: -1; 0; 1.
Функция чётная;
Заметим, если , то .
II. Функция определена, если
Найдём корни квадратного трёхчлена
тогда .
Перепишем систему неравенств в виде
(*)
Последняя система равносильна совокупности двух систем:
а) б)
На плоскости покажем графическое решение системы (*)
(см. рис.10).
рис.10).
Вероятно, что 3 целых числа в области определения функции следует искать среди чисел 0, 1, 2, 3 и, может быть, числа 4. Проведём дополнительные прямые , , , , и посмотрим, при каких выполняется условие задачи.
Очевидно, что в области определения функции ровно 3 целых числа при всех
Ответ:
Разобранные задачи достаточно убедительно демонстрируют эффективность предложенного метода. Однако, к сожалению, сфера применения этого метода ограничена трудностями, с которыми можно столкнуться при построении графического образа.
Задачи для самостоятельного решения
Задача 1. Найдите все значения параметра а, при каждом из которых система неравенств образует на числовой прямой отрезок длины 1.
Ответ: ; .
Задача 2. Найдите все значения параметра а,
при каждом из которых система неравенств имеет
единственное решение.
Ответ:
Задача 3. Найдите все значения параметра , при которых в множестве решений неравенства можно расположить два отрезка длиной 1 и длиной 4, которые не имеют общих точек.
Ответ: .
Задача 4. Найдите все значения параметра , при которых множество решений неравенства содержится в некотором отрезке длиной 4 и при этом содержит какой-нибудь отрезок длиной 2.
Ответ: .
Задача 5. Семь чисел образуют убывающую арифметическую прогрессию с разностью . Первый, второй и шестой члены этой прогрессии являются решениями неравенства , а остальные не являются решениями этого неравенства. Найдите множество всех возможных значений разности этой прогрессии.
Ответ: .
Уравнения с параметром — алгоритмы и примеры решения » Kupuk.net
В алгебре и других дисциплинах с физико-математическим уклоном существует вид уравнений с параметром, решение которых осуществляется по определенной методике. Чтобы к ней перейти, необходимы некоторые базовые знания нахождения корней тождеств с неизвестными. Математики рекомендуют изучить теоретические основы, а после этого переходить к их практическому применению во время решения задач.
Чтобы к ней перейти, необходимы некоторые базовые знания нахождения корней тождеств с неизвестными. Математики рекомендуют изучить теоретические основы, а после этого переходить к их практическому применению во время решения задач.
Общие сведения
Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.
Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.
Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.
Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.
Классификация уравнений
Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».
Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.
Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.
Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.
К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.
Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа.
После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.
Алгебраический вид
Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.
На основании последней характеристики они делятся на 5 типов:
Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.
Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.
Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.
Линейные и квадратичные
Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:
Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.
(½)]/(2А).
Записать результат. Выполнить проверку по отсеиванию ложных корней. Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.
Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.
Неполные решаются методом разложения на множители. Например, «v2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.
Кубичеcкие и биквадрaтные
Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной.
4−324=0 (истинно).
Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.
Пример решения
На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v4−32−4p-(v2 +4)+(v-2)(v+2)-v4+16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:
Записать равенство с неизвестным и параметром: 2v4−32−4p-(v2 +4)+(v-2)(v+2)-v4 +16=-4. Выполнить математические преобразования: 2v4−32−4p-v2+4+v2−4-v4+16+4=v4−16+4p+4=0. 4−16+4=16−16=0 (истина).
Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.
Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.
Уравнения с параметром — алгоритмы и примеры решения
В алгебре и других дисциплинах с физико-математическим уклоном существует вид уравнений с параметром, решение которых осуществляется по определенной методике. Чтобы к ней перейти, необходимы некоторые базовые знания нахождения корней тождеств с неизвестными. Математики рекомендуют изучить теоретические основы, а после этого переходить к их практическому применению во время решения задач.
Содержание
- Общие сведения
- Классификация уравнений
- Алгебраический вид
- Линейные и квадратичные
- Кубичеcкие и биквадрaтные
- Пример решения
Общие сведения
Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.
Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.
Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.
Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.
Классификация уравнений
Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».
Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма.
Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.
Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.
К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.
Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа.
После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.
Алгебраический вид
Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.
На основании последней характеристики они делятся на 5 типов:
Линейные. Квадратные (квадратичные). Кубические. Биквадратные. Высших порядков. Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.
Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями.
Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.
Линейные и квадратичные
Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:
Записывается искомое выражение. При необходимости раскрываются скобки и приводятся подобные элементы. Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо. Правая часть сокращается на коэффициент при неизвестной. Записывается результат. Выполняется проверка посредством подстановки корня в исходное выражение. Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.
(½)]/(2А).
Записать результат. Выполнить проверку по отсеиванию ложных корней. Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.
Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.
Неполные решаются методом разложения на множители. Например, «v2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.
Кубичеcкие и биквадрaтные
Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной.
4−324=0 (истинно).
Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.
Пример решения
На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v4−32−4p-(v2 +4)+(v-2)(v+2)-v4+16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:
Записать равенство с неизвестным и параметром: 2v4−32−4p-(v2 +4)+(v-2)(v+2)-v4 +16=-4. Выполнить математические преобразования: 2v4−32−4p-v2+4+v2−4-v4+16+4=v4−16+4p+4=0. 4−16+4=16−16=0 (истина).
Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.
Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.
Предыдущая
АлгебраЛинейные уравнения — алгоритмы и примеры решений с объяснением для 6 класса
Следующая
АлгебраАлгебра как наука — история появления, классификация раздела и понятия
Как найти значение параметра. Примеры с параметрами и методы их решения
Уравнение вида f (x ; a ) = 0 называется уравнением с переменной х и параметром а .

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х , удовлетворяющие этому уравнению.
Пример 1. ах = 0
Пример 2. ах = а
Пример 3.
х + 2 = ах
х – ах = -2
х(1 – а) = -2Если 1 – а = 0, т.е. а = 1, то х 0 = -2 корней нет
Если 1 – а 0, т.е. а 1, то х =
Пример 4.
(а 2 – 1) х = 2а 2 + а – 3
(а – 1)(а + 1)х = 2(а – 1)(а – 1,5)
(а – 1)(а + 1)х = (1а – 3)(а – 1)Если а = 1, то 0х = 0
х – любое действительное числоЕсли а = -1, то 0х = -2
Корней нетЕсли а 1, а -1, то х = (единственное решение).
Это значит, что каждому допустимому значению а соответствует единственное значение х .
Например:
если а = 5, то х = = ;
если а = 0, то х = 3 и т. д.
Дидактический материал
1. ах = х + 3
2. 4 + ах = 3х – 1
3. а = +
при а = 1 корней нет.
при а = 3 корней нет.
при а = 1 х – любое действительное число, кроме х = 1
при а = -1, а = 0 решений нет.
при а = 0, а = 2 решений нет.
при а = -3, а = 0, 5, а = -2 решений нет
при а = —с , с = 0 решений нет.
Квадратные уравнения с параметром
Пример 1. Решить уравнение
(а – 1)х 2 = 2(2а + 1)х + 4а + 3 = 0
При а = 1 6х + 7 = 0
В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.
Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16
20а + 16 = 0
20а = -16
Если а Д
Если а > -4/5 и а 1, то Д > 0,
х =
Если а = 4/5, то Д = 0,
Пример 2. При каких значениях параметра а уравнение
х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?
Д = 4(а + 1) 2 – 4(9а – 5) = 4а 2 – 28а + 24 = 4(а – 1)(а – 6)
4(а – 1)(а – 6) > 0
по т.
Виета: х 1 + х 2 = -2(а + 1)
х 1 х 2 = 9а – 5По условию х 1 х 2 а + 1) а – 5 > 0
В итоге 4(а – 1)(а – 6) > 0
— 2(а + 1) 9а – 5 > 0а 6
а > — 1
а > 5/9(Рис. 1 )
a a > 6
Пример 3. Найдите значения а , при которых данное уравнение имеет решение.
х 2 – 2(а – 1)х + 2а + 1 = 0
Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а
4а 2 – 16 0
4а (а – 4) 0
а(а – 4)) 0
а(а – 4) = 0
а = 0 или а – 4 = 0
а = 4(Рис.
2 )
Ответ: а 0 и а 4
Дидактический материал
1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?
2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?
3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2) = 0 имеет более двух корней?
4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?
5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?
1. При а = — 1/7, а = 0, а = 1
2. При а = 0
3. При а = 2
4.
При а = 10
5. При а = — 2
Показательные уравнения с параметром
Пример 1 .Найти все значения а , при которых уравнение
9 х – (а + 2)*3 х-1/х +2а *3 -2/х = 0 (1) имеет ровно два корня.
Решение. Умножив обе части уравнения (1) на 3 2/х, получим равносильное уравнение
3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)
Пусть 3 х+1/х = у , тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или
(у – 2)(у – а ) = 0, откуда у 1 =2, у 2 = а .
Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log 3 2 , или х 2 – х log 3 2 + 1 = 0.
Это уравнение не имеет действительных корней, так как его Д = log 2 3 2 – 4
Если у = а , т.е. 3 х+1/х = а то х + 1/х = log 3 а , или х 2 – х log 3 а + 1 = 0.
(3)
Уравнение (3) имеет ровно два корня тогда и только тогда, когда
Д = log 2 3 2 – 4 > 0, или |log 3 а| > 2.
Если log 3 а > 2, то а > 9, а если log 3 а а
Ответ: 0 а а > 9.
Пример 2 . При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?
Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х 1 = -3, х 2 = а = >
а – положительное число.
Ответ: при а > 0
Дидактический материал
1. Найти все значения а, при которых уравнение
25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.
2. При каких значениях а уравнение
2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?
3.
При каких значениях параметра а уравнение
4 х — (5а -3)2 х +4а 2 – 3а = 0 имеет единственное решение?
Логарифмические уравнения с параметром
Пример 1. Найти все значения а , при которых уравнение
log 4x (1 + ах ) = 1/2 (1)
имеет единственное решение.
Решение. Уравнение (1) равносильно уравнению
1 + ах = 2х при х > 0, х 1/4 (3)
х = у
ау 2 –у + 1 = 0 (4)
Не выполняется (2) условие из (3).
Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.Чтобы решить неравенство (3), построим графики функций Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение курса алгебры и математического анализа. – М.: Просвещение, 1990
Крамор В. С . Повторяем и систематизируем школьный курс алгебры и начал анализа. – М.: Просвещение, 1990.
Галицкий М.Л., Гольдман А.М., Звавич Л.И . Сборник задач по алгебре. – М.: Просвещение, 1994. Звавич Л.И., Шляпочник Л.Я. Алгебра и начала анализа. Решение экзаменационных задач. – М.: Дрофа, 1998. Макарычев Ю.Н. и др. Дидактические материалы по алгебре 7, 8, 9 кл. – М.: Просвещение, 2001. Саакян С.И., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа для 10–11-х классов. – М.: Просвещение, 1990. Журналы “Математика в школе”. Л.С. Лаппо и др. ЕГЭ. Учебное пособие. – М.: Экзамен, 2001–2008. К задачам с параметром можно отнести, например, поиск решения линейных и квадратных уравнений в общем виде, исследование уравнения на количество имеющихся корней в зависимости от значения параметра.
Не приводя подробных определений, в качестве примеров рассмотрим следующие уравнения:
у = kx, где x, y – переменные, k – параметр;
у = kx + b, где x, y – переменные, k и b – параметр;
аx 2 + bх + с = 0, где x – переменные, а, b и с – параметр.
Решить уравнение (неравенство, систему) с параметром это значит, как правило, решить бесконечное множество уравнений (неравенств, систем).
Задачи с параметром можно условно разделить на два типа:
а) в условии сказано: решить уравнение (неравенство, систему) – это значит, для всех значений параметра найти все решения. Если хотя бы один случай остался неисследованным, признать такое решение удовлетворительным нельзя.
б) требуется указать возможные значения параметра, при которых уравнение (неравенство, система) обладает определенными свойствами. Например, имеет одно решение, не имеет решений, имеет решения, принадлежащие промежутку и т. д. В таких заданиях необходимо четко указать, при каком значении параметра требуемое условие выполняется.
Параметр, являясь неизвестным фиксированным числом, имеет как бы особую двойственность. В первую очередь, необходимо учитывать, что предполагаемая известность говорит о том, что параметр необходимо воспринимать как число.
Во вторую очередь, свобода обращения с параметром ограничивается его неизвестностью. Так, например, операции деления на выражение, в котором присутствует параметр или извлечения корня четной степени из подобного выражения требуют предварительных исследований. Поэтому необходима аккуратность в обращении с параметром.
Например, чтобы сравнить два числа -6а и 3а, необходимо рассмотреть три случая:
1) -6a будет больше 3a, если а отрицательное число;
2) -6а = 3а в случае, когда а = 0;
3) -6а будет меньше, чем 3а, если а – число положительное 0.
Решение и будет являться ответом.
Пусть дано уравнение kx = b. Это уравнение – краткая запись бесконечного множества уравнений с одной переменной.
При решении таких уравнений могут быть случаи:
1. Пусть k – любое действительное число не равное нулю и b – любое число изR, тогда x = b/k.
2. Пусть k = 0 и b ≠ 0, исходное уравнение примет вид 0 · x = b. Очевидно, что у такого уравнения решений нет.
3.
Пусть k и b числа, равные нулю, тогда имеем равенство 0 · x = 0. Его решение – любое действительное число.
Алгоритм решения такого типа уравнений:
1. Определить «контрольные» значения параметра.
2. Решить исходное уравнение относительно х при тех значениях параметра, которые были определены в первом пункте.
3. Решить исходное уравнение относительно х при значениях параметра, отличающихся от выбранных в первом пункте.
4. Записать ответ можно в следующем виде:
1) при … (значения параметра), уравнение имеет корни …;
2) при … (значения параметра), в уравнении корней нет.
Пример 1.
Решить уравнение с параметром |6 – x| = a.
Решение.
Легко видеть, что здесь a ≥ 0.
По правилу модуля 6 – x = ±a, выразим х:
Ответ: х = 6 ± a, где a ≥ 0.
Пример 2.
Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.
Решение.
Раскроем скобки: aх – а + 2х – 2 = 0
Запишем уравнение в стандартном виде: х(а + 2) = а + 2.
В случае, если выражение а + 2 не нуль, т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.
В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое действительное число.
Ответ: х = 1 при а ≠ -2 и х € R при а = -2.
Пример 3.
Решить уравнение x/a + 1 = а + х относительно переменной х.
Решение.
Если а = 0, то преобразуем уравнение к виду а + х = а 2 + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.
Если а ≠ 1, то последнее уравнение примет вид х = -а.
Данное решение можно проиллюстрировать на координатной прямой (рис. 1)
Ответ: нет решений при а = 0; х – любое число при а = 1; х = -а при а ≠ 0 и а ≠ 1.
Графический метод
Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.
Пример 4.
Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?
Решение.
Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2) .
На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.
Ответ: корней у уравнения не будет, если а 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0
Пример 5.
При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?
Решение.
Изобразим графики функций y = 2|x| + |x – 1| и y = a. Для y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:
{-3x + 1, при x
y = {x + 1, при 0 ≤ x ≤ 1,
{3x – 1, при x > 1.
На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.
Ответ: а = 1.
Пример 6.
2 — 2y — 2a + 1 =0$. Дискриминант каждого из них равен $D = 16a-4$.
Заметим, что не может получиться так, что пара корней первого из квадратных уравнений совпадает с парой корней второго квадратного уравнения, так как сумма корней первого равна $-1$, а второго 1.
Значит, нужно, чтобы у каждого из этих уравнений было по одному корню, тогда у исходной системы их будет два решения. То есть $D = 16a — 4 = 0$.
Ответ. $a=\dfrac{1}{4}$
Найдите все значения параметра $a$, при каждом из которых уравнение $4x-|3x-|x+a||=9|x-3|$ имеет два корня.
Решение
Перепишем уравнение в виде:
$ 9|x-3|-4x+|3x-|x+a|| = 0. $
Рассмотрим функцию $f(x) = 9|x-3|-4x+|3x-|x+a||$.
При $x\geqslant 3$ первый модуль раскрывается со знаком плюс, и функция принимает вид: $f(x) = 5x-27+|3x-|x+a||$. Очевидно, что при любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом $k\geqslant 5-3-1=1>0$, то есть эта функция на данном промежутке неограниченно возрастает.
{-1}}\right\}$
1. Задача.
При каких значениях параметра a уравнение (a — 1)x 2 + 2x + a — 1 = 0 имеет ровно один корень?1. Решение.
При a = 1 уравнение имеет вид 2x = 0 и, очевидно, имеет единственный корень x = 0. Если a № 1, то данное уравнение является квадратным и имеет единственный корень при тех значениях параметра, при которых дискриминант квадратного трехчлена равен нулю. Приравнивая дискриминант к нулю, получаем уравнение относительно параметра a 4a 2 — 8a = 0, откуда a = 0 или a = 2.1. Ответ: уравнение имеет единственный корень при a О {0; 1; 2}.
2. Задача.
Найти все значения параметра a , при которых имеет два различных корня уравнение x 2 +4ax +8a +3 = 0.
2. Решение.
Уравнение x 2 +4ax +8a +3 = 0 имеет два различных корня тогда и только тогда, когда D = 16a 2 -4(8a +3) > 0.Получаем (после сокращения на общий множитель 4) 4a 2 -8a -3 > 0, откуда
2. Ответ:
a О (-Ґ ; 1 – Ц 7 2 ) И (1 + Ц 7 2 ; Ґ ). 3. Задача.
Известно, что
f 2 (x ) = 6x —x 2 -6.
а) Постройте график функции f 1 (x ) при a = 1.
б) При каком значении a графики функций f 1 (x ) и f 2 (x ) имеют единственную общую точку?3. Решение.
3.а. Преобразуем f 1 (x ) следующим образом
График этой функции при a = 1 изображен на рисунке справа.
3.б. Сразу отметим, что графики функций y = kx +b и y = ax 2 +bx +c (a № 0) пересекаются в единственной точке тогда и только тогда, когда квадратное уравнение kx +b = ax 2 +bx +c имеет единственный корень.Используя представление f 1 из 3.а , приравняем дискриминант уравнения a = 6x —x 2 -6 к нулю. Из уравнения 36-24-4a = 0 получаем a = 3. Проделав то же самое с уравнением 2x —a = 6x —x 2 -6 найдем a = 2. Нетрудно убедиться, что эти значения параметра удовлетворяют условиям задачи. Ответ: a = 2 или a = 3.
4. Задача.
Найти все значения a , при которых множество решений неравенства x 2 -2ax -3a і 0 содержит отрезок .4. Решение.
Первая координата вершины параболы f (x ) = x 2 -2ax -3a равна x 0 = a . Из свойств квадратичной функции условие f (x ) і 0 на отрезке равносильно совокупности трех систем
имеет ровно два решения?5. Решение.
Перепишем это уравнение в виде x 2 + (2a -2)x — 3a +7 = 0. Это квадратное уравнение, оно имеет ровно два решения, если его дискриминант строго больше нуля.Вычисляя дискриминант, получаем, что условием наличия ровно двух корней является выполнение неравенства a 2 +a -6 > 0. Решая неравенство, находим a a > 2. Первое из неравенств, очевидно, решений в натуральных числах не имеет, а наименьшим натуральным решением второго является число 3.
5. Ответ: 3.
6. Задача (10 кл.)
Найти все значения a , при которых график функции или, после очевидных преобразований, a -2 = | 2-a | . Последнее уравнение равносильно неравенству a і 2.6. Ответ: a О }
Квадратные уравнения с параметром: определение, пример решения
Понятие уравнения с параметром и его решения
Часто на практике создаётся такая математическая модель, в которой приходится решать не одно, а целое «семейство» похожих уравнений.
Рассмотрим несложный пример.
Пусть нам дан прямоугольный участок площадью a. С точки зрения практической, мы хотим обнести участок забором, т.
2 = 0, $$
один корень $x_0 = -2$
$$ D(a) \gt 0 при -3 \lt a \lt 1 $$
Уравнение имеет два корня:
$$ x_{1,2} = \frac{a-1 \pm \sqrt{-3(a-1)(a+3)}}{2} $$
$$ D(a) \lt 0 при a \lt -3 \cap a \gt 1 $$
Решений нет.
Ответ:
При a = -3 один корень $x_0 = -2$
При a = 1 один корень $x_0 = 0$
При $-3 \lt a \lt 1$ два корня $x_{1,2} = \frac{a-1 \pm \sqrt{-3(a-1)(a+3)}}{2}$
При других a решений нет.
Решение задач с параметром методом исследовательского анализа
На этой странице вы узнаете
- Категоричность или лояльность: чем отличается система от совокупности?
- Как проходит борьба за первенство между переменными?
- Как выглядят неравенства на графиках функций?
Как бы нам ни хотелось обратного, но научиться решать задачи с параметром, прочитав краткую инструкцию и выписав несколько формул, не получится. Нам обязательно потребуется аналитическое мышление, то есть способность разбивать информацию на небольшие части, исследовать и делать выводы.
Узнаем об этом в статье.
Системы уравнений с параметром
Что мы представляем, когда говорим про аналитику? Возможно, серьезных мужчин и женщин, которые много думают, сравнивают данные и делают на их основе сложные прогнозы. Они в строгих костюмах и очках, с серьезным сосредоточенным лицом.
Я предлагаю погрузиться в аналитику в параметрах. По желанию надеваем серьезный костюм и очки, и вперед.
Немного организационных вопросов перед нашим путешествием. Что подразумевает под собой аналитический способ решения параметров? В первую очередь, это использование алгебраических преобразований и рассуждений без привлечения графиков. Про «Графический способ решения параметров» можно прочесть в отдельной статье.
Как можно преобразовать системы уравнений? Рассмотрим пример.
Решим первое уравнение системы, получаем, что x=2 или
Что мы можем сказать про совокупность и про систему? Совокупность, которая обозначается квадратной скобочкой, выполняется в случае, если выполняется хотя бы одно, любое из ее уравнений.
Чтобы выполнялась система, необходимо, чтобы выполнялись все условия, которые в нее включены.
Категоричность или лояльность: чем отличается система от совокупности? Представим, что система и совокупность — это две дамы.
Система будет дамой категоричной. Ни одно из ее слов или условий не должны быть пропущены, иначе она обидится и не будет с нами сотрудничать.
А вот совокупность — дама лояльная. Она может простить, если не все ее условия выполнены. Для нее главное — понять, что мы ее слушали. А как это сделать? Выполнить хотя бы одно из поставленных ей условий.
Назовем уравнение y = 3 Кристиной. Кристина очень любит вязаных жабок (x = 2) и плюшевых ленивцев (x = — 2). Предположим, что Кристина пошла в магазин, чтобы купить новую игрушку. Скорее всего, она купит именно те игрушки, которые ей нравятся, поэтому система
будет обозначать, что Кристина купила жабку, которую очень любит.
А вот система
означает, что Кристина купила ленивца, которого также очень любит.

Разумеется, она может купить и жабку, и ленивца. Но что, если в магазине не будет одной из этих игрушек или у Кристины не хватит денег? Она купит только одну из них. А как показать это на языке математики? Совокупностью из двух систем:
Эта совокупность будет выполняться, даже если Кристина купит только жабку или только ленивца.
Так можно преобразовать любую систему или совокупность. Немного усложним в систему из двух совокупностей:
Переведем с языка математики. Нам было нужно, чтобы одновременно выполнялось А или В и С или D, то есть хотя бы по одному условию из каждой совокупности. Нам была необходима ситуация (А или В) и (С или D).
Следовательно, если выполняется условие А, то обязательно должно выполняться и условие С или D. Образуются две системы: “А и С” или “A и D”. Если выполняется условие В, то обязательно должно выполняться условие C или D, получаются две системы: “В и С” или “В и D”.
Для выполнения самой первой системы нужно выполнение хотя бы одной из получившихся четырех систем.
2 — 36a = a(41a — 36)
D > 0 => a(41a - 36) > 0Решаем неравенство методом интервалов и получаем, что a
a\in(-\infty;0)\cup(\frac{36}{41};+\infty)Шаг 9. В этот момент нам, как аналитикам, необходимо задуматься: а как объединить эти решения? Брать все получившиеся значения а или только те, которые удовлетворяют каждому из интервалов?
Представим, что нам нужно организовать праздник, на который придут два друга. Мы точно знаем, что один из них пьет только апельсиновый сок, а второй только апельсиновый или яблочный соки. Какой сок мы купим, чтобы все были довольны? Апельсиновый.
Точно также и здесь: чтобы обе системы были “довольны” и имели по два решения, нужно, чтобы все значения параметра а удовлетворяли условиям каждой из систем. Поэтому нам необходимо найти пересечение этих решений.
Шаг 10. Заметим, что
\frac{6-\sqrt{11}}{25}>\frac{6-\sqrt{36}}{25}Cледовательно,
\frac{6-\sqrt{11}}{25}>0\frac{36}{41}>\frac{6+\sqrt{11}}{25}Получаем, что
a\in(-\infty;0)\cup(\frac{36}{41};+\infty)Шаг 11.
Не забудем, что
a≠\frac{9}{8}Эту точку также нужно выколоть из ответа.
Получаем:
a\in(-\infty;0)\cup(\frac{36}{41};\frac{9}{8})\cup(\frac{9}{8};+\infty)Ответ:
a\in(-\infty;0)\cup(\frac{36}{41};\frac{9}{8})\cup(\frac{9}{8};+\infty)Выдохнем и вытрем испарину со лба: параметр решен. Если исключить достаточно трудоемкие вычисления, то остается только немного порассуждать.
Параметр как равноправная переменная
В рассмотренных ранее случаях параметр был темной лошадкой: он почти постоянно был на фоне, появлялся только под конец, чтобы внести свой вклад и показать свои способности, то есть значения. Но что, если вывести параметр на первый план?
Рассматривая функции, мы привыкли, что у — значение функции, которое зависит от переменной х. Однако в некоторых задачах с параметром от переменной х может зависеть и сам параметр.

В этом случае в борьбе между “у” и “а” выигрывает параметр и занимает место у. То есть параметр будет вести себя точно так же, как обычная функция, а изменение значения х будет менять и значение параметра.
Разумеется, можно построить и график такой функции, просто ось ординат будет подписана как “а”, а не “у”.
А может ли быть наоборот? Да. Параметрическую плоскость хОа можно использовать в двух случаях:
- параметр а — зависимая переменная, х — независимая;
- х — зависимая переменная, параметр а — независимая.
Как определить, какой из случаев использовать в конкретном примере? Нужно посмотреть, каким способом удобнее выразить одну переменную через другую. Например, в уравнении x2 + 5x — a = 0 намного удобнее выразить значение параметра a = x2 + 5x, чем пытаться вывести значение х.
В этом случае мы получим параболу.
Как проходит борьба за первенство между переменными? Между переменными в уравнениях всегда идет “борьба”: кто будет зависимой переменной, а кто независимой. Поскольку мы смотрим, с кем будет удобнее работать в качестве зависимой переменной, то сами выбираем победителя схватки.
Когда можно прибегнуть к такому методу решения параметров? Обычно его используют, если в уравнении, неравенстве или их системах есть только две переменные, одна из которых является параметром.
Пример 2. Найдите все значения параметра а, при которых система имеет хотя бы одно решение на промежутке [-3;1].
Решение. Если посмотреть на второе неравенство системы, то заметно, что удобнее выразить параметр через переменную х. Поэтому при решении параметр будет зависимой переменной, а х — независимой.

Шаг 1. Разберем первое неравенство системы и раскроем модули четырьмя способами. Подробнее про модули можно узнать в статье «Модуль». Также в дальнейшем будем использовать «Графический способ решения параметров».
x\geqslant0;a\geqslant0 => x+a\leqslant7=>a\leqslant7-xРассмотрим, как все условия будут выглядеть на графике.
x\geqslant0— плоскость, которая включает все значения х, больше 0.
a\geqslant0включают все точки, которые лежат выше линии а = 0.
А неравенство
a\leqslant7-xвключает все, что лежит ниже прямой 7 — x.
То есть каждый раз мы как бы разрезаем плоскость по одной из линий и отбрасываем все, что не удовлетворяет условию.
Как выглядят неравенства на графиках функций? В отличие от графиков обычных уравнений, неравенства задают не линию, а часть плоскости. То есть его решению будут удовлетворять все точки, которые попадут в нужную часть плоскости.

Неравенства очень жадные: они забирают себе не только точки, которые принадлежат определенной линии, но и все точки, которые лежат выше или ниже.
Наложим все три условия друг на друга и найдем место их пересечения.
Треугольник, в котором они пересекаются, и будет задаваться условием
x\geqslant0;a\geqslant0 => x+a\leqslant7=>a\leqslant7-xМы как бы трижды отрезали все ненужное, и в результате из всей плоскости у нас остался лишь маленький треугольник.
Аналогичным способом получаем еще три треугольника.
x<0;a\geqslant0 => -x+a\leqslant7=>a\leqslant7+xx<0;a<0 => -x-a\leqslant7=>a\geq-7-xx\geq0;a<0 => x-a\leqslant7=>a\geq-7+xОбъединив все графики, получим квадрат, ограниченный прямыми
a = x - 7, a = x + 7, a = - x - 7, a = - x + 7Шаг 2. Рассмотрим второе неравенство системы и преобразуем его.
x^2 + 4x < 8a + 368a > x^24x - 36a>\frac{1}{8}(x^2+4x-36)Это часть плоскости, ограниченная параболой
\frac{1}{8}(x^2+4x-36)Построим ее, вершина параболы будет лежать в точках:
x_{в}=-\frac{4}{2}=-2a_{в}=\frac{1}{8}((-2)^2+4(-2)-36)=\frac{1}{8}(4-8-36)=-5Поскольку знак неравенства строгий, то и сама парабола будет обозначаться пунктирной линией.
2+12x+20=0
D=144-4*1*20=144-80=64x_{1}=\frac{-12+8}{2}=-2x_{2}=\frac{-12-8}{2}=-20Поскольку точка А лежит в промежутке [-3;1], то x2 не подходит. Прямая и парабола пересекаются в точке x = — 2.
Найдем, чему равно значение параметра в точке А.
a=-(-2)-7=2-7=-5Шаг 6. Точка В — это вершина квадрата. А значит, точка В имеет координаты (0;7).
Шаг 7. Мы нашли значение параметра
-5< a\leq7Это и будет ответ.
Ответ:
-5< a\leq7Мы можем расслабиться, выйти из образа аналитика, снять очки и отдохнуть. Главное, мы можем гордиться собой, ведь мы разобрали два новых принципа решения параметров.
Фактчек
- Аналитический способ решения параметров — использование алгебраических преобразований и рассуждений без привлечения графических интерпретаций.
- Для решения параметров аналитическим способом важно уметь преобразовывать уравнения, неравенства и их системы.

- При решении параметров аналитикой важно уметь анализировать функции, их поведение и свойства. Это позволит прийти к правильным выводам при решении и правильно найти значения параметра.
- Некоторые примеры с параметров выгоднее решать в плоскости хОа. В этой плоскости параметр будет либо зависимой, либо независимой переменной.
Проверь себя
Задание 1.
В каких случаях у совокупности есть решения?
- Если выполняется хотя бы одно из ее условий.
- Если выполняются все условия.
- В любом случае, даже если ни одно из условий не будет выполнено.
- Нет верного ответа.
Задание 2.
В каких случаях у системы есть решения?
- Если выполняется хотя бы одно из ее условий.
- Если выполняются все условия.
- В любом случае, даже если ни одно из условий не будет выполнено.
- Нет верного ответа.

Задание 3.
Дана система из совокупности и уравнения. Как ее можно преобразовать?
- Все элементы можно записать отдельно.
- Все элементы можно записать только в систему.
- Можно получить совокупность двух систем.
- Можно получить систему из двух совокупностей.
Задание 4.
Может ли параметр быть независимой переменной в функции?
- Не может.
- Может.
- Параметр не может быть переменной в функции, это просто число.
- Нет верных ответов.
Задание 5.
Какая часть плоскости задается неравенством x>0
- Все, что лежит выше оси х, включая саму ось.
- Все, что лежит выше оси х, исключая саму ось.
- Все, что лежит правее оси х, включая саму ось.
- Все, что лежит правее оси х, исключая саму ось.
Ответы: 1. — 1 2. — 2 3. — 3 4. — 2 5.
— 4
Решение уравнений с параметрами
Творческое образование
Том 5 №11(2014), Статья ID:47178,6 страницы DOI: 10.4236/ce.2014.511110Решение уравнений с параметрами
Бат-Шева Илани 1 , Дина Хасидов 2
1 Колледж Бейт-Берл, Кфар-Саба, Израиль
2 Колледж Западной Галилеи, Акко, 770026, Израиль @netvision.net.il
Авторские права © 2014 принадлежат авторам и Scientific Research Publishing Inc.
Эта работа находится под лицензией Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Поступила в редакцию 23 апреля 2014 г.; пересмотрено 16 мая 2014 г.; принято 6 июня 2014 г.
АННОТАЦИЯ
В этом исследовании изучается, как учащиеся старших классов и студенты-учителя решают уравнения, представленные в различных формах. Некоторые представления нестандартны, например, приходится выражать «а» (обычно воспринимается как параметр) через «х» (обычно воспринимается как переменная). Мы исследуем, как испытуемые решают эти уравнения, а также различия между учениками и студентами-учителями. Наши результаты показывают, что уравнения, содержащие параметры, решить труднее, чем уравнения без параметров. Трудности связаны с буквами, которые должны быть выражены, и с расположением уравнения. Результаты данного исследования могут расширить знания учителей об уравнениях с параметрами и о конкретных трудностях, с которыми сталкиваются студенты в процессе решения.
Ключевые слова: Уравнения, Параметры, Учащиеся старших классов, Студенты-преподаватели, Математическое образование, Математические знания, Познание и математика
1.
Теоретическая основа
слабые места» (Седивый, 1976). Седиви также утверждает, что ученики сталкиваются с большими трудностями с уравнениями с параметрами, чем с уравнениями с числовыми коэффициентами. Алгебраические уравнения, содержащие параметры, представляют более широкие классы уравнений и более общие формы количественных отношений по сравнению с уравнениями без параметров.
Дэвис и Хенкин (1978) писали о важности квадратных уравнений вообще и с параметрическими коэффициентами в частности. Они описывают, как они интерпретируют понимание квадратных уравнений. Они предоставляют длинный список навыков, а также математические знания, необходимые для понимания и решения квадратных уравнений. Дэвис и Хенкин утверждают, что понимание и решение уравнений с параметрами улучшают понимание учащимися уравнений в целом.
Skemp (1987) утверждает, что изучение правил без причин позволяет ученику действовать только в узких рамках и решать только стандартные проблемы. Однако такой подход ограничивает понимание учащихся, и они не смогут справиться с более сложными задачами.
Понимание позволяет ученику решать нестандартные задачи, которые невозможно решить механическим применением формул. Fischbein и Muzicant (2002) указывают, что ученики обучались в основном процедурным образом и, следовательно, они часто не различали концептуальные и процедурные знания. Многим ученикам трудно понять, что буква представляет собой число, и они не знают, как работать с символическими значениями (Киран, 19 лет).92, 2014).
Общепризнанно, что учителям важно понимать, как их ученики воспринимают математические темы, в частности конкретные причины ошибок (Almog & Ilany, 2012).
На начальных курсах учащиеся привыкают к тому, что x (а позже y и z) являются переменными, а такие буквы, как a, b, c, являются константами или параметрами. Однако на более продвинутых курсах они сталкиваются с вопросами, где буквы используются по-другому, и это их очень сбивает с толку. Например, проблемы интеграции, где x фиксировано, а y является переменной. Или объемные вопросы, где в качестве переменных используются a, b, c.
Учащиеся решают в школе бесчисленное количество упражнений на уравнения, в которых буква x представляет собой переменную, которая должна быть выражена через буквы a, b, c и т. д. В этом исследовании испытуемым давали разнообразные уравнения с нестандартным представлением , как указано выше.
2. Цель
Целями исследования являются изучение и выявление трудностей старшеклассников и студентов-педагогов при решении уравнений с параметрами. Кроме того, выяснить, есть ли существенные различия между учениками и учениками-учителями в отношении решения таких уравнений. Какие процедуры используются и какие трудности возникают при решении уравнений с параметрами.
3. Исследовательские вопросы
1) Как испытуемые решают уравнения с параметрами, в которых они должны выражать различные буквы через другие буквы и параметры? В частности, когда уравнения расположены нестандартным образом.
2) Существуют ли различия между учениками и учениками-учителями в том, как они решают такие уравнения.
И если да, то в чем отличия.
Примеры уравнений, исследуемых в статье (нумерация вопросов соответствует номеру анкеты):
• Вопрос 16: Найдите x (через a) в (довольно стандартном уравнении с переменной x и параметром a).
• Вопрос 1: Найдите c (через x) в (менее стандартно, так как требуется выразить c через x).
• Вопрос 9: Найдите b (через x) в (менее стандартно, поскольку требуется перестроить уравнение «правильно», а затем выразить b через x).
• Вопрос 21: Следующее уравнение является линейным по x, хотя может ошибочно показаться квадратным относительно a:.
Знания, необходимые для решения простых уравнений, мы называем процедурными знаниями. Уравнения с нестандартными представлениями требуют более гибкого подхода.
4. Методика
Выборка исследования состояла из 115 студентов-учителей математики на третьем и четвертом курсах и 133 учащихся двенадцатого класса высшей математики (поток математики 5 единиц) в четырех средних школах.
Инструменты: Для исследования была разработана анкета, которая применялась в обеих группах. Часть анкеты состоит из шести вопросов, которые включают уравнения с параметрами. В этом исследовании сообщаются результаты двух вопросов об уравнениях первой степени (вопросы (5) и (21)) и трех вопросов об уравнениях второй степени (вопросы 16, 1 и 9).). Вопросы перечислены в Таблице 1 и Таблице 3
Процедура: Чтобы понять процесс решения предметов, были опрошены пять учеников и шесть студентов-преподавателей. Вопросы для интервью были составлены после заполнения и анализа анкеты. Цель состояла в том, чтобы уточнить и подтолкнуть к дальнейшим выводам анкеты. Кроме того, проводились открытые наблюдения, чтобы внимательно изучить ответы испытуемых.
Таблица 1. Вопросы 5 и 21, анализ результатов (уравнения первой степени с параметрами).
Примечание: (P = ученики, ST = студенты-учителя). * Субъекты правильно выразили x, но некоторые из них не смогли указать действительный домен, а затем упростить выражение.
Подробности см. в Таблице 2.
Анализ данных: Количественный анализ был проведен с помощью описательной статистики (таблицы, в которых указан процент успеха), тестов c 2 и t-тестов. Качественный анализ проводился путем наблюдения и интервью, как указано выше. Затем результаты были проанализированы в соответствии с новыми критериями.
5. Результаты
Результаты уравнений первой степени5 и 21 представлены в таблице 1
Таблица 1 показывает, что большой процент старшеклассников (22%) не ответили на вопрос 21. Очень небольшой процент испытуемых кто правильно выразил x через a, также указал правильную область решения. Некоторые испытуемые справились только со стандартными вопросами, которые требовали прямого подхода. В целом только 36% учеников и 73% студентов-учителей дали полное решение вопроса 219.0006
В вопросе 5 испытуемых просили выразить букву min через x. м — буква, которая обычно воспринимается как параметр (Илани, 1997, 1998). В этом вопросе мы имеем уравнение первой степени, для которого процесс решения должен быть простым, но только 67% учеников дали правильный ответ и 29% ошиблись.
Мы утверждаем, что ошибки возникают из-за путаницы, связанной с нестандартным использованием параметров и переменных (примеры приведены ниже). У студентов-преподавателей ситуация была лучше, 88% решали правильно и 10% допустили ошибки, связанные с нестандартным изложением.
В вопросе 21 уравнение имеет первую степень по x, и x нужно было выразить через a. Такое представление уравнения было связано с различными ошибками в процессе решения испытуемыми, поскольку x обычно воспринимается как переменная (Ilany, 1997). Стоит отметить, что уравнение 21 на самом деле линейно по x, так как x является переменной первой степени. Однако из-за наличия в уравнении a 2 некоторые студенты были сбиты с толку и восприняли уравнение как квадратное.
Чтобы решить приведенное выше уравнение, необходимо раскрыть скобки, собрать подобные выражения и переставить уравнение. Существует ограничение на a (a ≠ −1), и для решения уравнения требуется несколько алгебраических операций. Многочисленные ошибки были допущены испытуемыми, пытавшимися решить этот вопрос, особенно учащимися.
Только 36% учеников правильно выразили х через а. То есть они обнаружили, что:
Однако большинству студентов, которые правильно выразили x, не удалось указать допустимый домен и упростить полученное уравнение (см. Таблицу 2).
У студентов-учителей ситуация была лучше: 73% из них правильно ответили на вопрос 21. Анализ ошибок показал, что 41 % учеников по сравнению с 14 % студентов-преподавателей допустили ошибки, связанные с «нестандартными» буквами (см. табл. 1).
В этом исследовании мы решили исследовать три уравнения второй степени. В каждом уравнении требуется выразить данную букву через другую. Ошибки были разделены на два типа: ошибки в счете и ошибки, возникающие из-за путаницы, связанной с незнакомым употреблением букв: игнорирование букв, нахождение неправильной буквы и циклическое выражение букв. (Примеры будут приведены в таблице 3: вопросы 16, 1 и 9.).
Согласно таблице 3, высокий процент учеников (16%) не ответили на вопрос 9. Между студентами-учителями и старшеклассниками была значительная разница по всем трем вопросам.
Три уравнения имеют аналогичную структуру (табл. 3). Разница между ними в том, что в вопросе 16 (5x 2 + 8ax + 4a 2 = 0) нужно найти x, букву, воспринимаемую как переменную согласно Ilany (1997, 1998), а в другом уравнения
Таблица 2 . Вопрос 21 — Испытуемые, которые правильно выразили x (некоторые из них не завершили процесс).
Примечание: (P = ученики, ST = студенты-учителя).
Таблица 3. Вопросы 16, 1 и 9, анализ результатов.
Примечание: (P = ученики, ST = студенты-учителя).
буквы, которые должны быть найдены, это b или c. Эти буквы обычно воспринимаются как параметры, поэтому вызывают недоумение.
Результаты показывают, что больше учащихся правильно ответили на вопрос 16 по сравнению с вопросами 1 и 9 (см. Таблицу 3), которые касаются исследовательского вопроса 1. m (обычно функционируют как параметры) через x (который обычно обозначает переменную)
Значительная разница была обнаружена между студентами-учителями и учениками в двух отношениях.
Начнем с того, что студенты-учителя набрали больше баллов по всем вопросам. Кроме того, меньшая часть студентов-учителей, по-видимому, была сбита с толку изменением и перестановкой переменных (70% учеников правильно ответили на вопрос 16 по сравнению с 28% на вопрос 9).; соответствующие цифры для студентов-учителей составляют 88% против 43%).
В таблице 3 представлены три вопроса аналогичной структуры. Первый вопрос (16) довольно стандартный (выражение x через другие параметры).
Во втором вопросе (1) мы имеем нестандартное использование букв (выражение x через c).
В третьем вопросе также используется нестандартное использование переменных, поскольку b должно быть выражено через x. Кроме того, вы должны изменить уравнение, чтобы решить его.
Сравнение результатов ответов на вопросы 9 и 1 подчеркивает важность расположения уравнения. В вопросе 9 уравнение () похоже на уравнение в вопросе 1 (), но расположено не в обычном порядке, то есть первыми пишутся высшие показатели степени.
Здесь мы получили самые низкие результаты (только 28% учеников и 43% студентов-учителей правильно решили уравнение). Причины таких результатов связаны с трудностью составления уравнения и нахождением нестандартной буквы b через x.
Вопрос 1 также обсуждался в интервью. Интервьюер подчеркнул, что b или c должны быть выражены через x. Несмотря на это, большинство респондентов выразили x через b или c. Один из опрошенных, допустивший эту ошибку, сказал: «Даже если вы не хотите x, вы хотите b, я автоматически нахожу x, потому что это квадратное уравнение». Она сделала попытку выразить b, говоря: «Я не могу найти b, я знаю, что есть два решения, потому что D > 0, но я не могу его найти, я думаю, что это невозможно». В конце интервью мы вернулись к вопросу. На этот раз мы изменили уравнение как:, и интервьюируемый без труда выразил b через x. Другими словами, студентке было трудно даже начать процесс решения, когда она столкнулась с нестандартным расположением и буквами, хотя у нее не было технических трудностей при решении таких уравнений после правильной перестановки.
Тот же студент-учитель сумел переставить и успешно решить «неопрятное» уравнение, где x нужно было выразить через b, то есть стандартное использование букв. После интервью она сказала: «Отныне я буду просить своих учеников произносить разные буквы, не обязательно в обычном порядке».
Интересно отметить, что изменение уравнения в вопросе 9 является одним из способов его решения. Другой способ — поменять местами буквы, то есть поменять местами x и b, найти x и снова поменять местами буквы. Ни один из испытуемых не применил этот метод.
Примеры ошибок из-за использования нестандартных букв в приведенных выше вопросах:
Правильный ответ на вопрос 1:. В данном случае некоторым участникам было сложно принять «незавершенное решение», хотя дальше это выражение нельзя упростить, разве что указать домен.
Следовательно, некоторые испытуемые, правильно решившие вопрос, не удовлетворились своим ответом и зачеркнули его. Однако мы считали скрещенные решения правильными.
Связанная с этим ошибка заключалась в выражении x вместо c (2% студентов-учителей).
«Вы не можете найти с, так как это параметр» (5% студентов-учителей).
«c — это параметр, поэтому может быть любым числом».
Интересная ошибка в вопросе 16 заключалась в получении правильных ответов с пропуском «а» в этих ответах. То есть студент написал:
Аналогичной ошибкой было перепутать «х» и «а»:
Примеры ошибок в вопросе 9: Нахождение х вместо b (11% учеников, 5% студентов-учителей).
Выражение b через b. (6% учеников, 10% студентов-учителей):
Аналогично, в вопросе 21 4% старшеклассников выразили х через х, например:
Примеры ошибок, допущенных при попытке решить:
«Невозможно выразить x отдельно».
«Не знаю» (32% учащихся, 5% студентов-преподавателей).
Превратить x в x 2 (6% учащихся, 2% студентов-преподавателей).
Выразил а вместо х (3% учащихся).
Примеры ошибок, допущенных при попытке решить вопрос 5: Найдите m в:
Найдено x (3% учащихся).
«Невозможно» (10% студентов, 7% студентов-преподавателей).
Превратил уравнение в квадратное уравнение относительно m (3% учащихся).
6. Обсуждение
Результаты этого исследования показывают, что для уравнений с параметрами большой процент студентов-учителей и еще большая часть учеников ошибались из-за путаницы, связанной с нестандартным использованием букв, (например, нужно выразить а через х). Столкнувшись с уравнениями, в которых параметры и переменные не были расположены стандартным образом, испытуемым стало еще труднее решать эти уравнения.
Как правило, уравнения, содержащие параметры, решать сложнее, чем уравнения без параметров. Испытуемые склонны решать уравнения механически, поэтому допускают множество ошибок, когда сталкиваются с нестандартными вопросами, требующими более глубокого понимания.
Ключевыми факторами, которые часто создают проблемы для учащихся, являются тип буквы, которую необходимо выразить, расположение решаемого уравнения, мощность переменной, мощность параметра и тип требуемых алгебраических методов.
.
Последствия для обучения тому, как решать уравнения с параметрами Результаты этого исследования, в частности, большое количество ошибок, вызывают вопросы относительно эффективности обучения этой теме. Следовательно, чтобы улучшить понимание учащимися уравнений с параметрами, рекомендуется улучшить понимание учащимися использования букв в таких уравнениях. Например, внимательно прочитав, что требуется в вопросе, приняв более гибкий подход в отношении того, какие буквы могут быть выражены через другие буквы, убедившись, что выражение правильно упрощено, и осознавая различия и сходства между уравнениями с параметрами и без них.
Рекомендуем включать в школьную программу по математике больше уравнений с различными параметрами и переменными, а также уравнения, которые представлены не в обычном порядке. Это побудит студентов глубже задуматься над темой и получить более глубокое понимание.
Ссылки
- Альмог Н. и Илани Б.-С. (2012). Неравенство абсолютной ценности: решения и заблуждения старшеклассников.
Образовательные исследования по математике, 81 , 347-364. http://dx.doi.org/10.1007/s10649-012-9404-z
- Дэвис, Р. Б., и Хенкин, Л. (1978). Неадекватно протестированные аспекты обучения математике — тестирование, преподавание и обучение . Отчет о конференции по исследованиям в области тестирования, Национальный институт образования, 49-63.
- Фишбейн, Э., и Музикант, Б. (2002). Ричард Скемп и его концепция реляционного и инструментального понимания: открытые предложения и открытые фразы. В Д. Талл и М. Томас (ред.), Интеллект, обучение и понимание математики: дань уважения Ричарду Скемпу (стр. 49–77). Флакстон, Квинсленд: издательство Post Pressed.
- Илани, Б. (1998). Неуловимый параметр. В 23-е ежегодное собрание Международной группы психологии математического образования (том 4, стр. 265). Стелленбос: Стелленбосский университет.
- Илани, Б. (1997). Понятия о переменной и параметре учителей и старшеклассников .
Докторская диссертация, Тель-Авив: Тель-Авивский университет. (на иврите)
- Киран, К. (1992). Изучение и преподавание школьной алгебры. В DA Grouws (Ed.), Handbook of Research on Mathematics Teaching and Learning (стр. 390-419).
- Киран, К. (2014). Преподавание и изучение алгебры. Энциклопедия математического образования (стр. 27-32). Спрингер: Справочник по Спрингеру.
- Седиви, Дж. (1976). Примечание о роли параметров в обучении математике. Образовательные исследования по математике, 7 , 121-126. http://dx.doi.org/10.1007/BF00144365
- Скемп, Р. (1987). Психология обучения математике . Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates.
Примеры решения задачи введением новых параметров
Вопрос
Изменено 4 года, 8 месяцев назад
Просмотрено 396 раз
$\begingroup$
Сначала рассмотрим примеры:
Я видел много примеров вычисления определенных интегралов введением подходящего параметра, но до сих пор не могу понять, почему этот метод так эффективен, а вычисление интеграла напрямую может быть невероятно сложным .
Я помню, что в линейной алгебре мы можем доказать следующий факт, введя новый параметр $x$:
Факт: 9{-1})=\det(tE-BA)=\chi_{BA}(t).$$
Теперь, если и $A$, и $B$ вырождены, то мы можем найти, что, поскольку многочлен $f(x )=\det(A+xE)$ имеют только конечные корни и $f(0)=\det A=0,$, то существует удаленная окрестность $U(0)$ точки $0,$ такая, что $f( x)\neq 0,\ \forall\ x\in U(0).$Обозначим кольцо многочленов вещественных коэффициентов как $\mathbb R[t],$, затем заметим, что отображение $\varphi:\mathbb R\to \mathbb R[t],\ x\mapsto \chi_{(A+xE)B}(t)-\chi_{B(A+xE)}(t)$ является непрерывным, и $\varphi(x)=0,\ \forall\ x\in U(0),$, поэтому имеем $\varphi(0)=0,$ или $\chi_{A\cdot B}( t)=\chi_{B\cdot A} (t).$
Конец доказательства
- Еще один интересный пример: https://math.stackexchange.com/q/1395378
Меня очень интересует мотивация введения нового параметра и хотелось бы увидеть больше примеров решения проблем за счет введения нового параметра.
n}{q_n q_{n+1 }}.$$
Мое любимое доказательство этого включает введение дополнительной переменной $x$ и определение $$ f_n(x) = a_0 + \frac{1}{a_1 + \frac{1}{ \ddots \frac{1}{a_n + x}}}. $$ Затем, если вы проработаете несколько примеров, вы, естественно, придете к гипотезе, что $f_n(x) = \frac{p_n + p_{n-1} x}{q_n + q_{n-1} x}$. Смысл введения дополнительной переменной $x$ в том, что она позволяет производить подстановку внутри: $$ f_{n+1}(x) = f_n\left(\frac{1}{a_{n+1} + x}\right). $$ Это позволяет вам выразить $p_{n+1}$ и $q_{n+1}$ через $a_{n+1}$, $p_n$, $p_{n-1}$, $q_n$ , $q_{n-1}$, и оттуда становится просто показать желаемый результат по индукции. В то время как с исходной цепной дробью, но без этого трюка, казалось бы, нужно начинать вычисления для $\frac{p_n}{q_n}$ заново для каждого нового значения $n$, что очень затруднило бы попытаться найти отношения между различными $p_n$ и $q_n$. 9{n+1}$. Теперь из последнего уравнения следует, что $p_n$ и $q_n$ взаимно просты, и поэтому мы заключаем, что $\frac{p_n}{q_n} = f_n(0)$ действительно является представлением младших членов $n$-й частичной член цепной дроби.
)
$\endgroup$
$\begingroup$
Алгоритмы кратчайшего пути. Цель состоит в том, чтобы найти кратчайший путь от $s$ (для источника) до некоторого $v$, где $s$ и $v$ — вершины взвешенного ориентированного графа. Все приведенные ниже алгоритмы решают эту задачу путем решения более общей задачи.
Примеры:
Беллман-Форд : Найдите кратчайший путь между вершиной $s$ и любой другой вершиной $v$, которая имеет не более $k$ ребер . Алгоритм использует тот факт, что если известен ответ для $k$, то его легко найти для $k+1$.
Алгоритм Дейкстры : найти $k$ вершин, ближайших к вершине $s$. Опять же, если ответ известен для $k$, то его легче найти для $k+1$.
Все пары кратчайшего пути. Цель состоит в том, чтобы вывести матрицу, которая дает кратчайший путь между каждой парой вершин.
Примеры:
Floyd-Warshall : найти кратчайший путь между каждой парой вершин с учетом ограничения, что все промежуточных вершин в путях ограничены $\{1,\dotsc,k\} $.
Продолжайте увеличивать $k$. См. также алгоритм Клини для преобразования конечного автомата в регулярное выражение .
$\endgroup$
$\begingroup$
В Литтлвуде очень интересно «Математический сборник», на странице 21, он пишет о теореме благодаря М. Риссу для которого элегантное доказательство (Г. Торин («Теоремы выпуклости», Коммуникации Математический семинар Лундского университета, 9)) включает в себя вложенные верхние границы и самая внутренняя верхняя граница взят относительно переменной, которой нет.
В доказательстве верхняя граница относительно действительного $\sigma$ имеет $\сигма$ заменен на $s+it$ и новая верхняя граница вставлено то есть взятые относительно $t$.
$\endgroup$
$\begingroup$
Я видел много примеров вычисления определенных интегралов с введением подходящего параметра, но до сих пор не могу понять, почему этот метод настолько эффективен, а вычисление интеграла напрямую может быть невероятно сложным.
Я хочу отметить, что даже когда вы вычисляете определенный интеграл «напрямую», вы часто все же делаете это, неявно вводя параметр. Каждый раз, когда вы вычисляете определенный интеграл путем вычисления неопределенного интеграла путем вычисления первообразной, вы вводите новый параметр, а именно границы неопределенного интеграла. Причина, по которой вы это делаете, заключается в том, что вы можете дифференцировать по вашему новому параметру, а затем применить фундаментальную теорему исчисления.
Итак, позвольте мне немного порассуждать о том, почему это работает так хорошо. Дело в том, что понимание математического утверждения или объекта в отдельности часто бывает трудным, но понимание его в контексте семейства объектов часто намного проще, потому что вы можете использовать отношения между объектами, чтобы использовать свое понимание некоторых из них для понимания. другие. Это очень общий принцип, и он распространяется далеко за пределы интегралов.
0 = 1$, и используйте свое понимание, скажем, $I(0)$, чтобы понять $I(t)$ для любого $t$ и, следовательно, понять $I(1)$ или каким бы ни был ваш исходный интеграл.
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.Что такое параметры в математике?
Параметры — это специальный тип математической переменной. Параметрическое уравнение содержит одну или несколько параметрических переменных, которые могут иметь несколько возможных значений. Репетиторство по математике может помочь учащимся понять сложные концепции параметров, функций и значений. Значение каждого параметра сохраняется постоянным при использовании функции. В статистических разделах математики параметр представляет собой оценочное числовое значение характеристики совокупности.
Примеры параметрических уравненийКвадратное уравнение — известный пример, который можно записать в виде параметрического уравнения. В форме ax2 + bx + c = 0 a, b и c являются параметрами. Если параметрическим переменным присваиваются значения (например, a = 1, b = 2, c = 3), уравнение перестает быть параметрическим. x2 + 2x + 3 — отдельный член семейства квадратичных функций.
Другим известным примером является уравнение прямой линии, проведенной в декартовой системе координат. Наиболее общая форма уравнения: y = mx + b. Переменные m и b обычно называют наклоном и точкой пересечения соответственно. Варьируя m и b, можно получить бесконечное число различных прямых линий. Однако уравнение никогда не может дать параболу или окружность, независимо от того, какая комбинация m и b используется. Говорят, что уравнение производит семейство функций, потому что каждая функция дает один и тот же результат — прямую линию.
Как писать параметрические уравнения?Параметр может также использоваться для описания системы уравнений. Например, если мяч брошен и его траектория построена в декартовой системе координат, обе компоненты траектории x и y зависят от времени после того, как мяч был брошен, и от начальной скорости мяча. Уравнения могут выглядеть примерно так: x = vt и y = vt — 5t2. В данном случае параметрами являются скорость и время.
Более продвинутым применением параметров является метод вариации параметров, который используется для решения дифференциальных уравнений. В этом методе параметры фактически являются функциями, которые заменяют неизвестные константы в решении дифференциального уравнения. Решая эти параметрические функции, можно определить неизвестные константы и найти общее и частное решения дифференциального уравнения.
Параметры в статистикеСуществует множество способов использования параметров в реальных сценариях, например, в области статистики. В статистике параметр представляет собой оценку данной совокупности. Общие статистические параметры включают среднее значение и стандартное отклонение. Эти оценки используются в уравнениях для расчета тестовой статистики для различных статистических тестов.
Когда изучают параметры в средней школе?Учащиеся должны иметь четкое представление о параметрах для успеха в предварительном исчислении и исчислении, которые широко преподаются в средних школах.
Параметры часто изучаются вместе с другими математическими функциями в предварительном исчислении. Поскольку параметры преподаются в предварительном исчислении, учащиеся, скорее всего, узнают о них во второй половине своей карьеры в старшей школе.
Старшеклассники обычно изучают алгебру 1 в девятом классе, геометрию в десятом классе, алгебру 2 или тригонометрию в одиннадцатом классе и предварительный анализ или исчисление в двенадцатом классе. Тем не менее, отличники или учащиеся AP, скорее всего, будут изучать алгебру 1 в восьмом классе, геометрию в девятом классе, алгебру 2 или тригонометрию в десятом классе, предварительное исчисление в одиннадцатом классе и исчисление в двенадцатом классе. Это может отличаться от штата к штату, поскольку существуют некоторые различия в руководящих принципах штатов в отношении учебной программы по математике, преподаваемой в средних школах.
Для чего в реальной жизни используются параметрические уравнения?Параметрические уравнения часто используются для описания типов кривых, которые могут быть представлены на плоскости, но эти уравнения также используются, когда кривые на декартовой плоскости не могут быть описаны функцией.
Параметры позволяют отображать полное положение объекта во времени.
В повседневной жизни параметрические уравнения полезны для измерения кругового движения и движения снаряда. Например, вы можете использовать параметры для измерения кривой брошенного мяча или вашего положения на движущемся колесе обозрения.
Есть ли параметрические уравнения в SAT?Математический раздел SAT охватывает довольно широкий круг математических тем. Студенты должны понимать такие понятия, как операции, алгебра, функции, геометрия, измерения, анализ данных, статистика и вероятность, чтобы добиться успеха на SAT. Математический раздел SAT включает 19 вопросов по алгебре, 17 вопросов о решении задач и анализе данных, 16 вопросов, связанных с продвинутой математикой (например, решение квадратных уравнений и работа с полиномами), и 6 вопросов, связанных с дополнительными математическими темами (например, тригонометрия). , вычисление площади и объема и использование теорем, связанных с окружностями и линиями).
Вопросы SAT Math, скорее всего, проверят учащихся на их способность создавать и решать линейные уравнения, анализировать количественные данные, применять вероятности в контексте, создавать эквивалентные алгебраические выражения, решать задачи, связанные с площадью и объемом, работать с прямоугольными треугольниками и тригонометрическими функциями, и более. Математический раздел SAT вряд ли будет включать темы предварительного исчисления, такие как параметрические уравнения.
Однако, несмотря на то, что параметрические уравнения не являются основной частью теста SAT по математике, учащиеся все же должны сделать все возможное, чтобы понять эти концепции. Плохая успеваемость по предварительному исчислению или исчислению может негативно сказаться на успеваемости учащегося и его среднем балле.
Как репетиторы по математике могут помочь учащимсяОнлайн-репетитор — это отличный способ оказать учащимся поддержку, необходимую им для достижения успеха в математике на любом уровне.
Если учащегося пугают понятия, которые он изучает на уроке математики, репетитор может дать ему дополнительные инструменты и ресурсы для изучения материала в индивидуальной обстановке. Не менее важно и то, что работа с репетитором бесценна для укрепления уверенности учащихся. Точно так же, если учащийся преуспевает в математике, репетитор может предложить ему возможность выйти за рамки основ школьной программы, решить новые задачи и развить навыки критического мышления. Репетиторы по математике для учащихся — отличный способ помочь учащимся раскрыть свой истинный потенциал, независимо от их стиля обучения и академических потребностей.
Learner позволяет легко найти подходящего репетитора для каждого ребенка. Начать работу очень просто, и она полностью сосредоточена на академическом профиле учащегося. Первый шаг для родителей — ответить на вопросы об уникальных потребностях и опыте своего ребенка на веб-сайте Learner. Затем родители могут запланировать звонок академического тренера, чтобы определить цели и задачи обучения.
Наконец, Learner подберет для каждого ребенка подходящего репетитора. Первое занятие с репетитором Learner всегда на 100 % бесплатно, чтобы убедиться, что репетиторство подходит ребенку.
Ищете индивидуальные занятия по математике? Поговорите с нашим академическим консультантом, чтобы получить индивидуальное соответствие с вашим онлайн-репетитором по математике сегодня!
Часто задаваемые вопросы о параметрах Используют ли инженеры параметрические уравнения?Параметрические уравнения используются инженерами для поиска решений проблем. Эти уравнения можно использовать в качестве моделей для визуализации упрощений рассматриваемой системы и реального контекста, в котором работает система.
Можно ли использовать параметрические уравнения в текстовых задачах?Параметрические уравнения можно использовать в текстовых задачах, когда применяется математика параметров. Иногда у фактического параметра будет график, сопровождающий проблему вместе с параметрами.
Используют ли функции параметрические уравнения?В математике параметрическое уравнение определяет группу величин как функции одной или нескольких независимых переменных, называемых параметрами.
Что такое позиционные параметры?Позиционный параметр — это параметр, обозначаемый одной или несколькими цифрами, кроме одной цифры 0. Позиционные параметры связаны по положению, а позиционные параметры назначаются, но могут быть переназначены. Позиционные параметры могут называться одноместными параметрами.
Откуда взялся термин «параметр»?Термин «параметр» происходит от древнегреческих слов, означающих «помимо, вспомогательный» и «мера». Параметр определяется как величина, влияющая на результат поведения математического объекта. Он считается постоянным.
В чем разница между параметром и переменной?Переменная — это способ представления атрибута или количества.
Зависимая переменная — это переменная, которая зависит от других факторов. Другими словами, независимая переменная является причиной, а зависимая — следствием. В отличие от переменных параметр является константой в уравнении, описывающем модель.
Что такое параметр в статистике?
Вероятность и статистика > Базовая статистика > Что такое параметр в статистике?
Эта статья посвящена параметрам населения. Информацию о параметрах, которые можно использовать для определения распределения вероятностей, см. в разделе Что такое параметризация?
Что такое параметр в статистике?
В математике параметр — это что-то в уравнении, которое передается в уравнении. Это означает что-то другое в статистике. Это значение, которое говорит вам что-то о населения и противоположно статистике, которая говорит вам что-то о малая часть населения.
При переписи опрашиваются все.Параметр никогда не меняется , потому что все (или все) были опрошены, чтобы найти этот параметр.
Например, вас может интересовать средний возраст всех в вашем классе. Может быть, вы опросили всех и обнаружили, что средний возраст — 25 лет. Это параметр, потому что вы опросили всех в классе. Теперь предположим, что вы хотите узнать средний возраст всех учеников вашего класса или класса. Если вы используете эту информацию из своего класса, чтобы предположить средний возраст, то эта информация становится статистикой. Это потому, что вы не можете быть уверены, что ваша догадка верна (хотя она, вероятно, будет близка!).
Статистические данные различаются. Вы знаете, что средний возраст ваших одноклассников — 25 лет. Вы можете догадаться, что средний возраст всех ваших однокурсников — 24, 25 или 26 лет. Вы можете догадаться, что средний возраст в других колледжах в вашем районе такой же. И вы можете даже догадаться, что это средний возраст студентов колледжей в США. Возможно, это неплохие предположения, но это статистика, потому что вы не опрашивали всех.
Посмотрите это видео, чтобы увидеть больше примеров различий между параметрами и статистикой:
Как отличить статистику от параметра
Посмотрите это видео на YouTube.
Происхождение слова
ПараметрЭто слово встречается в 1914 г. в E. Czuber, Wahrscheinlichkeitsrechnung, Vol. I и в 1922 г. в книге Рональда А. Фишера «О математических основах теоретической статистики». Фишер — английский статистик, биолог и генетик.
Что такое параметр в статистике: обозначение
Параметры обычно представляют собой греческие буквы (например, σ) или заглавные буквы (например, P). Статистика обычно пишется латинскими буквами (например, s). В большинстве случаев, если вы видите строчную букву (например, p), это статистика. В этой таблице показаны различные символы. Некоторые могут выглядеть одинаково, но внимательно ищите строчные и заглавные буквы.
Совет: В статистике редко всплывает слово параметр. Это потому, что ВСЕ, с чем мы имеем дело, это статистика! Вы можете увидеть что-то вроде «среднее значение населения». Это делает более очевидным, что речь идет обо всем параметре. Когда вы видите просто «значительное», это обычно статистика.
Что такое параметр в статистике: точность.
Точность показывает, насколько ваша статистика близка к определенному параметру населения. Например, вы можете изучать вес беременных женщин. Если медиана выборки вашей совокупности составляет 150 фунтов, а статистика выборки — 149 фунтов, то вы можете сделать заявление о точности вашей выборки.
Статистика в целом не так точна, как хотелось бы, хотя это лучший инструмент, который у нас есть сейчас для прогнозирования населения. Согласно The Economist, научные статьи не очень надежны. Джон Лоаннисис, греческий эпидемиолог, считает, что целых 50 процентов научных работ оказываются ошибочными.
Факторы, способствующие получению ложных результатов, включают слишком малые размеры выборки, плохо спланированное исследование и предвзятость исследователя, вызванную финансовыми интересами или личными намерениями. Vioxx был снят с рынка после того, как он был связан с проблемами с сердцем. Опубликованные научные статьи о безопасности Vioxx оказались ложными.В. Как рассчитываемые статистические данные при переписи соотносятся с соответствующими параметрами населения?
Прежде чем начать, вы можете прочитать эту статью: Как отличить статистику от параметра.
Что на самом деле задает этот вопрос, насколько точна перепись? . Ответ таков (на удивление), что перепись очень точна, плюс-минус крошечный процент. Этот крошечный процент, скорее всего, составляют меньшинства, люди с низким доходом и люди, живущие в сельской местности.
На момент написания последней переписью была перепись 2010 года. Исторически перепись становится более точной: 903:00 По данным переписи 2010 года, общая численность населения США в 2010 году составляла 308 745 538 человек, что на 9,7% больше, чем по данным переписи 2000 года. Общая численность населения США была завышена на 0,01 процента. Это всего 36 000 человек — неплохо, если учесть, что население США составляет более 300 миллионов человек. Сравните это с переучетом в 0,49% в 2000 году (около миллиона человек) и занижением в 1,61% в 1990 году.
- Домовладельцев пересчитали.
- 2,1 процента чернокожих американцев были упущены. По данным Denver Post, это было огромным улучшением по сравнению с цифрами 1940 года, когда было подсчитано, что недоучет чернокожих составлял 8,4 процента.
- 1,5 процента выходцев из Латинской Америки были пропущены.
90 226 белых неиспаноязычных жителей были пересчитаны.Почему эти группы учитываются не так точно?
Доступность: С жителями сельской местности трудно или невозможно связаться по почте. В некоторых местах используются адреса «общей доставки», а не фиксированные адреса.
Языковой барьер и образование: Люди, изучающие английский язык, могут испытывать трудности с пониманием формы переписи. Люди с более низким уровнем образования и грамотности также могут не понимать важности участия в переписи.
Подозрение правительства: Некоторые люди могут подумать, что перепись будет использована против них.Некоторые люди не хотят быть в государственной базе данных. Например: нелегальные иммигранты, люди с ордерами на них, люди, имеющие долги или алименты.
Что такое параметр в статистике: Статья по теме:
Как отличить статистику от параметра.Ссылки
Гоник, Л. (1993). Мультяшный путеводитель по статистике. HarperPerennial.
Коц, С.; и др., ред. (2006), «Параметр», Энциклопедия статистических наук, Wiley.
Эверитт, Б.С.; Скрондал, А. (2010), Кембриджский статистический словарь, издательство Кембриджского университета.НАЗВАТЬ ЭТО КАК:
Стефани Глен . «Что такое параметр в статистике?» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/what-is-a-parameter-statisticshowto/————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Примеры
Next: Тонкости и ограничения Up: Пул решений Previous: Извлечение решений
Использование параметра
Давайте продолжим с несколькими примерами того, как параметры связанных с пулами решений, будет использовал. Представьте, что вы решаете MIP-модель с оптимальным (минимизация) цель 100. Далее представьте, что, используя значение по умолчанию параметры, решатель MIP находит четыре решения для этой модели с цели 100, 110, 120 и 130.
Если вы установите PoolSolutions значение 3 и снова решить модель, решатель MIP вернуться с 3 решениями в пуле решений (т. е. атрибут SolCount будет иметь значение 3). Если вместо этого установить Значение параметра PoolGap
0.2, решатель MIP отбрасывает любые решения, цель которых значение хуже 120 (что также оставило бы 3 решения в списке).пул растворов).
Если вы установите PoolSearchMode параметр на 1 и PoolSolutions значение 10, решатель MIP продолжит работу после того, как найдет оптимальное решение пытается найти и сохранить 10 решений, но без гарантия на качество дополнительных решений.
Если вы установите PoolSearchMode параметр на 2 и параметр PoolSolutions на 10, решатель MIP попытается найти 10 лучших решений для модель. Статус возврата
OPTIMALбудет означать, что либо (i) он нашел 10 лучших решений или (ii) нашел все возможные решения модели, а их было меньше 10. Если еще установить параметр PoolGap на значение 0.1, решатель MIP попытается найти 10 решений с целью no. хуже, чем 110. Хотя это может показаться эквивалентным запросу 10 решений и просто игнорирование тех, у которых цель хуже 110, решение обычно выполняется значительно быстрее с этим параметром набор, так как решателю не нужно тратить усилия на поиск решения, выходящие за пределы запрошенного пробела.Интерпретация атрибутивной информации
Давайте попробуем лучше понять атрибуты, связанные с пулами решений.
Рассмотрим снова задачу минимизации, когда настройки параметров
PoolSearchMode=2иPoolSolutions=10был использован.Во-первых, представьте, что решатель завершился с
ОПТИМАЛЬНЫМстатус возврата. Мы рассматриваем несколько возможных гипотетические значения некоторых атрибутов:
- Случай 1:
ObjVal=100,ObjBound=100,PoolObjBound=500, а целевое значение 10-го решения в бассейн 500р.Первое решение в пуле является оптимальным (поскольку
ObjValиObjBoundравны), и решатель смог найти 10 решений значения не более 500. ПосколькуPoolObjBound=500, мы знаем что все решения, которые решатель не нашел иметь целевое значение не менее 500. Поскольку последнее решение в пуле значение 500, 10 решений в пуле определенно являются 10 лучшими решениями.- Случай 2:
ObjVal=100,ObjBound=100,PoolObjBound=+infinity,SolCount=7, а значения 7-е и 8-е решения в пуле — это 350 и+ бесконечностьсоответственно.Решатель нашел 7 решений и доказал, что никакое другое допустимое решение для модели существует. Лучшее из этих 7 решений имеет цель 100, худший из них имеет цель 350.
Теперь представьте, что решатель завершил работу досрочно из-за ограничения по времени. (статус возврата
TIME_LIMIT). Опять же, мы рассматриваем несколько возможных гипотетические значения некоторых атрибутов:
- Случай 3:
ObjVal=100,ObjBound=50,PoolObjBound=50Поскольку
ObjBound<ObjVal, решатель сделал не доказывать оптимальность действующее решение (первое решение в пуле). Могут быть лучшие решения чем действующий.- Случай 4:
ObjVal=100,ObjBound=100,PoolObjBound=100, а целевое значение 10-го решения в пуле равно 500.Первое решение в пуле является оптимальным (поскольку
ObjValиObjBoundравны), и решатель смог найти 10 решений с целью стоимость не более 500.Поскольку
PoolObjBound=100, мы знаем, что все решения что решатель не нашел иметь объективное значение не менее 100. Поскольку значение последнее решение в пуле — 500, возможно, существуют 10 или более решений с целью менее 500 (но больше или равно 100). В частности, решения, которые в настоящее время находятся в пуле и имеют объективную ценность более 100 может не входить в 10 лучших решений.- Случай 5:
ObjVal=100,ObjBound=100,PoolObjBound=200, а целевые значения 4-го, 5-го и 10-го решений в пуле равны 180, 220 и 500 соответственно.Первое решение в пуле является оптимальным (поскольку
ObjValиObjBoundравны), и решатель смог найти 10 решений со значением не более 500. ПосколькуPoolObjBound=200, мы знаем, что все решения что решатель не нашел иметь объективную ценность не менее 200. Это означает, что первые 4 решения в пуле (до решения со значением 180) определенно лучшие четыре решения которые существуют.5-е решение со значением 220 (и последующие решения в пуле) может уступать другим неизведанным решениям.
Next: Тонкости и ограничения Up: Пул решений Previous: Получение решений
Проблемы — документация CVXPY 1.2
Класс
Проблемаявляется точкой входа в постановка и решение оптимизационных задач. КаждыйЭкземпляр задачиинкапсулирует оптимизацию проблема, т. е. цель и набор ограничений.solve()метод либо решает проблему кодируется экземпляром, возвращая оптимальное значение и устанавливая переменные значений в оптимальные точки, или сообщает, что проблема на самом деле неразрешима или неограниченный. Вы можете сконструировать проблему, решить ее и проверить как ее значение, и значения его переменных вот так:проблема = Проблема (Минимизация (выражение), ограничения) проблема решена() если проблема.статус не в ["недопустимый", "неограниченный"]: # В противном случае, problem.value равно inf или -inf соответственно. print("Оптимальное значение: %s" % проблема.значение) для переменной в problem.variables(): print("Переменная %s: значение %s" % (переменная.имя(), переменная.значение))
Проблемы являются неизменяемыми , за исключением спецификации
Значения параметра. Это означает что ты не может изменить цель или ограничения проблемы после того, как вы создал его. Если вы обнаружите, что хотите добавить ограничение к существующему проблему, вам следует вместо этого создать новую проблему, используя, например, следующая идиома:проблема = Проблема (Минимизация (выражение), ограничения) проблема = проблема (проблема.цель, проблема.ограничения + новые_ограничения)Большинству пользователей не нужно ничего знать о
Проблема класса, за исключением того, как его создать, как решить проблемные экземпляры (решить()), и как запросить результаты решателя (статусизначение).Информация о размере экземпляра проблемы и статистика о наиболее недавний вызов решения фиксируется
SizeMetricsиSolverStatsклассов соответственно и может быть доступ черезsize_metrics()иSolver_stats()свойстваЗадачакласса.
- класс cvxpy.Свернуть( выражение )[источник]
Цель оптимизации для минимизации.
- Параметры:
expr ( Expression ) — Минимизируемое выражение. Должен быть скаляром.
- Повышений:
ValueError — Если выражение не является скаляром.
- is_dcp( dpp: bool = False ) → bool[источник]
Объектив должен быть выпуклым.
- is_dgp( dpp: bool = False ) → bool[источник]
Объектив должен быть логарифмически выпуклым.
- class cvxpy.
Maximize( expr )[источник]
Цель оптимизации для максимизации.
- Параметры:
expr ( Expression ) — максимизируемое выражение. Должен быть скаляром.
- Повышений:
ValueError — Если выражение не является скаляром.
- is_dcp( dpp: bool = False ) → bool[источник]
Объектив должен быть вогнутым.
- is_dgp( dpp: bool = False ) → bool[источник]
Объектив должен быть логарифмически вогнутым.
- class cvxpy.Problem( цель: Union[Minimize, Maximize] , ограничения: Необязательный [Список[Ограничение]] = Нет )[источник]
Задача выпуклой оптимизации.
Проблемы неизменяемы, за исключением модификации через спецификацию
Параметр
- Параметры:
- атомы () → Список [Атом] [источник]
Метод доступа к атомам.
- Возвраты:
Список типов атомов в задаче; обратите внимание, что этот список содержит классы, а не экземпляры.
- Тип возврата:
список
Атом
- назад () → Нет [источник]
Вычислить градиент решения по параметру.
Этот метод отличается картой решения проблемы, получение градиента решения по Параметрам. Другими словами, он вычисляет чувствительность Параметров. по отношению к возмущениям оптимальных значений переменных. Этот может быть полезно для интеграции CVXPY в автоматическую дифференциацию наборы инструментов.
reverse()заполняет атрибутградиентакаждого параметра в проблеме как побочный эффект. Его можно вызвать только после вызоварешить()сrequire_grad=True.Ниже приведен простой пример:
импортировать cvxpy как cp импортировать numpy как np р = cp.Параметр() х = cp.Переменная() квадратичный = cp.square(x - 2 * p) проблема = cp.Problem(cp.Minimize(quadratic), [x >= 0]) р.значение = 3,0 problem.solve(requires_grad=True, eps=1e-10) # reverse() заполняет атрибут градиента параметров проблема.назад() # Поскольку x* = 2 * p, dx*/dp = 2 np.testing.assert_allclose (p.градиент, 2.0)
В приведенном выше примере градиент можно легко вычислить вручную.
reverse()полезен, потому что почти для всех задач градиент не может быть вычислен аналитически.Этот метод можно использовать для дифференциации через любой DCP или DGP проблема, если проблема совместима с DPP (т. е.
проблема.is_dcp(dpp=True)илипроблема.is_dgp(dpp=True)оценивается какПравда).Этот метод использует цепное правило для оценки градиентов скалярная функция переменных по отношению к параметрам. Например, пусть x будет переменной, а p — параметром; х и р могут быть скаляры, векторы или матрицы. Пусть f будет скалярнозначной функцией, с г = f (х).
Затем этот метод вычисляет dz/dp = (dz/dx) (dx/p). дз/дх по умолчанию выбирается в качестве вектора всех единиц, что соответствует выбор f в качестве функции суммы. Вы можете указать пользовательское значение для dz/dx, установив
градиентатрибут ваших переменных. Например,импортировать cvxpy как cp импортировать numpy как np б = cp.Параметр() х = cp.Переменная() квадратичный = cp.square(x - 2 * b) проблема = cp.Problem(cp.Minimize(quadratic), [x >= 0]) б.значение = 3. problem.solve(requires_grad=True, eps=1e-10) х.градиент = 4. проблема.назад() # dz/dp = dz/dx dx/dp = 4. * 2. == 8. np.testing.assert_allclose (б.градиент, 8.)Атрибут
градиентапеременной также можно интерпретировать как возмущения до оптимального значения.
- Повышение:
- константы () → Список [Константа] [источник]
Метод доступа к константам.
- Возвраты:
Список констант в задаче.
- Тип возврата:
список
Константа
- производная () → Нет [источник]
Применение производной карты решения к возмущениям в параметрах
Этот метод применяет производную карты решения к возмущениям в Параметры для получения возмущений в оптимальных значениях Переменные. Другими словами, он говорит вам, как оптимальные значения Переменные будут изменены небольшими изменениями в параметрах.
Вы можете указать возмущения в параметре, установив его
дельтуатрибут (если он не указан, возмущение по умолчанию равно 0).Этот метод заполняет атрибут
deltaпеременных как побочный эффект.Этот метод можно вызвать только после вызова
solve()стребует_град=Истина. Он совместим как с DCP, так и с DGP. проблемы (которые также совместимы с DPP).Ниже приведен простой пример:
импортировать cvxpy как cp импортировать numpy как np р = cp.Параметр() х = cp.Переменная() квадратичный = cp.square(x - 2 * p) проблема = cp.Problem(cp.Minimize(quadratic), [x >= 0]) р.значение = 3,0 problem.solve(requires_grad=True, eps=1e-10) # производная() заполняет дельта-атрибут переменных п.дельта = 1e-3 проблема.производная() # Так как x* = 2 * p, dx*/dp = 2, то (dx*/dp)(p.delta) == 2e-3 np.testing.assert_allclose (x.delta, 2e-3)
- Повышение:
- get_problem_data( решатель , gp: bool = False , force_dpp: bool = False , ignore_dpp: bool = False , verbose: bool = False )[80] 90 90
Возвращает данные о задаче, использованные при вызове решателя.
Когда проблема решена, CVXPY создает цепочку заключенных сокращений в
SolvingChain, и компилирует его в некоторое низкоуровневое представление, которое совместим с целевым решателем. Этот метод возвращает этот низкоуровневый представление.Для некоторых решаемых цепочек это низкоуровневое представление является словарем.
который содержит именно те аргументы, которые были переданы решателю; однако для других цепочек решения данные являются промежуточными представление, которое дополнительно компилируется интерфейсами решателя.
Решение эквивалентной низкоуровневой задачи может быть получено с помощью data путем вызова метода solve_via_data возвращенного решения цепочка, тонкая оболочка вокруг кода, внешнего по отношению к CVXPY, которая еще больше обрабатывает и решает проблему. Вызвать метод unpack_results восстановить решение исходной проблемы.
Например:
цель = ... ограничения = ... проблема = cp.Problem (цель, ограничения) данные, цепочка, обратные_данные = проблема.get_problem_data(cp.SCS) # вызывает SCS, используя `data` soln = chain.solve_via_data(проблема, данные) # распаковывает решение, возвращенное SCS, в `проблема` проблема.unpack_results(soln, chain, inverse_data)Кроме того, словарь данных , возвращаемый этим методом содержит достаточно информации, чтобы обойти CVXPY и вызвать решатель напрямую.
Например:
проблема = cp.Problem(цель, ограничения) данные, _, _ = проблема.get_problem_data(cp.SCS) импорт СК пробдата = { 'А': данные['А'], 'б': данные ['б'], 'с': данные ['с'], } конус_димс = данные['димс'] конусы = { "f": конус_димс.ноль, "l": конус_димс.nonneg, "q": конус_димс.soc, "эп": конус_димс.exp, «s»: конус_димс.psd, } soln = scs.solve(данные, конусы)Структура словаря данных, возвращаемого CVXPY, зависит от решатель. Для получения подробной информации обратитесь к интерфейсам решателя в cvxpy/редукции/решатели .
- Параметры:
решатель ( str ) — решатель, для которого предназначены данные задачи.
gp ( bool , необязательный ) — если True, то анализирует задачу как дисциплинированную геометрическую программу вместо дисциплинированной выпуклой программы.
force_dpp ( bool , необязательный ) — при значении True будет выдаваться ошибка DPPError при попытке анализа не-DPP.
проблема (а не просто предупреждение). По умолчанию имеет значение Ложь.
ignore_dpp ( bool , необязательный ) — при значении True проблемы DPP будут рассматриваться как не связанные с DPP, что может ускорить компиляцию. По умолчанию имеет значение Ложь.
verbose ( bool , необязательный ) — если True, вывести подробный вывод, связанный с компиляцией проблемы.
- Возвратов:
dict или object – низкоуровневое представление проблемы
SolvingChain — Цепочка решения, создавшая данные.
список — обратные данные, сгенерированные цепочкой.
- Повышений:
cvxpy.error.DPPError — Возникает, если настройки DPP недействительны.
- is_dcp( dpp: bool = False ) → bool[источник]
Удовлетворяет ли проблема правилам DCP?
- Параметры:
dpp ( bool , необязательный ) –
Если True, применить дисциплинированное параметризованное программирование (DPP) набор правил; уместно только тогда, когда проблема связана с параметрами.
DPP является мягким ограничением DCP. Когда проблема связана Параметры — DPP, последующие решения могут быть намного быстрее, чем первый. Для получения дополнительной информации обратитесь к документации на
https://www.cvxpy.org/tutorial/advanced/index.html#disciplined-parametrized-programming
- Возвратов:
Истина, если выражение — DCP, в противном случае — ложь.
- Тип возврата:
логический
- is_dgp( dpp: bool = False ) → bool[источник]
Удовлетворяет ли проблема правилам DGP?
- Параметры:
дпп ( логический , опционально ) –
Если True, применить дисциплинированное параметризованное программирование (DPP) набор правил; уместно только тогда, когда проблема связана с параметрами. DPP является мягким ограничением DGP. Когда проблема связана Параметры — DPP, последующие решения могут быть намного быстрее, чем первый.
.Для получения дополнительной информации обратитесь к документации по адресу
https://www.cvxpy.org/tutorial/advanced/index.html#disciplined-parametrized-programming
- Возвратов:
Истина, если Expression — DGP, в противном случае — ложь.
- Тип возврата:
логический
- is_dpp (контекст : str = ‘dcp’ ) → bool[источник]
Удовлетворяет ли проблема правилам DPP?
DPP — это мягкое ограничение DGP. Когда проблема связана Параметры — DPP, последующие решения могут быть намного быстрее, чем первый. Для получения дополнительной информации обратитесь к документации по адресу
.https://www.cvxpy.org/tutorial/advanced/index.html#disciplined-parametrized-programming
- Параметры:
контекст ( str ) – проверять соответствие DPP для DCP или DGP;
контекстдолжен быть либо'dcp', либо'dgp'.Вызов
проблема.is_dpp('dcp')эквивалентноproblem.is_dcp(dpp=True)и проблема.is_dpp(‘dgp’)` эквивалентно проблема.is_dgp(dpp=True) .- Возвратов:
Удовлетворяет ли проблема правилам DPP.
- Тип возврата:
логический
- is_dqcp() → bool[источник]
Удовлетворяет ли проблема правилам DQCP?
- is_qp() → bool[источник]
Является ли задача квадратичной программой?
- параметры () [источник]
Метод доступа к параметрам.
- Возвраты:
Список параметров задачи.
- Тип возврата:
список
Параметр
- classmethod register_solve( name: str , func ) → None[source]
Добавляет метод решения в класс Проблема.
- Параметры:
- решить( *аргументы , **kwargs )[источник]
Компилирует и решает задачу указанным методом.
Заполняет атрибуты состояния
и значенияна проблемный объект как побочный эффект.
- Параметры:
решатель ( str , дополнительный ) — решатель для использования. Например, «ECOS», «SCS» или «OSQP».
подробный ( логический , необязательный ) — переопределяет скрытие вывода решателя по умолчанию и печатает информация журнала, описывающая процесс компиляции CVXPY.
gp ( bool , необязательный ) — если True, анализирует задачу как дисциплинированную геометрическую программу. вместо дисциплинированной выпуклой программы.
qcp ( bool , необязательный ) — если True, анализирует проблему как дисциплинированную квазивыпуклую программу вместо дисциплинированной выпуклой программы.
required_grad ( bool , необязательный ) –
Позволяет вычислить градиенты решения относительно Параметры, вызывая
Problem.backward()после решения, или для вычислить возмущения переменных, заданных возмущениями параметров с помощью вызовproblem.derivative().Градиенты поддерживаются только для задач DCP и DGP, а не квазивыпуклые задачи. При вычислении градиентов (т. е. когда этот аргумент имеет значение True), проблема должна удовлетворять правилам DPP.
Enforce_dpp ( bool , необязательный ) — при значении True при попытке решить не-DPP будет выдаваться ошибка DPPError. проблема (а не просто предупреждение). Актуально только для проблем с участием параметров. По умолчанию имеет значение Ложь.
ignore_dpp ( bool , необязательный ) — при значении True проблемы DPP будут рассматриваться как не связанные с DPP, что может ускорить компиляцию.
По умолчанию имеет значение Ложь.
метод ( функция , дополнительный ) — Пользовательский метод решения для использования.
kwargs ( ключевых слов , необязательный ) — Дополнительные аргументы, специфичные для решателя. См. примечания ниже.
Примечания
интерфейса CVXPY с широким набором решателей; алгоритмы, используемые этими решателями иметь аргументы, касающиеся критериев остановки, и стратегии улучшения качества решения.
Не существует одного набора аргументов, идеально подходящего для любой задачи. Если вы не получив удовлетворительные результаты от решателя, вы можете попробовать изменить его аргументы. точный способ, которым это делается, зависит от конкретного решателя. Вот несколько примеров:
prob.solve(solver='ECOS', абстол=1e-6) prob.solve(solver='OSQP', max_iter=10000).mydict = {"MSK_DPAR_INTPNT_CO_TOL_NEAR_REL": 10} prob.solve(solver='MOSEK', mosek_params=mydict).
Вы должны обратиться к веб-документации CVXPY для получения подробной информации о том, как передать решатель аргументы решателя, доступные в
https://www.cvxpy.org/tutorial/advanced/index.html#setting-solver-options
- Возвраты:
Оптимальное значение для задачи или строка, указывающая почему проблема не может быть решена.
- Тип возврата:
поплавок
- Повышений:
cvxpy.error.DCPError — Возникает, если проблема не в DCP, а gp имеет значение False.
cvxpy.error.DGPError — Возникает, если проблема не в DGP и gp — True.
cvxpy.error.DPPError — возникает, если настройки DPP недействительны.
cvxpy.error.SolverError — Возникает, если среди установленных решателей нет подходящего решателя, или если произошла непредвиденная ошибка.
- unpack_results( решение , цепочка: SolvingChain , inverse_data ) → Нет[источник]
Обновляет состояние задачи с учетом результатов решателя.
Обновляет проблема.статус, проблема.значение и значение первичные и двойственные переменные.
- Параметры:
решение ( объект ) — Решение, полученное путем применения цепочки к задаче и вызов решателя для полученных данных.
цепочка ( SolvingChain ) — решающая цепочка, которая использовалась для решения задачи.
inverse_data ( list ) — обратные данные, возвращаемые применением цепочки к задаче.
- Повышений:
cvxpy.error.SolverError — Если решатель не удался
- переменные () → Список [переменная] [источник]
Метод доступа к переменным.
- Возвраты:
Список переменных задачи.
- Тип возврата:
список
Переменная
- свойство ограничения : Список [Ограничение]
Неглубокая копия ограничений задачи.
Обратите внимание, что ограничения нельзя переназначить, добавить или иным образом изменены после создания, кроме как через параметры.
- свойство цель : Союз [Свернуть, Развернуть]
Цель задачи.
Обратите внимание, что цель не может быть переназначена после создания, и изменение цели после создания приведет к неопределенное поведение.
- Тип:
Свернуть или развернуть
- свойство size_metrics : SizeMetrics
Информация о размере задачи.
- Тип:
SizeMetrics
- свойство Solver_stats : SolverStats
Информация, возвращенная решателем.
- Тип:
SolverStats
- недвижимость статус : ул
Статус последнего решения проблемы; один оптимальных, недопустимых или неограниченных (с или без суффикс неверный).
- Тип:
стр
- свойство значение
Значение последнего решения проблемы (или None, если не решено).
- Тип:
поплавок
- класс cvxpy.problems.problem.SizeMetrics (проблема : проблема ) [источник]
Сообщает различные показатели проблемы.
- число_скалярных_переменных
Количество скалярных переменных в задаче.
- Тип:
целое число
- num_scalar_data
Количество скалярных констант и параметров в задаче.
Количество константы, используемые во всех матрицах, векторах, в задаче. Некоторые константы не очевидны при построении задачи: например, Выражение sum_squares является оболочкой для выражения quad_over_lin с постоянная 1 в знаменателе.
- Тип:
целое число
- num_scalar_eq_constr
Количество ограничений скалярного равенства в задаче.
- Тип:
целое число
- num_scalar_leq_constr
- 92 по всем блокам данных задачи, где (большой) — это больший размер, а (маленький) — меньший размер. для каждого блока данных.
Количество ограничений скалярного неравенства в задаче.
- Тип:
целое число
- Тип:
целое число
- класс cvxpy.problems.problem.SolverStats ( results_dict , имя_решателя: str ) [источник]
Сообщает некоторую разную информацию, которая возвращается решателем после решения, но это не фиксируется непосредственно экземпляр Проблемы.

 После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.
После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее. (½)]/(2А).
(½)]/(2А). 4−324=0 (истинно).
4−324=0 (истинно). 4−16+4=16−16=0 (истина).
4−16+4=16−16=0 (истина).

 Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.
Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.
После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.
Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения. (½)]/(2А).
(½)]/(2А). 4−324=0 (истинно).
4−324=0 (истинно). 4−16+4=16−16=0 (истина).
4−16+4=16−16=0 (истина).


 Виета: х 1 + х 2 = -2(а + 1)
Виета: х 1 + х 2 = -2(а + 1) 2 )
2 ) При а = 10
При а = 10 (3)
(3) При каких значениях параметра а уравнение
При каких значениях параметра а уравнение С . Повторяем и систематизируем
школьный курс алгебры и начал анализа. – М.:
Просвещение, 1990.
С . Повторяем и систематизируем
школьный курс алгебры и начал анализа. – М.:
Просвещение, 1990.
 Во вторую очередь, свобода обращения с параметром ограничивается его неизвестностью. Так, например, операции деления на выражение, в котором присутствует параметр или извлечения корня четной степени из подобного выражения требуют предварительных исследований. Поэтому необходима аккуратность в обращении с параметром.
Во вторую очередь, свобода обращения с параметром ограничивается его неизвестностью. Так, например, операции деления на выражение, в котором присутствует параметр или извлечения корня четной степени из подобного выражения требуют предварительных исследований. Поэтому необходима аккуратность в обращении с параметром. Пусть k и b числа, равные нулю, тогда имеем равенство 0 · x = 0. Его решение – любое действительное число.
Пусть k и b числа, равные нулю, тогда имеем равенство 0 · x = 0. Его решение – любое действительное число.

 2 — 2y — 2a + 1 =0$. Дискриминант каждого из них равен $D = 16a-4$.
2 — 2y — 2a + 1 =0$. Дискриминант каждого из них равен $D = 16a-4$. {-1}}\right\}$
{-1}}\right\}$ Получаем (после сокращения
на общий множитель 4) 4a 2 -8a -3 > 0,
откуда
Получаем (после сокращения
на общий множитель 4) 4a 2 -8a -3 > 0,
откуда Используя представление f 1 из 3.а , приравняем
дискриминант уравнения a = 6x —x 2 -6 к нулю.
Из уравнения 36-24-4a = 0 получаем a = 3. Проделав то же
самое с уравнением 2x —a = 6x —x 2 -6
найдем a = 2. Нетрудно убедиться, что эти значения параметра
удовлетворяют условиям задачи. Ответ: a = 2 или a = 3.
Используя представление f 1 из 3.а , приравняем
дискриминант уравнения a = 6x —x 2 -6 к нулю.
Из уравнения 36-24-4a = 0 получаем a = 3. Проделав то же
самое с уравнением 2x —a = 6x —x 2 -6
найдем a = 2. Нетрудно убедиться, что эти значения параметра
удовлетворяют условиям задачи. Ответ: a = 2 или a = 3. Вычисляя дискриминант, получаем, что условием наличия ровно двух корней
является выполнение неравенства a 2 +a -6 > 0.
Решая неравенство, находим a a
> 2. Первое из
неравенств, очевидно, решений в натуральных числах не имеет, а наименьшим
натуральным решением второго является число 3.
Вычисляя дискриминант, получаем, что условием наличия ровно двух корней
является выполнение неравенства a 2 +a -6 > 0.
Решая неравенство, находим a a
> 2. Первое из
неравенств, очевидно, решений в натуральных числах не имеет, а наименьшим
натуральным решением второго является число 3. 2 = 0, $$
2 = 0, $$ Узнаем об этом в статье.
Узнаем об этом в статье.  Чтобы выполнялась система, необходимо, чтобы выполнялись все условия, которые в нее включены.
Чтобы выполнялась система, необходимо, чтобы выполнялись все условия, которые в нее включены. 
 2 — 36a = a(41a — 36)
2 — 36a = a(41a — 36) Не забудем, что
Не забудем, что
 В этом случае мы получим параболу.
В этом случае мы получим параболу. 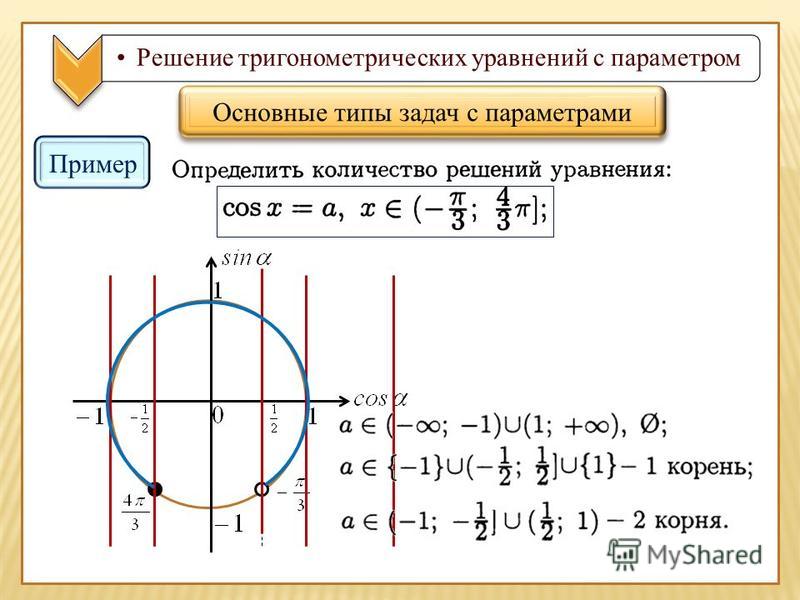

 2+12x+20=0
2+12x+20=0

 — 4
— 4
 Теоретическая основа
Теоретическая основа Понимание позволяет ученику решать нестандартные задачи, которые невозможно решить механическим применением формул. Fischbein и Muzicant (2002) указывают, что ученики обучались в основном процедурным образом и, следовательно, они часто не различали концептуальные и процедурные знания. Многим ученикам трудно понять, что буква представляет собой число, и они не знают, как работать с символическими значениями (Киран, 19 лет).92, 2014).
Понимание позволяет ученику решать нестандартные задачи, которые невозможно решить механическим применением формул. Fischbein и Muzicant (2002) указывают, что ученики обучались в основном процедурным образом и, следовательно, они часто не различали концептуальные и процедурные знания. Многим ученикам трудно понять, что буква представляет собой число, и они не знают, как работать с символическими значениями (Киран, 19 лет).92, 2014).