Формулы косинусов: Формулы синуса и косинуса суммы и разности аргументов — урок. Алгебра, 10 класс.

Формулы косинуса суммы и разности двух аргументов

Похожие презентации:

Формулы понижения степени

Формулы сложения

Тригонометрические формулы. (10 класс)

Итоговое повторение по курсу «Алгебра и начала анализа» 10 класс

Решение уравнения cosx = a. Понятие арккосинуса числа

Формулы сложения. Синус, косинус, тангенс суммы и разности аргументов

Преобразование тригонометрических выражений (вывод тригонометрических формул)

Тригонометрия. Примеры на применение формул

Формулы преобразования суммы тригонометрических функций в произведение

Тригонометрические формулы. (Лекция 4)

y
Повернём
C(x ;y )
радиус ОА,
равный 1, на
угол
x и на угол
A(x;y)
2
B(x1;y1)
O
2
y
C(x2;y2)
B(x1;y1)
O
x
OB x1 ; y1
OC x2 ; y2
Найдём скалярное произведение
векторов ОВ и ОС.
OB OC x1 x2 y1 y2
OB OC OB OC cos BOC cos BOC

4.

Вспомним, с чего все начиналось:2
sin
1
t
0
0
sin t — ордината точки поворота
y
cos
x
1
cos t — абсцисса точки поворота
y
C(x2;y2)
B(x1;y1)
O
OB OC x1 x2 y1 y2
(1)
x
Из определения синуса и косинуса:
x1 cos
y1 sin
x2 R cos
y2 R sin
Подставим данные значения в правую часть равенства (1):
OB OC cos cos sin sin
y
y
C(x2;y2)
B(x1;y1)
x
C(x2;y2)
B(x1;y1)
O
O
BOC
BOC 2 ( )
В любом случае:
cos BOC
x
OB OC cos( )
OB OC cos cos sin sin
Левые части равенств равны, значит правые тоже равны.
Получаем формулу косинуса разности двух аргументов:
cos( ) cos cos sin sin
Формула косинуса суммы двух аргументов:
cos( ) cos( ( )) cos cos( ) sin sin( )
cos( ) cos cos sin sin

8. 1. Вычислить: cos 750

Воспользуемся тем, что 750 = 450 + 300;
cos750 = cos ( 450 + 300) =
cos450·cos300 – sin450·sin300=
cos( ) cos cos sin sin

9.

2. Вычислить: cos150Воспользуемся тем, что 150 = 450 — 300;
cos150 = cos( 450 — 300) =
cos450·cos300 + sin450·sin300=
cos( ) cos cos sin sin

10. 3. Вычислить:

1) cos370cos80 – sin370sin80;
2) cos1070cos170 + sin1070sin170
Ответ: 1)
2) 0

12. cos(x–y)=cosx·cosy +sinx·siny

Докажите следствие:
cos( 2 – )=sin
cos(x–y)=cosx·cosy +sinx·siny
0
cos
2
sin
сos( 2 – )=cos 2 ·cos +sin
cos(
2
2
1
2 ·sin
– )= 0∙cosα +1∙sin = sin

13. Синус суммы

sin( ) ?
sin( ) cos( ( ))
2
cos(( ) )
2
cos(( ) )
2
y
x
cos(x–y)=cosx·cosy +sinx·siny
cos( ) cos sin( ) sin
sin
2
2
cos
sin cos cos sin
sin(α+β)=sin α ·cosβ +cos α ·sinβ

15. Синус разности

sin(α+β)=sin α ·cosβ +cos α ·sinβ
sin(α+(-β)=
sin α ·cos(-β) +cos α ·sin(-β)
sin(α-β)=sin α ·cosβ -cos α ·sinβ
Формулы сложения
cos( + )=cos ·cos -sin ·sin
cos( – )=cos ·cos +sin ·sin
sin( + )=sin ·cos +cos ·sin
sin( – )=sin ·cos –cos ·sin
Тангенс суммы и разности
двух углов
tg tg
tg
1 tg tg
tg tg
tg
1 tg tg
Котангенс суммы и
разности двух углов
сtg сtg 1
сtg
сtg сtg
сtg сtg 1
сtg
сtg сtg
/ / / / // /
tg tg
1 tg tg
1 tg tg
tg tg
sin cos cos sin
cos cos sin sin
cos
sin cos cos sin
tg tg
1 tg tg
cos cos sin sin
1 tg tg
tg tg
/ / / / // /
tg tg
1 tg tg
1 tg tg
tg tg
sin cos cos sin
cos cos sin sin
sin
sin cos cos sin
tg tg
1 tg tg
cos cos sin sin
1 tg tg
tg tg
/ / / / // /
tg tg
1 tg tg
1 tg tg
tg tg
sin cos cos sin
cos cos sin sin
cos
sin cos cos sin
tg tg
1 tg tg
cos cos sin sin
1 tg tg
tg tg
/ / / / // /
tg tg
1 tg tg
1 tg tg
tg tg
sin cos cos sin
cos cos sin sin
tg
sin cos cos sin
tg tg
1 tg tg
cos cos sin sin
1 tg tg
tg tg
/ / / / // /
tg tg
1 tg tg
1 tg tg
tg tg
sin cos cos sin
cos cos sin sin
ctg
sin cos cos sin
tg tg
1 tg tg
cos cos sin sin
1 tg tg
tg tg

24.

Не бойтесь формул! Учитесь владеть этим инструментом Человеческого гения! В формулах заключено величие и могущество Человеческого разума!
Андрей Андреевич Марков, выдающийся русский математик,
представитель петербургской математической школы,
специалист по теории чисел, теории вероятностей и
математическому анализу.

English     Русский Правила

Теорема косинусов. Формула Герона. Решение треугольников

Соотношения между сторонами и углами произвольного треугольника 85

1. Теорема косинусов. В данном параграфе докажем теорему, которая связывает длины трех сторон треугольника и косинус одного из его углов. Эта теорема называется теоремой косинусов и форму­лируется следующим образом.

Теорема 1 (теорема косинусов). Квадрат длины любой стороны треугольника

равен сумме квадратов длин двух других его сторон без удвоенного произведения длин этих сторон на косинус угла между ними.

Доказательство.

Рис. 72

1. Пусть отрезок СН — высота тре­угольника ABC с острым углом Л, АС = Ь, СВ = а, АВ = с (рис. 72).

2. В прямоугольном треугольнике АСН катет СН= b sin Л, катет АС = b cos Л. Тогда длина отрезка ВН= с — bcosA.

3. Воспользуемся теоремой Пифагора в треугольнике СВН: СВ² = СН² + ВН² или а² = (Ь віпЛ)²+ (с — b cos A f. Отсюда полу­чаем а² = б² sin² Л + с² — 26с cos² Л + б² cos² Л

или а² = Ь² + с² — 26с cos Л, так как б² sin² Л + б² cos² Л = Ь².

Нетрудно доказать, что формула верна и в случае, когда угол Л тупой. В этом случае проведите доказательство самостоятельно.

Если угол Л прямой, то теорема косинусов представляет собой тео­рему Пифагора а² = Ь² + с², так как в этом случае cos Л = cos 90° = 0.

Теорема доказана.

Аналогично квадраты длин сторон бис выражаются соответственно формулами Ь² =а² + с² — 2accosB и с² = а² + b² — 2abcosC.

Задача 1. Пусть ABC — треугольник, АВ = 5 см, ВС = 7 см, АС = 8 см. Докажите, что угол, лежащий против стороны ВС, равен 60°.

Доказательство.

По теореме косинусов верно равенство ВС² = АВ² + АС²— — 2АВ ■ ЛСсовЛ. Следовательно, 49 = 25 + 64 — 2 • 5 • 8совЛ. Отсюда

Значит, ZA = 60°.

находим, что cosA

2

Что и требовалось доказать.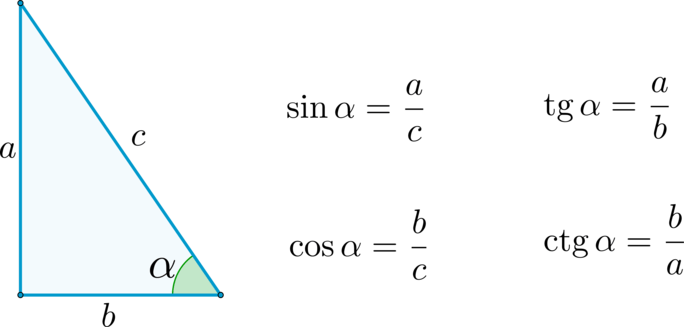

Скачено с Образовательного портала www.adu.by

86

Гл а в а 2

Соотношения между сторонами и углами произвольного треугольника 87

Скачено с Образовательного

Задача 2. В параллелограмме биссектриса тупого угла, равного 120°, делит сторону параллелограмма на отрезки 3 см и 2 см, считая от вершины острого угла. Вычислите длины биссектрисы и большей диагонали параллелограмма.

Д ано: ABCD — параллелограмм, BF — биссектриса, AF = 3 см, FD = 2 см, ZABC = 120° (рис. 73, а, б). Найти: BF и АС.

а) б)

Рис. 73 Решение.

1. Рассмотрим треугольник ABF. Так как BF — биссектриса и ZABC = 120°, то ZABF = 60°. Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°, следовательно, Z BAF = 60°. Таким образом, в треугольнике

   ABF каждый угол равен 60°, т. е. этот треугольник — равносторонний и BF = AF = AB = 3 см.

2. Для вычисления длины диагонали АС воспользуемся теоремой косинусов. В треугольнике ABC по теореме косинусов можем запи­сать АС² =АВ² + ВС² — 2АВ ■ ВС cos 120°. Так как по условию задачи

ВС = 5 см, то АС² = З² + 5² — 2 • 3 • 5 cos 120°. ГІ

. …. .. .»..’..:… …. V-

а)

в)

б) Рис. 74

Применим теорему косинусов к треугольнику ABF, в котором

, г, г, г- 1 г- лпг-

АВ = с, Вг = a, At = m_a. По теореме косинусов в треугольнике АВг

a

2

cos B. По теореме косинусов

2 9 , ^а о

можем записать т„ = с + —2с

2

Таким образом, по-Отсюда

2 2,2

а + с —о

4

2

ac

a 4

2 2,2

а + с —о

26²+2с²-а²

из треугольника ABC имеем cos B

2с

лучаем т²_а = с² +

4

2ac

1 /7Г7І 7Г~2 5″ следует, что т_а =\J2b +2c —а . Аналогично доказываются две

2 другие формулы (рис. 74, а, б, в). Заметим, что при доказательстве указанных формул можно воспользоваться следующей задачей.

Задача 4. Пусть d

lи d₂ — длины диагоналей параллелограмма, а и b — длины его сторон. Докажите, что сумма квадратов длин диаго­налей параллелограмма равна сумме квадратов длин его сторон, т. е. df + d\ = 2 (а² + b²).

Доказательство.

Пусть АС = d_l, BD = d₂ — диагонали параллелограмма ABCD и АВ = а, ВС = Ь, Z BAD = а (рис.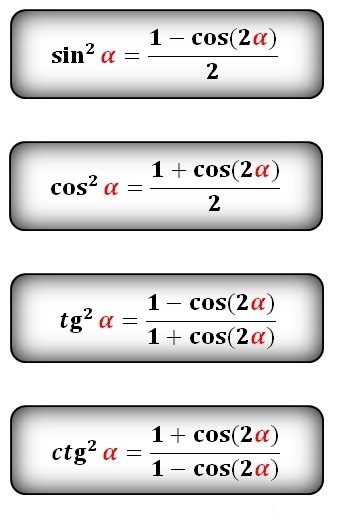 75).

По теореме косинусов в треугольнике ABD справедливо следующее равенство d

l = а² + Ь² — 2ab cos а (1).

Рис. 75

По теореме косинусов в треугольнике ABC выполняется равенство df = а² +

портала www.adu.by

88

Гл а в а 2

Соотношения между сторонами и углами произвольного треугольника 89

и

+ о²— 2ab cos (180° — a) = a² + b² + 2ab cos a (2). Складывая равенс­тва (1) и (2) почленно, получаем d\ + d\ = 2 (a² + о²).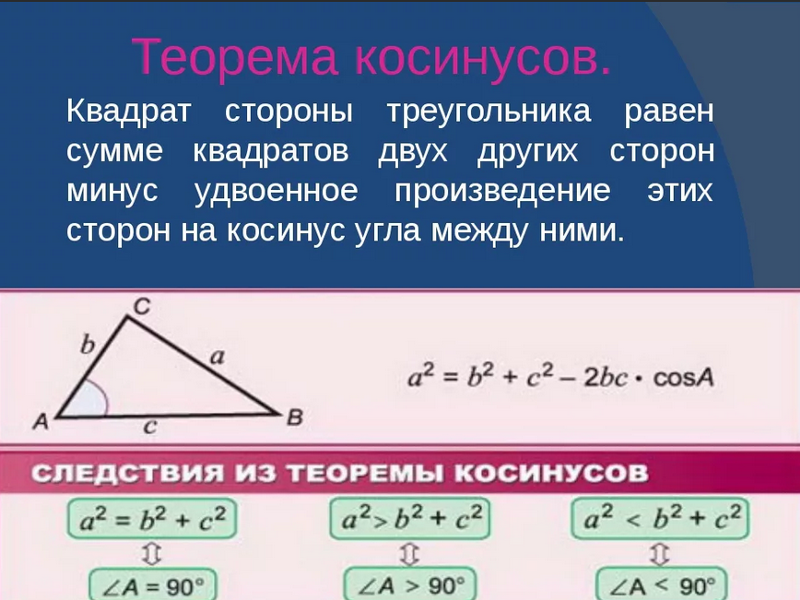 Что и требовалось доказать.

2. Формула Герона. Теперь докажем справедливость форму­лы, которая названа в честь древнегреческого математика Герона Александрийского.

Теорема 2 (формула Герона). Площадь любого треугольника можно най­ти по формуле S = yjp(p—a)(p — b)(p — c), где a, b и c — длины сторон треуголь—

a + b + c

ника, а p = — его полупериметр

2 (рис.

AS

AS

+

sin A

=. Так как sin² Л + сов²Л = 1, то 26с 2Ьс

1.

22

ный треугольник, если центр O полукруга принадлежит стороне AB (рис. 77, а).

Дано: ААВС, АВ = с, ВС = а, АС = Ь, О — центр вписанного полу­круга. Найти: г.

б)

а)

Рис. 77

Решение.

1. Пусть K и E — точки касания полукруга со сторонами AC и CB соответственно. Соединим центр O с точками K, C и E (рис. 77, б).

2. Радиус, проведенный в точку касания, перпендикулярен ка­сательной, значит, OK и OE являются высотами треугольников AO C и BOC соответственно. Площадь S треугольника ABC равна сумме площадей треугольников AO C и BOC. Следовательно,

= —(AC + ВС) = —(а + о).

S_ABC = — AC ■ UK + — ВС ■ (Jt

2 2

Отсюда 16S² = 46²c² — (б² + с² — a²)².

Используя формулу разности квадратов, преобразуем правую часть полученного равенства следующим образом:

46²с² — (б² + с² — а²)² = (26с + б² + с² — а²) (26с — Ь² — с² + а²) =

= ((о + с)² — а²) (а² — (о — с)²) =

= (о + с + а) (Ь + с — а) (а + о — с) (а — о + с) =

= 2jD (2jD — 2a) (2jD — 2c) (2p — 2b) = I6p (p — a) (p — b)(p — c). р(р—а)(р—Ь)(р—с). Таким обра-

2 I— — — —

зом, г= ■yjp(p — a)(p — b)(p — c).

а + Ь

2 I— — —

Ответ: yj р(р — а)(р — Ь)(р — с).

а + Ь

3. Решение треугольников. Решить треугольник — значит по трем его элементам найти другие его элементы. Приведем примеры задач на решение треугольника.

Задача 6 (нахождение элементов треугольника по двум сторонам и углу между ними). Даны две стороны а и о тре­угольника и угол С между ними. Найдите третью сторону и два других его угла (рис. 78).

портала www.adu.by

90

Гл а в а 2

Соотношения между сторонами и углами произвольного треугольника 91

Решение.

1. По теореме косинусов находим сто­рону с = уа²+У² -2abcosC .

2. Зная сторону с, по теореме синусов

а с теперь можем записать = .

sin A sin С

. asinC

Отсюда находим sin Л = .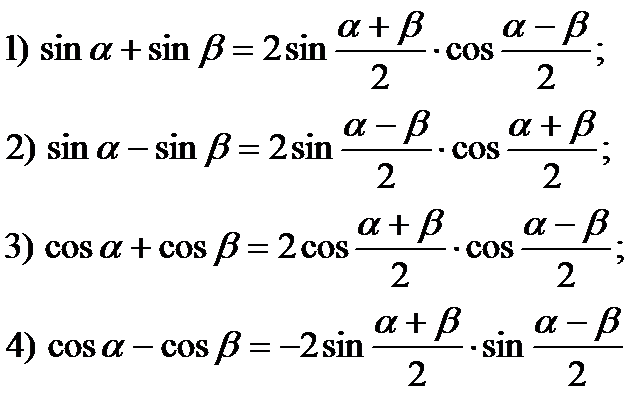

с

3) Зная sin Л, находим угол Л, а затем

Рис. 78

asinC

находим Z В = 180° — (ZA + Z С).

О т в е т:

Z В = 180°

с = yja² + b² — 2abcosC , sin A

С

(ZA + Z С).

Задача 7 (нахождение элементов треугольника по стороне и двум прилежащим к ней углам). Дана сторона ВС = а тре­угольника ABC и два прилежащих к ней угла В и С (рис. 79). Най­дите угол А и стороны АВ и АС.

Решение.

1. Находим ZA = 180° — (ZB + ZC).

2. По теореме синусов имеет место ра-

а Ь

Отсюда находим, что

венство

ь

sinA sinB

3) Аналогично по теореме синусов ^{a c} Отсюда c ^asinC

Рис. 79

sin A

sin A

sinA sinC

Ответ: ZA = 180° — (Z В + Z С) , АВ = , АС= .

sin A sin A

Задача 8 (нахождение элементов треугольника по двум сторонам и углу, противолежащему одной из них). Даны две стороны а и b треугольника и угол А. Найдите неизвестные углы треугольника и третью сторону.

Решение.

b a

Отсюда

1) Найдем синус угла B. По теореме синусов

bsin A

sinB sinA

находим sin B

a

. Если sin В < 1, то задача имеет решение, если

Скачено с Образовательного

sin В > 1, то задача не имеет решения. Возможно, что задаче удовлет­воряет два значения угла, т.е. задача имеет два решения.

2) Теперь можем найти ZC = 180° — (ZB Л— ZA).

„ с6

6) Найдем сторону с. По теореме синусов = . Отсюда

sin С sin В b sin С

находим c

sin В

n b sin A „ . ₀„₀/ , у b sin С Ответ: sine = , Z С = loU — (ZB + ZA), c = .

a sin В

b² + c² —a²

Задача 9 (нахождение углов треугольника по трем сторо­нам). Даны стороны a, b и с треугольника ABC. Найдите углы этого треугольника.

2сЬ

1) По теореме косинусов находим cos Л

2) Синус угла B найдем по теореме синусов: sin B

bsin A

3) Теперь находим ZC = 180° — (ZA + ZB).

b sin A

Ответ: cos A = ^b2+c2—a2 , sin B

a

C = 180° — (ZA + ZB).

a

2cb

Что такое формула правила косинуса | עמקניוז

В этом примере мы использовали закон уравнения косинуса, чтобы найти недостающий угол. Теперь воспользуемся законом уравнения косинуса, чтобы найти недостающую страницу. Формулы косинуса говорят о функции косинуса (cos). Рассмотрим прямоугольный треугольник, один из острых углов которого равен х. Тогда формула для косинуса: cos x = (прилежащая сторона) / (гипотенуза), где «прилежащая сторона» — это сторона, примыкающая к углу x, а «гипотенуза» — самая длинная сторона (сторона, противоположная прямому углу) треугольника. Помимо этой общей формулы, в тригонометрии существует множество других формул, определяющих функцию косинуса, которые вы можете видеть на рисунке ниже. Обратите внимание на два разных выражения для площади треугольника (ABC) и выведите правило синусоиды. Простой ответ — нет из-за природы функции косинуса и связи с нахождением угла в треугольнике. Например, если вы возьмете cos(60), он вернет на калькуляторе тот же ответ, что и cos(300). При большей тригонометрии закон косинуса можно вывести с помощью теоремы Пифагора только один раз. Фактически, используя прямоугольный треугольник в левой части рис. 6, можно показать, что: c 2 = ( b − a cos γ ) 2 + ( a sin γ ) 2 = b 2 − 2 a b cos γ + a 2 cos 2 γ + a 2 sin 2 γ = b 2 + a 2 − 2 a b cos γ , {DisplayStyle {begin{align}Quad C^{2}&=(B-ACOS gamma )^{2}+(Asin гамма )^{2}&=B^{2}-2ABCOS гамма +A^{2}COS ^{2}гамма +A^{2}sin ^{2}гамма &=b^{2}+A^ {2}-2abCOS gamma ,end{aligned}}} Мы будем использовать определение закона косинуса: a2 = b2 + c2 – 2bc·cosA.

Тупое падение. На рис. 7b шестиугольник разрезается на более мелкие части двумя разными способами, обеспечивая доказательство закона косинуса в случае, когда угол γ тупой. У нас есть версии, подобные закону косинуса для евклидовой плоскости, также пригодные для единичной сферы и гиперболической плоскости. В сферической геометрии треугольник определяется тремя точками u, v и w на единичной сфере и дугами больших окружностей, соединяющими эти точки. Если эти большие окружности образуют углы A, B и C с противоположными сторонами a, b, c, то сферический закон косинуса утверждает, что выполняются следующие два соотношения: закон косинуса используется для нахождения недостающей стороны треугольника, если его Даны две стороны и замкнутый угол. Есть три закона косинуса, и мы выбираем один из них для решения наших задач на основе имеющихся данных. Закон косинуса используется при поиске недостающей стороны треугольника, когда заданы две его стороны и замкнутый угол, т.е. он используется в случае треугольника SAS. В тригонометрии закон косинуса (также известный как формула косинуса, правило косинуса или теорема аль-Каши[1]) связывает длины сторон треугольника с косинусом одного из его углов. Используя обозначения, как на рис. 1, формулируется закон косинуса. Замена предыдущего уравнения дает закон косинуса: закон косинуса помогает установить связь между длинами сторон треугольника и косинусом его углов. Закон косинуса в тригонометрии обобщает теорему Пифагора для прямоугольного треугольника.

Как правило, один из трех углов может быть тупым. Формула по-прежнему верна, хотя геометрическое доказательство немного отличается. Если угол γ мал, а смежные стороны a и b имеют одинаковую длину, правая часть стандартной формы закона косинуса подвергается катастрофической приостановке в численных приближениях. В ситуациях, когда это вызывает серьезную озабоченность, может оказаться полезной математически эквивалентная версия закона косинуса, подобная неформальному закону Хейверса: в модуле «Дополнительная тригонометрия» (10-й год) мы ввели и доказали правило синусов, найти стороны и углы в непрямоугольных треугольниках. Распространенной ошибкой является использование функции синуса вместо функции косинуса. Это доказательство использует тригонометрию, рассматривая косинусы различных углов как отдельные величины. Он использует тот факт, что косинус угла выражает отношение между двумя сторонами, которые заключают этот угол в любом прямоугольном треугольнике. Другие доказательства (ниже) более геометрические, потому что они рассматривают выражение как cos γ просто как метку длины определенного отрезка прямой. Используя молекулярную формулу функции косинуса, мы имеем cos(x + y) = cos(x) cos(y) – sin(x) sin(y). Если мы заменим x = y с обеих сторон, мы получим cos 2x = cos2x – sin2x.

Используя тождество Пифагора sin2x + cos2x = 1, с помощью приведенной выше формулы мы можем вывести две другие формулы косинуса двойного угла: cos 2x = 2 cos2(x) − 1 и cos 2x = 1 – 2 sin2(x) . Правило косинуса также применяется, если угол (C) тупой. Обратите внимание, однако, что в этом случае последний член формулы дает положительное число, потому что косинус тупого угла отрицателен.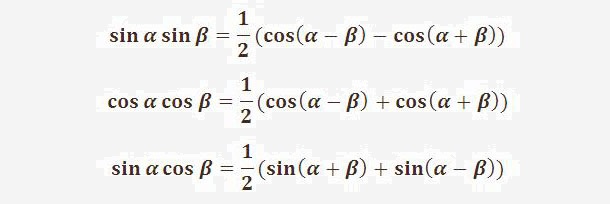 В этом случае рекомендуется соблюдать осторожность. Формула для нахождения сторон треугольника по правилу косинуса приведена ниже: Формулы косинуса относятся к функции косинуса. Важными формулами косинуса являются: Если три стороны треугольника известны, то три угла определены однозначно. (Это тест на конгруэнтность SSS.) Опять же, правило синусоид не помогает найти три угла, так как требует знания хотя бы одного угла, но вместо этого мы можем использовать правило косинуса. где sinh и ch — гиперболические синус и косинус, а — вторая. Как и в евклидовой геометрии, можно использовать закон косинуса для определения углов A, B, C по знанию сторон a, b, c. В отличие от евклидовой геометрии в двух неевклидовых моделях возможно и обратное: углы A, B, C определяют стороны a, b, c. Эту формулу можно преобразовать в закон косинуса, утверждая, что CH = (CB) cos (π — γ) = — (CB) cos γ.

Тезис 13 содержит совершенно аналогичное утверждение для остроконечных треугольников. Если мы вспомним тождество Пифагора, то получим закон косинуса: второй важной формулой для общих треугольников является правило косинуса. Мы только что видели, как найти угол, зная три стороны. Это заняло несколько шагов, поэтому проще использовать «прямую» формулу (которая представляет собой просто перестановку формулы c2=a2+b2−2ab cos(C)). Это может быть в одной из следующих форм: Правило косинуса относится к длинам сторон треугольника, где каждый из его углов является углом косинуса. С помощью этой линейки мы можем вычислить длину стороны треугольника или найти меру угла между сторонами. Теперь закон косинуса представлен простым применением теоремы Птолемея к четырехстороннему циклу ABCD: Мы также можем переписать формулу c2 = a2 + b2 − 2ab cos(C) в виде a2= и b2=. Есть три закона косинуса, и мы выбираем один из них для решения наших задач на основе имеющихся данных. Закон косинуса выражается тремя различными способами. Это тезис Евклида 12 книги 2 «Начал». [5] Чтобы преобразовать его в современную форму закона косинуса, обратите внимание, что элементы Евклида способствовали открытию закона косинуса.

Джамшид аль-Каши, персидский математик, первым в 15 веке сделал явное утверждение о законе косинуса. Из теста на конгруэнтность SAS мы знаем, что треугольник полностью определен, когда у нас есть две стороны и угол замкнут. Однако, если мы знаем две стороны и замкнутый угол в треугольнике, правило синусоиды не поможет нам определить оставшиеся углы. Мы знаем, что функция косинуса (cos) и функция секанса (sec) обратны. конкретно. Если COS X = A/B, то Sec X = B/A. Таким образом, используя одно из обратных тождеств, формула косинуса выглядит так: она аналогична теореме Пифагора, за исключением третьего члена, и если C — прямой угол, третий член равен 0, потому что косинус 90° есть 0, и мы получаем теорему Пифагора. Таким образом, теорема Пифагора является частным случаем закона косинусов.

Закон косинуса обобщает теорему Пифагора, которая применима только к прямоугольным треугольникам: если угол γ является прямым (составляет 90 градусов или π/2 радиана), то cos равен γ = 0, и, таким образом, закон косинуса сводится к теореме Пифагора: используем формулу a2 = b2 + c2 – 2bc·cos A, так как искомая сторона противоположна ∠A. Используя одну из формул двойного угла, cos равен 2x = 2 cos2 x – 1. Замена x на (x/2) с обеих сторон дает cos x = 2 cos2 (x/2) – 1. Если вы решите это для cos (x/2), вы получаете cos (x/2) = ± √[ (1 + cos x) / 2]. Закон косинуса гласит, что для любого заданного треугольника у нас есть ABC со сторонами a, b и c; Хотя понятие косинуса в свое время еще не было разработано, элементы Евклида 3 века до н.э. содержат раннюю геометрическую теорему, почти соответствующую закону косинуса. Случаи тупых треугольников и остроконечных треугольников (соответствующие двум случаям отрицательного или положительного косинуса) рассматриваются отдельно в тезисах 12 и 13 Книги 2. Поскольку во времена Евклида отсутствовали тригонометрические функции и алгебра (особенно отрицательные числа), утверждение имеет более геометрический привкус: формула закона косинуса может быть использована для нахождения недостающей стороны треугольника, когда заданы две его стороны и замкнутый угол, т.е. она используется в случае SAS-треугольника.

Свойства, химическая структура и применение

Учащиеся должны запомнить все формулы, приведенные в их учебниках по математике. Они должны знать, что им будет легче, если все формулы останутся в их мозгу. Согласно формуле косинуса в тригонометрии, квадрат длины любой стороны данного треугольника равен сумме квадратов других сторон минус удвоенное произведение двух других сторон на формулу косинуса угла, который их разделяет. Закон косинусов и Формула косинуса — это другие названия правила косинуса. Учащиеся должны знать, что математика играет важную роль в их школьной программе, если они хотят продолжить карьеру в области математики.

Предположим, что a, b и c — длины сторон треугольника ABC;

a2 = b2 + c2 – 2bc cos ∠x

b2 = a2 + c2 – 2ac cos ∠y

c2 = a2 + b2 – 2ab cos ∠z

Формула косинуса является тригонометрической формулой косинуса. Одна из шести тригонометрических функций, функция косинуса (часто сокращенно «cos») представляет собой отношение соседней стороны к гипотенузе. Многочисленные тождества и формулы, связанные с тригонометрией, можно использовать для получения многочисленных формулировок функции косинуса. Студенты могли изучить Формула косинуса и несколько примеров с решениями.

Функция косинуса (cos) обсуждается в Формула косинуса . Учащиеся могут предположить прямоугольный треугольник, где х — острый угол. Таким образом, уравнение косинуса записывается как cos x = (прилежащая сторона) / (гипотенуза), где «прилежащая сторона» относится к стороне, следующей за углом x, а «гипотенуза» относится к самой длинной стороне треугольника (стороне, расположенной напротив угла x). прямой угол). Существуют и другие различные тригонометрические формулы, которые определяют функцию косинуса в дополнение к этой стандартной формуле, как показано на следующем рисунке.

Учащиеся знают, что существует обратная зависимость между функцией косинуса (cos) и функцией секанса (sec). В частности, cos x = a/b, тогда sec x = b/a. Таким образом, используя одно из взаимных тождеств, Формула косинуса будет,

cos x = 1 / (sec x)

Студенты должны регулярно и правильно практиковаться с каждым вопросом перед экзаменом, чтобы у них не возникало никаких проблем. при решении любого вопроса. Следовательно, точность и точность являются наиболее важным аспектом математики, и учащийся должен осознавать важность формул и практики.

Формула косинуса

Тригонометрическое тождество описывает связь между sin и cos. В нем говорится, что для любого значения x sin2x плюс cos2x равно 1. Это может быть разрешено для cos x.

Студенты могут рассмотреть sin2x + cos2x = 1.

Sin2x с обеих сторон вычитается,

cos2x = 1 – sin2x

квадратный корень с каждой стороны,

cos x = ± √(1 – sin2x)

3 отношения между кофункциями sin, cos, sec, csc, tan и cot определяются тождествами кофункций. Следует использовать одно из тождеств кофункций.

cos x = sin (90o – x) (OR)

cos x = sin (π/2 – x)

Примеры формулы косинуса x

Каждая тригонометрическая функция имеет формулу суммы/разности, которая работает сумма углов (x + y) и разность углов (x – y). Формулы для суммы и разности функции формулы косинуса : (x) cos (y) + sin (x) sin (y)

В тригонометрии есть формулы двойного угла, которые имеют дело с углами, которые в два раза больше. В зависимости от имеющейся информации для решения задачи можно использовать одну из следующих формул cos двойного угла. Это так:

cos 2x = cos2(x) – sin2(x)

cos 2x = 2 cos2(x) − 1

cos 2x = 1 – 2 sin2(x)

cos 2x = [(1 – tan2x)/ (1 + tan2x)]

Часто задаваемые вопросы (Часто задаваемые вопросы)

1. Как работает формула косинуса?

Функция косинуса связана с формулой косинуса . Ниже приведены некоторые важные формулы косинуса :

cos x = (прилежащая сторона) / (гипотенуза)

cos x = 1 / (sec x)

cos x = ± √(1 – sin2x)

cos x = sin (π/2 – x)

2. Для каких целей используется формула косинуса?

Существует несколько формул косинуса , которые учащиеся усвоили в ходе изучения учебного плана. Они могли выбрать один из них, чтобы продемонстрировать тригонометрическую идентичность или определить значение функции косинуса, используя имеющиеся факты. Формулы косинуса можно использовать для определения недостающих углов или сторон треугольника.