Асимптоты кривой — Энциклопедия по экономике
V Пример 1. Найти асимптоты кривых [c.170]V Пример 2. Найти асимптоты кривой у — ж3 — 3 ж. [c.173]
Асимптота кривой при ->- оо есть Ь. Такая связь бывает часто, например, между объемом производства (х) и себестоимостью продукции (у). Действительно с ростом объема производства при определенных условиях себестоимость продукции монотонно снижается с уменьшающейся скоростью и при любом большом объеме производства не может быть ниже некоторого предела Ь, трактуемого в данном случае как условно-переменная часть себестоимости. [c.47]
Все три кривые имеют асимптотами оси координат, хотя и приближаются к ним. с разной скоростью. Это [c.62]
Эта кривая имеет две асимптоты. При L — + °° основные фонды К постоянно убывают, но стремятся не к нулю, как в случае функции Кобба — Дугласа, а к некоторому положительному числу [c.64]
Эта кривая имеет асимптоту, т. е. при бесконечном росте фондовооруженности производство не растет неограниченно, как в случае функции Кобба —
[c.65]
е. при бесконечном росте фондовооруженности производство не растет неограниченно, как в случае функции Кобба —
[c.65]
В свою очередь пределом накопленного роста ресурсов и запасов категорий С3 и С2 является оценка НСР на соответствующий момент времени. В разрезе пятилетнего планирования такая последовательность движения ресурсов приводит к тому, что на момент планирования объем возможной добычи предопределен на три пятилетки вперед (рис. 6). Если планирование начинается с задания плана добычи на момент t0, то оценка асимптоты аппроксимирующей кривой определит необходимый уровень состояния запасов категорий А + В + Q на момент предшествующей пятилетки и т. д. [c.23]
Большинство методов, рассматриваемых в этой книге, эффективны при долгосрочных стратегиях. На протяжении всей книги вы будете встречать термин асимптотический смысл , что означает возможный результат чего-либо, осуществленного бесконечное число раз, когда вероятность приближается к определенности при увеличении количества попыток.
 Другими словами, что-то, в чем мы можем быть почти уверены с течением времени. Смысл этого выражения содержится в математическом термине асимптота , которая является прямой и ограничивает кривую линию в том понимании, что расстояние между двигающейся точкой кривой и прямой линией приближается к нулю, когда точка удаляется на бесконечное расстояние от начала координат.
[c.5]
Другими словами, что-то, в чем мы можем быть почти уверены с течением времени. Смысл этого выражения содержится в математическом термине асимптота , которая является прямой и ограничивает кривую линию в том понимании, что расстояние между двигающейся точкой кривой и прямой линией приближается к нулю, когда точка удаляется на бесконечное расстояние от начала координат.
[c.5]Другое расхожее заблуждение состоит в том, что будто бы увеличение числа компонентов портфеля снижает его эффективность, или что в пределе выгода от увеличения числа компонентов убывает, то есть достигает некоторой асимптоты. Это не так кривая зависимости между этими факторами отличается от логарифмической и, скорее всего, представляет собой прямую линию, поднимающуюся снизу вверх и слева направо, ибо с помощью диверсификации мы достигаем только увеличения Т. Всякий прирост Т соответствующим образом увеличивает прирост счета, который не имеет асимптот. [c.69]
Следовательно, кривая имеет вертикальную асимптоту х = 1.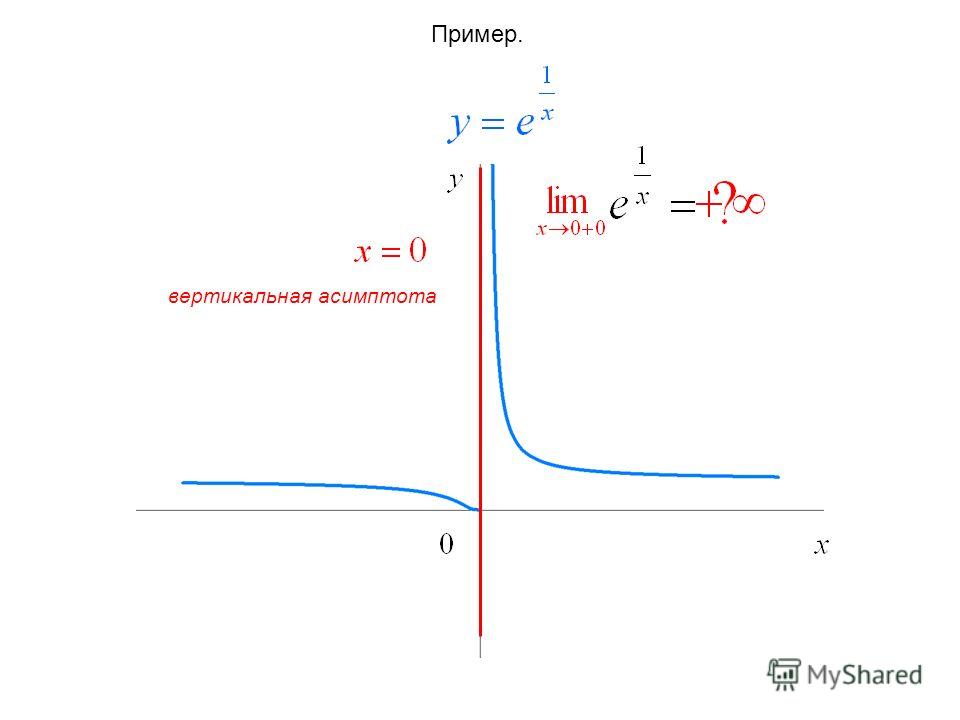 2) Найдем наклонные и горизонтальные асимптоты (если они есть). Для этого вычислим соответствующие пределы [c.171]
2) Найдем наклонные и горизонтальные асимптоты (если они есть). Для этого вычислим соответствующие пределы [c.171]
Кривая имеет перегиб в точке x — 4nb и асимптоту у = а. По-видимому, логистической кривой удобно описывать процесс изменения объема производства предприятия [c.47]
Этот тип кривых (рис. 6.3) характеризуется двумя асимптотами (прямыми, к которым график функции неограниченно приближается, не достигая их) горизонтальной у = а и вертикальной х = 0, а также параметром искривления Ь. С помощью преобразования независимой переменной х = l/х (т. е. перехода к новому аргументу) эта зависимость приводится к линейному виду у = а + Ьх [c.185]
Рассматриваемые кривые (рис. 6.5) имеют горизонтальную асимптоту у = На, вертикальную асимптоту х — — Ыа и характеристику искривления, равную — b/а 2. С помощью [c.186] Кривые (рис. 6.6) проходят через точку (0,Л), причем ось х является их горизонтальной асимптотой. Если вместо т] (соответственно y j) в качестве зависимой переменной рассмотреть величину т] = In ц (соответственно / = In то данная зависимость преобразуется к линейному виду — а + Ьх, в котором а == In A [c.
 187]
187]При b > 0 кривая (рис. 6.7, а) имеет горизонтальную асимптоту у = А и вертикальную асимптоту х = 0. При Ь [c.187]
Частный случай так называемой логистической кривой показан на рис. 6.8. Кривая имеет две горизонтальные асимптоты у = 0 и у = На и точку перегиба (In ( /a ), 1/2я). Линеаризация этой зависимости производится с помощью перехода к новым переменным т] = 1/т (соответственно yt = и А = ег . [c.188]
Все кривые на рисунке проходят через точку (1, Л), причем если Ъ > 0, то они проходят еще и через начало координат — точку (0, 0), а если b [c.189]
Кривые на рисунке проходят через точку (1, а ) и имеют в качестве вертикальной асимптоты ось у (т. е. х = 0). Переход к линейному виду зависимости осуществляется с помощью логарифмического преобразования аргумента х = In х. [c.189]
Обычно дифференциальное уравнение является уравнением второго порядка в х, так как q = dx/dt и требует, таким образом, двух конечных условий. Одно из них х = О при t = 0.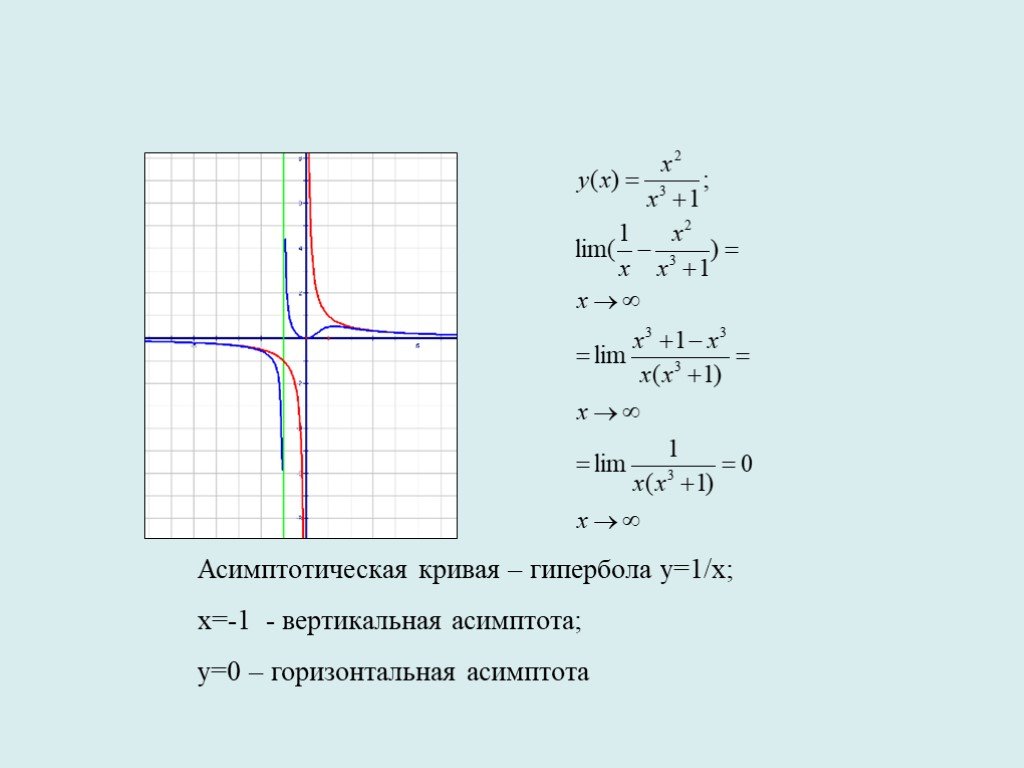 Другой конец кривой, представляющий х как функцию t, может быть в любом месте на линии х = а, или кривая может иметь эту линию как асимптоту. Эту неопределенность можно
[c.279]
Другой конец кривой, представляющий х как функцию t, может быть в любом месте на линии х = а, или кривая может иметь эту линию как асимптоту. Эту неопределенность можно
[c.279]
На нулевой итерации в качестве оценок при переменных емкостях складов закладываются условно постоянные затраты /а,-(о) = ао, Що) = а°/, взятые из уравнений (1) и соответствующие асимптотам гиперболических кривых после решения задачи, т. е. вычисления плана я(0), корректируем коэффициенты удельных затрат по формулам (1), исходя из плана л(0> [c.396]
А и а — положительные параметры. Из данного уравнения следует если х > О, то у > 0, если у > О, то х > 0. Кривая Парето имеет две асимптоты х = а и у = 0. Если ось у перенести в точку Р, соответствующую минимальному из рассматриваемых доходов, то а = О и уравнение кривой Парето имеет следующий вид [c.225]
Постройте кривые безразличия функции полезности y=xt х2 при уровнях полезности.равных 2 иЗ. Найдите их асимптоты. [c.41]
Кривые спроса замкнуты, следовательно, в гиперболах количества. Можно также сказать, что обычно эти кривые пересекают оси координат и не являются их асимптотами.
[c.48]
Можно также сказать, что обычно эти кривые пересекают оси координат и не являются их асимптотами.
[c.48]
Термин асимптота введен древнегреческим ученым Аполлонием Пергским при изучении гиперболы и происходит от греческого слова асимтотос , означающего несовпадающий . Пусть это слово не вводит вас в заблуждение. Асимптоты гиперболы действительно не пересекают график функции (т. е. являются в некотором смысле несовпадающими ). Однако, согласно современным представлениям об асимптоте, кривая может пересекать свою асимптоту (например, график затухающих колебаний, изображенный на рис. 9.18). [c.165]
При выборе кривой следует определять, может ли данное явление (процесс) насыщаться, т. е. приближаться к пределу. Например, гиперболическая функция, модифицированная экспоненциальная функция, кривая Гомперца, логическая кривая имеют асимптоту и могут применяться лишь для аналитическое го выравнивания процессов, имеющих тенденцию к насыщению,. т. е. ограниченных в своем росте. [c.29]
[c.29]
Более наглядное представление о динамике разведанной части ресурсов и добычи дают так называемые кривые освоения ресурсов. В работах [48, 6, 27, 18, 24] оценка НСР принималась в качестве асимптоты, ограничивающей рост накопленных запасов и добычи. К. С. Баймухаметов и М. М. Саттаров предложили при построении кривой накопленных запасов учитывать лишь достоверную часть НСР, а также анализировать кривые освоения запасов различных категорий. М. Д. Белонин и др. [4] более детально исследовали временной аспект в освоении ресурсов нефти и газа различных категорий ло пятилеткам. [c.22]
Исследование динамики социальных и экономических процессов выявило довольно сильную распространенность эффекта насыщения выхода на асимптоту при достижении определенных значений показателей. В силу этого в эконометрике большое распт ространение получили так называемые кривые с насыщением. К этому типу кривых относится кривая Гомперца — s-образная кривая, предложенная Б. Гомперцем (1799—1865), которая имеет вид
[c.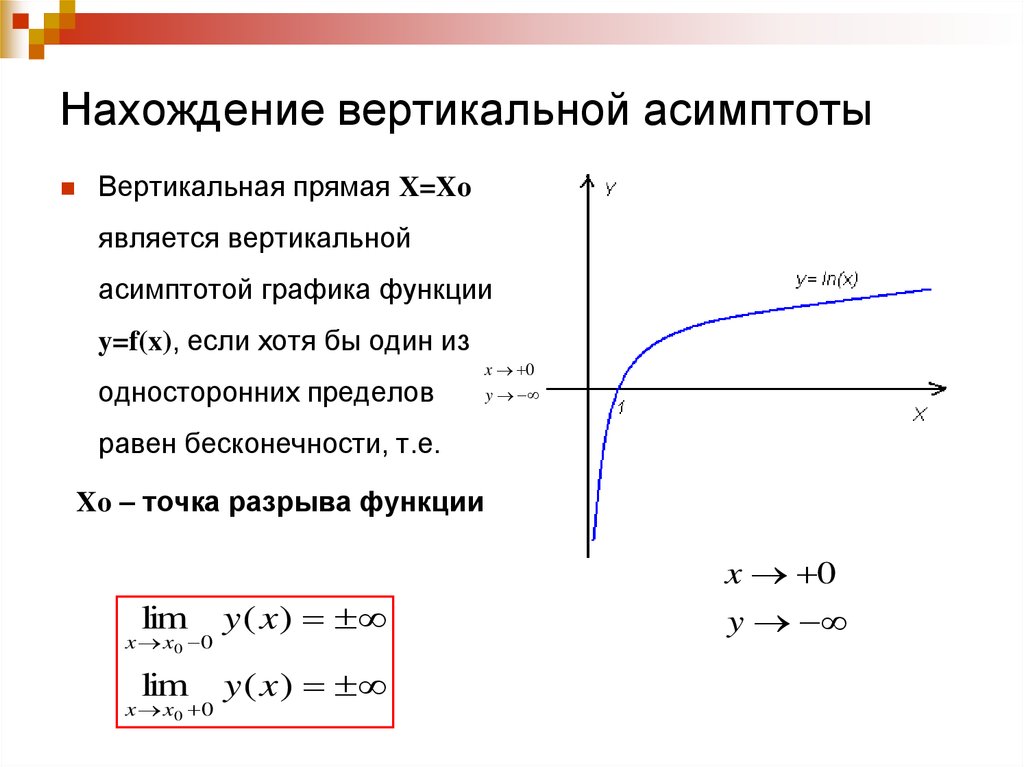
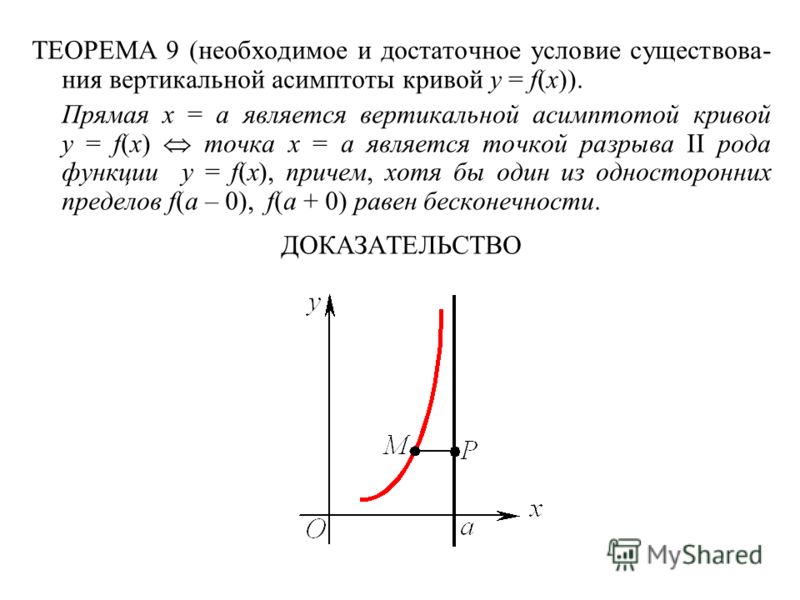
АСИМПТОТА [asymptote] — прямая, к которой стремится (никогда не достигая ее) имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент приближается к некоторому заданному значению, неограниченно возрастает или уменьшается. Напр., в функции у = с + + Их значение у приближается с возрастанием х к величине с сколь угодно близко («асимптотически стремится к ней»). [c.24]
Следовательно, кривая sBS представляет собой логарифмическую кривую, подкасательная которой всегда равна Ь, а асимптотой является прямая Qq.»1 [c.17]
Следует, однако, учесть, что возрастание темпов роста Уд не может быть бесконечным. По мере включения в сферу разработки взаимодействий ОМФ с внешней средой, сложность их реализации возрастает, поскольку приходится включать в сферу деятельности задачи и процессы, требующие все более высоких инвестиционных затрат для реализации. Поэтому в некоторой точке И, соответствующей уровню актуализации У , будет достигнут максимальный темп роста, т.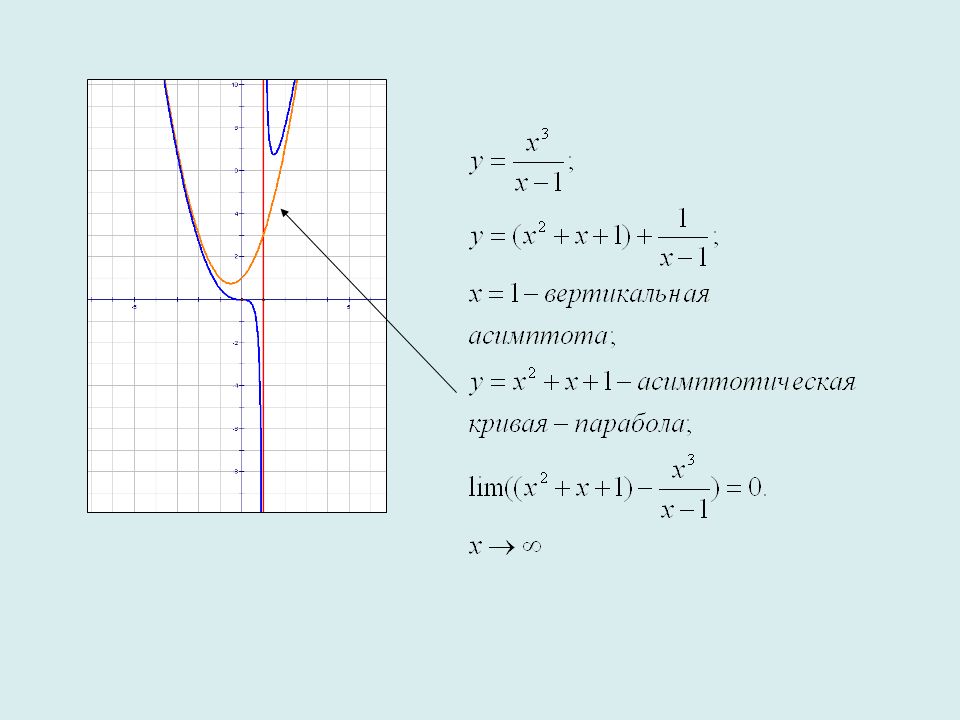
Дисперсионная кривая для уравнения (4.27) изображена на рис. 48. Согласно формулам (4.23), (4.24) и (4.27) она количественна правильно описывает поведение дисперсионной кривой в области длинных волн.. Кроме того, при больших Re А , имеется качественно правильное соответствие кривая выходит на асимптоту o.
До сих пор в ходе нашего обсуждения мы предполагали, что кривые спроса AdAp, BdBp, B dB p пересекают обе оси координат. Надо рассмотреть крайний случай, когда кривые спроса, совпадая с гиперболами наличного количества, оказываются асимптотами к этим осям. [c.58]
Как найти асимптоты кривой?
Как найти асимптоты кривой? | Ответы MyTutor>Дополнительная математика>Уровень A>Статья
Асимптоты кривой — это линии или кривые, которые очень близко подходят к данной кривой, но фактически не касаются ее. Они значительно упрощают рисование кривых. У вас, вероятно, будут только асимптоты, которые являются линиями, и в этом случае у вас будут либо горизонтальные асимптоты, либо вертикальные асимптоты. Горизонтальные асимптоты Чтобы найти горизонтальные асимптоты, мы хотим увидеть поведение кривой при стремлении x к бесконечности. Итак , мы смотрим на порядок числителя и знаменателя: Случай 1 : Если порядок числителя больше, чем порядок знаменателя (например, если функция f(x) = x 3 /(2x 2 +1 ) поскольку x 3 имеет порядок 3, а x 2 имеет порядок 2), то горизонтальных асимптот не будет. Случай 2 : если порядок числителя меньше порядка знаменателя (например, если функция f(x) = 1/x), то горизонтальная асимптота будет y=0 Случай 3 : если порядок числителя такой же, как и порядок знаменателя, например, функция f(x) = (2x 2 — 4) / (x 2 — 1), тогда мы смотрим на член высшего порядка для обеих сторон и посмотрите на коэффициент этого. Другими словами, мы игнорируем все остальные члены, кроме 2x 2 и x 2 , поэтому 2x 2 /x 2 = 2. Итак, в этом случае асимптота y=2. Но почему это работает? Для горизонтальных асимптот мы эффективно смотрим на то, что будет делать наша кривая, когда x стремится к бесконечности. Таким образом, в случае 1, когда числитель больше знаменателя, поскольку x стремится к бесконечности, y стремится к бесконечности, поэтому асимптота отсутствует. В случае 2, когда x стремится к бесконечности, мы находим, что y стремится к нулю. В случае 3 при стремлении x к бесконечности все меньшие члены становятся незначимыми.
Случай 2 : если порядок числителя меньше порядка знаменателя (например, если функция f(x) = 1/x), то горизонтальная асимптота будет y=0 Случай 3 : если порядок числителя такой же, как и порядок знаменателя, например, функция f(x) = (2x 2 — 4) / (x 2 — 1), тогда мы смотрим на член высшего порядка для обеих сторон и посмотрите на коэффициент этого. Другими словами, мы игнорируем все остальные члены, кроме 2x 2 и x 2 , поэтому 2x 2 /x 2 = 2. Итак, в этом случае асимптота y=2. Но почему это работает? Для горизонтальных асимптот мы эффективно смотрим на то, что будет делать наша кривая, когда x стремится к бесконечности. Таким образом, в случае 1, когда числитель больше знаменателя, поскольку x стремится к бесконечности, y стремится к бесконечности, поэтому асимптота отсутствует. В случае 2, когда x стремится к бесконечности, мы находим, что y стремится к нулю. В случае 3 при стремлении x к бесконечности все меньшие члены становятся незначимыми. Давайте посмотрим поближе. Чтобы полностью понять, мы можем заменить x = 1000 (или любое другое большое число), чтобы примерно увидеть, что происходит. Случай 1: f(x) = x 3 /(2x 2 +1). Установив x=1000, мы получим f(1000)= 1000 3 /(2(1000) 2 +1) = 500, и если мы установим x= 10000, то f(x)=5000, поэтому горизонтальной асимптоты нет здесь. Случай 2: f(x) = 1/x. Установив x = 1000, мы получим f(1000)=0,001, что близко к нулю. Точно так же f(10000) = 0,0001, поэтому при увеличении x f(x) стремится к нулю. Вот почему асимтота y=0 Случай 3: f(x) = (2x 2 — 4) / (x 2 -1). f(1000) = (2(1000) 2 — 4) / ((1000) 2 -1)= 1,999998, что примерно равно 2. Если мы увеличим x еще больше, то f(10000)= 1,99999998, что четно ближе к 2. Именно поэтому асимптота y=2 Вертикальные асимптоты: Здесь мы фактически наблюдаем поведение кривой, когда f(x)=y стремится к бесконечности.
Давайте посмотрим поближе. Чтобы полностью понять, мы можем заменить x = 1000 (или любое другое большое число), чтобы примерно увидеть, что происходит. Случай 1: f(x) = x 3 /(2x 2 +1). Установив x=1000, мы получим f(1000)= 1000 3 /(2(1000) 2 +1) = 500, и если мы установим x= 10000, то f(x)=5000, поэтому горизонтальной асимптоты нет здесь. Случай 2: f(x) = 1/x. Установив x = 1000, мы получим f(1000)=0,001, что близко к нулю. Точно так же f(10000) = 0,0001, поэтому при увеличении x f(x) стремится к нулю. Вот почему асимтота y=0 Случай 3: f(x) = (2x 2 — 4) / (x 2 -1). f(1000) = (2(1000) 2 — 4) / ((1000) 2 -1)= 1,999998, что примерно равно 2. Если мы увеличим x еще больше, то f(10000)= 1,99999998, что четно ближе к 2. Именно поэтому асимптота y=2 Вертикальные асимптоты: Здесь мы фактически наблюдаем поведение кривой, когда f(x)=y стремится к бесконечности.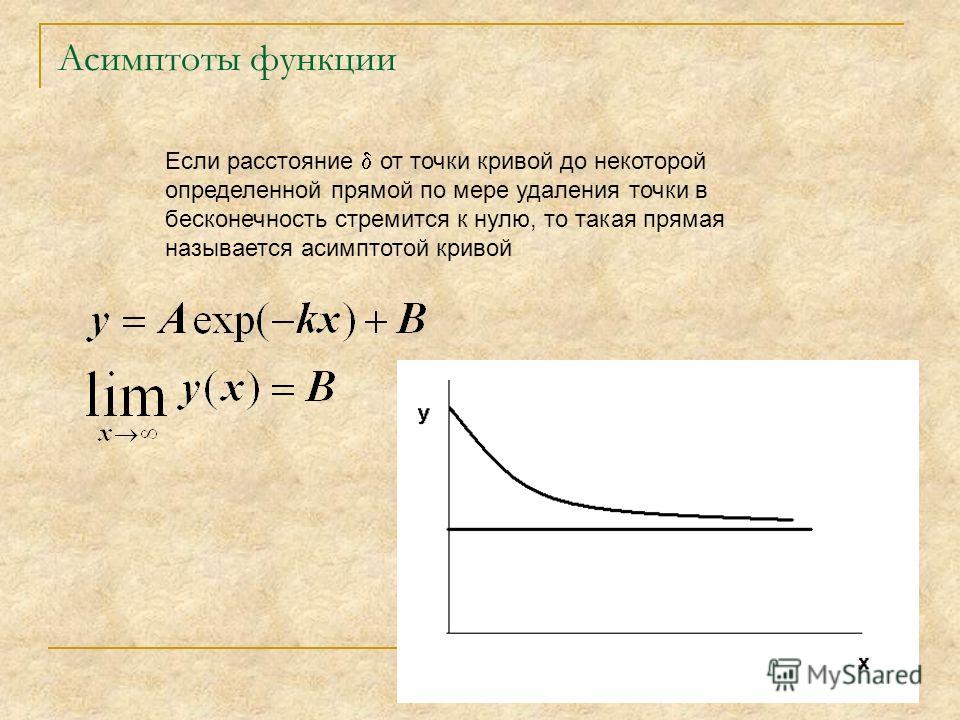 Единственный раз, когда будут вертикальные асимптоты, это когда порядок знаменателя дроби больше, чем порядок числителя. Поскольку f(x) будет стремиться к бесконечности, знаменатель нашей кривой будет стремиться к нулю. Например, рассмотрим кривую f(x) = (2x 92 — 2x + 2 = 0 имеет корни A и B, найдите значения A + B и A * B.
Единственный раз, когда будут вертикальные асимптоты, это когда порядок знаменателя дроби больше, чем порядок числителя. Поскольку f(x) будет стремиться к бесконечности, знаменатель нашей кривой будет стремиться к нулю. Например, рассмотрим кривую f(x) = (2x 92 — 2x + 2 = 0 имеет корни A и B, найдите значения A + B и A * B.
Brilliant Math & Science Wiki
Основная статья: Вертикальные асимптоты.
Одним из самых простых примеров кривой с асимптотами будет y=1x.y=\frac{1}{x}.y=x1. Обратите внимание, что это рациональная функция. Чтобы найти ее асимптоты, мы берем пределы всех значений, где функция не определена, а именно −∞,0,-\infty, 0,−∞,0 и ∞.\infty.∞. Для x→0,x\rightarrow 0,x→0 мы должны проверить как правый, так и левый пределы. Тогда у нас есть 9{+},x→0+, кривая идет бесконечно вверх, сходясь к положительной стороне оси yyy.
Таким образом, асимптотами y=1xy=\frac{1}{x}y=x1 являются оси xxx и yyy. Теперь взгляните сами на график кривой и убедитесь, что наш вывод соответствует рисунку.
Вы, наверное, заметили, что лучший способ найти асимптоты — просто нарисовать график, и вы правы! Итак, если график кривой, с которой мы имеем дело, вам знаком, просто нарисуйте график и попытайтесь понять, где должны быть асимптоты. Для сложных функций было бы полезно оценить их график дифференцированием. Давайте рассмотрим некоторые случаи и посмотрим, как это делается. 9{-x} y=e−x
y=arctanxy = \arctan xy=arctanx
- На первом графике оба предела limx→∞f(x) \displaystyle \lim _{x \to \infty } f(x) x→∞limf(x) и limx→−∞f(x) \displaystyle \lim _{x \to — \infty } f(x) x→−∞lim f(x) не конечны. Поэтому на первом графике отсутствуют горизонтальные асимптоты.
- Во втором графике только один из пределов конечен, а значит, имеет только одну горизонтальную асимптоту.
- На третьем графике оба предела постоянны, но оба предела равны, поэтому имеется только одна горизонтальная асимптота.
- На четвертом графике оба предела конечны, и оба предела различны, поэтому он имеет две различные горизонтальные асимптоты.

Можете ли вы назвать функцию, которая имеет три или более горизонтальных асимптот?
Невозможно иметь функцию с более чем двумя горизонтальными асимптотами. Однако у нас могут быть кривые, которые не являются функциями, имеющими более двух асимптот.
Найдите горизонтальные асимптоты y=arctanx y = \arctan x y=arctanx. 9x=0f′′(x)=-(1+x)ex=0 дает x=-1.x=-1.x=-1.
Затем проверка знаков f′(x)f'(x)f′(x) и f′′(x)f»(x)f′′(x) вокруг x=−1x=-1x=− 1 и x=0,x=0,x=0, получим следующую таблицу:x⋯−1⋯0⋯f′(x)(+)(+)(+)0(−)f′′(x)(+)0(−)(−)(−)f(x)( вогнутый вверх)2e(вогнутый вниз)1(вогнутый вниз) \begin{массив} { c c c c c c } х & \cdots & -1 & \cdots & 0 & \cdots \\ \\ f'(x) & (+) & (+) & (+) & 0 & (-) \\ f»(x) & (+) & 0 & (-) &(-) & (-) \\ f(x) & \text{(вогнутый вверх)} & \frac{2}{e} & \text{(вогнутый вниз)} & 1 & \text{(вогнутый вниз)} \end{массив} xf′(x)f′′(x)f(x)⋯(+)(+)(вогнутый вверх)−1(+)0e2⋯(+)(−)(вогнутый вниз)00(−)1⋯(−)(−)(вогнутый вниз)
Теперь, проверяя пределы f(x)f(x)f(x) в качестве последнего шага, мы имеем
limx→∞f(x)=−∞,limx→−∞f(x)=0.
\lim_{x \rightarrow \infty} f(x) =-\infty, \lim_{x \ стрелка вправо -\infty} f(x) =0.x→∞limf(x)=−∞,x→−∞limf(x)=0.
Таким образом, в интервале [−1, ∞), [-1, \infty), [−1, ∞) кривая вогнута вниз, достигает максимума при x=0x=0x=0 и бесконечно снижается по мере того, как значение xxx приближается к ∞.\infty.∞.
В интервале (−∞,−1],(-\infty,-1],(−∞,−1] кривая вогнута вверх, приближаясь к оси xxx по мере приближения значения xxx − ∞.-\infty.−∞ Используя эту информацию, мы можем грубо нарисовать график y=f(x),y=f(x),y=f(x), который будет выглядеть как на рисунке ниже: 92+1}{2x}?y=2xx2+1?Пусть y=f(x),y=f(x),y=f(x), тогда областью определения f(x)f(x)f(x) являются все действительные числа xxx такие, что x≠ 0x\ne 0x=0, так как знаменатель не может быть равен нулю. Кроме того, график y=f(x)y=f(x)y=f(x) симметричен относительно начала координат, поскольку f(-x)=-f(x).f(-x)=-f (x).f(−x)=−f(x).
Теперь, чтобы лучше понять, как выглядит график, мы получим первую и вторую производные от f(x)f(x)f(x) следующим образом:
f′(x)=(2x)⋅(2x)−(x2+1)⋅2(2x)2=2×2−24×2=(x+1)(x−1)2x2f′′(x)=(2x )⋅(2×2)−(x2−1)⋅(4x)(2×2)2=1×3.
3}. \end{выровнено}f′(x)f′′(x)=(2x)2(2x)⋅(2x)−(x2+1)⋅2=4x22x2−2=2×2(x+1) (x−1)=(2×2)2(2x)⋅(2×2)−(x2−1)⋅(4x)=x31. 93}=0f′′(x)=x31=0 не дает решения, а это означает, что график не имеет точек перегиба.
Затем, проверяя знаки f′(x)f’(x)f′(x) и f′′(x)f’’(x)f′′(x) вокруг x=−1,x=0, x=-1,x=0,x=-1,x=0 и x=1,x=1,x=1, получаем следующую таблицу:
x⋯−1⋯0⋯1⋯f′(x)(+)0(−)(−)0(+)f′′(x)(−)(−)(−)(+)(+) (+)f(x)(вогнутый вниз)−1(вогнутый вниз)(вогнутый вверх)1(вогнутый вверх) \begin{array} { c c c c c c c } х & \cdots & -1 & \cdots &0 & \cdots & 1 & \cdots \\ \\ f'(x) & (+) & 0 &(-) & & (-) & 0 & (+) \\ f»(x) & (-) & (-) &(-) & & (+) &(+) & (+) \\ f(x) &\text{(вогнутость вниз)} &-1 &\text{(вогнутость вниз)} & &\text{(вогнутость вверх)} & 1 & \text{(вогнутость вверх)} \end{массив} xf′(x)f′′(x)f(x)⋯(+)(-)(вогнутый вниз)−10(-)−1⋯(-)(-)(вогнутый вниз)0⋯(−)(+)(вогнутая вверх)10(+)1⋯(+)(+)(вогнутая вверх) 92+1}{2x}=\frac{1}{2x}+\frac{1}{2}x.f(x)=2xx2+1=2×1+21x. Затем проверка пределов f(x)f(x)f(x), так как наш последний шаг дает
limx→+0f(x)=∞,limx→−0f(x)=−∞\lim_{x \rightarrow +0} f(x) =\infty, \lim_{x \rightarrow -0 } f(x) =-\inftyx→+0limf(x)=∞,x→−0limf(x)=−∞
и
limx→∞(f(x)−12x)=0,limx→−∞(f(x)−12x)=0.
\lim_{x \rightarrow \infty} \left(f(x) -\frac{1}{2}x\right)=0, \lim_{x \rightarrow -\infty} \left(f(x)-\frac{1}{2}x\right)=0.x →∞lim(f(x)−21x)=0,x→-∞lim(f(x)−21x)=0.
Таким образом, в интервале (0,∞),(0, \infty),(0,∞) кривая вогнута вниз, бесконечно приближаясь к оси yyy при x→0x\rightarrow 0x→0 и к линия y=12xy=\frac{1}{2}xy=21x при x→∞.x\стрелка вправо \infty.x→∞.
Кроме того, в интервале (−∞,0),(-\infty, 0),(−∞,0) кривая вогнута вверх, бесконечно приближаясь к оси yyy при x→0x\rightarrow 0x→ 0 и к прямой y=12xy=\frac{1}{2}xy=21x при x→−∞.x\стрелка вправо -\infty.x→−∞. Теперь мы можем нарисовать график y=f(x),y=f(x),y=f(x), который будет выглядеть как на рисунке ниже: 92}>0,4+x21>0, что означает, что кривая не имеет точек перегиба.
Затем проверка знаков f′(x)f'(x)f′(x) и f′′(x)f»(x)f′′(x) вокруг x=12,x=\frac{ 1}{2},x=21, получаем следующую таблицу:
x0⋯12⋯f′(x)(−)0(+)f′′(x)(+)(+)(+)f(x)(вогнутый вверх)(12−ln12)(вогнутый вверх ) \begin{массив} { c c c c } х &0 & \cdots & \frac{1}{2} & \cdots \\ \\ f'(x) & & (-) & 0 & (+) \\ f»(x) & & (+) & (+) & (+) \\ f(x) & & \text{(вогнутый вверх)} & \left(\frac{1}{2}-\ln \frac{1}{2}\right) & \text{(вогнутый вверх)} \end{массив} xf′(x)f′′(x)f(x)0⋯(−)(+)(вогнутый вверх)210(+)(21-ln21)⋯ (+)(+)(вогнутая вверх)
Теперь, проверяя пределы f(x)f(x)f(x) в качестве последнего шага, мы имеем
limx→+0f(x)=∞,limx→∞f(x)=∞.

 \lim_{x \rightarrow \infty} f(x) =-\infty, \lim_{x \ стрелка вправо -\infty} f(x) =0.x→∞limf(x)=−∞,x→−∞limf(x)=0.
\lim_{x \rightarrow \infty} f(x) =-\infty, \lim_{x \ стрелка вправо -\infty} f(x) =0.x→∞limf(x)=−∞,x→−∞limf(x)=0. 3}.
\end{выровнено}f′(x)f′′(x)=(2x)2(2x)⋅(2x)−(x2+1)⋅2=4x22x2−2=2×2(x+1) (x−1)=(2×2)2(2x)⋅(2×2)−(x2−1)⋅(4x)=x31. 93}=0f′′(x)=x31=0 не дает решения, а это означает, что график не имеет точек перегиба.
3}.
\end{выровнено}f′(x)f′′(x)=(2x)2(2x)⋅(2x)−(x2+1)⋅2=4x22x2−2=2×2(x+1) (x−1)=(2×2)2(2x)⋅(2×2)−(x2−1)⋅(4x)=x31. 93}=0f′′(x)=x31=0 не дает решения, а это означает, что график не имеет точек перегиба.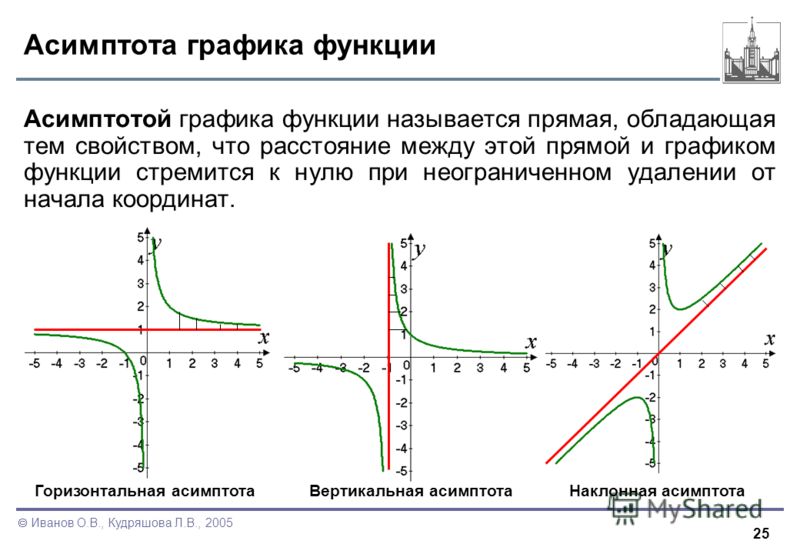 \lim_{x \rightarrow \infty} \left(f(x) -\frac{1}{2}x\right)=0, \lim_{x \rightarrow -\infty} \left(f(x)-\frac{1}{2}x\right)=0.x →∞lim(f(x)−21x)=0,x→-∞lim(f(x)−21x)=0.
\lim_{x \rightarrow \infty} \left(f(x) -\frac{1}{2}x\right)=0, \lim_{x \rightarrow -\infty} \left(f(x)-\frac{1}{2}x\right)=0.x →∞lim(f(x)−21x)=0,x→-∞lim(f(x)−21x)=0.