Применение квадратичной функции и её графика
Применение квадратичной функции и её графика
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Алдошкина М.Л. 1
1МБОУ «Лицей №9 имени К.Э.Циолковского» г.Калуги
Рылова И.Г. 1
1МБОУ «Лицей №9 имени К.Э.Циолковского» г.Калуги
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
«Устройство нашего мира непостижимо без знания математики».
Роджер Бэкон
Математика, как систематическая наука, появилась только в Древней Греции, её история начинается уже с возникновения таких понятий, как: натуральное число и геометрическая фигура.
В 1692 году Го́тфрид Ви́льгельм Лейбниц впервые использовал термин «функция». Первоначально её понятие было неотличимо от понятия аналитического представления. Впоследствии появилось несколько определение функции. Наконец, единая формулировка была дана Николаем Ивановичем Лобачевским в 1834 году: «Общее понятие требует, чтобы функцией от x называть число, которое дастся для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подает средство испытывать все числа и выбирать одно из них; или, наконец, зависимость может существовать и оставаться неизвестной …»
Существуют разные виды функциональных зависимостей: линейная, показательная, логарифмическая, тригонометрические, степенная, квадратичная и многие другие.
Актуальность исследования:
Проблема:
Если по какой-то причине пропущен урок, на котором изучалась квадратичная функция, объяснялись роль каждого коэффициента, входящего в уравнение, задающее квадратичную функцию, появляются трудности при решении задач по нахождению формулы, заданной квадратичной.
Гипотеза исследования – существуют различные способы определения коэффициентов квадратичной функции по графику этой функции.
Цель исследования – найти и изучить множество способов задания функциональной зависимости квадратичной функции по заданному графику, определить некоторые области жизнедеятельности человека, в которых применяется квадратичная функция или ее график.
Данная цель отвечает следующим задачам:
Выяснить роль каждого коэффициента квадратичной функции.
Изучить движение графика квадратичной функции в декартовой системе координат, в зависимости от коэффициента, входящего в формулу функции.
Составить банк задач по восстановлению формул, задающей квадратичную функцию, в зависимости от её графика.
Определить, где применяется квадратичная функция.
Систематизация данных в №9 раздела «Парабола» в зависимости от данных(math.100)
Объект исследования – алгебра, аналитическая геометрия, математический анализ.
Предмет исследования –квадратичная функция и её график.
Теоретическая значимость исследования: полученные результаты исследования составят полноценное представление о практической значимости квадратичной функции.Практическая значимость исследования заключается в том, что результаты работы могут быть использованы изучающими квадратичную функцию учениками 7-11 классов.
Квадратичная функция в математике.
Составление формулы задания квадратичной функции по ее графику есть в ЕГЭ №9. Я решила рассмотреть некоторые из них.(см. Таблицу №2)
Таблица 2. Классификация графиков квадратичной функции в зависимости от заданного коэффициента и особых точек.
|
Группа |
|
№ заданий |
|
1 группа |
Вершина параболы — узловая точка; Коэффициент a известен; Коэффициенты b, c не известны; График не пересекает оcь Oy; |
№2, №4 |
|
2 группа |
Вершина параболы – не узловая точка; Коэффициент с известен; Коэффициенты a, b не известны; График пересекает оcь Oy; |
№9, №10, №11 |
|
3 группа |
Вершина параболы — узловая точка;
Коэффициенты a, b, с не известны; График не пересекает оcь O. |
№15, №18, №19 |
1 группа: №2, №4
№ 2 На рисунке 1 изображён график функции . Найдите
Рисунок 1
№ 4. На рисунке 2 изображён график функции . Найдите
Рисунок 2
2 группа: №9, №10, №11
№ 9 На рисунке 3 изображён график функции . Найдите
Рисунок 3
№ 10 На рисунке 4 изображён график функции . Найдите
Рисунок 4
№ 11. На рисунке 5 изображён график функции . Найдите
3 группа: №15, №18, №19.
№ 15. На рисунке 6 изображён график функции . Найдите
Рисунок 6
№ 18. На рисунке 7 изображён график функции , где a, b и c – целые. Найдите
Рисунок 7
№ 19. На рисунке 8 изображён график функции , где a, b и c – целые. Найдите
На рисунке 8 изображён график функции , где a, b и c – целые. Найдите
Рисунок 8
Квадратичная функция в архитектуре
Гуляя по городу, мы часто видим дугообразные конструкции. Архитекторы используют параболическую форму в проектировании арок, мостов, куполов, потолков. Во-первых, именно такая форма придает эстетичный вид, во-вторых, параболическим конструкциям присуща прочность, потому что сила, создаваемая нагрузкой на мост или арку, не толкает вниз, а распределяется вдоль дуги, то есть эти строения поддерживают сами себя. В куполах всех храмов и церквей используется этот же принцип.
Из истории архитектурыАрхитекту́ра — искусство и наука строить, проектировать здания и сооружения (включая их комплексы), а также сама совокупность зданий и сооружений, создающих пространственную среду для жизни и деятельности человека.
В архитектуре часто встречаются сооружения и конструкции, в основе которых лежит парабола, ветви которой направлены вниз. Эта форма широко распространена не только из-за эстетичного внешнего вида, но и из-за способности выдерживать нагрузки, вызываемые весом самого сооружения и дополнительными факторами (сейсмическая активность в регионе, транспорт и т.д.). Архитекторы используют параболическую форму в проектировании арок, мостов, куполов, потолков. Параболическим конструкциям присуща прочность, потому что сила, создаваемая нагрузкой на мост или арку, не толкает вниз, а распределяется вдоль дуги, то есть эти строения поддерживают сами себя. [5]
Эта форма широко распространена не только из-за эстетичного внешнего вида, но и из-за способности выдерживать нагрузки, вызываемые весом самого сооружения и дополнительными факторами (сейсмическая активность в регионе, транспорт и т.д.). Архитекторы используют параболическую форму в проектировании арок, мостов, куполов, потолков. Параболическим конструкциям присуща прочность, потому что сила, создаваемая нагрузкой на мост или арку, не толкает вниз, а распределяется вдоль дуги, то есть эти строения поддерживают сами себя. [5]
Арочные мосты
Арочный мост — мост с пролётными строениями, основными несущим конструкциями которых служат арки.
О сновные размеры элементов арочных мостов – высота и ширина балок, толщина плиты, высота и ширина арок, количество арматуры и т.п. (рисунок 9) – окончательно устанавливаются на основании расчета сооружения в соответствии с действующими на сооружение нагрузками и качеством материалов, из которых строится мост.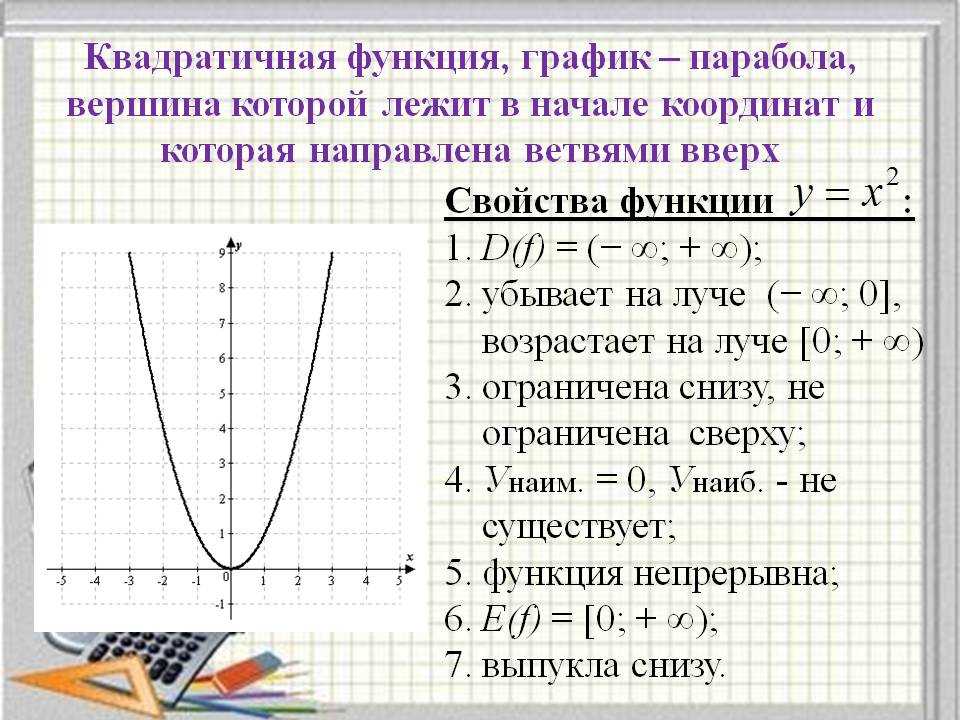 Рисунок 9
Рисунок 9
В ыбор толщины арки затруднителен вследствие большого разнообразия факторов, влияющих на этот выбор, таких как величина нагрузки, марка бетона и т.д. Примерно можно принимать: , где d – толщина арки, l – расчетный пролет арки.
Также для строения моста необходимо рассчитать максимально возможную нагрузку на конструкцию. Для этого используется формула Журавского. (Рисунок 10)
Рисунок 10
К аменный мост
Каменный мост (Рисунок 11) через Березуйский овраг в Калуге — старейший и крупнейший каменный виадук в России, построенный в 1785 году по проекту архитектора Петра Романовича Никитина. Мост опирается на 15 крупных каменных арок, три центральные арки сделаны в 2 этажа. Более 220 лет Каменный мост служит городу, хотя и не был рассчитан на современные транспортные нагрузки. Здесь проходит оживленная транспортная артерия, с Рисунок 11 моста открывается прекрасный вид.
Арки
Московские ворота
М есто, где сегодня находится Калужской областная филармония, в XVIII веке называлось Ямской слободой, и в 1775 году здесь появилась одна из главных достопримечательностей Калуги дореволюционного периода каменная калужская триумфальная арка «Московские ворота» (Рисунок 12) или «Екатерининские ворота».
Н а первый взгляд ничего не приходит в голову при упоминании квадратичной функции в биологии, но это не так. Параболу можно встретить, глядя на растения (Рисунок 14) [12], животных (Рисунок 13), морские волны (Рисунок 13) [13], радугу (Рисунок 14) [14], горы (Рисунок 15) [16].
Рисунок 13 Рисунок 14
Р исунок 15
Рисунок 16
Парабола в физике
М ожно привести немало примеров применения квадратичной функции в физике, из которых самый известный — уравнение пути равномерно-переменного движения с начальной скоростью.
Множество траекторий полёта в однородном гравитационном поле без сопротивления воздуха какого-либо объекта, например мяча, соответствует параболе (Рисунок 17) [16]
Рисунок 17
С вязь с космическим миром.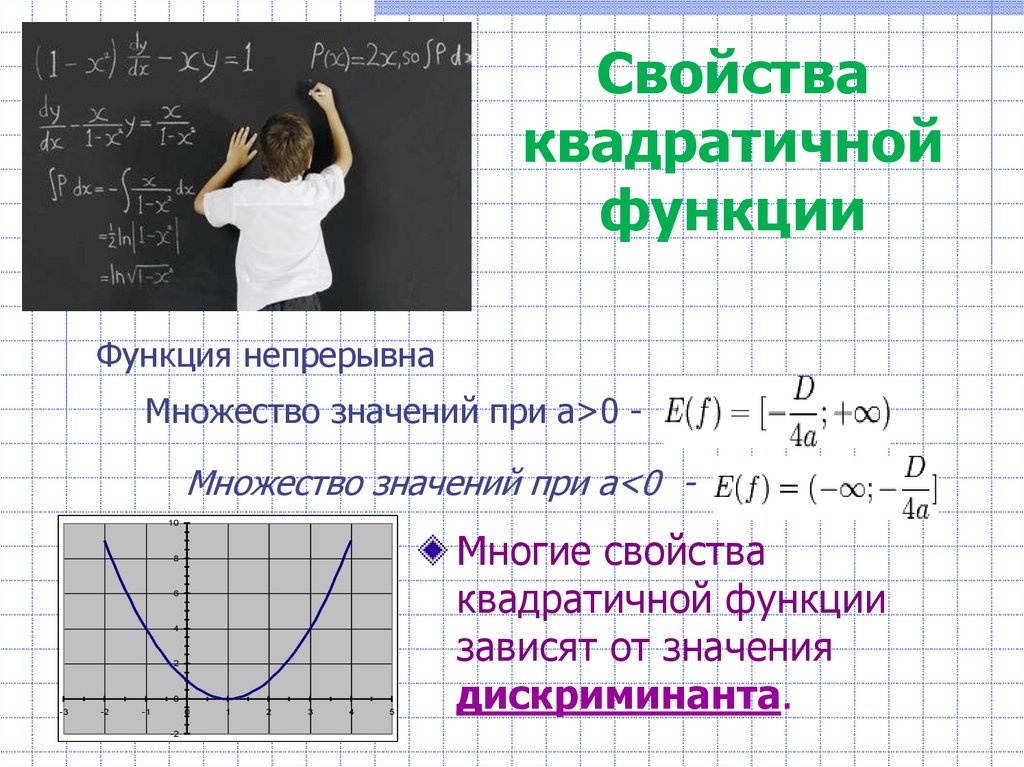 Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (нейтронной звезды, чёрной дыры или просто планеты) на достаточно большой скорости имеют форму параболы (Рисунок 18) [18]. Эти тела вследствие своей большой скорости и малой массы не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности аппаратов Вояджер). [17]
Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (нейтронной звезды, чёрной дыры или просто планеты) на достаточно большой скорости имеют форму параболы (Рисунок 18) [18]. Эти тела вследствие своей большой скорости и малой массы не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности аппаратов Вояджер). [17]
Рисунок 18
Парабола в геометрии
П араболой называется линия, которая в некоторой прямоугольной системе координат определяется каноническим уравнением , при условии, что .
Из уравнения вытекает, что для всех точек параболы . Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы. (Рисунок 19) Рисунок 19
Форма параболы известна из курса средней школы, где она встречается в качестве графика функции . Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством .
Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством .
Фокусом параболы называется точка F с координатами в канонической системе координат. Директрисой параболы называется прямая с уравнением в канонической системе координат. [19]
Цель моего проекта достигнута, я нашла и изучила множество способов задания функциональной зависимости квадратичной функции по заданному графику, определила некоторые области жизнедеятельности человека, в которых применяется квадратичная функция или ее график.
Достигла поставленных задач:
Выяснила роль каждого коэффициента квадратичной функции.
Изучила движение графика квадратичной функции в декартовой системе координат, в зависимости от коэффициента, входящего в формулу функции.
Составила банк задач по восстановлению формул, задающей квадратичную функцию, в зависимости от её графика.
Определила, где применяется квадратичная функция.
Систематизировала данные в №9 раздела «Парабола» в зависимости от данных(math.100)
Выдвинутая в проекте гипотеза подтвердилась. Существует несколько различных способов определение квадратичной функции по её графику. Например, в №5(см.Таблицу 1) вершина параболы – узловая точка, с помощью которой можно найти коэффициент a.
|
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
№7 |
№8 |
№9 |
№10 |
||||||||||||
|
Коэффициент а |
известен |
да |
да |
да |
да |
нет |
нет |
нет |
нет |
нет |
нет |
||||||||||
|
вершина а — узловая точка? |
нет |
да |
да |
да |
да |
нет |
нет |
да |
нет |
нет |
|||||||||||
|
Коэффициент b |
известен |
нет |
нет |
нет |
нет |
нет |
да |
да |
да |
нет |
нет |
||||||||||
|
Коэффициент с |
известен |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
да |
да |
||||||||||
|
пресекает ось ординат? |
да |
нет |
да |
нет |
да |
да |
да |
нет |
да |
да |
|||||||||||
Таблица 1. 2 Анализ графиков квадратичной функции в зависимости от заданного коэффициента и особых точек.
2 Анализ графиков квадратичной функции в зависимости от заданного коэффициента и особых точек.
Таблица 1.2. Анализ графиков квадратичной функции в зависимости от заданного коэффициента и особых точек.
|
№11 |
№12 |
№13 |
№14 |
№15 |
№16 |
№17 |
№18 |
№19 |
№20 |
||
|
Коэффициент а |
известен |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
|
вершина а — узловая точка? |
нет |
да |
нет |
нет |
да |
нет |
нет |
да |
да |
нет |
|
|
Коэффициент b |
известен |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
|
Коэффициент с |
известен |
да |
да |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
|
пресекает ось ординат? |
да |
да |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
нет |
|
Таким образом, составление формулы квадратичной функции зависит от того, как заданы точки, лежащие на параболе, является ли вершина параболы узловой точкой или пресекает ли ось ординат одна из ветвей.
Электронные источники:
История математики. / Википедия. URL :https://ru.wikipedia.org/wiki/%D0%98%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8F_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B8 (дата обращения: 27.11.2020).
Возникновение математики. / Википедия. URL :https://ru.wikipedia.org/wiki/%D0%92%D0%BE%D0%B7%D0%BD%D0%B8%D0%BA%D0%BD%D0%BE%D0%B2%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B8 (дата обращения: 27.11.2020).
Функция (математика). / Википедия. URL : https://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)(дата обращения: 27.11.2020).
Квадратичная функция одной переменной. / Википедия. URL : https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%B8%D1%87%D0%BD%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%BE%D0%B4%D0%BD%D0%BE%D0%B9_%D0%BF%D0%B5%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%BD%D0%BE%D0%B9 (дата обращения: 27. 11.2020)
11.2020)
Архитектура. / Википедия. URL : https://ru.wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D1%82%D0%B5%D0%BA%D1%82%D1%83%D1%80%D0%B0#%D0%90%D1%80%D1%85%D0%B8%D1%82%D0%B5%D0%BA%D1%82%D1%83%D1%80%D0%B0_%D0%BA%D0%B0%D0%BA_%D0%B2%D0%B8%D0%B4_%D0%B8%D1%81%D0%BA%D1%83%D1%81%D1%81%D1%82%D0%B2%D0%B0 (дата обращения: 28.11.2020)
Парабола. / Википедия. URL :https://ru.wikipedia.org/wiki/%D0%9F%D0%B0%D1%80%D0%B0%D0%B1%D0%BE%D0%BB%D0%B0 (дата обращения: 28.11.2020)
Параболы в арочных мостах. / Обучёнок. URL :https://obuchonok.ru/node/6541 (дата обращения: 28.11.2020)
Триумфальная арка в Париже – зеркало истории Франции. / Пути-дороги. URL :https://putidorogi-nn.ru/evropa/400-triumfalnaia-arka-v-parizhe (дата обращения: 28.11.2020)
Арка Константина. / Туристер. URL :https://www.tourister.ru/world/europe/italy/city/roma/placeofinterest/3168 (дата обращения: 28.11.2020)
Сиднейский оперный театр. / Belcanto.ru. URL:https://www.belcanto.ru/sydney.html (дата обращения: 28.11.2020)
/ Belcanto.ru. URL:https://www.belcanto.ru/sydney.html (дата обращения: 28.11.2020)
Гигантский лотос в Китае – шедевр экологического проектирования от австралийских архитекторов. / Строительная компания №1 Стиль. Качество. Надежность. URL:https://skn1.ru/news/gigantskiy-lotos-v-kitae-the-lotus-building/ (дата обращения: 26.01.2021)
Картинки. / Яндекс. URL: https://cloud.prezentacii.org/19/05/146571/images/screen24.jpg (дата обращения: 26.01.2021)
Картинки. / Яндекс https://masyamba.ru/%D0%B4%D0%B5%D0%BB%D1%8C%D1%84%D0%B8%D0%BD%D1%8B-%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8/3-%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8-%D0%BF%D1%80%D0%BE-%D0%B4%D0%B5%D0%BB%D1%8C%D1%84%D0%B8%D0%BD%D0%BE%D0%B2.jpg (дата обращения: 26.01.2021)
Картинки. / Яндекс URL:https://cdn.photosight.ru/sight/2008/01/04/2487092.jpg (дата обращения: 26.01.2021)
Картинки. / Яндекс URL: https://mtdata.ru/u20/photoF80C/20981393775-0/original. jpeg (дата обращения: 26.01.2021)
jpeg (дата обращения: 26.01.2021)
Картинки. / Google URL: https://static.wixstatic.com/media/64285d_5af50e464b464f65b016efd69ccb1c7f~mv2.jpg/v1/fill/w_1800,h_1159,al_c/64285d_5af50e464b464f65b016efd69ccb1c7f~mv2.jpg (дата обращения: 27.01.2021)
Геометрические и оптические свойства параболы. / Saratov FIO Wiki URL: https://wiki.soiro.ru/%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%B8_%D0%BE%D0%BF%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D1%81%D0%B2%D0%BE%D0%B9%D1%81%D1%82%D0%B2%D0%B0_%D0%BF%D0%B0%D1%80%D0%B0%D0%B1%D0%BE%D0%BB%D1%8B (дата обращения: 27.01.2021)
Картинки. / Яндекс URL: https://spaceflight.nasa.gov/gallery/images/skylab/skylab4/hires/s73-37273.jpg (дата обращения: 27.01.2021)
Парабола, её форма, фокус и директриса. / The univerlib URL: https://univerlib.com/analytic_geometry/second_order_lines_and_surfaces/parabola (дата обращения : 27.01.2021)
Просмотров работы: 393
Квадратичное уравнение Квадратичная формула Квадратичная функция Математика, формула, угол, текст, прямоугольник png
Квадратичное уравнение Квадратичная формула Квадратичная функция Математика, формула, угол, текст, прямоугольник pngтеги
- угол,
- текст,
- прямоугольник,
- логотип,
- число,
- черный,
- константа,
- параллель,
- парабола,
- точка,
- полином,
- написание,
- квадратный корень,
- символ,
- переменная,
- площадь,
- черный И белый,
- бренд,
- каллиграфия,
- круг,
- коэффициент,
- диаграмма,
- дискриминант,
- уравнение,
- формула,
- почерк,
- линия,
- алгебра,
- ноль функции,
- квадратное уравнение,
- квадратная формула,
- квадратичная функция,
- математика,
- png,
- прозрачный,
- бесплатная загрузка
Об этом PNG
- Размер изображения
- 1500x673px
- Размер файла
- 7.
 22KB
22KB - MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Лицензия
Некоммерческое использование, DMCA Contact Us
- Квадратичное уравнение Квадратичная функция График функции Ноль функции, OneNote, синий, угол, текст png 2000x1714px 101.53KB
- Квадратичное уравнение Квадратичная функция Квадратичная формула Завершая квадрат, формула, угол, текст, прямоугольник png 2000x617px 30.38KB
- Квадратичное уравнение Квадратичная формула Квадратичная функция Ноль функции, Математика, угол, белый, текст png
1705x586px
10.
 08KB
08KB - Квадратичное уравнение Квадратичная формула Алгебра Квадратичная функция, формула функции, угол, текст, прямоугольник png 1280x395px 13.9KB
- Математическая формула Алгебра Евклидова, Математическая формула, угол, текст, монохромный png 2244x2244px 134.04KB
- Математические уравнения, Формула Математика Функция Евклида, Оси математических функций, синий, угол, текст png 800x800px 366.32KB
- Формула Математика Евклидова, математическая формула, угол, текст, монохромный png 3500x3313px 875.77KB
- Квадратичное уравнение Квадратичная функция Квадратичная формула, формула, угол, текст, логотип png
2211x557px
27.
 73KB
73KB - Математика геометрия формула евклидово уравнение, математические заметки, угол, текст, треугольник png 6354x6354px 911.07KB
- Квадратичная функция Квадратичное уравнение Парабола Алгебра, Математика, угол, текст, симметрия png 700x750px 58.63KB
- Кривая параболы Квадратичная функция График функции Математика, Математика, угол, треугольник, график функции png 1024x620px 15.48KB
- математические уравнения, математические формулы, математические обозначения, cdr, угол, текст png 1080x763px 356.8KB
- График функции Математическое производное уравнение, математическое уравнение, угол, белый, текст png
1600x625px
8.
 41KB
41KB - Математическая нотация Математический символ Номер, математические символы, угол, белый, текст png 1024x683px 56.5KB
- Число Фибоначчи Золотая спираль Золотое сечение Последовательность, спираль, угол, белый, текст png 1600x1012px 47.16KB
- Число Десятичная Математика Прямоугольник Квадрат, черно-белая сетка, разное, угол, белый png 1024x1024px 8.29KB
- Алгебра Математика Решение уравнений с переменными, угол, текст, логотип png 1050x1024px 68.67KB
- Квадратный корень n-й корень математика квадратное число ноль функции, математика, угол, текст, прямоугольник png
500x549px
9.
 46KB
46KB - Квадратичное уравнение Квадратичная функция Квадратичная формула Ноль функции, топор, угол, белый, текст png 1600x565px 24.22KB
- Длинное деление Математика Математическая запись Символ Квадратный корень, Математика, угол, текст, прямоугольник png 1000x1000px 10.76KB
- Квадратное уравнение Квадратный корень из 3-го корня Формула, математический вопрос, угол, текст, логотип png 1000x1000px 7.85KB
- Золотая спираль Золотое сечение число Фибоначчи Золотой прямоугольник, евклидов, угол, белый, текст png 1600x1012px 42.47KB
- График функции Математика Интегральное исчисление, Математика, угол, текст, логотип png
901x534px
9.
 74KB
74KB - График функции Родительская функция Квадратичная функция Экспоненциальная функция, Математика, угол, текст, прямоугольник png 2000x2000px 75.49KB
- математические уравнения, математическое уравнение евклидовой формулы, математический набросок материала, угол, текст, цифровой png 918x670px 147.15KB
- иллюстрация в черно-серой рамке, Диаграммная бумага, текстура, угол, белый png 1501x1501px 14.69KB
- Квадрантная декартова система координат График функции Квадратичная функция Математика, 12 бис, угол, текст, прямоугольник png 907x907px 30.58KB
- Математика Число Точка Уравнение Геометрия, математическая формула, угол, текст, прямоугольник png
1546x646px
8.
 84KB
84KB - Математика евклидова геометрия формула, математика, угол, текст, треугольник png 4050x4050px 420.75KB
- Система уравнений Математика Квадратичное уравнение Решение уравнений, рукописная математическая формула, угол, текст, число png 1920x2010px 152.49KB
- Система линейных уравнений Система уравнений Решение уравнений, др., разное, угол, белый png 2266x1200px 31.69KB
- Квадратичная функция Квадратичное уравнение Квадратичная формула, Математика, угол, белый, текст png 1512x661px 8.6KB
- Система линейных уравнений Математика, Математика, синий, угол, текст png
597x599px
16.
 58KB
58KB - Квадратичная функциональная линия, Квадратичное уравнение, Степень, Полиномиальная функция, График функции, График, Парабола, Коэффициент, угол, площадь, круг png 1630x1553px 75.08KB
- Решение уравнений Математика Математическая запись Формула, администратор, текст, число, математик png 792x658px 240.21KB
- Математика евклидова формула бумаги, математические различные формулы, угол, текст, монохромный png 4050x4050px 627.53KB
- Число Фибоначчи Золотая спираль Золотое сечение Последовательность Золотой прямоугольник, Математика, угол, белый, текст png 2000x1266px 39.05KB org/ImageObject»> Математика Математическая запись Компьютерные иконки Математик, Математика, угол, текст, логотип png 600x564px 12.32KB
- головоломки, шаблон головоломки, шаблон кусочек головоломки, угол, текст, прямоугольник png 750x500px 229.4KB
- Физика Скоростная формула Ускорение, линия, угол, текст, логотип png 1161x861px 9.11KB
- Математика Геометрия Формула Тригонометрия Куб, Математика, угол, треугольник, монохромный png 1920x1308px 921.05KB
- Математика Уравнение Угол Почерк, рукописная математическая формула, белый, текст, прямоугольник png 900x1111px 11.38KB org/ImageObject»> Пи Дня Окружность квадратного корня Математическая константа, пи математика, разное, угол, белый png 2000x455px 26.99KB
- Эквивалентность массы – энергии уравнения поля Эйнштейна Теория формулы относительности, Математика, угол, текст, число png 735x861px 210.86KB
- черные линии сетки, правило третей Составная линия, сетка, угол, белый, мебель png 1800x1200px 77.09KB
- Бразилия подпись президента, Линха до темпа, угол, белый, текст png 1200x592px 34.46KB
- Теорема Пифагора Угол Числовая линия, Угол, угол, текст, прямоугольник png 2400x2384px 40.82KB org/ImageObject»> Декартова система координат График функции Диаграмма бумаги Плоскость, др., угол, прямоугольник, треугольник png 800x800px 30.81KB
- Корень квадратный Радикальный символ Математика Квадрат номер n th корень квадратный фон, угол, текст, рука png 512x512px 5.1KB
- Цифровая подпись, Tiff, разное, угол, белый png 2656x1932px 154.08KB
Квадратичные формулы и функции — Квадратичные функции
Сложность построения графика квадратичной функции зависит от формы, в которой вы ее найдете. Мы начнем относительно легко.
f ( x ) = a ( x – h ) 2 + k , мы не лжем вам
,; что есть квадратичная функция. Давай, умножай.
f ( x ) = AX 2 + (-2 AH ) x + ( AH 2 + K )
ah ) и ( ah 2 + k ) также являются константами, которые мы могли бы назвать, скажем, b и c . Видите, вы можете нам доверять, это полностью квадратично.
Видите, вы можете нам доверять, это полностью квадратично.
Когда у вас есть парабола, записанная как f ( x ) = a ( x – h ) 2 + k , это в вершинной форме . С вершинной формой вы сразу же получаете несколько фрагментов важной информации. Когда вы впервые встречаете кого-то, ваше первое впечатление, как правило, остается с вами. То же самое и с этим уравнением.
Знак a говорит вам, открывается ли парабола вверх или вниз. Если и положительны, он открывается. Если и являются Негативной Нэнси, парабола раскрывается вниз. Вы также знаете, что вершина параболы находится в точке ( ч , к ). Однако будьте осторожны со знаком h .
Задача выборки
График Функция F ( x ) = ( x — 2) 2 — 1.
Вертекс параболы составляет ( H , K ) = = (2, –1). Мы также можем видеть, что парабола открывается вверх. Однако нам нужно еще несколько очков. Мы могли бы составить таблицу и начать подставлять значения x , но обычно есть более простой способ: найти точки пересечения х и х (если они существуют). Начиная с точки пересечения y , которая происходит при x = 0.
Мы также можем видеть, что парабола открывается вверх. Однако нам нужно еще несколько очков. Мы могли бы составить таблицу и начать подставлять значения x , но обычно есть более простой способ: найти точки пересечения х и х (если они существуют). Начиная с точки пересечения y , которая происходит при x = 0.
f (0) = (0 – 2) 2 – 1 = 4 – 1 = 3
Прямо на: (0 , 3) — точка на нашей параболе. Теперь перейдите к x -перехватам, которые происходят, когда y = 0, если они есть.
0 = ( x – 2) 2 – 1
0 = x 2 – 4 x + 4 – 1
0 = x 2 – 4 x + 3
Это квадратное уравнение можно разложить на множители.
0 = ( x – 3)( x – 1)
Итак, (1, 0) и (3, 0) также являются точками параболы. Соединив все вместе, мы получаем:
Видишь? Математика умнее, а не сложнее.
Пример задачи
Нарисуйте график функции f ( x ) = -2( x + 1) 2 – 2.
Сразу видно, что вершина находится в (-1, -2) , а парабола направлена вниз. Время выследить нашу г -перехват.
f (0) = -2(0 + 1) 2 – 2 = -2(1) – 2 = -4
Сладкий. Перехват y равен (0, -4). Теперь охотимся за x -перехватами. Некоторые говорят, что использование динамита во время охоты неспортивно. Наверное, они правы.
0 = -2 ( x + 1) 2 -2
0 = -2 ( x 2 + 2 x + 1) -2
0 = -2 x 2 – 4 х — 2 — 2
0 = -2 x 2 — 4 x — 4
0 = — x 2 — 2 x — 2
. стена. Дискриминант этого уравнения равен:
b 2 – 4 ac =(-2) 2 – 4(-1)(-2) = 4 – 8 = -4
Отрицательно, поэтому действительных корней у этого уравнения нет. Это означает, что функция никогда не пересечет ось x , поэтому нет x — перехваты. Это имеет смысл, учитывая, что вершина находится в точке (-1, -2), а парабола направлена вниз, поэтому функция не будет двигаться вверх к оси x . Думаю, нам не понадобится этот динамит в конце концов.
Это означает, что функция никогда не пересечет ось x , поэтому нет x — перехваты. Это имеет смысл, учитывая, что вершина находится в точке (-1, -2), а парабола направлена вниз, поэтому функция не будет двигаться вверх к оси x . Думаю, нам не понадобится этот динамит в конце концов.
Вместо использования точек пересечения x мы вставим несколько дополнительных значений x и нанесем их на график.
| x | f ( x ) |
| -3 | 8 -10|
| -4 | -20 |
Мы почти готовы закончить этот график. Однако это будет проще сделать с еще несколькими точками. Помните, что ось симметрии проходит через вершину; теперь мы можем использовать это, чтобы найти еще несколько точек, поскольку у нас есть точки с обеих сторон вершины.
Сравните (0, -4) с вершиной в (-1, -2), например. Это 1 справа по оси x и 2 ниже по оси y . Поскольку функция симметрична, 1 пробел слева от вершины также будет на 2 ниже на y — ось, точка (-2, -4). Точно так же (-3, -10) — это 2 пробела слева от вершины и 8 вниз, а (-4, -20) — 3 пробела влево и 18 пробелов вниз. Отразите их на правую сторону вершины, и мы увидим, что (1, -10) и (2, -20) также являются точками на параболе. Теперь мы можем уверенно изобразить этого плохого мальчика.
Вершинная парабола Стратегия
Когда вы рисуете параболу в форме вершины, вот что вы делаете.
- Проверьте знак и , чтобы увидеть, открывается ли он вверх или вниз.
- Найдите вершину и точку пересечения y .
- Определите, есть ли пересечения x , либо путем сравнения формы параболы и вершины, либо путем проверки дискриминанта расширенной функции.
- Найти x -отрезков, если они существуют.

- Проверьте, достаточно ли у вас очков, чтобы закончить график. Если да, то ура.
- Если нет, бу. Постройте еще несколько точек и используйте симметрию функции, чтобы найти больше точек.
- Заканчивайте и закругляйтесь.
Что такое квадратичная формула?
Почти каждый школьник сталкивается с квадратной формулой в математике, и это популярный способ вычислить корни квадратного уравнения.
В реальной жизни квадратичная формула помогает нам определить площадь пространства, скорость движущегося объекта, величину прибыли, полученной от продукта, и многое другое. Даже траектория космической ракеты описывается квадратным уравнением. Таким образом, квадратичная формула имеет большое значение не только в математике, но и в реальном мире.
Что такое квадратичная формула?
Часто сложно разложить на множители некоторые конкретные типы квадратных уравнений; однако корни (также называемые точками пересечения или нулями) таких уравнений можно легко вычислить с помощью квадратичной формулы. Квадратичная функция графически представлена параболой с вершиной, расположенной в начале координат ниже оси x или выше оси x . Следовательно, квадратичная функция может иметь один, два или нулевые корни.
Квадратичная функция графически представлена параболой с вершиной, расположенной в начале координат ниже оси x или выше оси x . Следовательно, квадратичная функция может иметь один, два или нулевые корни.
Квадратное уравнение обычно записывается как:
ax 2 +bx+c = 0
Чтобы найти корни квадратной функции, мы можем положить f ( x ) = 0 и решить уравнение, заполнив уравнение . Когда мы делаем это, мы приходим к квадратной формуле, которая задается как:
x = [-b ± √(b² — 4ac)] /2a
Решая приведенное выше уравнение, значение x (корень) определяется, а сумма корней и произведение корней уравнения также могут быть выведены далее.
Терм b 2 −4 ac называется дискриминантом. Дискриминант важен, потому что он говорит вам, сколько корней имеет квадратичная функция. В частности, если:
В частности, если:
B 2 −4 AC <0 Нет реальных корней
B 2 — 4 AC = 0 Существует один реальный корень
— 4 AC = 0 Существует один реальный корень
9000 2 — 4 .0006 b 2 −4 ac > 0 Имеются два действительных корня
На графике для любой параболы, которая описывается как y = x 2 +b 7 9079 x 900 точки (или значения), где парабола пересекает ось x.
- Дискриминант в квадратичной формуле
Природа корней, полученных из квадратичной формулы, определяется дискриминантом (D), который определяется как:
Самые популярные
D = b 2 -4ac
Когда значение D равно нулю, говорят, что корни действительны и равны. Если значение D положительное, полученные корни вещественные и неравные, а когда D отрицательное, то корни являются комплексно-сопряженными, поэтому действительных корней нет.
Факторизация и завершение метода квадратов — два других способа решения квадратного уравнения. Однако квадратичная формула считается более эффективной, поскольку она применима ко всем уравнениям и действует как единственная формула, которая может вычислять корни любого квадратного уравнения. Более того, по сравнению с двумя другими методами, проще объяснить природу корней с помощью квадратичной формулы, исходя из значения D.
- Типы квадратных уравнений
Квадратное уравнение можно записать в трех различных формах:
Стандартная форма: y = ax 2 + bx + c
Факторизованная форма: d)
Форма вершины: y = a(x + b) 2 + c
Вы можете преобразовать квадратное уравнение из одной формы в другую в зависимости от ваших требований. Например, если вам нужно найти нули стандартного квадратного уравнения, вы можете сначала преобразовать его в факторизованную форму.
Кто изобрел квадратную формулу?
История квадратной формулы восходит к древним египтянам. Теория состоит в том, что египтяне знали, как вычислить площадь различных форм, но не знали, как вычислить длину сторон данной формы, например. размер стены, необходимый для создания данного плана этажа.
Чтобы решить практическую задачу, примерно к 1500 г. до н.э. египетские математики создали таблицу площадей и длин сторон различных фигур. Эту таблицу можно использовать, например, для определения размера сеновала, необходимого для хранения определенного количества сена.
Хотя этот метод работал нормально, это не было универсальным решением. Следующий подход мог исходить от вавилонян, у которых было преимущество перед египтянами в том, что их система счисления была больше похожа на ту, которую мы используем сегодня (хотя она была шестидесятеричной или с основанием 60). Это упростило сложение и умножение. Считается, что примерно к 400 г. до н.э. вавилоняне разработали метод заполнения квадрата для решения общих задач, связанных с областями.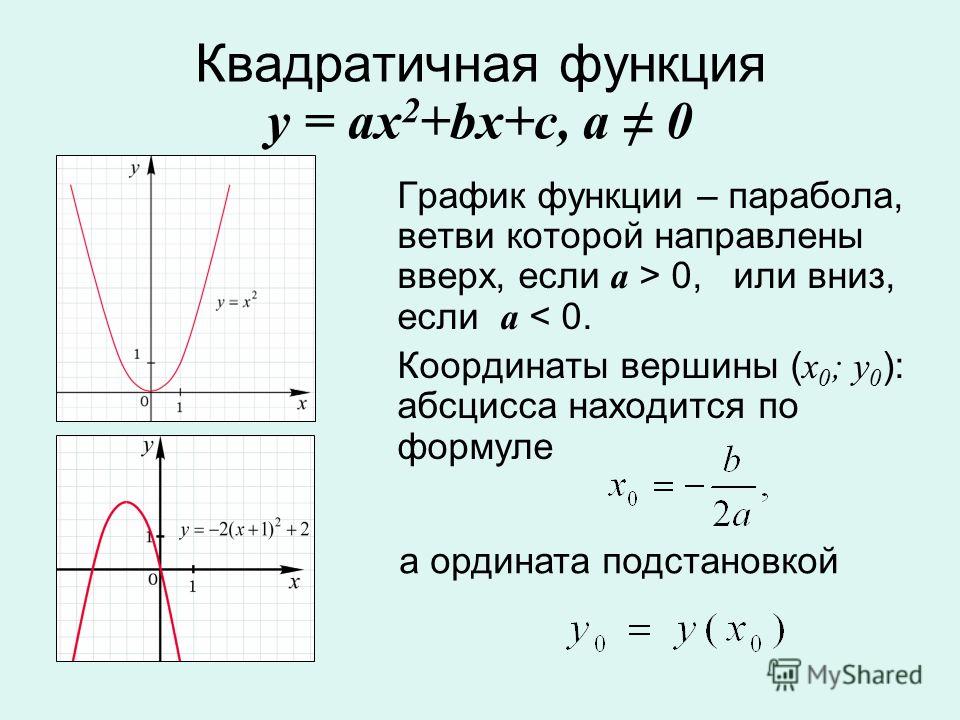 Аналогичный метод появляется и в китайских документах примерно в то же время.
Аналогичный метод появляется и в китайских документах примерно в то же время.
Метод полного квадрата позволил вавилонянам и китайцам перепроверить значения площади, рассчитанные ими для разных целей.
Первые попытки найти более общую формулу для решения квадратных уравнений, возможно, были предприняты греческими философами Пифагором (ок. 500 г. до н.э.) и Евклидом (ок. 300 г. до н.э.), которые оба использовали геометрический подход к выводу общей процедуры для решение квадратного уравнения.
Пифагор заметил, что значение квадратного корня не всегда является целым числом. Однако он отказывался допускать нерациональные пропорции. Евклид в своем математическом трактате Elements, предположил, что иррациональные квадратные корни также возможны.
Однако из-за того, что древние греки не пользовались той системой счисления, которую используем мы сейчас, вычислить квадратный корень вручную, в чем очень нуждались архитекторы и инженеры, было невозможно.
Именно индийский математик Брахмагупта нашел решение квадратного уравнения в своем трактате 628 г. н.э.0006′) .
Индийская математика использовала десятичную систему. У нее также было еще одно преимущество перед системой, использовавшейся древними египтянами и греками — ноль. Ноль позволил математикам не только теоретизировать об иррациональных числах, но и использовать их в уравнениях.
Брахмагупта понял, что решение квадратного уравнения имеет два корня, и описал формулу квадратного уравнения так: «К абсолютному числу, умноженному на четырехкратный [коэффициент] квадрата, прибавьте квадрат [коэффициента] средний член; квадратный корень из того же, за вычетом [коэффициента] среднего члена, деленный на удвоенный [коэффициент] квадрата, является значением». Это может быть записано как:
x = [ √(4ac+b 2 ) — b ] /2a
4 90 В последующие годы индийский астроном Бхаскара математически подтвердил возможность того, что любое положительное число имеет два квадратных корня.
Около 820 г. н.э. персидский математик Мухаммад ибн Муса аль-Хорезми, который был знаком с нулем, используемым в индийской математике, разработал то, что мы сейчас знаем как алгебру. Он решил квадратное уравнение, используя алгебраические выражения (хотя и отвергал отрицательные решения), и его часто называют отцом алгебры. Его работа попала в Европу примерно к 1100 году нашей эры, где была переведена на латынь.
К 1545 году итальянский ученый Джероламо Кардано собрал работы, связанные с квадратными уравнениями, включая решение Аль-Хорезми и евклидову геометрию. В своих работах он допускает существование корней отрицательных чисел.
Фламандский инженер и физик Симон Стевин дал общее решение квадратного уравнения для всех случаев в своей книге Арифметика в 1594 году. Позже французский ученый Рене Декарт опубликовал частные случаи квадратной формулы в своей работе 1637 года La Géométrie , в котором также использовались математические обозначения и символы, разработанные математиком Франсуа Виете. Работа Декарта включала квадратичную формулу в той форме, которую мы знаем сегодня.
Работа Декарта включала квадратичную формулу в той форме, которую мы знаем сегодня.
Квадратное уравнение в реальной жизни
Квадратное уравнение появилось из-за простой необходимости удобного нахождения площади квадратных и прямоугольных тел, но с момента своего появления это популярное математическое уравнение прошло долгий путь доказать свою значимость в реальном мире.
- Спортивные аналитики и сборщики команд используют различные квадратные уравнения для анализа результатов спортсменов за определенный период времени. Кроме того, в спортивных соревнованиях, таких как метание копья и баскетбол, используются квадратичные формулы для определения точной дистанции, скорости или времени, необходимых для получения большего количества очков.
- Военные и правоохранительные органы используют квадратичные формулы для расчета скорости ракет, движущихся транспортных средств и самолетов. Координаты посадки самолетов, танков и реактивных самолетов также определяются по формулам из квадратных уравнений.

- Автомобильные детали, такие как тормоза и криволинейные элементы, рассчитываются на основе квадратичной формулы. Пенсионные планы, модели страхования, производительность труда сотрудников; все эти параметры рассчитываются с помощью квадратных уравнений. Кроме того, по формуле квадрата измеряются границы сельскохозяйственных угодий и площади полей с наибольшей урожайностью.
- Строительство памятников, офисов, квартир, дорог, мостов и т. д. требует сложных расчетов и измерений площади, поэтому все эти математические сложности решаются с помощью различных квадратных формул.
- Углы, под которыми устанавливается спутниковая антенна для приема сигналов, также определяются с помощью квадратных уравнений. Кроме того, чтобы выяснить, как тарелка принимает сигналы от нескольких спутников одновременно, принимается во внимание квадратное уравнение.
Квадратичная формула является одним из фундаментальных принципов современной математики.


 22KB
22KB 08KB
08KB 73KB
73KB 41KB
41KB 46KB
46KB 74KB
74KB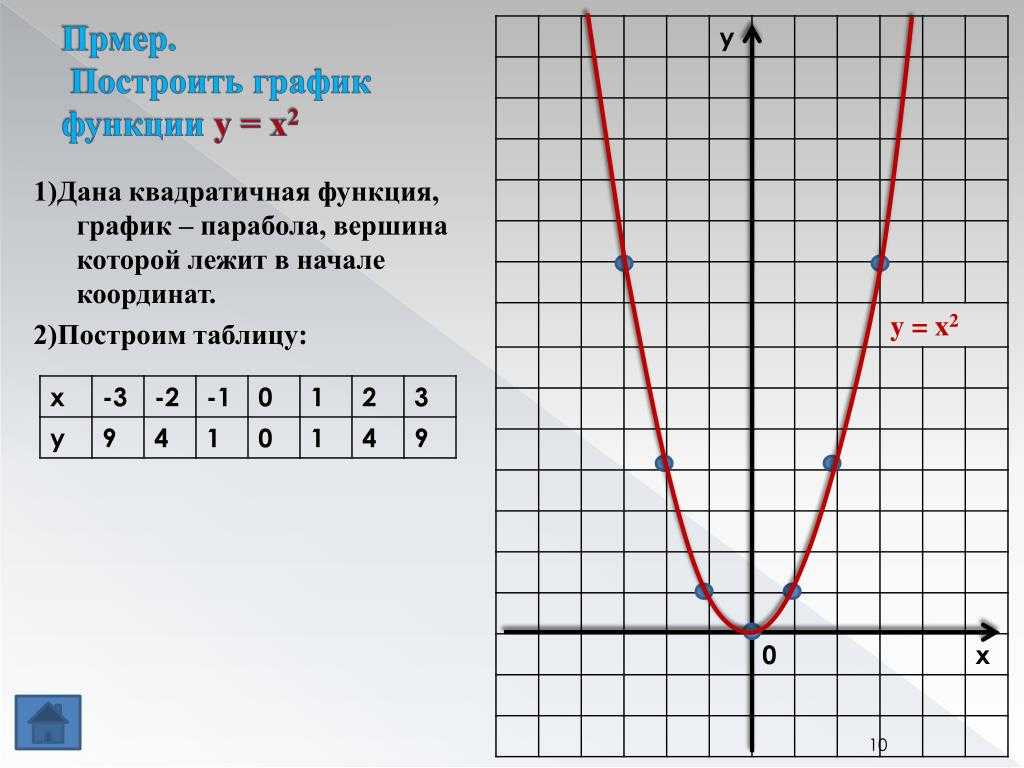 84KB
84KB 58KB
58KB