Формулы параллелограмма, трапеции, квадрата, прямоугольника и ромба
Содержание статьи
1. Понятие четырехугольника
2. Параллелограмм
3. Трапеция
4. Квадрат
5. Прямоугольник
6. Ромб
7. Пример задачи
Понятие четырехугольника
Введем для начала понятие многоугольника вообще.
Определение 1
Многоугольником называется геометрическая фигура в плоскости, которая состоит из попарно соединенных между собой отрезков, соседние из которых не лежат на одной прямой.
При этом отрезки называются сторонами многоугольника, а их концы — вершинами многоугольника.
Определение 2
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольники могут быть выпуклыми и невыпуклыми.
Определение 3
Если четырехугольник всегда будет лежать по одну сторону от любой прямой, проходящей через его стороны, то он называется выпуклым (рис. 1).
1).
Рисунок 1. Выпуклый четырехугольник
Определение 4
Если четырехугольник лежит по разные стороны хотя бы одной прямой, проходящей через его стороны, то он называется невыпуклым (рис. 2).
Рисунок 2. Невыпуклый четырехугольник
Классическими примерами выпуклых четырехугольников являются квадрат, прямоугольник, трапеция, ромб, параллелограмм. Рассмотрим далее эти фигуры по отдельности.
Параллелограмм
Определение 5
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 3).
Рисунок 3. Параллелограмм
\[P=2(a+b)\] \[S=ah\] \[S=absin\alpha \]
Трапеция
Определение 6
Трапеция — это четырехугольник, в котором две противоположные стороны параллельны между собой, а другие две противоположные стороны не параллельны между собой (рис.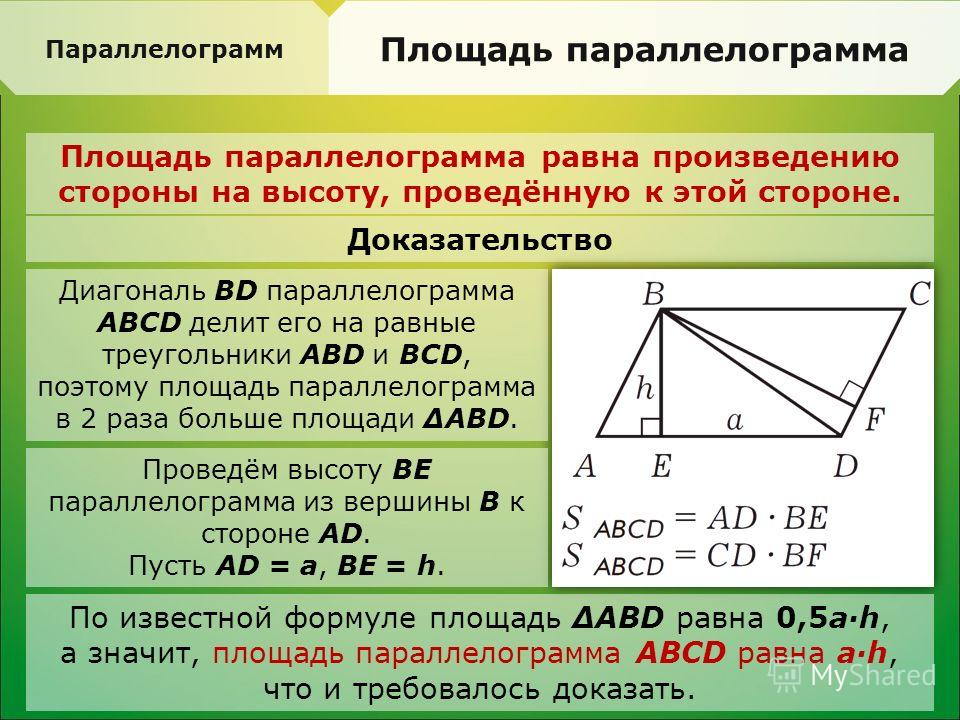 2=n⋅m\)
2=n⋅m\)
\(r=\frac{a+b−c}{2}\)
\( sin\ α=\frac{a}{c}\)
\( cos\ α=\frac{b}{c}\)
\(tan\ α=\frac{a}{b}\)
\(cot \ α=\frac{b}{a}\)
Треугольник: формулы площадей
\(S=\frac{1}{2}ch_c\)
\(S=\frac{1}{2} \ ab \ sin\ γ \)
\(S=\sqrt{p(p−a)(p−b)(p−c)}\)
\(S=pr\)
\(S=\frac{abc}{4R}\)
Параллелограмм. Формулы площади
\(S=AB⋅DE=BC⋅DF \)
\(S=AB⋅AD \ sinα\)
\(S=\frac{1}{2} AC⋅BD \ sin\ γ\)
Площадь четырехугольника
\(S=\frac{1}{2} AC⋅BD \ sin\ φ\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Алла Александровна Коледа
Репетитор по математике
Стаж (лет)
Образование:
Барановичский высший педагогический колледж
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Ольга Яновна Савинова
Репетитор по математике
Стаж (лет)
Образование:
Гродненский государственный университет имени Янки Купалы
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Анна Фёдоровна Ринкман
Репетитор по математике
Стаж (лет)
Образование:
Коми государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Физика
- Химия
- Русский язык
- Английский язык
- Обществознание
- История России
- Биология
- География
- Информатика
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Подготовка к ОГЭ по математике
- Репетитор по алгебре
- Подготовка к ЕГЭ по математике (профильный уровень)
- Подготовка к ЕГЭ по русскому языку
- Грамматика русского языка
- Подготовка к ЕГЭ по английскому языку
- ВПР по математике
- Подготовка к ОГЭ по информатике
Похожие статьи
- Как перевести м/мин в км/час
- ФГУ МГУ: проходгной балл, предметы ЕГЭ, отзывы студентов
- ИВТ (НИУ ВШЭ) | Информатика и вычислительная техника
- РУДН: факультет Государственного и Муниципального Управления (ГМУ)
- ЕГЭ по математике, базовый уровень.
 Простейшие уравнения (вариант 3)
Простейшие уравнения (вариант 3) - Как не умереть от скуки в детском лагере?
- Летнее меню: рацион школьника летом
- Учимся оказывать первую помощь себе и друзьям
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Формулы параллелограмма — GeeksforGeeks
Геометрия — это область изучения, которая изучает формы и их свойства. Формы изучаются на основе их размеров, состава, углов и других свойств. Поле занимается расчетом площади, объема, периметра и других параметров конкретной формы.
Что такое параллелограмм?
Параллелограмм представляет собой плоскую или двумерную фигуру с четырьмя сторонами, каждая пара противоположных сторон параллельна. Даже противоположные внутренние углы, как и стороны параллелограмма, всегда равны.
Даже противоположные внутренние углы, как и стороны параллелограмма, всегда равны.
Следовательно, параллелограмм представляет собой объемную фигуру, состоящую из двумерных четырехугольников, у которых четыре стороны каждой противоположной пары параллельны друг другу.
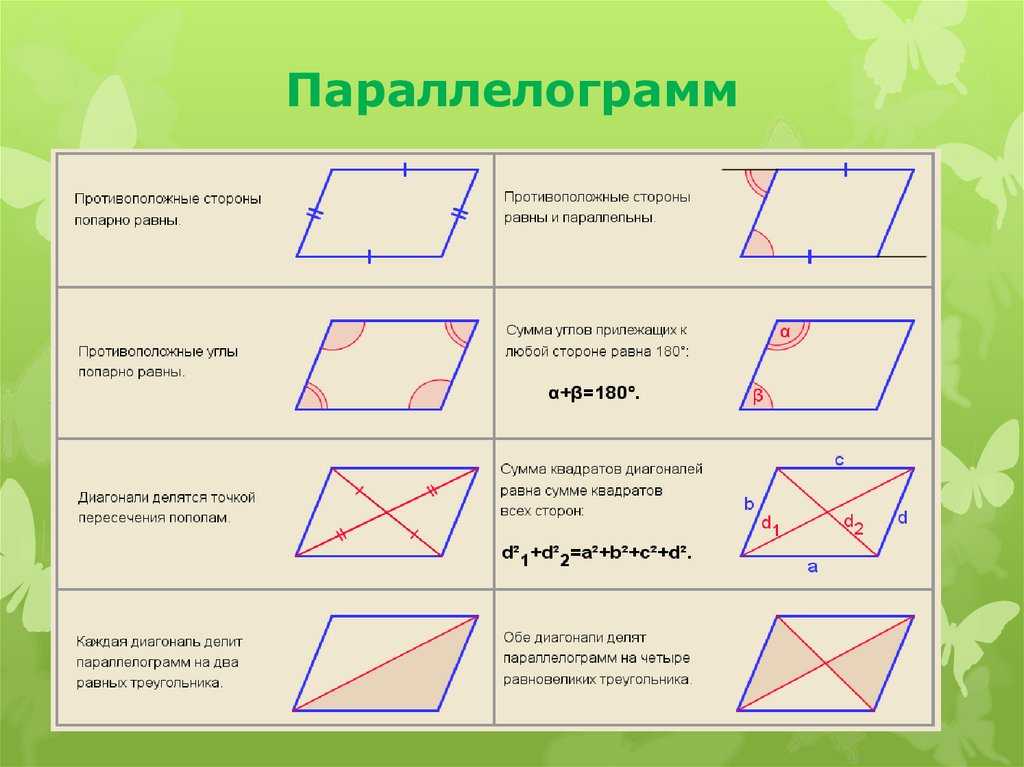
Свойства параллелограмма
- Противоположные стороны параллелограмма всегда равны.
- Противоположные углы параллелограмма равны.
- Если один из углов параллелограмма образует прямой угол, то и остальные три угла тоже прямые.
- Диагонали параллелограмма делятся пополам в центре фигуры.
Формула параллелограмма
Параллелограмм, как объяснялось выше, представляет собой двумерную структуру, изучаемую геометрией. Фигура имеет свои свойства, а также параметры. Поэтому для определения этих параметров приведены некоторые стандартные формулы.
Комбинированный расчет площади и периметра параллелограмма известен как формула параллелограмма.
Площадь параллелограмма
Площадь известна как общая поверхность, занимаемая фигурой, а площадь параллелограмма будет равна поверхности, покрытой или занятой ею. Для расчета площади параллелограмма предусмотрено три разных метода. Площадь параллелограмма можно определить с помощью высоты фигуры, длин сторон или диагоналей.
Площадь параллелограмма по высоте
Площадь параллелограмма по высоте получается произведением основания и высоты.
Математически,
Площадь параллеограммы = B x H
, где
B является основанием параллеграммы
, а H — высота параллелограмма
Область параллеляграммы по длине. Площадь параллелограмма по длине стороны определяется длиной его стороны и прилежащего к ней угла.
Математически,
Площадь параллелограммы = AB SINθ
, где,
A и B — длина сторон
, а θ — смежный угол
область диаг. два отрезка, пересекающиеся в центре данной фигуры. Площадь параллелограмма определяется двумя диагоналями и углом между этими диагоналями.
два отрезка, пересекающиеся в центре данной фигуры. Площадь параллелограмма определяется двумя диагоналями и углом между этими диагоналями.
Математически,
Площадь параллелограмма = 1/2 x d1 x d2 sin(x)
где,
d1 и d2 — диагонали
, а x — угол между диагоналями — общая длина или расстояние границы данной фигуры, а периметр параллелограмма — общая длина границы параллелограмма. Периметр параллелограмма определяется его длиной и шириной.
Математически формула периметра записывается как
Периметр параллелограмма = 2(a+b)
где,
a и b — стороны параллелограмма измерения 6см и 8см по формуле параллелограмма.
Решение:
Дано
Стороны параллелограмма равны 6см и 8см.
Пусть a=6см и b=8см
Имеем,
Периметр=2(a+b)
=>2(6+8)
=>2 x 14
=>28 см
Задача 2.
Вычислите периметр параллелограмма со сторонами 5 см и 4 см по формуле параллелограмма.
Решение:
Дано
Стороны параллелограмма равны 5см и 4см.
Пусть a=5см и b=4см.
Имеем,
Периметр=2(a+b)
=>2(5+4)
=>2 x 9
=>18см
Задача 3. Вычислить периметр параллелограмма со сторонами 12см и 8см по формуле параллелограмма.
Решение:
Дано
Стороны параллелограмма равны 12см и 8см.
Пусть a=12см и b=8см
Имеем,
Периметр=2(a+b)
=>2(12+8)
=>40см.
Задача 4. Вычислить площадь параллелограмма с основание 5 см и высота 8 см, используя формулу параллелограмма.
Решение:
Указано
Основание составляет 5 см
Высота 8 см
,
Площадь = B x
=> 5 x 8
=> 40CM 2
=> 5 x 8
=> 40CM 29 39003
=> 40CM 29.
Задача 5. Вычислите площадь параллелограмма с основанием 20 см и высотой 10 см по формуле параллелограмма.
Solution:
Given
The base is 20cm
The height is 10cm
We have,
Area = b x h
=>20 x 10
=>200cm 2
Все формулы параллелограмма — Калькулятор онлайн
Стороны параллелограмма
1. Стороны параллелограмма, если известны диагонали и угол между ними или другая сторона
— Меньшая сторона
— Большая сторона
,- Диагонали
,- Углы между диагоналями
Найти длину параллельграммы, если дать диагональ и угол между диагейнами ( ( ( ( ( ( ( a b ) :
Найдите длину сторон параллелограмма и другую сторону, если даны
0259 A B ):
2.
Стороны параллелограммы. высота измеряется под прямым углом к основанию
— высота измеряется под прямым углом к основанию
Найдите стороны параллелограмма, если известны угол и высота ( а б ) :
Find the length of the diagonal of a parallelogram
1. Diagonals of a parallelogram if you know sides and angle or sides and other diagonal
— smaller diagonal
— larger diagonal
, — стороны
— острый угол
— тупой угол
Найти длину диагонали параллелограммы, если заданные стороны и угол ( D D /):
параллелограмм, если даны стороны и другие диагонали ( D d ) :
2.
0260
— меньший диагональный — Большая диагональная
,- Углы между диагоналями
— Площадь параллелограммы
Найти длину диагональной диагональной диагональной диагональной диагональной диагональной диагональной диагональной диагональной диагональной области. и другая диагональ ( D d ) :
Углы параллелограмма
— меньший диагональный
— больший диагональный
,- стороны
— Острый угол
— Потушенный угол
— Площадь параллелограммы
. стороны и диагональ :
Найдите угол параллелограмма , если известны стороны и площадь:
Уравнения отношения острого и тупого углов: :
Углы между диагоналями параллелограмма
— меньший диагональный
— Большая диагональная
,- стороны
— Острый угол между диагоналями
— Угол-претуп между диагоналами
9.0002- Площадь параллелограмма
Найдите угловой между диагонали, если даны стороны и диагонали:
Найдите диагональ между диагоналами, если дайте область параллеляграмма и дневники:
.
Тождества для отношения острых и тупых углов между диагоналями: :
Высота параллелограмма и угол пересечения высот
, — сторон
— Острый угол
— тупой угол
— Высота до основания
— Высота до основания
Найдите длину высоты параллелограммы
без площади, если заданная сторона и угол:
Острый угол пересечения высот равен острому углу параллелограмма. :
Тупой угол пересечения высот равен тупому углу параллелограмма. :
сумма квадратов диагоналей параллелограмма0003
— Большая сторона
— Острый угол между диагоналями
Уравнение для суммы квадратных диагоналей :
Уравнение для разностей разностей складов: 9
9003 .
Уравнение различий в разностях складов: 9
9003 . :
Длина и свойства биссектрисы параллелограмма
1. Свойства бисектора параллелограммаПо определению Бискектор делит угол на половинках :
. треугольники ABF и DKC ) :
0002 бисекторы из противоположных углов являются равными и параллельными :
— Бискектор с острым углом
— бисектор с тупым углом
, боли параллелграма
— ах угол
— тупой угол
Поскольку треугольники ABF и DKC равнобедренные, выполняются следующие тождества :
2.

 Простейшие уравнения (вариант 3)
Простейшие уравнения (вариант 3)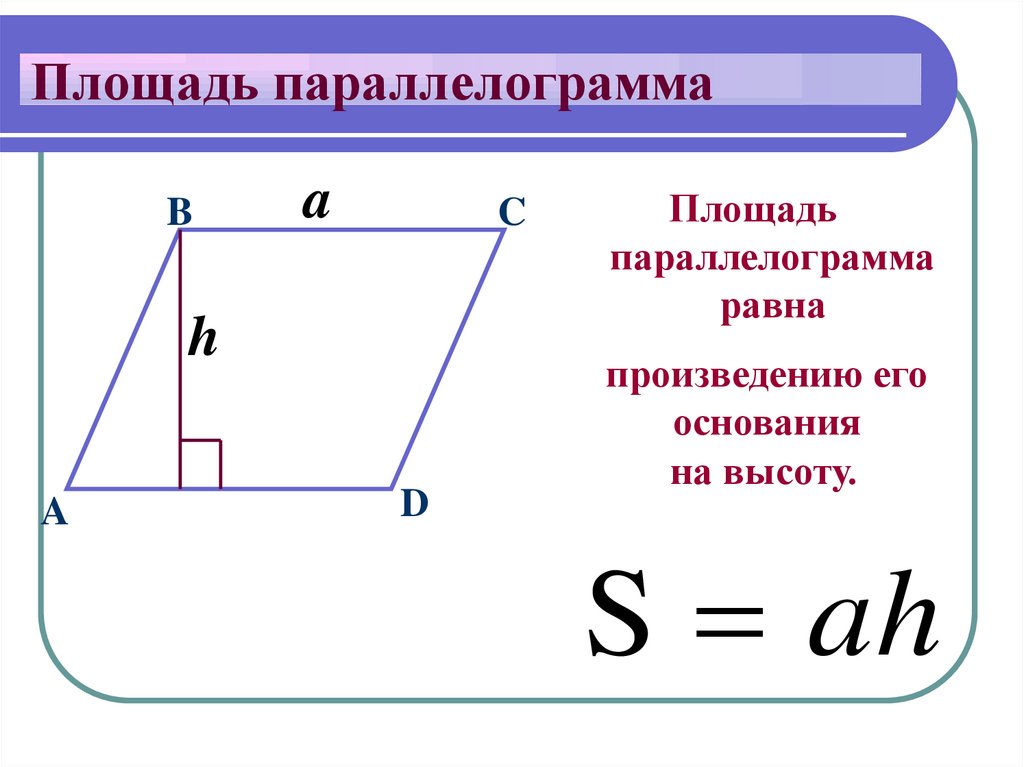 Вычислите периметр параллелограмма со сторонами 5 см и 4 см по формуле параллелограмма.
Вычислите периметр параллелограмма со сторонами 5 см и 4 см по формуле параллелограмма. 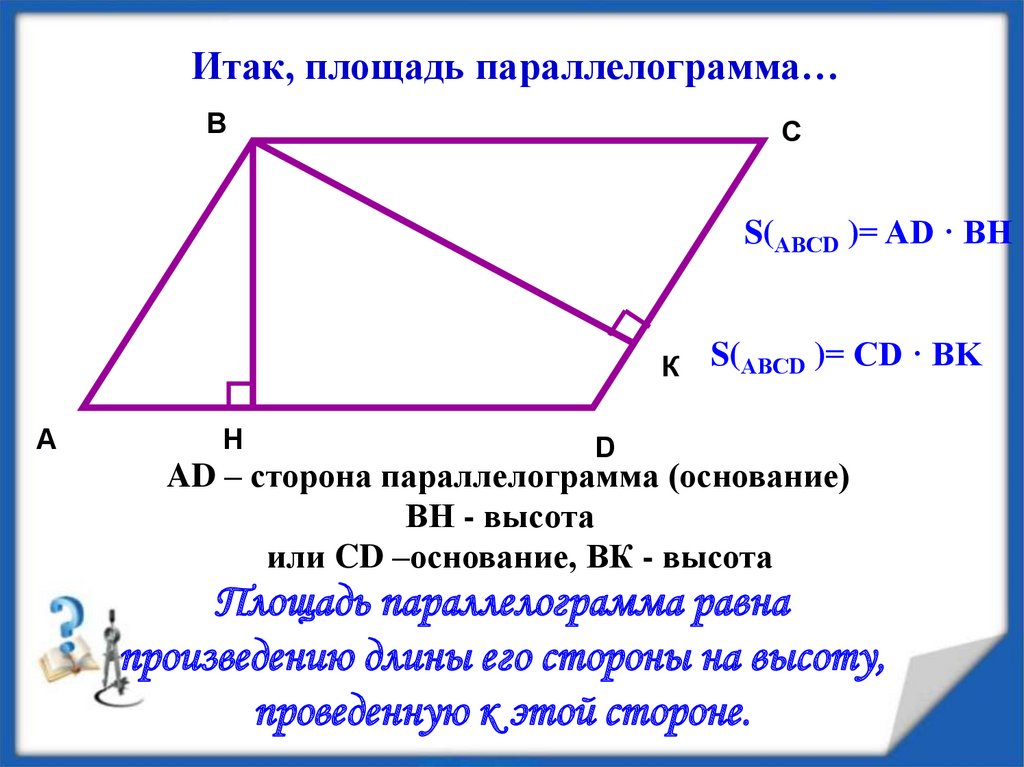
 Стороны параллелограммы. высота измеряется под прямым углом к основанию
Стороны параллелограммы. высота измеряется под прямым углом к основанию 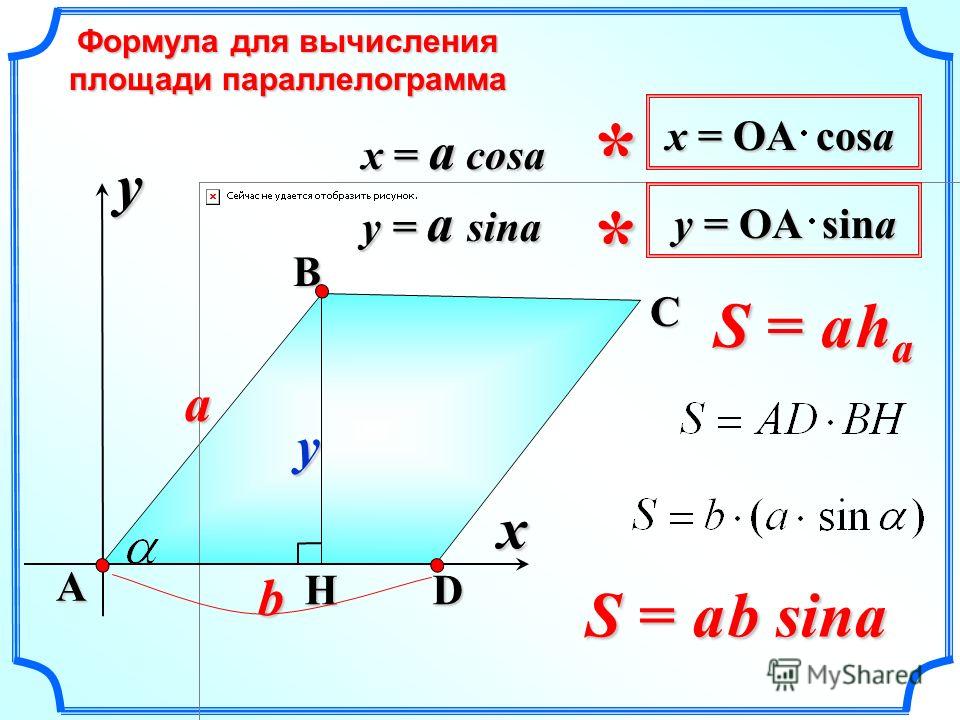 0260
0260 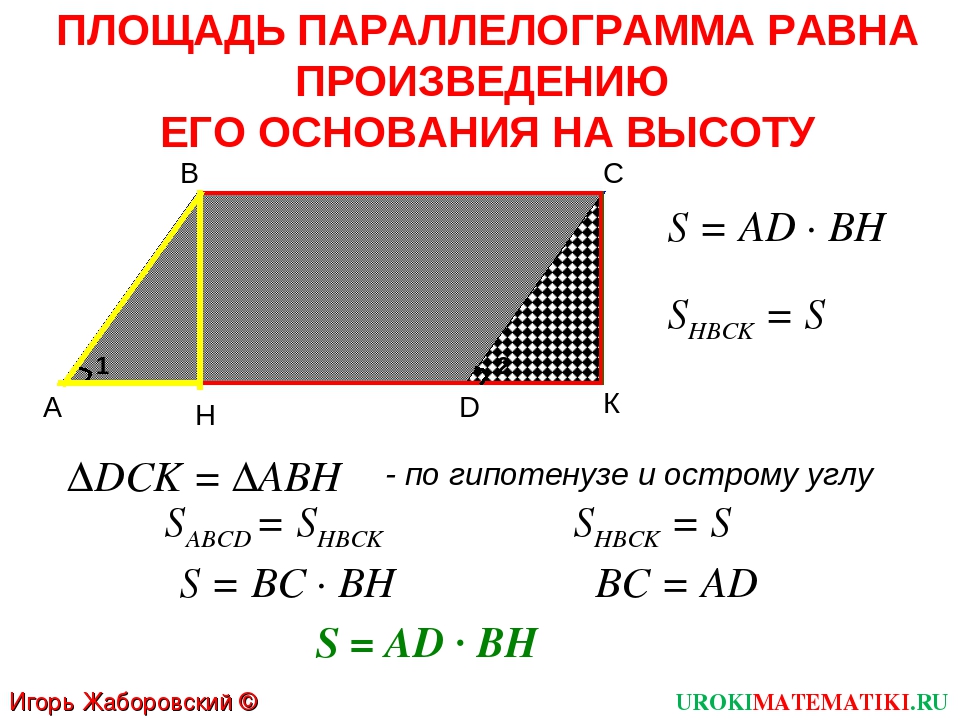 0002- Площадь параллелограмма
0002- Площадь параллелограмма Уравнение различий в разностях складов: 9
Уравнение различий в разностях складов: 9