Определитель 2 порядка определение. Определители и их свойства
Практическое занятие
Тема: Вычисление определителей.
Цели: закрепить понятия определителей и их свойств, сформировать и закрепить умения и навыки вычислять определители 2-го и 3-го порядков; развивать умения обобщать полученные знания, проводить анализ и сравнения, способствовать развитию логического мышления; воспитывать у обучающихся сознательное отношение к процессу обучения.
I. Общие теоретические положения
Определителем второго порядка называют число
Определителем третьего порядка называют число
Свойства определителей
Свойство 1.
Определитель не изменится, если все строки заменить соответствующими столбцами и наоборот.
Свойство 2.
При перестановке двух каких-либо строк или столбцов местами определитель изменяет знак.
Свойство 3.
Определитель равен нулю, если он имеет две равные строки (столбца).
Свойство 4.
Множитель, общий для всех элементов строки или столбца, можно выносить за знак определителя.
Свойство 5.
Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, то определитель не изменится.
Следствие из свойств 4 и 5: Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на некоторое число, то определитель не изменится.
Контрольные вопросы:
1.Дать определение матрицы.
2. Что означает символ ?
3. Какая матрица называется транспонированной по отношению к матрице А?
4. Какую матрицу называют квадратной порядка n?
5. Дать определение определителя 2-го порядка.
6. Дать определение определителя 3-го порядка.
7. Чему равен определитель транспонированной матрицы?
8. Как изменится величина определителя, если в матрице поменять местами 2 строки (столбца)?
9. Можно ли вынести за знак определителя общий множитель строки или столбца?
10. Чему равен определитель, если все элементы некоторой строки (столбца) равны 0?
Чему равен определитель, если все элементы некоторой строки (столбца) равны 0?
11.Чему равен определитель, если он имеет две одинаковых строки (столбца)?
12. Сформулируйте правило вычисления определителя 2-го порядка.
13. Сформулируйте правило вычисления определителя 3-го порядка.
II . Формирование умений и навыков.
Пример 1. Вы числить определитель: а) по правилу треугольника б) по правилу Саррюса;
в) методом разложения по элементам первой строки
Решение:
б) припишем два первых столбца и вычислим произведения из трех элементов по главной диагонали и параллельно к ней со знаком (+), а затем по побочной диагонали и параллельно к ней со знаком (-):
получаем:
Пример 2. Вычислить определитель двумя способами: с помощью разложения по первой строке и по правилу треугольника.
Решение:
Пример 3 . Вычислить определитель, используя свойства:
III . Закрепление изученного материала.
Закрепление изученного материала.
№1. Вычислить определители:
№ 2. Решить уравнения:
№ 4. Вычислить определители, используя свойства:
1
.
. 2.
. 3.
. 4
.
.
Литература
1. Письменный, Д. Т. Конспект лекций по высшей математике: полный курс Д. Т. Письменный. – 9-е изд. – М.: Айрис-пресс, 2009. 608 с.: ил. – (Высшее образование).
2. Лунгу, К. Н. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу, Д. Т. Письменный, С. Н. Федин, Ю. А. Шевченко. – 7-е изд. – М.: Айрис-пресс, 2008. 576 с.: – (Высшее образование).
Определители и правило Крамера. Определители 2-го и 3-го порядка. Правило Крамера. Миноры и алгебраические дополнения. Разложение определителя по строке или столбцу. Основные свойства определителей Метод элементарных преобразований.
2. ОПРЕДЕЛИТЕЛИ И ПРАВИЛО КРАМЕРА
2.1. Определители второго порядка
Понятие определителя возникло также в связи с задачей решения систем линейных уравнений. Определитель (или детерминант ) есть число, характеризующее квадратную матрицу A и обозначается обычно символами: detA , | A | или . Если матрица задана явно, в виде таблицы, то определитель обозначают, заключая таблицу в вертикальные линии.
Определитель (или детерминант ) есть число, характеризующее квадратную матрицу A и обозначается обычно символами: detA , | A | или . Если матрица задана явно, в виде таблицы, то определитель обозначают, заключая таблицу в вертикальные линии.
Определитель матрицы второго порядка находится следующим образом :
(2.1)
Он равен произведению элементов главной диагонали матрицы минус произведение элементов второй диагонали
Например,
Следует еще раз подчеркнуть, что матрица есть таблица чисел, тогда как определитель есть число, определяемое через элементы квадратной матрицы.
Рассмотрим теперь систему двух линейных уравнений с двумя неизвестными:
Используя понятие определителя 2-го порядка, решение этой системы можно записать в виде:
(2.2)
Это есть правило Крамера решения системы двух линейных уравнений с двумя неизвестными при условии, что 0.
Пример 2.1. Решить систему линейных уравнений, используя правило Крамера:
Решение . Найдем определители:
Историческая справка. Идея понятия «определителя» могла бы принадлежать Г. Лейбницу (1646-1716), если бы он развил и опубликовал свои идеи относительно определителей, к которым он пришел в 1693 г. Поэтому приоритет в разработке метода определителей решения систем линейных уравнений принадлежит Г. Крамеру (1704-1752), который опубликовал свои исследования по этой теме в 1750 г. Однако Крамер не построил полноценной теории определителей, к тому же ему не доставало удобного обозначения. Первое обширное исследование , посвященное определителям, было А. Вандермондом (1735-1796) в 1772 г. Он дал логическое изложение теории определителей и ввел правило разложения определителя с помощью миноров. Полное изложение теории определителей было дано лишь в 1812 г.
Ж. Бине (1786-1856) и О. Коши (1789-1858). Термин «определитель» («детерминант» ) в современном его значении был введен Коши (ранее этот термин использовался К. Гауссом для обозначения дискриминанта квадратичной формы).
Коши (1789-1858). Термин «определитель» («детерминант» ) в современном его значении был введен Коши (ранее этот термин использовался К. Гауссом для обозначения дискриминанта квадратичной формы).
2.2. Определители третьего порядка
Определитель матрицы 3-го порядка находится следующим образом
(2.3)
Естественно, что запомнить эту формулу довольно трудно. Однако есть правила, которые облегчают выписывание выражения для определителя 3-го порядка.
Правило треугольников : три слагаемых, входящих в исходное выражение со знаком плюс, есть произведения элементов главной диагонали или треугольников, основания которых параллельны этой диагонали. Остальные три слагаемых, входящих со знаком минус, находятся таким же образом, но относительно второй диагонали.
Правило Саррюса : припишем к матрице справа первый, а затем второй столбец. Тогда «положительные» слагаемые будут находиться на линиях параллельных главной диагонали, а «отрицательные» на линиях, параллельных второй диагонали .
2.3. Правило Крамера
Рассмотрим систему 3-х уравнений с тремя неизвестными
Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т.е.
(2.4)
если 0. Здесь
Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .
Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:
Решение . Находим определитель основной матрицы системы
Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:
Проверка:
Следовательно, решение найдено правильно.
Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место
 Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам
Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам (2.5)
где – определитель основной матрицы , i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.
Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.
2.4. Определители n-го порядка
Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т. е. A ij = (–1) i + j M ij .
е. A ij = (–1) i + j M ij .
Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя
Получаем
Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n -го порядка по строке или столбцу .
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:
(2.6)
Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя
т. е. алгебраические дополнения записывают в явном виде через миноры.
е. алгебраические дополнения записывают в явном виде через миноры.
Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.
2.5. Основные свойства определителей
Разлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс , можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.
Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.
Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т.е. при транспонировании матрицы:
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).
Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя.
Например,
Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.
Свойство 4 . Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число.
Например,
Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:
2.6.
Теорема 2.2. Определитель треугольной матрицы равен произведению элементов главной диагонали:
Элементарными преобразованиями матрицы называются следующие преобразования: 1) умножение строки (столбца) на число, не равное нулю; 2) прибавление одной строки (столбца) к другой; 3) перестановка двух строк (столбцов).
Метод элементарных преобразований заключается в том, чтобы при помощи элементарных преобразований, учитывая свойства определителей, привести матрицу к треугольному виду.
Пример 2.5. Вычислить определитель при помощи элементарных преобразований, приведя их к треугольному виду:
Пример 2. 6. Вычислить определитель:
6. Вычислить определитель:
.
Решение . Упростим данный определитель , а затем вычислим его:
.
Пример 2.7. Вычислить определитель
.
Решение . Способ 1 .При помощи элементарных преобразований матрицы, учитывая свойства определителей, будем получать в какой-либо строке или столбце нули, а затем будем разлагать полученный определитель по этой строке или столбцу:
–6
2
-2
.
Способ 2 .При помощи элементарных преобразований матрицы, учитывая свойства определителей, приведем матрицу к треугольному виду:
.
Вычисление определителей при помощи элементарных преобразований, путем приведения его к треугольному виду, является одним из самых распространенных методов. Это связано с тем, что он является основным методом при реализации вычислений определителей на ЭВМ. Точнее он является одной из модификаций метода Гаусса , который обычно используется при решении систем линейных уравнений.
Пример 2.8. Вычислить определитель методом Гаусса:
Решение. Рассмотрим первый столбец и выберем в нем ту строку, которая содержит 1. Если единиц нет, то нужно эту единицу создать при помощи элементарных преобразований: переставляя строки или столбцы, складывая или вычитая их друг с другом, умножая или деля их на какое-либо число (учитывая при этом, конечно свойства определителей). Возьмем за основу вторую строку и получим при помощи ее нули в первом столбце:
После этого на первую строку больше внимания не обращаем. Рассмотрим 2-й столбец.
В результате, получилась треугольная матрица. Для того чтобы вычислить определитель, осталось только перемножить элементы матрицы, находящиеся на главной диагонали. Таким образом, получаем ответ: –2(–1)(–1)1334 = –264.
Определение 6 . Определителем третьего порядка, соответствующим матрице системы (1.4), назовем число D , равное
Для того, чтобы вычислить определитель
третьего порядка применяют две вычислительные схемы, позволяющие вычислять определители третьего порядка без особых хлопот. Эти схемы известны как » правило треугольника » (или «правило звездочки») и » правило Саррюса «.
Эти схемы известны как » правило треугольника » (или «правило звездочки») и » правило Саррюса «.
По правилу треугольника сначала перемножаются и складываются элементы, соединенными на схеме линиями
т.е. получаем сумму произведений: a 11 a 22 a 33 +a 12 a 23 a 31 +a 21 a 13 a 32 .
Обратите внимание, что перемножаются элементы, соединенные одной линией, прямой или ломанной, а потом полученные произведения складываются.
Затем перемножаются и складываются элементы, соединенные на схеме
т.е. получаем другую сумму произведений a 13 a 22 a 31 +a 12 a 21 a 33 +a 11 a 23 a 32 . И, наконец, чтобы вычислить определитель , из первой суммы вычитают вторую. Тогда окончательно получаем формулу вычисления определителя третьего порядка:
D=(a 11 a 22 a 33 +a 12 a 23 a 31 +a 21 a 13 a 32)-(a 13 a 22 a 31 +a 12 a 21 a 33 +a 11 a 23 a 32).
По
правилу Саррюса к определителю справа дописывают два первых столбца, а затем считают сумму произведений элементов определителя в одном направлении и из нее вычитают сумму произведений элементов в другом направлении (см.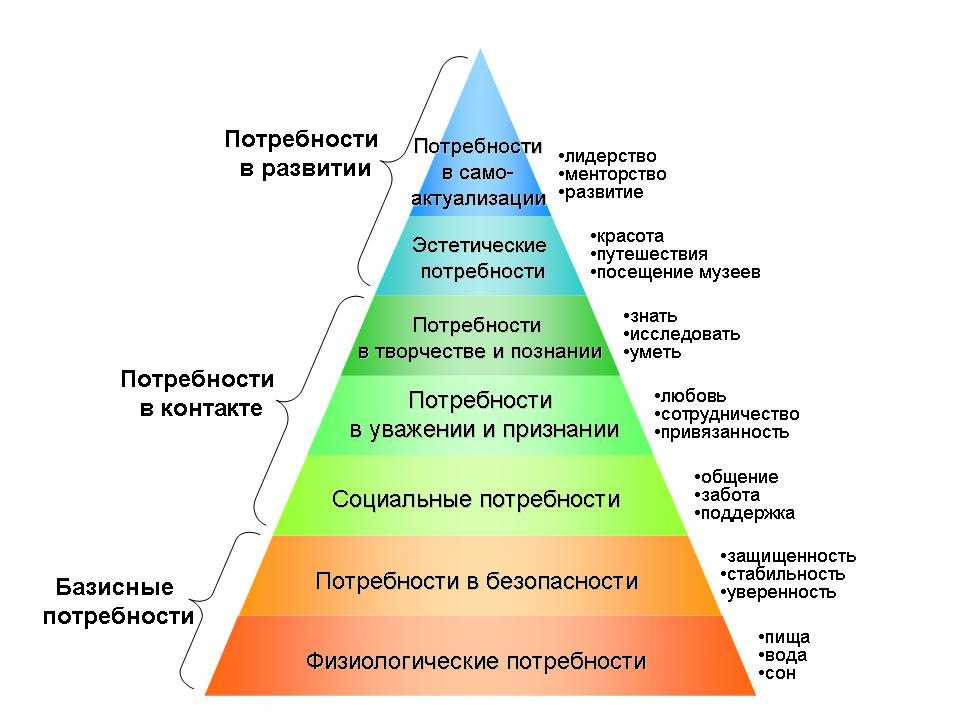 схему):
схему):
Можно убедиться, что результат будет таким же, что и при вычислении определителя по правилу треугольника.
Пример . Вычислить определитель
Решение . Вычислим определитель по правилу звездочки
И по правилу Саррюса
Т.е. получаем одинаковый результат для обеих вычислительных схем, как и ожидалось.
Заметим, что все свойства, сформулированные для определителей второго порядка, справедливы для определителей третьего порядка, в чем можно убедиться самостоятельно. На основании этих свойств сформулируем общие свойства для определителей любого порядка.
определителей
Определение. Матрицей размера mn называется прямоугольная таблица чисел, состоящая из m строк и n столбцов :
. (1)
Числа
стоящие в матрице
называются ее элементами и обозначаются буквой с двумя индексами,
первый из которых равен номеру строки,
а второй
номеру столбца в пересечении которых
находится данный элемент. Элементы
матрицы обычно обозначаются малыми
буквами, а сами матрицы
соответствующими заглавными. Если
матрица задаётся перечислением своих
элементов, то таблица элементов
заключается в круглые или квадратные
скобки.
Элементы
матрицы обычно обозначаются малыми
буквами, а сами матрицы
соответствующими заглавными. Если
матрица задаётся перечислением своих
элементов, то таблица элементов
заключается в круглые или квадратные
скобки.
Например, матрица a размера 23 записывается в виде:
Эта матрица состоит из 6 элементов , гдеi =1,2 – есть номер строки, j =1,2,3 – номер столбца. Матрицы используются в технических науках и в экономике для записи табличной информации. В программировании матрицы называются двумерными массивами.
Матрица у которой число строк равно числу столбцов называется квадратной , а число строк (столбцов) этой квадратной матрицы называется ее порядком . Квадратная матрица n – го порядка состоит из n 2 элементов:
. (2)
Каждой квадратной матрице по определённому правилу сопоставляется число, которое называется определителем этой матрицы. Определитель, в отличие от матрицы обозначается вертикальными линиями:
.
Сформулируем правила вычисления определителей 1-го, 2-го, 3-го порядков.
Определителем матрицы 2-го порядка называется число
.
Например:
.
2. Определителем матрицы 3-го порядка называется число
Это правило называется правилом треугольников (Саррюса) . Для его запоминания используется следующая схематическая запись, где элементы, расположенные на месте черных точек перемножаются:
Например:
Определение: Транспонированной матрицей для матрицы A называется матрица A T , столбцами которой являются соответствующие строки матрицы A. Диагональ, исходящая из левого верхнего угла матрицы, называется её главной диагональю . Для квадратной матрицы (2) транспонированная матрица записывается так:
Рассмотрим теперь
свойства определителей, справедливые
для определителей любого порядка. Для
определённости будем их записывать для
определителей 3-го порядка.
І. Определители квадратной матрицы A и её транспонированной A T совпадают, т.е. |A|=|A T |.
Дальнейшие свойства определителей мы будем формулировать для его строк. Из первого свойства следует, что все они справедливы и для столбцов.
ІІ. При перемене местами двух строк матрицы, её определитель меняет свой знак на противоположный .
Например:
.
В определителе поменяли местами вторую и третью строки.
ІІІ . Определитель матрицы с двумя одинаковыми строками равен 0 .
В самом деле, при перемене местами этих строк, согласно свойству 2, определитель должен удовлетворять уравнению . Отсюда,, следовательно.
І V . Если все элементы одной строки квадратной матрицы умножить на число , то её определитель умножится на это число .
Например: .
V . Если
квадратная матрица содержит нулевую
строку, то её определитель равен 0 .
Это свойство получается из предыдущего при = 0.
V І . Если одна из строк определителя записывается в виде суммы двух строк, то определитель записывается в виде суммы двух определителей у которых на месте этой строки стоят соответственно первые и вторые слагаемые. Остальные соответствующие строки всех трёх определителей равны .
Например:
V ІІ. Если к одной строке матрицы прибавить другую её строку, умноженную на число , то определитель матрицы при этом не изменится .
Определителем квадратной матрицы называется число, которое вычисляется следующим образом:
а) Если порядок квадратной матрицы равен 1, т.е. она состоит из 1 числа, то определитель равен этому числу;
б)Если порядок квадратной матрицы равен 2, т.е. она состоит из 4 чисел, то определитель равен разности произведения элементов главной диагонали и произведения элементов побочной диагонали;
в)Если порядок квадратной матрицы равен 3, т. е. она состоит из 9 чисел, то определитель равен сумме произведений элементов главной диагонали и двух треугольников параллельных этой диагонали, из которой вычли сумму произведений элементов побочной диагонали и двух треугольников параллельных этой диагонали.
е. она состоит из 9 чисел, то определитель равен сумме произведений элементов главной диагонали и двух треугольников параллельных этой диагонали, из которой вычли сумму произведений элементов побочной диагонали и двух треугольников параллельных этой диагонали.
Примеры
Свойства определителей
1. Определитель не изменится, если строки заменить столбцами, а столбцы – строками
- Определитель, имеющий 2 одинаковых ряда, равен нулю
- Общий множитель какого – либо ряда (строки или столбца) определителя можно вынести за знак определителя
4. При перестановке двух параллельных рядов определитель меняет знак на противоположный
5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей
6. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число
Минор элемента определителя и его алгебраическое дополнение
Минором элемента a IJ определителя n-го порядка называется определитель n-1 порядка, полученный из исходного с помощью вычеркивания i-той строки и j-того столбца
Алгебраическое дополнение элемента a IJ определителя – это его минор, умноженный на (-1) i+ j
Пример
Обратная матрица
Матрица называется невырожденной , если ее определитель не равен нулю, в противном случае, матрицу называют вырожденной
Матрица называется союзной , если она состоит из соответствующих алгебраических дополнений и транспонирована
Матрица называется обратной к данной матрице, если их произведение равно единичной матрице того же порядка, что и данная матрица
Теорема о существовании обратной матрицы
Любая невырожденная матрица имеет обратную, равную союзной матрице, деленной на определитель данной матрицы
Алгоритм нахождения обратной матрицы А
- Вычислить определитель
- Транспонировать матрицу
- Составить союзную матрицу, вычислить все алгебраические дополнения транспонированной матрицы
- Воспользоваться формулой:
Минором матрицы называется определитель, состоящий из элементов, находящихся на пересечении выделенных k строк и k столбцов данной матрицы размера mxn
Рангом матрицы называется наибольший порядок того минора матрицы, который отличен от нуля
Обозначение r(A), rangA
Ранг равен количеству ненулевых строк ступенчатой матрицы.
Пример
Системы линейных уравнений.
Системой линейных уравнений, содержащей m уравнений и n неизвестных, называется система вида
где числа a IJ — коэффициенты системы,числа b i — свободные члены
Матричная форма записи системы линейных уравнений
Решением системы называются n значений неизвестных c 1 , c 2 ,…, c n , при подстановке которых в систему все уравнения системы обращаются в верные равенства. Решение системы можно записать в виде вектор – столбца.
Система уравнений называется совместной , если она имеет хотя бы одно решение, и несовместной , если решений не имеет.
Теорема Кронекера – Капелли
Система ЛУ совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной
Методы решения системы ЛУ
1. Метод Гаусса (расширенную матрицу с помощью элементарных преобразований свести к ступенчатой, а потом к канонической)
К элементарным преобразованиям относятся:
Перестановка строк (столбцов)
Прибавление к одной строке (столбцу) другой, умноженной на число, отличное от 0.
Составим расширенную матрицу:
Выберем ведущий элемент, стоящий в первом столбце и первой строке, элемент 1., назовем его ведущим. Строка, в которой находится ведущий элемент меняться не будет. Обнулим элементы под главной диагональю. Для этого прибавим ко второй строке первую, умноженную на (-2). Прибавим к третьей строке первую, умноженную на (-1), получим:
Поменяем вторую и третью строки местами. Мысленно вычеркиваем первый столбец и первую строку и продолжаем алгоритм для оставшейся матрицы. К третьей строке прибавляем 2-ю, умноженную на 5.
Привели расширенную матрицу к ступенчатому виду. Возвращаясь к уравнениям системы, начиная с последней строки и двигаясь вверх, поочередно определяем неизвестные.
2. Матричный метод (AX=B, A -1 AX=A -1 B, X=A -1 B; матрицу, обратную к основной матрице умножить на столбец свободных членов)
3. Метод Крамера.
Решение системы находится по формуле:
Где -определитель измененной основной матрицы, в которой i-й столбец изменен на столбец свободных членов, а — главный определитель, состоящий из коэффициентов при неизвестных.
Векторы.
Вектор – это направленный отрезок
Любой вектор задается длиной (модулем) и направлением.
Обозначение: или
где А – начало вектора, В – конец вектора, – длина вектора.
Классификация векторов
Нулевой вектор – это вектор, длина которого равна нулю
Единичный вектор – это вектор, длина которого равна единице
Равные векторы – это два вектора, у которых совпадают длина и направление
Противоположные векторы – это два вектора, у которых длины равны, а направления – противоположные
Коллинеарные векторы – это два вектора, которые лежат на одной прямой или на параллельных прямых
Сонаправленные векторы – это два коллинеарных вектора с одинаковым направлением
Противоположно направленные векторы– это два коллинеарных вектора с противоположным направлением
Компланарные векторы – это три вектора, которые лежат в одной плоскости или на параллельных плоскостях
Прямоугольная система координат на плоскости – это две взаимно перпендикулярные прямые с выбранным направлением и началом отсчета, при этом горизонтальная прямая называется осью абсцисс, а вертикальная – осью ординат
Каждой точке в прямоугольной системе координат поставим в соответствие два числа: абсциссу и ординату
Прямоугольная система координат в пространстве – это три взаимно перпендикулярные прямые с выбранным направлением и началом отсчета, при этом горизонтальная прямая, направленная на нас, называется осью абсцисс, горизонтальная прямая, направленная вправо от нас — осью ординат, а вертикальная прямая, направленная вверх – осью аппликат
Каждой точке в прямоугольной системе координат поставим в соответствие три числа: абсциссу, ординату и аппликату
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы. Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Интересное: Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒ Определители определены только для квадратных матриц. Определителем второго порядка называется число, которое вычисляется по формуле: . Пример. Вычислить определитель матрицы . Решение. . Ответ: . Определителем третьего порядка называется число, которое вычисляется по формуле: Запомнить эту формулу помогает схема, которая называется «правилом треугольника»: Эти 3 слагаемых берутся Эти 3 слагаемых берутся со знаком «+» со знаком «–»
Пример. Вычислить определитель третьего порядка . Решение. Используя приведенные выше схемы, получим Ответ: 105. Минором элемента определителя -го порядка называется определитель -го порядка, который получается в результате вычеркивания в определителе n-го порядка строки и столбца, содержащих элемент . Алгебраическим дополнением элемента называется его минор, умноженный на : . Пример. Дан определитель . Вычислить минор и алгебраическое дополнение элемента . Решение. Вычислим минор элемента : . Теперь вычислим алгебраическое дополнение элемента : Ответ: , Любой определитель равен сумме произведений элементов произвольной строки (столбца) на их алгебраические дополнения. Этот способ вычисления определителя называется вычислением определителя с помощью разложения по строке (столбцу). Пример. Вычислить определитель . Решение. Вычислим этот определитель с помощью разложения по первой строке. Такой же ответ получится, если определитель вычислять разложением по любой другой строке или столбцу. Ответ: 105. Обратная матрица
Матрица называется обратной по отношению к квадратной матрице , если выполняется равенство: (1) Матрица имеет единственную обратную матрицу тогда и только тогда когда ее определитель отличен от нуля. Алгоритм вычисления обратной матрицы: 1. Вычислить определитель матрицы . Если определитель этой матрицы равен нулю, то не существует. Если же определитель этой матрицы не равен нулю, то существует. 2. Вычислить транспонированную матрицу . 3. Вычислить алгебраические дополнения матрицы . 4. Вычислить обратную матрицу по формуле: . 5. Проверить правильность вычислений по формуле (1). Выполнение данного пункта не является обязательным. Пример.Вычислить обратную матрицу , если . Решение. 1. Вычислим определитель данной матрицы. 2. Вычислим транспонированную матрицу : . 3. Вычислим алгебраические дополнения матрицы : ; ; ; ; ; ; ; ; . 4. Вычислим обратную матрицу: .
Система линейных алгебраических уравнений (СЛАУ) Основные понятия Рассмотрим систему из m линейных уравнений с n переменными: (2) где – коэффициенты при переменных, – свободные члены уравнений. Совокупность чисел называется решением системы (2), если при их подстановке каждое уравнение системы обращается в верное равенство. Система, не имеющая решений, называется несовместной. Система, имеющая решения называется совместной. Совместная система, имеющая единственное решение называется определенной. Совместная система, имеющая более одного решения называется неопределенной. Выпишем коэффициенты при переменных в системе (2) в виде матрицы: . Матрица называется матрицей системы. Выписав из системы все переменные, получим матрицу-столбец переменных: . Выписав все свободные члены, получим матрицу-столбец свободных членов: . Матрица называется расширенной матрицей системы. Метод Гаусса Рассмотрим решение системы (2) методом Гаусса (методом последовательного исключения переменных). Прямой ход. Выпишем расширенную матрицу системы (2) и приведем матрицу к ступенчатому виду, то есть к виду, для которого выполняются условия: 1) все ненулевые строки (имеющие, по крайней мере, один ненулевой элемент) располагаются над всеми чисто нулевыми строками; 2) ведущий элемент, то есть первый ненулевой элемент строки при отсчёте слева направо каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной. . Каждую прямоугольную матрицу с помощью элементарных преобразований можно привести к ступенчатому виду. Элементарные преобразования матрицы – это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, заданной с помощью этой матрицы. К элементарным преобразованиям матрицы относится: 1) умножение любой строки на числовой коэффициент ; 2) прибавление к какой-либо строке другой строки, умноженной на числовой коэффициент; 3) перестановка местами любых двух строк. Обратный ход. Вернемся от расширенной матрицы ступенчатого вида к системе уравнений, которая соответствует этой матрице. Затем начиная с последних по номеру переменных, последовательно найдем все переменные. Пример. Решить систему линейных уравнений: Решение. Решим эту систему уравнений методом Гаусса. Выпишем расширенную матрицу и с помощью элементарных преобразований приведем ее к ступенчатому виду: Прокомментируем каждый шаг алгоритма: 1-й шаг: умножаем первую строку на (-2) и прибавляем к третьей строке. В результате получим в первом столбце все нули, кроме верхнего элемента. 2-й шаг: умножим вторую строку на . 3-й шаг: умножим вторую строку на 5 и прибавим к третьей строке. В результате мы получим расширенную матрицу ступенчатого вида. Далее от полученной расширенной матрицы вернемся к соответствующей ей системе уравнений: Отсюда, из третьего уравнения найдем . Подставляя полученное значение во второе уравнение, найдем . Ответ: .
Формулы Крамера Рассмотрим систему (2), в которой число уравнений равно числу переменных, то есть . В этом случае матрица системы будет квадратной, а ее определитель называется определителем системы. Если определитель матрицы системы не равен нулю , то система имеет единственное решение, которое определяется по формулам: , , …, , (3)
где − определитель матрицы системы, − определитель, получаемый из определителя заменой — го столбца столбцом свободных членов. Формулы (3) называются формулами Крамера. Пример. Решить систему линейных уравнений: Решение. Решим систему линейных уравнений с помощью формул Крамера. Составим определитель матрицы системы уравнений. Для этого выпишем коэффициенты при переменных , и в определитель и вычислим его по «правилу треугольника»: Заменив первый столбец определителя столбцом свободных членов, получим определитель: Заменив второй столбец определителя столбцом свободных членов, получим определитель: Заменив третий столбец определителя столбцом свободных членов, получим определитель: По формулам Крамера находим: , , . Ответ: , , .
Векторы и операции над ними Вектором называется направленный отрезок, который можно перемещать параллельно самому себе. Векторы могут обозначается несколькими способами. Например, либоa, или, где точка означает начало вектора, а точка – конец вектора. Длиной вектора называется число, равное длине отрезка , изображающего вектор. Длина вектора обозначается . Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Вектор, длина которого равна нулю, называется нуль-вектором. Нуль-вектор обозначается . Произведением вектора на число называется вектор , имеющий длину , направление которого совпадает с направлением вектора , если , и противоположно ему, если . Противоположным вектором называется вектор . Определим понятие суммы двух векторов. Также сумму двух векторов можно построить по правилу параллелограмма. Для этого берут произвольную точку и откладывают от нее два вектора и . Далее на этих векторах достраивают параллелограмм . Диагональ является суммой векторов и . (см. рис. 2) Разностью двух векторов и называется вектор . (см. рис. 3) Введем понятие координат вектора. Для этого совместим начало вектора с началом координат. Тогда координатами вектора называются координаты его конечной точки. Пусть точка имеет координаты , а точка – . Тогда координаты вектора . Суммой векторов и является вектор . Разностью векторов и является вектор . Произведением вектора на число называется вектор . Длина вектора равна . Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: , где – угол между векторами и . Если вектора и заданы с помощью координат, то скалярное произведение векторов равно: . Заметим, что скалярный квадрат вектора равен квадрату его длины: . Угол между векторами и вычисляется по формуле: . Пример. Даны два вектора и . Найти угол между этими векторами. Решение. Вычислим косинус угла между этими векторами: . Следовательно, . Ответ: .
Векторное произведение (другое обозначение ) двух векторов и есть третий вектор , модуль которого (т. Если векторы и коллинеарны ( ), то =0. Свойства векторного произведения: ; ; ; ; . Базисные единичные векторы декартовой прямоугольной системы координат удовлетворяют следующим соотношениям: ; ; ; . Если векторы и заданы своими декартовыми координатами: , , то их векторное произведение . Смешанным произведением векторовназывается произведение , результатом которого является скаляр (число). Для компланарных векторов их смешанное произведение . Если векторы , и образуют правую тройку, то , если – левую, то . Смешанное произведение равно объему параллелепипеда , построенного на векторах , и , взятому со знаком «+», если векторы , и образуют правую тройку, и со знаком «–», если – левую: . Если векторы , и заданы своими декартовыми координатами: , , , то их смешанное произведение . Пример. Даны координаты вершин треугольника: , , . Найти площадь . Решение. Направим из вершины треугольника векторы в вершины и (рис. 6). Учитывая, что площадь равна половине площади параллелограмма, построенного на этих векторах, площадь которого, в свою очередь, можно выразить через векторное произведение, будем иметь . Находим координаты векторов: , . Находим векторное произведение = . Таким образом, (кв. ед.). Пример. Найти объем параллелепипеда, построенного на векторах , , . Решение. Вычисляем смешанное произведение данных векторов: = . Объем параллелепипеда .
⇐ Предыдущая1234Следующая ⇒ Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим. Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
Общий метод вычисления определителей
Мы знаем, что вычисление определителя третьего порядка занимает довольно много времени. Количество операций велико, и оно будет еще больше, когда необходимо вычислить определители четвертого порядка или выше.
Мы также знаем, что правило Сарруса справедливо только для вычисления определителей третьего порядка. Давайте теперь рассмотрим более общий метод.
Давайте начнем с нескольких примеров определителей $$3 \times 3$$, чтобы проверить, поможет ли ваша интуиция найти общее правило для вычисления определителей.
$$$\слева| \begin{matrix} 1 & 0 & 2 \\ 2 & 4 & 5 \\ 1 & 0 & 2 \end{matrix}\right|=1 \cdot \left|\begin{matrix} 4 & 5 \\ 0 & 2\end{matrix}\right|-0 \cdot \left|\begin{matrix}2 & 5 \\ 1 & 2\end{matrix}\right|+2 \cdot \left|\begin{matrix} 2 & 4 \\ 1 & 0\end{matrix}\right|=$$$
$$$=1 \cdot (4 \cdot 2-5\cdot 0)-0+2\cdot (2\cdot 0-4\cdot 1)=8-0-8=0$$$
$$$\left|\begin{matrix}1 & 2 & 3 \\ 4 & 5 & 6\\ 7 & 8 & 9\end{matrix}\right|=1 \cdot \left|\begin{matrix}5 & 6 \\ 8 & 9\end{matrix}\right|-2 \cdot \left|\begin{matrix}4 & 6 \\ 7 & 9 \end{matrix}\right|+3 \cdot \left|\begin{matrix} 4 & 5 \\ 7 & 8 \end{matrix}\right|=$$$
$$ $=1 \cdot (5 \cdot 9- 6 \cdot 8)-2 \cdot (4 \cdot 9- 6\cdot 7 )+3\cdot (4 \cdot 8 -5 \cdot 7)=-3+ 12-9=0$$$
Как видите, процедура проста. Определитель матрицы – это сумма произведений элементов одной строки на их сомножители.
Определитель матрицы – это сумма произведений элементов одной строки на их сомножители.
В этих двух решенных случаях мы выбрали первую строку, и каждый из ее элементов был умножен на соответствующий коэффициент.
Давайте рассмотрим тот же пример и действуем шаг за шагом:
$$$\left|\begin{matrix}1 & 2 & 3 \\ 4 & 5 & 6\\ 7 & 8 & 9\end {matrix}\right|$$$
Выбираем одну строку, например, первую $$(1 2 3)$$, и начинаем с первого элемента: $$1$$.
- Рассчитывается его кофактор.
$$$\left|\begin{matrix}\rlap{/}1 & \rlap{/}2 & \rlap{/}3 \\ \rlap{/}4 & 5 & 6\\ \rlap {/}7 & 8 & 9\end{matrix}\right|=5 \cdot 9-8\cdot 6=-3$$$
(знак менять нельзя, так как $$1+1=2$ $, пара.)
- Умножаем выбранный член, то есть $$1$$, на соответствующий ему коэффициент.
$$$1 \cdot \left| \begin{matrix}5 & 6 \\ 8 & 9 \end{matrix}\right|= 1 \cdot (5 \cdot 9-6 \cdot 8)=-3$$$
И так далее со следующими элементы.
Выбран второй член, то есть $$2$$.
- Рассчитывается его кофактор.
$$$\слева| \begin{matrix}\rlap{/}1 & \rlap{/}2 & \rlap{/} 3\\ 4 & \rlap{/}5 и 6\\ 7 & \rlap{/}8 & 9\ end{matrix}\right|$$$
Не забывайте знак минус!!! ($$1+2=3$$, что нечетно).
$$$-2 \cdot \left| \begin{matrix}4 & 6 \\ 7 & 9\end{matrix}\right|=-2 \cdot (4 \cdot 9 — 6 \cdot 7)=12$$$
- Выбираем последний член и повторите процесс, теперь уже с положительным знаком.
$$$\слева| \begin{matrix}\rlap{/}1 & \rlap{/}2 & \rlap{/} 3\\ 4 &5 & \rlap{/}6\\ 7 & 8 & \rlap{/}9\end {матрица}\справа|=3 \cdot \слева| \begin{matrix}4 & \\ 7 & 8 \end{matrix}\right|=3 \cdot (4 \cdot 8 — 5 \cdot 7)=3 \cdot (4 \cdot 8- 5 \cdot 7) = 3 \cdot (-3)=-9$$$
- Наконец, мы суммируем все три случая. В этом примере результат равен нулю.
Подытожим:
$$$\left| \begin{матрица}1 и 2 и 3 \\ 4 и 5 и 6\\ 7 и 8 и 9\end{matrix}\right|=\left| \begin{matrix}\rlap{/}1 & \rlap{/}2 & \rlap{/}3 \\ \rlap{/}4 & 5 & 6\\ \rlap{/}7 & 8 & 9\ конец{матрица}\право|-\лево| \begin{matrix}\rlap{/}1 & \rlap{/}2 & \rlap{/}3 \\ 4 & \rlap{/}5 и 6\\ 7 & \rlap{/}8 & 9\ конец{матрица}\право|+\лево| \begin{matrix}\rlap{/}1 & \rlap{/}2 & \rlap{/}3 \\ 4 & 5 & \rlap{/}6\\ 7 & 8 & \rlap{/}9\ конец{матрица}\справа|=1 \cdot \слева| \begin{matrix}5 и 6 \\ 8 и 9 \end{matrix}\right|-2 \cdot \left| \begin{matrix}4 и 6 \\ 7 и 9\end{matrix}\right|+3 \cdot \left| \begin{matrix}4 & \\ 7 & 8 \end{matrix}\right|$$$
и, используя то, что мы узнали об определителях второго порядка, решим этот случай.
Мы будем использовать тот же метод. Элементы строки умножаются на соответствующие им кофакторы. То есть:
$$$\left| \begin{matrix}1 & 0 & 2 & 1 \\ 0 & 3 & 2 & 1 \\ 2 & 4 & 1 & 2 \\ 3 & 1 & 0 & 2\end{matrix}\right|= \left | \begin{matrix}\rlap{/}1 & \rlap{/}0 & \rlap{/}2 & \rlap{/}1 \\ \rlap{/}0 & 3 & 2 & 1 \\ \rlap {/}2 & 4 & 1 & 2 \\ \rlap{/}3 & 1 & 0 & 2\end{matrix}\right| -\влево| \begin{matrix}\rlap{/}1 & \rlap{/}0 & \rlap{/}2 & \rlap{/}1 \\ 0 & \rlap{/}3 & 2 & 1 \\ 2 & \rlap{/}4 & 1 & 2 \\ 3 & \rlap{/}1 & 0 & 2\end{matrix}\right| +\влево| \begin{matrix}\rlap{/}1 & \rlap{/}0 & \rlap{/}2 & \rlap{/}1 \\ 0 & 3 & \rlap{/}2 & 1 \\ 2 & 4 & \rlap{/}1 & 2 \\ 3 & 1 & \rlap{/}0 & 2\end{matrix}\right|-\left| \begin{matrix}\rlap{/}1 & \rlap{/}0 & \rlap{/}2 & \rlap{/}1 \\ 0 & 3 & 2 & \rlap{/}1 \\ 2 & 4 & 1 & \rlap{/}2 \\ 3 & 1 & 0 & \rlap{/}2\end{matrix}\right| $$$
Как и в случае с определителями третьего порядка, это сводится к умножению каждого элемента первой строки на определители «что не зачеркнуто», помня всегда соответствующий знак. То есть
То есть
$$$\left| \begin{matrix}1 & 0 & 2 & 1 \\ 0 & 3 & 2 & 1 \\ 2 & 4 & 1 & 2 \\ 3 & 1 & 0 & 2\end{matrix}\right|= 1 \ cdot \влево| \begin{matrix} 3 & 2 & 1 \\ 4 & 1 & 2 \\ 1 & 0 & 2\end{matrix}\right|- 0 \cdot \left| \begin{matrix}0 & 2 & 1 \\ 2 & 1 & 2 \\ 3 & 0 & 2\end{matrix}\right|+2 \cdot \left| \begin{matrix} 0 & 3 & 1 \\ 2 & 4 & 2 \\ 3 & 1 & 2\end{matrix}\right|-1 \cdot \left| \begin{matrix}0 & 3 & 2 \\ 2 & 4 & 1\\ 3 & 1 & 0 \end{matrix}\right|$$$
Итак, решая четыре определителя третьего порядка и используя предыдущее выражение, мы можем вычислить определитель матрицы $$4 \times 4$$.
Тот же метод можно использовать для вычисления высших определителей. Таким образом, для вычисления определителя 5-го порядка необходимо вычислить $$5$$ определителей четвертого порядка, которые, в свою очередь, требуют вычисления $$4$$ определителей третьего порядка, и так далее. Таким образом, мы видим, что метод достаточно медленный и утомительный, чтобы гарантировать, что использование мощных вычислителей совершенно необходимо.
KryssTal : Дополнительная алгебра
KryssTal : Дополнительная алгебра [Домашняя страница] [Введение в числа] [Отзывы читателей (математика)] [Язык] | |
Введение
Определитель представляет собой набор чисел, расположенных в строках и столбцах и заключенных в квадратные скобки []. Каждое отдельное значение называется элементом . Определители имеют столько же строк, сколько и столбцов. Определитель с n строк и столбцов называется определителем n-го порядка .
Каждое отдельное значение называется элементом . Определители имеют столько же строк, сколько и столбцов. Определитель с n строк и столбцов называется определителем n-го порядка .Например, определитель ниже равен Определитель второго порядка :
Это пример определителя третьего порядка :
Оценка детерминантов
Определитель имеет значение. Чтобы вычислить определитель второго порядка, диагональные элементы перемножаются и вычитаются, как показано ниже.Использование формулы дает значение -7:

Затем каждый определитель второго порядка можно оценить отдельно и умножить на член снаружи, потому что:
Оценка проводится в два этапа по трем меньшим детерминантам:
Вычисление определителя можно упростить. Если строка или столбец имеют общий множитель, этот множитель можно удалить за пределы определителя, если затем все строки/столбцы разделить на этот множитель. Это может привести к значительному упрощению арифметики. В определителе ниже 6 удаляется из столбца 1, затем 2 удаляется из строки 1.
Решение одновременных уравнений
Детерминанты можно использовать для решения одновременных уравнений. Рассмотрим следующую пару одновременных уравнений с двумя неизвестными ( x и y ): 2 у + с 2 = 0 Во «Введении в алгебру» одновременные уравнения решались путем манипулирования ими до тех пор, пока не оставалась одна переменная.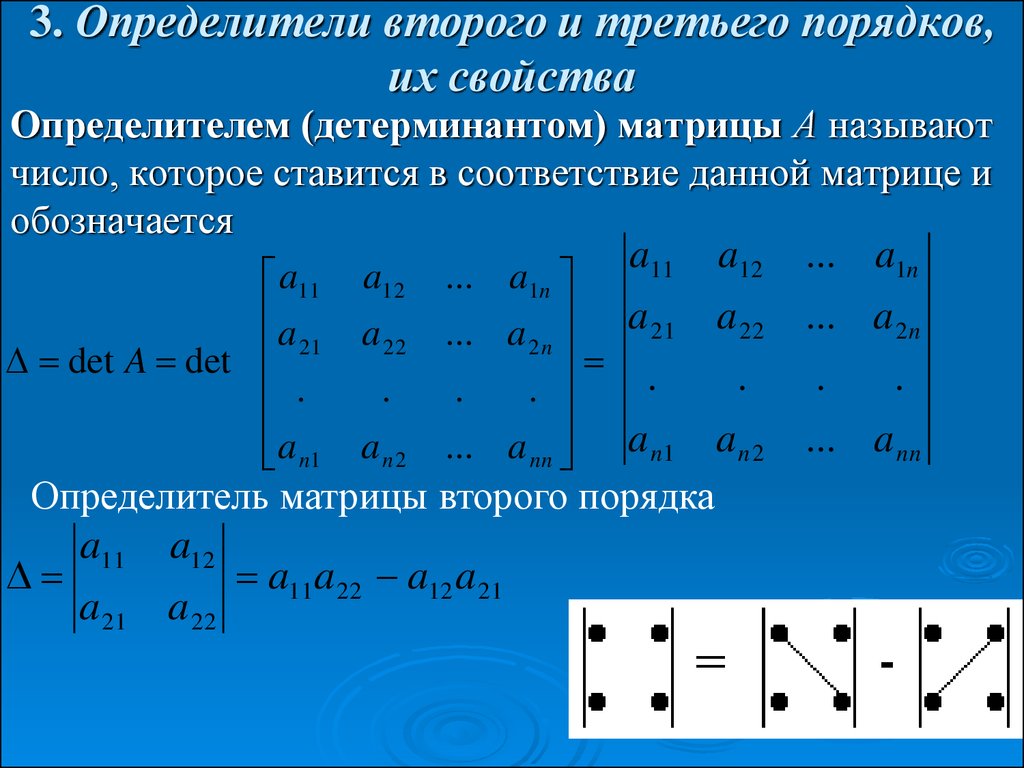
Это метод решения одновременных уравнений с использованием определителей.
- Составьте определитель, называемый D(n) , коэффициентов x и y .
- Составьте определитель, называемый D(x) , из коэффициентов y и чисел.
- Составьте определитель, называемый D(y) , из коэффициентов x и чисел.
- Решение уравнений дается по формуле ниже. Обратите внимание на чередующийся знак минус.
Создайте и оцените три определителя.

Приравнивание дроби, содержащей x, к дроби, состоящей только из чисел, дает:
Приравнивание дроби, содержащей y, к дроби, состоящей только из чисел, дает:
Таким образом, решения равны x = 5 и y = -2 .
Аналогичным образом можно решить три одновременных уравнения с тремя неизвестными ( x , y , z ). Четыре определителя третьего порядка получены с использованием коэффициентов и чисел, как указано выше, чтобы получить D(n) , D(x) , D(y) и D(z) . Формула для решения одновременных уравнений:x + 2y — z — 7 = 0
2x + 3y + 2z — 4 = 0
 D(n) содержит коэффициенты x, y и z. Это имеет значение 33.
D(n) содержит коэффициенты x, y и z. Это имеет значение 33. D(x) содержит все коэффициенты и числа, кроме x. Его значение равно -33.
D(y) содержит все коэффициенты и числа, кроме тех, что относятся к y. Его значение равно 66.
D(z) содержит все коэффициенты и числа, кроме z. Его значение также равно 66.
Наконец, примените формулу и замените значениями определителей.
Приравнивая каждую дробь, содержащую неизвестное, к дроби, содержащей числа, мы можем показать, что
х = 1 , у = 2 , z = -2 .
Столь же легко решаются одновременные уравнения более высокого порядка с большим количеством неизвестных.Рассмотрим дробную функцию вида, показанного ниже, где a , b , c , d и e это номера:
Во многих задачах полезно иметь возможность выразить это в виде частичных дробей примерно так
где A , B и f , g — числа.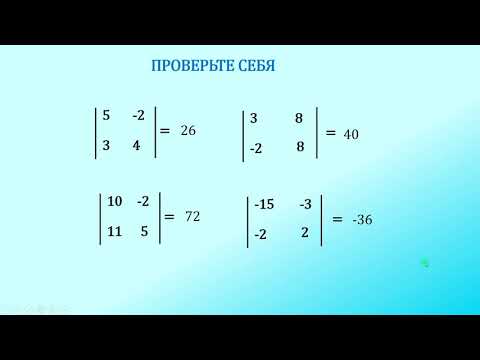 Выражения x + f и x + g являются двумя множителями знаменателя исходной функции (нижняя часть).
Выражения x + f и x + g являются двумя множителями знаменателя исходной функции (нижняя часть).
Метод преобразования дробных функций в неполные дроби включает разложение знаменателя исходной дроби на множители, а затем вычисление чисел А и В . Пример — самый простой способ показать метод.
Пример 6. Преобразуйте приведенную ниже дробную функцию в неполные дроби.Сначала мы факторизуем знаменатель, как показано ниже. Мы используем знак идентичности (три строки), а не знак равенства (=), потому что мы меняем формат, не затрагивая никаких значений.
Затем мы разделяем функцию на две новые дроби, каждая с одним из множителей в качестве знаменателя. Числа в числителях (верхние части), A и B, на данном этапе неизвестны, и их необходимо будет вычислить.
На следующем этапе мы складываем дроби, используя обычные правила дробной алгебры. Мы пытаемся воссоздать исходную дробь, но с буквами А и В в числителе: Числитель первой дроби (А) умножается на знаменатель второй дроби (х+2). Числитель второй дроби (В) умножается на знаменатель первой дроби (х — 1). Затем объединенный числитель расширяется, и различные члены группируются вместе с точки зрения x и констант.
Числитель первой дроби (А) умножается на знаменатель второй дроби (х+2). Числитель второй дроби (В) умножается на знаменатель первой дроби (х — 1). Затем объединенный числитель расширяется, и различные члены группируются вместе с точки зрения x и констант.
Теперь мы можем сравнить исходную дробную функцию с новой версией, которую мы создали.
Левая сторона идентична правой стороне. Это означает, что коэффициенты x можно приравнять с обеих сторон и числа тоже можно приравнять. Это дает пару одновременных уравнений с двумя неизвестными (A и B).
Эти уравнения можно легко решить, чтобы получить А = 1 и В = 3 , поэтому
Что такое предел?
Идея ограничения странная. Он использовался в математике на протяжении тысячелетий для придания значения вещам, которые невозможно точно вычислить.
Например, рассмотрим бесконечный ряд ниже:
. Ряд имеет бесконечное количество членов. Сумма ряда (сколько это всего) может быть переписана с использованием символа суммирования (греческая заглавная буква, сигма Σ) следующим образом
 Мы можем использовать идею предела, чтобы сказать, что:
Мы можем использовать идею предела, чтобы сказать, что:Существует краткий способ написания этого заявления:
. Следующий предел
означает
Это означает
Производная x
2 Пределы очень полезны математически. Одним из примеров является дифференциальное исчисление. Мы уже ввели идею о том, что производная x 2 2x. Сейчас это будет доказано.Рассмотрим функцию
 Чтобы найти значение y, просто возведите значение x в квадрат. Когда мы находим производную, мы пытаемся увидеть, как эта функция изменяется при заданном значении x. Мы можем аппроксимировать это, добавив небольшую величину к x и посмотрев, как это повлияет на y.
Чтобы найти значение y, просто возведите значение x в квадрат. Когда мы находим производную, мы пытаемся увидеть, как эта функция изменяется при заданном значении x. Мы можем аппроксимировать это, добавив небольшую величину к x и посмотрев, как это повлияет на y.Небольшое дополнение к x обозначается символом Δx. Точно так же небольшое дополнение к y обозначается символом Δy. Суммы должны быть небольшими, иначе мы не найдем вариации в определенной точке. Когда мы делаем сложение, мы получаем:
Мы можем расширить правую сторону
Теперь вычтите y из обеих сторон
Помните, что у = х 2
Разделите обе части на Δx, чтобы получить
 Это мера того, как изменяется y при незначительном изменении x. Чем меньше мы делаем Δx, тем ближе выражение приближается к скорости изменения в данной точке, мгновенной скорости изменения . Мы не можем просто установить Δx равным 0, потому что мы не можем делить на ноль.
Это мера того, как изменяется y при незначительном изменении x. Чем меньше мы делаем Δx, тем ближе выражение приближается к скорости изменения в данной точке, мгновенной скорости изменения . Мы не можем просто установить Δx равным 0, потому что мы не можем делить на ноль.Но мы можем использовать ограничения. Мы можем позволить Δx приблизиться к 0 и посмотреть, каков предел. Это можно выразить:
Правило Лопиталя
Правило Лопиталя позволяет найти пределы дробных функций, если их можно дифференцировать. Если две функции равны f(x) и g(x) и если их отдельные производные равны F(x) и G(x) соответственно, то правило Лопиталя гласит: Если производные не дают предела, то процесс можно повторить. Использование этого правила лучше всего показать на примере.
Использование этого правила лучше всего показать на примере.
Ищем следующий предел.
Производная от 1 — cos(x) равна sin(x) . производная от x 2 равна 2x . Поэтому ищем следующий предел:
Это не лучше, потому что предел равен 0/0, когда x приближается к нулю.
Мы можем продолжить и снова различать верх и низ.

 ..
..




 Метод Гаусса состоит из прямого и обратного хода.
Метод Гаусса состоит из прямого и обратного хода.
 Подставляя вместо и полученные значения, из первого уравнения найдем .
Подставляя вместо и полученные значения, из первого уравнения найдем .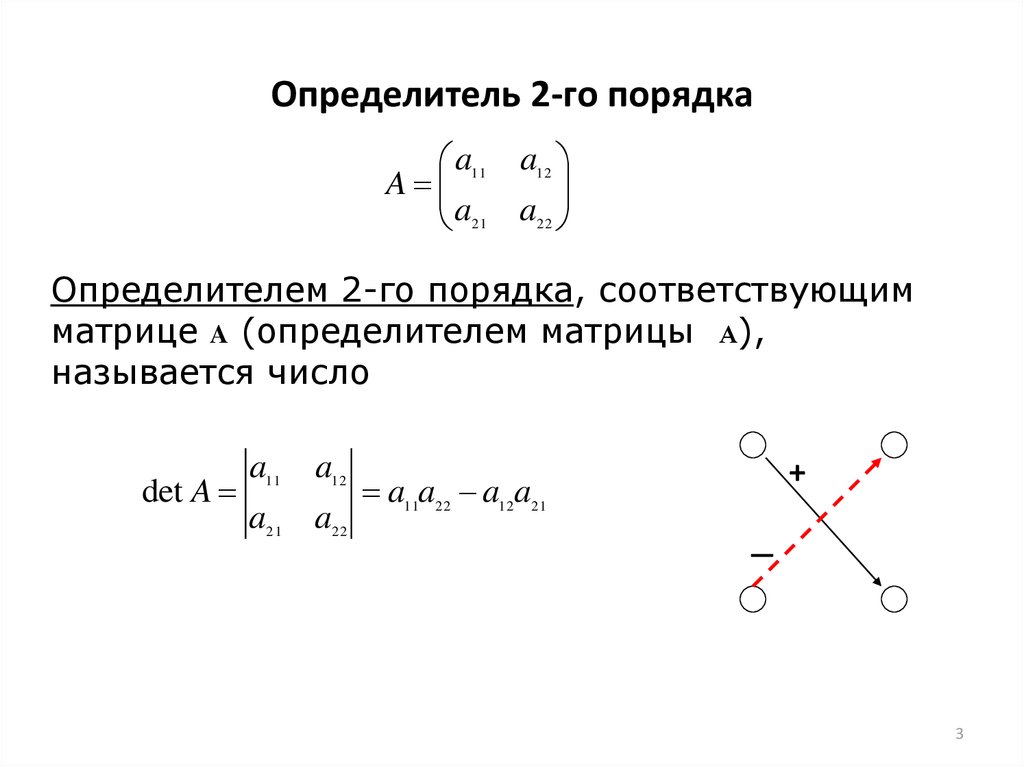
 Пусть и – два произвольных вектора. Возьмем произвольную точку и построим вектор . От точки отложим вектор . Вектор , соединяющий начало первого вектора с концом второго, называется суммой векторов и : . (см. рис. 1) Это правило сложения векторов называется правилом треугольника.
Пусть и – два произвольных вектора. Возьмем произвольную точку и построим вектор . От точки отложим вектор . Вектор , соединяющий начало первого вектора с концом второго, называется суммой векторов и : . (см. рис. 1) Это правило сложения векторов называется правилом треугольника.
 е. равен площади параллелограмма, построенного на векторах и ), а направление перпендикулярно к обоим векторам и (т. е. плоскости упомянутого параллелограмма) и совпадает с направлением поступательного движения правого винта при его повороте от к на угол, меньший . Из этого определения векторного произведения следует, что векторы , и образуют правую систему.
е. равен площади параллелограмма, построенного на векторах и ), а направление перпендикулярно к обоим векторам и (т. е. плоскости упомянутого параллелограмма) и совпадает с направлением поступательного движения правого винта при его повороте от к на угол, меньший . Из этого определения векторного произведения следует, что векторы , и образуют правую систему.

 ..
..