Калькулятор многоугольника
Поиск для:
Правильный многоугольник — плоская замкнутая ломаная, состоящая из прямых отрезков. Все стороны и углы правильного многоугольника равны между собой.
Калькулятор расчета площади и периметра правильного многоугольника.
| Расчет площади многоугольника по длине стороны:[ ((длина стороны)2×N)/(4Tan(π/N)) ] | |
| Введите длину стороны = | |
| Введите количество сторон = | |
| Площадь многоугольника = |
|
Расчет периметра Многоугольника: [ N×(side) ] | |
| Введите длину стороны = | |
| Введите кол-во сторон = | |
| Периметр Многоугольника = |
Расчет площади по длине стороны:
Площадь Многоугольника = ((side)² * N) / (4Tan(π / N))
Периметр Многоугольника = N * (side)
Расчет площади по радиусу описанной окружности :
Площадь Многоугольника = ½ * R² * Sin(2π / N)
Расчет площади по радиусу вписанного круга :
Площадь Многоугольника = A² * N * Tan(π / N)
где, A = R * Cos(π / N)
По радиусу вписанного круга и длине стороны :
Площадь Многоугольника = (A * P) / 2
где A = сторона / (2 * Tan(π / N))
где,
- N = Количество сторон,
- A = Радиус вписанного круга,
- R = Радиус описанной окрудности,
- P = Периметр
Примеры:
Задача 1: Найдите площадь и периметр многоугольника, если длина стороны = 2 и количество сторон = 4.
Шаг 1: Найдем площадь.
Площадь = ((длина стороны)² * N) / (4Tan(π / N))
= ((2)² * 4) / (4 * Tan(3.14 / 4))
= 16 / 4 * 0.999
= 16 / 3.996
Площадь = 4.
Шаг 2: Найдем периметр.
Периметр = (N * (длина стороны) = 4 * 2 = 8
Задача 2: Найдите площадь и периметр многоугольника, если радиус описанной окружности = 2, количество сторон многоугольника = 5.
Шаг 1: Найдем площадь.
Площадь = ½ * R² * Sin(2π / N)
= (0.5) * 2² * Sin(2 * 3.14 / 5)
= 0.5 * 4 * Sin(6.28 / 5)
= 2 * Sin(1.26)
= 2 * 0.95
Площадь = 1.9.
Задача 3:Найдите площадь многоугольника с радиусом описанной окружности равному 2 и количеству сторон 5, используя радиус вписанного круга.
Шаг 1: Найдем радиус вписанного круга.
А = R * Cos(π / N)
= 2 * Cos(3.14 / 5)
= 2 * Cos(0.63)
= 2 * 0.81
Апофема (радиус вписанного круга) = 1.62.
Шаг 2: Найдем площадь.
Площадь = A² * N * Tan(π / N)
= 1.62² * 5 * Tan(3.14 / 5)
= 2.62 * 5 * Tan(0.63)
= 13.1 * 0.73
Площадь = 9.5.
Задача 4: Найти площадь многоугольника используя Апофему (радиус вписанного круга), если длина стороны равна 2, а количество сторон 5.
Step 1: Найдем Апофему.
Апофема = длина стороны / (2 * Tan(π / N))
= 2 / (2 * Tan(π / 4))
= 2 / (2 * Tan(0.785))
= 2 / (2 * 0.999)
= 2 / 1.998
Апофема (А) = 1.
Шаг 2: Найдем периметр.
Периметр (P) = (N * (длина стороны) = 4 * 2 = 8
Шаг 3: Найдем площадь.
Площадь = (A * P) / 2
= (1 * 8) / 2
= 8 / 2
Площадь = 4.
Приведенные выше примеры показывают, как вычислить площадь и периметр многоугольника вручную.
людей нашли эту статью полезной. А Вы?
0Оставьте комментарий! Напишите, что думаете по поводу статьи.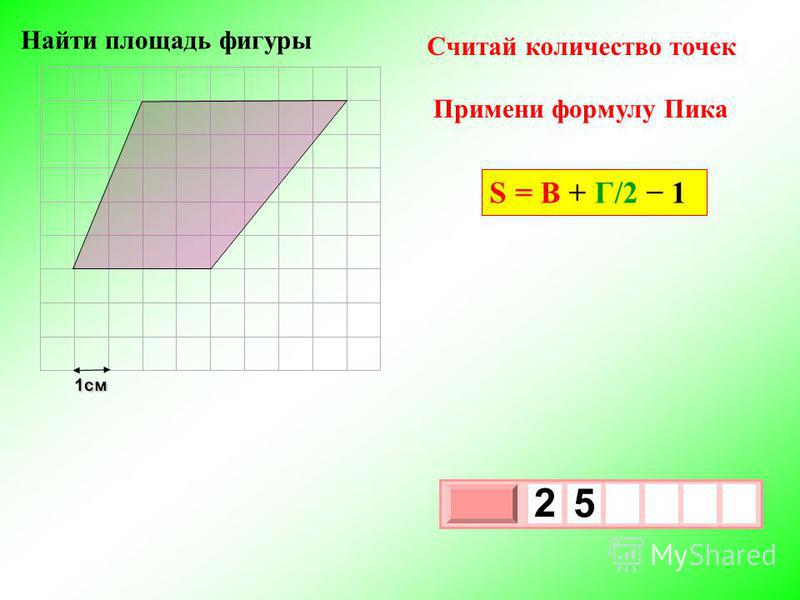
x
Площадь многоугольника
Получи беслпатные курсы подготовки к ЕГЭ и ОГЭ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2016-11-10
Площадь многоугольника. Друзья! К вашему вниманию пару задачек с многоугольником и вписанной в него окружностью. Существует формула, которой связывается радиус указанной окружности и периметр с площадью такого многоугольника. Вот она:
Как выводится эта формула? Просто!
Имеем многоугольник и вписанную окружность. *Рассмотрим вывод на примере пятиугольника. Разобьём его на треугольники (соединим центр окружности и вершины отрезками). Получается, что у каждого треугольника основание является стороной многоугольника, а высоты образованных треугольников равны радиусу вписанной окружности:
Используя формулу площади треугольника можем записать:
Вынесем общие множители:
Уверен, сам принцип вам понятен.
*При выводе формулы количество сторон взятого многоугольника не имеет значения.
В общем виде вывод формулы выглядел бы так:
*Дополнительная информация!
Известна формула радиуса окружности вписанной в треугольник
Не трудно заметить, что она исходит из полученной нами формулы, посмотрите (a,b,c – это стороны треугольника):
27640. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Вычисляем:
Ответ: 30
Ещё пара задач с многоугольниками.
27930. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 540. Найдите n.
Если угол между радиусом окружности и стороной многоугольника равен 540, то угол между сторонами многоугольника будет равен 1080. Тут необходимо вспомнить формулу угла правильного многоугольника:
Остаётся подставить в формулу значение угла и вычислить n:
Ответ: 5
27595.
Периметры двух подобных многоугольников относятся как 2:7. Площадь меньшего многоугольника равна 28. Найдите площадь большего многоугольника.
Здесь нужно вспомнить о том, что если линейные размеры фигуры увеличивается в k раз, то площадь фигуры увеличивается в k2 раз. *Свойство подобия фигур.
Периметр большего многоугольника больше периметра меньшего в 7/2 раза, значит площадь увеличилась в (7/2)2 раза. Таким образом, площадь большего многоугольника равна:
Ответ: 343
27639. Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.
Посмотреть решение
27641. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Посмотреть решение
27595. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Ответ: 50
Всего доброго! Учитесь с удовольствием!
С уважением, Александр.
Категория: Площади фигур | ЕГЭ-№1Формулы
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Площадь неправильного многоугольника
Площадь неправильного многоугольника — Открытый справочник по математикеОткрытый справочник по математике
Главная Контакт О Тематический указатель
В отличие от правильного многоугольника, если вы не знаете координаты вершин, нет простой формулы для площади неправильного многоугольника. Каждая сторона может быть разной длины, и каждый внутренний угол может быть разным. Он также может быть выпуклым или вогнутым.
Если известны координаты вершин многоугольника, есть два способа:
- Ручной метод. См. Площадь многоугольника (Координатная геометрия).
- Компьютер алгоритм. См. Алгоритм нахождения площади любого многоугольника.
Итак, как это сделать?
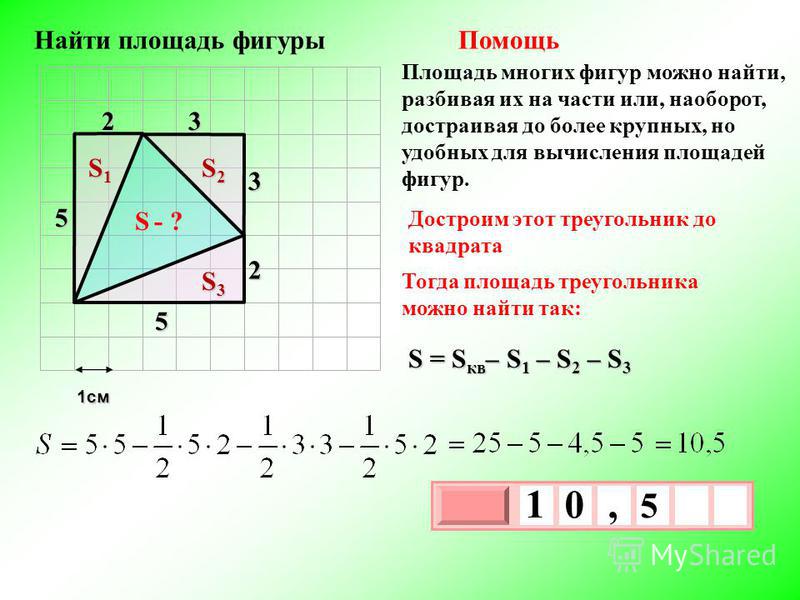
Один из подходов состоит в том, чтобы разбить фигуру на части, которые вы можете решить — обычно это треугольники, так как есть много способов вычислить площадь треугольников. Как именно вы это сделаете, зависит от того, что вам дано для начала. Поскольку это очень изменчиво, нет простого правила, как это сделать. В приведенных ниже примерах представлены некоторые основные подходы, которые можно попробовать.
1. Разбить на треугольники, затем добавить
На рисунке выше многоугольник можно разбить на треугольники, проведя все диагонали. из одной из вершин. Если вы знаете достаточно сторон и углов, чтобы найти площадь каждой из них, то вы можете просто сложить их, чтобы найти сумму. Не бойтесь рисовать лишние линии в любом месте, если они помогут найти фигуры, которые вы сможете разгадать. Здесь неправильный шестиугольник разделен на 4 треугольника добавлением красных линий.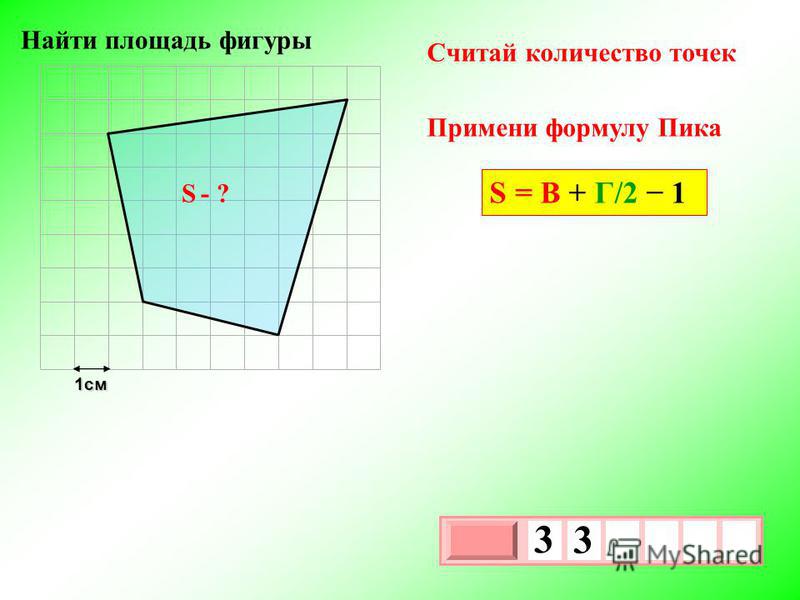
2. Найдите «недостающие» треугольники, затем вычтите
На рисунке выше общая форма представляет собой правильный шестиугольник, но отсутствует треугольная часть.Мы знаем, как найти площадь правильного многоугольника, поэтому мы просто вычитаем площадь «недостающего» треугольника, созданного путем рисования красной линии. (См. Площадь правильного многоугольника и Площадь треугольника.)
3. Рассмотрим другие формы
На рисунке выше фигура представляет собой неправильный шестиугольник, но его симметрия позволяет разбить его на два параллелограмма. нарисовав красную пунктирную линию. (при условии, конечно, что линии, которые выглядят параллельными, на самом деле таковыми являются!)Мы знаем, как найти площадь параллелограмма, поэтому мы просто находим площади каждого из них и складываем их вместе. (См. Площадь параллелограмма).
Как видите, существует бесконечное количество способов разбить фигуру на части, которыми легче управлять.
4. Если известны координаты вершин
Если известны координаты x,y вершин (углов) фигуры, существует метод прямого нахождения площади. См. Площадь многоугольника (Координатная геометрия). Это работает для всех типов полигонов (правильных, неправильных, выпуклых, вогнутых). Также есть компьютер алгоритм это делает то же самое. См. Алгоритм нахождения площади любого многоугольника.Другие темы полигонов
Общий
- Общее определение многоугольника
- Четырехугольник
- Правильный многоугольник
- Неправильный многоугольник
- Выпуклые многоугольники
- Вогнутые многоугольники
- Диагонали многоугольника
- Многоугольные треугольники
- Апофема правильного многоугольника
- Центр полигона
- Радиус правильного многоугольника
- Вписанная окружность правильного многоугольника
- Центр правильного многоугольника
- Окружность многоугольника
- Параллелограмм, вписанный в четырехугольник
Типы полигонов
- Квадрат
- Диагонали квадрата
- Прямоугольник
- Диагонали прямоугольника
- Золотой прямоугольник
- Параллелограмм
- Ромб
- Трапеция
- Медиана трапеции
- Воздушный змей
- Вписанный (вписанный) четырехугольник
- Вписанные внутренние углы четырехугольника
- Площадь вписанного четырехугольника
- Диагонали вписанного четырехугольника
Площадь полигонов различных типов
- Площадь правильного многоугольника
- Область неправильного многоугольника
- Площадь ромба
- Кайт-площадка
- Площадь прямоугольника
- Площадь трапеции
- Площадь параллелограмма
Периметр различных типов полигонов
- Периметр многоугольника (правильного и неправильного)
- Периметр треугольника
- Периметр прямоугольника
- Периметр квадрата
- Периметр параллелограмма
- Периметр ромба
- Периметр трапеции
- Периметр воздушного змея
Углы, связанные с многоугольниками
- Внешние углы многоугольника
- Внутренние углы многоугольника
- Соотношение внутренних и внешних углов
- Центральный угол многоугольника
Именованные полигоны
- Четырехугольник, 4 стороны
- Пятиугольник, 5 сторон
- Шестигранник, 6 сторон
- Семиугольник, 7 сторон
- Октагон, 8 сторон
- Нонагон Эннеагон, 9 сторон
- Десятиугольник, 10 сторон
- Undecagon, 11 сторон
- Додекагон, 12 сторон
(C) 2011 Copyright Math Open Reference.
Все права защищены
Площадь правильного многоугольника с решенными примерами
Любой многоугольник с равными сторонами и углами называется правильным. Учитывая это, метод, используемый для определения площади правильных многоугольников, основан на формулах, присвоенных каждому многоугольнику.
Многоугольник — это плоская фигура, описываемая конечным числом прямолинейных отрезков, соединенных в замкнутую многоугольную цепь (или многоугольный контур). Ограниченная плоская область, ограничивающая цепь или то и другое вместе могут называться многоугольником в евклидовой геометрии.
Некоторые важные термины и информация о многоугольнике:- Стороны – сегменты многоугольника
- Вершины — место встречи двух сторон многоугольника
- Кузов – салон полигон
- «угольник» относится к сторонам многоугольника. Четырехугольник — это 4-угольник.
- Многоугольник — это двухмерная фигура.
- Апофема правильного многоугольника (иногда сокращенно апо) — это отрезок прямой от центра до середины одной из его сторон.
- Внутренний угол: угол, образованный вершиной многоугольника, лежащей внутри области, заключенной в многоугольник.
- Центр правильного многоугольника: точка внутри многоугольника, от которой все вершины многоугольника равноудалены.
- Конгруэнтные многоугольники: Многоугольники, все стороны которых конгруэнтны
- Внешний угол: угол, образованный вершиной многоугольника, лежащей вне области, заключенной в многоугольник.
Длина сторон, диагоналей и вычисление углов, медиан, периметров и площадей правильных многоугольников входят в учебную программу измерения и геометрии.
Некоторые из популярных имен полигонов (по количеству сторон) с их свойствами:| Имя | Стороны | Свойства |
| моногон | 1 | Обычно не признается многоугольником, хотя в некоторых дисциплинах, таких как теория графов, иногда используется этот термин. |
| двуугольник | 2 | Обычно не признается многоугольником на евклидовой плоскости, хотя может существовать как сферический многоугольник. |
| треугольник (или треугольник) | 3 | Простейший многоугольник, который может существовать на евклидовой плоскости. Может замочить самолет. |
| четырехугольник (или четырехугольник) | 4 | Простейший многоугольник может пересекаться; простейший многоугольник, который может быть вогнутым; простейший многоугольник может быть нециклическим. Может замочить самолет. |
| пятиугольник | 5 | Простейший многоугольник может существовать как правильная звезда. Звездный пятиугольник известен как пентаграмма или пентакль. |
| шестигранник | 6 | Может замостить плоскость. |
| семиугольник (или септагон) | 7 | Простейший многоугольник таков, что правильная форма не может быть построена с помощью циркуля и линейки. Однако его можно построить с помощью конструкции neusis. |
- Выпуклость означает, что любая линия, проведенная через многоугольник (не касающаяся стороны или угла), пересекает его границу ровно дважды. В результате ни один из его внутренних углов не превышает 180°. С другой стороны, любой отрезок с концами на границе проходит только через внутренние точки между его концами.
- Вогнутая: невыпуклая и прямая. По крайней мере один внутренний угол больше 180°.
- Простой: граница полигона не пересекает саму себя. Все выпуклые многоугольники простые.
- Звездчатый многоугольник — это многоугольник, который регулярно пересекает сам себя. Многоугольник не может быть одновременно звездой и иметь форму звезды. Следует помнить о разнице между этим и следующим, пока мы пытаемся найти площадь правильного многоугольника.
- Звездообразный: по крайней мере из одной точки видна вся внутренняя часть без пересечения каких-либо краев. Многоугольник должен быть простым и может быть как выпуклым, так и вогнутым. Все выпуклые многоугольники имеют форму звезды.
- Невыпуклая: можно найти линию, пересекающую границу более двух раз. Отрезок линии существует между двумя граничными точками, которые проходят за пределами многоугольника.
- Простой: граница полигона не пересекает саму себя. Все выпуклые многоугольники простые.
- Вогнутая: невыпуклая и прямая. По крайней мере один внутренний угол больше 180°.
- Самопересекающийся: граница многоугольника пересекает сама себя. Термин сложный иногда используется в отличие от простого, но это может сбить с толку концепцию сложного многоугольника как многоугольника, существующего на сложной гильбертовой плоскости и имеющего два сложных измерения.
В результате ни один из его внутренних углов не превышает 180°. С другой стороны, любой отрезок с концами на границе проходит только через внутренние точки между его концами.
По аспектам равенства и симметрии
- Равноугольный: означает, что все углы равны.
- Равносторонний: Это означает, что все ребра имеют одинаковую длину.
- Обычные: равносторонние и равноугольные по форме.
- Циклический: все четыре угла расположены на одной окружности, известной как описанная окружность.
- Другой способ определить правильность состоит в том, что многоугольник является правильным, если он одновременно изогональный и изотоксальный, или, что то же самое, если он одновременно циклический и равносторонний. Правильный звездчатый многоугольник — это невыпуклый правильный многоугольник.
- Изотоксальный или реберно-транзитивный: все стороны имеют одну и ту же орбиту симметрии. Кроме того, многоугольник является равносторонним и касательным.
- Касательная: это означает, что все стороны окружности касаются.
- Изогональные или вершинно-транзитивные: все углы находятся на одной орбите симметрии. Кроме того, многоугольник циклический и равноугольный.
/918870b1bc4a305.s.siteapi.org/img/edee03ad2caaea20a8e609afa923e1cfd0151aa3.jpg)
Правильный звездчатый многоугольник — это невыпуклый правильный многоугольник.Как найти площадь правильного многоугольника?
Площади правильных многоугольников описываются площадью, ограниченной сторонами/границами многоугольника. Впоследствии можно было бы сказать, что для нахождения площади правильного многоугольника нужно вычислить область, которую он занимает.
Разница между периметром и площадью правильных многоугольников Периметр и площадь часто путают. Однако их единственное сходство состоит в том, что площадь и периметр не зависят от внутренних углов многоугольника; скорее, они зависят от длины сторон.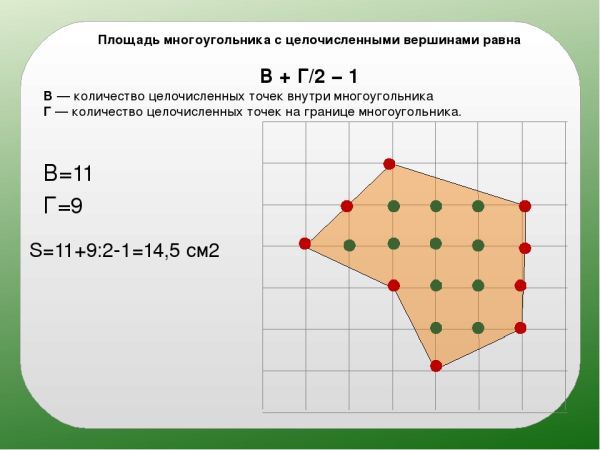
Сначала необходимо понять основные различия, чтобы устранить путаницу между этими двумя измеримыми тождествами.
| Критерии | Периметр многоугольника | Площадь многоугольника | |||||||||||||
| Определение | Определяется как общая длина границы многоугольника, которая может быть получена путем сложения длин всех его сторон. | Определяется как область пространства, ограниченная любым многоугольником. | |||||||||||||
| Формула | Периметр многоугольника = длина стороны 1 + длина стороны 2 + …+ длина стороны N (для N-стороннего многоугольника) | Площадь многоугольника может быть найдена по разным формулам в зависимости от того, многоугольник правильный или неправильный. | |||||||||||||
| Единица измерения | метры, сантиметры, дюймы, футы и т. д. правильный многоугольник Формулы для некоторых известных правильных многоугольников приведены ниже
Мы также можем найти площадь треугольника, если известны длины его сторон, используя формулу Герона, то есть площадь = √s(s−a)(s−b)(s−c)s(s− a)(s−b)(s−c), где s = периметр/2 = (a + b + c)/2, a, b и c — длины его сторон.
В двух словах, как найти площадь каждого правильного многоугольника:
Как найти площадь правильного многоугольника, если известно количество его сторон? Площади правильных многоугольников = (количество сторон × длина одной стороны × апофема)/2, где длина апофемы определяется как l/(2tan(180/n)), где l — длина стороны, а n — количество сторон правильного многоугольника.
Пример: найти площадь правильного многоугольника с пятью сторонами, каждая из которых имеет длину 10 см
Пример: Найдите площадь правильного многоугольника с тремя сторонами, основанием 6 см и высотой 10 см l
1/2 × основание × высота
В этих примерах нахождение площади каждого правильного многоугольника становится намного проще, если использовать базовые формулы. Часто задаваемые вопросы1. Что такое определение площади многоугольника?Ответ. Площадь многоугольника — это площадь, которую он заключает. Поскольку многоугольники представляют собой замкнутые плоские формы, их площадь — это пространство, которое они занимают в двумерной плоскости. Площадь любого многоугольника всегда измеряется в квадратных единицах. 2. Как найти площадь многоугольника?Ответ. Чтобы найти площадь многоугольника, нужно знать, сколько у него сторон и какой он формы. Площадь многоугольника равна половине произведения его периметра и длины одной стороны. Вот пример: вычислите площадь треугольника со сторонами 3, 7 и 5 единиц длины. Длина периметра равна 15 единицам, поэтому: Площадь = ½ × 15 × (3 + 7 + 5) = 0,75 × 15 = 10,25 единиц² 3. |
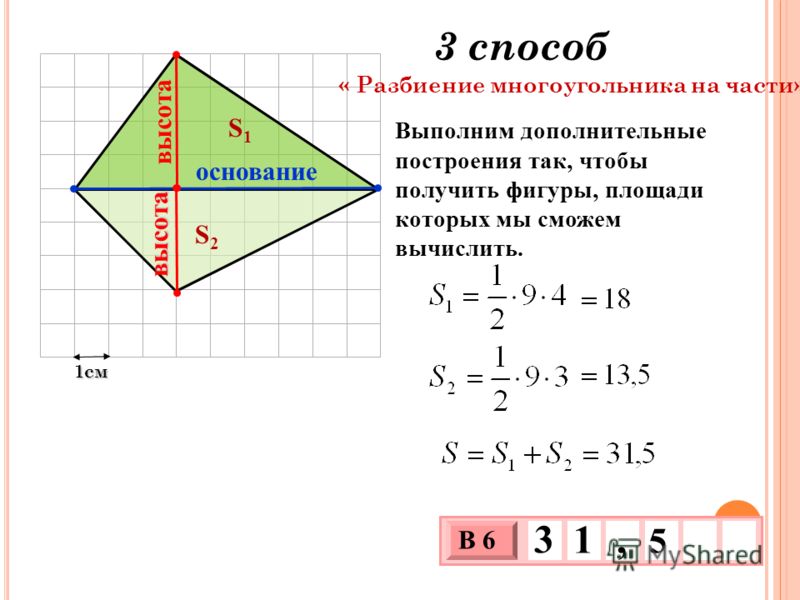
Другие формулы для углубленного изучения также говорят о внутренних и внешних углах и неправильных многоугольниках. Здесь описаны основы нахождения площадей правильных многоугольников.