Построение треугольников. Признаки равенства треугольников.
Построение треугольников по одному или двум элементам
Пусть требуется построить треугольник по данной стороне а. Так как об углах треугольника и о других его сторонах ничего не сказано, то можем построить сколько угодно различных треугольников, у которых одна сторона будет равна отрезку а
Пусть требуется построить треугольник по данному углу α. В этом случае также можно построить сколько угодно различных треугольников, имеющих данный угол,
Точно так же можно построить сколько угодно различных треугольников по двум сторонам, или по двум углам, или по углу и стороне (см. рис.).
Таким образом, если будут заданы только один или два элемента треугольника, то по этим элементам можно построить сколько угодно различных треугольников.
Далее о построении треугольников не по одному и не по двум, а по трём элементам:
1.
 Построение треугольника по двум данным его сторонам и углу между ними.
Построение треугольника по двум данным его сторонам и углу между ними.Первый признак равенства треугольников
Пусть требуется построить треугольник, одна сторона которого равна, например,
35 мм, другая сторона равна 32 мм и угол, заключённый между этими сторонами, равен 46°.
Построим с помощью транспортира ∠A, равный 46°, и на его сторонах отложим отрезки АВ и АС, соответственно равные 35 мм и 32 мм. Соединив точки В и С, получим искомый треугольник ABC.
По тем же данным построим другой треугольник — Δ А’В’С’.
Докажем, что эти треугольники равны между собой.
Для этого наложим Δ А’В’С на Δ AВС так, чтобы вершины А’ и А совместились. Сторону А’С’ направим по стороне АС. Тогда точка С совместится с точкой С’, потому что А’С’ = АС.
Сторона А’В’ пойдёт по стороне АВ, так как ∠A’ = ∠A. Точка В’ совместится с точкой В, так как А’В’ = АВ. Если точки С и С’, В и В’ совместились, то совместятся и стороны В’С’ и ВС.
Треугольники ABC и А’В’С’ совпали, значит, они равны.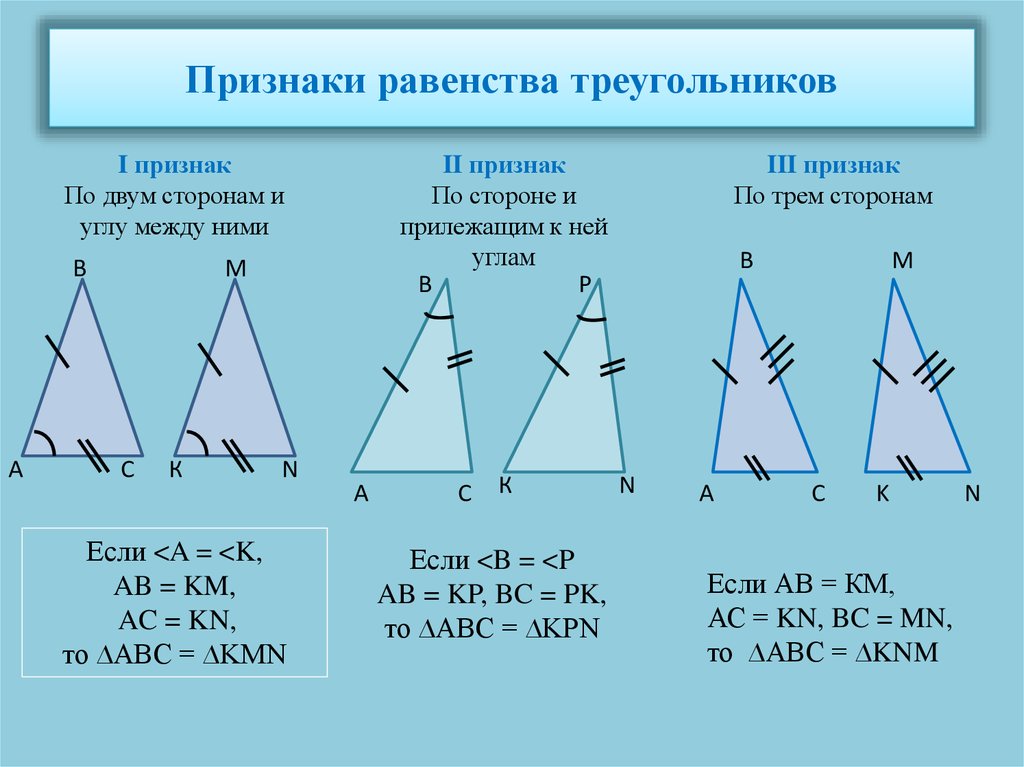
Мы можем по этим же данным построить сколько угодно треугольников, и все они будут равны между собой.
Таким образом, если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны между собой.
Назовём это первым признаком равенства треугольников.
Построение треугольника по стороне и двум прилежащим к ней углам.
Второй признак равенства треугольников
Пусть требуется построить треугольник, одна сторона которого равна, например, 40 мм, а углы, прилежащие к ней, равны 50° и 48°.
На произвольной прямой построим отрезок АС, равный 40 мм. Затем на этом отрезке при точке А построим угол, равный 50°, а при точке С — угол, равный 48°.
Если мы достаточно продолжим стороны этих углов, то они пересекутся в некоторой точке В. Получим треугольник ABC.
По тем же данным построим другой треугольник — Δ А’В’С’ и докажем, что эти треугольники будут равны между собой.
Для этого наложим Δ А’В’С’ на Δ ABC так, чтобы совместились равные стороны АС и А’С’. Тогда сторона А’В’ пойдёт по стороне АВ, так как ∠A’ = ∠A, и сторона С’В’ пойдёт по стороне СВ, так как ∠C’ = ∠C. Точка В’ одновременно должна быть и на стороне АВ, и на стороне СВ, следовательно, она совместится с точкой В, так как две прямые могут пересечься только в одной точке.
Треугольники ABC и А’В’С’ совпали, значит, они равные. По этим же данным можно построить сколько угодно треугольников, и все они будут равны между собой.
Таким образом, если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны между собой.
Назовём это вторым признаком равенства треугольников.
Построение треугольника по трём данным его сторонам.
Третий признак равенства треугольников
Пусть требуется построить треугольник по трём его сторонам, например, сторона а = 30 мм, сторона с = 40 мм и сторона b = 42 мм.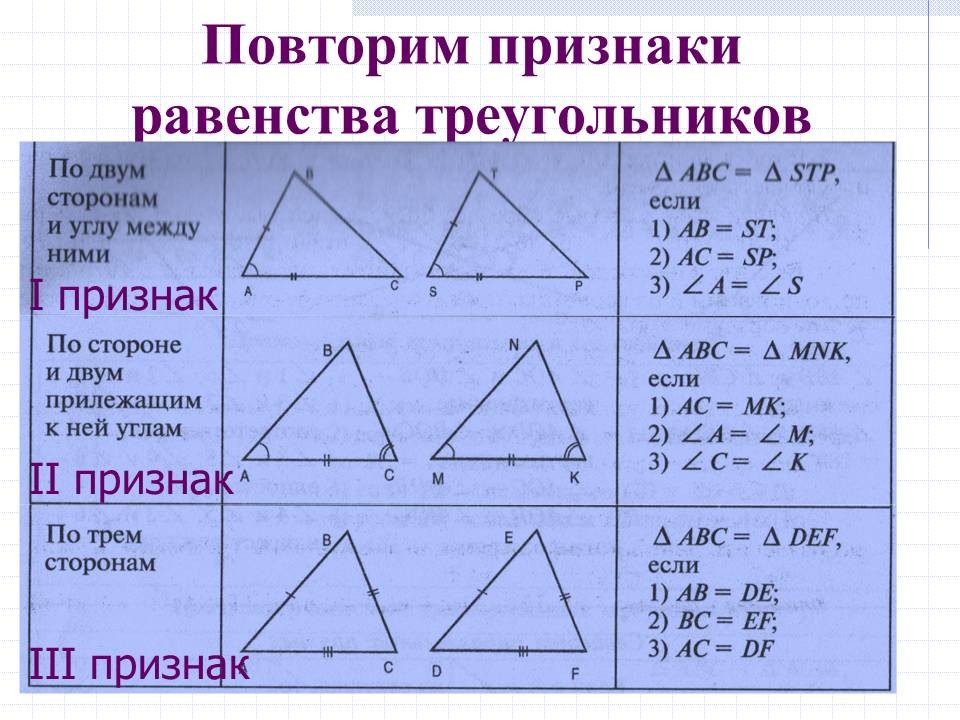 (Заданные размеры должны удовлетворять условию: сумма двух любых сторон треугольника больше третьей стороны.)
(Заданные размеры должны удовлетворять условию: сумма двух любых сторон треугольника больше третьей стороны.)
Сначала на произвольной прямой построим отрезок АС, равный данному отрезку b, т. е. 42 мм; мы сразу получим две вершины искомого треугольника — А и С.
Так как длина второй и третьей сторон соответственно равна отрезкам с и а (в данном случае 40 мм и 30 мм), то третья вершина треугольника должна находиться как на дуге, описанной из центра А радиусом, равным 40 мм, так и на дуге, описанной из центра С радиусом, равным 30 мм. Следовательно, третьей вершиной треугольника будет точка пересечения этих дуг. Обозначив эту точку буквой В и соединив её отрезками с точками А и С, получим искомый треугольник ABC.
По тем же данным построим второй треугольник — Δ А’В’С’ и докажем,
что Δ АВС = Δ А’В’С’. Для этого приложим треугольник А’В’С’ к треугольнику ABC так, чтобы их равные стороны А’С’ и AС совместились, причём точка А’ совпала бы с точкой А, точка С — с точкой С. Тогда треугольник А’В’С’ примет положение АВ»С. Сторона АВ будет равна стороне АВ» и сторона ВС — стороне В»С.
Тогда треугольник А’В’С’ примет положение АВ»С. Сторона АВ будет равна стороне АВ» и сторона ВС — стороне В»С.
Соединив отрезком прямой точки В и В», получим два равнобедренных треугольника ВАВ» и ВСВ», у которых ∠1 = ∠2, а ∠3 = ∠4, откуда ∠B = ∠B».
Следовательно, Δ АВС = Δ АВ»С, но тогда и Δ АВС = Δ А’В’С’.
По этим же данным можно построить сколько угодно треугольников, и все они будут равны между собой.
Мы доказали, что если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны между собой.
Назовём это третьим признаком равенства треугольников.
Замечания. 1. Во всех трёх признаках равенства треугольников в число трёх данных элементов входит хотя бы одна сторона треугольника.
2. В равных треугольниках против равных сторон лежат равные углы и, обратно, против равных углов лежат равные стороны.
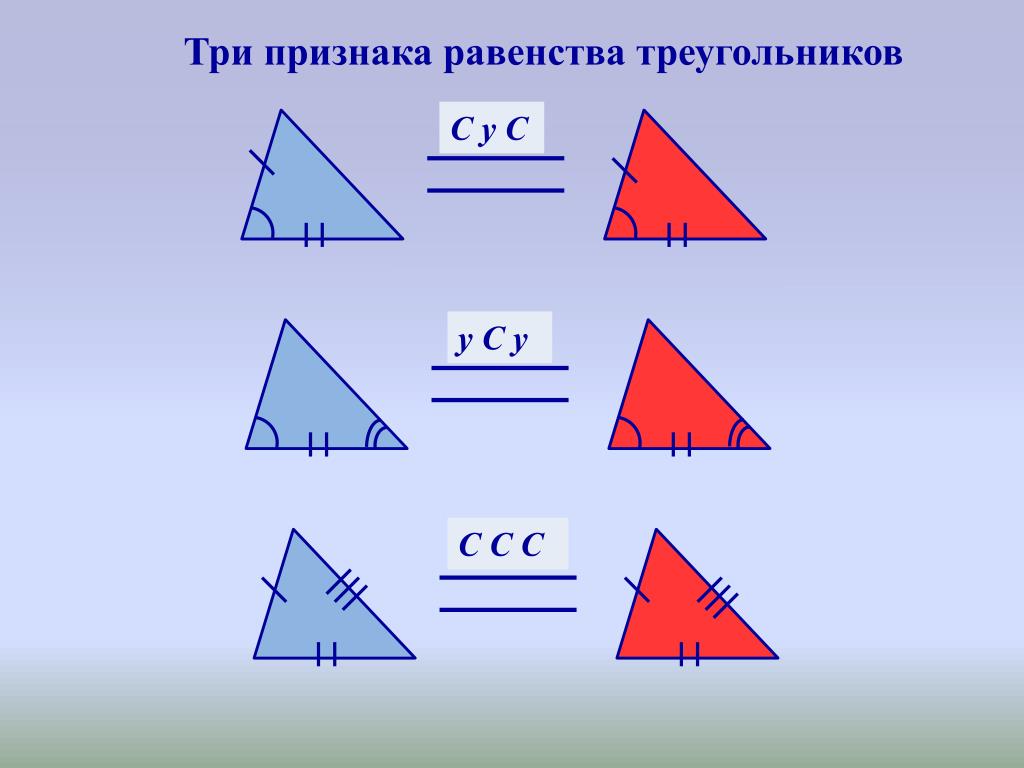
Итак, три признака равенства треугольников:
1.Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны между собой
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны между собой
3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны между собой
Признаки Треугольников
Главная » геометрия
Обновлено
Признаки треугольника — это признаки, с помощью
которых можно доказать, что геометрическая фигура
является треугольником.
При решении задач, так или иначе связанных с треугольником,
бывает нужно определить, что за фигуру нужно решить в задаче.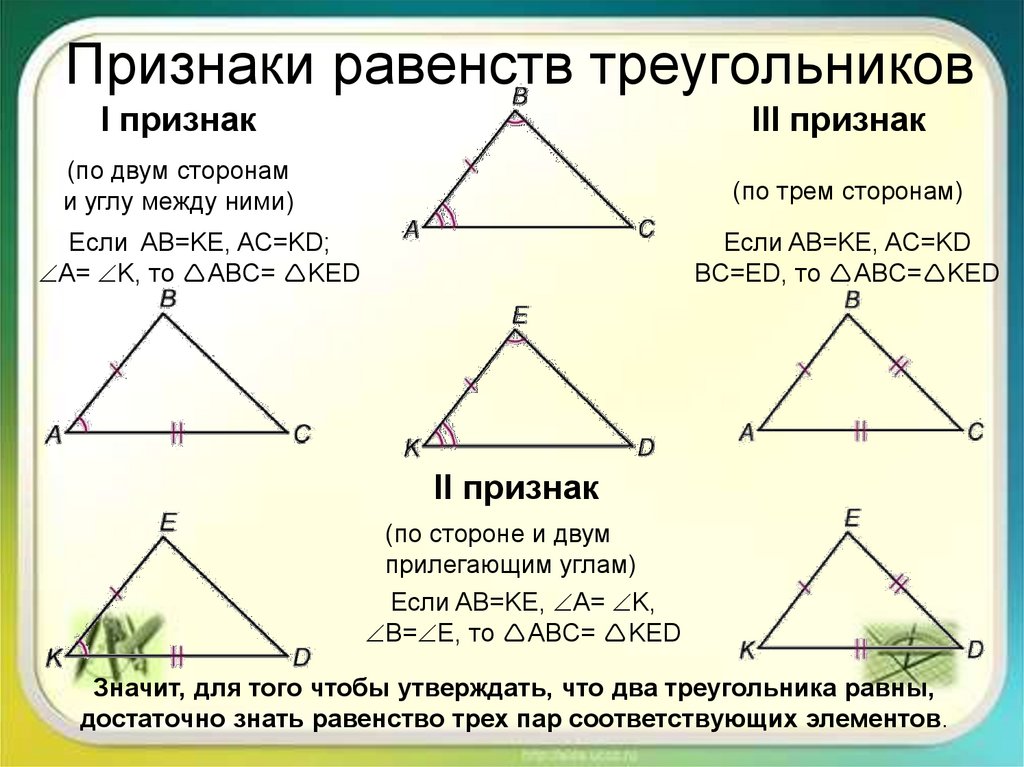
Для определения типа и вида геометрической фигуры нужно знать
признаки. В этой статье рассмотрено три признака треугольника, пять
признаков равнобедренного треугольника, четыре признака
равностороннего треугольника, и три признака прямоугольного треугольника.
геометрическая фигура треугольником.
Содержание
- III признака треугольника
- V признаков равнобедренного треугольника
- IV признака равностороннего треугольника
- III признака прямоугольного треугольника
III признака треугольника
- Геометрическая фигура является треугольником, если состоит из трёх точек,
не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. - Геометрическая фигура является треугольником, если у нее три стороны и три угла.
- Геометрическая фигура является треугольником, если сумма всех углов 180°.

Кроме просто треугольника есть еще виды треугольников. Существует три
основных вида треугольников: равнобедренный, равносторонний, прямоугольный.
Кроме признаков треугольника мы рассмотрим еще и признаки видов треугольника.
V признаков равнобедренного треугольника
- Треугольник является равнобедренным, если
два угла одинаковы и равны. - Треугольник является равнобедренным, если
две стороны одинаковы и равны. - Треугольник является равнобедренным, если
биссектриса является медианой либо высотой. - Треугольник является равнобедренным, если
медиана является биссектрисой либо высотой. - Треугольник является равнобедренным, если
высота является медианой либо биссектрисой.
IV признака равностороннего треугольника
- Треугольник является равносторонним, если три стороны равны.
- Треугольник является равносторонним, если три угла равны.
- Треугольник является равносторонним, если все три угла одинаковы и равны 60°.

- Треугольник является равносторонним, если медианы, высоты, биссектрисы пересекаются в центре треугольника.
III признака прямоугольного треугольника
- Треугольник является прямоугольным, если один из углов в треугольнике 90°.
- Треугольник является прямоугольным, если одну из сторон можно вычислить по Теореме Пифагора.
- Треугольник является прямоугольным, если медиана, проведенная из вершины угла, равна радиусу описанной окружности.
Услуги треугольных знаков
Услуги треугольных знаковНаше наследие
Основанная в 1931 году, мы помогаем нашим клиентам формировать имидж бренда и распространять ценности бренда. наша кровь. Начиная с местных проектов вывесок в нашем родном городе Балтимор, штат Мэриленд, наша устойчивый рост поставил нас в авангарде отрасли, поддерживая национальные развертывания и международные брендинговые проекты любого уровня сложности.
На самом деле, сегодня наши инновационные вывески и системы освещения, изготовленные по индивидуальному заказу, можно найти в магазинах, корпоративных комплексах, медицинских учреждениях, спортивных и образовательных учреждениях по всей стране и за ее пределами.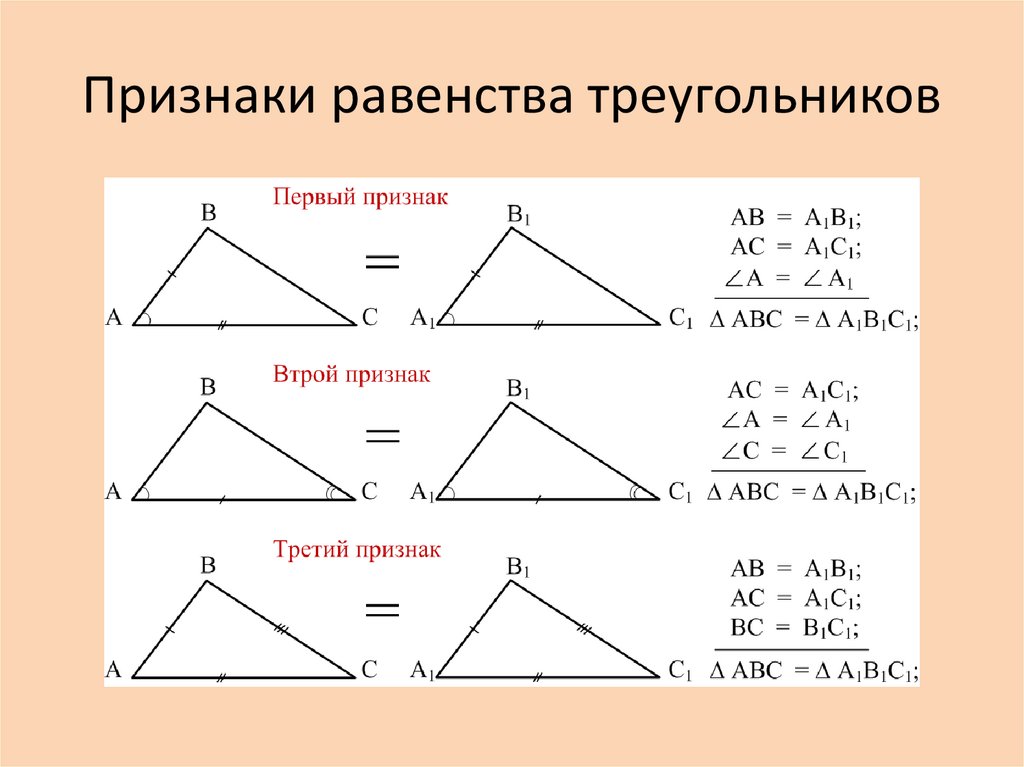
Подробнее +
Впереди
Наш успех проистекает из качества наших сотрудников. Это наши самые ценные активы. Команда лидеров мирового класса Triangle оказывает им жизненно важную поддержку, необходимую для расширения навыков, способностей и опыта, которые необходимы для нашей приверженности обслуживанию клиентов. Они здесь для вас и хотят приступить к работе по внедрению вашего бренда.
Стив Альтшулер
Президент
Джим ДеСтефано
Вице-президент по административным вопросам
MJ Fratianni
Исполнительный директор по продажам и маркетингу
Роб Маунт
Вице -президент по операциям
Scott Moody
Исполнительный директор по развитию бизнеса
Danielle Almand
Директор по национальному управлению проектами
Bryan Walker
9004 400154. 9004 9004 9004 9004 9004 9004 9004
9004 9004 9004 9004 9004 9004 90049004 9004 9004 40004 9004 400154
9004 40004 40004 40004 40004 40004
40004 40004 40004 40004
4 Директор по обслуживанию объектов
Крис Шиффлетт
Директор по управлению местными проектами/специальными проектами
Сара Лориган
Менеджер по персоналу
Джон Кубель
Директор завода
Community Outreach
Каждый год Triangle Signs участвует в мероприятиях и благотворительных инициативах, которые влияют на жизнь
тех, кто живет и работает в сообществах. Мы гордимся тем, что оказываем постоянную поддержку
организациям, чья миссия сосредоточена на образовании, социальном и экономическом равенстве, здравоохранении, сохранении
и других вопросах, приобретающих все большее значение в нашей повседневной жизни.
Меняем мир к лучшему
Компания Triangle стремится к обществу
В Casey Cares мы знаем, насколько трудной может быть жизнь семей с тяжелобольными детьми.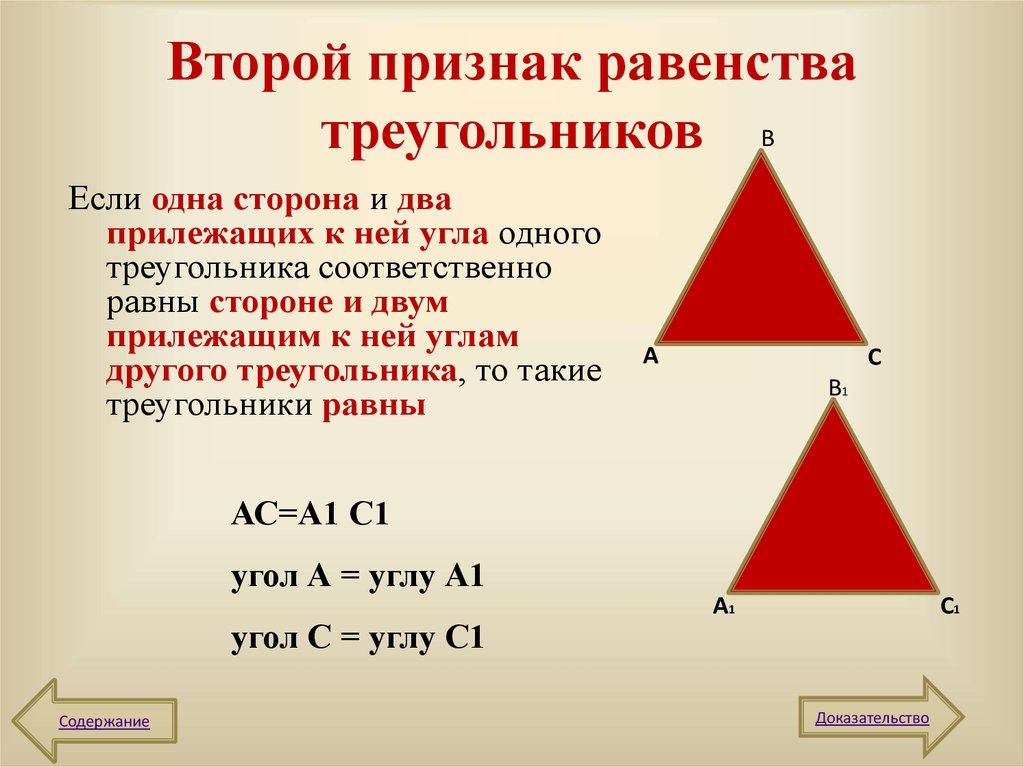 Мы помогаем поддерживать хорошее настроение семьям, организуя программы — будь то простой вечер кино и свежая пара пижам или посещение крупного спортивного мероприятия. Casey Cares делает жизнь намного лучше, добавляя индивидуальный подход в течение года и оставляя незабываемые воспоминания для семей в Среднеатлантическом регионе и некоторых частях Среднего Запада. Чтобы узнать больше, посетите сайт caseycares.org
Мы помогаем поддерживать хорошее настроение семьям, организуя программы — будь то простой вечер кино и свежая пара пижам или посещение крупного спортивного мероприятия. Casey Cares делает жизнь намного лучше, добавляя индивидуальный подход в течение года и оставляя незабываемые воспоминания для семей в Среднеатлантическом регионе и некоторых частях Среднего Запада. Чтобы узнать больше, посетите сайт caseycares.org
Сеть поставщиков Triangle
Мы всегда стремимся добавить в нашу сеть надежных и качественных поставщиков. По мере того, как присутствие Triangle по всей стране продолжает расти, растет и наша потребность в помощи в установке и обслуживании наших инновационных вывесок и осветительных решений.
Наши партнеры-поставщики разделяют наше стремление приносить исключительную пользу каждому клиенту за счет качества изготовления, профессионализма и обслуживания. Если это похоже на вас, и вы хотели бы изучить эту возможность дальше, заполните прилагаемое заявление.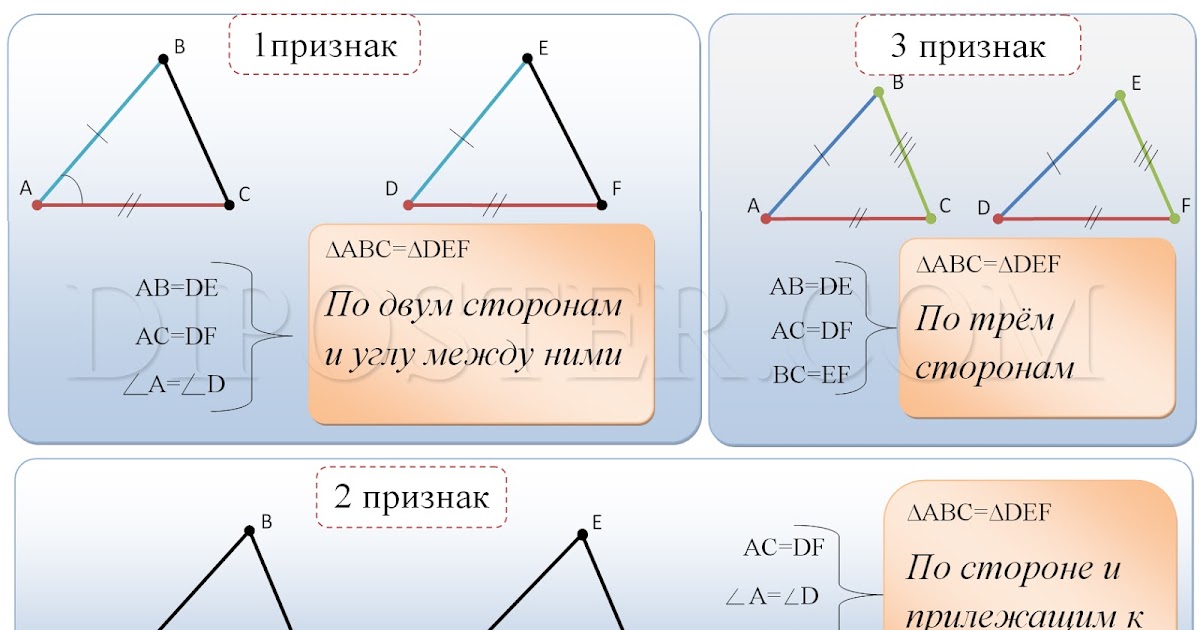

 Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны между собой
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны между собой
