Как видим, площади, найденные обоими способами, равны.
Рисунок 3.
Рисунок 4.
Отрезок $AC$ делит прямоугольник на два равных треугольника: $ABC$ и $ADC$. Значит площадь каждого из треугольников равна половине площади всего прямоугольника.
Определение 2
Прямоугольник с равными сторонами называется квадратом .
Если обозначить сторону квадрата буквой $a$, то площадь квадрата будет находится по формуле:
Отсюда и название квадрат числа $a$.
Пример 2
Например, если сторона квадрата равна $5$ см, то его площадь:
Объемы
С развитием торговли и строительства еще во времена древних цивилизаций появилась необходимость в нахождении объемов. В математике существует раздел геометрии, который занимается изучением пространственных фигур, называемый стереометрией. Упоминания об этом отдельном направлении математики встречались уже в $IV$ веке до н.э.
Древними математиками был выведен способ вычисления объема несложных фигур — куба и параллелепипеда. Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Объем прямоугольного параллелепипеда
Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.
Рисунок 5.
Сравнить объемы двух сосудов можно, наполнив один водой и перелив ее во второй сосуд. Если второй сосуд окажется полностью заполненным, то сосуды имеют равные объемы. Если при этом в первой вода останется, то объем первого сосуда больше объема второго. Если при переливании воды из первого сосуда не удается полностью заполнить второй сосуд, значит объем первого сосуда меньше объема второго.
Объем измеряется с помощью следующих единиц:
$мм^3$ — миллиметр кубический,
$см^3$ — сантиметр кубический,
$дм^3$ — дециметр кубический,
$м^3$ — метр кубический,
$км^3$ — километр кубический.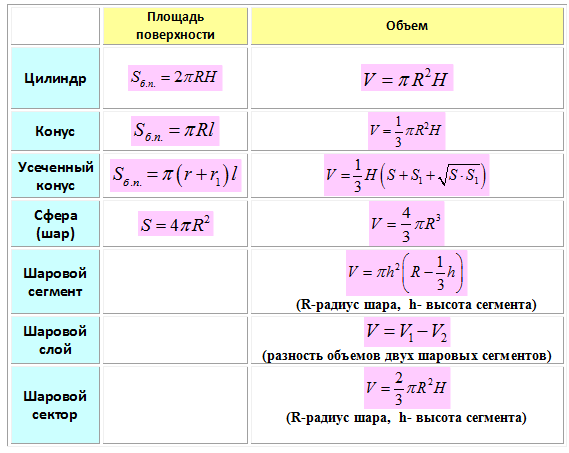
Любое геометрическое тело можно охарактеризовать площадью (S) поверхности и объемом (V). Площадь и объем совсем не одно и то же. Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Параллелепипед: определение, виды и свойства
Параллелепипед – это четырехугольная призма, в основании которой находится параллелограмм. Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.
У фигуры 6 граней – параллелограммов и 12 ребер, две произвольно выбранные грани называют основаниями. Параллелепипед может быть нескольких видов. Различия обусловлены углами между смежными ребрами. Формулы для нахождения V-ов различных многоугольников немного отличаются.
Формулы для нахождения V-ов различных многоугольников немного отличаются.
Если 6 граней геометрической фигуры представляют собой прямоугольники, то ее тоже называют прямоугольной. Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Для решения задач понадобятся знания не только готовых формул, но свойств фигуры. Перечень основных свойств прямоугольной призмы невелик и очень прост для понимания:
- Противолежащие грани фигуры равны и параллельны. Это значит, что ребра расположенные напротив одинаковы по длине и углу наклона.
- Все боковые грани прямого параллелепипеда – прямоугольники.
- Четыре главные диагонали геометрической фигуры пересекаются в одной точкой, и делятся ею пополам.
- Квадрат диагонали параллелепипеда равен суме квадратов измерений фигуры (следует из теоремы Пифагора).
Теорема Пифагора гласит, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.
Доказательство последнего свойства можно разобрать на изображении представленном ниже. Ход решения поставленной задачи прост и не требует подробных объяснений.
Формула объема прямоугольного параллелепипеда
Формула нахождения для всех видов геометрической фигуры одна: V=S*h, где V- искомый объем, S – площадь основания параллелепипеда, h – высота, опущенная из противоположной вершины и перпендикулярная основанию. В прямоугольнике h совпадает с одной из сторон фигуры, поэтому чтобы найти объем прямоугольной призмы необходимо перемножить три измерения.
Объем принято выражать в см3. Зная все три значения a, b и c найти объем фигуры совсем не сложно. Наиболее часто встречающийся тип задач в ЕГЭ – это поиск объема или диагонали параллелепипеда. Решить многие типовые задания ЕГЭ без формулы объема прямоугольника – невозможно. Пример задания и оформления его решения приведен на рисунке ниже.
Примечание 1 . Площадь поверхности прямоугольной призмы можно найти, если умножить на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ac).
Примечание 2 . Площадь поверхности боковых граней легко узнать умножив периметр основания на высоту параллелепипеда.
Исходя из первого свойства параллелепипедов AB = A1B1, а грань B1D1 = BD. Согласно следствиям из теоремы Пифагора сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла в 30°, равен гипотенузы. Применив данные знания для треугольника, легко находим длину сторон AB и AD. Затем перемножаем полученные значения и вычисляем объем параллелепипеда.
Формула для нахождения объема наклонного параллелепипеда
Чтобы найти объем наклонного параллелепипеда необходимо площадь основания фигуры умножить на высоту, опущенную на данное основание из противоположного угла.
Таким образом, искомый V можно представить в виде h — количества листов с площадью S основания, так объем колоды складывается из V-ов всех карт.
Примеры решения задач
Задания единого экзамена должны быть выполнены за определенное время. Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Как видно из примера на изображении выше, ничего сложного в решении подобных задач нет. Задания из более сложных разделов предполагают знания теоремы Пифагора и ее следствий, а так же формулу длины диагонали фигуры. Для успешного решения заданий тестов достаточно заранее ознакомится с образцами типовых задач.
А древние египтяне пользовались методами вычисления площадей различных фигур, похожими на наши методы.
В своих книгах «Начала» известный древнегреческий математик Евклид описывал достаточно большое число способов вычисления площадей многих геометрических фигур. Первые рукописи на Руси, в которых содержатся геометрические сведения, были написаны в $XVI$ веке. В них описаны правила нахождения площадей фигур различных форм.
Как видим, площади, найденные обоими способами, равны.
Рисунок 3.
Рисунок 4.
Отрезок $AC$ делит прямоугольник на два равных треугольника: $ABC$ и $ADC$. Значит площадь каждого из треугольников равна половине площади всего прямоугольника.
Определение 2
Прямоугольник с равными сторонами называется квадратом .
Если обозначить сторону квадрата буквой $a$, то площадь квадрата будет находится по формуле:
Отсюда и название квадрат числа $a$.
Пример 2
Например, если сторона квадрата равна $5$ см, то его площадь:
Объемы
С развитием торговли и строительства еще во времена древних цивилизаций появилась необходимость в нахождении объемов. В математике существует раздел геометрии, который занимается изучением пространственных фигур, называемый стереометрией. Упоминания об этом отдельном направлении математики встречались уже в $IV$ веке до н.э.
Древними математиками был выведен способ вычисления объема несложных фигур — куба и параллелепипеда. Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Объем прямоугольного параллелепипеда
Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.
Рисунок 5.
Сравнить объемы двух сосудов можно, наполнив один водой и перелив ее во второй сосуд. Если второй сосуд окажется полностью заполненным, то сосуды имеют равные объемы. Если при этом в первой вода останется, то объем первого сосуда больше объема второго. Если при переливании воды из первого сосуда не удается полностью заполнить второй сосуд, значит объем первого сосуда меньше объема второго.
Объем измеряется с помощью следующих единиц:
$мм^3$ — миллиметр кубический,
$см^3$ — сантиметр кубический,
$дм^3$ — дециметр кубический,
$м^3$ — метр кубический,
$км^3$ — километр кубический.
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Общий обзор. Формулы стереометрии!
Здравствуйте, Дорогие друзья! В этой статье решил сделать общий обзор задач по стереометрии, которые будут на ЕГЭ по математик е. Нужно сказать, что задачи из этой группы довольно разнообразны, но не сложны. Это задачи на нахождение геометрических величин: длин, углов, площадей, объёмов.
Рассматриваются: куб, прямоугольный параллелепипед, призма, пирамида, составной многогранник, цилиндр, конус, шар. Печалит тот факт, что некоторые выпускники на самом экзамене за такие задачи даже не берутся., хотя более 50% из них решаются элементарно, практически устно.
Остальные требуют небольших усилий, знаний и специальных приёмов. В будущих статьях мы с вами будем рассмотривать эти задачи, не пропустите, подпишитесь на обновление блога.
Для решения необходимо знать формулы площадей поверхности и объёмов параллелепипеда, пирамиды, призмы, цилиндра, конуса и шара. Сложных задач нет, все они решаются в 2-3 действия, важно «увидеть» какую формулу необходимо применить.
Сложных задач нет, все они решаются в 2-3 действия, важно «увидеть» какую формулу необходимо применить.
Все нужные формулы представлены ниже:
Шар или сфера. Шаровой, или сферической поверхностью (иногда просто сферой) называется геометрическое место точек пространства, равноудаленных от одной точки — центра шара.
Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.
Круглый конус может быть получен вращениемпрямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называт также конусом вращения. См. также Площадь поверхности круглого конуса
Объем круглого конуса равен трети произведения площади основания S на высоту H:
(H — высота ребра куба)
Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипедимеет шесть граней, и все они — параллелограммы.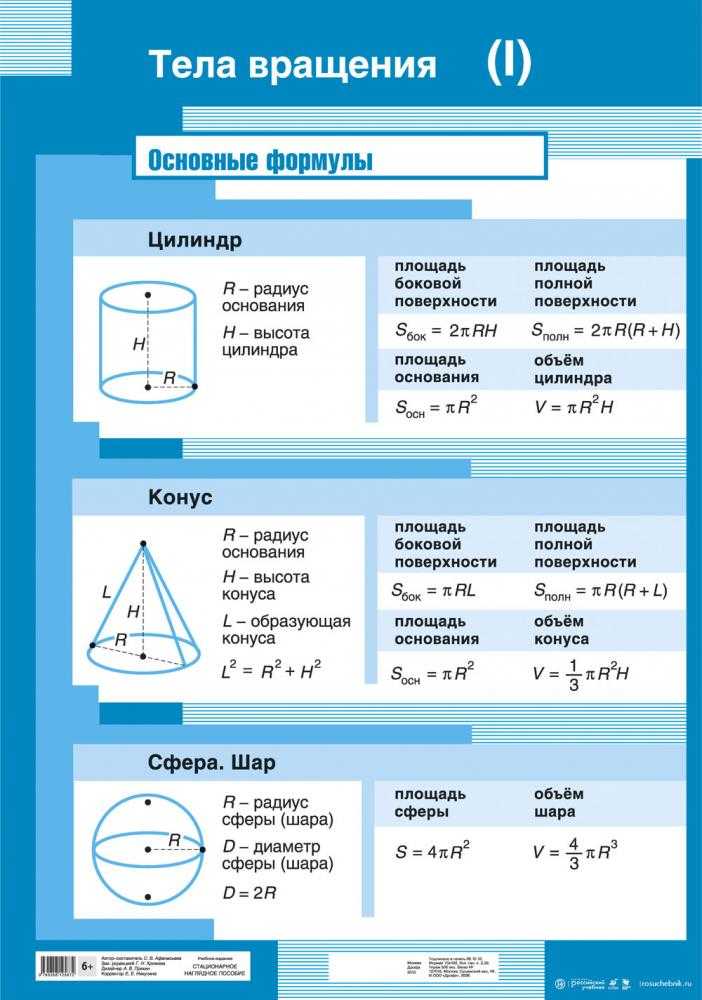 Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.
Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:
(S — площадь основания пирамиды, h — высота пирамиды)
Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды.
Сечение параллельное основанию пирамиды делит пирамиду на две части. Часть пирамиды между ее основанием и этим сечением — это усеченная пирамида.
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1 (abcde) , нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.
| 1. | V = |
n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника — основания правильной пирамиды
h — высота правильной пирамиды
Правильная треугольная пирамида — этомногогранник, у которого одна грань — основание пирамиды — правильныйтреугольник, а остальные — боковые грани — равные треугольники с общей вершиной.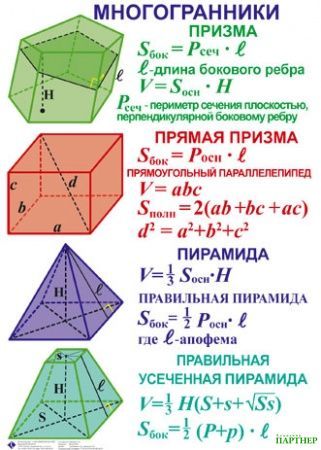 Высота опускается в центр основания из вершины.
Высота опускается в центр основания из вершины.
Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC) на высоту h (OS)
a — сторона правильного треугольника — основания правильной треугольной пирамиды
h — высота правильной треугольной пирамиды
Вывод формулы объема тетраэдра
Объем тетраэдра расчитывается по классической формуле объема пирамиды. В нее необходимо подставитьвысоту тетраэдра и площадь правильного (равностороннего) треугольника.
Объем тетраэдра — равен дроби в числителе которой корень квадратный из двух в знаменателе двенадцать, помноженной на куб длины ребра тетраэдра
(h — длина стороны ромба)
Длина окружности p составляет примерно три целых и одну седьмую длины диаметра круга. Точное отношение длины окружности к ее диаметру обозначается греческой буквой π
В итоге периметр круга или длина окружности вычисляется по формуле
(r — радиус дуги, n — центральный угол дуги в градусах.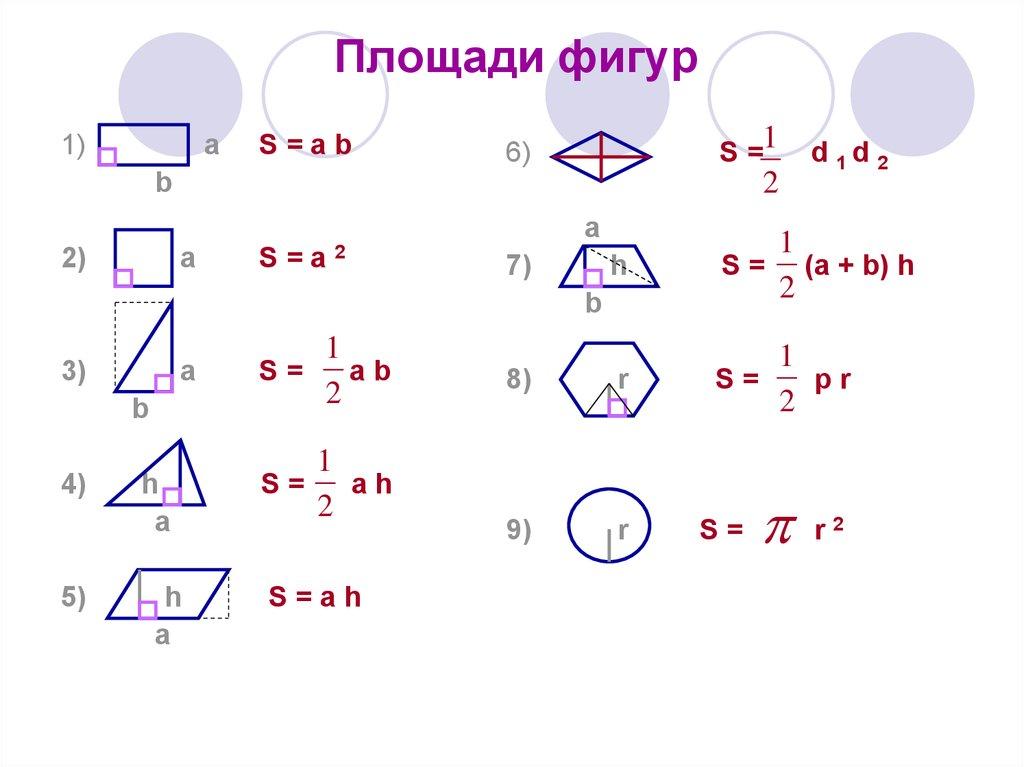 )
)
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: | |||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим.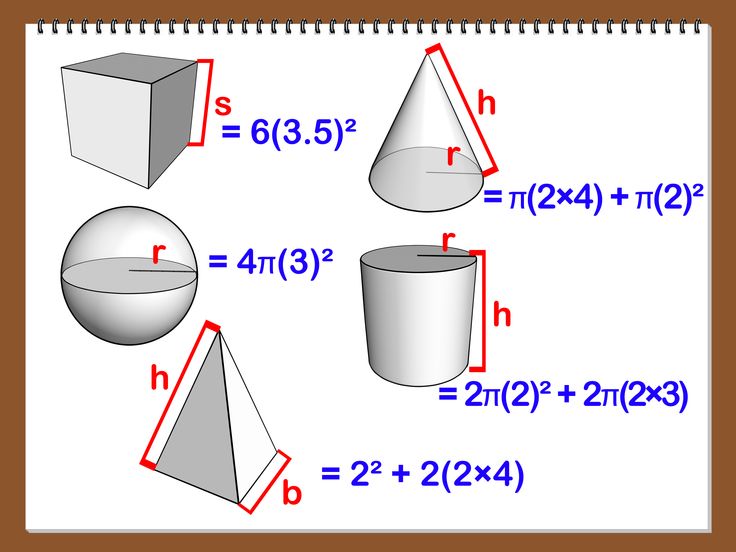 | |||
Узнайте об объеме и площади поверхности
В этом видео вы узнаете, как рассчитать объем и площадь поверхности некоторых твердых фигур, таких как призма, сфера, конус, цилиндр и пирамида.
объем трехмерной фигуры — это количество места, которое она занимает.
Боковая площадь трехмерной фигуры представляет собой сумму самых внешних слоев фигуры, за исключением оснований.
Площадь поверхности трехмерной фигуры представляет собой сумму самых внешних слоев фигуры.
Prism
Объем:
Боковая площадь:
Площадь поверхности:
Пирамида
Объем:
Боковая площадь:
Площадь поверхности:
.
Прямой круговой конус
Объем:
Боковая площадь:
Площадь поверхности:
Сфера
Объем:
Боковая площадь:
Площадь поверхности:
.
У нас есть твердая цифра, формула объема и формула площади поверхности или площади земли
Начнем с призмы.
Призма может быть, например, прямоугольной. Где верх и низ одинаковы и вытянуты по вертикали. Нижний прямоугольник и верхний тоже прямоугольник. Куб также является призмой. У нас есть квадрат со всех шести сторон. У нас также может быть треугольная призма. Верх и низ представляют собой треугольник, а вертикальные линии вытянуты вверх.
Объем равен
, где площадь основания, нам просто нужно узнать, что такое площадь основания, а затем мы должны умножить ее на высоту.
Для куба мы должны выяснить, чему равна площадь основания квадрата, умноженная на его высоту.
И для этого треугольника мы должны найти площадь основания треугольника, умноженную на его высоту.
Это нахождение объема призмы.
Что такое боковая площадь?
Боковая площадь – это площадь сторон.
Площадь передней, задней, левой и правой сторон. Нам нужно найти боковую площадь по всему периметру.
Чтобы найти боковую площадь вокруг него, вам просто нужно умножить высоту на периметр.
Нам нужно узнать периметр основания. Для этого нам просто нужно сложить длины, умноженные на его высоту.
Нам нужно найти общую площадь поверхности, мы должны найти площадь верха и низа и прибавить ее к общей боковой площади.
Теперь давайте посмотрим на объем и площадь поверхности пирамиды.
Пирамида имеет квадратное основание и расширяется до точки над ней. Это выглядит примерно так.
У нас есть квадратное или прямоугольное основание, а все стороны — треугольники.
Формула объема пирамиды
где площадь основания, в данном случае основание квадрат.
Итак, нам нужно вычислить площадь квадрата, умножив ее на высоту.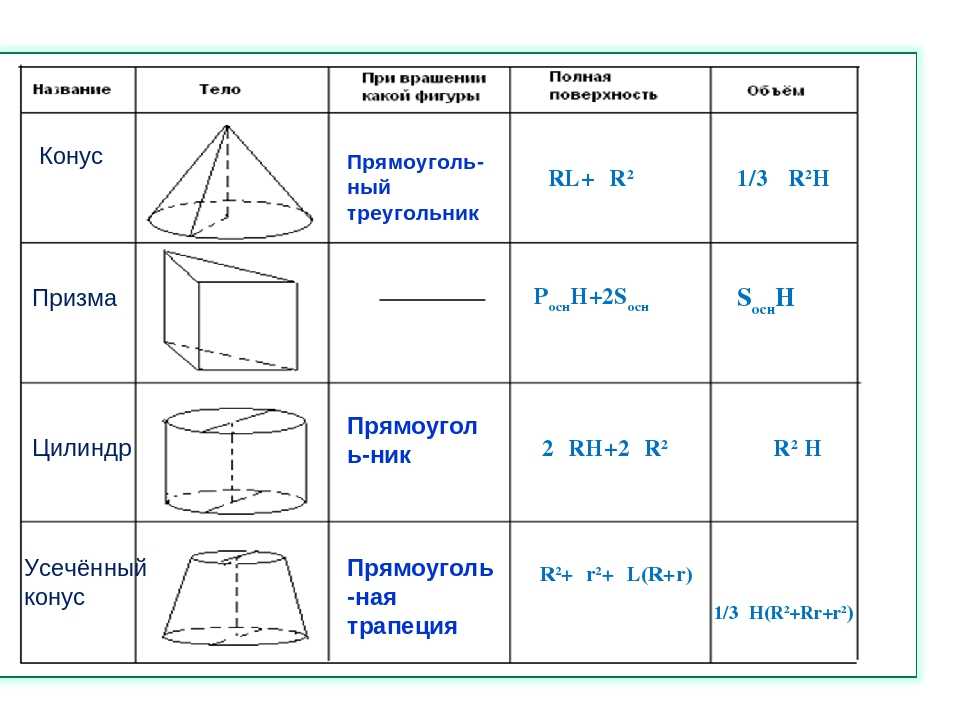
Высота от дна до самой высокой точки, то есть, если вы внутри, она идет прямо вниз и образует прямой угол с основанием.
Чтобы вычислить боковую площадь пирамиды:
P — периметр основания.
В данном случае это квадрат. Просто сложите все стороны, умножьте на высоту и сделайте это, вы получите боковую площадь.
Боковая площадь – это площадь сторон. Без учета площади основания. Вот почему мы должны найти площадь квадратного основания и добавить ее.
Теперь посмотрим на цилиндр.
Цилиндр имеет круглую верхнюю и нижнюю часть, как у банки, и имеет высоту.
Объем
очень похож на призму.
Здесь основанием является круг.
Нам нужно найти площадь круга, который равен .
Теперь наша формула
Площадь поперечного сечения
Вот формула длины окружности.
У нас есть расстояние от основания круга, умноженное на его высоту.
По сравнению с формулой призмы, где высота умножается на периметр, здесь высота умножается на длину окружности.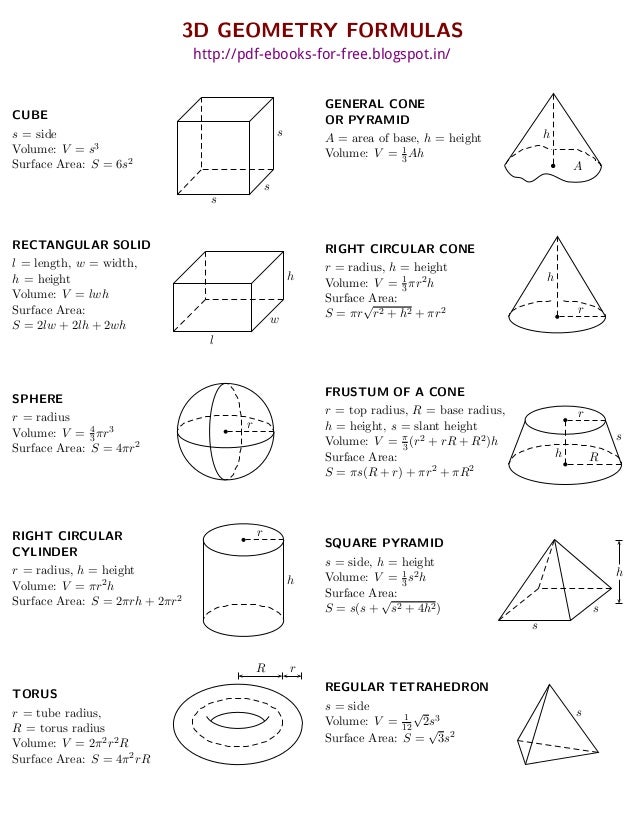
Боковая зона – это площадь вокруг цилиндра. Но это не касается верха и низа. Если бы нам нужно было найти общую площадь поверхности цилиндра, мы должны были бы вычислить площади верхней и нижней части, а затем прибавить их.
Таким образом, общая площадь поверхности в этом случае равна
, включая верх и низ.
Общая боковая площадь просто проходит по сторонам.
Теперь давайте пройдемся по правому круглому конусу.
Основанием прямого кругового конуса является круг. Затем он поднимается до точки или вершины.
Объем равен
, где площадь основания и высота, вычисленная от самого верха до низа.
Основание — круг, поэтому
Наша формула для объема теперь
Теперь давайте посмотрим на боковую область.
Боковая площадь
где длина стороны конуса.
Это прямоугольный конус, поэтому, если мы проведем высоту посередине и продолжим радиус до этой точки, у нас получится прямой угол.
Итак, у нас будет прямоугольный треугольник с высотой и радиусом.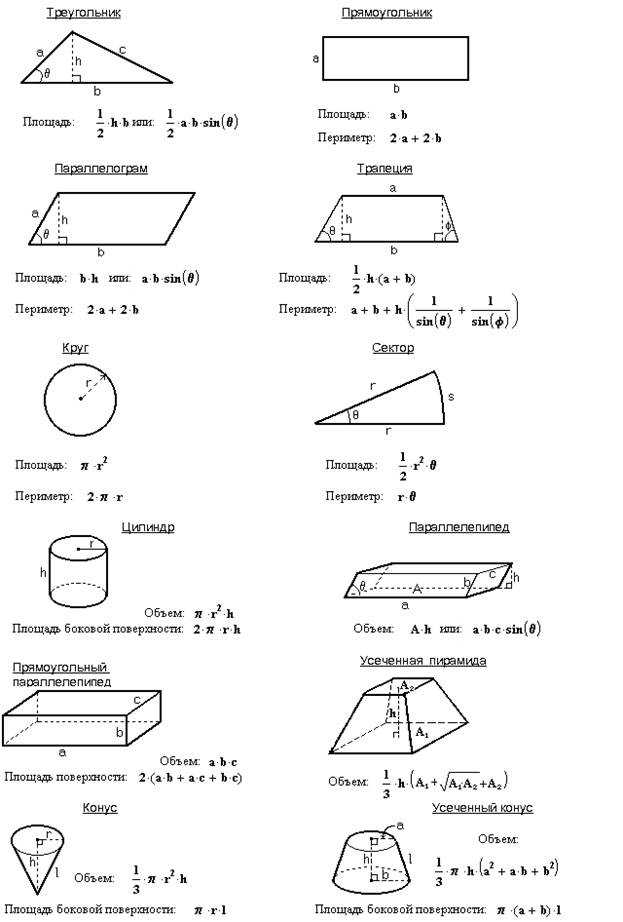
Теперь, когда у нас есть прямоугольный треугольник, мы можем найти его длину, если она не дана, используя теорему Пифагора.
Да.
Боковая область даст нам площадь вокруг конуса, но не будет включать его дно.
Если нам нужна общая площадь поверхности, включая базовый круг, мы должны вычислить боковую площадь плюс площадь базового круга.
Пройдемся по объему и площади поверхности сферы.
Сфера похожа на шар или мрамор. Это круглая трехмерная форма.
Объем сферы
и площадь поверхности
Радиус идет от центра к краю.
Можно подумать о площади поверхности, если вы делаете кожаный баскетбольный мяч. Вы можете использовать площадь поверхности, чтобы определить, сколько кожи вам понадобится для изготовления мяча. Какой площади вам понадобится, чтобы сделать шар.
В любительских регионах ближней сцены хорошо то, что вам дают формулы. От вас не ожидают, что вы запомните каждую формулу из этого списка.
На самом деле они дают вам формулу объема пирамиды, но не формулу площади ее боковых сторон.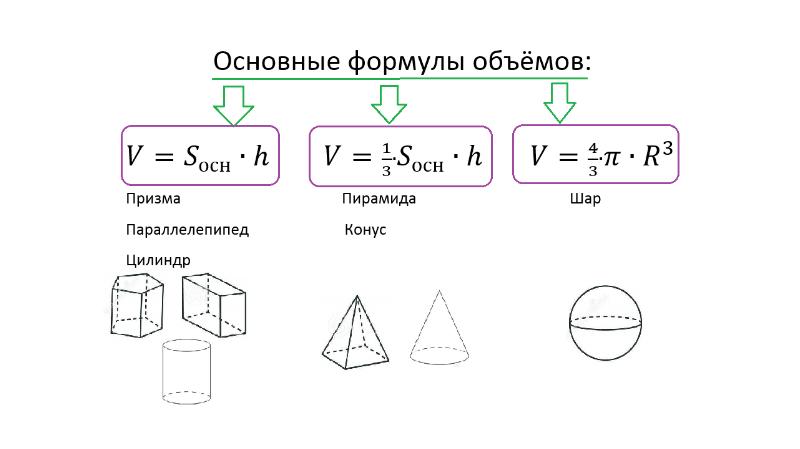
Также они дают вам формулу объема и поперечной площади цилиндра.
Они дают вам формулу объема и поперечной площади прямого круглого конуса.
Кроме того, они также дают формулы для объема и площади поверхности сферы.
Но помните, когда вы вычисляете боковую площадь цилиндра и прямоугольного конуса, это не проблема.
Но если вас спросят о площади поверхности, вы должны указать боковую площадь плюс площадь основания.
У цилиндра есть основание вверху и внизу.
Итак, вам нужно умножить основание на два.
Правильный круглый конус
имеет только одно основание.
Формулы площади и объема геометрии роялти бесплатно векторное изображение
Формулы площади и объема геометрии роялти бесплатно векторное изображение- лицензионные векторы org/ListItem»> Площадь векторов
ЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Расшир. | |
|---|---|---|
| Печатная / редакционная | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и изменять | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по требованию |
Право собственности Учить больше
Эксклюзивный Если вы хотите купить исключительно этот вектор, отправьте художнику запрос ниже: Хотите, чтобы это векторное изображение было только у вас? Эксклюзивный выкуп обеспечивает все права этого вектора.
Мы удалим этот вектор из нашей библиотеки, а художник прекратит продажу работ.
Способы покупкиСравнить
Плата за изображение $ 14,99 Кредиты $ 1,00 Подписка $ 0,69Оплатить стандартные лицензии можно тремя способами. Цены $ долларов США.
| Оплата с | Цена изображения |
|---|---|
| Плата за изображение $ 14,99 Одноразовый платеж | |
| Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р. | |
| План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Способы покупкиСравнить
Плата за изображение $ 39,99 Кредиты $ 30,00 Существует два способа оплаты расширенных лицензий. Цены $ $ .
Цены $ $ .
| Оплата с | Стоимость изображения |
|---|---|
| Плата за изображение $ 39,99 Оплата разовая, регистрация не требуется. | |
| Предоплаченные кредиты $ 30 Загружайте изображения по запросу (1 кредит = 1 доллар США). | |
Оплата
Плата за изображение $ 499Дополнительные услугиПодробнее
Настроить изображение Доступно только с оплатой за изображение $ 85,00Нравится изображение, но нужны лишь некоторые модификации? Пусть наши талантливые художники сделают всю работу за вас!
Мы свяжем вас с дизайнером, который сможет внести изменения и отправить вам изображение в выбранном вами формате.
Примеры
- Изменить текст
- Изменить цвета
- Изменение размера до новых размеров
- Включить логотип или символ
- Добавьте название своей компании или компании
Включенные файлы
Подробности загрузки.

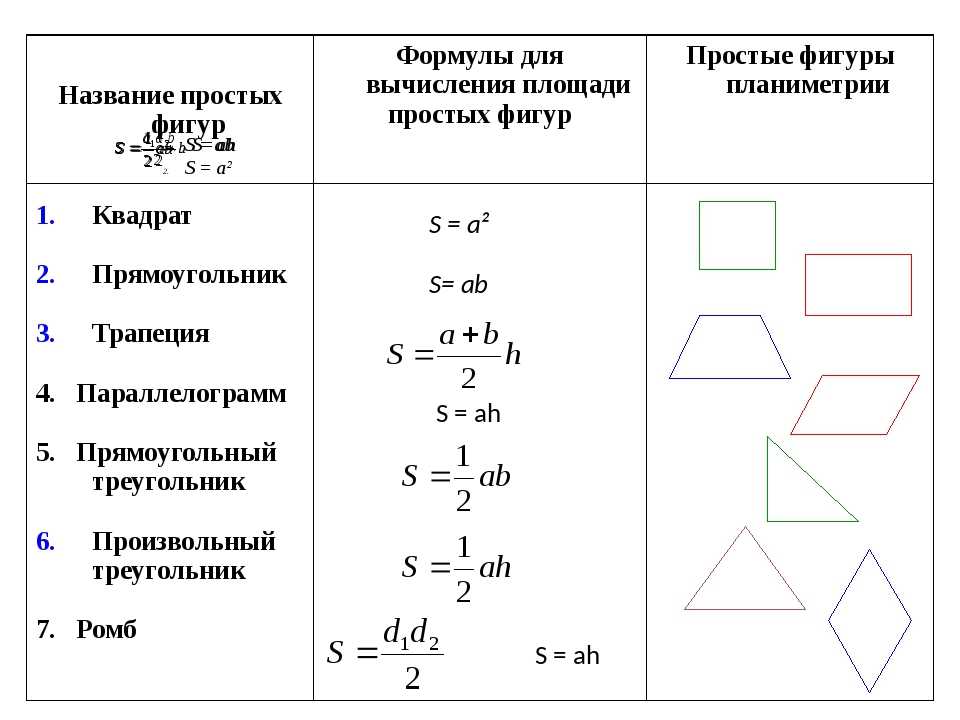 Треугольники, Прямоугольники и т.д. Градусы в радианы.
Треугольники, Прямоугольники и т.д. Градусы в радианы. Сочленение труб и резервуаров. Пересечение труб, штуцеров, сгонов.
Сочленение труб и резервуаров. Пересечение труб, штуцеров, сгонов.