Формулы площади четырехугольников: параллелограмма, трапеции, ромба, прямоугольника, квадрата.

Как найти площадь выпуклого четырехугольника: формула

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади выпуклого четырехугольника: формула и пример

Выпуклый четырехугольник – это геометрическая фигура, полученная путем соединения на плоскости четырех точек, которые не должны лежать на одной прямой. При этом образованные таким образом стороны не должны пересекаться.

• Формула вычисления площади
  • По диагоналям и углу между ними
  • По четырем сторонам (формула Брахмагупты)
  • По радиусу вписанной окружности и сторонам
• Пример задачи

Формула вычисления площади

По диагоналям и углу между ними

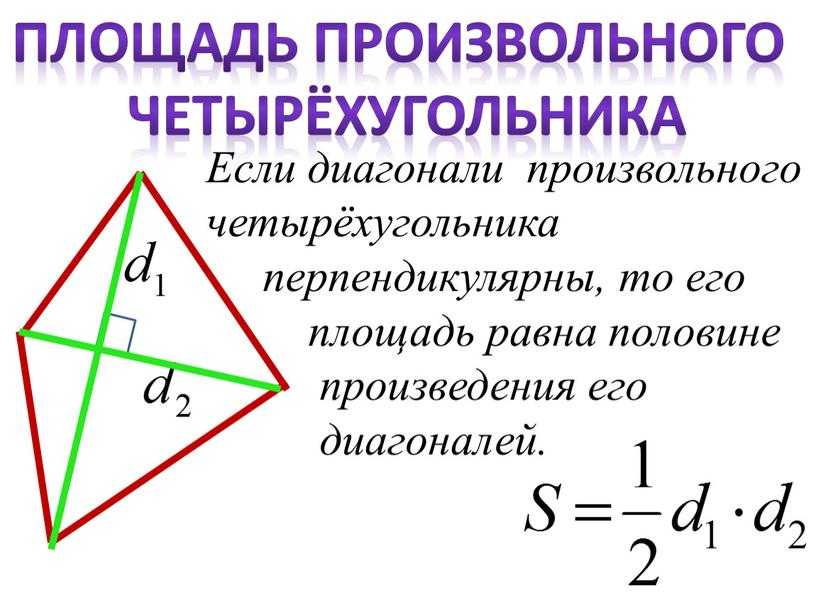
Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними.

По четырем сторонам (формула Брахмагупты)

Чтобы воспользоваться формулой, необходимо знать длины всех сторон фигуры. Также вокруг четырехугольника должна быть возможность описать окружность.

p – полупериметр, вычисляется следующим образом:

По радиусу вписанной окружности и сторонам

Если в четырехугольник можно вписать окружность, вычислить его площадь можно, воспользовавшись формулой:

S = p ⋅ r

r – радиус окружности.

Пример задачи

Найдите площадь выпуклого четырехугольника, если его диагонали равны 5 и 9 см, а угол между ними составляет 30°.

Решение:
Подставляем в формулу известные нам значения и получаем: S = 1/2 * 5 см * 9 см * sin 30° = 11,25 см².

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Четырехугольники.

Площади четырехугольников

Вопросы занятия:

·  вывести формулы для вычисления площадей различных четырёхугольников.

Материал урока

Наряду с понятием длины, понятие площади является основным в геометрии.

Напомним, что за единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков. Т.е. площадь квадрата со стороной, равной одной единице измерения длины, равна одной квадратной единице. Если же сторона квадрата равна а единиц измерения длины, то его площадь равна а² квадратных единиц.

Понятно, что равные фигуры имеют равные площади.

Если же фигура составлена из нескольких фигур, то её площадь равна сумме площадей составляющих её фигур.

Также напомним, что фигуры, имеющие равные площади, называют равновеликими.

А начнём мы повторение с площади прямоугольника

.

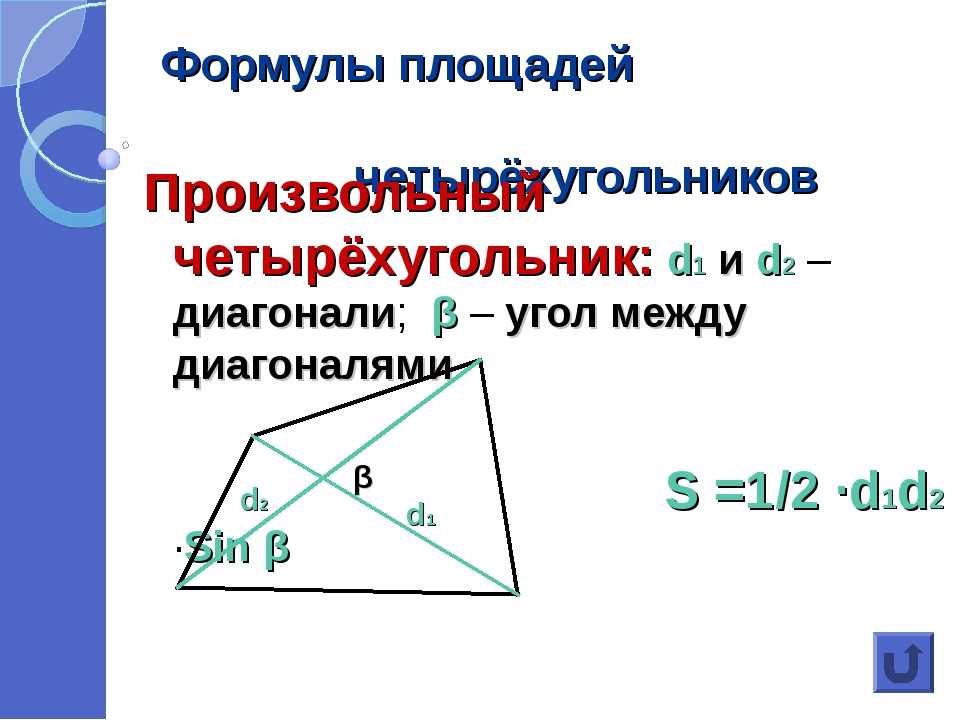
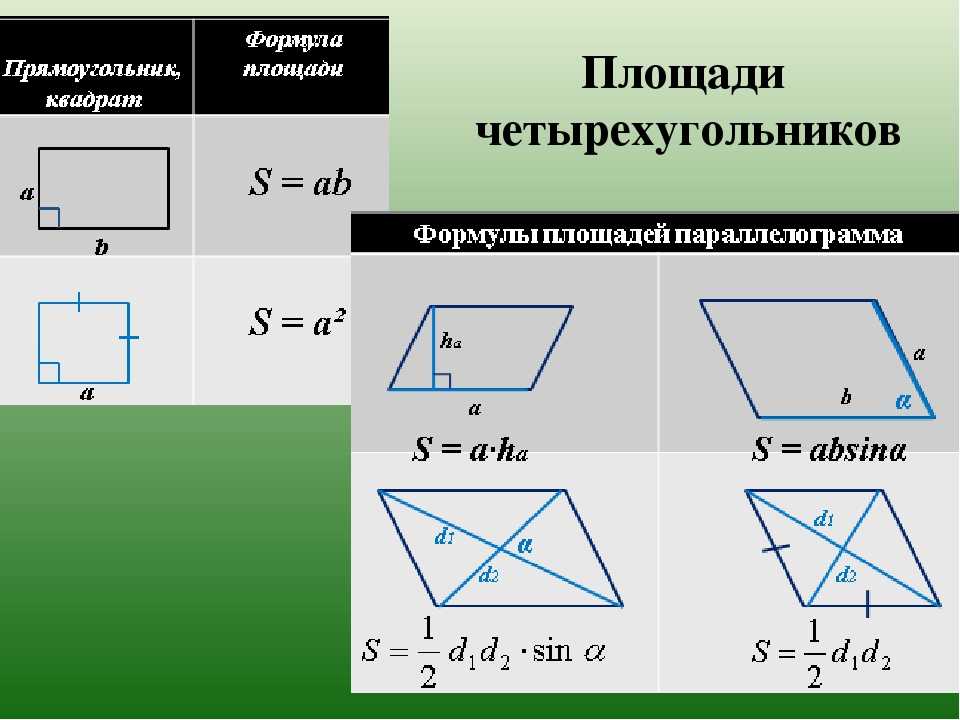
Площадь прямоугольника равна произведению его измерений, т.е. произведению длины и ширины.

Или ещё можно сказать, что площадь прямоугольника равна произведению его соседних сторон.

Давайте докажем это.

Пусть дан прямоугольник со сторонами  и  и площадью . Достроим его до квадрата со стороной .

Так как площадь квадрата равна квадрату его стороны, то площадь построенного квадрата равна .

Но ведь, с другой стороны, площадь этого квадрата равна сумме площадей .

Так как равны левые части данных равенств, то можем приравнять и их правые части.

Преобразуем получившееся выражение. Приведём подобные слагаемые в правой части. Затем перенесём  в правую часть, а  в левую. Раскроем скобки в правой части, применив формулу квадрата суммы (при этом обратите внимание, что перед скобками стоит знак минус). Теперь приведём подобные слагаемые в правой части.

Разделим обе части равенства на – 2. В результате получим,

То есть площадь прямоугольника со сторонами  и  равна произведению его соседних сторон.

Что и требовалось доказать.

Задача.

Стороны прямоугольника равны 72 метра и 8 метров. Определите сторону равновеликого ему квадрата.

Так как прямоугольник и квадрат равновелики, то их площади равны.

По формуле площади прямоугольника имеем, что площадь нашего прямоугольника равна

А значит, и площадь равновеликого ему квадрата также равна  (м²).

Пусть сторона квадрата равна х. Так как площадь квадрата равна квадрату его стороны, то получим, что сторона данного квадрата равна

Следующей вспомним площадь параллелограмма.

Площадь параллелограмма равна произведению длины стороны на высоту, проведённую к ней.

Докажем это утверждение. Пусть  – некоторый параллелограмм.  – высота . Докажем, что площадь параллелограмма равна .

Проведём к прямой, содержащей сторону , высоту . Тогда четырёхугольник  является прямоугольником. Докажем, что .

Рассмотрим прямоугольные треугольники  и . У них гипотенузы  как противолежащие стороны параллелограмма . А катеты , так как являются высотами проведёнными к одной стороне. Следовательно, треугольники  по гипотенузе и катету. Из равенства этих треугольников следует и равенство их площадей .

Так как трапеция  состоит из параллелограмма   и треугольника , то .

Также трапеция  является объединением треугольника  и прямоугольника . Следовательно, .

А так как , то .

Площадь прямоугольника  равна . Тогда и площадь параллелограмма  равна .

В параллелограмме  стороны  и  равны как противоположные. Значит, площадь параллелограмма  равна .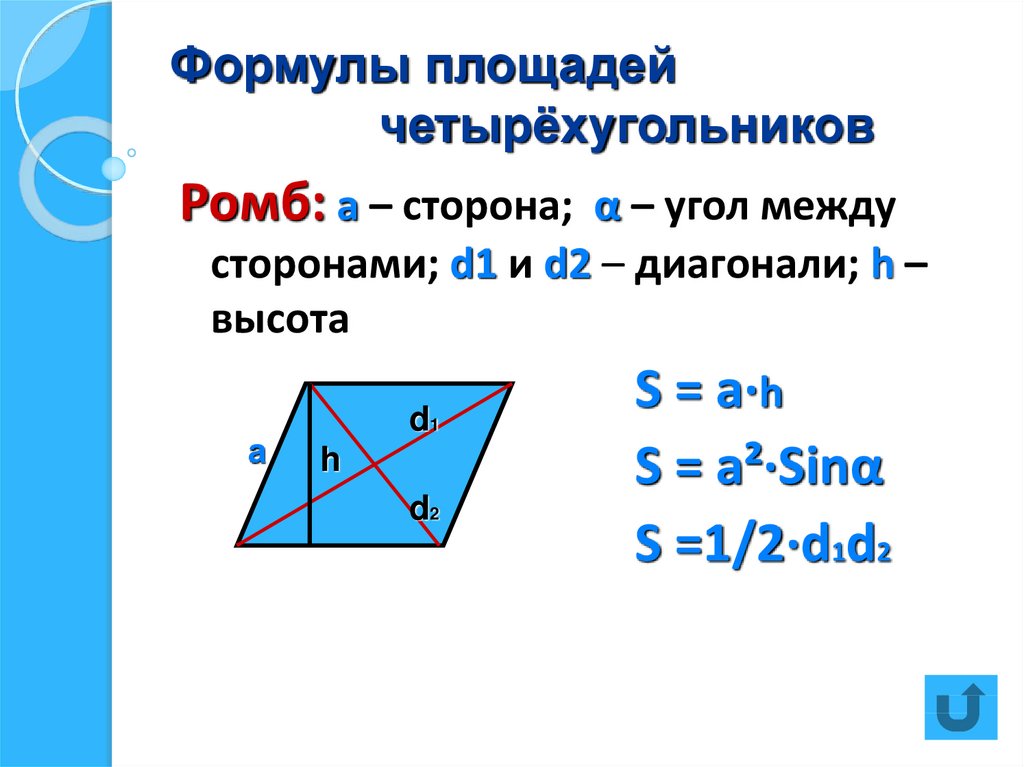 То есть площадь параллелограмма равна произведению длины стороны на высоту, проведённую к ней.

Что и требовалось доказать.

Задача.

Высоты параллелограмма равны  см и  см, а угол между ними равен . Найдите площадь параллелограмма.

Пусть  см,  см, .

Напомним, что угол между высотами параллелограмма, проведёнными из вершины тупого угла, равен острому углу параллелограмма. Тогда в параллелограмме  угол .

Рассмотрим треугольник . Он прямоугольный, так как  высота по условию. По свойству катета лежащего против угла в 30^о, получаем, что  (см).

Так как в параллелограмме  стороны  как противоположные, то площадь параллелограмма равна

Перейдём к площади трапеции.

Площадь трапеции равна произведению половины суммы её оснований на высоту.

Докажем это утверждение. Пусть дана трапеция .  и  – основания, – высота .

Докажем, что площадь трапеции  равна .

Проведём диагональ . Она разбивает трапецию на два треугольника  и . Понятно, что площадь трапеции равна сумме площадей этих треугольников .

Напомним, что площадь треугольника равна . Тогда площадь треугольника  равна , а площадь треугольника  равна .

Площадь трапеции  равна сумме площадей этих треугольников.

А тогда имеем, площадь трапеции  равна . То есть площадь трапеции равна произведению половины суммы её оснований на высоту.

Что и требовалось доказать.

Задача.

В прямоугольной трапеции основания равны  см и  см, а большая боковая сторона –  см. Найдите площадь трапеции.

Пусть дана трапеция .  перпендикулярно , ,  и .

Проведём высоту . Получим прямоугольник . По свойству сторон прямоугольника имеем ,  см.

Рассмотрим треугольник . Он прямоугольный, так как  высота по построению.  в по условию.  (см). Тогда по теореме Пифагора можем выразить сторону .

А тогда подставляя все известные данные в формулу площади трапеции, получим, что площадь нашей трапеции равна  (см²).

И последней вспомним площадь ромба.

Площадь ромба равна половине произведения его диагоналей.

Пусть дан ромб .  и  – его диагонали.

Докажем, что площадь ромба .

Проведём диагональ . Она разбивает ромб на два треугольника и . Понятно, что площадь ромба равна сумме площадей этих треугольников.

Напомним, что площадь треугольника равна половине произведения длины стороны треугольника на длину высоту, проведённую к ней. Напомним, что диагонали ромба взаимно перпендикулярны. Тогда площадь треугольника  , а площадь треугольника  равна .

Площадь ромба  равна сумме площадей этих треугольников.

Получаем, что площадь ромба  равна . То есть площадь ромба равна половине произведения его диагоналей.

Что и требовалось доказать.

Задача.

Диагонали ромба относятся как . Найдите площадь ромба, если его периметр равен  см.

Так как диагонали ромба точкой пересечения делятся пополам, то .

Рассмотрим треугольник . Он прямоугольный, так как диагонали ромба взаимно перпендикулярны. Напомним, что стороны ромба равны, а тогда сторона  (см) . Так как , то можем ввести следующие обозначения: .

По теореме Пифагора имеем

А тогда , .

А значит, диагонали ромба равны: , .

Подставим наши диагонали в формулу площади ромба. Посчитаем. И получим, что площадь нашего ромба равна

Итоги урока

На этом уроке мы говорили о «четырёхугольниках». А точнее вспомнили формулы для вычисления их площадей.

Формула площади

для четырехугольника — объяснение, типы и часто задаваемые вопросы

Дата последнего обновления: 18 апреля 2023 г.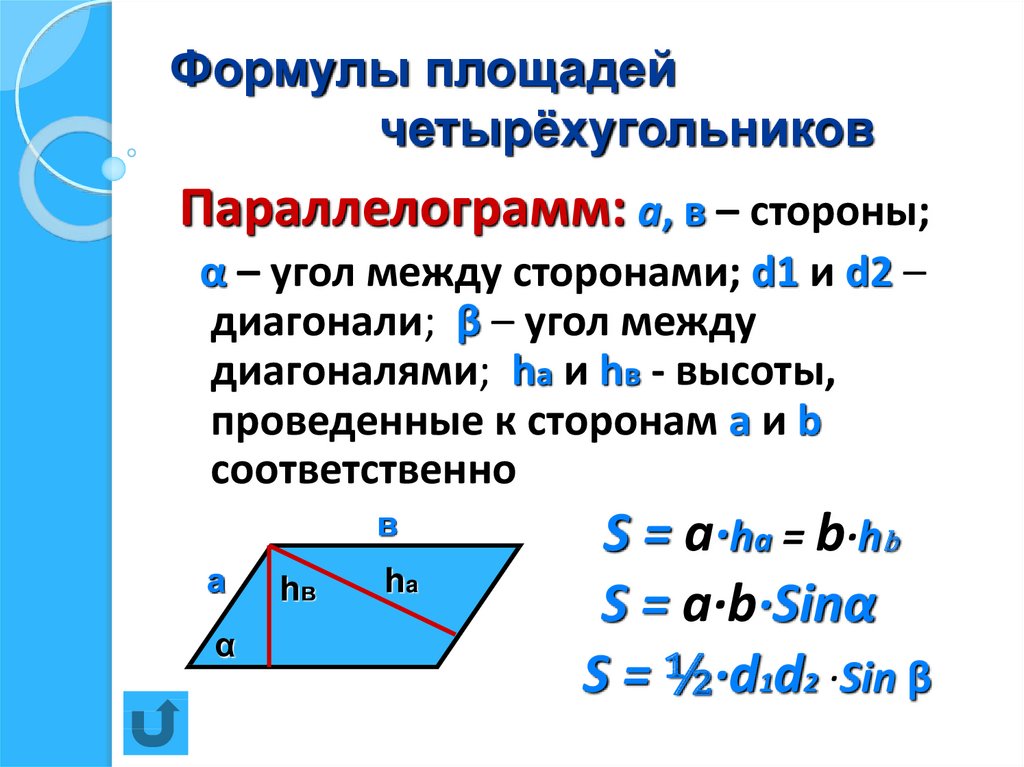 ;white-space:pre-wrap;»>Четырехугольником называется четырехсторонняя двумерная геометрическая фигура, сумма всех четырех внутренних углов которой равна 360 ^o . Также он имеет 4 ребра (стороны) и четыре вершины ( Четырехугольники бывают двух разных типов, а именно правильные четырехугольники и неправильные четырехугольники. Несколько известных примеров четырехугольников: квадрат, прямоугольник, трапеция, ромб, воздушный змей и параллелограмм.0003

Площадь четырехугольника — это количество квадратных единиц, которые можно составить из него. Здесь мы рассмотрим важные формулы площади для четырехугольников и то, как найти площадь четырехугольника.

Общая формула площади четырехугольника

Давайте научимся выводить общую формулу площади четырехугольника. Рассмотрим четырехугольник PQRS, приведенный ниже:

• Мы можем наблюдать следующий четырехугольник как комбинацию двух треугольников, рассматривая диагональ PQ как общее основание.

• h₁ и h₂ — высоты треугольников PQR и PSR соответственно.

Площадь четырехугольника PQRS можно рассчитать, сложив площади двух треугольников, то есть PQR и PSR.

Вычислим площадь треугольника PQR и площадь треугольника PSR.

Площадь ΔPSR = 1/2 x основание x высота = 1/2 x PR x h ₁

Площадь ΔPQR = 1/2 x основание x высота = 1/2 x PR x h площадь четырехугольника PQRS равна

Площадь ΔPSR + Площадь ΔPQR = 1/2 x PR x h ₁ + 1/2 x PR x h ₂ = PR(h ₁ + h ₂ /2)

9001/2)

9001/2 PR (h ₁ + h ₂ )

Следовательно, формула для нахождения площади четырехугольника получается следующим образом:

Площадь общего четырехугольника Формула = 1/2 x длина диагоналей x (сумма высот два треугольника).

Формулы площади четырехугольника в тригонометрических терминах

Формула для нахождения площади четырехугольника в тригонометрических терминах имеет вид:

Площадь = ½ x ab x Sin θ

Где a и b — длины диагоналей четырехугольника и угол между ними.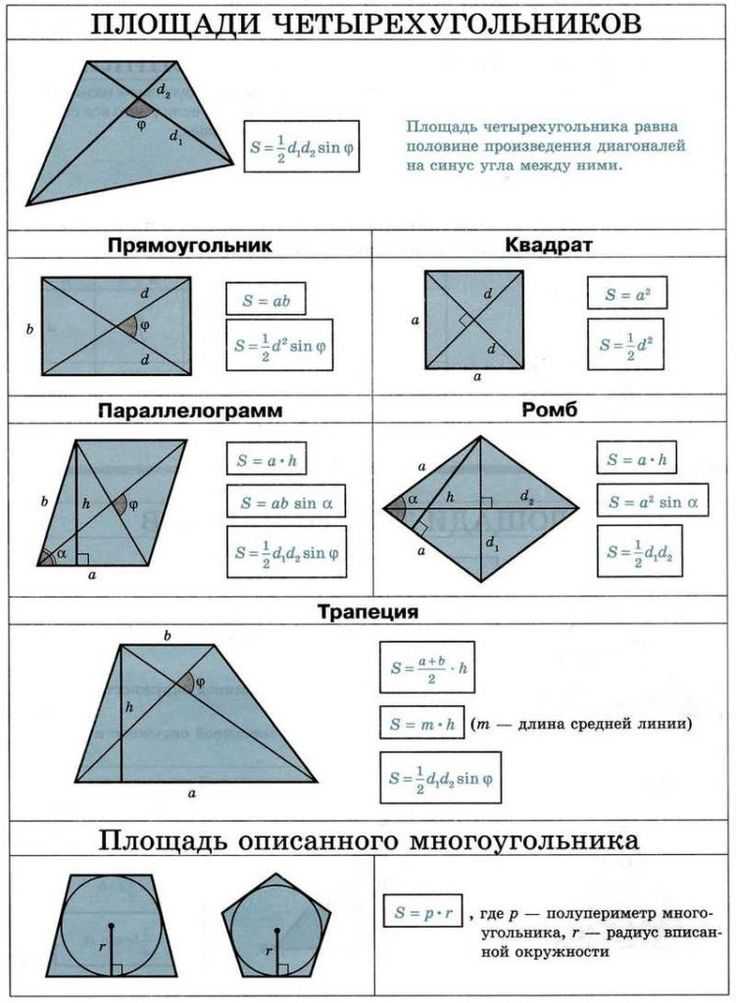

В случае ортогональных четырехугольников (таких как квадрат, воздушный змей и ромб) формулы минимизируются до

Площадь = ½ x ab (поскольку θ равно 90 ^o ).

Площадь четырехугольника Формула Координаты Геометрия

Если ABCD — четырехугольник с диагональю AC, то мы можем разделить четырехугольник на два треугольника ABC и ACD.

Теперь, используя формулу площади треугольника с учетом его вершин, мы можем определить площади треугольников ABC и ACD

Следовательно, площадь четырехугольника по формуле координатной геометрии задается как:

Площадь четырехугольника ABCD = площадь треугольника ABC + Площадь треугольника ACD

Используя эту информацию, мы можем найти площадь четырехугольника, если известны его вершины:

Пусть вершины четырехугольника ABCD равны A ( x₁,y₁), B(x₂,y₂), C( х₃,у₃), D(х₄,у₄)

Площадь четырехсторонней ABCD = площадь треугольника ABD + область треугольника BCD

+1/2 {(x₁y₂ + x₂y₄ + x₄y₁) — (x₂y₁ + x₄y₂ + x₁y₄)}

= 1/2 {(x₂y₃ + x₁y₄)}

= 1/2 (x₂y₃ + x₁y₄} + х₄у₂) — (х₃у₂ + х₄у₃ + х₂у₄)}

= 1/2{(х₁у₂ + х₂у₃ + х₃у₄ + х₄у₁) — (х₂у₁ + х₃у₂ + х₄у₃)000₄993} 12 =1/2(х₁ — х₃) (y₂ — y₄) -(x₂ -x₄) (y₁ — y₃) sq. unit

Формулы для нахождения площади четырехугольника 

Вот список формул для нахождения площади четырехугольников, таких как квадрат, воздушный змей, параллелограмм , трапеция, прямоугольник и ромб.

89

9

Воздушный змей

Четырехугольник	Фигура	Формула площади	93	Квадрат		Сторона² или x²
Прямоугольник		Длина(l) x Ширина(b)
Равнобедренная трапеция		1/2 Сумма параллельных сторон Расстояние между ними или 1/2(a + b)h
Параллелограмм		Высота основания
	1/2 диагонали 1 х диагональ 2
Ромб		1/2 х диагональ 1 х диагональ 911038 2 8

Заключение

Здесь мы обсудили формулу площади для различных виды четырехугольников.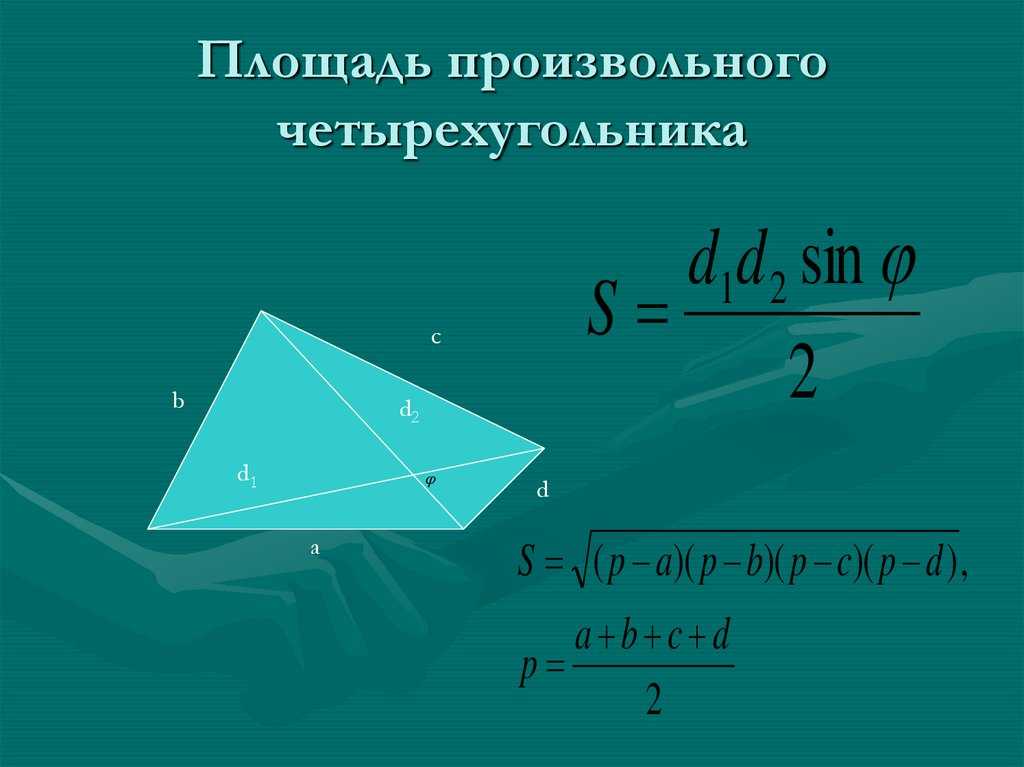 Эти формулы четырехугольника помогут вам вычислить площадь квадрата, прямоугольника, параллелограмма, воздушного змея, ромба и трапеции. Мы также обсудили площадь четырехугольника с формулой координатной геометрии, которая получается путем деления четырехугольника на два треугольника, вычисления площади каждого треугольника с учетом его вершин и сложения этих значений для получения общей площади четырехугольника.

Площадь четырехугольника – формулы, вывод и пример

Площадь четырехугольника обычно определяется как область, занимаемая внутри границ четырехугольника или плоского объекта или фигуры.

Площадь измеряется в квадратных единицах. Стандартной единицей измерения являются квадратные метры (м ² ).

О четырехугольнике

Четырехугольник — это четырехугольник, сумма внутренних углов которого равна 360 ^o .

Свойства четырехугольника:

• 4 вершины и 4 стороны.
• Сумма внутренних углов = 360 ^o
• Обычно могут иметь стороны разной длины и углы разной величины.

Примерами четырехугольника являются квадрат, прямоугольник, параллелограмм, трапеция, ромб и воздушный змей.

Примеры четырехугольников (источник)

Вычисление площади четырехугольника

В приведенном выше четырехугольнике h ₁ и h ₂ являются высотами треугольников ABC и ADC соответственно. BE и DF перпендикулярны диагонали AC.

Теперь, 

площадь (четверка ABCD) = площадь (△ABC) + площадь (△ADC)

площадь (△ABC) = \(\frac{(\mbox{основание * высота})}{2} = \frac{(AC*h_1)}{2}\)

площадь(△ADC) = \(\frac{(\mbox{основание * высота})}{2} = \frac{(AC*h_2)} {2}\)

⇒ площадь (четверка ABCD) = \(\frac{(AC*h_1)}{2} + \frac{(AC*h_2)}{2} = AC \left( \frac{h_1 + h_2}{2} \right) = \frac{1}{2}*AC*(h2+h3)\)

∴ Площадь четырехугольника = \(\frac{1}{2}\) * диагональ * Сумма высот двух треугольников

Площади различных четырехугольников Площадь квадрата 90 13 2

Четырехугольники	Площади
Площадь прямоугольника	Длина * ширина
Площадь воздушного змея	\(\frac{1}{2}\) * Произведение диагоналей
Площадь параллелограмма	\(\mbox{основание} * \mbox{высота}\)
Площадь трапеции	\(\frac{\mbox{основание}_1 + \mbox{основание}_2}{2} * \mbox{высота}\)
Площадь ромба	\(\frac {1}{2} диагональ_1 \cdot диагональ_2\)

Решенный пример

Вопрос.

No related posts.