Все возможные площади фигур формулы. Как найти площадь геометрических фигур
Что такое площадь?Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).
Как найти площадь треугольника?
S = a · h
где a – длина основания, h – высота треугольника, проведенная к основанию.
Причем, основание не обязательно должно находиться снизу. Так тоже сойдет.
Если треугольник тупоугольный , то высота опускается на продолжение основания:
Если треугольник прямоугольный , то основанием и высотой являются его катеты:
2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
S =
a · b · sinα где a и b – две стороны треугольника, sinα – синус угла между этими сторонами.
Главное условие – угол берется между двумя известными сторонами.
3. Формула площади по трем сторонам (формула Герона):
S =
где a , b и с – стороны треугольника, а р – полупериметр. p = (a + b + c )/2.
4. Формула площади треугольника через радиус описанной окружности:
S =
где a , b и с – стороны треугольника, а R – радиус описанной окружности.
5. Формула площади треугольника через радиус вписанной окружности:
Как найти площадь прямоугольника?S = p · r
где р – полупериметр треугольника, а r –
радиус вписанной окружности.
1. Площадь прямоугольника находится довольно-таки просто:
S = a · b
Никаких подвохов.
1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:
S = a · a = a 2
2. Также площадь квадрата можно найти через его диагональ:
S = d 2
Как найти площадь параллелограмма?
1. Площадь параллелограмма находится по формуле:
S = a · h
Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:
2. Также площадь параллелограмма можно найти через угол между двумя сторонами:
S = a · b · sinα
Как найти площадь ромба?Ромб по своей сути является параллелограммом, у которого все стороны равны.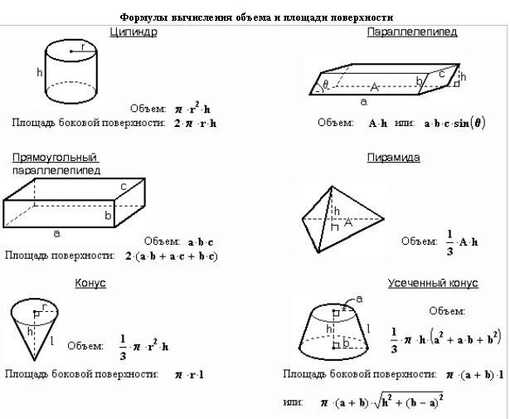 Поэтому для него применяются те же формулы площади.
Поэтому для него применяются те же формулы площади.
1. Площадь ромба через высоту:
S = a · h
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
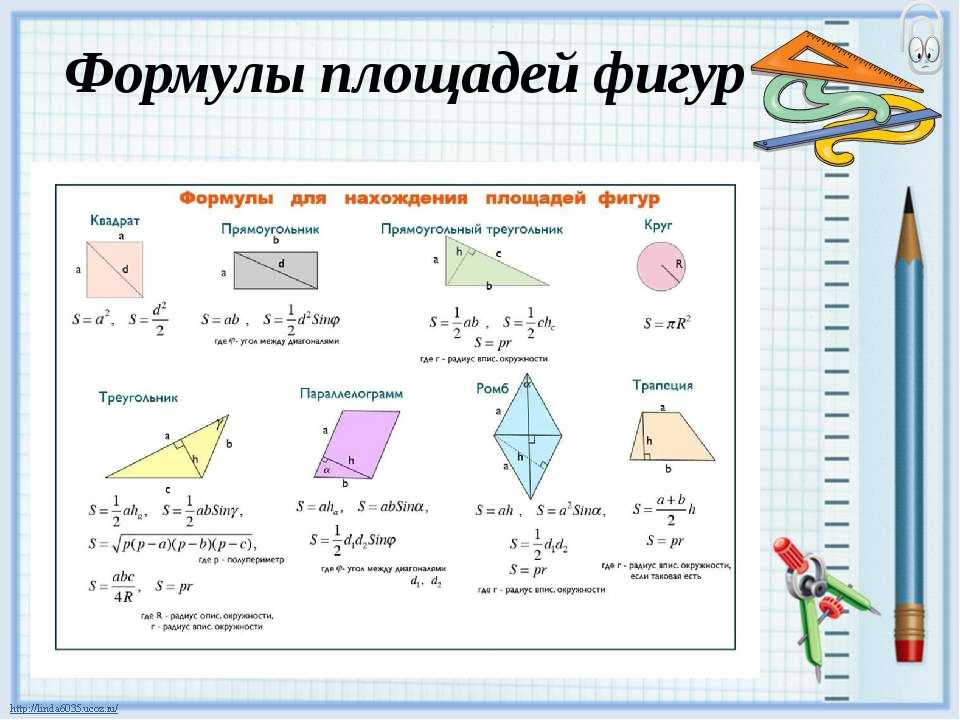
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности.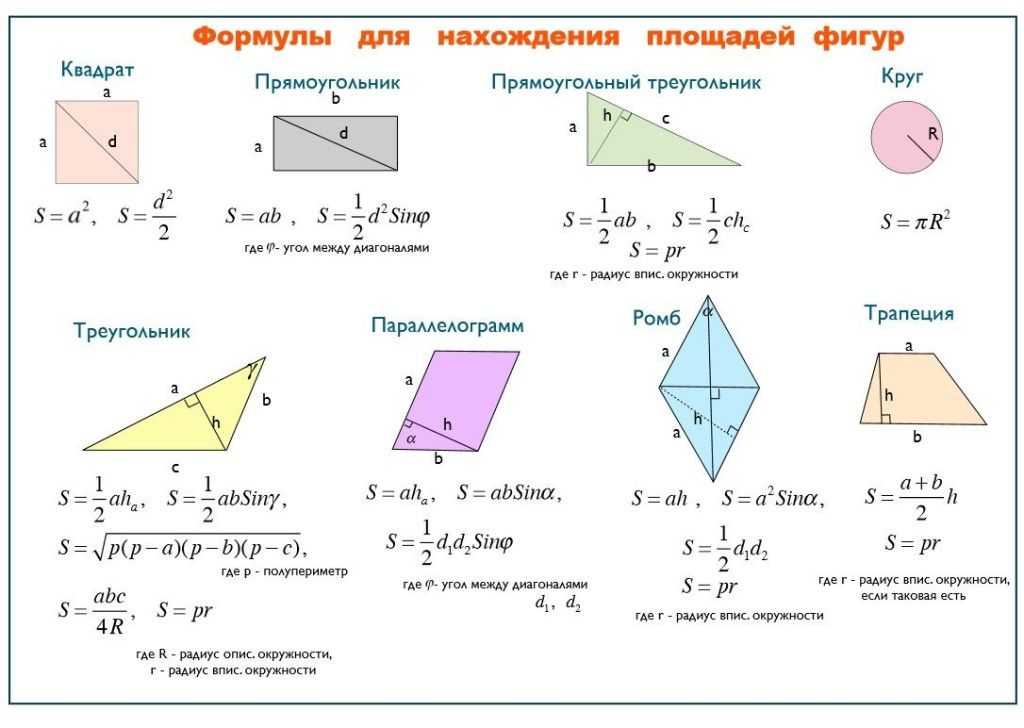 Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Все формулы площади плоских фигур
Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобедренной трапеции через радиус вписанной окружности
R- радиус вписанной окружности
D- диаметр вписанной окружности
O- центр вписанной окружности
H- высота трапеции
α, β — углы трапеции
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3.
d- диагональ трапеции
α,β- углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c- боковая сторона
m- средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,
(S):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь треугольника по стороне и двум углам, формула.
a, b, c- стороны треугольника
α, β, γ- противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формула площади правильного многоугольника
a — сторона многоугольника
n — количество сторон
Площадь правильного многоугольника, (S):
Формула (Герона) площади треугольника через полупериметр (S):
Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего
треугольника.
a — сторона треугольника
h – высота
Как вычислить площадь равнобедренного треугольника?
b — основание треугольника
a — равные стороны
h – высота
3. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
h — высота
Формула радиуса описанной окружности трапеции, (R)
найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b — стороны треугольника
Радиус описанной окружности равнобедренного треугольника (R):
Радиус вписанной окружности в шестиугольник
a — сторона шестиугольника
Радиус вписанной окружности в шестиугольник, (r):
Радиус вписанной окружности в ромб
r — радиус вписанной окружности
a — сторона ромба
D, d — диагонали
h — высота ромба
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Радиус вписанной окружности в прямоугольный треугольник
a, b — катеты треугольника
с — гипотенуза
Радиус вписанной окружности в равнобедренный треугольник
a, b — стороны треугольника
Доказать, что площадь вписанного четырёхугольника равна
\/(р — а)(р — b) (р — с) (р — d),
где р — полупериметр и а, b, с и d —
стороны четырёхугольника.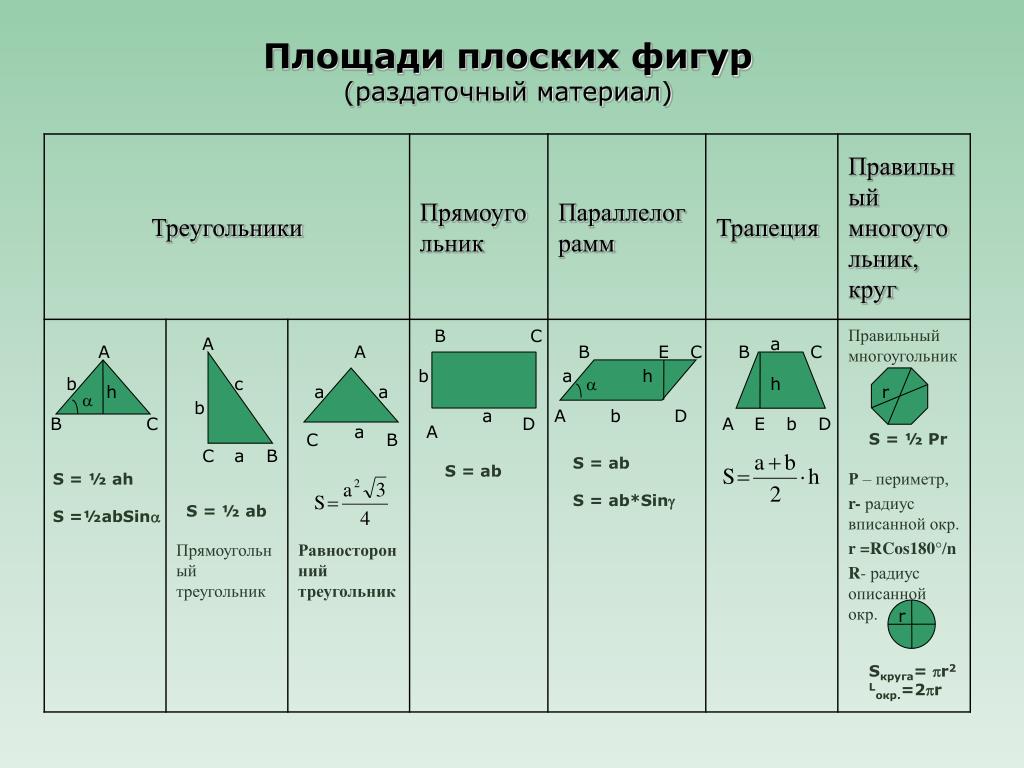
Доказать, что площадь вписанного в круг четырёхугольника равна
1/2 (ab + cb) · sin α , где а, b, с и d — стороны четырёхугольника и α — угол между сторонами а и b.
S = √[ a ƀ c d] sin ½ (α + β). — Читайте подробнее на FB.ru:
Площадь произвольного четырёхугольника (рис. 1.13) можно выразить через его стороны а, b, c и сумму пары противоположных углов:
где р – полупериметр четырёхугольника.
Площадь вписанного в окружность четырёхугольника () (рис. 1.14, а) вычисляется по формуле Брахмагупты
а описанного (рис. 1.14, б) () – по формуле
Если же четырёхугольник вписан и описан одновременно (рис. 1.14, в), то формула становится совсем простой:
Формула Пика
Чтобы оценить площадь многоугольника
на клетчатой бумаге, достаточно
подсчитать, сколько клеток покрывает
этот многоугольник (площадь клетки мы
принимаем за единицу). Точнее, если S –
площадь многоугольника, — число клеток,
которые целиком лежат внутри многоугольника,
и — число клеток, которые имеют с
внутренностью многоугольника хоть одну
общую точку.
Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:
где — площадь, r – число узлов, которые лежат строго внутри многоугольника.
Эту формулу называют «формула Пика» — по имени математика, открывшего её в 1899 году.
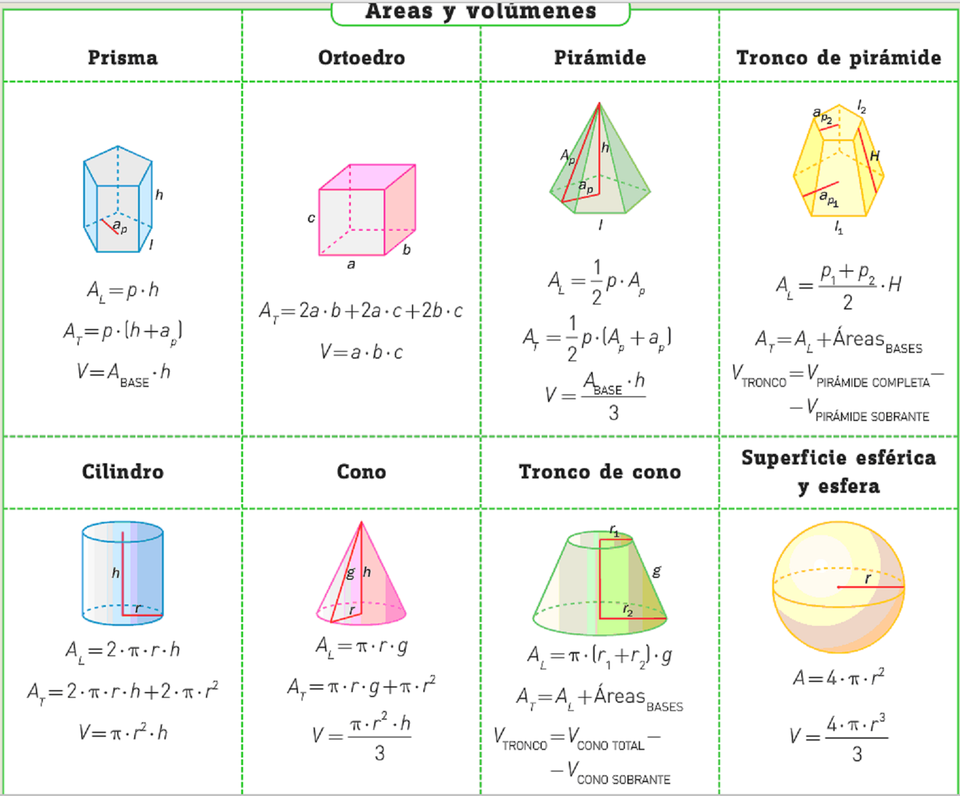
Формулы площадей и объёмов геометрических фигур
Формулы по математике площадей
В данной теме выложены вспомогательные картинки для учеников и студентов с формулами площадей и объемов фигур. Ниже расположены основные формулы, которые потребуются при решении задач по геометрии на нахождение объемов и площадей поверхности таких фигур, как квадрат, прямоугольник, параллелограмм, ромб, треугольник, прямоугольный треугольник, трапеция, круг, куб, параллелепипед, прямоугольный параллелепипед, призма, пирамида, цилиндр, конус и шар.
Формулы площадей и объёмов геометрических фигур.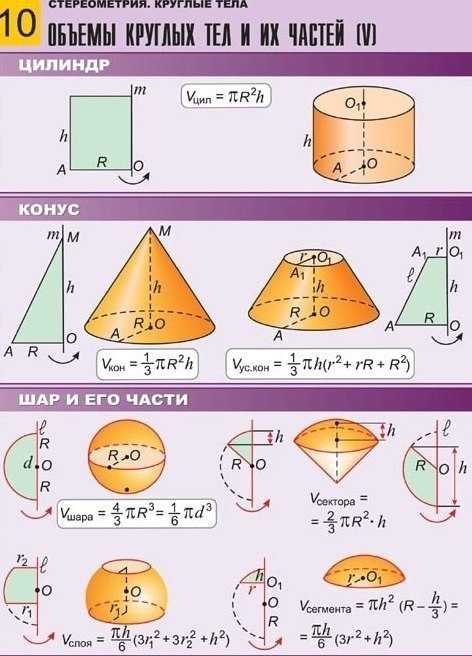
Vopvet. ru
12.06.2018 22:48:15
2018-06-12 22:48:15
Источники:
Https://vopvet. ru/news/formuly_ploshhadej_i_objomov_geometricheskikh_figur/2015-09-13-1863
Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса. » /> » /> .keyword { color: red; }
Формулы по математике площадей
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
| S = | 1 | A · h |
| 2 |
Формула Герона
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.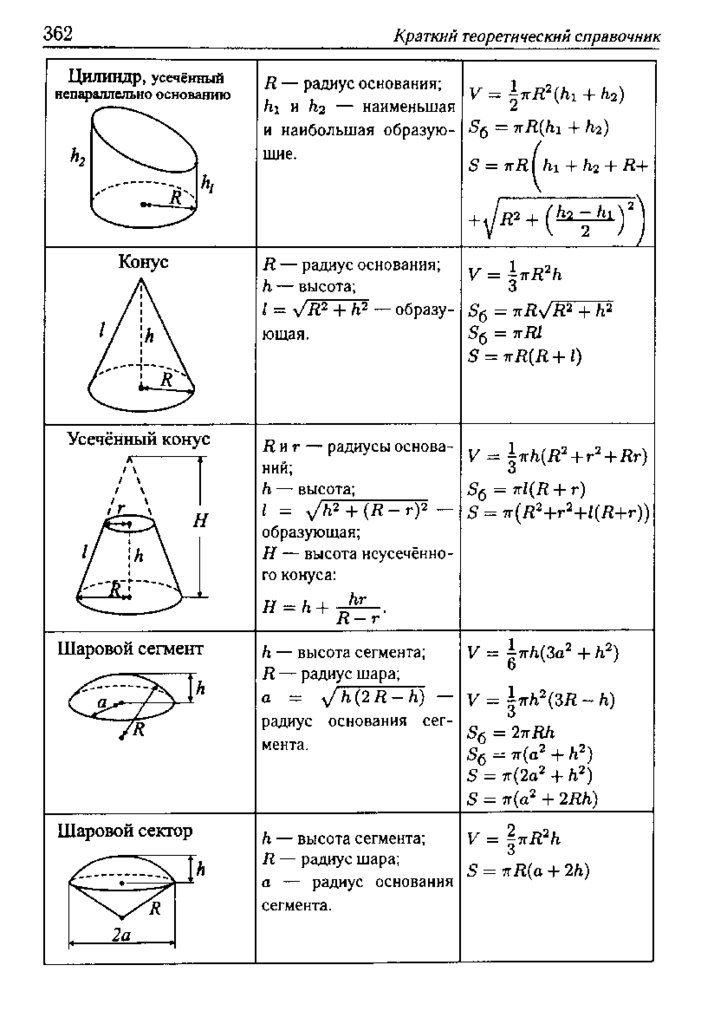
| S = | 1 | A · b · sin γ |
| 2 |
| S = | 1 | A · c · sin β |
| 2 |
| S = | 1 | B · c · sin α |
| 2 |
| S = | A · b · с |
| 4R |
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
| S = | 1 | D 2 |
| 2 |
Формула площади прямоугольника
Формулы площади параллелограмма
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.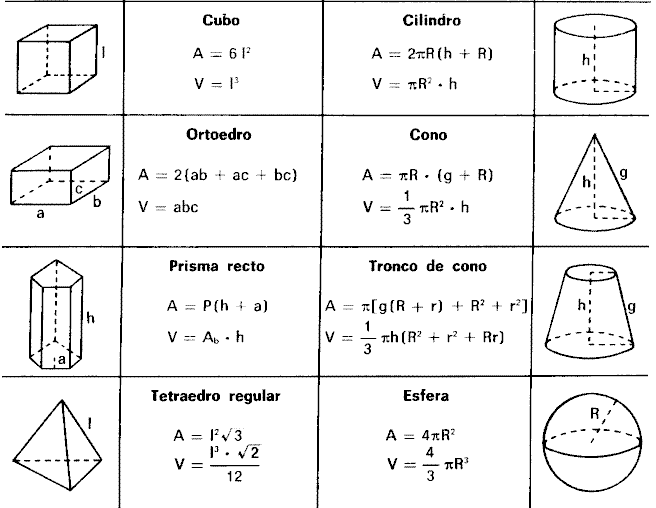
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
| S = | 1 | D 1 d 2 sin γ |
| 2 |
Формулы площади ромба
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
| S = | 1 | D 1 · d 2 |
| 2 |
Формулы площади трапеции
Формула Герона для трапеции
| S = | A + b | √ ( p-a )( p-b )( p-a-c )( p-a-d ) |
| | a — b | |
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту
| S = | 1 | ( a + b ) · h |
| 2 |
Формулы площади выпуклого четырехугольника
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
| S = | 1 | D 1 d 2 sin α |
| 2 |
Где S — площадь четырехугольника,
D 1, d 2 — длины диагоналей четырехугольника,
Α — угол между диагоналями четырехугольника./918870b1bc4a305.s.siteapi.org/img/da030ac2a7fb5c233f7bae5e5994c9ac4d7727d0.jpg)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
Формула площади четырехугольника по длине сторон и значению противоположных углов
A, b, c, d — длины сторон четырехугольника,
P = a + b + c + d 2 — полупериметр четырехугольника,
Θ = α + β 2 — полусумма двух противоположных углов четырехугольника.
Формула площади четырехугольника, вокруг которого можно описать окружность
Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.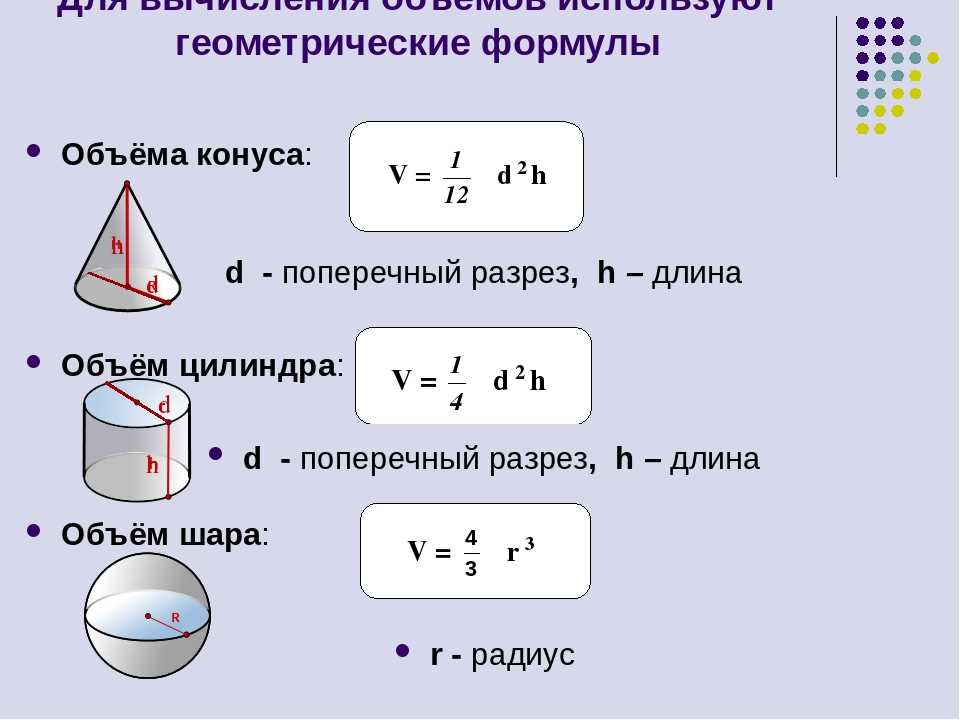
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
| S = | 1 | A · h |
| 2 |
Формула Герона
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
| S = | 1 | A · b · sin γ |
| 2 |
| S = | 1 | A · c · sin β |
| 2 |
| S = | 1 | B · c · sin α |
| 2 |
| S = | A · b · с |
| 4R |
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Формула площади треугольника по стороне и высоте Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
Ru. onlinemschool. com
16.06.2017 6:14:08
2017-06-16 06:14:08
Источники:
Https://ru. onlinemschool. com/math/formula/area/
Формулы объемов и площадей геометрических фигур | ЕГЭ по математике » /> » /> .keyword { color: red; }
Формулы по математике площадей
Подготовка к ЕГЭ по математике не может обойтись без Изучения геометрии. Задачи на расчет площади и объема фигур, нахождение углов и длин сторон встречаются и в первой, и во второй части. В базовой математике ЕГЭ формулы на объем и площадь представлены в справочных материалах. Тем, кто сдает профильную, придется выучить их. Рассмотрим основную теорию.
Площадь — величина, которая есть у плоских фигур. Ее можно посчитать для квадрата, прямоугольника, параллелограмма, треугольника, ромба, трапеции, круга. Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус. Объемные тела условно делят на многогранники (состоят из нескольких многоугольников) и поверхности вращения (есть условная линия, вдоль которой вращается плоская фигура). На вычисление объема это не влияет.
Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус. Объемные тела условно делят на многогранники (состоят из нескольких многоугольников) и поверхности вращения (есть условная линия, вдоль которой вращается плоская фигура). На вычисление объема это не влияет.
В таблицах представлены основные формулы объемов и площадей фигур для ЕГЭ. Мы советуем сохранить их себе, чтобы пользоваться при подготовке к ЕГЭ и быстро повторить теорию перед экзаменом.
Формулы объемов и площадей геометрических фигур.
Unikum. rudn. ru
10.02.2017 12:14:16
2017-02-10 12:14:16
Источники:
Https://unikum. rudn. ru/news/formuly-obemov-i-ploshchadey-geometricheskikh-figur
Площадь s фигуры. Площадь фигур на клетчатой бумаге. Полная инструкция (2020). Сбор и использование персональной информации
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Формула площади необходима для определения площадь фигуры, которая является вещественнозначной функцией, определённой на некотором классе фигур евклидовой плоскости и удовлетворяющая 4м условиям:
- Положительность — Площадь не может быть меньше нуля;
- Нормировка — квадрат со стороной единица имеет площадь 1;
- Конгруэнтность — конгруэнтные фигуры имеют равную площадь;
- Аддитивность — площадь объединения 2х фигур без общих внутренних точек равна сумме площадей этих фигур.
| Геометрическая фигура | Формула | Чертеж |
|---|---|---|
Результат сложения расстояний между серединами противоположных сторон выпуклого четырехугольника будут равна его полупериметру. | ||
Сектор круга. Площадь сектора круга равна произведению его дуги на половину радиуса. | ||
Сегмент круга. Чтобы получить площадь сегмента ASB, достаточно из площади сектора AOB вычесть площадь треугольника AOB. | S = 1 / 2 R(s — AС) | |
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи. | ||
Эллипс . Еще один вариант как вычислить площадь эллипса — через два его радиуса. | ||
Треугольник. Через основание и высоту. Формула площади круга через его радиус и диаметр. | ||
Квадрат . Через его сторону. Площадь квадрата равна квадрату длины его стороны. | ||
Квадрат. Через его диагонали . Площадь квадрата равна половине квадрата длины его диагонали. | ||
Правильный многоугольник . Для определения площади правильного многоугольника необходимо разбить его на равные треугольники, которые бы имели общую вершину в центре вписанной окружности. | S= r·p = 1/2 r·n·a |
Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.
Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении.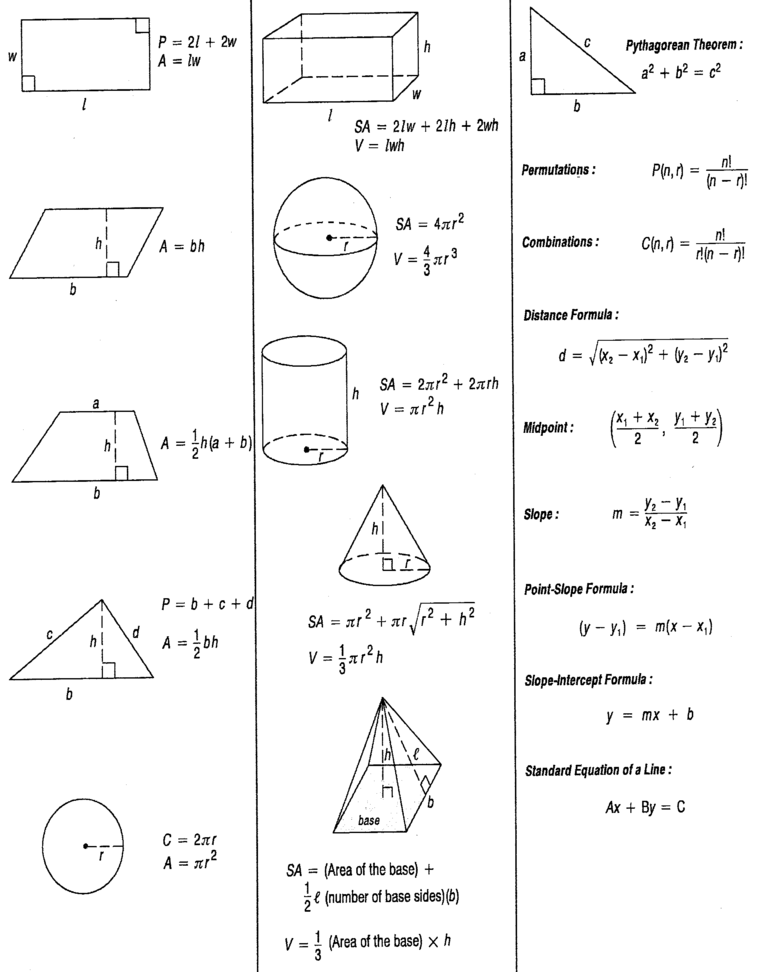 Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:
2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении. Такая формула площади прямоугольника имеет вид:
Такая формула площади прямоугольника имеет вид:
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.
Как найти площадь фигуры?
Знать и уметь рассчитывать площади различных фигур необходимо не только для решения простых геометрических задач. Не обойтись без этих знаний и при составлении или проверке смет на ремонт помещений, расчета количества необходимых расходных материалов. Поэтому давайте разберемся, как находить площади разных фигур.
Часть плоскости, заключенная внутри замкнутого контура, называется площадью этой плоскости. Выражается площадь количеством заключенных в ней квадратных единиц.
Чтобы вычислить площадь основных геометрических фигур, необходимо использовать правильную формулу.
Площадь треугольника
Обозначения:
- Если известны h, a, то площадь искомого треугольника определяется как произведение длин стороны и высоты треугольника, опущенной к этой стороне, разделенное пополам: S=(a·h)/2
- Если известны a, b, c, то искомая площадь рассчитывается по формуле Герона: корень квадратный, взятый из произведения половины периметра треугольника и трех разностей половины периметра и каждой стороны треугольника: S = √(p·(p — a)·(p — b)·(p — c)).

- Если известны a, b, γ, то площадь треугольника определяется как половина произведения 2-х сторон, умноженная на значение синуса угла между этими сторонами: S=(a·b·sin γ)/2
- Если известны a, b, c, R, то искомая площадь определяется как деление произведения длин всех сторон треугольника на четыре радиуса описанной окружности: S=(a·b·c)/4R
- Если известны p, r, то искомая площадь треугольника определяется умножением половины периметра на радиус вписанной в него окружности: S=p·r
Площадь квадрата
Обозначения:
- Если известна сторона, то площадь данной фигуры определяется как квадрат длины его стороны: S=a 2
- Если известна d, то площадь квадрата определяется как половина квадрата длины его диагонали: S=d 2 /2
Площадь прямоугольника
Обозначения:
- S — определяемая площадь,
- a, b — длины сторон прямоугольника.
- Если известны a, b, то площадь данного прямоугольника определяется произведением длин двух его сторон: S=a·b
- Если длины сторон неизвестны, то площадь прямоугольника нужно разбить на треугольники.
 В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.
В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.
Площадь параллелограмма
Обозначения:
- S — искомая площадь,
- a, b — длины сторон,
- h — длина высоты данного параллелограмма,
- d1, d2 — длины двух диагоналей,
- α — угол, находящийся между сторонами,
- γ — угол, находящийся между диагоналями.
- Если известны a, h, то искомая площадь определяется перемножением длин стороны и высоты, опущенной на эту сторону: S=a·h
- Если известны a, b, α, то площадь параллелограмма определяется перемножением длин сторон параллелограмма и значения синуса угла между этими сторонами: S=a·b·sin α
- Если известны d 1 , d 2 , γ то площадь параллелограмма определяется как половина произведения длин диагоналей и значения синуса угла между этими диагоналями: S=(d 1 ·d 2 ·sinγ)/2
Площадь ромба
Обозначения:
- S — искомая площадь,
- a — длина стороны,
- h — длина высоты,
- α — меньший угол между двумя сторонами,
- d1, d2 — длины двух диагоналей.

- Если известны a, h, то площадь ромба определяется умножением длины стороны на длину высоты, которая опущена на эту сторону: S=a·h
- Если известны a, α, то площадь ромба определяется перемножением квадрата длины стороны на синус угла между сторонами: S=a 2 ·sin α
- Если известны d 1 и d 2 , то искомая площадь определяется как половина произведения длин диагоналей ромба: S=(d 1 ·d 2)/2
Площадь трапеции
Обозначения:
- Если известны a, b, c, d, то искомая площадь определяется по формуле: S= (a+b) /2 *√ .
- При известных a, b, h, искомая площадь определяется как произведение половины суммы оснований и высоты трапеции: S=(a+b)/2·h
Площадь выпуклого четырехугольника
Обозначения:
- Если известны d 1 , d 2 , α, то площадь выпуклого четырехугольника определяется как половина произведения диагоналей четырехугольника, умноженная на величину синуса угла между этими диагоналями: S=(d 1 · d 2 ·sin α)/2
- При известных p, r площадь выпуклого четырехугольника определяется как произведение полупериметра четырехугольника на радиус окружности, вписанной в этот четырехугольник: S=p·r
- Если известны a, b, c, d, θ, то площадь выпуклого четырехугольника определяется как корень квадратный из произведений разницы полупериметра и длины каждой стороны за минусом произведения длин всех сторон и квадрата косинуса половины суммы двух противоположных углов: S 2 = (p — a)(p — b)(p — c)(p — d) — abcd·cos 2 ((α+β)/2)
Площадь круга
Обозначения:
Если известен r, то искомая площадь определяется как произведение числа π на радиус в квадрате: S=π r 2
Если известна d, то площадь круга определяется как произведение числа π на квадрат диаметра, поделенное на четыре: S=(π·d 2)/4
Площадь сложной фигуры
Сложную можно разбить на простые геометрические фигуры. Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.
Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.
Обозначение:
- S — площадь кольца,
- R, r — радиусы внешней окружности и внутренней соответственно,
- D, d — диаметры внешней окружности и внутренней соответственно.
Для того чтобы найти площадь кольца, надо из площади большего круга отнять площадь меньшего круга. S = S1-S2 = πR 2 -πr 2 = π (R 2 -r 2).
Таким образом, если известны R и r, то площадь кольца определяется как разница квадратов радиусов внешней и внутренней окружностей, умноженная на число пи: S=π(R 2 -r 2).
Если известны D и d, то площадь кольца определяется как четверть разницы квадратов диаметров внешней и внутренней окружностей, умноженная на число пи: S= (1/4)(D 2 -d 2) π.
Площадь закрашенной фигуры
Предположим, что внутри одного квадрата (А) находится другой (Б) (меньшего размера), и нам нужно найти закрашенную полость между фигурами «А» и «Б». Скажем так, «рамку» маленького квадрата. Для этого:
Скажем так, «рамку» маленького квадрата. Для этого:
- Находим площадь фигуры «А» (вычисляется по формуле нахождения площади квадрата).
- Аналогичным образом находим площадь фигуры «Б».
- Вычитаем из площади «А» площадь «Б». И таким образом получаем площадь закрашенной фигуры.
Теперь вы знаете, как находить площади разных фигур.
геометрических формул и уравнений | Примеры, Методы, Таблица
Примечание: эта страница содержит устаревшие ресурсы, которые больше не поддерживаются. Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.
Квадрат – это четырехугольник, у которого четыре равные стороны и четыре прямых угла.
Для квадрата, сторона которого состоит из s единиц:
Площадь квадрата = сторона x сторона = s 2 кв. единиц
Например, если у нас есть квадрат, одна сторона которого равна 6 см, его площадь будет рассчитана как:
Площадь = сторона x сторона = 6 x 6 = 36 см 2
Прямоугольник является разновидностью четырехугольника равные противоположным сторонам и четырем прямым углам.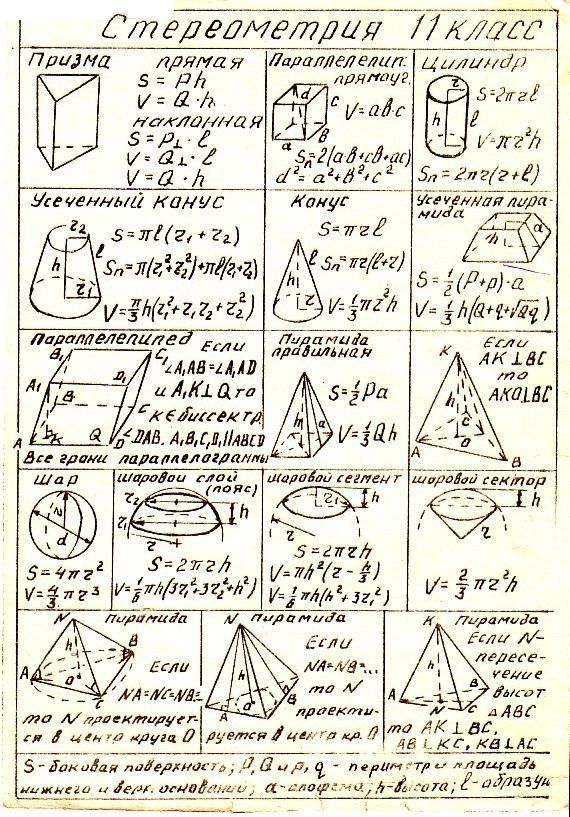
Площадь прямоугольника с длиной ‘ l ‘ и шириной ‘b’ равна l x b
Например, рассмотрим прямоугольник длиной 8 см и шириной 7 см, как показано на рис. рисунок ниже.
Треугольник — это многоугольник, состоящий из трех ребер и трех вершин. Вершины соединяются вместе, образуя три стороны треугольника. Площадь, занимаемая этими тремя сторонами, называется площадью треугольника.
Площадь треугольника определяется как: 1/2 x b x h
Где b = основание треугольника (или любая сторона треугольника)
И
H = высота треугольника от этого основания (или стороны )
На следующем рисунке показаны основание и высота треугольника:
Приведенная выше формула применима независимо от того, является ли треугольник разносторонним (у него разные стороны), равнобедренным треугольником (у которого две стороны равны) или равносторонним треугольником (у которого все стороны равны).
Давайте лучше разберемся на примере. Предположим, у нас есть треугольник, одна сторона которого равна 6 см, а высота основания равна 8 см, как показано на следующем рисунке:
Предположим, у нас есть треугольник, одна сторона которого равна 6 см, а высота основания равна 8 см, как показано на следующем рисунке:
Площадь этого треугольника равна
1/2 x b x h
Где b = 6 см, а h = 8 см
Следовательно, площадь = 1/2 x 6 x 8 = 24 см 2
Пространство, занимаемое кругом, называется его площадью.
Площадь круга с радиусом r (расстояние от центра до точки на границе) определяется как πr 2 , где π = 22/7 или 3,14 (приблизительно)
Например, предположим, что у нас есть круг с радиусом 7 см, как показано на рисунке ниже.
Его площадь определяется как:
Площадь = πr 2 = (22/7) x 7 x 7 = 154 см 2
Предположим, что вместо радиуса нам дан диаметр круга, как мы вычисляем площадь?
Мы знаем, что в круге радиус равен половине диаметра. Математически
r = d/2, где d — диаметр, а r — радиус.
Итак, делим заданный диаметр наполовину и получаем радиус.
Пример
Предположим, нам нужно найти площадь круга диаметром 4,2 см.
Здесь диаметр (d) = 4,2 см
Из соотношения между радиусом и диаметром имеем r = d/2.
Отсюда r = 4,2/2 = 2,1 см
Теперь площадь этого круга = = πr 2 = (22/7) x 4,2 x 4,2 = 55,44 см 2
Длина, равная границе круг называется его окружностью . Он определяется как 2πr, где r — радиус. Другими словами, окружность круга — это то же, что периметр для других геометрических фигур, таких как прямоугольник квадрата.
Рассмотрим круг радиусом 7 см. Для того, чтобы найти его длину окружности, нам нужно воспользоваться формулой 2πr.
Следовательно, длина окружности этого круга = 2πr = 2 x (22/7) x 7 = 44 см.
Обратите внимание на единицы измерения периметра и площади. В то время как единицы площади всегда выражены в квадратных единицах, в случае периметра они всегда выражены в стандартных единицах длины, таких как м, см, дм, км и т. д.
д.
Многогранник, содержащий две пары конгруэнтных параллельных оснований, называется прямоугольная призма. Он считается призмой из-за поперечного сечения по длине. Основание прямоугольной призмы представляет собой прямоугольник. Он имеет три измерения, как показано на рисунке ниже:
Объем прямоугольной призмы определяется как:
V = длина x ширина x высота
Где
l = длина основания призмы
w = ширина основания призмы
h = высота призмы
Например, у нас есть прямоугольная призма, длина основания которой равна 6 см; ширина основания 5 см, а высота 4 см. Тогда объем будет равен:
Объем (V) = l x w x h
Где
l = 6 см, w = 5 см и h = 4 см
Объем = 6 х 5 х 4 = 120 куб. см
Не единицы объема. Объем любой геометрической фигуры всегда выражается в кубических единицах.
Количество (в любой форме), которое может удержаться в цилиндре, называется его объемом. Другими словами, объем цилиндра – это занимаемое им пространство. Основание правильного круглого цилиндра представляет собой круг на обоих концах, которые проходят параллельно друг другу, как показано на рисунке ниже.
Другими словами, объем цилиндра – это занимаемое им пространство. Основание правильного круглого цилиндра представляет собой круг на обоих концах, которые проходят параллельно друг другу, как показано на рисунке ниже.
Объем прямого кругового цилиндра определяется как:
| Объем = площадь основания x высота цилиндра становится πr 2 h Пример Предположим, мы хотим найти объем правильного круглого цилиндра, радиус которого в основании равен 5 см, а высота цилиндра равна 7 см. На следующем рисунке показаны заданные размеры этого цилиндра. Его объем определяется как πr 2 ч = (22/7) x 5 x 5 x 7 = 550 куб. см Конус представляет собой пирамиду с круглым основанием. Его объем равен 1/3πr 2 ч, где «r» — радиус основания конуса, а «h» — его высота. Предположим, мы хотим вычислить объем конуса с радиусом 6 см и высотой 14 см. Его объем будет равен: V = 1/3πr 2 h = (1/3) x (22/7) x 6 x 14 = 88 куб. Приведенные выше формулы можно обобщить в таблице ниже. Приведенные ниже формулы обычно требуются в геометрии для расчета длин, площадей и объемов. Вы можете использовать их, чтобы помочь детям с домашним заданием по математике. Список формул
Мы тратим много времени на изучение и сбор информации на этом сайте. Геометрическая формула Диаграмма Мастер 7 столбов школы успеха Улучшить свои оценки и снизить стресс . Шпаргалка по геометрии для старшей школы Формулы геометрии Очень красивая страница с формулами геометрии для печати. Включает в себя типичные формы плюс формулы, обычно не встречающиеся, такие как кольцо, эллипс, тор. Страница 1 Страница 2 Скачать Полный список здесь. Таблица формул для геометрии Страница 1 Страница 2
Таблица формул для геометрии. Нажмите на картинку, чтобы загрузить всю таблицу Нахождение площади: формула и исчисление, фигураДавайте посмотрим, как найти площадь некоторых распространенных геометрических фигур, таких как треугольники, круги, параллелограммы и прямоугольники, как а также менее распространенные формы. Как найти площадь треугольникаПлощадь треугольника можно найти разными способами: с помощью длин или с помощью тригонометрии. Использование длинПлощадь треугольника равна , где b соответствует длине основания треугольника, а h соответствует его высоте, перпендикулярной основанию. Высота и основание треугольников Вопросы могут заключаться в том, чтобы найти площадь треугольника по его размерам или найти неизвестную длину по его площади. Найдите площадь треугольника с длиной основания 7 см и высотой 50 см. Здесь см и см. Используя формулу площади, Площадь треугольника равна 17,5 см² Найдите длину основания и высоту треугольника с площадью 9 см², зная, что высота в два раза больше основания. Пусть длина основания b = x, поэтому h = 2x. Подстановка известных значений в уравнение площади, Следовательно, Поскольку x — это длина, -3 отбрасывается и x = 3. Длина основания равна 3 см, а длина высоты равна 2 x 3 = 6 см Используя тригонометрию:Площадь треугольника можно вычислить, если известны 2 длины и угол между ними (в случае SAS — сторона, угол, сторона) треугольник со сторонами и углами, обозначенными a, b, с т В этом случае формула площади треугольника . Известные длины умножаются на синус угла между ними. Две формулы, используемые для вычисления площади треугольника, кажутся разными, но первое уравнение, использующее просто длины, получено из второго уравнения с помощью тригонометрии. Докажем это: Найдите площадь треугольника по формуле Если длины a и b перпендикулярны друг другу, то одна из них является основанием треугольника, а другая — его высотой. Кроме того, угол между ними будет 90° или π/2 радиан. Так как , эту формулу можно записать в виде , что эквивалентно первой формуле. Вот пример использования тригонометрической формы формулы. Чему равна площадь треугольного двора с точностью до ближайшего квадратного метра, если два соседних забора двора имеют длину 10 и 12 м, а угол между ними равен 78°? Для этого вопроса мы воспользуемся тригонометрической формулой, так как нам даны 2 стороны и 1 угол. Площадь двора 59 кв.м² с точностью до ближайшего квадратного метра. Как найти площадь кругаПлощадь круга можно рассчитать по формуле , в которой r представляет собой радиус круга (половину длины диаметра), а π — иррациональное число 3,14159265 … π — постоянное отношение длины окружности к ее диаметру. Любой сектор круга также можно рассчитать, взяв долю площади. Эта дробь есть. Например, для вычисления площади полукруга используется формула (или ), так как полуокружность – это сектор, состоящий из половины окружности. Найдите площадь круга радиусом 3 см, оставив ответ в точной форме. Мы будем использовать формулу. подставляя известный радиус, Следовательно, круг имеет площадь 9π см² в точной форме. Какова площадь сектора с углом 34° окружности радиусом 2км? Дайте ответ с точностью до двух знаков после запятой. Поскольку необходимо вычислить площадь сектора круга, будет взята только часть его площади. Чтобы вычислить это, мы возьмем часть полной площади круга, так как круг состоит из 360 градусов. Следовательно, площадь сектора Так как вопрос требует ответа с точностью до 2 dp, площадь сектора равна 1,19 км² Как найти площадь параллелограмма Площадь параллелограмма может быть рассчитывается по длине его основания и перпендикулярной высоте. Площадь параллелограмма в два раза больше площади одного из треугольников, на которые его можно разделить: Площадь параллелограмма также можно определить с помощью тригонометрического метода нахождения площади треугольника. Таким образом, площадь параллелограмма можно вычислить как :, где a и b — две смежные длины, а C — угол между ними. Параллелограмм, разделенный на два треугольника Рассмотрим пример для практики: Если основание параллелограмма в три раза больше его высоты, а площадь равна 108 м², найдите основание . Пусть высота = x. Основание в три раза больше высоты, поэтому основание = 3x. Сформулируем уравнение площади через x: Площадь параллелограмма 3x² или 108м². Поскольку х — это длина, она не может быть отрицательной, поэтому х = 6 м. Основание равно 3x, следовательно, основание = (3) (6) = 18 м. Как найти площадь прямоугольникаПлощадь прямоугольника находится тем же методом, что и площадь параллелограмма. Формула площади прямоугольника , где ширина и длина перпендикулярны друг другу. Квадрат — это особый тип прямоугольника, у которого все стороны равны. И w, и l равны определенному значению. Пусть это значение будет х. Площадь квадрата равна просто Вот пример: Если площадь прямоугольника 120 м², а одна из его сторон 6 м, каков его периметр? Чтобы найти недостающую длину, воспользуемся формулой площади и переставим ее. Длина недостающей стороны 20м. Прямоугольник состоит из 2 наборов по 2 параллельных одинаковых стороны. Следовательно, периметр равен m. Будьте осторожны с единицами измерения вашего ответа: Площадь фигуры выражается в единицах², а ее периметр, который является длиной, выражается в единицах. Как найти площадь фигурыЧтобы найти площадь менее распространенных или неизвестных фигур, может потребоваться разделить эту фигуру на более мелкие фигуры, для которых легко вычислить площадь. Важно отличать простые формы от более сложных, таких как полукруги, прикрепленные к каждому концу прямоугольника, образующие форму беговой дорожки: Прямоугольник с полуокружностями Кроме того, правильные многоугольники с n сторонами можно разделить на n равнобедренных треугольников одинакового размера и формы. Например, квадрат (четыре стороны) можно разделить на четыре треугольника, как показано на рисунке. Квадрат, разделенный на четыре треугольника Австралийская монета номиналом 50 центов имеет форму правильного двенадцатиугольника (12 сторон). Поскольку мы не знаем формулы для непосредственного нахождения площади двенадцатиугольника, для решения этой задачи нам нужно разделить фигуры на более мелкие известные фигуры. Додекагон является правильным многоугольником, поэтому его можно разделить на двенадцать равнобедренных треугольников одинакового размера с вершиной в центре додекагона, как показано на рисунке. Додекагон. Изображение: общественное достояние Две стороны каждого треугольника имеют одинаковую длину, соответствующую радиусу двенадцатиугольника (длина от центра до любой вершины). Угол между этими длинами равен градусам. Размеры монет и банкноты неизвестны. Пусть радиус = r. Следовательно, мы можем вычислить площадь каждого треугольника через r: единиц² В каждом додекагоне двенадцать треугольников, а в банкноте восемь додекагонов. |




 В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.
В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.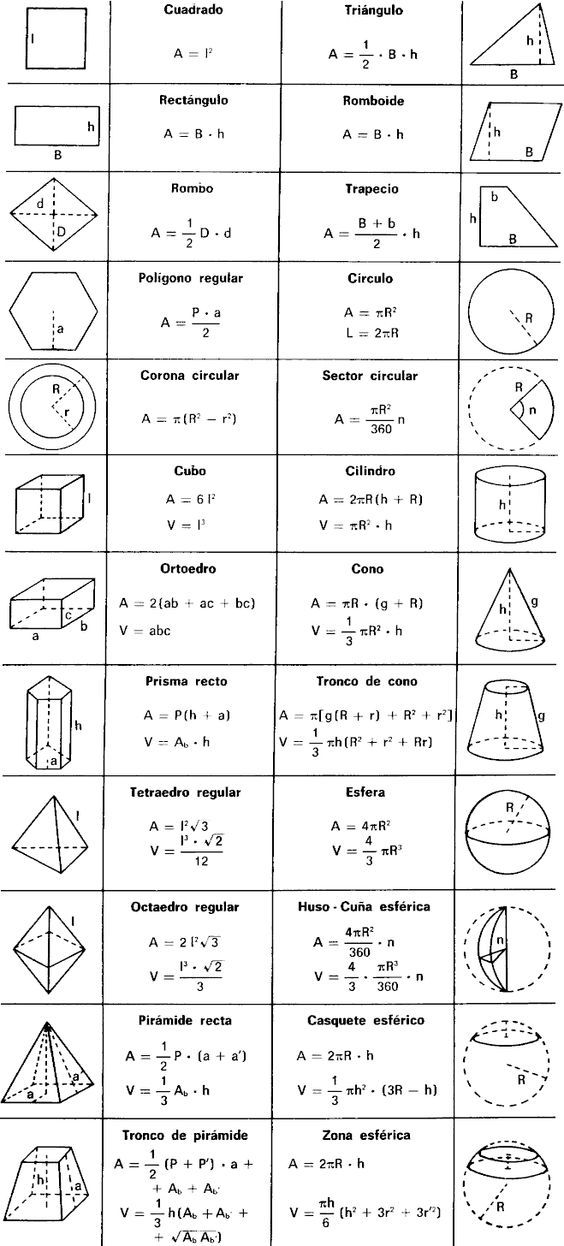
 см
см Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку! Используйте эти формулы геометрии для расчета периметра, площади, площади основания, поперечной площади и площади поверхности для различных геометрических фигур, а также формулу расстояния и уравнение окружности. Включено более 70 формул. Таблица формул геометрии также доступна для скачивания. Надеюсь поможет
Используйте эти формулы геометрии для расчета периметра, площади, площади основания, поперечной площади и площади поверхности для различных геометрических фигур, а также формулу расстояния и уравнение окружности. Включено более 70 формул. Таблица формул геометрии также доступна для скачивания. Надеюсь поможет 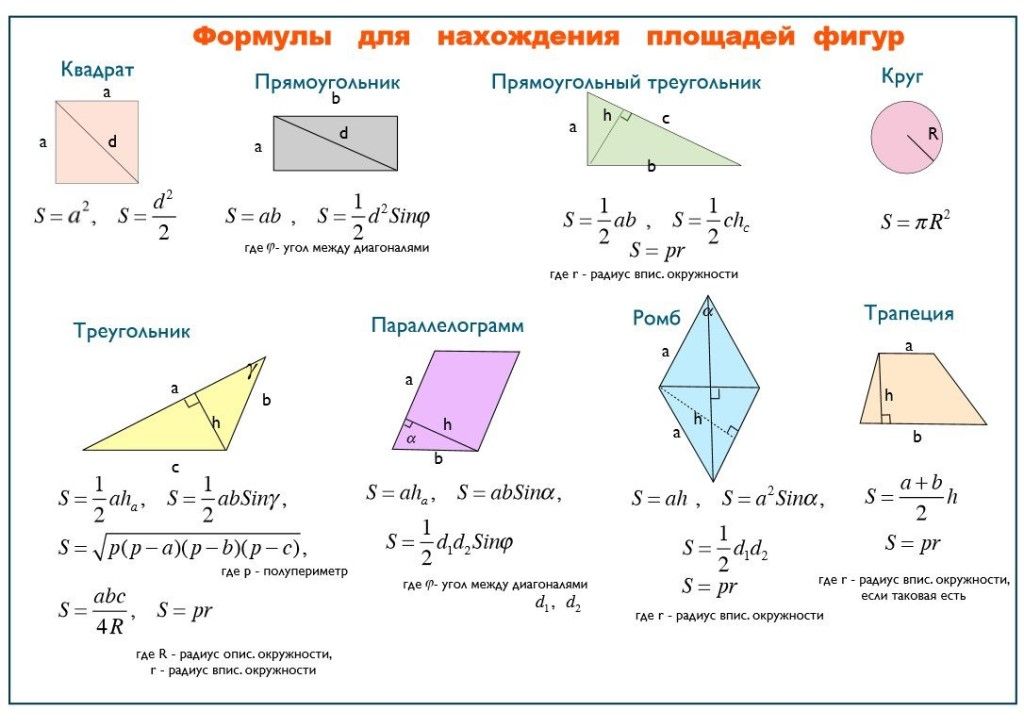

 Формула, связывающая их вместе, равна , в которой b соответствует длине основания параллелограмма, а h соответствует его перпендикулярной высоте. Эта формула связана с формулой площади треугольника, поскольку параллелограмм всегда можно разделить на 2 одинаковых треугольника, если параллелограмм разделен диагональю.
Формула, связывающая их вместе, равна , в которой b соответствует длине основания параллелограмма, а h соответствует его перпендикулярной высоте. Эта формула связана с формулой площади треугольника, поскольку параллелограмм всегда можно разделить на 2 одинаковых треугольника, если параллелограмм разделен диагональю.

 Восемь из этих 50-центовых монет с номерами n помещаются на банкноте в 5 австралийских долларов. Какая часть купюры не покрыта?
Восемь из этих 50-центовых монет с номерами n помещаются на банкноте в 5 австралийских долларов. Какая часть купюры не покрыта? 