Формула доверительного интервала: Доверительный интервал онлайн

Содержание

Доверительный интервал для математического ожидания

Точечная и интервальная оценки среднего значения
Точечная и интервальная оценки удельного веса

Доверительный интервал для математического ожидания — это такой вычисленный по данным интервал, который с известной вероятностью содержит математическое ожидание генеральной совокупности. Естественной оценкой для математического ожидания является среднее арифметическое её наблюденных значений. Поэтому далее в течение урока мы будем пользоваться терминами «среднее», «среднее значение». В задачах рассчёта доверительного интервала чаще всего требуется ответ типа «Доверительный интервал [95%; 90%; 99%] среднего числа [величина в конкретной задаче] находится от [меньшее значение] до [большее значение]». С помощью доверительного интервала можно оценивать не только средние значения, но и удельный вес того или иного признака генеральной совокупности. Средние значения, дисперсия, стандартное отклонение и погрешность, через которые мы будем приходить к новым определениям и формулам, разобраны на уроке

Характеристики выборки и генеральной совокупности.

Если среднее значение генеральной совокупности оценивается числом (точкой), то за оценку неизвестной средней величины генеральной совокупности принимается конкретное среднее, которое рассчитано по выборке наблюдений. В таком случае значение среднего выборки — случайной величины — не совпадает со средним значением генеральной совокупности. Поэтому, указывая среднее значение выборки, одновременно нужно указывать и ошибку выборки. В качестве меры ошибки выборки используется стандартная ошибка , которая выражена в тех же единицах измерения, что и среднее. Поэтому часто используется следующая запись: .

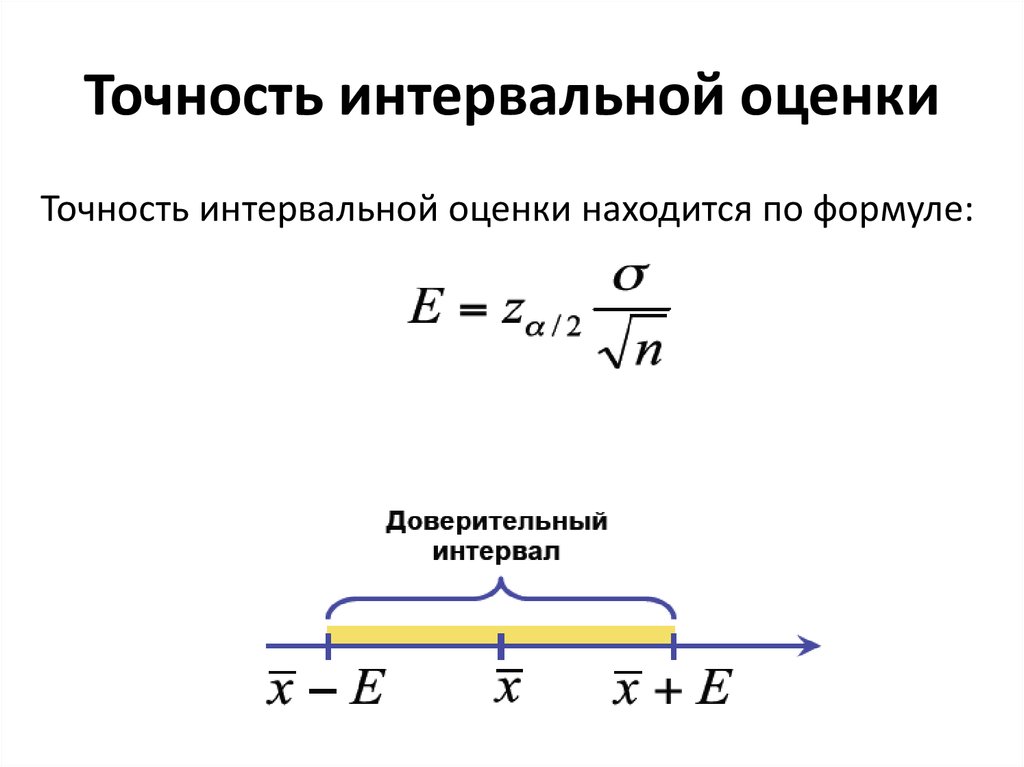
Если оценку среднего требуется связать с определённой вероятностью, то интересующий параметр генеральной совокупности нужно оценивать не одним числом, а интервалом. Доверительным интервалом называют интервал, в котором с определённой вероятностью

P находится значение оцениваемого показателя генеральной совокупности. Доверительный интервал, в котором с вероятностью P = 1 — α находится случайная величина , рассчитывается следующим образом:

где — критическое значение стандартного нормального распределения для уровня значимости α = 1 — P, которое можно найти в приложении к практически любой книге по статистике.

На практике среднее значение генеральной совокупности и дисперсия не известны, поэтому дисперсия генеральной совокупности заменяется дисперсией выборки , а среднее генеральной совокупности — средним значением выборки . Таким образом, доверительный интервал в большинстве случаев рассчитывается так:

Формулу доверительного интервала можно использовать для оценки среднего генеральной совокупности, если

известно стандартное отклонение генеральной совокупности;
или стандартное отклонение генеральной совокупности не известно, но объём выборки — больше 30.

Среднее значение выборки является несмещённой оценкой среднего генеральной совокупности . В свою очередь, дисперсия выборки не является несмещённой оценкой дисперсии генеральной совокупности . Для получения несмещённой оценки дисперсии генеральной совокупности в формуле дисперсии выборки объём выборки n следует заменить на n-1.

Пример 1. Собрана информация из 100 случайно выбранных кафе в некотором городе о том, что среднее число работников в них составляет 10,5 со стандартным отклонением 4,6. Определить доверительный интервал 95% числа работников кафе.

Решение:

где — критическое значение стандартного нормального распределения для уровня значимости α = 0,05.

Таким образом, доверительный интервал 95% среднего числа работников кафе составил от 9,6 до 11,4.

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Пример 2. Для случайной выборки из генеральной совокупности из 64 наблюдений вычислены следующие суммарные величины:

сумма значений в наблюдениях ,

сумма квадратов отклонения значений от среднего .

Вычислить доверительный интервал 95 % для математического ожидания.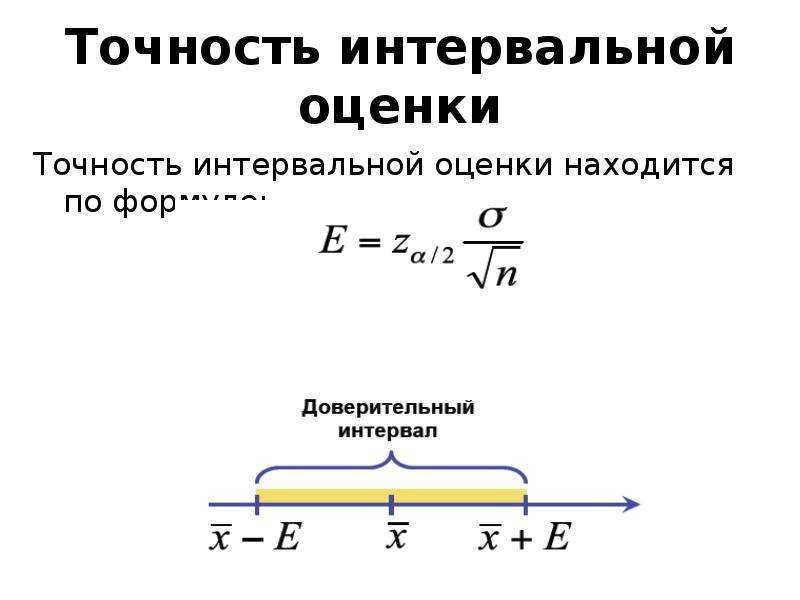

Решение:

вычислим стандартное отклонение:

вычислим среднее значение:

Подставляем значения в выражение для доверительного интервала:

где — критическое значение стандартного нормального распределения для уровня значимости α = 0,05.

Получаем:

Таким образом, доверительный интервал 95% для математического ожидания данной выборки составил от 7,484 до 11,266.

Пример 3. Для случайной выборки из генеральной совокупности из 100 наблюдений вычислено среднее значение 15,2 и стандартное отклонение 3,2. Вычислить доверительный интервал 95 % для математического ожидания, затем доверительный интервал 99 %. Если мощность выборки и её вариация остаются неизменными, а увеличивается доверительный коэффициент, то доверительный интервал сузится или расширится?

Решение:

Подставляем данные значения в выражение для доверительного интервала:

где — критическое значение стандартного нормального распределения для уровня значимости α = 0,05.

Получаем:

Таким образом, доверительный интервал 95% для среднего данной выборки составил от 14,57 до 15,82.

Вновь подставляем данные значения в выражение для доверительного интервала:

где — критическое значение стандартного нормального распределения для уровня значимости α = 0,01.

Получаем:

Таким образом, доверительный интервал 99% для среднего данной выборки составил от 14,37 до 16,02.

Как видим, при увеличении доверительного коэффициента увеличивается также критическое значение стандартного нормального распределения, а, следовательно, начальная и конечная точки интервала расположены дальше от среднего, и, таким образом, доверительный интервал для математического ожидания увеличивается.

Удельный вес некоторого признака выборки можно интерпретировать как точечную оценку удельного веса p этого же признака в генеральной совокупности. Если же эту величину нужно связать с вероятностью, то следует рассчитать доверительный интервал удельного веса p признака в генеральной совокупности с вероятностью P = 1 — α:

Пример 4. В некотором городе два кандидата A и B претендуют на пост мэра. Случайным образом были опрошены 200 жителей города, из которых 46% ответили, что будут голосовать за кандидата

A, 26% — за кандидата B и 28% не знают, за кого будут голосовать. Определить доверительный интервал 95% для удельного веса жителей города, поддерживающих кандидата A.

Решение:

Таким образом, доверительный интервал 95% удельного веса горожан, поддерживающих кандидата A, составил от 0,391 до 0,529.

Пример 5. Чтобы проверить отношение покупателей к новому квасу, проведён опрос случайной выборки в 50 человек. Результаты обобщены в следующей таблице (0 — не понравился, 1 — понравился, 2 — нет ответа):

1	0	0	1	2
0	1	0	2	0
1	0	0	0	0
0	1	0	0	1
0	2	0	0	1
0	1	1	0	0
2	2	0	0	1
1	0	2	0	0
0	0	1	0	1
1	0	0	0	1

Найти доверительный интервал 95 % удельного веса покупателей, которым новый квас не понравился.

Решение.

Найдём удельный вес указанных покупателей в выборке: 29/50 = 0,58. Таким образом, , . Мощность выборки известна (n = 50). Критическое значение стандартного нормального распределения для уровня значимости

α = 0,05 равно 1,96. Подставляем имеющиеся показатели в выражение интервала для удельного веса:

Таким образом, доверительный интервал 95% удельного веса покупателей, которым новый квас не понравился, составил от 0,45 до 0,71.

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Пройти тест по теме Теория вероятностей и математическая статистика

К началу страницы

Назад

Листать

Вперёд>>>

Всё по теме «Математическая статистика»

Характеристики выборки и генеральной совокупности: среднее значение, дисперсия, погрешности выборки

Проверка статистических гипотез

Парная линейная регрессия.

Задачи регрессионного анализа

Множественная корреляция, её коэффициент. Частная корреляция

Множественная линейная регрессия. Улучшение модели регрессии

Дисперсионный анализ: соединение теории и практики

Доверительный интервал — формула и примеры определения вероятности » Kupuk.net

В математической статистике при анализе и систематизации различных данных для подведения практических выводов часто используют метод доверительных интервалов. С его помощью выполняют определённую выборку среднего или доли с учётом стандартной ошибки. Благодаря этому достоверность вероятности увеличивается, так как оценка расширяется в обе стороны от исследуемой величины.

Общая схема построения

По сути, метод основан на модели классической математической статистики, подразумевающей бесконечно возможные выборки в генеральной совокупности. Пусть имеется главная выборка эпсилон с функцией распределения известной до некого параметра тау (Fe (x, τ)). Из этой генеральной совокупности получена выборка объёмом эн, включающая диапазон от x1 до xn. Этот параметр можно считать одномерным и принадлежащим диапазону от τ до R. Математически такое положение описывают как τ є T c R.

Если предположить, что для некоторого интервала йод, лежащего от нуля до единицы, существуют статистики S-(X|n|, J) и S+(X|n|, J), при этом им соответствует неравенство P{ S-(X|n|, J) < τ < S+(X|n|, J)}, то рассматриваемый интервал принято называть доверительным касательно параметра τ. Причём уровень доверия или величина доверительного интервала зависит от значения статистики S и выборки. Вероятность попадания истинного параметра тэта в интервал от S-1 до S+1 находится из выражения: P = 1 — J.

Общий метод построения доверительных функций может быть использован при изучении статистики Y (S (X|n|, t), где: t — оцениваемый параметр, S (X|n| — точечная оценка. При этом известны следующие свойства:

функция распределения Fy (x), где игрек принимает случайное известное значение, не подвержена влиянию тау.
график функция статистики непрерывный и монотонный по тау.

После того как такая функция найдена, необходимо задать уровень значимости j. Как правило, его величина берётся небольшой, чтобы доверительная вероятность P была как можно больше. Тогда построенный интервал обязательно будет включать истинное значение параметра. А также при построении графика учитывают, чтобы вероятность попадания вне интервала по обе стороны равнялись друг другу: (inf, S-(X|n|, j)), (S+(X|n|, j + inf).

Затем необходимо найти квантили статистики игрек порядка y (j/2) и y (1 — j/2). Исходя из определения квантили можно утверждать, что вероятность попадания статистики игрек в рассматриваемой интервале будет определяться разницей функции распределения соответствующих точек и равняться P = 1 — j. Описать это можно следующим выражением: P (y (j/2) < Y (S (X|n|), t) < y (1-j/2) = F (y (1-j/2) — F (y (j/2) = 1 — j.

Так как статистика по игреку строится таким образом, чтобы она была монотонной и непрерывной по тэте, то можно найти обратную функцию y-1. Для определённости принимают, что игрек по тэта монотонно возрастает. Тогда вероятность расположения будет эквивалентна неравенству: y-1(j/2) < t < y-1(-j/2). Отсюда можно получить доверительный интервал для тэта: P (S -(X | n |, j) < t < S +(X | n |, j)) = 1 — j. Где: S -(X | n |, j) = Y-1(y (a /2)), S +(X | n |, j) = Y-1(y (1- a /2).

Таким образом, определить доверительную вероятность попадания тэта в интервал от S- до S+ можно от значения обратной функции в точках, равняющихся квантили статистики игрек порядка j/2 и 1 — j/2. При этом когда рассматриваемая функция монотонно убывает, знаки в неравенстве меняются на противоположные.

Пользуясь общим подходом расчёта доверительных интервалов, можно посчитать вероятность для нормальной генеральной совокупности, опираясь на ряд утверждений. Пусть известна выборка X|n,| взятая из совокупности E ~ N (j, ς2), то есть имеющей нормальный закон распределения с математическим ожиданием j и дисперсией сигма в квадрате. Для такого состояния справедливо следующее:

Функция вида (X-j) * √ n / ς соответствует стандартному нормальному закону распределения. Икс — это математическое ожидание неизвестного, из которого вычитается истинное значение для получения величины, имеющей нулевую вероятность. После этого величина центруется путём деления на среднее квадратичное отклонение: ς / √ n. Так как закон исходной генеральной совокупности нормальный, то и среднее арифметическое случайных величин будет являться нормально распределённой случайной величиной.

Если статистика S2 не смещена от точки дисперсии, то функция (X — a) * √n / S будет подчиняться распределению Стьюдента с n — 1 степенью свободы.

Статистика n — 1, умноженная на несмещённый центр дисперсии и отнесённая к истинному значению, подчиняется распределению хи-квадрат.

В числителе формулы находится сумма квадратов нормальных распределений, которые приводятся к нормальным стандартам.

Когда рассматривается смещённая оценка дисперсии, то статистика nS2 / ς2 соответствует распределению хи-квадрат с эн степенями свободы.

Точный интервал

Существует ряд правил, позволяющих построить точные интервалы для математического ожидания и дисперсии нормально распределённой случайной величины. Есть два случая — при одном дисперсия может быть известной, а при другом нет. Следует обратить внимание, что точная доверительная вероятность строится с помощью общей схемы. Используют следующие правила для предоставления точных прогнозов:

При построении доверительного интервала с погрешностью 1 — E он определяется границами: P{ X — (ς / √n) * Z (1-E/2) и X + (ς / √n) * Z (1-E/2)}. Где: 1-E/2 — квантиль стандартного нормального распределения, которое симметричное.

Когда дисперсия неизвестна, в качестве оценки берётся несмещённая оценка S2.

Формула распределения в этом случае будет иметь вид: P{ X — (s / √n) * t (1-E/2) и X + (s / √n) * t (1-E/2)}. Значение t (1-E/2)} соответствует квантилю распределения Стьюдента с n — 1 свободной степенью.

Если ожидание неизвестно, то справедлива следующая формула: P {(n — 1) * s2 / U (1- e /2) < ς2 < (n — 1) * s 2 / U (e /2) } = 1 — E. Доверительный интервал при известном j можно рассматривать как оценку математического ожидания: S2 = 1/n Σ (xi-j)2, то есть равенство истинной дисперсии. Она с вероятностью 1 — E находится в интервале от n * S2, делённая на квантиль распределения V (1-E/2) c уровнями свободы энной степени.

Измерение ожидания равняется истинной дисперсии, которая лежит в области от n * S2, делённая на хи-квадрат с 1- E/2 степенью свободы, до n * S2 с квантилей E /2. Если же ожидание неизвестно, в качестве дисперсии берётся несмещённая оценка S2. При этом изменяется число степеней свободы хи-квадрат. Она становится n — 1. Всё остальное остаётся без изменений.

Асимптотическое приближение

Однако не всегда можно рассчитать точный доверительный интервал. В этом случае строится приближённая вероятность — асимптотическая. Пусть для некоторого j Є (0,1) существует набор статистик S-(X|n|, j) и S-(X|n|, j), причём такие, что lim P{ S-(X|n|, j) < t < S-(X|n|, j), } = 1- j, при эн, стремящемуся к бесконечности, тогда область, ограниченная интервалом (S-(X|n|, j), S-(X|n|, j)), является асимптотической приближённой. Её построение основывается на свойствах нормальных оценок. То есть для начала необходимо для параметра выбрать оценку, обладающую свойством асимптотической нормальностью.

Оценку тэты можно выполнить по формуле: t = t (x|n|), при этом √n (t-t) * (d / n → ∞) ~ N (0, ς2), а ς2 — коэффициент асимптотического рассеивания. Если делается несколько анализов одного параметра, то считается лучшим тот, у которого коэффициент будет меньше.

Применив теорему непрерывности к статистике, можно показать, что функция вида √n (t — t), отнесённая к среднестатистическому отклонению ς (t) по распределению, при n → ∞ сходится к случайной величине, имеющей стандартное распределение. То есть для последовательности случайных векторов справедливо выражение: kn = (k (n1), …, (k (nm). И если заданная функция непрерывна H: Rm →R, то H (k (n) * d / n → ∞, то имеет место сходимость: (√n (t — t) / ς (t)) / *(d / n → ∞) k ~ N (0, 1).

Отсюда будет справедливым следующее соотношение: P{-z (1-j/2) < z (1-j/2} → 1 — j = 1 / √2p ∫ (e -y2/2) dy. Таким образом, вероятность попадания будет находиться в области P є (z (1 — j/2), — z (1 — j/2)) и будет стремиться к минусу йод. Здесь z является квантилем 1- j/2. Точность интервальной оценки характеризуется шириной доверительной области. Чем больше объём выборки, тем уже будет рассматриваемый интервал (меньше ширина) и тем точнее будет интервальная оценка.

Примеры решения задач

Пусть имеется энное количество испытаний, из которых m являются успешными. Выборочный результат описывается функцией X|n| = (a1, …, an) и включает в себя нули и единицы. Статистика правдоподобия имеет вид: L (X|n|, p) = pm * q n-m, p є t = (0, 1). Для оценки правдоподобия необходимо составить функцию и найти оценки параметра P. Статистика имеет вид: ln L = mLnp + (n-m) ln (1-p). Максимальный результат выпадения единицы описывают выражением: d ln L / dP = (m / p) — (n — m) / (1 — p) = (m — mp -np + mp) / p (1 — p) = 0.

Отсюда получают оценку: p = m / n. Теперь нужно убедиться, что p максимизирует функцию правдоподобия. То есть d2LnL / dp2 = — m / p2 — (n — m) / (1 — p)2 < 0. Несложно доказать, что результат оценки будет асимптотически нормальным: √n ((m/n) — p) = (m -np) / √n = (Σ (ς i-p) / √n) (d / n → ∞) ~ N (0, pq). Воспользовавшись утверждением, довольно легко показать следующую сходимость: √n ((m/n) — p) / (√m/n (1 — m/n))) (d / n → ∞) ~ N (0, 1). Анализируя полученное, можно утверждать, что формула расчёта доверительного интервала будет иметь вид: ((m / n) — z (1-j/2) √m / n (1- m / n) / √n, (m / n + — z (1-j/2) √m / n (1- m / n) / √n)).

Более практичной является следующая задача. Пусть имеется предприятие, на котором решили узнать среднюю зарплату. В каких единицах она будет измеряться — значения не имеет. Для этого произвольно отобрали тридцать сотрудников, по анализу дохода которых выявили, что в месяц зарплата их составляет 30 тысяч с учётом среднего квадратичного отклонения в пять тысяч. Нужно рассчитать среднюю заработную плату за середину месяца с погрешностью менее 0,01 процента.

Сперва следует кратко записать условие. Известно, что n = 30, Xs = 30000, S = 5000, а P = 0,99. Для решения задачи необходимо использовать таблицу, соответствующую теореме Стьюдента. В ней собраны справочные величины для t — критерии с разной вероятностью. Согласно ей, для заданных значений n и P критерий равняется 2,756.

Подставив исходные данные в формулу и выполнив вычисления, можно утверждать, что необходимая доверительная область ограничивается интервалом от 27484 до 32516: 30000 — 2,756 * (5000 / √30) < Xs < 3000 + 2,756 * (5000 / √30). То есть средняя зарплата сотрудников за половину месяца лежит в интервале (13742, 16258). Задача решена.

Использование онлайн-калькулятора

На практике довольно часто вычислить доверительную область не так уж и просто. Всё дело в том, что высокая вероятность часто находится в выборке большого объёма, поэтому приходится выполнять громоздкие вычисления. Учитывая, что доверительная вероятность определяет точность полученных результатов, другими словами, показывает, с какой вероятностью неправильное решение попадает в найденный интервал, обычно используют процент выборки от 95 до 99,9%.

Для высокой точности получения диапазона как раз и используют сервисы, которые в последнее время начали называться онлайн-калькуляторами. Это специализированные сайты, умеющие в автоматическом режиме решать различные математические задания. Особенность этих сайтов в том, что они предоставляют услуги бесплатно, при этом от их пользователей не требуется никаких знаний.

Всё что им нужно — это ввести в пролагаемую форму данные и нажать кнопку «Рассчитать». Система автоматически вычислит ответ и выведет его на экран. Из наиболее популярных можно отметить следующие сервисы:

Webstarstudio.

MathSemestr.

Allcalc.

Они доступны на русском языке, их интерфейс интуитивно понятен, поэтому воспользоваться их услугами сможет любой заинтересованный, имеющий доступ к интернету. Автоматический расчёт занимает буквально секунды, что составляет существенную разность по сравнению с затратой времени при самостоятельном вычислении.

Функция ДОВЕРИТ

В этой статье описаны синтаксис формулы и использование в Microsoft Excel.

Описание

Возвращает доверительный интервал для среднего генеральной совокупности с нормальным распределением.

Доверительный интервал — это диапазон значений. Выборка «x» находится в центре этого диапазона, а диапазон — x ± ДОВЕРИТ. Например, если x — это пример времени доставки продуктов, заказаных по почте, то x ± ДОВЕРИТ — это диапазон средств численности населения. Для любого средней численности населения (μ0) в этом диапазоне вероятность получения выборки от μ0 больше, чем x, больше, чем альфа; для любого средней численности населения (μ0, не в этом диапазоне), вероятность получения выборки от μ0 больше, чем x, меньше, чем альфа. Другими словами, предположим, что для построения двунамерного теста на уровне значимости альфа гипотезы о том, что это μ0, используются значения x, standard_dev и размер. Тогда мы не отклонить эту гипотезу, если μ0 находится через доверительный интервал, и отклонить эту гипотезу, если μ0 не находится в доверительный интервал. Доверительный интервал не позволяет нам сделать вывод о том, что вероятность 1 — альфа, что следующий пакет займет время доставки через доверительный интервал.

Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.

Чтобы узнать больше о новых функциях, см. в разделах Функция ДОВЕРИТ.НОРМ и Функция ДОВЕРИТ.СТЬЮДЕНТ.

Синтаксис

ДОВЕРИТ(альфа;стандартное_откл;размер)

Аргументы функции ДОВЕРИТ описаны ниже.

Альфа — обязательный аргумент. Уровень значимости, используемый для вычисления доверительного уровня. Доверительный уровень равен 100*(1 — альфа) процентам или, иными словами, значение аргумента «альфа», равное 0,05, означает 95-процентный доверительный уровень.
Стандартное_откл — обязательный аргумент. Стандартное отклонение генеральной совокупности для диапазона данных, предполагается известным.
Размер — обязательный аргумент. Размер выборки.

Замечания

Если какой-либо из аргументов не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.
Если альфа ≤ 0 или ≥ 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.
Если Standard_dev ≤ 0, возвращается #NUM! значение ошибки #ЗНАЧ!.
Если значение аргумента «размер» не является целым числом, оно усекается.
Если размер < 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.
Если предположить, что альфа = 0,05, то нужно вычислить область под стандартной нормальной кривой, которая равна (1 — альфа), или 95 процентам. Это значение равно ± 1,96. Следовательно, доверительный интервал определяется по формуле:

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,05	Уровень значимости
2,5	Стандартное отклонение для генеральной совокупности
50	Размер выборки
Формула	Описание	Результат
=ДОВЕРИТ(A2;A3;A4)	Доверительный интервал для математического ожидания генеральной совокупности. Иными словами, доверительный интервал средней продолжительности поездки на работу для генеральной совокупности составляет 30 ± 0,692952 минуты или от 29,3 до 30,7 минут.	0,692951912

Формула доверительного интервала

| Калькулятор (пример с шаблоном Excel)

Формула доверительного интервала (оглавление)

Формула
Примеры
Калькулятор

В статистике термин «доверительный интервал» относится к диапазону значений, в пределах которого будет лежать истинное значение совокупности в случае выборки из совокупности. Другими словами, доверительный интервал представляет собой величину неопределенности, ожидаемую при определении оценки выборочной совокупности или среднего значения истинной совокупности. Использование доверительных интервалов делает оценку выборочной совокупности более управляемой.

Формулу для доверительного интервала можно рассчитать, вычитая и добавляя предел погрешности из среднего значения выборки и к нему. Погрешность вычисляется на основе заданного уровня достоверности, стандартного отклонения генеральной совокупности и количества наблюдений в выборке. Математически формула для доверительного интервала представлена как0006

или

Доверительный интервал = X̄ ± Z * ơ / √n

Где,

X̄: Среднее значение выборки
z: Коэффициент достоверности
ơ: Стандартное отклонение населения
n: Размер образца

Пример формулы доверительного интервала (с шаблоном Excel)

Давайте рассмотрим пример, чтобы лучше понять расчет формулы доверительного интервала.

Вы можете скачать этот шаблон Excel с формулой доверительного интервала здесь — Шаблон Excel с формулой доверительного интервала

Формула доверительного интервала — пример № 1

Возьмем в качестве примера 100 респондентов, которые были опрошены на предмет их отзывов об обслуживании клиентов. Опрос проводился по шкале от 1 до 5, где 5 был лучшим, и было обнаружено, что средний отзыв респондентов составил 3,3 при стандартном отклонении населения 0,5. Определить доверительный интервал для –

Уровень достоверности 90%
Уровень достоверности 95%
Уровень достоверности 98%
Уровень достоверности 99%

Решение:

Достоверный интервал рассчитывается с использованием формулы, приведенной ниже

Доверительный интервал = ( x̄ — z * ơ / √n) до ( x̄ + z * ơ / √n) √n)

Общий расчет для верхнего предела и нижнего предела, как ниже

для 90%

Достоверный интервал = (3,30 — 1,645 * 0,5 / √100) до (3,30 + 1,645 * 0,5 / √100 )
Доверительный интервал = от 3,22 до 3,38

Таким образом, доверительный интервал при уровне достоверности 90% составляет от 3,22 до 3,38.

Для 95%

Доверительный интервал = (3,30 – 1,96 * 0,5 / √100) до (3,30 + 1,96 * 0,5 / √100)
Доверительный интервал = от 3,20 до 3,40

Таким образом, доверительный интервал при доверительном уровне 95 % составляет от 3,20 до 3,40.

Для 98%

Доверительный интервал = (3,30 – 2,33 * 0,5 / √100) до (3,30 + 2,33 * 0,5 / √100)
Доверительный интервал = от 3,18 до 3,42

Таким образом, доверительный интервал при доверительном уровне 98 % составляет от 3,18 до 3,42.

Для 99%

Доверительный интервал = (3,30 – 2,58 * 0,5 / √100) до (3,30 + 2,58 * 0,5 / √100)
Доверительный интервал = от 3,17 до 3,43

Таким образом, доверительный интервал при доверительном уровне 99 % составляет от 3,17 до 3,43.

На приведенном выше рисунке видно, что доверительный интервал выборки расширяется с увеличением уровня достоверности.

Объяснение

Формулу доверительного интервала можно рассчитать, выполнив следующие шаги:

Шаг 1: Во-первых, определите выборочное среднее на основе выборочных наблюдений из набора данных совокупности. Обозначается .

Шаг 2: Затем определите размер выборки, который представляет собой количество наблюдений в выборке. Обозначается н.

Шаг 3: Затем определите стандартное отклонение генеральной совокупности на основе выборочных наблюдений, среднего значения и размера выборки. Обозначается ơ.

Шаг 4: Затем определите коэффициент достоверности или z-оценку на основе желаемого уровня достоверности.

Шаг 5: Затем вычислите предел погрешности, используя размер выборки (шаг 2), стандартное отклонение генеральной совокупности (шаг 3) и коэффициент достоверности (шаг 4).

Погрешность = z * ơ / √n

Шаг 6: Наконец, формулу для доверительного интервала можно рассчитать, вычитая и добавляя погрешность (шаг 5) из выборочного среднего значения и к нему. (шаг 1), как показано ниже:

Доверительный интервал = ( x̄ – z * ơ / √n) до ( x̄ + z * ơ / √n)

или

доверительный интервал = X̄ ± z * ơ / √n

.

Вы можете использовать следующий калькулятор формулы доверительного интервала

x̄
z
ơ
n
Confidence Interval

Доверительный интервал =	(x̄ — z * ơ / √n) до (x̄ + z * ơ / √n)
	(0 — 0 * 0 / √0) до (0 + 0 * 0 / √0) =	0

Релевантность и использование формулы доверительного интервала

Важно понимать концепцию доверительного интервала, поскольку он показывает точность метода выборки. По сути, он указывает, насколько устойчива оценка выборочной совокупности, так что будет минимальное отклонение от исходной оценки в случае повторения выборки снова и снова. Существует некоторая путаница в отношении того, что такое доверительный интервал и уровень достоверности. Обратите внимание, что 9Уровень достоверности 5% не означает, что существует 95%-ная вероятность того, что параметр популяции попадет в заданный интервал. Уровень достоверности 95% означает, что процедура оценки или метод выборки надежны на 95%.

8.

3 Доверительный интервал для доли населения – вводная бизнес-статистика
В год выборов мы видим в газетах статьи, в которых доверительные интервалы указываются в пропорциях или процентах. Например, опрос конкретного кандидата, баллотирующегося на пост президента, может показать, что кандидат имеет 40% голосов в пределах трех процентных пунктов (если выборка достаточно велика). Часто предвыборные опросы рассчитываются с 95% достоверности, поэтому социологи будут на 95% уверены, что истинная доля избирателей, поддерживающих кандидата, будет между 0,37 и 0,43.
Инвесторов на фондовом рынке интересует истинное соотношение акций, которые растут и падают каждую неделю. Предприятия, продающие персональные компьютеры, интересуются долей домохозяйств в США, владеющих персональными компьютерами. Доверительные интервалы можно рассчитать для истинной доли акций, которые растут или падают каждую неделю, и для истинной доли домохозяйств в США, владеющих персональными компьютерами.
Процедура определения доверительного интервала для доли населения аналогична процедуре для среднего значения населения, но формулы немного отличаются, хотя концептуально идентичны. Хотя формулы разные, они основаны на одной и той же математической основе, данной нам Центральной предельной теоремой. Из-за этого мы увидим тот же базовый формат, использующий те же три части информации: выборочное значение рассматриваемого параметра, стандартное отклонение соответствующего выборочного распределения и количество стандартных отклонений, которое нам нужно, чтобы быть уверенными в нашей достоверности. оценить, что мы желаем.
Откуда вы знаете, что имеете дело с проблемой пропорций? Во-первых, основное распределение имеет двоичную случайную величину и, следовательно, является биномиальным распределением . (Нет упоминания о среднем или среднем значении.) Если X — биномиальная случайная величина, то X ~ B ( n , p ), где n — количество испытаний, а p — вероятность успеха. Чтобы составить пробную пропорцию, возьмите 9, читай «P hat».)
p′ = оценочная доля успехов или выборочная доля успехов ( p′ — это точечная оценка для p , истинная доля населения, и, таким образом, q — вероятность неудачи в любом одном испытании.)
x = число успехов в выборке
n = размер выборки
Формула доверительного интервала для доля населения следует тому же формату, что и для оценки среднего значения населения. Вспоминая выборочное распределение доли из главы 7, стандартное отклонение оказалось равным:
σp’=p(1−p)nσp’=p(1−p)n
Таким образом, доверительный интервал для доли населения принимает вид:
p=p′±[Z(a2)p′( 1−p′)n]p=p′±[Z(a2)p′(1−p′)n]
Z(a2)Z(a2) устанавливается в соответствии с нашей желаемой степенью уверенности, а p′( 1−p′)np′(1−p′)n — стандартное отклонение выборочного распределения.
Пропорции выборки p′ и q′ являются оценками неизвестных долей совокупности p и q . Расчетные пропорции p’ и q’ используются, потому что p и q неизвестны.
Помните, что чем дальше p от 0,5, тем биномиальное распределение становится менее симметричным. Поскольку мы оцениваем бином с симметричным нормальным распределением, чем дальше от симметричного становится бином, тем меньше у нас уверенности в оценке.
Этот вывод можно продемонстрировать с помощью следующего анализа. Пропорции основаны на биномиальном распределении вероятностей. Возможные исходы бинарны: либо «успех», либо «неудача». Это приводит к пропорции, означающей процент результатов, которые являются «успехами». Было показано, что биномиальное распределение можно было бы полностью понять, если бы мы знали только вероятность успеха в любом одном испытании, называемом р. Среднее значение и стандартное отклонение бинома оказались равными:
м = нп м = нп
σ=npqσ=npq
Также было показано, что биномиальное распределение можно оценить с помощью нормального распределения, если ОБА np И nq больше 5. Из приведенного выше обсуждения было обнаружено, что стандартизирующая формула для биномиального распределения имеет вид :
Z=p’-p(pqn)Z=p’-p(pqn)
, что является не чем иным, как переформулировкой общей стандартизирующей формулы с соответствующими заменами μ и σ из бинома. Мы можем использовать стандартное нормальное распределение, причина Z в уравнении, потому что нормальное распределение является предельным распределением бинома. Это еще один пример центральной предельной теоремы. Мы уже видели, что выборочное распределение средних распределено нормально. Вспомните расширенное обсуждение в главе 7, касающееся выборочного распределения долей и выводов центральной предельной теоремы.
Теперь мы можем манипулировать этой формулой точно так же, как мы делали это для нахождения доверительных интервалов для среднего, но для нахождения доверительного интервала для биномиального параметра генеральной совокупности, p.
p’-Zαp’q’n ≤ p ≤ p’+Zαp’q’np’-Zαp’q’n ≤ p ≤ p’+Zαp’q’n
Где p’ = x/n, точечная оценка p, взятая из выборки. Обратите внимание, что p’ заменил p в формуле. Это потому, что мы не знаем p, на самом деле это как раз то, что мы пытаемся оценить.
К сожалению, не существует поправочного коэффициента для случаев, когда размер выборки мал, поэтому np’ и nq’ всегда должны быть больше 5, чтобы получить интервальную оценку для p.
Пример 8,6
Проблема
Предположим, что фирма, занимающаяся исследованием рынка, нанята для оценки процента взрослых, живущих в большом городе, у которых есть сотовые телефоны. Пятьсот случайно выбранных взрослых жителей этого города опрашиваются, чтобы определить, есть ли у них сотовые телефоны. Из из 500 опрошенных 421 человек ответил утвердительно, у них есть сотовые телефоны. Используя уровень достоверности 95%, вычислите оценку доверительного интервала для истинной доли взрослых жителей этого города, имеющих мобильные телефоны.
Решение 1
Пошаговое решение.
Пусть X = количество людей в выборке, у которых есть сотовые телефоны. X является биномиальным: случайная величина двоичная, у людей либо есть мобильный телефон, либо его нет.
Чтобы вычислить доверительный интервал, мы должны найти p′ , q′ .
n = 500
x = количество успехов в выборке = 421
p′=xn=421500=0,842p′=xn=421500=0,842
p′ = 0,842 – доля выборки; это точечная оценка доли населения.
Q ′ = 1 — P ′ = 1 — 0,842 = 0,158
, поскольку запрошенный уровень достоверности составляет CL = 0,95, затем α = 1 — Cl = 1 – 0.95 = 0.95 = 0.95 = 0.95 = 0.95 = 0.95 = 0.95 = 0,95 = 0,95 = 0,95 = 0,95 = 0,95 = 0,95 = 0,95 = 0,95 = 0,95 = 0,95 α = 1 — . α2)(α2) = 0,025.
Тогда zα2=z0,025=1,96zα2=z0,025=1,96
Это можно найти с помощью таблицы стандартных нормальных вероятностей в Приложении A Статистические таблицы. Это также можно найти в таблице студентов t в столбце 0,025 и бесконечных степенях свободы, потому что при бесконечных степенях свободы студенты t -распределение становится стандартным нормальным распределением, Z.
Доверительный интервал для истинной биномиальной доли населения равен
q’n≤p≤p’+Zαp’q’n
Подставляя значения выше, мы находим доверительный интервал: 0,810≤p≤0,874 Подставляя значения выше, мы находим доверительный интервал: 0,810≤p ≤0,874
Интерпретация
Мы оцениваем с достоверностью 95%, что от 81% до 87,4% всех взрослых жителей этого города имеют сотовые телефоны.
Объяснение 95% уровня достоверности
Девяносто пять процентов построенных таким образом доверительных интервалов будут содержать истинное значение доли всех взрослых жителей этого города, имеющих мобильные телефоны.
Пример 8,7
Проблема
Школа дрессировки собак Данди имеет большую, чем в среднем, долю клиентов, которые участвуют в профессиональных соревнованиях. Строится доверительный интервал для доли в популяции собак, которые участвуют в профессиональных соревнованиях из 150 различных школ дрессировки. Нижний предел определен равным 0,08, а верхний предел определен равным 0,16. Определите уровень достоверности, используемый для построения интервала доли собак в популяции, участвующих в профессиональных соревнованиях.
Решение 1
Начнем с формулы доверительного интервала для пропорции, поскольку случайная величина является двоичной; либо клиент участвует в профессиональных соревнованиях с собаками, либо нет.
p=p′±[Z(a2)p′(1−p′)n]p=p′±[Z(a2)p′(1−p′)n]
Далее находим долю выборки :
p′=0,08+0,162=0,12p′=0,08+0,162=0,12
Таким образом, ±, составляющий доверительный интервал, равен 0,04; 0,12 + 0,04 = 0,16 и 0,12 — 0,04 = 0,08 — границы доверительного интервала. Наконец, мы решаем на З .
[Z⋅0,12(1−0,12)150]=0,04[Z⋅0,12(1−0,12)150]=0,04, , следовательно, Z = 1,51
стандартная нормальная таблица.
p(Z=1,51)=0,4345p(Z=1,51)=0,4345, p(Z)⋅2=0,8690p(Z)⋅2=0,8690 или 86,90%86,90%.
Пример 8,8
Проблема
Финансовый директор компании хочет оценить процент дебиторской задолженности, просроченной более чем на 30 дней. Он просматривает 500 счетов и обнаруживает, что 300 из них просрочены более чем на 30 дней. Вычислить 90% доверительный интервал для истинного процента дебиторской задолженности, просроченной более чем на 30 дней, и интерпретировать доверительный интервал.
Решение 1
Решение пошаговое:
x = 300 и n = 500
p’=xn=300500=0,600p’=xn=300500=0,600
q′=1-p′=1-0,600=0,400q′=1-p′=1-0,600=0,400
Поскольку уровень достоверности = 0,90, то α = 1 – уровень достоверности = (1 – 0,90) = 0,10(α2)(α2) = 0,05
Zα2Zα2 = Z _0,05 = 1,645
Это значение Z можно найти с помощью стандартной таблицы нормальных вероятностей. Также можно использовать t-таблицу Стьюдента, введя таблицу в столбец 0,05 и прочитав строку для бесконечных степеней свободы. Т-распределение — это нормальное распределение при бесконечных степенях свободы. Это удобный прием, который следует помнить при поиске Z-значений для часто используемых уровней достоверности. Мы используем эту формулу для доверительного интервала для пропорции:
p’-Zαp’q’n ≤ p ≤ p’+Zαp’q’np’-Zαp’q’n ≤ p ≤ p’+Zαp’q’n
Подставляя значения сверху, находим доверительный интервал для истинной биномиальной доли населения составляет 0,564 ≤ p ≤ 0,636
Интерпретация
По нашим оценкам с достоверностью 90%, истинный процент всей дебиторской задолженности, просроченной на 30 дней, составляет от 56,4% до 63,6%.
Альтернативная формулировка: по нашим оценкам с достоверностью 90%, от 56,4% до 63,6% ВСЕХ счетов просрочены на 30 дней.
Объяснение уровня достоверности 90%
Девяносто процентов всех доверительных интервалов, построенных таким образом, содержат истинное значение процента дебиторской задолженности, просроченной на 30 дней, для генеральной совокупности.
Понимание доверительных интервалов | Простые примеры и формулы
Опубликован в 7 августа 2020 г. по Ребекка Беванс. Отредактировано 9 июля 2022 г.
Когда вы делаете оценку в статистике, будь то сводная статистика или тестовая статистика, вокруг этой оценки всегда присутствует неопределенность, поскольку число основано на выборке изучаемой вами совокупности.
Доверительный интервал — это диапазон значений, который, как вы ожидаете, попадет в вашу оценку в определенный процент времени, если вы снова запустите эксперимент или повторите выборку населения таким же образом.
доверительный уровень — это процент времени, когда вы ожидаете воспроизвести оценку между верхней и нижней границами доверительного интервала, и задается значением альфа.
Содержание
Что такое доверительный интервал?
Расчет доверительного интервала: что вам нужно знать
Доверительный интервал для среднего значения данных с нормальным распределением
Доверительный интервал для пропорций
Доверительный интервал для данных с ненормальным распределением
Сообщение о доверительных интервалах
Предостережение при использовании доверительных интервалов
Часто задаваемые вопросы о доверительных интервалах
Что такое доверительный интервал?
Доверительный интервал — это среднее значение вашей оценки плюс минус вариация этой оценки. Это диапазон значений, между которыми, как вы ожидаете, будет находиться ваша оценка, если вы повторите тест с определенным уровнем достоверности.
Уверенность , в статистике, это еще один способ описать вероятность. Например, если вы строите доверительный интервал с 9Уровень достоверности 5% означает, что в 95 случаях из 100 оценка будет находиться между верхним и нижним значениями, указанными в доверительном интервале.
Ваш желаемый уровень достоверности обычно равен единице минус значение альфа ( a ), которое вы использовали в своем статистическом тесте:
Уровень достоверности = 1 − a
Таким образом, если вы используете значение альфа p < 0,05 для статистической значимости, то ваш уровень достоверности будет 1 − 0,05 = 0,95, или 95%.
Когда вы используете доверительные интервалы?
Вы можете рассчитать доверительные интервалы для многих видов статистических оценок, в том числе:
Пропорции
Население означает
Различия между средними значениями или пропорциями населения
Оценки различий между группами
Все это точечные оценки, и они не дают никакой информации о вариации числа. Доверительные интервалы полезны для сообщения об отклонении от точечной оценки.
Пример: отклонение от оценки. Вы опросили 100 британцев и 100 американцев об их привычках смотреть телевизор и обнаружили, что обе группы смотрят телевизор в среднем 35 часов в неделю.
Тем не менее, у опрошенных британцев наблюдались большие различия в количестве часов просмотра, в то время как у всех американцев наблюдалось одинаковое количество часов.
Несмотря на то, что обе группы имеют одинаковую точечную оценку (среднее количество часов просмотра), британская оценка будет иметь более широкий доверительный интервал, чем американская оценка, поскольку данные больше разнятся.
Расчет доверительного интервала: что нужно знать
Большинство статистических программ включают доверительный интервал оценки при выполнении статистического теста.
Если вы хотите самостоятельно рассчитать доверительный интервал, вам необходимо знать:
Точечная оценка, которую вы строите доверительный интервал для
Критические значения тестовой статистики
Стандартное отклонение выборки
Размер выборки
Зная каждый из этих компонентов, вы можете рассчитать доверительный интервал для своей оценки, подставив их в формулу доверительного интервала, соответствующую вашим данным.
Точечная оценка
Точечной оценкой вашего доверительного интервала будет любая статистическая оценка, которую вы делаете (например, среднее значение генеральной совокупности, разница между средними значениями генеральной совокупности, пропорции, различия между группами).
Пример: балльная оценка. В примере с просмотром телепередач балльная оценка представляет собой среднее количество часов просмотра: 35,9.0062 Нахождение критического значения
Критические значения сообщают вам, на сколько стандартных отклонений от среднего вам нужно уйти, чтобы достичь желаемого уровня достоверности для вашего доверительного интервала.
Есть три шага, чтобы найти критическое значение.
Выберите значение альфа ( a ).
Значение альфа является порогом вероятности для статистической значимости. Наиболее распространенное значение альфа p = 0,05, но иногда используются 0,1, 0,01 и даже 0,001. Лучше всего просмотреть статьи, опубликованные в вашей области, чтобы решить, какое значение альфа использовать.
Решите, нужен ли вам односторонний или двусторонний интервал.
Скорее всего, вы будете использовать двусторонний интервал, если вы не выполняете односторонний t-критерий.
Для двустороннего интервала разделите альфу на два, чтобы получить значение альфы для верхнего и нижнего хвостов.
Найдите критическое значение, соответствующее альфа-значению.
Если ваши данные подчиняются нормальному распределению или у вас большой размер выборки ( n > 30), который примерно нормально распределен, вы можете использовать распределение z , чтобы найти ваши критические значения.
Для статистики z некоторые из наиболее распространенных значений показаны в этой таблице:
Уровень достоверности 90% 95% 99%
альфа для одностороннего КИ 0,1 0,05 0,01
альфа для двусторонней ДИ 0,05 0,025 0,005
z -статистика 1,64 1,96 2,57
Если вы используете небольшой набор данных (n ≤ 30) с приблизительно нормальным распределением, вместо этого используйте распределение t .
Распределение t имеет ту же форму, что и распределение z , но с поправкой на небольшие размеры выборки. Для распределения t вам необходимо знать свои степени свободы (размер выборки минус 1).
Ознакомьтесь с набором таблиц t , чтобы найти статистику t . Автор включил уровень достоверности и p -значения как для односторонних, так и для двусторонних тестов, чтобы помочь вам найти нужное t -значение.
Для нормальных распределений, таких как t -распределение и z -распределение, критическое значение одинаково по обе стороны от среднего.
Пример: критическое значение. В опросе о просмотре телепередач имеется более 30 наблюдений, и данные имеют примерно нормальное распределение (колоколообразная кривая), поэтому мы можем использовать z — раздача для нашей тестовой статистики.
Для двустороннего 95% доверительного интервала значение альфа равно 0,025, а соответствующее критическое значение равно 1,96.
Это означает, что для расчета верхней и нижней границ доверительного интервала мы можем взять среднее значение ±1,96 стандартного отклонения от среднего.
Определение стандартного отклонения
Большинство статистических программ имеют встроенную функцию для расчета стандартного отклонения, но чтобы найти его вручную, вы можете сначала найти свою выборочную дисперсию, а затем извлечь квадратный корень, чтобы получить стандартное отклонение.
Найти выборочную дисперсию
Выборочная дисперсия определяется как сумма квадратов отличий от среднего, также известная как среднеквадратическая ошибка (MSE):
Чтобы найти MSE, вычтите среднее значение выборки из каждого значения в наборе данных, возведите полученное число в квадрат и разделите это число на n − 1 (размер выборки минус 1).
Затем сложите все эти числа, чтобы получить общую выборочную дисперсию ( s ²). Для больших выборок проще всего это сделать в Excel.
Найдите стандартное отклонение.
Стандартное отклонение вашей оценки ( s ) равно квадратному корню выборочной дисперсии/ошибки выборки ( s ² ):

Пример: стандартное отклонение. В опросе телезрителей дисперсия оценки Великобритании составляет 100, тогда как дисперсия оценки США равна 25. Извлечение квадратного корня из дисперсии дает нам стандартное отклонение выборки ( с ) из:
10 для оценки ГБ.
5 для оценки США.
Размер образца
Размер выборки — это количество наблюдений в вашем наборе данных.
Пример: Размер выборки В нашем опросе американцев и британцев размер выборки составляет 100 человек для каждой группы.
Получение отзывов о языке, структуре и форматировании
Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание:
Академический стиль
Расплывчатые предложения
Грамматика
Согласованность стиля
См. пример
Доверительный интервал для среднего значения нормально распределенных данных
Нормально распределенные данные образуют форму колокола при нанесении на график со средним значением выборки в середине, а остальные данные распределены достаточно равномерно по обе стороны от среднего.
Доверительный интервал для данных, соответствующих стандартному нормальному распределению:
Где:
ДИ = доверительный интервал
X̄ = среднее значение населения
Z* = критическое значение z -распределения
σ = стандартное отклонение совокупности
√n = квадратный корень из численности населения
Доверительный интервал для t-распределения соответствует той же формуле, но заменяет Z * на t *.
В реальной жизни вы никогда не узнаете истинные значения численности населения (если только вы не можете провести полную перепись). Вместо этого мы заменяем значения генеральной совокупности значениями из наших выборочных данных, поэтому формула принимает следующий вид:
Где:
ˆx = выборочное среднее
с = стандартное отклонение выборки
Пример: расчет доверительного интервала. В исследовании привычек американцев и британцев смотреть телевизор мы можем использовать среднее значение выборки, стандартное отклонение выборки и размер выборки вместо среднего значения генеральной совокупности, стандартного отклонения генеральной совокупности и размера генеральной совокупности.
Чтобы рассчитать доверительный интервал 95%, мы можем просто подставить значения в формулу.
Для США:

Итак, для США нижняя и верхняя границы 95% доверительного интервала составляют 34,02 и 35,98.
Для ГБ:

Итак, для ГБ нижняя и верхняя границы 95% доверительного интервала составляют 33,04 и 36,96.
Доверительный интервал пропорций
Доверительный интервал для пропорции следует той же схеме, что и доверительный интервал для средних, но вместо стандартного отклонения вы используете пропорцию выборки, умноженную на единицу минус пропорцию:
Где:
ˆp = доля в вашей выборке (например, доля респондентов, которые вообще не смотрели телевизор)
Z*= критическое значение z -распределения
n = объем выборки
Доверительный интервал для ненормально распределенных данных
Чтобы вычислить доверительный интервал вокруг среднего значения данных, которые не имеют нормального распределения, у вас есть два варианта:
Вы можете найти распределение, соответствующее форме ваших данных, и использовать это распределение для расчета доверительного интервала.
Вы можете выполнить преобразование данных, чтобы привести их к нормальному распределению, а затем найти доверительный интервал для преобразованных данных.
Выполнение преобразований данных очень распространено в статистике, например, когда данные следуют логарифмической кривой, но мы хотим использовать их вместе с линейными данными. Вам просто нужно не забыть выполнить обратное преобразование ваших данных, когда вы вычисляете верхнюю и нижнюю границы доверительного интервала.
Представление доверительных интервалов
Доверительные интервалы иногда приводятся в статьях, хотя исследователи чаще сообщают о стандартном отклонении своих оценок.
Если вас попросят указать доверительный интервал, вы должны указать верхнюю и нижнюю границы доверительного интервала.
Пример: отчет о доверительном интервале «Мы обнаружили, что и в США, и в Великобритании в среднем 35 часов просмотра телевидения в неделю, хотя в оценке Великобритании разброс больше (9 часов). 5% ДИ = 33,04, 36,96), чем для США (95% ДИ = 34,02, 35,98)».
Одним из мест, где доверительные интервалы часто используются, являются графики. При отображении различий между группами или построении линейной регрессии исследователи часто включают доверительный интервал, чтобы дать визуальное представление о вариации вокруг оценки.
Пример: доверительный интервал на графике. Вы можете построить точечные оценки среднего количества часов просмотра телевизора в США и Великобритании с 95% доверительный интервал вокруг среднего значения.
Предостережение при использовании доверительных интервалов
Доверительные интервалы иногда интерпретируются как говорящие о том, что «истинное значение» вашей оценки находится в пределах доверительного интервала.
Это не так. Доверительный интервал не может сказать вам, насколько вероятно, что вы нашли истинное значение вашей статистической оценки, потому что она основана на выборке, а не на всей совокупности.
Доверительный интервал только говорит вам, какой диапазон значений вы можете ожидать, если вы повторно сделаете выборку или проведете эксперимент снова точно таким же образом.
Чем точнее ваш план отбора проб или реалистичнее ваш эксперимент, тем выше вероятность того, что ваш доверительный интервал включает истинное значение вашей оценки. Но эта точность определяется вашими методами исследования, а не статистикой, которую вы делаете после того, как собрали данные!
Часто задаваемые вопросы о доверительных интервалах
Чем отличается доверительный интервал от доверительного уровня?
Уровень достоверности — это процент случаев, когда вы ожидаете приблизиться к той же оценке, если вы снова запустите свой эксперимент или повторите выборку населения таким же образом.
Доверительный интервал состоит из верхней и нижней границ оценки, которую вы ожидаете получить при заданном уровне достоверности.
Например, если вы оцениваете 95-процентный доверительный интервал вокруг средней доли младенцев женского пола, рождающихся каждый год на основе случайной выборки младенцев, вы можете найти верхнюю границу 0,56 и нижнюю границу 0,48. Это верхняя и нижняя границы доверительного интервала. Уровень достоверности 95%.
Как рассчитать доверительный интервал?
Для расчета доверительного интервала необходимо знать:
Точечную оценку, которую вы строите доверительный интервал для
Критические значения тестовой статистики
Стандартное отклонение выборки
Размер выборки
Затем вы можете подставить эти компоненты в формулу доверительного интервала, соответствующую вашим данным. Формула зависит от типа оценки (например, среднее значение или пропорция) и от распределения ваших данных.
Что такое z-показатели и t-показатели?
z -оценка и t -оценка (также известные как z -значение и t -значение) показывают, на сколько стандартных отклонений от среднего значения распределения вы находитесь, предполагая, что ваши данные соответствуют распределению z или т -распределение.
Эти оценки используются в статистических тестах, чтобы показать, насколько далека от среднего значения прогнозируемого распределения ваша статистическая оценка. Если ваш тест дает z -оценку 2,5, это означает, что ваша оценка составляет 2,5 стандартных отклонения от предсказанного среднего значения.
Прогнозируемое среднее значение и распределение вашей оценки генерируются нулевой гипотезой статистического теста, который вы используете. Чем больше стандартных отклонений от предсказанного среднего в вашей оценке, тем меньше вероятность того, что оценка могла быть получена при нулевой гипотезе.
Что такое критическое значение?
Критическое значение — это значение статистики теста, которое определяет верхнюю и нижнюю границы доверительного интервала или порог статистической значимости в статистическом тесте. Он описывает, как далеко от среднего значения распределения вам нужно пройти, чтобы охватить определенную часть общей вариации данных (т. е. 90%, 95%, 99%).
Если вы строите 95% доверительный интервал и используете порог статистической значимости p = 0,05, то ваше критическое значение будет одинаковым в обоих случаях.
Что значит, если мой доверительный интервал включает ноль?
Если ваш доверительный интервал для различий между группами включает ноль, это означает, что если вы проведете эксперимент еще раз, у вас есть хорошие шансы не обнаружить различий между группами.
Если ваш доверительный интервал для корреляции или регрессии включает ноль, это означает, что если вы снова запустите свой эксперимент, есть большая вероятность, что в ваших данных не будет найдено никакой корреляции.
В обоих этих случаях вы также обнаружите высокое значение p при выполнении статистического теста, что означает, что ваши результаты могли быть получены при нулевой гипотезе об отсутствии связи между переменными или отсутствии различий между группами.
Источники в этой статье
Мы настоятельно рекомендуем учащимся использовать источники в своей работе. Вы можете процитировать нашу статью (стиль APA) или глубоко погрузиться в статьи ниже.
Эта статья Scribbr
Беванс, Р. (9 июля 2022 г.). Понимание доверительных интервалов | Простые примеры и формулы. Скриббр. Проверено 11 октября 2022 г., из https://www.scribbr.com/statistics/confidence-interval/
Процитировать эту статью
Полезна ли эта статья?
Вы уже проголосовали. Спасибо 🙂 Ваш голос сохранен 🙂 Обработка вашего голоса.
No related posts.