Формулы преобразования координат: Глава 7. Преобразование координат

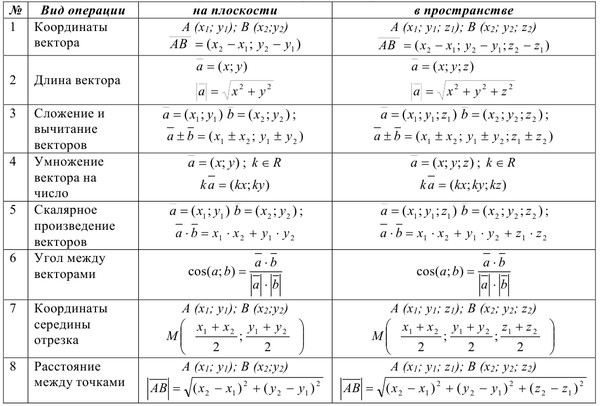
1.4. Преобразование координат и упрощение

уравнений кривых второго порядка

■ Преобразование координат. Задача преобразования координат на плоскости состоит в том, чтобы, зная координаты любой точки плоскости М(х, у), найти координаты этой же точки в другой системе координат. Формулы, связывающие координаты точки М в «старой» и «новой» системах координат, называются формулами преобразования координат. При удачном выборе новой системы координат можно добиться, чтобы уравнение линии приняло наиболее простой канонический вид (что позволит исследовать свойства линии и облегчит ее построение).

1-й случай. Пусть требуется перейти от системы координат хОу к новой системе координат , начало которой находится в точке (где а и b – координаты точки в старой системе координат), а новые оси и параллельны старым осям Ох и Оу (и одинаково с ними направлены).

Тогда между координатами произвольной точки в этих двух системах координат имеется следующая зависимость:

(1)

Эти формулы позволяют выразить первоначальные координаты точки x, y через ее новые координаты и координаты нового начала в старой системе координат.

Если же требуются формулы обратного перехода, выражающие новые координаты через старые, то из (1) легко видеть, что

(2)

Пример 1. Даны координаты точки в системе хОу. Перенесем начало координат в точку , сохраняя направления осей. Найти новые координаты точки М.

Решение. Имеем , ; тогда по формулам (2) , .

Ответ: .

Пример 2. С помощью параллельного переноса осей координат (без изменения их направления) упростить уравнение линии .

Решение.

Выделим в левой части уравнения полные квадраты:

или ,

откуда .

Воспользуемся формулами (2):

.

Отсюда видно, что если взять , , т.е. перенести начало координат в точку , то в новой системе координат уравнение примет вид , откуда видно, что исходное уравнение определяет гиперболу, действительная полуось которой , мнимая полуось , а центр находится в точке .

2-й случай. Пусть требуется перейти от системы координат хОу к новой системе координат (с тем же самым началом О), которая получается при повороте осей координат на угол (рис. 6). Тогда имеют место соотношения

. (3)

Формулы обратного перехода имеют вид

. (4)

Пример 3. Дана точка . Найти ее координаты в системе координат , повернутой на угол 30° против часовой стрелки относительно исходной системы (без изменения начала координат).

Решение. Имеем , , . Тогда по формулам (4)

,

.

Ответ: .

Замечание. Можно объединить соотношения (1) и (3), получая формулы преобразования координат при параллельном переносе и повороте системы координат:

.

Тогда формулы обратного перехода будут иметь вид

.

■ Упрощение уравнений кривых второго порядка. Общее уравнение второй степени имеет вид

(5)

(где коэффициенты

А, В, С не равны нулю одновременно).

Рассмотренные выше окружность, эллипс, гипербола и парабола имеют уравнения, которые являются частными случаями общего уравнения (5) (поэтому их называют кривыми второго порядка). Однако этому уравнению могут соответствовать и другие геометрические образы, иллюстрируемые следующими примерами.

Пример 4. Уравнение определяет пару пересекающихся прямых, т.к. его можно записать в виде , откуда получаем и .

Пример 5. Уравнению отвечает пара параллельных прямых и .

Пример 6. Уравнению , которое можно переписать в виде , отвечает одна прямая (или, как еще говорят, пара слившихся прямых).

Пример 7. Уравнению удовлетворяют только значения , , т.е. оно определяет одну точку («вырожденный эллипс»).

Пример 8. Уравнению не удовлетворяют никакие значения х и у, так что оно не определяет никакого геометрического образа («мнимый эллипс»).

Можно доказать, что все возможные случаи, которые могут встретиться при исследовании общего уравнения второй степени (5), исчерпываются либо кривыми второго порядка; либо ситуациями в Примерах 4 – 8.

Составим из коэффициентов уравнения два определителя:

и .

В зависимости от значений этих определителей уравнение (5) определяет следующий геометрический образ (см. таблицу):

	Эллипс (или нет геометрического образа)	Точка
	Гипербола	Пара пересекающихся прямых
	Парабола	Пара параллельных прямых или одна прямая

Задача упрощения уравнения (5) состоит в том, чтобы при переходе к новой системе координат добиться устранения члена с произведением координат. Практически такой переход можно осуществить следующим образом.

1-й случай. Если , то геометрический образ имеет центр симметрии . Координаты центра находятся из системы уравнений

. (6)

После переноса начала координат в новый центр уравнение (5) в системе координат примет вид

. (7)

Далее повернем систему координат на угол , определяемый формулой (если , то угол поворота 45°). При этом координаты , заменяются на новые координаты , по формулам поворота:

(8)

Теперь последнее уравнение примет канонический вид

,

из которого легко распознать вид геометрического образа и расположение на плоскости.

2-й случай. Если , то отвечающий уравнению (5) геометрический образ не имеет определенного центра симметрии. При этом система уравнений (6) либо совсем не имеет решений, либо имеет бесконечно много решений. Тогда рекомендуется действовать иначе, чем в случае, когда .

Если повернуть оси координат на угол , определяемый как в предыдущем случае, старые координаты х, у выразятся через новые координаты , по формулам (3), произведение координат исчезнет, а уравнение (5) примет вид:

, или

.

Остается выделить полный квадрат, вид геометрического образа и его расположение на плоскости.

Замечание. В подробных курсах аналитической геометрии приводится ряд других приемов процедуры приведения общего уравнения кривой второго порядка к каноническому виду.

Пример 9. Выяснить, какую линию определяет уравнение и привести его к каноническому виду.

Решение. 1) Составим определители и (см. стр. ___):

, .

Так как , , то данная линия является эллипсом (см. таблицу на стр.

___).

2) Составим систему уравнений для нахождения координат центра эллипса :

,

откуда , .

3) Перенесем начало координат в центр (без поворота осей). Тогда в системе координат уравнение кривой примет вид (7):

.

4) Теперь повернем систему координат на угол (против часовой стрелки), так как здесь . При этом новые координаты , связаны с координатами , соотношениями (8):

,

.

Если преобразовать по этим формулам последнее уравнение, то, согласно общей теории, член с произведением координат исчезнет и мы получим или – каноническое уравнение эллипса с полуосями , , фокусы которог о расположены на оси (см. рис. 7).

§4 Преобразование координат на плоскости. Применение преобразования координат к упрощению уравнений кривых второго порядка

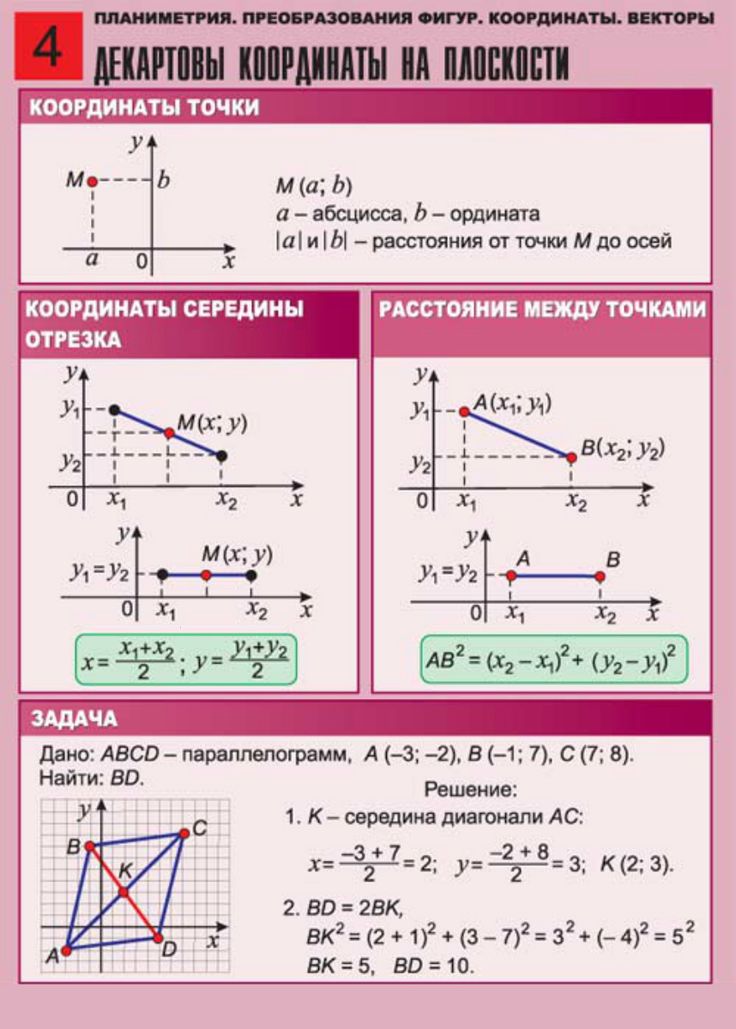
1749 §4 Преобразование координат на плоскости. М в системе осей с началом О (рис. 24). Пусть (a,b) — координаты точки O в системе осей х, у. Очевидно ОО+ОМ=ОМ. Поскольку при параллельном переносе осей координатный базис не изменяется, то при прибавлении векторов можно складывать их соответствующие координаты. А потому х=х+а; у=у+b (1) Мы получили формулы для перехода от «старых» координат точки М к «новым» ее координатам. Из (1) следуют формулы х=х-а; у=у-b (2), которые выражают «новые» координаты через «старые». Пример 1.199 Установить, как изменяется уравнение х2-4х+2у2+8у-10=0 при параллельном переносе осей координат, если начало координат перенесено в точку О'(2;-2). Решение. Согласно формул (1) имеем х=х+2, у= у-2. Подставляя эти выражения в заданное уравнение, получим (х+2)2-4(х+2)+2(в-2)2+8(в-2)-10=0 х2+2у2=22, Таким образом, исходному уравнению отвечает эллипс с полуосями , с центром симметрии в точке (2;-2) и осями симметрии, параллельными осям координат. Тогда получим или Таким образом, исходное уравнение определяет гиперболу с действительной осью 2, воображаемой и центром симметрии в точке (3;-1). Оси симметрии гиперболы параллельны осям координат. Ранее отмечалось, что уравнение у2=2рх (р>0) определяет параболу, в которой ось симметрии совпадает с осью абсцисс и вершина находится в начале координат. Уравнению х2=2ру или, что одно и то же, уравнению у=ах2 отвечает, очевидно, парабола, у которой ось симметрии совпадает с осью ординат, а вершина, как и ранее, находится в начале координат. Покажем, что к виду у=ах2 можно привести с помощью параллельного переноса осей уравнение y=ax2+bx+c. Пусть (a1;b1) — координаты нового начала в старой системе координат. Тогда х=х`+а1, у=у`+b1 и уравнение y=ax2+bx+c приобретет вид y+b1=a(x+a1)2+b(x+a1)+c или y=ax2+(2aa1+b)x+aa12+ba1+c-b1 Числа a1 и b1 были пока что произвольные. Выберем их так, чтобы выполнялось равенство 2aa1+b=0 aa12+ba1+c-b1=0 Решая эту систему, получим . Таким образом, если перенести начало координат (при сохранении направления осей координат) в точку О, тогда исходное уравнение y=ax2+bx+c будет иметь вид y=ax2. Но это означает, что исходное уравнение есть уравнением параболы с вершиной в точке О и осью симметрии, параллельной оси ординат. Рассмотрим теперь преобразование, что включает в себя поворот координатных осей при сохранении положения начала координат. Пусть х, у — старые оси координат, х, у — новые оси (рис. 25) и  — угол поворота, то есть угол между «новой» и одноименной «старой» осью (поскольку мы рассматриваем задачу на плоскости, то можно фиксировать направление отсчета углов; угол высчитывается от положительного направления старой оси против часовой стрелки). В рассматриваемом случае координатный базис, очевидно, изменяется: вместо базиса — имеем новый базис , при чем угол между равен , угол между равен (или ), угол между равен , угол между и равен . А потому в ортонормированном базисе Пусть М — произвольная точка плоскости, (х;у) ее старые, а (х; у) новые координаты. Тогда , то есть имеем: (3), формулы, которые выражают старые координаты через новые. Решая систему уравнений (3) относительно х и у, получим (4), формулы (3) и (4) и есть формулами преобразования поворота координатных осей. Пример 1.201. Преобразовать уравнение ху=с (с0) (график обратно пропорциональной зависимости), выбрав за новые оси биссектрисы координатных осей. Решение. Угол поворота  в этом случае равен . А потому Таким образом, кривая ху=с (с0) есть равносторонняя гипербола, действительная ось которой направлена по биссектрисе 3-го и 1-го координатных углов, центр симметрии находится в начале координат, и полуоси равняются . Мы рассматривали отдельно преобразование параллельного переноса и преобразование поворота координатных осей. Возможно, конечно, последовательно провести эти два преобразования, осуществить и поворот, и перенос координатных осей. Укажем, не делая конкретных вычислений, как можно с помощью рассмотренных методов привести общее уравнение кривой 2-го порядка Ax2+Bxy+Cy2+Dx+Ey+F=0 (5) к каноническим уравнениям эллипса, параболы и гиперболы, или к случаям их «вырождения». Отметим, во-первых, что при преобразованиях уравнения (5) с помощью формул (1) и (3) не может измениться порядок уравнения. Он естественно не сможет повыситься (то есть стать больше, чем 2), поскольку в формулах (1) и (3) х и у выражается линейно через х и у, но не может и понизиться. Действительно, если мы из уравнений (5) с помощью формул (1) и (3) получили бы уравнение вида А1х+В1у+С1=0, то, возвращаясь с помощью равенств (2) и (4) к исходным переменным х и у, мы не получили бы уравнения 2-й степени — исходное уравнение (5). Таким образом, порядок (степень) уравнения при наших преобразованиях сохраняется. С помощью поворота осей всегда можно избавиться от члена с произведением координат. Действительно, подставляя в (5) вместо х и у их выражения согласно формул (3), получим новое уравнение A1x2+B1xy+C1y2+D1x+E1y+F=0, коэффициенты которого и, в частности , коэффициент В1, содержит тригонометрические функции угла . Приравнивая коэффициент В1 к нулю, получим тригонометрическое уравнение. Решая его, найдем значение угла поворота , при котором в уравнение уже не будет входить произведение координат, и которое будет иметь вид A1x2+C1y2+D1x+E1y+F=0 Если коэффициенты А1 и С1 отличны от нуля, тогда всегда можно, как это показано на примерах 1 и 2, с помощью переноса осей координат (формулы 1) избавиться от членов с первыми степенями переменных координат и привести уравнение (6) к виду A1x2+C1y2+F1=0 (7) Но отсюда видно, что мы имеем или эллипс (если А1 и С1 имеют один знак, а F1 противоположный), или воображаемое место точек (если А1, С1 и F1 имеют один и тот же знак; в таком случае говорят, что имеет место случай «вырождения» эллипса в «воображаемое место точек»), или одну точку (если А1 и С1 одного знака и F1 =0 — «вырождение» эллипса в точку), или гиперболу (если А1 и С1 различных знаков і), или две прямые, которые пересекаются (если А1 и C1 разных знаков и F1=0 — «вырождение» гиперболы в 2 прямые, которые пересекаются). Если ж в уравнении (6) один из коэффициентов А1 и С1, например, С1, превращается в нуль, тогда, как показано в начале параграфа, можно такое уравнение с помощью переноса осей привести к виду y=ax2 при или к виду ax2+d=0 при Е1=0. В первом случае получаем параболу, во втором «вырождение» параболы (2 параллельные прямые или одна прямая, или воображаемое место точек). Отсюда следует, что, как уже указывалось выше, любая кривая 2-го порядка есть или эллипс, или гипербола, или парабола, или представляет собой их «вырождение».

Преобразование координат

Введение

Преобразования координат достаточно неинтуитивны в 2D, и положительно болезненный в 3-D. Эта страница решает их в следующем порядке: (i) векторы в 2-D, (ii) тензоры в 2-D, (iii) векторы в трехмерном пространстве, (iv) тензоры в трехмерном пространстве и, наконец, (v) тензорные преобразования 4-го ранга.

Основным аспектом преобразования координат является оценка матрицы преобразования, особенно в 3D. Это затрагивается здесь и подробно обсуждается на Следующая страница.

Очень важно понимать, что все преобразования координат на этой странице являются поворотами. системы координат, в то время как сам объект остается неподвижным. «Объект» может быть вектором, таким как сила или скорость, или тензор, такой как напряжение или напряжение в компоненте. Повороты объектов обсуждаются в следующих разделах.

---

Двухмерные координатные преобразования векторов

Академический картофель представляет собой отличный пример того, как преобразование координат применяются к векторам, подчеркивая при этом, что это система координат, которая вращается, а не вектор… или картошка.

Картофель слева имеет вектор. Но без система координат, нет никакого способа описать вектор. Таким образом, к картофелю была добавлена ​​система координат, как показано справа, что позволяет вектор теперь описывается как \({\bf v} = 2{\bf i} + 9{\bf j}\).

Итак, теперь мы вводим повернутую систему координат, показанную синим цветом ниже, используя \(х’\) и \(у’\). Новая система повернута против часовой стрелки на угол \(\theta\), от исходной системы координат. Обратите внимание, что вектор сам совсем не меняется. Это все тот же вектор как прежде. Но он описывается другими числовыми значениями в новой системе координат. В этом случае вектор более точно параллелен к новой оси \(x’\), чем ось \(y’\), поэтому компонент \({\bf i’}\) будет больше компонента \({\bf j’}\). Преобразование приведен под рисунком.

Уравнения двумерного векторного преобразования:

\[ v’_x = \;\;\; v_x \cos\тета + v_y \sin\тета \] \[ v’_y = -v_x \sin\theta + v_y\cos\theta \]
Это можно увидеть, отметив, что

• часть \(v_x\), лежащая вдоль оси \(x’\), равна \(v_x \cos \theta\)
• часть \(v_y\), лежащая вдоль оси \(x’\), равна \(v_y \sin \theta\)
• часть \(v_x\), лежащая вдоль оси \(y’\), равна \(-v_x \sin \theta\) 9\круг = 4,25 \]
  Компонент \(v’_x\) действительно больше, чем компонент \(v’_y\), как и ожидалось.
  

  Матрица трансформации

  Удобнее писать (и работать) уравнения преобразования с помощью матриц.

  \[ \left\{ \matrix {v’_x \\ v’_y} \right\} = \left[ \matrix {\;\;\;\cos \theta & \sin \theta\\ -\sin\theta & \cos\theta}\right] \left\{ \matrix {v_x \\ v_y} \right\} \]
  Члены \(\cos \theta\) находятся на диагонали матрицы, а \(\sin \theta\) термины недиагональны. Единственный потенциал попался вспоминает что Термин \(\sin\theta\) имеет знак минус. Это всегда нижний левый член.

  Приведенное выше уравнение записано в матричной записи как

  \[ {\bf v’} = {\bf Q} \cdot {\bf v} \]
  , где \({\bf Q}\) — обычная буква, выбранная для матрицы преобразования.
  

  Преобразование против матриц вращения

  Если эта тема уже недостаточно сложна, многие книги и веб-сайты дополняют ее. путаница из-за неясности того, что неподвижно, а что вращается. На этой странице и во-вторых, это система координат, которая вращается, в то время как объект остается неподвижным. Итак, термин 9Матрица преобразования 0014 используется здесь, чтобы подчеркнуть это.

  Однако позже мы рассмотрим ситуации, когда объект вращается, когда система координат остается неизменной. В этом сценарии термин матрица вращения будет использоваться, чтобы подчеркнуть, что объект вращается.

  Много путаницы возникает из-за удивительного факта, что каждый матрица (преобразование и вращение) — это просто транспонирование другого! Так что они очень похожи. В двумерных задачах единственная практическая разница заключается в том, стоит ли знак минус перед \(\sin\theta\) находится в термине \(q_{12}\) или в термине \(q_{21}\).
  

  Свойства матрицы преобразования

  Матрицы преобразования обладают несколькими особыми свойствами, которые, хотя и легко увидеть в этом обсуждение двумерных векторов, в равной степени применимы к трехмерным приложения тоже. Этот список полезен для проверки точности преобразования. Матрица, если возникнут вопросы. Хотя матрица все еще может быть неправильно, даже если он проходит все эти проверки, это определенно неправильно, если он не проходит хотя бы одну!

  Определитель \({\bf Q}\) равен единице. Транспонирование \({\bf Q}\) является его обратным. Скалярное произведение любой строки или столбца на себя равно единице. Пример: \( (\cos \theta \; {\bf i} + \sin \theta \; {\bf j}) \cdot (\cos \theta \; {\bf i} + \sin \theta \; {\bf j}) = 1 \) Скалярное произведение любой строки на любую другую строку равно нулю. Пример: \( (\cos \theta \; {\bf i} + \sin \theta \; {\bf j}) \cdot (-\sin \theta \; {\bf i} + \cos \theta \; {\bf j}) = 0 \) Скалярное произведение любого столбца на любой другой столбец равно нулю. Пример: \( (\cos \theta \; {\bf i} — \sin \theta \; {\bf j}) \cdot (\ sin \ theta \; {\ bf i} + \ cos \ theta \; {\ bf j}) = 0 \)

  \[ {\ бф Q} = \left[ \matrix {\;\;\;\cos \theta & \sin \theta\\ -\sin\theta & \cos\theta}\right] \]

  Существует общий метод формулирования матриц преобразования на основе косинусов углов между осями двух систем координат, т. е. направляющие косинусы. (Это также относится к трехмерным преобразованиям.) Матрица преобразования может быть записана как 9\circ + \theta) = -\sin \theta\).
  

  Состав матрицы трансформации

  Другой способ построения матрицы преобразования (и мой любимый) заключается в следующем.

  \[ {\ бф Q} = \ влево [ \matrix { \left( \matrix{\text{x-comp} \\ \text{of} {\bf i’}} \right) & \left( \matrix{\text{y-comp} \\ \text{of} {\bf i’}} \right) \\ \left( \matrix{\text{x-comp} \\ \text{of} {\bf j’}} \right) & \left( \matrix{\text{y-comp} \\ \text{of} {\bf j’}} \right)} \Правильно] \]
  «x-comp of \({\bf i’}\)» означает x-компоненту единичного вектора \({\bf i’}\). Обратите особое внимание на то, какие термины имеют штрихи, а какие нет. Не путайте это с «x’-компонентой», потому что «x’-comp of \({\bf i’}\)» равно просто 1. Еще один способ сказать это: «первая компонента \({\bf i’}\) единичный вектор в нештрихованной системе координат \(x-y\).

  Подводя итог,

  • x-comp числа \({\bf i’}\) равно \(\cos \theta\)
  • y-компенсация \({\bf i’}\) равна \(\sin \theta\)
  • x-comp числа \({\bf j’}\) равно \(-\sin \theta\)
  • y-компенсация \({\bf j’}\) равна \(\cos \theta\)

    Тензорная нотация

    Преобразование координат записывается в тензорной записи как

    \[ v’_i = \lambda_{ij} v_j \]
    , где \(\lambda_{ij}\) — матрица преобразования \({\bf Q}\). (я не знаю почему \({\bf Q}\) используется в матричных обозначениях, но \(\lambda_{ij}\), не \(q_{ij}\), используется в тензорной записи.) \(\lambda_{ij}\) определяется как

    \[ \lambda_{ij} = \cos(x’_i,x_j) \]
    Например, если \(i = 1\) и \(j = 2\), то

    \[ \lambda_{12} = \cos(x’_1,x_2) = \cos(x’,y) \]
    \(\lambda_{ij}\) — направляющий косинус угла между ось \(x’_i\) и ось \(x_j\). Опять же, это одинаково применимо и к трехмерным преобразованиям.
    

    Умножение матриц преобразования

    Напомним, что скалярное произведение любых двух разных строк или столбцов матрица преобразования равна нулю, а скалярное произведение любой строки или столбца сам с собой един. Это можно записать в матричных и тензорных обозначениях как 9Т знак равно {\bf I} \qquad \qquad \text{и} \qquad \qquad \lambda_{ik} \lambda_{jk} = \delta_{ij} \]
    Это показывает, что транспонирование матрицы преобразования также это обратное.

    ---

    Двухмерные координатные преобразования тензоров

    В этом разделе будут представлены , что и , как тензорных преобразований. Почему придется подождать, пока позже.

    Координатные преобразования тензоров 2-го ранга включают те же \({\bf Q}\) матрица как векторное преобразование. Преобразование тензора напряжений \(\boldsymbol{\sigma}\), из эталонной системы координат \(xy\) в \(\boldsymbol{\sigma’}\) в новой \(x’-y’\) система делается следующим образом. 9Т \]
    Явная запись матриц дает

    \[ \left[ \matrix{\sigma’_{xx} & \sigma’_{xy} \\ \sigma’_{xy} & \sigma’_{yy} } \right] = \влево[\матрица{\;\;\; \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta } \right] \left[ \matrix{\sigma_{xx} & \sigma_{xy} \\ \sigma_{xy} & \sigma_{yy} } \right] \left[ \matrix{\cos\theta & -\sin\theta\\ \sin\theta&\;\;\; \cos\тета} \право] \]
    (Обратите внимание, что тензор напряжений всегда симметричен, даже после преобразований. ) 92 \ тета) \end{эквнаррай} \]
    Эти три уравнения в точности представляют собой двумерное преобразование тензора напряжений, полученное из суммирование сил на дифференциальном элементе и установление равновесия. Это тоже представлена ​​кругом Мора.

    Преобразования векторов и тензоров

    Обратите внимание, что каждый компонент напряжения в приведенном выше уравнение умножается ровно на две триггерные функции. Наоборот, только одна триггерная функция умножается на любой вектор компонент векторного преобразования. Пример: \( v’_x = v_x \cos \theta + v_y \sin \theta \). Это не совпадение. Каждая триггерная функция исходит из матрицы преобразования \({\bf Q}\). Один матрица используется для преобразования тензоров 1-го ранга (т. Е. Векторов) и две матрицы используются для преобразования тензоров 2-го ранга, таких как напряжение и напряжение. 9\цирк } \справа] \\ \\ знак равно \left[ \matrix{4.143 & \;\;\;\; 0,638 \\ 0,638 & -0,143 } \справа] \end{эквнаррай} \]
    Как и в приведенном выше векторном примере, напряженное состояние совсем не изменился. Отличаются только значения в матрицах, потому что ориентации систем координат различны.

    Тензорная нотация

    Преобразование координат записывается в тензорной записи как

    \[ \sigma’_{mn} = \lambda_{mi} \lambda_{nj} \sigma_{ij} \]
    Как обычно, тензорная нотация обеспечивает понимание процесса. На этот раз понимание исходит из нижних индексов на лямбды. Каждая лямбда эффективно объединяет нижний индекс в \(\boldsymbol{\sigma’}\) с одним на \(\boldsymbol{\sigma}\). Это верно независимо от ранга тензора.

    ---

    Трехмерные координатные преобразования векторов

    Многие из общих уравнений, используемых в двумерных преобразованиях, также применимы в трехмерных. Примеры включают

    \[ {\bf v’} = {\bf Q} \cdot {\bf v} \qquad \qquad \qquad \qquad v’_i = \lambda_{ij} v_j \qquad \qquad \qquad \qquad \lambda_{ij} = \cos(x’_i,x_j) \]
    Только теперь детали другие. Векторы имеют z-компоненты и преобразование матрицы 3х3 вместо 2х2.

    \[ {\bf v} = \left\{ \matrix {v_x \\ v_y \\ v_z} \right\} \qquad \qquad \text{и} \qquad \qquad {\ бф Q} = \ влево [ \matrix { \cos(x’,x) & \cos(x’,y) & \cos(x’,z) \\ \cos(y’,x) & \cos(y’,y) & \cos(y’,z) \\ \cos(z’,x) & \cos(z’,y) & \cos(z’,z) } \right] \]
    \[ {\ бф Q} = \ влево [ \matrix { \left( \matrix{\text{x-comp} \\ \text{of} {\bf i’}} \right) & \left( \matrix{\text{y-comp} \\ \text{of} {\bf i’}} \right) & \left( \matrix{\text{z-comp} \\ \text{of} {\bf i’}} \right) \\ \left( \matrix{\text{x-comp} \\ \text{of} {\bf j’}} \right) & \left( \matrix{\text{y-comp} \\ \text{of} {\bf j’}} \right) & \left( \matrix{\text{z-comp} \\ \text{of} {\bf j’}} \right) \\ \left( \matrix{\text{x-comp} \\ \text{of} {\bf k’}} \right) & \left( \matrix{\text{y-comp} \\ \text{of} {\bf k’}} \right) & \left( \matrix{\text{z-comp} \\ \text{of} {\bf k’}} \right)} \Правильно] \]
    \[ \left\{ \matrix { v’_x \\ v’_y \\ v’_z } \right\} = \оставил[ \matrix { \cos(x’,x) & \cos(x’,y) & \cos(x’,z) \\ \cos(y’,x) & \cos(y’,y) & \cos(y’,z) \\ \cos(z’,x) & \cos(z’,y) & \cos(z’,z) } \right] \left\{ \matrix { v_x \\ v_y \\ v_z } \right\} \]
    

    ---

    Трехмерные координатные преобразования тензоров

    Опять же, правила не меняются, меняются только детали. T \qquad \qquad \qquad \qquad \sigma’_{mn} = \lambda_{mi} \lambda_{nj} \sigma_{ij} \qquad \qquad \qquad \qquad \lambda_{ij} = \cos(x’_i,x_j) \]
    Явная запись матриц дает

    \[ \оставил[ \matrix{\sigma’_{xx} & \sigma’_{xy} & \sigma’_{xz} \\ \sigma’_{xy} & \sigma’_{yy} & \sigma’_{yz} \\ \sigma’_{xz} & \sigma’_{yz} & \sigma’_{zz} } \справа] = \оставил[ \matrix { \cos(x’,x) & \cos(x’,y) & \cos(x’,z) \\ \cos(y’,x) & \cos(y’,y) & \cos(y’,z) \\ \cos(z’,x) & \cos(z’,y) & \cos(z’,z) } \Правильно] \оставил[ \matrix{\sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{xy} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{xz} & \sigma_{yz} & \sigma_{zz} } \Правильно] \оставил[ \matrix { \cos(x’,x) & \cos(y’,x) & \cos(z’,x) \\ \cos(x’,y) & \cos(y’,y) & \cos(z’,y) \\ \cos(x’,z) & \cos(y’,z) & \cos(z’,z) } \Правильно] \]
    Эта веб-страница выполняет преобразования координат трехмерных тензоров. Попробуйте.

    ---

    Координатные преобразования тензоров 4-го ранга

    мы увидим в разделе Закон Гука о том, что тензор жесткости равен 4-й ряд, т. е. 3х3х3х3 (не 4х4). Он пишется как \(C_{ijkl}\), потому что относится любой компонент деформации, \(\epsilon_{kl}\), к любому компонент напряжения, \(\sigma_{ij}\), т. е. \(\sigma_{ij} = C_{ijkl} \epsilon_{kl}\). Закон преобразования координат для тензора жесткости 4-го ранга легко записывается в тензорной записи как 9Т \]

    Пример тензорного преобразования 4-го ранга

    На слайдах ниже показан расчет жесткости типичный однослойный стальной ремень. Угол \(\альфа\) представляет собой вращение тросов относительно продольной оси. Обратите внимание, как уравнения содержат триггерные функции в 4-й степени, это согласуется с использованием четырех \({\bf Q}\) матриц в преобразовании уравнения.

    Ссылка: МакГинти, Р. Д., Райн, Т. Б., и Крон, С. М., «Аналитическое решение для Напряжения, возникающие в +/- наклонных ремнях радиальных шин, Наука и технология шин, ТСТКА, Том. 36, № 4, октябрь декабрь 2008 г., стр. 244-274. 9Т \qquad \qquad \text{и} \qquad \qquad \sigma’_{mn} = \lambda_{mi} \lambda_{nj} \sigma_{ij} \]
    Обратите внимание, что \({\bf Q}\) и \(\lambda_{ij}\) являются одной и той же матрицей преобразования.

    В 2D \({\bf Q}\) и \(\lambda_{ij}\) определяются как

    \[ {\ бф Q} = \left[ \matrix {\;\;\;\cos \theta & \sin \theta\\ -\sin\theta & \cos\theta}\right] \]
    , что является частным случаем более общей трехмерной формы.

    \[ {\ бф Q} = \оставил[ \matrix { \cos(x’,x) & \cos(x’,y) & \cos(x’,z) \\ \cos(y’,x) & \cos(y’,y) & \cos(y’,z) \\ \cos(z’,x) & \cos(z’,y) & \cos(z’,z) } \Правильно] \] 9Т \]
    в матричной записи и

    \[ C’_{ijkl} = \lambda_{im} \lambda_{jn} \lambda_{ko} \lambda_{lp} C_{mnop} \]
    в тензорной записи.

    Типы, правила, формулы, графики, примеры

    Преобразования — это изменения фигур на координатной плоскости путем поворота, отражения или перемещения. В 19 веке Феликс Кляйн предложил новую точку зрения на геометрию, известную как трансформационная геометрия. Большинство доказательств в геометрии основано на преобразованиях объектов. Мы можем изменить любое изображение в координатной плоскости с помощью преобразований. Графика, используемая в видеоиграх, лучше понимается с применением правил преобразования. Давайте научимся идентифицировать преобразования, поймем правила преобразования функций и изучим типы преобразований.

    1.	Что такое трансформации?
    2.	Типы трансформаций
    3.	Правила трансформации
    4.	Формула превращений
    5.	Часто задаваемые вопросы о преобразованиях

    Что такое преобразования в математике?

    Функция f, которая отображается сама на себя, называется преобразованием, т. е. f: X → X. Прообраз X становится изображением X после преобразования. Это преобразование может быть любым или комбинацией операций, таких как перемещение, вращение, отражение и расширение. Перевод — это перемещение функции в определенном направлении, вращение — это вращение функции вокруг точки, отражение — это зеркальное отображение функции, а расширение — это масштабирование функции. Преобразования в математике описывают, как двумерные фигуры перемещаются по координатной плоскости.

    Типы трансформаций

    Существует четыре распространенных типа преобразований: перемещение, вращение, отражение и расширение. Из определения преобразования у нас есть вращение вокруг любой точки, отражение по любой линии и перемещение по любому вектору. Это жесткие преобразования, при которых изображение конгруэнтно своему прообразу. Они также известны как изометрические преобразования. Расширение выполняется практически в любой точке и не является изометрическим. Здесь образ подобен своему прообразу.

    Трансформация	Функция	Результат
    Вращение	Вращает или поворачивает прообраз вокруг оси	Без изменения размера или формы
    Отражение	Переворачивает предварительное изображение и создает зеркальное изображение	Без изменений размера, формы или ориентации
    Перевод	Скользит или перемещает прообраз	Без изменения размера или формы; Изменяет только направление формы
    Расширение	Растягивает или сжимает прообраз	Расширяет или сужает форму

    Правила трансформаций

    Рассмотрим функцию f(x). На координатной сетке мы используем оси x и y для измерения движения. Вот правила преобразования функций, которые можно применить к графикам функций. Преобразования могут быть представлены алгебраически и графически. Преобразования обычно встречаются в алгебраических функциях. Мы можем использовать формулу преобразований в графических функциях, чтобы получить график, просто преобразуя базовую или родительскую функцию, и тем самым перемещать график, а не табулировать значения координат. Преобразования помогают нам визуализировать и изучать уравнения в алгебре.

    Преобразование перемещения

    Перемещение двумерной формы вызывает скольжение этой формы. Чтобы описать положение синей фигуры относительно красной фигуры, давайте посмотрим на взаимное расположение их вершин. Нам нужно найти положения A′, B′ и C′, сравнивая их положение относительно точек A, B и C. Мы находим, что A′, B′ и C′ равны:

    • 8 единиц слева от A, B и C соответственно.
    • На 3 единицы ниже A, B и C соответственно.

    Этот перевод можно алгебраически перевести как 8 единиц влево и 3 единицы вниз. то есть (x, y) → (x-8, y-3)

    Преобразование квадратичных функций

    Мы можем применить правила преобразования к графикам квадратичных функций. Этот прообраз в первой функции показывает функцию f(x) = x ² . Преобразование f(x) = (x+2) ² сдвигает параболу на 2 шага вправо.

    Трансформация отражения

    Тип преобразования, происходящего при отражении каждой точки фигуры от линии, называется отражением. Когда точки отражаются над линией, изображение находится на том же расстоянии от линии, что и прообраз, но с другой стороны линии. Каждая точка (p, q) отражается на точку изображения (q, p). Если точка A находится на расстоянии 3 единиц от линии отражения справа от линии, то точка A’ будет на расстоянии 3 единиц от линии отражения слева от линии. Таким образом, линия отражения действует как серединный перпендикуляр между соответствующими точками изображения и прообраза.

    Вот график квадратичной функции, показывающий преобразование отражения. Функция f(x) = x ³ . Преобразование f(x) равно g(x) = — x ³ , что является отражением f(x) относительно оси x.

    Преобразование вращения

    Преобразование, которое поворачивает каждую точку фигуры на определенное число градусов вокруг этой точки, называется вращением. Фигура вращается против часовой стрелки, если число градусов положительное, и по часовой стрелке, если число градусов отрицательное. Общее правило преобразования вращения вокруг начала координат следующее.

    Повернуть на 90º: (x,y) → (-y, x)

    Повернуть на 180º (x,y) → (-x,-y)

    Повернуть на 270º (x,y) → (y, -x)

    На приведенном ниже графике функции мы наблюдаем преобразование вращения, при котором прообраз поворачивается на 180º в центре вращения в точке (0,1). Давайте проследим, как здесь применяется правило поворота от (x, y) к каждой вершине. Здесь происходит преобразование из (x,y) → (-x, 2-y)

    (-2,4) →(2,-2), (-3,1) → (3,1 ) и (0,1 ) → (0,1)

    Преобразование расширения

    Преобразование, которое заставляет двухмерную форму растягиваться или сжиматься по вертикали или горизонтали с постоянным коэффициентом, называется расширением. Вертикальное растяжение задается уравнением y = a.f(x). Если a > 1, функция растягивается относительно оси y. Если a < 1, функция сжимается по оси y. Горизонтальное растяжение определяется как y = f.(ax). Если a > 1, функция сжимается по оси x. Если a < 1, функция растягивается относительно оси x.

    Рассмотрим родительскую функцию y = x ² +x. После горизонтального сжатия в 5 раз измененная функция становится равной 5x ² +5x в точке (1/5x, y). После горизонтального растяжения с коэффициентом 1/5 преобразованная функция становится равной 1/5 x ² +1/5 x в точке (5x,y). После вертикального сжатия в 5 раз измененная функция становится равной 5x ² +5x в точке (x, 5y). После вертикального растяжения в 1/5 преобразованная функция становится равной 1/5 x ² +1/5 x в точке (x, 1/5y).

    Формула Превращений

    Рассмотрим граф f(x) = x ²

    • Допустим, нам нужно построить график f(x) = x ² -3, сдвинем вершину на 3 единицы вниз.
    • Допустим, нам нужно построить график f(x) = 3x ² + 2, сдвинем вершину на две единицы вверх и растянем по вертикали в три раза.
    • Допустим, нам нужно построить график f(x) = 2(x-1) ² , сдвинем вершину на единицу вправо и растянем по вертикали в 2 9 раз0033
    • Таким образом, мы получаем общую формулу преобразований в виде

    f(x) =a(bx-h) ⁿ +k

    где k — вертикальное смещение,

    h — горизонтальное смещение,

    a — вертикальное растяжение и

    b — горизонтальная растяжка.

    Аналогично, f(x) можно преобразовывать разными способами. В этой таблице показан результирующий график после применения преобразования к f(x).

    Преобразование f(x)	Преобразование графа	Изменить (х, у) на
    -ф(х)	отражает f(x) по оси x	(х, у)
    ф(-х)	отражает f(x) по оси Y	(-х, у)
    ф(х)+а	сдвиг f(x) вверх на единицу	(х, у+а)
    ф(х) — а	сдвиг f(x) вниз на единицу	(х, у-а)
    ф(х+а)	сдвиг f(x) влево на единицу	(х-а, у)
    ф(х-а)	сдвиг f(x) вправо на единицу	(х+а,у)
    а. ф(х)	растягивание/сжатие f(x) по вертикали	(х, ау)
    ф(акс)	растягивание/сжатие f(x) по горизонтали	(х/а,у)

    Важные замечания по преобразованиям

    • Преобразования в геометрии можно комбинировать. Форма может быть отражена или повернута, перемещена или расширена, или может иметь комбинацию этих преобразований.
    • Преобразования выражаются алгебраически в функциях графика.

    ☛ Похожие темы:

    • Графические функции

    Часто задаваемые вопросы о преобразованиях

    Что такое трансформации?

    Преобразования — это изменения, выполняемые с функцией путем перемещения, отражения, поворота и расширения. Исходное изображение, известное как предварительное изображение, изменяется, чтобы получить изображение.

    Каковы 4 типа трансформации?

    Перевод, отражение, вращение и расширение — это 4 типа преобразований. Перевод — это перемещение формы в определенном направлении, отражение — создание зеркального отображения формы, вращение переворачивает форму относительно точки в градусах, а расширение — растяжение или сжатие формы на постоянный коэффициент.

    Почему в математике важны преобразования?

    Математика предназначена для выявления закономерностей и понимания взаимосвязей между понятиями для выработки решения проблемы. Преобразования важны в математике, чтобы в основном знать конгруэнтность и подобие фигур на плоскости. Мы могли бы изменить положение точки, линии или двумерной фигуры, используя 4 преобразования.

    Как построить отражение и какие трансформации происходят?

    Когда мы отражаем точку по оси x, координата y преобразуется, а координата x остается прежней. x-координата будет иметь тот же знак, но изменится знак y-координаты.

    Какова формула трансформации?

    Общая формула преобразований: f(x) =a(bx-h) ⁿ +k

    где k — вертикальное смещение,

    h — горизонтальное смещение,

    a — вертикальное растяжение

    b — горизонтальная вытяжка.

    No related posts.