Формулы приведения: таблица, примеры, правила
Поможем понять и полюбить математику
Начать учиться
Из этой статьи вы узнаете, как привести тригонометрические функции огромных аргументов к функциям аргумента из промежутка [0; π/2]. А еще — как в этом занятии поможет лошадка и кому она кивает. 🐴
Вы наверняка помните значения тригонометрических функций основных аргументов:
Но что делать, если в задаче просят вычислить ? В этом и других случаях, когда из огромного аргумента нам нужно получить аргумент в пределе от 0 до 90 градусов, работают формулы приведения.
Всего формул приведения тридцать две штуки, но прежде чем мы перейдем к формулам, давайте договоримся, что точку тригонометрической окружности, отвечающую углу , где n — целое число, мы будем называть опорной точкой.
Список формул приведения
Формулы приведения c опорной точкой (случай n = 1):
;
;
;
;
;
;
;
.
Формулы приведения c опорной точкой (случай n = 2):
;
;
;
;
;
;
;
.

Формулы приведения c опорной точкой (случай n = 3):
;
;
;
;
;
;
;
- .
Формулы приведения c опорной точкой (случай n = 4):
;
;
;
;
;
;
;
.

Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Доказательство формул
Чтобы убедиться, что формулы рабочие, рассмотрим примеры доказательств нескольких из них.
Для этого нам нужно будет вспомнить формулы сложения для синуса и косинуса:
;
.
Формула приведения с синусом
Разберем первый пример формулы приведения с синусом: . Нужно доказать, что левая часть равна правой.
По формуле синуса суммы представим левую часть выражения:
Вычислим и в получившемся выражении:
Таким образом, , что и требовалось доказать.
Формула приведения с косинусом
Рассмотрим также пример формулы приведения с косинусом и докажем ее:
Аналогично распишем левую часть по формуле косинуса суммы:
Вычислим и
Следовательно, , что и требовалось доказать.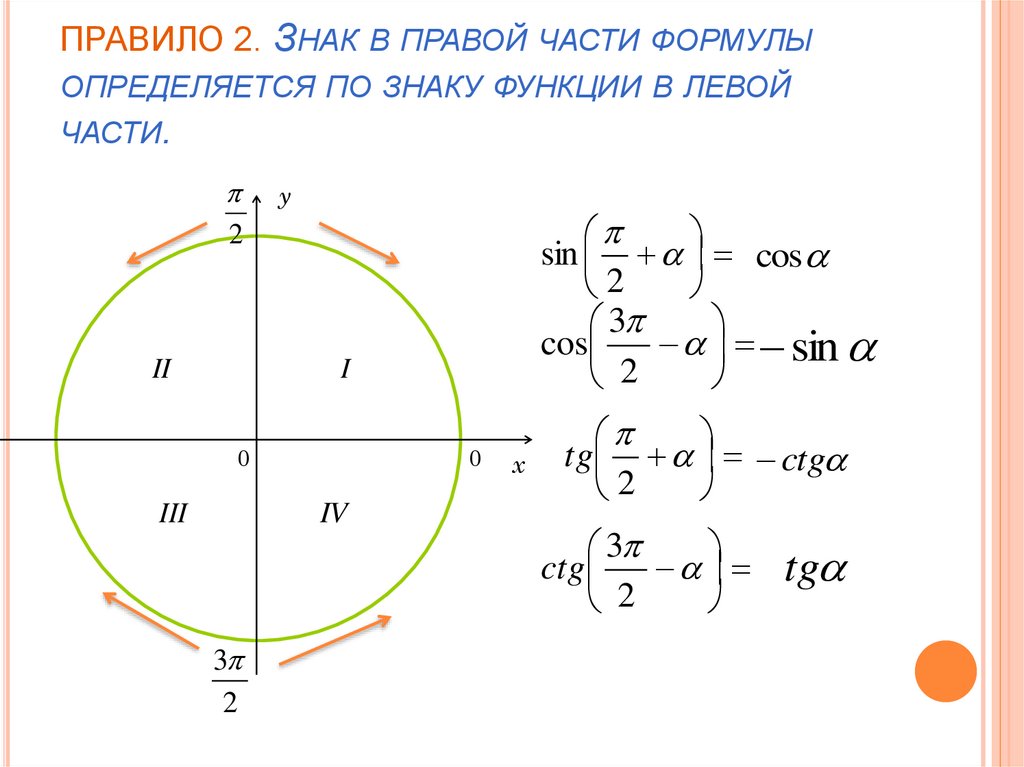
Формула приведения с тангенсом
Чтобы доказать формулу приведения с тангенсом, нужно вспомнить, что тангенс — это отношение синуса к косинусу. Тогда для доказательства нужно лишь дважды использовать формулы сложения — попробуйте сами на формуле и сравните с примером.
При желании таким образом вы сможете доказать справедливость всех формул.
Таблица формул приведения
Нередко можно встретить такой вариант оформления формул приведения — в виде таблицы.
Для того чтобы воспользоваться этой таблицей, выберите строку с нужной функцией и столбец с необходимым аргументом — на их пересечении вы узнаете ответ.
Например, нужно упростить . говорит нам о том, что нужно выбрать первую строку, указывает на шестую колонку. На их пересечении нашли ответ: . Значит,
Маленькую распечатанную таблицу формул приведения тригонометрических функций удобно иметь в пенале на случай неожиданных контрольных.
Как запомнить формулы приведения
Одно дело — воспользоваться формулами, а совсем другое — выучить их. Знать наизусть все формулы приведения или всю таблицу — дело нелегкое и, к счастью, абсолютно ненужное.
Поэтому познакомимся с мнемоническим алгоритмом:
Представьте аргумент в виде , где n — целое число, а — острый угол, то есть принадлежит отрезку
Изобразите (на листе или мысленно) на единичной окружности данный угол.
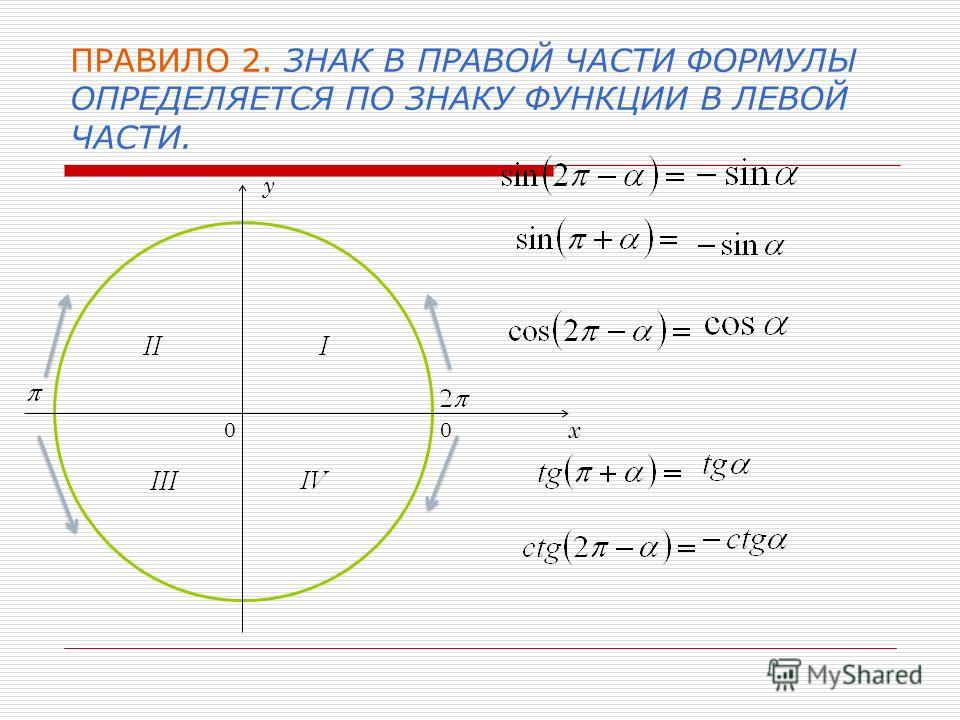
С помощью окружности определите знак исходной функции. Полученная функция в правой части будет иметь такой же знак.
Напоминаю знаки тригонометрических функций во всех четвертях тригонометрической окружности:
Если в аргументе у опорной точки n — нечетное число, то исходную функцию замените на кофункцию, то есть на противоположную функцию (синус меняется на косинус, тангенс — на котангенс, и наоборот).

Если в аргументе у опорной точки n — четное число, то функция не меняется.
Вот с этим пунктом изменения или сохранения функции возникает постоянная путаница. А запомнить поможет «правило лошадки».
Правило лошадки 🐴
Таким образом, формулы приведения — это тригонометрические тождества вида
Задание 1
Найдите значение выражения
Вы видите, что каждое слагаемое выражения — это формула приведения тригонометрической функции. Упростим их по отдельности.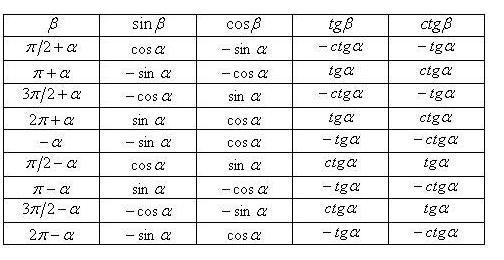
Сначала нужно представить аргумент в виде , где n — целое число, а — острый угол. Здесь этот шаг уже выполнен, поэтому пропускаем его.
Далее изображаем данный угол на тригонометрической окружности:
Определяем знак исходной функции, то есть синуса. Синус этого угла принимает положительные значения.
В конце определяем, меняется ли функция. В этом нам поможет «правило лошадки»: опорная точка лежит на горизонтальной оси, значит, функция не меняется на кофункцию, то есть синус не меняется на косинус.
Значит, .
Приведем аналогичные рассуждения для всех слагаемых в выражении.
Аргумент уже представлен в виде , где n — целое число, а — острый угол.

Косинус во второй четверти тригонометрической окружности принимает отрицательные значения.
Опорная точка лежит на вертикальной оси — это случай, когда косинус меняется на синус.
Значит, .
Аргумент уже представлен в виде , где n — целое число, а — острый угол.
Косинус в третьей четверти тригонометрической окружности принимает отрицательные значения.
Опорная точка лежит на вертикальной оси — это случай, когда косинус меняется на синус.
Значит, .
А теперь запишем преобразованные выражения в наше исходное и упростим:
Обратите внимание, к какому простому виду удалось привести это сложное, на первый взгляд, выражение.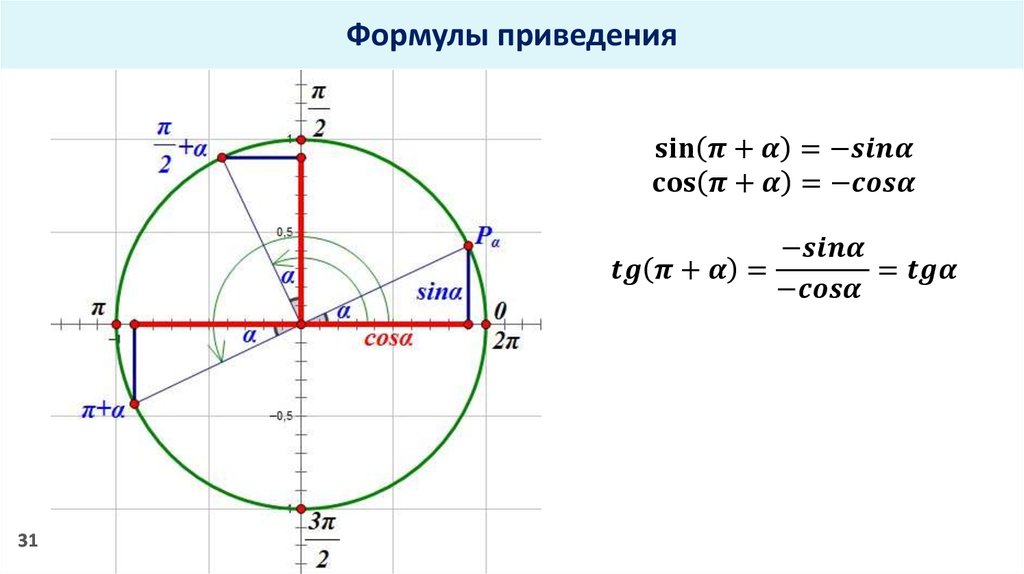
Задание 2
До этого момента мы говорили о формулах приведения тригонометрических функций углов, выраженных в радианах. Однако мы понимаем, что градусы и радианы — это разные способы представления одних и тех же углов или аргументов, поэтому тригонометрические формулы приведения работают и для выражений с градусами.
Разберем на примере: найдите значение выражения .
В этом случае важно заметить, что , а значит, одну из функций, например , можно представить в виде , то есть в виде, необходимом для использования формулы приведения.
Так как первый шаг выполнен, то продолжаем идти по алгоритму.
Опорная точка лежит на вертикальной оси, поэтому косинус меняется на синус.
Значит,
Запишем преобразованные выражения в наше исходное и упростим:
Формулы приведения в тригонометрии занимают второе место по важности и частоте использования после основного тригонометрического тождества, так что осваивайте теоретические материалы, практикуйтесь на задачках, а за другими полезными формулами и самыми хитрыми заданиями приходите на онлайн-курсы математики для детей в Skysmart.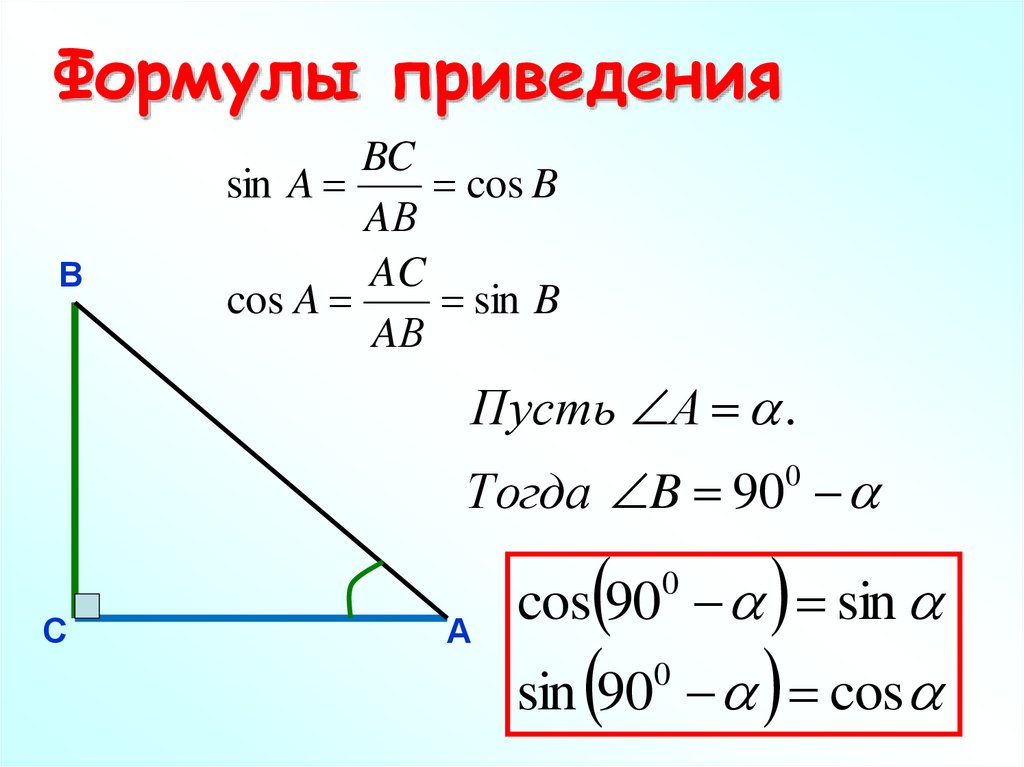
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Кристина Тоскина
К предыдущей статье
Уравнение касательной к графику функции
К следующей статье
209.3K
Логарифмы
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Формулы приведения
Бизнес с Oriflame — рост и РАЗВИТИЕ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2012-10-06
Формулы приведения! Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
*А тем, кто хочет набить руку решая задачи, вот здесь разобраны 22 примера от простых до самых сложных.
Перечислю лишь некоторые задачи, типы которых возможны на экзамене, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
Формулы приведения:
угол альфа лежит пределах от 0 до 90 градусов
* * *
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
Определите знак функции в соответствующей четверти.
Напомню их:
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен.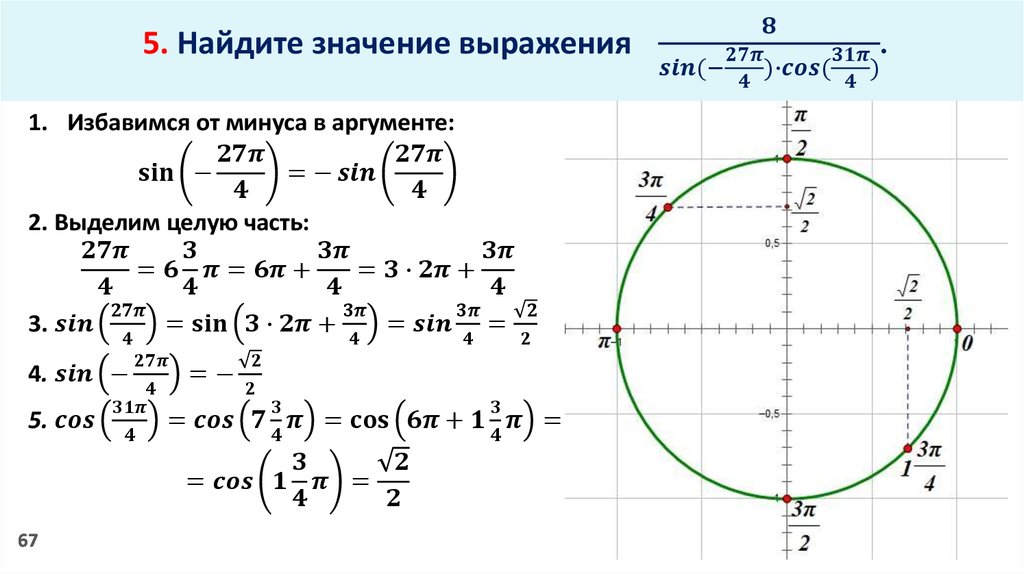 Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
***
В статье на решение прямоугольного треугольника был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
И наоборот – косинус одного острого угла в прямоугольном треугольнике равен синусу другого острого угла в нём. Вот вам и подтверждение этого с помощью формул приведения:
Конечно, определить значения углов можно и без формул приведения, по тригонометрической окружности. И если вы умеете это делать, то очень хорошо. Но поняв, как работают формулы приведения, вы сможете делать это очень быстро.
Данные формулы можно также выразить в табличной форме:
В дальнейшем, применяя свойство периодичности, четности (нечётности) вы без труда определите значение любого угла: 10500, -7500, 23700 и любые другие. Статья об этом в будущем обязательно будет, не пропустите!
Статья об этом в будущем обязательно будет, не пропустите!
Когда в решениях задач буду использовать формулы приведения, то обязательно буду ссылаться на эту статью, чтобы вы всегда смогли освежить в памяти представленную выше теорию. На этом всё. Надеюсь, материал был вам полезен.
Получить материал статьи в формате PDF
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Формулы Теория | Как запомнитьТригонометрияФормулы
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Формулы двойного угла, полуугла и приведения · Алгебра и тригонометрия
Формулы двойного угла, полуугла и приведения · Алгебра и тригонометрияВ этом разделе вы:
- Используйте формулы двойного угла, чтобы найти точные значения.

- Используйте формулы двойного угла для проверки тождества.
- Используйте формулы сокращения для упрощения выражения.
- Используйте формулы половинного угла, чтобы найти точные значения.
Велосипедные рампы, изготовленные для соревнований (см. [ссылка]), должны различаться по высоте в зависимости от уровня квалификации участников. Для продвинутых участников угол, образованный рампой и землей, должен составлять θ
., так что tan θ=53.
Угол разделен пополам для новичков. Какая крутизна пандуса для новичков? В этом разделе мы исследуем три дополнительные категории тождеств, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
Использование формул двойного угла для нахождения точных значений
В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций. Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где α=β.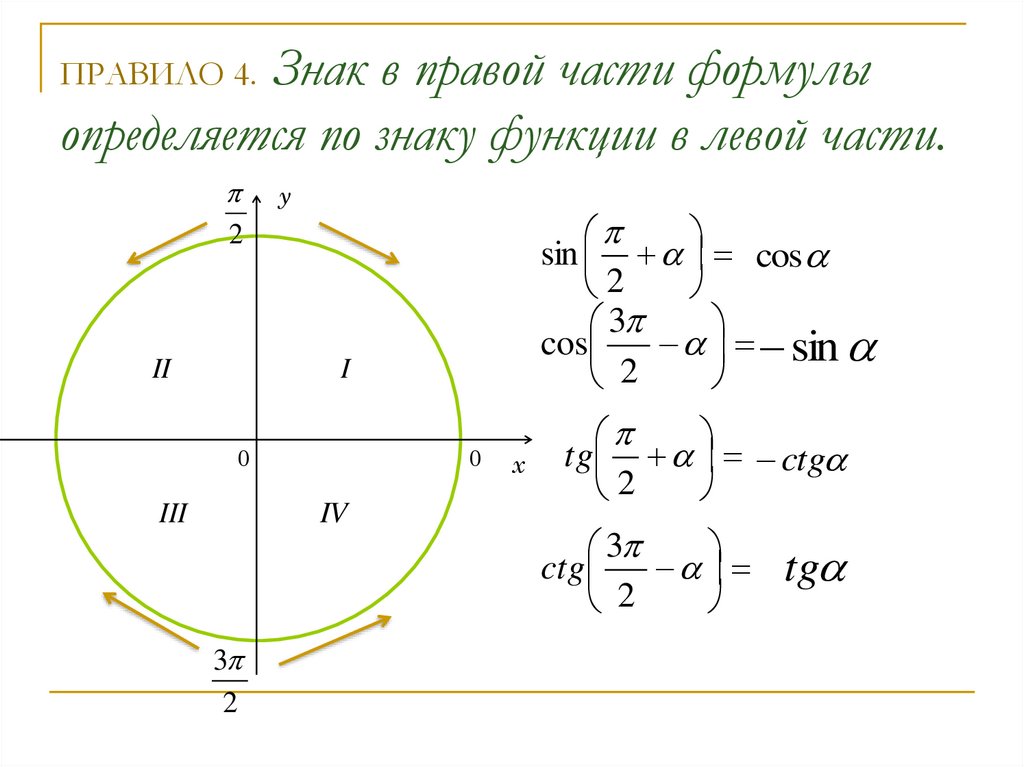
Вывод формулы двойного угла для синуса начинается с формулы суммы,
sin(α+β)=sin α cos β+cos α sin β
Если мы допустим α=β=θ,
тогда у нас есть
sin(θ+θ)=sin θ cos θ+cos θ sin θsin(2θ)=2sin θ cos θ
Получение двойного угла для косинуса дает нам три варианта. Во-первых, исходя из формулы суммы, cos(α+β)=cos α cos β−sin α sin β,
и пусть α=β=θ,
у нас есть
cos(θ+θ)=cos θ cos θ−sin θ sin θcos(2θ)=cos2θ−sin2θ
Используя свойства Пифагора, мы можем расширить эту формулу двойного угла для косинуса и получить еще два варианта. Первый вариант:
cos(2θ)=cos2θ−sin2θ=(1−sin2θ)−sin2θ=1−2sin2θ
Второй вариант:
cos(2θ)=cos2θ−sin2θ=cos2θ−(1−cos2θ)=2 cos2θ−1
Аналогично, чтобы вывести формулу тангенса двойного угла, заменив α=β=θ
в формуле суммы дает
tan(α+β)=tan α+tan β1−tan α tan βtan(θ+θ)=tan θ+tan θ1−tan θ tan θtan(2θ)=2tan θ1−tan2θ
Формулы двойного угла
Формулы двойного угла резюмируются следующим образом:
sin(2θ)=2 sin θ cos θ −1
тангенс(2θ)=2 тангенс θ1−тангенс2θ
Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение.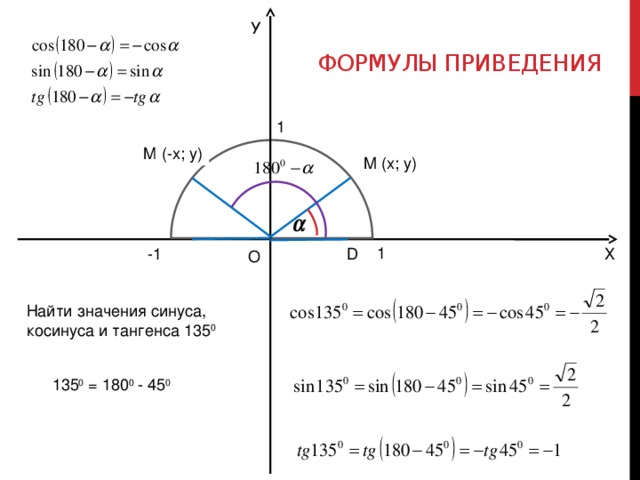
- Нарисуйте треугольник, чтобы отразить данную информацию.
- Определите правильную формулу двойного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.
Использование формулы двойного угла для нахождения точного значения, включающего тангенс
Учитывая, что tan θ=−34
и θ
находится в квадранте II, найдите следующее:
- грех (2θ)
- cos(2θ)
- загар (2θ)
Если мы нарисуем треугольник, отражающий предоставленную информацию, мы сможем найти значения, необходимые для решения задач на изображении. Нам дано tan θ=−34,
, так что θ
находится в квадранте II. Тангенс угла равен противолежащей стороне относительно прилежащей, а так как θ
находится во втором квадранте, соседняя сторона находится на оси x и является отрицательной. Используйте Теорему Пифагора , чтобы найти длину гипотенузы:
Используйте Теорему Пифагора , чтобы найти длину гипотенузы:
(−4)2+(3)2=c216+9=c225=c2c=5
Теперь мы можем нарисовать треугольник, подобный показанному на рис. [связь].
- Начнем с того, что напишем формулу двойного угла для синуса.
sin(2θ)=2 sin θ cos θ
Видим, что нужно найти sin θ
и cos θ.
По [ссылке] мы видим, что гипотенуза равна 5, значит sin θ=35,
и cos θ=-45.
Подставьте эти значения в уравнение и упростите.
Таким образом,
sin(2θ)=2(35)(−45)=−2425
- Запишите формулу косинуса двойного угла.
cos(2θ)=cos2θ−sin2θ
Снова подставьте значения синуса и косинуса в уравнение и упростите.
cos(2θ)=(−45)2−(35)2=1625−925=725
- Запишите формулу тангенса двойного угла.

тангенс(2θ)=2 тангенс θ1−тангенс2θ
В этой формуле нам нужен тангенс, который мы получили как tan θ=−34.
Подставьте это значение в уравнение и упростите.
тангенс(2θ)=2(-34)1-(-34)2=-321-916=-32(167)=-247
Учитывая sin α=58,
с θ
в квадранте I, найти cos(2α).
cos(2α)=732
Использование формулы двойного угла для косинуса без точных значений
Используйте формулу двойного угла для косинуса, чтобы записать cos(6x)
в единицах cos(3x).
cos(6x)=cos(2(3x))=2cos2(3x)−1
Анализ
Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений. Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.
Использование формул двойного угла для проверки подлинности
Установление тождеств с помощью формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для вывода формул суммы и разности.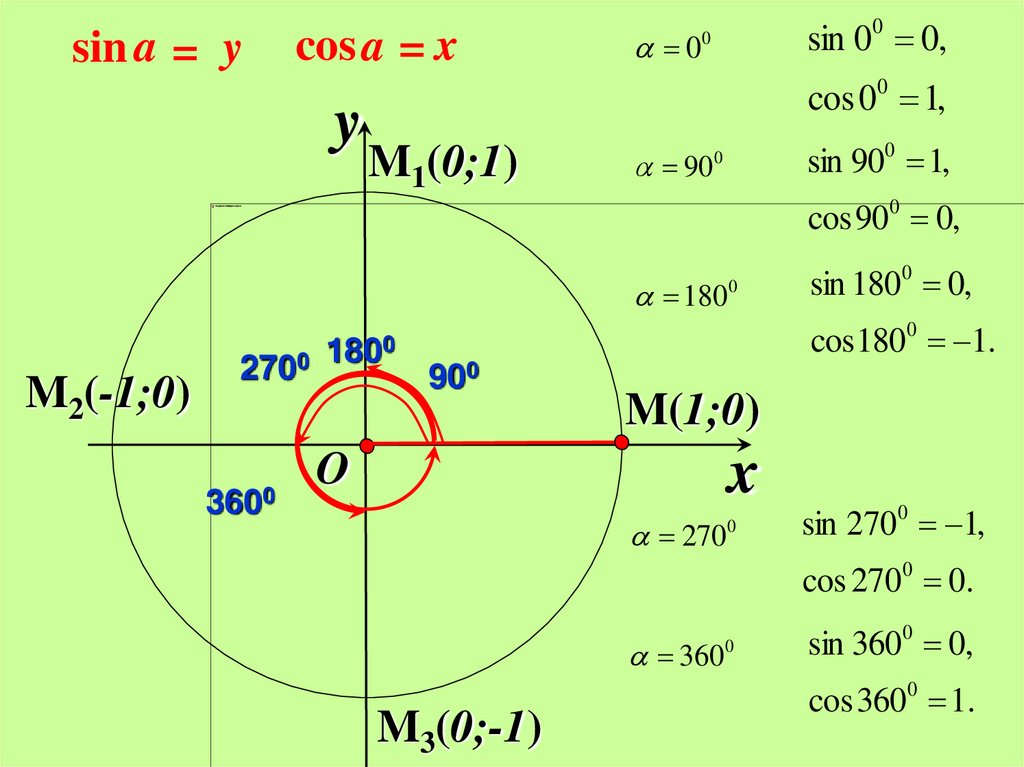 Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной.
Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной.
Использование формул двойного угла для проверки тождества
С помощью формул двойного угла проверьте следующее тождество:
1+sin(2θ)=(sin θ+cos θ)2
знак равенства и перепишите выражение, пока оно не совпадет с левой частью. 9Анализ
Этот процесс не сложен, если вспомнить формулу идеального квадрата из алгебры:
(a±b)2=a2±2ab+b2
, где a=sin θ
и b=cos θ.
Одним из условий успеха в математике является умение распознавать закономерности. Хотя термины или символы могут меняться, алгебра остается неизменной.
Проверить тождество: cos4θ−sin4θ=cos(2θ).
cos4θ−sin4θ=(cos2θ+sin2θ)(cos2θ−sin2θ)=cos(2θ)
Проверка идентичности двойного угла для касательной
Проверка идентичности:
tan(2θ)=2cot θ−tan θ
В этом случае мы будем работать с левой частью уравнения и упростим или перепишем, пока она не будет равна правая часть уравнения.
tan(2θ)=2 tan θ1−tan2θФормула двойного угла=2 tan θ(1tan θ)(1−tan2θ)(1tan θ) Умножить на член, который дает желаемый числитель.=21tan θ−tan2θ=2tan θ θ−tan θИспользовать взаимное тождество для 1tan θ.
Анализ
Вот случай, когда более сложная часть исходного уравнения появилась справа, но мы решили работать с левой частью. Однако, если бы мы выбрали для перезаписи левую часть, мы бы работали в обратном направлении, чтобы получить эквивалентность. Например, предположим, что мы хотели показать
2tan θ1−tan2θ=2cot θ−tan θ
Давайте работать с правой стороной.
2cot θ−tan θ=21tan θ−tan θ(tan θtan θ)=2 tan θ1tan θ(tan θ)−tan θ(tan θ)=2 tan θ1−tan2θ
При использовании тождеств для упрощения тригонометрического выражения или решения тригонометрического уравнения обычно существует несколько путей к желаемому результату. Не существует установленного правила относительно того, какой стороной следует манипулировать. Тем не менее, мы должны начать с руководящих принципов, изложенных ранее.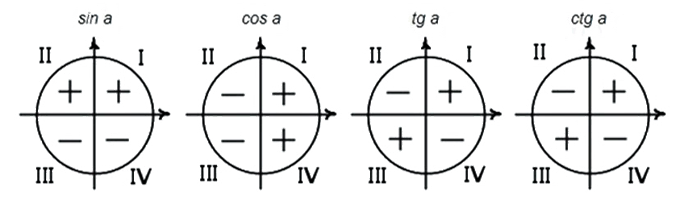
Проверить тождество: cos(2θ)cos θ=cos3θ−cos θ sin2θ.
cos(2θ)cos θ=(cos2θ−sin2θ)cos θ=cos3θ−cos θsin2θ
Использование формул сокращения для упрощения выражения
Формулы двойного угла можно использовать для получения формулы приведения , которые являются формулами, которые мы можем использовать для уменьшения мощности данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны в курсах математики более высокого уровня, в частности исчисления. Также называемые формулами уменьшения степени, включены три тождества, которые легко выводятся из формул двойного угла.
Мы можем использовать две из трех формул двойного угла для косинуса, чтобы вывести формулы приведения для синуса и косинуса. Начнем с cos(2θ)=1−2 sin2θ.
Решите для sin2θ:
cos(2θ)=1−2 sin2θ2 sin2θ=1−cos(2θ)sin2θ=1−cos(2θ)2
Далее используем формулу cos(2θ)=2 cos2θ−1.
Решите для cos2θ:
cos(2θ)= 2 cos2θ−11+cos(2θ)=2 cos2θ1+cos(2θ)2=cos2θ
Последняя формула приведения получается путем записи тангенса через синус и косинус:
tan2θ=sin2θcos2θ=1−cos(2θ)21+cos(2θ)2Подставить формулы редукции.=(1−cos(2θ)2)(21+cos(2θ))=1−cos(2θ)1+cos (2θ)
Формулы приведения
Формулы приведения резюмируются следующим образом:
Написание эквивалентного выражения, не содержащего степеней больше 1
Напишите эквивалентное выражение для cos4x
, которое не содержит степеней синуса или косинуса больше 1.
Мы дважды применим формулу редукции для косинуса.
cos4x=(cos2x)2=(1+cos(2x)2)2Подставьте формулу приведения вместо cos2x.=14(1+2cos(2x)+cos2(2x))=14+12 cos(2x)+14( 1+cos2(2x)2) Подставить формулу приведения вместо cos2x.=14+12 cos(2x)+18+18 cos(4x)=38+12 cos(2x)+18 cos(4x)
Анализ
Решение находится путем двойного использования формулы приведения, как уже отмечалось, и формулы полного квадрата из алгебры.
Использование формул уменьшения степени для доказательства тождества
Использование формул уменьшения степени для доказательства
sin3(2x)=[12 sin(2x)] [1−cos(4x)]
левая часть уравнения:
sin3(2x)=[sin(2x)][sin2(2x)]=sin(2x)[1−cos(4x)2]Подставьте формулу уменьшения мощности.=sin( 2x)(12)[1-cos(4x)]=12[sin(2x)][1-cos(4x)]
Анализ
Обратите внимание, что в этом примере мы заменили
1-cos(4x)2
на sin2(2x).
Формула гласит:
sin2θ=1−cos(2θ)2
Положим θ=2x,
, значит 2θ=4x.
Используйте формулы понижения мощности, чтобы доказать, что 10 cos4x=154+5 cos(2x)+54 cos(4x).
10cos4x=10(cos2x)2=10[1+cos(2x)2]2Подставьте формулу приведения вместо cos2x.=104[1+2cos(2x)+cos2(2x)]=104+102cos(2x)+104 (1+cos2(2x)2) Подставить формулу приведения вместо cos2x.=104+102cos(2x)+108+108cos(4x)=308+5cos(2x)+108cos(4x)=154+5cos(2x)+54cos (4x)
Использование формул половинного угла для нахождения точных значений
Следующим набором тождеств является набор из формул половинного угла , которые могут быть получены из формул редукции и могут использоваться, когда у нас есть угол, который в два раза меньше специального угла. Если мы заменим θ
Если мы заменим θ
с α2,
Формула половинного угла для синуса находится путем упрощения уравнения и решения для sin(α2).
Обратите внимание, что формулам половинного угла предшествует a ±
9знак 0002. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором α2завершается.
Формула половинного угла для синуса получается следующим образом:
sin2θ=1−cos(2θ)2sin2(α2)=1−(cos2⋅α2)2=1−cos α2sin(α2)=±1−cos α2
Чтобы вывести формулу косинуса половины угла, мы имеем
cos2θ=1+cos(2θ)2cos2(α2)=1+cos(2⋅α2)2=1+cos α2cos(α2)=±1+cos α2
Для тождества касательной имеем
tan2θ=1−cos(2θ)1+cos(2θ)tan2(α2)=1−cos(2⋅α2)1+cos(2⋅α2)=1−cos α1+cos αtan(α2)=±1 −cos α1+cos α
Формулы половин угла
Формулы половин угла следующие: 1 -cos α1+cos α = sin α1+cos α = 1 -cos αsin α
Использование формулы половинного угла для нахождения точного значения функции синуса
Найдите sin(15°)
с помощью формулы половинного угла.
Так как 15°=30°2,
используем формулу половинного угла для синуса:
sin 30°2=1−cos30°2=1−322=2−322=2−34=2−32
Помните, что мы можем проверить ответ с помощью графического калькулятора.
Анализ
Обратите внимание, что мы использовали только положительный корень, потому что sin(15°)
является положительным.
Зная тангенс угла и квадрант, в котором находится угол, найдите точные значения тригонометрических функций половины угла.
- Нарисуйте треугольник для представления данной информации.
- Определите правильную формулу половинного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.
Нахождение точных значений с помощью тождеств половин углов
Учитывая, что tan α=815
и α
лежит в квадранте III, найдите точное значение следующего:
- грех(α2)
- cos(α2)
- загар (α2)
Используя данную информацию, мы можем нарисовать треугольник, показанный на [ссылка].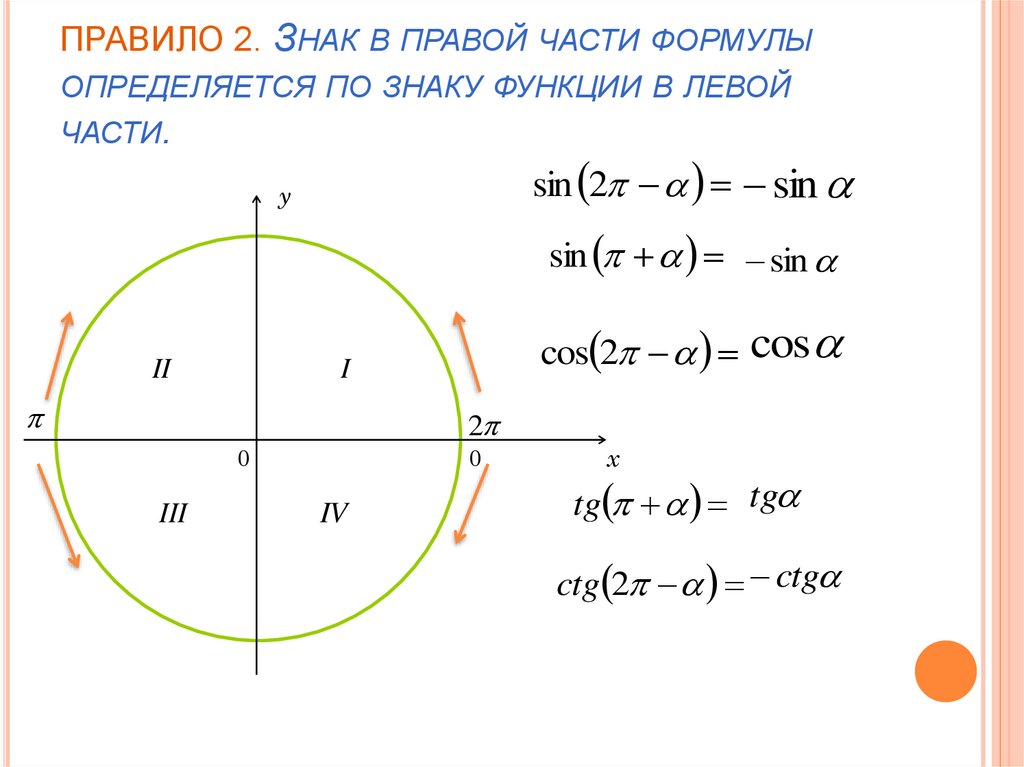 Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sin α=−817
Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sin α=−817
и cos α=−1517.
- Прежде чем мы начнем, мы должны помнить, что если
α
находится в квадранте III, затем
180°<α<270°,, поэтому
180°2<α2<270°2.Это означает, что клеммная сторона
α2находится в квадранте II, так как
90°<α2<135°.Чтобы найти sin α2,
начнем с записи формулы половинного угла для синуса. Затем подставляем найденное значение косинуса из треугольника в [ссылка] и упрощаем.
sin α2=±1−cos α2=±1−(−1517)2=±32172=±3217⋅12=±1617=±417=41717
Выбираем положительное значение sin α2
, потому что угол заканчивается в квадранте II, а синус положителен в квадранте II.
- Найти
cos α2,
запишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника в [ссылка], и упростим.

cos α2=±1+cos α2=±1+(−1517)2=±2172=±217⋅12=±117=−1717
Выбираем отрицательное значение cos α2
, потому что угол находится в квадранте II, потому что косинус отрицателен в квадранте II.
- Найти
тангенс α2,
пишем формулу тангенса половины угла. Снова подставляем найденное значение косинуса из треугольника в [ссылка] и упрощаем.
тангенс α2=±1−cos α1+cos α=±1−(−1517)1+(−1517)=±3217217=±322=−16=−4
Выбираем отрицательное значение tan α2
потому что α2
лежит в квадранте II, а тангенс отрицателен в квадранте II.
Учитывая, что sin α=−45
и α
лежит в квадранте IV, найдите точное значение cos (α2).
−25
Нахождение измерения половинного угла
Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа построена для соревнований высокого уровня с углом θ
, образованным рампой и землей. Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если tan θ=53
Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если tan θ=53
для соревнований более высокого уровня, каково измерение угла для соревнований новичков?
Поскольку угол для начинающих соревнований измеряет половину крутизны угла для соревнований высокого уровня, а tan θ=53
для высоких соревнований, мы можем найти cos θ
из прямоугольного треугольника и теоремы Пифагора, так что мы можно использовать тождества половинного угла. См. [ссылка].
32+52=34c=34
Мы видим, что cos θ=334=33434.
Мы можем использовать формулу половинного угла для тангенса: tan θ2=1−cos θ1+cos θ.
Так как tan θ
находится в первом квадранте, поэтому tan θ2.
tan θ2=1−334341+33434=34−3343434+33434=34−33434+334≈0,57
Возьмем арктангенс, чтобы найти угол: tan−1(0,57)≈29,7°.
Таким образом, угол рампы для соревнований новичков составляет ≈29,7°.
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с формулами двойного угла, половинного угла и сокращения.
- Двухугольные тождества
- Полуугольные тождества
Ключевые уравнения
| Формулы двойного угла | sin(2θ)=2sin θ cos θcos(2θ)=cos2θ−sin2θ=1−2sin2θ=2cos2θ−1tan(2θ)=2tan θ1−tan2θ |
| Формулы приведения | sin2θ=1−cos(2θ)2cos2θ=1+cos(2θ)2tan2θ=1−cos(2θ)1+cos(2θ) |
| Формулы полууглов | sin α2=±1−cos α2cos α2=±1+cos α2tan α2=±1−cos α1+cos α=sin α1+cos α=1−cos αsin α |
Ключевые понятия
- Тождества двойного угла получаются из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса. См. [ссылка], [ссылка], [ссылка] и [ссылка].
- Формулы редукции особенно полезны в математических вычислениях, поскольку они позволяют уменьшить мощность тригонометрического члена.
 См. [ссылка] и [ссылка].
См. [ссылка] и [ссылка]. - Формулы половинного угла позволяют нам найти значение тригонометрических функций, содержащих половинные углы, независимо от того, известен исходный угол или нет. См. [ссылка], [ссылка] и [ссылка].
Раздел Упражнения
Устный
Объясните, как определить редукционные тождества из тождества двойного угла cos(2x)=cos2x−sin2x.
Используйте тождества Пифагора и изолируйте квадрат члена.
Объясните, как определить формулу двойного угла для tan(2x)
, используя формулы двойного угла для cos(2x)
и sin(2x).
Мы можем определить формулу половинного угла для tan(x2)=1−cos x1+cos x
, разделив формулу для sin(x2) на
by cos(x2).
Объясните, как определить две формулы для tan(x2)
, которые не содержат квадратных корней.
1−cos xsin x,sin x1+cos x,
, умножая верх и низ на 1−cos x
и 1+cos x,
соответственно.
Для формулы половинного угла, приведенной в предыдущем упражнении для tan(x2),
объясните, почему деление на 0 не имеет значения. (Подсказка: проверьте значения cos x
, необходимые для того, чтобы знаменатель был равен 0.)
Алгебраический
Для следующих упражнений найдите точные значения a) sin(2x),
б) cos(2x),
и в) загар(2x)
без решения x.
Если sin x=18,
и x
находится в I квадранте.
Если cos x=23,
и x
находится в квадранте I.
Если cos x=−12,
и x
находится в квадранте III.
а) 32
б) −12
в) −3
Если tan x=−8,
и x
находится в квадранте IV.
В следующих упражнениях найдите значения шести тригонометрических функций, если выполнены указанные условия.
cos(2θ)=35
и 90°≤θ≤180°
cos θ=−255,sin θ=55,tan θ=−12,csc θ=5,sec θ=−52,cot θ= −2
cos(2θ)=12
и 180°≤θ≤270°
Для следующих упражнений упростите до одного тригонометрического выражения.
2 sin(π4) 2 cos(π4)
2 sin(π2)
4 sin(π8) cos(π8)
Для следующих упражнений найдите точное значение, используя формулы половинного угла.
sin(π8)
2−22
соз(-11π12)
sin(11π12)
2−32
потому что (7π8)
тан(5π12)
2+3
тангенс (−3π12)
тангенс(−3π8)
−1−2
Для следующих упражнений найдите точные значения a) sin(x2),
б) cos(x2),
и в) загар(х2)
без решения для x,
, когда 0°≤x≤360°.
Если tan x=−43,
и x
находится в квадранте IV.
Если sin x=−1213,
и x
находится в квадранте III.
а) 31313
б) −21313
в) −32
Если csc x=7,
и x
находится в квадранте II.
Если сек x=−4,
и x
находится в квадранте II.
а) 104
б) 64
в) 153
В следующих упражнениях используйте [ссылка] для нахождения требуемых половинных и двойных углов.
Найти sin(2θ),cos(2θ),
и tan(2θ).
Найти sin(2α),cos(2α),
и tan(2α).
120169,–119169,–120119
Найти sin(θ2),cos(θ2),
и tan(θ2).
Найти sin(α2),cos(α2),
и tan(α2).
21313,31313,23
В следующих упражнениях упростите каждое выражение. Не оценивайте.
cos2(28°)−sin2(28°)
2cos2(37°)−1
cos(74°)
1−2 sin2(17°)
cos2(9x)−sin2(9x)
cos(18x)
4 sin(8x) cos(8x)
6 sin(5x) cos(5x)
3sin(10x)
Для следующих упражнений докажите данное тождество.
(sin t−cos t)2=1−sin(2t)
sin(2x)=−2 sin(−x) cos(−x)
−2 sin(−x)cos(−x)=−2(−sin(x)cos(x))=sin(2x )
детская кроватка x−tan x=2 кроватка(2x)
sin(2θ)1+cos(2θ)tan2θ=tan3 θ
sin(2θ)1+cos(2θ)tan2θ=2sin(θ)cos(θ)1+cos2θ−sin2θtan2θ=2sin(θ)cos(θ) )2cos2θtan2θ=sin(θ)cos θtan2θ=cot(θ)tan2θ=tan3 θ
Для следующих упражнений перепишите выражение с показателем степени не выше 1.
cos2(5x)
cos2(6x)
1+cos(12x)2
sin4(8x)
sin4(3x)
3+cos(12x)−4cos(6x)8
cos2x sin4x
cos4x sin2x
2+cos(2x)−2cos(4x)−cos(6x)32
загар2x sin2x
Технология
Для следующих упражнений уменьшите уравнения до степени единицы, а затем проверьте ответ графически.
tan4x
3+cos(4x)−4cos(2x)3+cos(4x)+4cos(2x)
sin2(2x)
sin2x cos2x
1−cos(4x)8
tan2x sin x
tan4x cos2x
3+cos(4x)−4cos(2x)4(cos(2x)+1)
cos2x sin(2x)
cos2(2x)sin x
(1+cos(4x))sin x2
тангенс2(х2) sin х
Для следующих упражнений алгебраически найдите эквивалентную функцию только с точки зрения sin x
и/или cos x,
, а затем проверьте ответ, построив график обеих функций.
sin(4x)
4sin xcos x(cos2x−sin2x)
cos(4x)
Расширения
Для следующих упражнений докажите тождества.
sin(2x)=2 tan x1+tan2x
2tan x1+tan2x=2sin xcos x1+sin2xcos2x=2sin xcos xcos2x+sin2xcos2x=2sin xcos x=s.cos2x1=2sin0003
cos(2α)=1−tan2α1+tan2α
tan(2x)=2 sin x cos x2cos2x−1
2sin xcos x2cos2x−1=sin(2x)cos(2x)=tan(2x)
(sin2x−1)2=cos(2x)+sin4x
sin(3x)=3 sin x cos2x−sin3x sin3x+2sin xcos2x=3sin xcos2x−sin3x
cos(3x)=cos3x−3sin2x cos x
1+cos(2t)sin(2t)−cos t=2 cos t2 sin t−1 )=2cost2sint−1
sin(16x)=16 sin x cos x cos(2x)cos(4x)cos(8x)
cos(16x)=(cos2(4x)−sin2(4x)−sin(8x))(cos2(4x)−sin2(4x)+sin(8x))
(cos2(4x)−sin2(4x) −sin(8x))(cos2(4x)−sin2(4x)+sin(8x))==(cos(8x)−sin(8x))(cos(8x)+sin(8x))=cos2(8x )−sin2(8x)=cos(16x)
Глоссарий
- формулы двойного угла
- тождеств, полученных из формул суммы синуса, косинуса и тангенса, в которых углы равны
- формулы половинного угла
- тождества, полученные из формул приведения и используемые для определения значений половинных углов тригонометрических функций
- формулы приведения
- тождеств, полученных из формул двойного угла и используемых для уменьшения степени тригонометрической функции
Эта работа находится под лицензией Creative Commons Attribution 4.
 0 International License.
0 International License.Вы также можете бесплатно скачать на http://cnx.org/contents/[email protected]
Атрибуция:
- По вопросам, касающимся этой лицензии, обращайтесь по адресу [email protected].
- Если вы используете данный учебник в качестве библиографической ссылки, то цитировать его следует следующим образом: Колледж OpenStax, алгебра и тригонометрия. OpenStax CNX. http://cnx.org/contents/[email protected].
- Если вы распространяете этот учебник в печатном формате, вы должны указать на каждой физической странице следующее указание авторства: «Скачать бесплатно на http://cnx.org/contents/[email protected].»
- Если вы распространяете часть этого учебника, вы должны сохранять при каждом просмотре страницы в цифровом формате (включая, помимо прочего, EPUB, PDF и HTML) и на каждой физической печатной странице следующее указание авторства:
«Загрузите бесплатно по адресу http://cnx.
 org/contents/[email protected]».
org/contents/[email protected]».
Формула приведения — Что такое формула приведения? Примеры
Формула приведения часто используется при интегрировании для вычисления интегралов более высокого порядка. Работать с выражениями более высокой степени долго и утомительно, и здесь формулы приведения даны в виде простых выражений со степенью n для решения этих выражений более высокой степени. Эти формулы приведения были получены из базовых формул интегрирования и работают по тем же правилам интегрирования. 9{2}(2 x)+1 / 2 \ln \sec (2 x)+C\)
Часто задаваемые вопросы о формуле приведения
Что такое формула приведения?
Формула приведения часто используется при интегрировании для вычисления интегралов более высокого порядка. Работать с выражениями более высокой степени долго и утомительно, и здесь формулы приведения даны в виде простых выражений со степенью n для решения этих выражений более высокой степени. Следующие формулы приведения полезны для работы с выражениями более высокой степени, включающими алгебраические переменные, функции тригонометрии, логарифмические функции.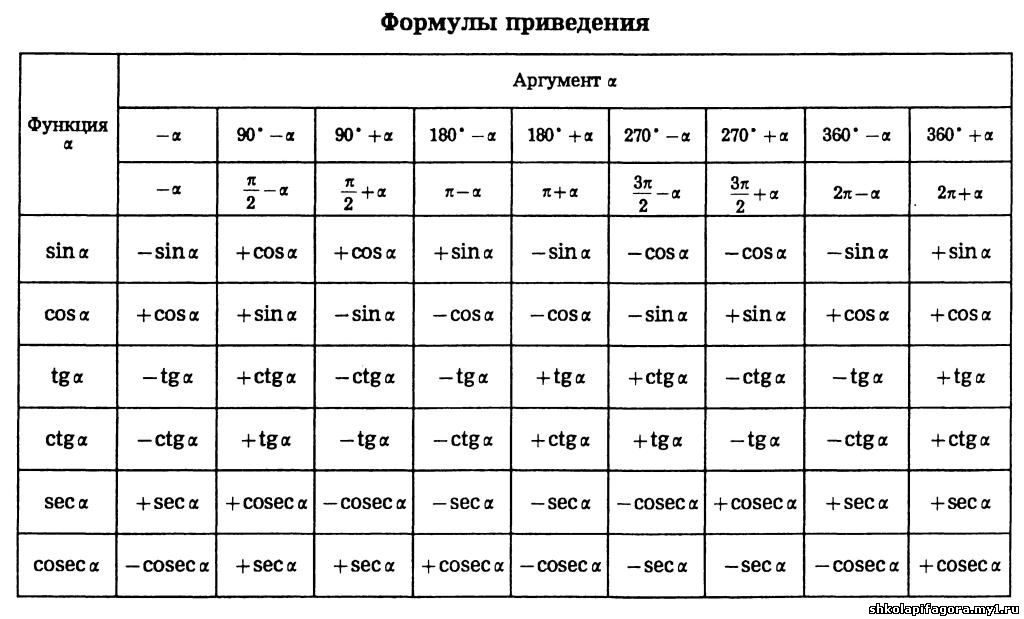








 См. [ссылка] и [ссылка].
См. [ссылка] и [ссылка]. org/contents/
org/contents/