Все главные формулы по математике — Математика — Теория, тесты, формулы и задачи
Оглавление:
- Формулы сокращенного умножения
- Квадратное уравнение и формула разложения квадратного трехчлена на множители
- Свойства степеней и корней
- Формулы с логарифмами
- Арифметическая прогрессия
- Геометрическая прогрессия
- Тригонометрия
- Тригонометрические уравнения
- Геометрия на плоскости (планиметрия)
- Геометрия в пространстве (стереометрия)
- Координаты
- Таблица умножения
- Таблица квадратов двухзначных чисел
- Расширенная PDF версия документа «Все главные формулы по школьной математике»
Формулы сокращенного умножения
К оглавлению…
Квадрат суммы:
Квадрат разности:
Разность квадратов:
Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению. ..
..
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения может быть вычислено по формуле:
Парабола
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:
Икс вершины:
Игрек вершины параболы:
Свойства степеней и корней
К оглавлению…
Основные свойства степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.
Основные свойства математических корней:
Для арифметических корней:
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:
Для корня четной степени имеется следующее свойство:
Формулы с логарифмами
К оглавлению…
Определение логарифма:
Определение логарифма можно записать и другим способом:
Свойства логарифмов:
Логарифм произведения:
Логарифм дроби:
Вынесение степени за знак логарифма:
Другие полезные свойства логарифмов:
Арифметическая прогрессия
К оглавлению. ..
..
Формулы n-го члена арифметической прогрессии:
Соотношение между тремя соседними членами арифметической прогрессии:
Формула суммы арифметической прогрессии:
Свойство арифметической прогрессии:
Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:
Соотношение между тремя соседними членами геометрической прогрессии:
Формула суммы геометрической прогрессии:
Формула суммы бесконечно убывающей геометрической прогрессии:
Свойство геометрической прогрессии:
Тригонометрия
К оглавлению…
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму
Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению. ..
..
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.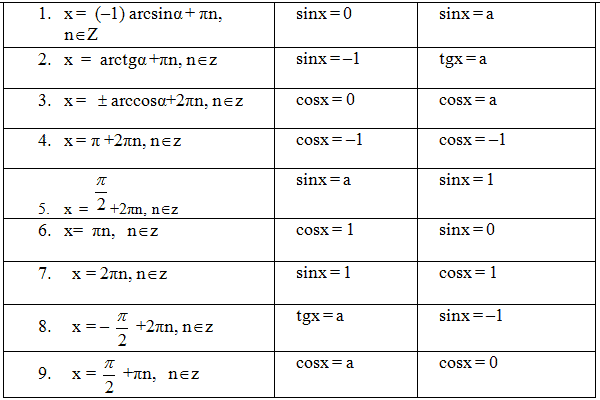 е. в том числе для любых треугольников):
е. в том числе для любых треугольников):
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:
Центральный угол правильного n-угольника:
Площадь правильного n-угольника:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Геометрия в пространстве (стереометрия)
К оглавлению. ..
..
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (или, другими словами, площадь сферы):
Координаты
К оглавлению. ..
..
Длина отрезка на координатной оси:
Длина отрезка на координатной плоскости:
Длина отрезка в трёхмерной системе координат:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):
Таблица умножения
К оглавлению…
Таблица квадратов двухзначных чисел
К оглавлению…
Расширенная PDF версия документа «Все главные формулы по школьной математике»:
К оглавлению…
Создание простой формулы в Excel
Excel
Формулы и функции
Формулы
Формулы
Создание простой формулы в Excel
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Еще.
Вы можете создать простую формулу для с суммы, вычитания, умножения и деления значений на вашем компьютере. Простые формулы всегда начинаются со знака равной(=),за которым следуют константы, которые являются числами и операторами вычислений, такими как «плюс»(+),«минус» (— ),«звездочка»*или «косая черта»(/)в начале.
В качестве примера рассмотрим простую формулу.
-
Выделите на листе ячейку, в которую необходимо ввести формулу.
-
Введите = (знак равенства), а затем константы и операторы (не более 8192 знаков), которые нужно использовать при вычислении.
В нашем примере введите =1+1.

Примечания:
-
Вместо ввода констант в формуле можно выбрать ячейки с нужными значениями и ввести операторы между ними.
-
В соответствии со стандартным порядком математических операций, умножение и деление выполняются до сложения и вычитания.
-
Нажмите клавишу ВВОД (Windows) или Return (Mac).
Рассмотрим другой вариант простой формулы. Введите =5+2*3 в другой ячейке и нажмите клавишу ВВОД или Return. Excel перемножит два последних числа и добавит первое число к результату умножения.
Использование автосуммирования
Для быстрого суммирования чисел в столбце или строке можно использовать кнопку «Автосумма». Выберите ячейку рядом с числами, которые необходимо сложить, нажмите кнопку Автосумма на вкладке Главная, а затем нажмите клавишу ВВОД (Windows) или Return (Mac).
Когда вы нажимаете кнопку Автосумма, Excel автоматически вводит формулу для суммирования чисел (в которой используется функция СУММ).
Примечание: Также в ячейке можно ввести ALT+= (Windows) или ALT++= (Mac), и Excel автоматически вставит функцию СУММ.
Приведем пример. Чтобы сложить числа за январь в бюджете «Развлечения», выберите ячейку B7, которая непосредственно под столбцом чисел. Затем нажмите кнопку «Автоумма». Формула появится в ячейке B7, а Excel выделит ячейки, которые вы суммируете.
Чтобы отобразить результат (95,94) в ячейке В7, нажмите клавишу ВВОД. Формула также отображается в строке формул вверху окна Excel.
Формула также отображается в строке формул вверху окна Excel.
Примечания:
Чтобы сложить числа в столбце, выберите ячейку под последним числом в столбце. Чтобы сложить числа в строке, выберите первую ячейку справа.
-
Создав формулу один раз, ее можно копировать в другие ячейки, а не вводить снова и снова. Например, при копировании формулы из ячейки B7 в ячейку C7 формула в ячейке C7 автоматически настроится под новое расположение и подсчитает числа в ячейках C3:C6.
-
Кроме того, вы можете использовать функцию «Автосумма» сразу для нескольких ячеек.
 Например, можно выделить ячейки B7 и C7, нажать кнопку Автосумма и суммировать два столбца одновременно.
Например, можно выделить ячейки B7 и C7, нажать кнопку Автосумма и суммировать два столбца одновременно.
Скопируйте данные из таблицы ниже и вставьте их в ячейку A1 нового листа Excel. При необходимости измените ширину столбцов, чтобы видеть все данные.
Примечание: Чтобы эти формулы выводили результат, выделите их и нажмите клавишу F2, а затем — ВВОД (Windows) или Return (Mac).
|
Данные |
||
|
2 |
||
|
5 |
||
|
|
Описание |
Результат |
|
=A2+A3 |
Сумма значений в ячейках A1 и A2 |
=A2+A3 |
|
=A2-A3 |
Разность значений в ячейках A1 и A2 |
=A2-A3 |
|
=A2/A3 |
Частное от деления значений в ячейках A1 и A2 |
=A2/A3 |
|
=A2*A3 |
Произведение значений в ячейках A1 и A2 |
=A2*A3 |
|
=A2^A3 |
Значение в ячейке A1 в степени, указанной в ячейке A2 |
=A2^A3 |
|
Формула |
Описание |
Результат |
|
=5+2 |
Сумма чисел 5 и 2 |
=5+2 |
|
=5-2 |
Разность чисел 5 и 2 |
=5-2 |
|
=5/2 |
Частное от деления 5 на 2 |
=5/2 |
|
=5*2 |
Произведение чисел 5 и 2 |
=5*2 |
|
=5^2 |
Число 5 во второй степени |
=5^2 |
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Создание простой формулы
Excel для Интернета Еще…Меньше
Вы можете создать простую формулу для с суммы, вычитания, умножения и деления значений на вашем компьютере. Простые формулы всегда начинаются со знака равной(=),за которым следуют константы, которые являются числами и операторами вычислений, такими как «плюс»(+),«минус»(-),«звездочка»*или «косая черта»(/)в начале.
Например, при вводе формулы =5+2*3последние два числа умножаются и добавляются к первому числу, чтобы получить результат. В стандартном порядке математических операций умножение выполняется перед с добавлением.
-
На сайте щелкните ячейку, в которой вы хотите ввести формулу.
org/ListItem»>
-
Нажмите клавишу ВВОД.
Примечания:
-
Чтобы быстро сложить значения, можно использовать авто сумму, а не вводить формулу вручную(вкладка «Главная», группа «Редактирование»).
-
Для вычисления значений на вашем компьютере также можно использовать функцию (например, функцию СУММ).
-
Чтобы сделать это на один шаг дальше, используйте в формуле ссылки на ячейки вместо фактических значений в простой формуле.

-
Введите знак =(знак равно), за которым следуют константы и операторы, которые вы хотите использовать в вычислениях.
В формулу можно ввести до 8192 знаков.
Совет: Вместо того чтобы вводить константы в формулу, вы можете выбрать ячейки (например, B12:B15), содержащие нужные значения, и ввести операторы между ними.
В приведенной ниже книге показаны примеры простых формул. Вы можете изменить любую из существующих формул или ввести собственные, чтобы узнать, как они работают и посмотреть результаты.
|
Данные |
||
|
2 |
||
|
5 |
||
|
Формула |
Описание |
Результат |
|
‘=A2+A3 |
Сумма значений в ячейках A1 и A2 |
=A2+A3 |
|
‘=A2-A3 |
Разность значений в ячейках A1 и A2 |
=A2-A3 |
|
‘=A2/A3 |
Частное от деления значений в ячейках A1 и A2 |
=A2/A3 |
|
‘=A2*A3 |
Произведение значений в ячейках A1 и A2 |
=A2*A3 |
|
‘=A2^A3 |
Значение в ячейке A1 в степени, указанной в ячейке A2 |
=A2^A3 |
|
Формула |
Описание |
Результат |
|
‘=5+2 |
Сумма чисел 5 и 2 |
=5+2 |
|
‘=5-2 |
Разность чисел 5 и 2 |
=5-2 |
|
‘=5/2 |
Частное от деления 5 на 2 |
=5/2 |
|
‘=5*2 |
Произведение чисел 5 и 2 |
=5*2 |
|
‘=5^2 |
Число 5 во второй степени |
=5^2 |
Как математика помогает выходить из сложных ситуаций»
Математическая формула может пригодиться вам в самой неожиданной ситуации. Например, если вам нужно спасти человечество в разгар энергетического кризиса, предотвратить разлив нефти, сохранить шедевр в Лувре или поставить сложный трюк для голливудского блокбастера. В книге «Формулы на все случаи жизни: Как математика помогает выходить из сложных ситуаций» (издательство «Альпина Паблишер»), переведенной на русский язык Анной Туровской, британский математик Крис Уоринг рассказывает о пользе уравнений на примере не только бытовых, но и экстраординарных событий. Предлагаем вам ознакомиться с фрагментом, посвященным поиску простого числа, состоящего из ста миллионов знаков.
Например, если вам нужно спасти человечество в разгар энергетического кризиса, предотвратить разлив нефти, сохранить шедевр в Лувре или поставить сложный трюк для голливудского блокбастера. В книге «Формулы на все случаи жизни: Как математика помогает выходить из сложных ситуаций» (издательство «Альпина Паблишер»), переведенной на русский язык Анной Туровской, британский математик Крис Уоринг рассказывает о пользе уравнений на примере не только бытовых, но и экстраординарных событий. Предлагаем вам ознакомиться с фрагментом, посвященным поиску простого числа, состоящего из ста миллионов знаков.
Непростое положение
Послание от внеземной цивилизации расшифровано! Вам, старшему IT-специалисту института SETI, поручили ознакомиться с ним и составить ответ. Похоже, что инопланетяне, вступившие в контакт, высокоразвиты, дружелюбны и бескорыстны, поэтому готовы поделиться своими достижениями с другими цивилизациями, которые уже достигли соответствующего уровня научно- технического прогресса. Решим поставленную перед нами задачу — докажем состоятельность человечества. От нас требуется найти простое число, состоящее из ста миллионов знаков. За это инопланетяне в подробностях поведают о своих наиболее важных достижениях. Благодаря им мы сумеем свести к нулю выбросы углекислого газа и, остановив таким образом глобальное потепление, спасем собственную планету. Сумеете ли вы обнаружить настолько монструозное число?
Решим поставленную перед нами задачу — докажем состоятельность человечества. От нас требуется найти простое число, состоящее из ста миллионов знаков. За это инопланетяне в подробностях поведают о своих наиболее важных достижениях. Благодаря им мы сумеем свести к нулю выбросы углекислого газа и, остановив таким образом глобальное потепление, спасем собственную планету. Сумеете ли вы обнаружить настолько монструозное число?
Давайте вспомним, что такое простое число. Исходя из количества делителей, все целые положительные числа можно распределить по трем категориям:
- с одним делителем;
- с двумя делителями;
- с тремя и более делителями.
Делитель — то, на что без остатка делится целое положительное число. Поскольку абсолютно любое число можно поделить на единицу, она является делителем для любого целого положительного числа. К примеру, 6 без остатка делится на 1, 2, 3 и 6: таким образом, у числа 6 четыре делителя, поэтому его можно спокойно поместить в третью категорию с составными числами (скоро вы поймете, почему они называются именно так). Первая категория мала: один-единственный делитель есть только у единицы. Вторая категория включает простые числа, которые делятся на нее и на себя. Вот несколько первых простых чисел: 2, 3, 5, 7, 11, 13, 17. Доказано, что существует бесконечное множество простых чисел. Они стоят особняком и могут здорово помочь вам при совершении покупок в интернете (этот момент мы разберем в подробностях чуть позже).
Первая категория мала: один-единственный делитель есть только у единицы. Вторая категория включает простые числа, которые делятся на нее и на себя. Вот несколько первых простых чисел: 2, 3, 5, 7, 11, 13, 17. Доказано, что существует бесконечное множество простых чисел. Они стоят особняком и могут здорово помочь вам при совершении покупок в интернете (этот момент мы разберем в подробностях чуть позже).
Существует удивительно элегантный математический факт — фундаментальная теорема арифметики. Ее суть полностью соответствует звучному наименованию. Во-первых, в теореме говорится: каждое целое положительное число, от личное от единицы, является либо простым, либо произведением простых чисел. Таким образом, составными называются числа, составленные из последовательно умноженных простых чисел. Во-вторых, теорема заявляет, что каждое составное число может быть представлено в виде произведения простых чисел одним- единственным способом. Например, 6 = 2 × 3. Или, скажем, 123 456 = 2 × 2 × 2 × 3 × 3 × 173. Каждый из приведенных примеров — уникальный, единственно возможный вариант представления составных чисел при разложении на простые множители. Поэтому мы вправе утверждать, что простые числа — своего рода ДНК всех прочих чисел.
Каждый из приведенных примеров — уникальный, единственно возможный вариант представления составных чисел при разложении на простые множители. Поэтому мы вправе утверждать, что простые числа — своего рода ДНК всех прочих чисел.
Поделиться
Невозможно точно определить, является ли то или иное число простым: не существует ни формулы, ни особого способа. Можно лишь попытаться разложить его на меньшие множители. Поэтому так трудно выявлять большие простые числа, поэтому инопланетяне и рассматривают свое задание как тест на уровень развития человечества.
Более 2000 лет назад Эратосфен, древнегреческий математик и глава легендарной Александрийской библиотеки, придумал алгоритм поиска простых чисел. Метод, ныне известный как «решето Эратосфена», включает в себя фильтрацию списка целых положительных чисел. Первое простое число — это 2. Отметив его как простое, вычеркиваете все остальные числа, кратные двум: они в любом случае будут составными. Переходите к следующему невычеркнутому числу — это будет 3. А затем избавляетесь от невычеркнутых чисел, кратных тройке. Возобновляете процесс: следующее число, которым вы еще не занимались, должно быть простым, в чем вы убедитесь, попытавшись разложить его на меньшие множители.
Переходите к следующему невычеркнутому числу — это будет 3. А затем избавляетесь от невычеркнутых чисел, кратных тройке. Возобновляете процесс: следующее число, которым вы еще не занимались, должно быть простым, в чем вы убедитесь, попытавшись разложить его на меньшие множители.
Поделиться
Алгоритм хорош, но трудоемок. Если надо узнать, является ли 323 простым числом, придется делить его на меньшие простые числа, пытаясь установить его кратность 2 (нет), 3 (нет), 5 (нет), 7 (нет), 11 (нет), 13 (нет), 17 (да!). Поскольку 323 делится на 17, вы понимаете, что у него имеются как минимум три делителя (1, 17 и 323), и, следовательно, это число является не простым, а составным. Кстати, 323 = 17 × 19. Если составное число раскладывается только на действительно большие простые множители, то поиск таковых занимает много времени.
Есть ли в этом какой-то смысл? Ладно, вам интересны прибамбасы, которые вы можете получить от более развитой инопланетной цивилизации. Ну а кому-нибудь еще нужны эти простые числа? Да, нужны. Простые числа используются для шифрования сетевого трафика, а в наши дни без интернета не проживешь.
Ну а кому-нибудь еще нужны эти простые числа? Да, нужны. Простые числа используются для шифрования сетевого трафика, а в наши дни без интернета не проживешь.
Поделиться
Простые числа играют большую роль в средствах крипто графической защиты информации в интернете: взять, к при меру, алгоритм компании RSA Security, названной в честь ее основателей — по первым буквам их фамилий: Рональда Ривеста (Rivest), Ади Шамира (Shamir) и Леонарда Адлемана (Adleman). Это пример шифрования с открытым ключом: открытый ключ передается по открытому каналу и используется для шифрования сообщений, а расшифровка сообщений осуществляется при помощи закрытого ключа. Открытый ключ — это произведение двух больших простых чисел: суть в том, что сообщение легко шифруется, однако на его рас шифровку без закрытого ключа могут уйти годы. Чем большие простые числа вы используете для создания публичного ключа, тем надежнее защищены ваши данные. Именно по этому вы можете быть спокойны, делая покупки в интернете: на страже ваших банковских данных стоят простые числа.
Именно по этому вы можете быть спокойны, делая покупки в интернете: на страже ваших банковских данных стоят простые числа.
А еще большие простые числа могут принести большие деньги. Фонд электронных рубежей (Electronic Frontier Foundation) — некоммерческая организация, выступающая за цифровую конфиденциальность, — предлагает премию в размере 150 000 долларов первому, кто найдет простое число, состоящее из 100 миллионов знаков*. Так что вы можете не только спасти Землю, но и подзаработать! Однако для этого вам придется много делить, так что попробуйте повысить свои шансы дать миру новое простое число.
*Также предлагается 250 000 долларов за нахождение простого числа из более 1 млрд знаков. — Прим. науч. ред.
Поделиться
От половины чисел со 100 миллионами знаков можете сразу отмахнуться: ни одно четное число (кроме 2) не будет простым — ведь они по определению кратны 2. Спокойно избавляйтесь еще от одной десятой всех чисел — просто исключите все, которые заканчиваются пятеркой, поскольку они делятся на 5. Есть и другие ухищрения, но даже если вычеркнуть 90 процентов чисел со 100 миллионами знаков, вас тем не менее ждет уйма работы с очень большими числами. Допустим, у вас есть самый мощный в мире компьютер, который проанализирует оставшиеся числа, — но все равно на поиск и проверку нужного числа уйдут долгие годы.
Есть и другие ухищрения, но даже если вычеркнуть 90 процентов чисел со 100 миллионами знаков, вас тем не менее ждет уйма работы с очень большими числами. Допустим, у вас есть самый мощный в мире компьютер, который проанализирует оставшиеся числа, — но все равно на поиск и проверку нужного числа уйдут долгие годы.
Шкала Кардашева
Поиски внеземного разума велись и в Советском Союзе. В них принимал участие советский астрофизик Николай Кардашев. По мнению ученого, существующие инопланетные культуры, скорее всего, оказались бы — и наверняка окажутся — куда прогрессивнее землян. Для классификации цивилизаций он предложил специальную шкалу, оценивающую уровень технологического развития Достичь хотя бы первого уровня человечеству может помочь антиматерия (подробнее см. главу 18).
Достичь хотя бы первого уровня человечеству может помочь антиматерия (подробнее см. главу 18).
**В шкале, описанной Н. Кардашевым в 1964 году в работе «Передача информации внеземными цивилизациями», действительно фигурировали только три типа цивилизаций (ученый ранжировал их по количеству создаваемой и потребляемой энергии), но сейчас эта шкала состоит из семи уровней, включая нулевой, к которому относятся земляне. — Прим. пер.
Поделиться
Что ж, прежде чем прибегнуть к грубой силе — простому перебору, давайте поищем: нет ли какой-нибудь уловки, способной помочь? В нашей ситуации пригодится идея Марена Мерсенна, французского священника XVII века. Мерсенн был чрезвычайно разносторонним человеком, у него есть музыкальные, философские и религиозные работы, но нас интересуют его труды, посвященные математике. Мерсенн писал о числах, представляющих собой разность между 2 в той или иной степени и 1. Эти числа известны как числа Мерсенна, а их формула выглядит так:
Mn = 2n – 1.
Чтобы найти первое число Мерсенна, принимаем n равным 1:
М1 = 21 – 1
= 2 – 1
= 1.
То же самое для n = 2:
М2 = 22 – 1
= 4 – 1
= 3.
Идея понятна. Вот первые одиннадцать чисел Мерсенна: 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047. Отлично! Но как эта формула поможет нам с простыми числами? Мерсенн обратил внимание, что если n — простое число, то и M
Поделиться
В приведенном примере число 2047 представляет собой 23 × 89, что и делает его составным. Простые числа Мерсенна привлекли пристальное внимание научного сообщества, но, разумеется, без ошибок не обошлось — ведь электронные вычисления были еще невозможны. M67, которое, по мнению Мерсенна, являлось простым числом, оказалось составным: 267 – 1 соответствует 147 573 952 589 676 412 927, что, в свою очередь, равняется 193 707 721 × 761 838 257 287. Это было выявлено в 1903 году, спустя 250 лет после смерти Мерсенна.
Это было выявлено в 1903 году, спустя 250 лет после смерти Мерсенна.
Поделиться
Уже после Второй мировой войны, когда появились электронные калькуляторы, проверка простых чисел Мерсенна, которая и без того не прекращалась, набрала обороты. В 1952 году группа исследователей из Калифорнийского университета за несколько часов проверила два новых простых числа Мерсенна — M521 и M607. В общей сложности к текущему моменту обнаружено 51 простое число Мерсенна: они занимают семь верхних строчек в списке самых больших простых чисел, известных науке. Всякий раз, когда ученые находят новое простое число — по формуле Мерсенна или иным образом, — его можно использовать для проверки другого простого числа Мерсенна. Именно поэтому при помощи электронных вычислений по-прежнему ищут новые простые числа: раз от раза они становятся все больше и больше. На сегодня самое большое простое число Мерсенна — это M82589933, в котором почти 25 миллионов знаков.
Чтобы установить, в каком из чисел Мерсенна будет не меньше 100 миллионов знаков, воспользуемся известным нам математическим фактом: при возведении в степень основания 10 результат на один знак меньше, чем у показателя степени. Например:
101 = 10 (2 цифры)
102 = 100 (3 цифры)
103 = 1000 (4 цифры).
Выходит, что 1099999999 будет иметь 100 миллионов знаков. Взглянем для начала на простые числа Мерсенна — по крайней мере, на такие же большие:
2n – 1 ≥ 1099999999.
Это позволит нам пренебречь –1. Достаточно просто взглянуть на число из 100 миллионов знаков, как вычитание единицы тут же теряет всякий смысл. Теперь формула выглядит так:
2n > 1099999999.
Нужно найти n — в данном выражении это степень, — поэтому мы обращаемся к логарифмам (см. главу 13):
n > log2 (1099999999).
Если вы попытаетесь вычислить значение n с помощью калькулятора, тот выдаст ошибку: 1099999999 — это слишком много для устройства. Но есть одно ухищрение. Возведение в степень — это результат многократного умножения числа на себя. К этой хитрости и прибегнем. 1099999999 — это 10, умноженное само на себя 99 999 999 раз. Будь у вас достаточно времени (и бумаги), вы могли бы записать нужное выражение таким образом:
Но есть одно ухищрение. Возведение в степень — это результат многократного умножения числа на себя. К этой хитрости и прибегнем. 1099999999 — это 10, умноженное само на себя 99 999 999 раз. Будь у вас достаточно времени (и бумаги), вы могли бы записать нужное выражение таким образом:
1099999999 = 10 × 10 × 10 × … × 10.
Почему это важно? Потому что мы можем обратиться к основному свойству логарифмов: вне зависимости от основания log (a × a) = log (a) + log (a). Итак:
log2(1099999999) = log2(10) + log2(10) + log2(10) +…+ log2(10).
Всего у вас 99 999 999 членов log2 (10), то есть 99 999 999 × log2 (10). Такое выражение калькулятору по силам:
n > 99 999 999 log2(10)
n > 332 192 806.
Получившееся число — 332 192 806 — сравнительно невелико и имеет всего девять знаков, так что вы можете начать поиск с любого уже проверенного простого числа, которое больше него. Экспресс-анализ сообщает, что в M31, обнаруженном Леонардом Эйлером в 1772 году (2 147 483 647), уже 10 цифр. Как знать, может, победителем станет M2147483647?
Экспресс-анализ сообщает, что в M31, обнаруженном Леонардом Эйлером в 1772 году (2 147 483 647), уже 10 цифр. Как знать, может, победителем станет M2147483647?
Последние семнадцать простых чисел Мерсенна были обнаружены благодаря проекту распределенных вычислений GIMPS (англ. — Great Internet Mersenne Prime Search). Участники проверяют простые числа Мерсенна с привлечением принадлежащего GIMPS программного обеспечения и собственной компьютерной техники любой доступной мощности. Такие хитрые ходы действительно помогают вам сузить поле поиска, однако оно все равно остается очень, очень широким.
Вы осознаете: своими силами институту SETI не обойтись, но можно официально опубликовать задачу и привлечь сторонние ресурсы. Чем больше у вас будет помощников, тем быстрее вы найдете нужное простое число и получите обещанное вознаграждение от дружественных инопланетян. Вы сообщаете руководству: миру пора узнать, что мы не одиноки во Вселенной.
Подробнее читайте:
Уоринг, К. Формулы на все случаи жизни: Как математика помогает выходить из сложных ситуаций / Крис Уоринг : Пер. с англ. [Анны Туровской] — М.: Альпина Паблишер, 2022. — 194 с., ил.
Формулы на все случаи жизни: Как математика помогает выходить из сложных ситуаций / Крис Уоринг : Пер. с англ. [Анны Туровской] — М.: Альпина Паблишер, 2022. — 194 с., ил.
как пользоваться, создавать и изменять
Формулы Excel используют, когда данных очень много. Например, чтобы посчитать сумму нескольких чисел быстрее, чем на калькуляторе. Преимуществ много, поэтому работодатели часто указывают эту программу в требованиях. В конце марта 2022 года 64 225 вакансий на хедхантере содержали формулировки вроде «уверенный пользователь Excel», «работа с формулами в Excel».
Кому важно знать Excel и где выучить основы
Из чего состоит формула в Excel
Основные виды
Простые
Сложные
Комбинированные
Встроенные
Как скопировать
Как обозначить постоянную ячейку
Как поставить «плюс», «равно» без формулы
Главное о формулах в Excel
Кому важно знать Excel и где выучить основы
Excel нужен бухгалтерам, чтобы вести учет в таблицах. Экономистам, чтобы делать перерасчет цен, анализировать показатели компании. Менеджерам — вести базу клиентов. Аналитикам — строить и проверять гипотезы.
Экономистам, чтобы делать перерасчет цен, анализировать показатели компании. Менеджерам — вести базу клиентов. Аналитикам — строить и проверять гипотезы.
Программу можно освоить самостоятельно, например по статьям в интернете. Но это поможет понять только основные формулы. Если нужны глубокие знания — как строить сложные прогнозы, собирать калькулятор юнит-экономики, — пройдите курсы.
На онлайн-курсе Skypro «Аналитик данных» научитесь владеть базовыми формулами Excel, работать с нестандартными данными, статистикой. Кроме Excel вы изучите Metabase, SQL, Power BI, язык программирования Python. Программа подойдет даже тем, у кого совсем нет опыта в анализе и кто не любит математику. Вас ждут живые вебинары, мастер-классы, домашки с разбором, помощь наставников.
Урок из курса «Аналитик данных» в Skypro
Из чего состоит формула в Excel
Основные знаки:
= с него начинают любую формулу;
( ) заключают формулу и ее части;
; применяют, чтобы указать очередность ячеек или действий;
: ставят, чтобы обозначить диапазон ячеек, а не выбирать всё подряд вручную.
Еще используют символы сравнения:
равенство =
меньше <
больше >
меньше либо равно <=
больше либо равно >=
не равно <>
Основные виды
Все формулы в Excel делятся на простые, сложные и комбинированные. Их можно написать самостоятельно или воспользоваться встроенными.
Простые
Применяют, когда нужно совершить одно простое действие, например сложить или умножить.
✅ СУММ. Складывает несколько чисел. Сумму можно посчитать для нескольких ячеек или целого диапазона.
=СУММ(А1;В1) — для соседних ячеек;
=СУММ(А1;С1;h2) — для определенных ячеек;
=СУММ(А1:Е1) — для диапазона.
Сумма всех чисел в ячейках от А1 до Е1
✅ ПРОИЗВЕД. Умножает числа в соседних, выбранных вручную ячейках или диапазоне.
=ПРОИЗВЕД(А1;В1)
=ПРОИЗВЕД(А1;С1;h2)
=ПРОИЗВЕД(А1:Е1)
Произведение всех чисел в ячейках от А1 до Е1
✅ ОКРУГЛ. Округляет дробное число до целого в большую или меньшую сторону. Укажите ячейку с нужным числом, в качестве второго значения — 0.
Округляет дробное число до целого в большую или меньшую сторону. Укажите ячейку с нужным числом, в качестве второго значения — 0.
=ОКРУГЛВВЕРХ(А1;0) — к большему целому числу;
=ОКРУГЛВНИЗ(А1;0) — к меньшему.
Округление в меньшую сторону
✅ ВПР. Находит данные в таблице или определенном диапазоне.
=ВПР(С1;А1:В6;2)
- С1 — ячейка, в которую выписывают известные данные. В примере это код цвета.
- А1 по В6 — диапазон ячеек. Ищем название цвета по коду.
- 2 — порядковый номер столбца для поиска. В нём указаны названия цвета.
Формула вычислила, какой цвет соответствует коду
✅ СЦЕПИТЬ. Объединяет данные диапазона ячеек, например текст или цифры. Между содержимым ячеек можно добавить пробел, если объединяете слова в предложения.
=СЦЕПИТЬ(А1;В1;С1) — текст без пробелов;
=СЦЕПИТЬ(А1;" ";В1;" "С1) — с пробелами.
Формула объединила три слова в одно предложение
✅ КОРЕНЬ. Вычисляет квадратный корень числа в ячейке.
Вычисляет квадратный корень числа в ячейке.
=КОРЕНЬ(А1)
Квадратный корень числа в ячейке А1
✅ ПРОПИСН. Преобразует текст в верхний регистр, то есть делает буквы заглавными.
=ПРОПИСН(А1:С1)
Формула преобразовала строчные буквы в прописные
✅ СТРОЧН. Переводит текст в нижний регистр, то есть делает из больших букв маленькие.
=СТРОЧН(А2)
✅ СЧЕТ. Считает количество ячеек с числами.
=СЧЕТ(А1:В5)
Формула вычислила, что в диапазоне А1:В5 четыре ячейки с числами
✅ СЖПРОБЕЛЫ. Убирает лишние пробелы. Например, когда переносите текст из другого документа и сомневаетесь, правильно ли там стоят пробелы.
=СЖПРОБЕЛЫ(А1)
Формула удалила двойные и тройные пробелы
Сложные
✅ ПСТР. Выделяет определенное количество знаков в тексте, например одно слово.
=ПСТР(А1;9;5)
- Введите =ПСТР.
- Кликните на ячейку, где нужно выделить знаки.
- Укажите номер начального знака: например, с какого символа начинается слово. Пробелы тоже считайте.
- Поставьте количество знаков, которые нужно выделить из текста. Например, если слово состоит из пяти букв, впишите цифру 5.
В ячейке А1 формула выделила 5 символов, начиная с 9-го
✅ ЕСЛИ. Анализирует данные по условию. Например, когда нужно сравнить одно с другим.
=ЕСЛИ(A1>25;"больше 25";"меньше или равно 25")
В формуле указали:
- А1 — ячейку с данными;
- >25 — логическое выражение;
- больше 25, меньше или равно 25 — истинное и ложное значения.
Первый результат возвращается, если сравнение истинно. Второй — если ложно.
Число в А1 больше 25. Поэтому формула показывает первый результат — больше 25.
✅ СУММЕСЛИ. Складывает числа, которые соответствуют критерию. Обычно критерий — числовой промежуток или предел.
Обычно критерий — числовой промежуток или предел.
=СУММЕСЛИ(В2:В5;">10")
В формуле указали:
- В2:В5 — диапазон ячеек;
- >10 — критерий, то есть числа меньше 10 не будут суммироваться.
Число 8 меньше указанного в условии, то есть 10. Поэтому оно не вошло в сумму.
✅ СУММЕСЛИМН. Складывает числа, когда условий несколько. В формуле указывают диапазоны — ячейки, которые нужно учитывать. И условия — содержание подходящих ячеек. Например:
=СУММЕСЛИМН(D2:D6;C2:C6;"сувениры";B2:B6;"ООО ХY")
- D2:D6 — диапазон, из которого суммируем числа;
- C2:C6 — диапазон ячеек для категории;
- сувениры — условие, то есть числа другой категории учитываться не будут;
- B2:B6 — диапазон ячеек для компании;
- ООО XY — условие, то есть числа другой компании учитываться не будут.
Под условия подошли только ячейки D3 и D6: их сумму и вывела формула
Комбинированные
В Excel можно комбинировать несколько функций: сложение, умножение, сравнение и другие. Например, вам нужно найти сумму двух чисел. Если значение больше 65, сумму нужно умножить на 1,5. Если меньше — на 2.
Например, вам нужно найти сумму двух чисел. Если значение больше 65, сумму нужно умножить на 1,5. Если меньше — на 2.
=ЕСЛИ(СУММ(A1;B1)<65;СУММ(A1;B1)*1,5;(СУММ(A1;B1)*2))
То есть если сумма двух чисел в А1 и В1 окажется меньше 65, программа посчитает первое условие — СУММ(А1;В1)*1,5. Больше 65 — Excel задействует второе условие — СУММ(А1;В1)*2.
Сумма в А1 и В1 больше 65, поэтому формула посчитала по второму условию: умножила на 2
Встроенные
Используйте их, если удобнее пользоваться готовыми формулами, а не вписывать вручную.
- Поместите курсор в нужную ячейку.
- Откройте диалоговое окно мастера: нажмите клавиши Shift + F3. Откроется список функций.
- Выберите нужную формулу. Нажмите на нее, затем на «ОК». Откроется окно «Аргументы функций».
- Внесите нужные данные. Например, числа, которые нужно сложить.
Ищите формулу по алфавиту или тематике, выбирайте любую из тех, что использовали недавно
Как скопировать
Если для разных ячеек нужны однотипные действия, например сложить числа не в одной, а в нескольких строках, скопируйте формулу.
- Впишите функцию в ячейку и кликните на нее.
- Наведите курсор на правый нижний угол — курсор примет форму креста.
- Нажмите левую кнопку мыши, удерживайте ее и тяните до нужной ячейки.
- Отпустите кнопку. Появится итог.
Посчитали сумму ячеек в трех строках
Как обозначить постоянную ячейку
Это нужно, чтобы, когда вы протягивали формулу, ссылка на ячейку не смещалась.
- Нажмите на ячейку с формулой.
- Поместите курсор в нужную ячейку и нажмите F4.
- В формуле фрагмент с описанием ячейки приобретет вид $A$1. Если вы протянете формулу, то ссылка на ячейку $A$1 останется на месте.
Как поставить «плюс», «равно» без формулы
Когда нужна не формула, а данные, например +10 °С:
- Кликните правой кнопкой по ячейке.
- Выберите «Формат ячеек».
- Отметьте «Текстовый», нажмите «ОК».
- Поставьте = или +, затем нужное число.
- Нажмите Enter.
Главное о формулах в Excel
- Формула состоит из математических знаков.
 Чтобы ее вписать, используют символы = ( ) ; : .
Чтобы ее вписать, используют символы = ( ) ; : . - С помощью простых формул числа складывают, умножают, округляют, извлекают из них квадратный корень. Чтобы отредактировать текст, используют формулы поиска, изменения регистра, удаления лишних пробелов.
- Сложные и комбинированные формулы помогают делать объемные вычисления, когда нужно соблюдать несколько условий.
Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.
Площадь плоских фигур
Площадь треугольника
Площадь прямоугольного треугольника
Площадь треугольника формула Герона
Площадь равнобедренного треугольника
Площадь равностороннего треугольника
Площадь треугольника через две стороны и угол
Площадь треугольника через сторону и два угла
Площадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь ромба
Площадь произвольной трапеции
Площадь равнобедренной трапеции
Площадь правильного многоугольника
Площадь круга
Площадь сектора круга
Площадь сегмента круга
Площадь кольца
Площадь сектора кольца
Площадь эллипса
Все формулы раздела
Площадь поверхности тел
Площадь поверхности куба
Площадь поверхности параллелепипеда
Площадь поверхности сферы
Площадь поверхности шарового сегмента
Площадь поверхности шарового слоя
Площадь поверхности шарового сектора
Площадь поверхности цилиндра
Площадь поверхности конуса
Площадь поверхности усеченного конуса
Площадь поверхности правильной пирамиды
Боковая поверхность правильной усеченной пирамиды
Все формулы раздела
Объем тел
Объем куба
Объем параллелепипеда
Объем шара
Объем шарового сегмента
Объем шарового слоя
Объем шарового сектора
Объем цилиндра
Объем конуса
Объем усеченного конуса
Объем пирамиды
Объем усеченной пирамиды
Объем правильной пирамиды
Объем правильной треугольной пирамиды
Объем правильной четырехугольной пирамиды
Объем правильного тетраэдра
Все формулы раздела
Периметр фигур
Периметр круга или длина окружности
Длина дуги
Периметр треугольника
Периметр прямоугольника
Периметр квадрата
Периметр параллелограмма
Периметр ромба
Периметр трапеции
Длина дуги, формула Гюйгенса
Все формулы раздела
Радиус описанной окружности
Радиус описанной окружности треугольника
Радиус описанной окружности равностороннего треугольника
Радиус описанной окружности равнобедренного треугольника
Радиус описанной окружности прямоугольного треугольника
Радиус описанной окружности квадрата
Радиус описанной окружности прямоугольника
Радиус описанной окружности равнобокой трапеции
Радиус описанной окружности правильного шестиугольника
Радиус описанной окружности правильного многоугольника
Все формулы раздела
Радиус вписанной окружности
Радиус вписанной окружности в треугольник
Радиус вписанной окружности в равносторонний треугольник
Радиус вписанной окружности в равнобедренный треугольник
Радиус вписанной окружности в прямоугольный треугольник
Радиус вписанной окружности в квадрат
Радиус вписанной окружности в ромб
Радиус вписанной окружности в трапецию
Радиус вписанной окружности в правильный многоугольник
Радиус вписанной окружности в правильный шестиугольник
Все формулы раздела
Формулы для параллелограмма
Длина стороны параллелограмма
Длина диагоналей параллелограмма
Сумма квадратов диагоналей
Углы параллелограмма
Углы между диагоналями параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Формулы для ромба
Диагонали ромба
Сторона ромба
Углы ромба
Формулы для окружности, круга
Радиус окружности
Длина хорды окружности
Высота сегмента круга, окружности
Площадь круга
Длина окружности
Формулы для квадрата и прямоугольника
Сторона квадрата
Диагонали квадрата
Диагональ и углы прямоугольника
Формулы для треугольника
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все формулы раздела
Формулы для произвольной трапеции
Стороны трапеции
Диагональ трапеции
Средняя линия трапеции
Высота трапеции
Формулы для равнобедренной трапеции
Стороны равнобедренной трапеции
Диагональ равнобедренной трапеции
Высота равнобедренной трапеции
Средняя линия равнобедренной трапеции
Формулы для прямоугольной трапеции
Основания прямоугольной трапеции
Диагональ прямоугольной трапеции
Боковые стороны прямоугольной трапеции
Средняя линия прямоугольной трапеции
Тригонометрические тождества
sin, cos, tg, ctg
Сумма углов: sin(α+β), cos(α+β), tg(α+β), ctg(α+β)
Разность углов: sin(α-β), cos(α-β), tg(α-β), ctg(α-β)
Двойной угол: sin(2α), cos(2α), tg(2α), ctg(2α)
Тройной угол: sin(3α), cos(3α), tg(3α), ctg(3α)
Половинный угол: sin(α/2), cos(α/2), tg(α/2), ctg(α/2)
Квадрат функций: sin2(α), cos2(α), tg2(α), ctg2(α)
Куб функций: sin3(α), cos3(α), tg3(α), ctg3(α)
Сумма функций: sin(α), cos(α), tg(α), ctg(α)
Разность функций: sin(α), cos(α), tg(α), ctg(α)
Произведение функций: sin(α), cos(α), tg(α), ctg(α)
Формулы приведения функций: sin(α), cos(α), tg(α), ctg(α)
Понятие, что такое: sin(α), cos(α), tg(α), ctg(α)
Все формулы раздела
Теоремы
Теорема синусов
Теорема косинусов
Теорема Пифагора
Формулы сокращенного умножения
Квадрат суммы (a+b)2
Квадрат разности (a-b)2
Разность квадратов a2 — b2
Куб суммы (a+b)3
Куб разности (a-b)3
Сумма кубов a3 +b3
Разность кубов a3 — b3
Разность n степеней an — bn
Все формулы раздела
Производные
Производная функции Y(X)
Производная сложной функции (V, U)
Одночлены Многочлены
Правила возведения в степень
Одночлен, многочлен и действия над ними
Факториал числа
Биномиальные коэффициенты
Треугольник Паскаля
Бином Ньютона
Кинематика
Свободное падение тел
Скорость, расстояние, время и координата тела падающего вертикально вниз с нулевой начальной скоростью
Скорость, расстояние, время и координата тела падающего вертикально вниз с не нулевой начальной скоростью
Скорость, время, высота тела брошенного вертикально вверх
Скорость, время, расстояние, высота тела брошенного горизонтально
Бросок под углом к горизонту, максимальные значения
Бросок под углом к горизонту, высота
Бросок под углом к горизонту, время
На сайте, в простой и понятной форме, выложены основные формулы по геометрии, алгебре, которые вы найдете по ссылкам выше.
Формула через основание и высоту:
Любая формула в один клик с главной страницы.
Так же на основных страницах, есть боковые меню (если вы зашли с компьютера) и эти же меню, вы найдете внизу страницы (если используете мобильное устройство). Эти меню позволяет быстро перемещаться по сайту и находить необходимую информацию. Есть различные калькуляторы для расчетов необходимых значений.
Формулы регулярно добавляются
2011-08-21
- Подробности
- Автор: Сергей Кондратов
Рейтинг: 5 / 5
Пожалуйста, оцените Оценка 1Оценка 2Оценка 3Оценка 4Оценка 5Создать простую формулу
Excel для Интернета Дополнительно. .. Меньше
.. Меньше
Вы можете создать простую формулу для сложения, вычитания, умножения или деления значений на листе. Простые формулы всегда начинаются со знака равенства ( = ), за которым следуют константы, представляющие собой числовые значения, и операторы вычисления, такие как плюс ( + ), минус ( — ), звездочка ( * ) или косая черта. ( / ) знаки.
Например, когда вы вводите формулу =5+2*3 , последние два числа умножаются и добавляются к первому числу, чтобы получить результат. Следуя стандартному порядку математических операций, умножение выполняется перед сложением.
На рабочем листе щелкните ячейку, в которую вы хотите ввести формулу.
Введите = (знак равенства), а затем константы и операторы, которые вы хотите использовать в расчетах.

Вы можете ввести в формулу столько констант и операторов, сколько вам нужно, до 8192 символов.
Совет: Вместо того, чтобы вводить константы в формулу, вы можете выбрать ячейки (например, B12:B15), которые содержат значения, которые вы хотите использовать, и ввести операторы между выбранными ячейками.
Нажмите Enter.
Примечания:
Для быстрого добавления значений можно использовать AutoSum вместо ввода формулы вручную ( вкладка Главная , группа Редактирование ).
Вы также можете использовать функцию (например, функцию СУММ) для вычисления значений на листе.
Чтобы сделать еще один шаг вперед, вы можете использовать ссылки на ячейки в формуле вместо фактических значений в простой формуле.

В рабочей тетради ниже показаны примеры простых формул. Вы можете изменить любую из существующих формул или ввести свои собственные формулы, чтобы узнать, как они работают, и увидеть их результаты.
Данные | ||
2 | ||
5 | ||
Формула | Описание | Результат |
‘=А2+А3 | Складывает значения в ячейках A1 и A2 | =А2+А3 |
‘=А2-А3 | Вычитает значение в ячейке A2 из значения в ячейке A1 | =А2-А3 |
‘=А2/А3 | Делит значение в ячейке A1 на значение в ячейке A2 | =А2/А3 |
‘=А2*А3 9А3 | ||
Формула | Описание | Результат |
‘=5+2 | Добавляет 5 и 2 | =5+2 |
‘=5-2 | Вычесть 2 из 5 | =5-2 |
‘=5/2 | Делит 5 на 2 | 92
Создание простой формулы в Excel
Excel
Формулы и функции
Формулы
Формулы
Создать простую формулу в Excel
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Больше. ..Меньше
..Меньше
Вы можете создать простую формулу для сложения, вычитания, умножения или деления значений на листе. Простые формулы всегда начинаются со знака равенства ( = ), за которым следуют константы, представляющие собой числовые значения, и операторы вычисления, такие как плюс ( + ), минус ( — ), звездочка ( * ) или косая черта. ( / ) знаки.
Возьмем пример простой формулы.
На рабочем листе щелкните ячейку, в которую вы хотите ввести формулу.
Введите = (знак равенства), а затем константы и операторы (до 8192 символов), которые вы хотите использовать в расчетах.
В нашем примере введите =1+1 .

Примечания:
Вместо того, чтобы вводить константы в формулу, вы можете выбрать ячейки, содержащие значения, которые вы хотите использовать, и ввести операторы между выбранными ячейками.
В соответствии со стандартным порядком математических операций умножение и деление выполняются перед сложением и вычитанием.
Нажмите Введите (Windows) или Верните (Mac).
Возьмем еще один вариант простой формулы. Введите =5+2*3 в другую ячейку и нажмите Введите или Верните . Excel умножает два последних числа и прибавляет к результату первое число.
Excel умножает два последних числа и прибавляет к результату первое число.
Использовать автосумму
Вы можете использовать автосумму для быстрого суммирования столбца, строки или чисел. Выберите ячейку рядом с числами, которые вы хотите просуммировать, щелкните AutoSum на вкладке Home , нажмите Enter (Windows) или Return (Mac), и все!
Когда вы нажимаете Автосумма , Excel автоматически вводит формулу (которая использует функцию СУММ) для суммирования чисел.
Примечание: Вы также можете ввести ALT+= (Windows) или ALT++= (Mac) в ячейку, и Excel автоматически вставит функцию СУММ.
Вот пример. Чтобы добавить числа за январь в этот бюджет развлечений, выберите ячейку B7, ячейку непосредственно под столбцом чисел. Затем нажмите AutoSum . В ячейке B7 появляется формула, и Excel выделяет ячейки, которые вы суммируете.
Нажмите Enter, чтобы отобразить результат (95.94) в ячейке В7. Вы также можете увидеть формулу в строке формул в верхней части окна Excel.
Примечания:
Чтобы просуммировать столбец чисел, выберите ячейку непосредственно под последним числом в столбце. Чтобы просуммировать ряд чисел, выберите ячейку сразу справа.
Создав формулу, вы можете скопировать ее в другие ячейки вместо того, чтобы вводить ее снова и снова. Например, если вы скопируете формулу из ячейки B7 в ячейку C7, формула в ячейке C7 автоматически подстроится под новое местоположение и вычислит числа в ячейках C3:C6.
org/ListItem»>
Вы также можете использовать автосумму для нескольких ячеек одновременно. Например, вы можете выделить ячейки B7 и C7, щелкнуть Автосумма и одновременно подвести итоги по обоим столбцам.
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
Примечание. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Введите (Windows) или Верните (Mac).
Данные | ||
2 | ||
5 | ||
Формула | Описание | Результат |
=А2+А3 | Складывает значения в ячейках A1 и A2 | =А2+А3 |
=А2-А3 | Вычитает значение в ячейке A2 из значения в ячейке A1 | =А2-А3 |
=А2/А3 | Делит значение в ячейке A1 на значение в ячейке A2 | =А2/А3 |
=А2*А3 | Умножает значение в ячейке A1 на значение в ячейке A2 9А3 | |
Формула | Описание | Результат |
=5+2 | Добавляет 5 и 2 | =5+2 |
=5-2 | Вычесть 2 из 5 | =5-2 |
=5/2 | Делит 5 на 2 | =5/2 | 92
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
Формулы Excel: простые формулы
Урок 2: простые формулы
/en/excelformulas/about-this-tutorial/content/
Введение
Одной из самых мощных функций Excel является возможность вычислить числовую информацию, используя формулы . Как и калькулятор, Excel может складывать, вычитать, умножать и делить. В этом уроке мы покажем вам, как использовать ссылок на ячейки для создания простых формул.
Дополнительно: загрузите нашу рабочую тетрадь.
Посмотрите видео ниже, чтобы узнать, как создавать формулы в Excel.
Математические операторы
Excel использует стандартные операторы для формул, такие как знак плюс 9 ) для показателей.
Стандартные операторы
Все формулы в Excel должны начинаться со знака равенства ( = ). Это связано с тем, что ячейка содержит или равна формуле и вычисляемому ею значению.
Это связано с тем, что ячейка содержит или равна формуле и вычисляемому ею значению.
Понимание ссылок на ячейки
Хотя вы можете создавать простые формулы в Excel вручную (например, =2+2 или =5*5 ), большую часть времени вы будете использовать адресов ячеек для создания формулы . Это известно как создание номер ячейки . Использование ссылок на ячейки гарантирует, что ваши формулы всегда будут точными, поскольку вы можете изменить значение ячеек, на которые ссылаются, без необходимости переписывать формулу.
Использование ссылок на ячейки для пересчета формулы
Комбинируя математический оператор со ссылками на ячейки, вы можете создавать различные простые формулы в Excel. Формулы также могут включать комбинацию ссылок на ячейки и номеров, как в примерах ниже:
Примеры простых формул
Чтобы создать формулу:
В приведенном ниже примере мы будем использовать простую формулу и ссылки на ячейки для расчета бюджета.
- Выберите ячейку , которая будет содержать формулу. В нашем примере мы выберем ячейку B3 .
Выбор ячейки B3
- Введите знак равенства (=) . Обратите внимание, как он отображается в ячейке и в формуле bar .
Ввод знака =
- Введите ячейка адрес ячейки, на которую вы хотите сослаться первой в формуле: ячейка B1 в нашем примере. Вокруг указанной ячейки появится синяя рамка .
Ссылка на ячейку B1
- Введите математический оператор , который вы хотите использовать. В нашем примере мы введем знак добавления ( + ).
- Введите адрес ячейки ячейки, на которую вы хотите сослаться второй в формуле: ячейка B2 в нашем примере.
 Вокруг указанной ячейки появится красная рамка .
Вокруг указанной ячейки появится красная рамка .Ссылка на ячейку B2
- Нажмите Введите на клавиатуре. Формула будет рассчитана , а в ячейке будет отображаться значение .
Полная формула и расчетное значение
Если результат формулы слишком велик для отображения в ячейке, он может отображаться в виде знаков фунта стерлингов (#######) вместо значения. Это означает, что ширина столбца недостаточно широка для отображения содержимого ячейки. Просто увеличьте ширину столбца для отображения содержимого ячейки.
Изменение значений с помощью ссылок на ячейки
Истинное преимущество ссылок на ячейки заключается в том, что они позволяют обновлять данные на листе без необходимости переписывать формулы. В приведенном ниже примере мы изменили значение ячейки B1 с 1200 до 1800 долларов. Формула в ячейке B3 автоматически пересчитает и отобразит новое значение в ячейке B3.
Формула в ячейке B3 автоматически пересчитает и отобразит новое значение в ячейке B3.
Пересчитанное значение ячейки
Excel не всегда будет сообщать вам , если ваша формула содержит ошибку, поэтому вы должны проверить все свои формулы. Чтобы узнать, как это сделать, вы можете прочитать урок «Перепроверьте свои формулы» из нашего учебника по формулам Excel.
Чтобы создать формулу методом «укажи и щелкни»:
Вместо того, чтобы вводить адреса ячеек вручную, вы можете указать и щелкнуть ячейки, которые вы хотите включить в формулу. Этот метод может сэкономить много времени и усилий при создании формул. В приведенном ниже примере мы создадим формулу для расчета стоимости заказа нескольких коробок пластиковых столовых приборов.
- Выберите ячейку , которая будет содержать формулу. В нашем примере мы выберем ячейку D3 .
Выбор ячейки D3
- Введите знак равенства (=) .

- Выберите ячейку , на которую вы хотите сослаться первой в формуле: ячейка B3 в нашем примере. В формуле появится адрес ячейки , а вокруг указанной ячейки появится пунктирная синяя линия .
Ссылочная ячейка B3
- Введите математический оператор , который вы хотите использовать. В нашем примере мы введем знак умножения (*) .
- Выберите ячейку , на которую вы хотите сослаться второй в формуле: ячейка C3 в нашем примере. В формуле появится адрес ячейки , а вокруг указанной ячейки появится пунктирная красная линия .
Ссылка на ячейку C3
- Нажмите Введите на клавиатуре. Формула будет вычислил , и в ячейке отобразится значение .
Завершенная формула и вычисленное значение
Формулы также могут быть скопированы в соседние ячейки с помощью заполнения ручки , что может сэкономить много времени и усилий, если вам нужно выполнить одно и то же вычисление кратное раз на листе.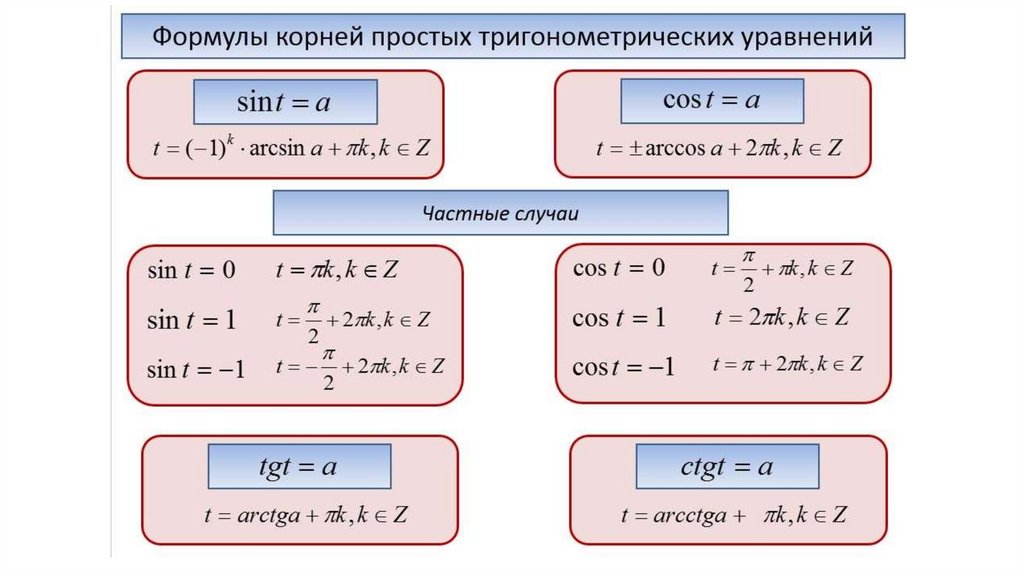 Просмотрите наш урок об относительных и абсолютных ссылках на ячейки, чтобы узнать больше.
Просмотрите наш урок об относительных и абсолютных ссылках на ячейки, чтобы узнать больше.
Копирование формулы в соседние ячейки с помощью маркера заполнения
Чтобы изменить формулу:
Иногда вам может понадобиться изменить существующую формулу. В приведенном ниже примере мы ввели неверный адрес ячейки в нашу формулу, поэтому нам нужно его исправить.
- Выберите ячейку , содержащую формулу, которую вы хотите изменить. В нашем примере мы выберем ячейку B3 .
Выбор ячейки B3
- Щелкните строку формул , чтобы изменить формулу. Вы также можете дважды щелкнуть ячейку, чтобы просмотреть и изменить формулу непосредственно в ячейке.
Выбор формулы для редактирования
- Рамка появится вокруг любых ячеек, на которые есть ссылки. В нашем примере мы изменим вторую часть формулы, указав ссылку на ячейку B2 вместо ячейки C2 .

Неуместная ссылка на ячейку
- Когда вы закончите, нажмите Введите на клавиатуре или щелкните галочкой в строке формул.
Редактирование формулы
- Формула будет обновлена , а в ячейке будет отображаться новое значение .
Новое рассчитанное значение
Если вы передумаете, вы можете нажать клавишу Esc на клавиатуре, чтобы случайно не внести изменения в формулу.
Чтобы отобразить все формулы в электронной таблице, вы можете, удерживая клавишу Ctrl , нажать ` (большое ударение). Клавиша серьезного акцента обычно находится в верхнем левом углу клавиатуры. Вы можете нажать Ctrl+` еще раз, чтобы вернуться к обычному виду.
Вызов!
- Откройте существующую книгу Excel.
 Если вы хотите, вы можете использовать нашу рабочую тетрадь.
Если вы хотите, вы можете использовать нашу рабочую тетрадь. - Создайте простую формулу сложения, используя ссылок на ячейки . Если вы используете пример, создайте формулу в ячейке B4 для расчета общего бюджета.
- Попробуйте изменить значение ячейки, на которую ссылается формула. Если вы используете пример, измените значение ячейки B2 до 2000 долларов. Обратите внимание, как формула в ячейке B4 пересчитывает итог.
- Попробуйте использовать метод «укажи и щелкни» для создания формулы. Если вы используете пример, создайте формулу в ячейке G5 , которая умножает стоимость салфеток на количество , необходимое для расчета общей стоимости .
- Редактировать формулу с помощью строки формул. Если вы используете пример, отредактируйте формулу в ячейке B9 9.0648, чтобы изменить знак деления ( / ) на знак минус ( — ).

Предыдущий: Об этом учебнике
Далее:Сложные формулы
/en/excelformulas/complex-formulas/content/
Список 10 лучших основных формул и функций Excel (с примерами)
Вот список 10 основных формул и функций в Excel.
- Сумма
- COUN
- COUNTA
- COUNTBLANK
- Среднее
- MIN Excel
- MAX Excel
- LEN Excel
- Excel
- IAL Excel
- Excel
- IT Excel
- EXCEL LIT LIT EXEL
- IT Excel
- Excel Excel
- IT Excel
- IN EXCEL
- IT Excel .
- Список 10 основных основных формул и функций Excel
- #1 СУММ в Excel
- Пример
- #2 Функция Excel Excel
- Пример
- #3 Counta в Excel
- Пример
- #4 Countblank в Excel
- Пример
- #4 Countblank в Excel
- 40044 4004444444444444444444444444444.

- #4.
- Формула #6 MIN в Excel
- Пример
- Формула #7 MAX в Excel
- Пример
- #8 LEN в Excel
- 4 Пример 3
- #9 Триминация в Excel
- Пример
- #10, если в Excel
- Пример
- . Шаблон Excel с формулами здесь — Шаблон Excel с основными формулами
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Основные формулы Excel (wallstreetmojo.com)#1 СУММ в Excel
Эта базовая формула Excel используется для получения суммы значений в одной или нескольких ячейках или диапазонах.
Пример
=СУММ(A1 :A5 )
Результат = 41 (см. рисунок ниже)
#2 COUNT Функция Excel
Эта базовая функция Excel подсчитывает числовые значения в одной или нескольких ячейках или нескольких диапазонах.
 .
.Пример
=СЧЁТ(A1:A5)
Результат = 4 (Это исключит ячейку A3, поскольку эта формула вычисляет только числовое значение. См. изображение ниже).
#3 COUNTA в Excel
Эта формула подсчитывает значение в одной или нескольких ячейках (при этом будут измеряться ячейки независимо от числового или текстового значения).
Пример
=СЧЕТЧАС(A1:A5)
Результат = 5 (Это будет включать ячейку A3, так как эта формула вычисляет как текст, так и числовое значение. См. изображение ниже).
#4 СЧИТАТЬ ПРОПУСТЫ в Excel
Эта базовая функция Excel подсчитывает пустое значение в диапазоне. (Примечание: мы не будем считать только пробел в ячейке пустой ячейкой).
Пример
=СЧИТАТЬПУСТОТЫ(A1:A5)
Результат = 2 (Это подсчитает количество пустых ячеек в диапазоне. См. изображение ниже).
#5 СРЗНАЧ в Excel
Эта базовая формула в Excel используется для получения среднего значения в одной или нескольких ячейках или диапазонах.

Пример
=СРЗНАЧ(A1:A5)
Результат = 4 (см. изображение ниже)
#6 Формула MIN в Excel
Эта базовая функция Excel используется для получения минимального значения в ячейках или диапазоне.
Пример
= МИН(A1:A5). Результат = 2 (см. изображение ниже)
#7 Формула MAX в Excel
Эта базовая функция Excel используется для получения максимального значения в ячейках или диапазоне.
Пример
=MAX(A1:A5)
Результат = 9 (см. изображение ниже)
#8 ДЛСТР в Excel
Эта базовая функция Excel используется для подсчета количества символов в ячейке или тексте.
Пример=LEN(A1)
Значением ячейки A1 является Shivam, длина которого составляет 6 символов. Таким образом, результат будет 6 (см. изображение ниже).
#9 ОБРЕЗКА в Excel
Эта базовая функция Excel удаляет ненужные пробелы в ячейке или тексте.

СИНТАКСИС: TRIM(TEXT)
Пример
=TRIM(A1)
В ячейке A1 есть два пробела между именем, отчеством и фамилией. Эта функция удалит лишнее пространство, чтобы дать результат. (См. изображение ниже).
#10 ЕСЛИ в Excel
Функция ЕСЛИ может выполнять логический тест в excelЛогический тест в ExcelЛогический тест в Excel приводит к аналитическому выводу, который может быть либо истинным, либо ложным. Оператор равенства «=» является наиболее часто используемой логической проверкой.Подробнее.
Пример= ЕСЛИ (A1> 33, «P», «F»). Значение в ячейке A1 равно 50, и логическая проверка выполняется, если значение больше 33. Тогда результатом будет P. В противном случае результатом будет F.
Поскольку значение 50 больше 33, результатом будет быть P. (см. изображение ниже).
Что следует помнить
- Формула всегда должна начинаться со знака равенства.
 В противном случае он покажет ошибку.
В противном случае он покажет ошибку. - Если мы вводим любое текстовое значение вместо указания адреса ячейки, мы должны указать текстовое значение в кавычках («»).
- Перед вводом функции в ячейку убедитесь, что формат ячейки является общим. Если выбран текстовый формат, то формула не будет работать.
- Пробел (_) всегда считается одним символом. Итак, если вы работаете с пустыми ячейками, помните, что если в ячейке есть только пробел, она не будет считаться пустой ячейкой.
Видео с основными формулами Excel
Рекомендуемые статьи
Это руководство по основным формулам в Excel. Здесь мы обсуждаем список 10 лучших основных формул и функций в Excel, включая СУММ, СЧЕТЧИК, СЧЕТЧИК, СЧИТАТЬПУСТОТЫ, МАКС, МИН и т. д. с загружаемым шаблоном Excel. Вы можете узнать больше об Excel из следующих статей —
- Формула ЕСЛИ ExcelExcel Функция ЕСЛИ ФормулаЕСЛИ в Excel оценивает, выполняется ли заданное условие, и возвращает значение в зависимости от того, является ли результат «истинным» или «ложным».
 Это условная функция Excel, которая возвращает результат на основе выполнения или невыполнения заданных критериев.
читать далее
Это условная функция Excel, которая возвращает результат на основе выполнения или невыполнения заданных критериев.
читать далее - Среднее значение FormulaAverage FormulaAverage — это значение, которое используется для представления набора значений данных, как среднее значение, рассчитанное из всех данных, и эта формула рассчитывается путем сложения всех значений заданного набора, обозначаемого суммированием X и разделив его на количество значений, данных в наборе, обозначенном N.читать далее
- Как использовать функцию режима в Excel?Как использовать функцию режима в Excel?Функция режима в Excel — это статистическая функция, которая возвращает наиболее часто встречающееся значение в наборе данных. Если есть несколько режимов, он вернет самый низкий. читать далее
- Примеры VBA TRIM Примеры VBA TRIM VBA TRIM классифицируется как строковая и текстовая функция. Это функция рабочего листа в VBA, которая, как и ссылка на рабочий лист, используется для обрезки или удаления ненужных пробелов из строки.
 Он принимает один аргумент, являющийся входной строкой, и возвращает выходную строку.Подробнее
Он принимает один аргумент, являющийся входной строкой, и возвращает выходную строку.Подробнее
Базовые математические формулы — GeeksforGeeks
Математика включает в себя бесконечный спектр исследований и исследований в области чисел и их операций. Каждая область математики имеет дело с чем-то другим. Филиалы исследуют новые методы и стандарты расчета, чтобы сделать ежедневную торговлю еще более удобной.
Математика делится на различные разделы в соответствии с используемыми способами вычислений и темами, которые они охватывают. Ветви включают геометрию, алгебру, арифметику, проценты, экспоненты и т. Д. Математика также предоставляет стандартные производные формулы, чтобы сделать операции или расчеты точными. В данной статье представлены все основные формулы, имеющиеся в математике по разным ее разделам или областям.
Основные математические формулы
Формула – это математическое выражение или определенное правило, которое выводится из отношения между двумя или более величинами, а полученный конечный продукт выражается в символах.
 Математические формулы включали числа, известные как константы, буквы, представляющие неизвестные значения и известные как переменные, математические символы, известные как знаки, и в некоторых случаях экспоненциальные степени.
Математические формулы включали числа, известные как константы, буквы, представляющие неизвестные значения и известные как переменные, математические символы, известные как знаки, и в некоторых случаях экспоненциальные степени.Арифметика
Арифметика – древнейший метод вычислений, известный до сих пор. Слово арифметика происходит от греческих слов «арифмос», что буквально означает числа. Брахмагупта индийский математик известен как «отец арифметики ». И Фундаментальная теория теории чисел была предложена Карлом Фридрихом Гауссом в 1801 году.
Основными операциями, используемыми в арифметике, являются сложение, вычитание, умножение и деление.
Арифметическая формула
Среднее арифметическое (среднее) = Сумма значений/Количество значений.
Алгебра
Алгебра — это элементарный предмет математики, который занимается изучением оценки чисел и символов.
 Алгебраические операции выполняются для определения неизвестных значений, которые выражаются буквами. Алгебраические уравнения представляют собой выражения, образованные комбинацией переменных, констант, факторов и коэффициентов переменных.
Алгебраические операции выполняются для определения неизвестных значений, которые выражаются буквами. Алгебраические уравнения представляют собой выражения, образованные комбинацией переменных, констант, факторов и коэффициентов переменных.Основная алгебраическая формула
- a 2 – b 2 = (a – b)(a + b)
- (a + b) 2 b5 2 9
2 = a 2
- a 2 + b 2 = (a + b) 2 – 2ab
- (a – b) 2 = a 2 – 2ab + b 2
- ( a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca
- (a – b – c) 2 = A 2 + B 2 + C 2 — 2AB + 2BC — 2CA
- (A + B) 3 = A 3 + 3A 2 = A 3 + 3A 2
- 9292929292929292 .
 + b 2
+ b 2 - (a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3
- a 3 – b 3 = (a – b)(a 2 + ab + b 2 )
- a 3 + b 3 = (a + b)(a 2 – ab + b 2 )
- (a + b) 4 = a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4
- (a – b ) 4 = a 4 – 4a 3 b + 6a 2 b 2 – 4ab 3 + b 4
- a 4 – b 4 = (a – b )(a + b)(a 2 + b 2 )
- (a m )(a n ) = a m + n
- (ab) m = a m b m
- (a m ) n = a mn
Geometry
Geometry is a part of mathematics that is concerned with the изучение форм, размеров, параметров, измерений, свойств и размеров.
 Обычно существует три типа геометрии. Это евклидова геометрия, сферическая геометрия и гиперболическая геометрия.
Обычно существует три типа геометрии. Это евклидова геометрия, сферическая геометрия и гиперболическая геометрия.Формула базовой геометрии
- Rectangle
- Perimeter of Rectangle = 2(l + b)
- The area of Rectangle = l × b
Where ‘l’ is Length and ‘b’ is Breadth
- Square
- The area of Square = a 2
- The perimeter of Square = 4a
Where ‘a’ is the length of the sides of a Square
- Triangle
Area треугольника = 1/2 × b × h
Где «b» — основание треугольника, а «h» — высота треугольника
- Трапеция
Площадь трапеции = 1/2 7 × (b 7 1 8 ) × h
, где B 1 и B 2 являются основаниями трапеции
и, H = высота трапеции
- Circle 9003
- .
 r 2
r 2 - Длина окружности = 2πr
- Формула всегда должна начинаться со знака равенства.
- #1 СУММ в Excel
Содержание
, где ‘r’ — это радиус круга
- Куб
Площадь поверхности куба = 6A 2
, где » — это длина по всей длине по всей длине по длине
- Цилиндр
- Площадь кричащей поверхности цилиндра = 2πrh
- Общая площадь поверхности цилиндра = 2πr (r + h)
- Объем цилиндра = v = πr
92929292929292929292929292929292929292929292929292929н 900 2929 2929292929292929292929292929292929292929 292929 2929 2929 2929 2929 2
- .
Где «r» — радиус основания цилиндра
А, «h» — высота цилиндра
- Конус
- Общая площадь криволинейной поверхности конуса = πr4 5 поверхности площадь конуса = πr(r + l) = πr[r + √(h 2 + r 2 )]
- Здесь ‘r’ — радиус основания конуса, а h = высота конуса
- Сфера
.
Вероятность — это математический термин, используемый для определения вероятности наступления определенного события. Вероятность можно просто определить как возможность возникновения события. Она выражается по линейной шкале от 0 до 1. Существует три типа теоретической вероятности, экспериментальной вероятности и субъективной вероятности.
Базовая формула вероятности
P(A) = n(A)/n(S)
Где
P(A) — вероятность события.
n(A) — количество благоприятных исходов
n(S) — общее количество событий
Дробь
Дробь — это число, выраженное целыми числами, в котором числитель делится на знаменатель. Дробь — это в основном частное от деления.
Формула основных фракций
- (а + b/c) = (a × c) + b/c
- (a/b + d/b) = (a + d)/b
- (a/b + c/d ) = (a × d + b × c/b × d)
- a/b × c/d = ac/bd
- (a/b)/(c/d) = a/b × d/c
Процент
Процент — это числовое значение или отношение, выраженное в виде доли от 100.
Обычно оно обозначается знаком %.
Базовая формула процентов
Процент = (Сумма в категории/Общая стоимость) × 100
Примеры задач
Вопрос 1: Определите вероятность получения туза из карты, взятой из колоды.
Решение:
Дано:
Общее количество благоприятных исходов n(S) = 52
Количество лицевых карт в колоде = 12 Теперь
P(A) = n(A)/n(S)
=> 12/52
=> 3/13
Следовательно, вероятность получить лицевую карту из колоды карт равна 3/ 13.
Вопрос 2: Упростить 3/(x – 1) + 1/(x(x – 1) = 2/x
Решение:
=> 3x + 1/x(x – 1) ) = 2(x – 1)/x(x – 1)
=> 3x + 1 = 2(x – 1)
=> x = -3
Вопрос 3: Если x + 1/x = 3. Найдите значение x 2 + 1/x 2 .
.
=> х 2 + 2 × x × 1/x + (1/x) 2 = 9
=> x 2 + 1/x 2 + 2 = 9
=> x 2 + 1/ x 2 = 7
Вопрос 4: Если радиус окружности равен 21см. Найдите площадь данного круга.
Решение:
Дано:
Радиус круга равен 21см.
Имеем,
Площадь круга (A) = πr 2
=> 22/7 × 21 × 21
=> 1386см 2
Следовательно, площадь данного круга равна 1386см 2
Вопрос 5: Найдите площадь треугольника с основанием 100см и высотой 20см.
Решение:
Дано:
Основание треугольника равно 100см.
Высота треугольника 20см.
У нас есть,
Площадь(A) = 1/2 × b × h
=> 1/2 × 10 × 20
=> 1000см 2
Вопрос 6: Пунам имеет 4/5 части поля, 2/5 из которых она использует для ведения сельского хозяйства.
Какая часть фермы остается для других целей?
Решение:
Дано:
Общая доля земли 4/5.
Общая фракция, используемая для фарма 2/5.
Сейчас,
=> 4/5 – 2/5
=> 4 – 2/5
=> 2/5
Следовательно, осталось 2/5 часть поля.
Вопрос 7: Сколько будет 20% от 240 кг?
Решение:
=> 20/100 × 240
=> 48 кг
Следовательно, 20% от 240 кг будет 48 кг.
10 формул Excel, которые должен знать каждый новичок – Excel для бизнеса
Формулы Excel упрощают расчет чисел и осмысление больших объемов данных . Зная несколько ключевых формул , вы сможете выполнять различные действия в Excel, которые повысят вашу производительность и снизят риск ошибок в вычислениях. Мы собрали 10 формул Excel, которые вам понадобятся для начала работы.
Существует множество сложных формул, но хорошая формула не обязательно должна быть сложной.
На самом деле некоторые из самых простых формул являются наиболее полезными и помогут вам максимально использовать возможности Excel.
Вот 10 формул Excel, которые вы должны знать , включая несколько простых формул, которые не имеют ничего общего с анализом данных, если вы используете Excel и для организации информации.
1. 10 формул Excel =СУММ=СУММ – отличная базовая формула, особенно потому, что она позволяет складывать числа разными способами. Excel легко выполнит эту формулу за вас, но есть несколько приемов =СУММ, которые обеспечивают еще больше возможностей для добавления данных.
Во-первых, =СУММ может суммировать целые строки чисел или только определенные ячейки в строке. Вот как это выглядит:
=СУММ(A2:A9) складывает значения в ячейках A2 от до A9
=СУММ(A2, A9) складывает значения в ячейках A2 и A9
. В этом примере =СУММ (A2:A9)/5 суммирует значения в ячейках с A2 по A9, а затем делит сумму на 5.
2. 10 Формулы Excel =МАКС. и =МИН. электронная таблица с большим количеством чисел, это полезная формула. С =MAX вы можете немедленно найдет наибольшее число в вашем наборе данных , а с помощью =MIN вы можете найти наименьшее .Используйте =MAX(ВЫБЕРИТЕ КЛЕТКИ:ВЫБЕРИТЕ КЛЕТКИ).
= MAX (A2: A9)
= мин (A2: A9)
3. 10 Формулы Excel = IFс этой формулой, Excel A Excel Will Wyl Wyk . выполняется определенное условие . Например, вам может понадобиться узнать, какие значения в столбце А больше 3. Используя формулу =ЕСЛИ, вы можете заставить Excel автоматически заполнять «да» для каждой ячейки, которая больше 3, и «нет». ” для каждого значения меньше 3. ЕСЛИ этого выражения нет в ваших 10 лучших формулах Excel, вы многое упускаете!
=ЕСЛИ(A2>=3, «Да», «Нет»)
4.10 формул Excel =TRIM
При копировании и вставке данных в электронную таблицу есть вероятность, что вставленные данные будут беспорядочными. Это означает, что в нем могут быть лишние пробелы или скрытые символы, и они испортят формулы, потому что Excel нужны чистые данные без этих лишних пробелов.
=TRIM очищает вставленные данные, чтобы они были совместимы с Excel.
В приведенном ниже примере животные в ячейках A3, A6, A8, A10 и A 12 имеют лишние пробелы в начале. Использование =TRIM(SELECT A CELL) исправит это.
Слева видно, как формула использовалась в столбце D, а лишние пробелы исчезли.
5. 10 Формулы Excel =СЦЕПИТЬ=СЦЕПИТЬ – полезная формула, которая берет значения из нескольких ячеек и объединяет их в одну ячейку. Эта формула экономит время и нервы, когда вам нужно объединить информацию из нескольких ячеек в одну ячейку. Вместо того, чтобы делать это вручную, =CONCATENATE может сделать это вдвое быстрее и вдвое быстрее.
В этом примере столбец A содержит имена, а столбец B — фамилии. Используя =CONCATENATE(SELECT CELL, SELECT CELL), эти ячейки можно легко объединить, что отражено в столбце D, где полные имена теперь находятся в одной ячейке. Подумайте обо всех копиях/вставках этой формулы, только что сохраненных!
6. 10 формул Excel = СЕГОДНЯВам может понадобиться отметка времени для электронной таблицы при каждом ее просмотре.
Вместо ввода даты вручную используйте =СЕГОДНЯ(). Правильно — вам даже не нужно помещать значение в круглые скобки, и каждый раз, когда электронная таблица открывается, она будет обновляться с текущей датой.
7. 10 формул Excel =PROPERExcel предназначен не только для анализа данных; это также хорошая платформа для организации и сортировки информации. При вводе больших объемов текста в Excel формула =ПРОП. 1869 преобразует ячейку текста в правильный регистр
, где первая буква каждого слова заглавная, а остальные буквы строчные.В этом примере довольно много имен в столбце А не пишутся с заглавной буквы. Вместо того, чтобы щелкать в каждой ячейке, удалять первую букву каждого имени и вводить заглавную букву (что требует много дополнительных кликов и времени), =PROPER делает это мгновенно, как вы можете видеть в столбце D.
Используйте =Proper(SELECT A CELL) для этой формулы.
8. 10 формул Excel =ЧЕТНЫЕ и =НЕЧЕТНЫЕЭта формула пригодится, если вы работаете с данными, содержащими много десятичных знаков. =EVEN округляет число до ближайшего четного числа, и =ODD округляет число до ближайшего нечетного числа. Если вы работаете с отрицательными числами, эти формулы по-прежнему работают, округляя до ближайшего четного или нечетного числа.
В этом примере в столбце D используется формула =ЧЕТНЫЙ, а в столбце Е используется формула =НЕЧЕТНЫЙ.
Используйте =ЧЕТНЫЕ(ВЫБЕРИТЕ ЯЧЕЙКУ) и =НЕЧЕТНЫЕ(ВЫБЕРИТЕ ЯЧЕЙКУ) для этой формулы.
9. 10 Формулы Excel КОНЕЦ МЕСЯЦА=КОНЕЧНАЯМЕСЯЦ можно использовать, чтобы найти последний день текущего месяца или предстоящих месяцев. Вместо перехода между календарем и электронной таблицей используйте =КОНМЕСЯЦ(ДАТА НАЧАЛА, 0). Сделайте еще один шаг в этой формуле и рассчитайте следующий месяц, добавив =КОНМЕСЯЦ(дата начала, 1).
Обратите внимание, как в примере можно рассчитать будущие месяцы, увеличивая число в конце формулы.
Еще одна особенность этой формулы: при вводе даты начала обязательно используйте функцию ДАТА (2019,1,8) — 8 января 2019 г., чтобы формула работала в настоящее время. Если формула возвращает #ЧИСЛО! ошибка, скорее всего, дата имеет неправильный формат.
10. 10 Формулы Excel ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛТаблицу можно легко использовать для выбора случайных чисел, используя =СЛУЧМЕЖДУ(ВЫБРАТЬ ЗНАЧЕНИЯ).


 Например, можно выделить ячейки B7 и C7, нажать кнопку Автосумма и суммировать два столбца одновременно.
Например, можно выделить ячейки B7 и C7, нажать кнопку Автосумма и суммировать два столбца одновременно.
 Чтобы ее вписать, используют символы = ( ) ; : .
Чтобы ее вписать, используют символы = ( ) ; : .


 Вокруг указанной ячейки появится красная рамка .
Вокруг указанной ячейки появится красная рамка .

 Если вы хотите, вы можете использовать нашу рабочую тетрадь.
Если вы хотите, вы можете использовать нашу рабочую тетрадь.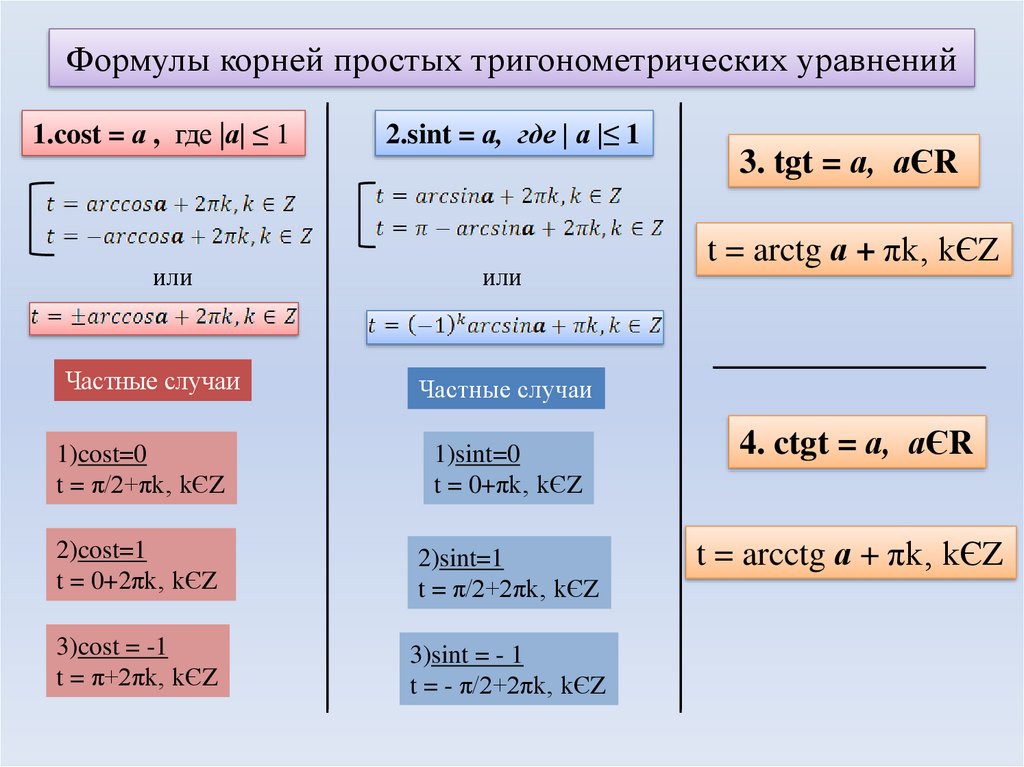

 .
.

 В противном случае он покажет ошибку.
В противном случае он покажет ошибку. Это условная функция Excel, которая возвращает результат на основе выполнения или невыполнения заданных критериев.
читать далее
Это условная функция Excel, которая возвращает результат на основе выполнения или невыполнения заданных критериев.
читать далее