Системы линейных неравенств и выпуклые множества точек
- Понятие системы линейных неравенств
- Решение линейных неравенств с любым числом неизвестных
- Выпуклые множества точек
Неравенство — это два числа или математических выражения, соединённых одним из знаков: > (больше, в случае строгих неравенств), < (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
Неравенство является линейным при тех же условиях, что и уравнение: оно содержит переменные только в первой степени и не содержит произведений переменных.
Решение линейных неравенств и систем линейных неравенств неразрывно связано
с их геометрическим смыслом: решением линейного неравенства является некоторая полуплоскость,
на которые всю плоскость делит прямая, уравнением которой задано линейное неравенство. Эту
полуплоскость, а в случае системы линейных неравенств — часть плоскости, ограниченную
несколькими прямыми, требуется найти на чертеже.
К решению систем линейных неравенств с большим числом переменных сводятся многие экономические задачи, в частности, задачи линейного программирования, в которых требуется найти максимум или минимум функции.
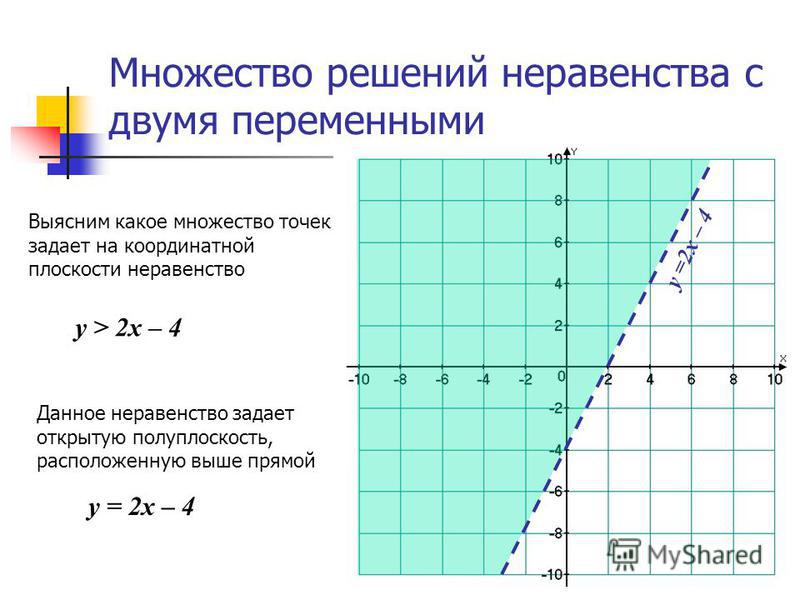
Сначала разберём линейные неравенства на плоскости. Рассмотрим одно неравенство с двумя переменными и :
,
где — коэффициенты при переменных (некоторые числа), — свободный член (также некоторое число).
Одно неравенство с двумя неизвестными, так же как и уравнение, имеет бесчисленное множество решений. Решением данного неравенства назовём пару чисел , удовлетворяющих этому неравенству. Геометрически множество решений неравенства изображается в виде полуплоскости, ограниченной прямой
,
которую назовём граничной прямой.
Шаг 1. Построить прямую, ограничивающую множество решений линейного неравенства
Для этого надо знать какие-либо две точки этой прямой. Найдём точки
пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1).
Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу
после этого теретического экскурса.
Найдём точки
пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1).
Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу
после этого теретического экскурса.
Абсциссу найдём, решая как систему уравнение прямой с уравнением оси .
Найдём пересечение с осью :
Подставляя значение в первое уравнение, получаем
, откуда .
Таким образом, нашли абсциссу точки A .
Найдём координаты точки пересечения с осью .
Абсцисса точки B равна нулю. Решим уравнение граничной прямой с уравнением оси координат:
Решение:
,
следовательно, координаты точки B: .
Шаг 2. Начертить прямую, ограничивающую множество решений неравенства. Зная точки A и B пересечения граничной прямой с осями
координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две
части, лежащие справа и слева (выше и ниже) от этой прямой.
Зная точки A и B пересечения граничной прямой с осями
координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две
части, лежащие справа и слева (выше и ниже) от этой прямой.
Шаг 3. Установить, которая из полуплоскостей является решением данного неравенства. Для этого нужно в это неравенство подставить начало координат (0; 0). Если координаты начала удовлетворяют неравенству, то решением неравенства является полуплоскость, в которой находится начало координат. Если же координаты не удовлетворяют неравенству, то решением неравенства является полуплоскость, которая не содержит начала координат. Полуплоскость решения неравенства будем обозначать штрихами от прямой внутрь полуплоскости, как на рисунке 1.
Если решаем систему линейных неравенств, то каждый шаг выполняется для каждого из неравенств системы.
Пример 1. Решить неравенство
Решение. Начертим прямую
Начертим прямую
Подставив в уравнение прямой , получим , а подставив , получим . Следовательно, координаты точек пересечения с осями будут A(3; 0), B(0; 2). Через эти точки проведём прямую (опять рисунок 1).
Выберем полуплоскость решений неравенства. Для этого в неравенство подставим координаты начала (0; 0):
,
получим , т. е. координаты начала удовлетворяют данному неравенству. Следовательно, решением неравенства является полуплоскость, содержащая в себе начало координат, т. е. левая (она же нижняя) полуплоскость.
Если бы данное неравенство было строгим, то есть имело бы вид
,
то точки граничной прямой не являлись бы решением, так как они не удовлетворяют неравенству.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Теперь рассмотрим систему линейных неравенств с двумя неизвестными:
Каждое из неравенств этой системы на плоскости определяет полуплоскость. Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и
несовместной, если она не имеет решений. Решением системы линейных неравенств называется
любая пара чисел (),
удовлетворяющая всем неравенствам данной системы.
Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и
несовместной, если она не имеет решений. Решением системы линейных неравенств называется
любая пара чисел (),
удовлетворяющая всем неравенствам данной системы.
Геометрически решением системы линейных неравенств является множество точек, удовлетворяющих всем неравенствам системы, то есть, общая часть получаемых полуплоскостей. Поэтому геометрически в общем случае решение может быть изображено в виде некоторого многоугольника, в частном случае — может быть линия, отрезок и даже точка. Если система линейных неравенств несовместна, то на плоскости не существует ни одной точки, удовлетворяющей всем неравенствам системы.
Пример 2. Решить систему линейных неравенств
Решение. Итак, требуется найти многоугольник решений этой системы неравенств.
Построим граничную прямую для первого неравенства, то есть прямую ,
и граничную прямую для второго неравенства, то есть прямую .
Делаем это пошагово, как было показано в теоретической справке и в примере 1, тем более, что в примере 1 строили граничную прямую для неравенства, которое является первым в данной системе.
Полуплоскости решений, соответствующие неравенствам данной системы, на рисунке 2 заштрихованы вовнутрь. Общая часть полуплоскостей решений представляет собой открытый угол ABC. Это означает, что множество точек плоскости, составляющих открытый угол ABC, является решением как первого, так и второго неравенства системы, то есть, является решением системы двух линейных неравенств. Иначе говоря, кординаты любой точки из этого множества удовлетворяют обоим неравенствам системы.
Пример 3. Решить систему линейных неравенств
Решение. Построим граничные прямые, соответствующие неравенствам системы.
Делаем это, выполняя шаги, данные в теоретической справке, для каждого неравенства. Теперь
определим полуплоскости решений для каждого неравенства (рисунок 3).
Теперь
определим полуплоскости решений для каждого неравенства (рисунок 3).
Полуплоскости решений, соответствующие неравенствам данной системы, заштрихованы вовнутрь. Пересечение полуплоскостей решений изображается, как показано на рисунке, в виде четырёхугольника ABCE. Получили, что многоугольник решений системы линейных неравенств с двумя переменными является четырёхугольником ABCE.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Всё описанное выше о системах линейных неравенств с двумя неизвестными
относится и к системе неравенств с любым числом неизвестных, с той лишь разницей, что решением
неравенства с
Так же, как и в двухмерном пространстве (на плоскости), каждое из
неравенств системы определяет n-мерное полупространство. Пересечение всех этих
полупространств образует многогранник решений. Но изобразить этот многогранник (называемый
симплексом) геометрически невозможно. Лишь в случае, когда число неизвестных не больше трёх, то есть
в действительном пространстве, многогранник решений можно изобразить геометрически.
Пересечение всех этих
полупространств образует многогранник решений. Но изобразить этот многогранник (называемый
симплексом) геометрически невозможно. Лишь в случае, когда число неизвестных не больше трёх, то есть
в действительном пространстве, многогранник решений можно изобразить геометрически.
Множество решений линейных неравенств геометрически составляет выпуклый многогранник или выпуклое множество точек.
Как уже отмечалось, системы линейных неравенств играют важную роль в линейном программировании. Теоремы линейного программирования содержат такие понятия, как выпуклые множества и крайние точки. Разберёмся бегло, о чём речь.
Множество точек называется выпуклым, если вместе с его любыми двумя
точками ему принадлежит и весь отрезок, соединяющий их. Если же существует хотя бы такая
пара точек множества, что отрезок, соединяющий эти точки, не принадлежит целиком этому
множеству, то такое множество называется невыпуклым. На рисунке 4 слева изображено
выпуклое множество, а справа — невыпуклое.
На рисунке 4 слева изображено
выпуклое множество, а справа — невыпуклое.
Выпуклые множества обладают важным свойством, которое устанавливается следующей теоремой.
Теорема. Пересечение двух выпуклых множеств — также выпуклое множество.
Через любую внутреннюю точку выпуклого множества можно провести отрезок, для которого она является внутренней, а сам отрезок целиком принадлежит этому множеству. Но есть точки (для выпуклого многоугольника это его вершины), для которых такое построение выполнить нельзя: нет ни одного отрезка, для которого вершина являлась бы внутренней, а отрезок целиком бы принадлежал мноргоугольнику.
Точка выпуклого множества называется угловой (или крайней), если через неё нельзя провести ни одного отрезка, состоящего только из точек данного множества и для которого она была бы внутренней.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Всё по теме «Линейное программирование
Продолжение темы «Систем уравнений и неравенств»
Решение систем линейных уравнений методом Крамера
Решение систем линейных уравнений методом Гаусса
Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли
Теорема Кронекера-Капелли
Решение систем линейных уравнений матричным методом (обратной матрицы)
Начало темы «Линейная алгебра»
Определители
Матрицы
Поделиться с друзьями
§ 8. Системы линейных уравнений и неравенств.
Линейным неравенством называют неравенство вида: , где — некоторые числа, — координаты точки пространства . Совокупность всех точек , координаты которых удовлетворяют неравенству, называют областью решений данного неравенства.
В линейное неравенство имеет вид .
Его областью решений является одна из
полуплоскостей, на которые граничная
прямая делит плоскость .
Для того, чтобы установить какая из
полуплоскостей удовлетворяет данному
неравенству выбирают «пробную» точку
и проверяют, удовлетворяет ли она
ограничению-неравенству. Если
удовлетворяет, то неравенство выполняется
в полуплоскости, содержащей «пробную»
точку, в противном случае берётся другая
полуплоскость. В качестве «пробной»
точки выбирают любую точку, не принадлежащую
граничной прямой. Полуплоскость,
в которой неравенство выполняется,
отмечают стрелками, направленными
внутрь данной полуплоскости.
В качестве «пробной»
точки выбирают любую точку, не принадлежащую
граничной прямой. Полуплоскость,
в которой неравенство выполняется,
отмечают стрелками, направленными
внутрь данной полуплоскости.
Системой линейных неравенств называют систему неравенств вида:
, где — коэффициенты системы, — свободные члены системы. Совокупность всех точек , координаты которых удовлетворяют каждому из неравенств, называют областью решений системы неравенств.
В система линейных неравенств имеет вид: .
Её областью решений является пересечение полуплоскостей, ограниченных прямыми, уравнения которых получают из неравенств заменой в них знаков неравенств на знаки равенств
Переход
от системы линейных уравнений с
условиями неотрицательности для
переменных (
),
к эквивалентной системе линейных
неравенств осуществляется следующим
способом. Сначала (методом Гаусса)
систему уравнений преобразуют к виду,
в котором базисные переменные
представляются в виде линейных комбинаций
свободных переменных, затем в полученных
равенствах опускают неотрицательные
базисные переменные и переходят к
эквивалентным неравенствам.
Ограничения-неравенства , преобразуются в ограничения-равенства путём прибавления (вычитания) к левым частям дополнительных (балансовых) неотрицательных переменных : .
Частное решение системы линейных уравнений, в котором базисные переменные принимают неотрицательные значения, а свободные переменные равны нулю, называется опорным.
1.188 Построить графически область решений следующих систем неравенств:
а); б); в);
г); д); е);
ж); з) .
1.189. Системы линейных уравнений преобразовать в эквивалентные системы линейных неравенств и построить графически область их решений.
а) ; б) ;
в) ; г) .
1.190 Смешанные
системы линейных уравнений и неравенств
преобразовать в эквивалентные системы
линейных уравнений и найти какие-нибудь
их опорные решения.
а) ; б) ;
в) ; г) .
1.191 Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа В и 675 заготовок типа С. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице 1. Записать условия выполнения задания и определить количество листов материала, раскраиваемых первым, вторым и третьим способами.
Таблица 1.
Тип Заготовки | Способ раскроя | ||
1 | 2 | 3 | |
А | 3 | 2 | 1 |
В | 1 | 6 | 2 |
С | 4 | 1 | 5 |
1. 192 Из
Казани в Наб.Челны необходимо перевезти
оборудование трех типов: I
типа- 95 ед., II
типа – 100 ед., III
типа – 185 ед. Для перевозки оборудования
завод может заказать три вида транспорта.
Количество оборудования каждого типа,
вмещаемого на определенный вид транспорта,
приведено в таблице 2. Записать условия
перевозки оборудования из Казани в
Наб.Челны и установить, сколько единиц
транспорта каждого вида для этого
потребуется.
192 Из
Казани в Наб.Челны необходимо перевезти
оборудование трех типов: I
типа- 95 ед., II
типа – 100 ед., III
типа – 185 ед. Для перевозки оборудования
завод может заказать три вида транспорта.
Количество оборудования каждого типа,
вмещаемого на определенный вид транспорта,
приведено в таблице 2. Записать условия
перевозки оборудования из Казани в
Наб.Челны и установить, сколько единиц
транспорта каждого вида для этого
потребуется.
Таблица 2.
Тип
Оборудования
Вид транспорта
Т1
Т2
Т3
I
3
2
1
II
4
1
2
III
3
5
4
1. 193 На
товарные станции А1 и А2 прибыло по 45
комплектов мебели. Перевозка одного
комплекта со станции А1 в магазины М1,
М2 и М3 обходится соответственно в 1, 3 и
5 ден. ед., а перевозка комплекта со
станции А2 в те же магазины – в 3, 5 и 4
ден. ед.. В каждый магазин надо доставить
одинаковое количество мебели. Записать
в математической форме условия доставки
мебели в магазины, если транспортные
расходы определены в 270 ден. ед. и найти
план перевозки мебели со станций в
магазины.
193 На
товарные станции А1 и А2 прибыло по 45
комплектов мебели. Перевозка одного
комплекта со станции А1 в магазины М1,
М2 и М3 обходится соответственно в 1, 3 и
5 ден. ед., а перевозка комплекта со
станции А2 в те же магазины – в 3, 5 и 4
ден. ед.. В каждый магазин надо доставить
одинаковое количество мебели. Записать
в математической форме условия доставки
мебели в магазины, если транспортные
расходы определены в 270 ден. ед. и найти
план перевозки мебели со станций в
магазины.
1.194 На предприятии освоено 4 технологических способа изготовления изделий А и В из некоторого сырья. В таблице 3 указано количество изделий, которое может быть произведено из единицы сырья каждым из способов.
Таблица 3.
Изделие
Выход из единицы сырья
I
II
III
IV
А
2
1
7
4
В
6
12
2
3
Записать условия
выбора технологий при производстве из
94 единиц сырья 574 изделий А и 328 изделий
В. Определить какое количество сырья
следует перерабатывать по каждой
технологии, чтобы выполнить плановое
задание по выпуску изделий.
Определить какое количество сырья
следует перерабатывать по каждой
технологии, чтобы выполнить плановое
задание по выпуску изделий.
1.195 Для откорма кроликов на ферме в ежедневный рацион каждого животного включается 6 единиц питательного вещества А и 7 единиц вещества В. При этом используются корма К1,К2 и К3. Данные о содержании веществ в одной весовой единице корма и ее стоимости приведены в таблице 4.
Таблица 4.
Корм | Содержание питательного вещества | Стоимость единицы корма, ден.ед. | |
А | В | ||
К1 | 2 | 1 | 5 |
К2 | 1 | 2 | 1 |
К3 | 3 | 1,5 | 3 |
Записать условия
составления ежедневного рациона
стоимостью 7 денежных единиц, содержащего
норму питательных веществ и определить
его состав.
1.196 Для выполнения полевых работ сельскохозяйственное предприятие может купить тракторы марок Т1 и Т2.Все необходимые данные приведены в таблице 5.
Таблица 5.
Вид Работ | Объем работы | Производительность трактора | |
Т1 | Т2 | ||
Р1 | 60 | 4 | 3 |
Р2 | 40 | 8 | 1 |
Цена трактора, ден. | 7 | 2 | |
Записать условия выполнения всего комплекса полевых работ приобретенными тракторами, если на их покупку отпущено 53 ден. ед. Установить, сколько тракторов той и другой марки следует приобрести предприятию для выполнения запланированного объема работ.
1.197 Цех выпускает
трансформаторы видов А и В. На один
трансформатор вида А расходуется 5 кг
трансформаторного железа и 3 кг проволоки,
а на трансформатор вида В – 3кг железа
и 2 кг проволоки. От реализации
трансформатора вида А прибыль составляет
12 ден. ед., а вида В – 10 ден. ед. Сменный
фонд железа – 480 кг, проволоки – 300 кг.
Записать условия, которым должен
удовлетворять план выпуска трансформаторов,
если расход ресурсов не должен превышать
выделенных фондов, а прибыль должна
быть не менее 900 ден. ед. за смену. Построить
графически область допустимых планов
выпуска трансформаторов.
1.198 На судно грузоподъемностью 1000 т и емкостью трюмов 2400 необходимо погрузить товары А и В. Объемные коэффициенты товаров составляют соответственно 3 /т и 1,2 /т. На складе имеется 800 т товара В и большое количество товара А. Записать ограничения на количество погружаемых на судно товаров, не позволяющие превысить грузоподъемность судна, емкость его трюмов и запас товара В. Построить графически область допустимых вариантов загрузки трюма судна.
1.199 Со станции ежедневно можно отправлять пассажирские и скорые поезда. Данные приведены в таблице 6.
Таблица 6.
Количество вагонов в составе | |||
Тип поезда | плацкартный | Купейный | мягкий |
Пассажирский | 5 | 6 | 3 |
Скорый | 8 | 4 | 1 |
Резерв вагонов | 80 | 72 | 21 |
Записать условия,
не позволяющие превысить наличный парк
вагонов при формировании пассажирских
и скорых поездов, ежедневно отправляемых
со станции.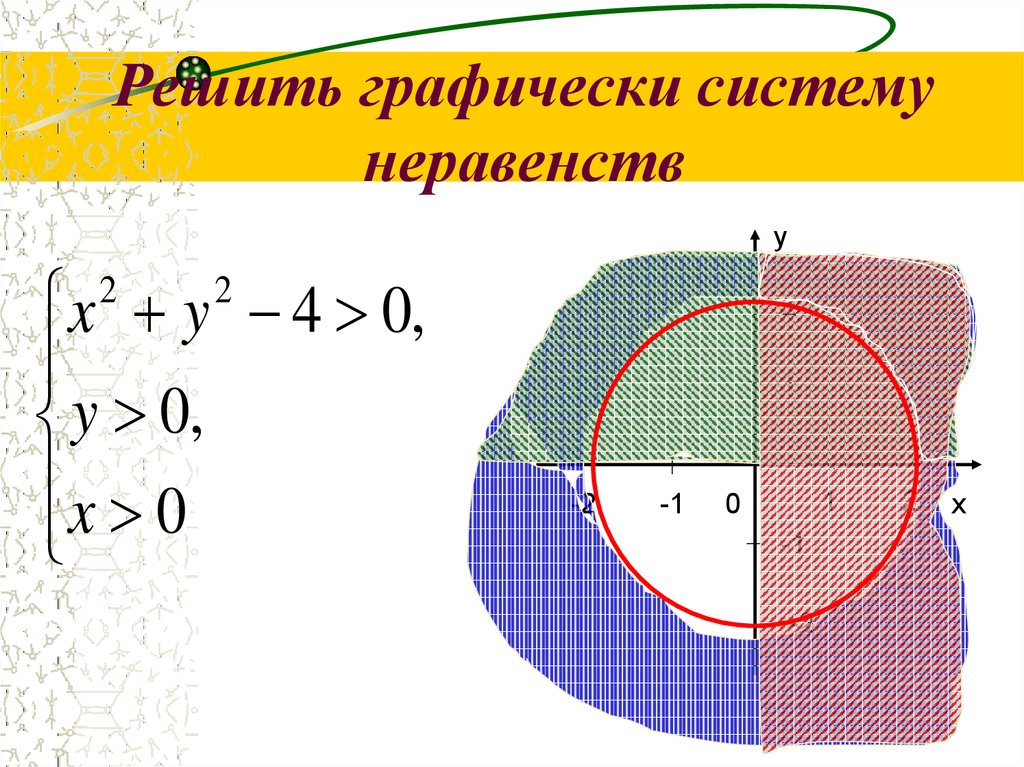 Построить графически область
допустимых вариантов формирования
поездов.
Построить графически область
допустимых вариантов формирования
поездов.
1.200 Предприятию задан план производства по времени и номенклатуре: не более чем за 6 часов необходимо выпустить ровно 30 ед. продукции вида П1 и ровно 96 ед. продукции вида П2. Машина А за 1 час производит либо 6 ед. продукции П1, либо 24 ед. продукции П2, а машина В – соответственно 13 и 13 ед.. Записать условия, которым должно удовлетворять время работы каждой из машин по выпуску продукции при точном выполнении плана по отдельным ее видам. Построить графически область допустимых вариантов использования времени работы машин, для выполнения плана выпуска продукции.
Задание фигур на координатной плоскости уравнениями и неравенствами
Репетиторы ❯ Математика ❯ Задание фигур на координатной плоскости уравнениями и неравенствами
Автор: Ольга Л., онлайн репетитор по математике
●
12. 12.2011
12.2011
●
Раздел: Математика
Пусть задано уравнение с двумя переменными F(x; y). Вы уже познакомились со способами решения таких уравнений аналитически. Множество решений таких уравнений можно представить и в виде графика.
Графиком уравнения F(x; y) называют множество точек координатной плоскости xOy, координаты которых удовлетворяют уравнению.
Для построения графика уравнения с двумя переменными сначала выражают в уравнении переменную y через переменную x.
Наверняка вы уже умеете строить разнообразные графики уравнений с двумя переменными: ax + b = c – прямая, yx = k – гипербола, (x – a)2 + (y – b)2 = R2 – окружность, радиус которой равен R, а центр находится в точке O(a; b).
Пример 1.
Построить график уравнения x2 – 9y2 = 0.
Решение.
Разложим на множители левую часть уравнения.
(x – 3y)(x+ 3y) = 0, то есть y = x/3 или y = -x/3.
Ответ: рисунок 1.
Особое место занимает задание фигур на плоскости уравнениями, содержащими знак абсолютной величины, на которых мы подробно остановимся. Рассмотрим этапы построения графиков уравнений вида |y| = f(x) и |y| = |f(x)|.
Первое уравнение равносильно системе
{f(x) ≥ 0,
{y = f(x) или y = -f(x).
То есть его график состоит из графиков двух функций: y = f(x) и y = -f(x), где f(x) ≥ 0.
Для построения графика второго уравнения строят графики двух функций: y = f(x) и y = -f(x).
Пример 2.
Построить график уравнения |y| = 2 + x.
Решение.
Заданное уравнение равносильно системе
{x + 2 ≥ 0,
{y = x + 2 или y = -x – 2.
Строим множество точек.
Ответ: рисунок 2.
Пример 3.
Построить график уравнения |y – x| = 1.
Решение.
Если y ≥ x, то y = x + 1, если y ≤ x, то y = x – 1.
Ответ: рисунок 3.
При построении графиков уравнений, содержащих переменную под знаком модуля, удобно и рационально использовать метод областей, основанный на разбиении координатной плоскости на части, в которых каждое подмодульное выражение сохраняет свой знак.
Пример 4.
Построить график уравнения x + |x| + y + |y| = 2.
Решение.
В данном примере знак каждого подмодульного выражения зависит от координатной четверти.
1) В первой координатной четверти x ≥ 0 и y ≥ 0. После раскрытия модуля заданное уравнение будет иметь вид:
2x + 2y = 2, а после упрощения x + y = 1.
2) Во второй четверти, где x < 0, а y ≥ 0, уравнение будет иметь вид: 0 + 2y = 2 или y = 1.
3) В третьей четверти x < 0, y < 0 будем иметь: x – x + y – y = 2. Перепишем этот результат в виде уравнения 0 · x + 0 · y = 2.
4) В четвертой четверти, при x ≥ 0, а y < 0 получим, что x = 1.
График данного уравнения будем строить по четвертям.
Ответ: рисунок 4.
Пример 5.
Изобразить множество точек, у которых координаты удовлетворяют равенству |x – 1| + |y – 1| = 1.
Решение.
Нули подмодульных выражений x = 1 и y = 1 разбивают координатную плоскость на четыре области. Раскроем модули по областям. Оформим это в виде таблицы.
| Область | Знак подмодульного выражения | Полученное уравнение после раскрытия модуля |
| I | x ≥ 1 и y ≥ 1 | x + y = 3 |
| II | x < 1 и y ≥ 1 | -x + y = 1 |
| III | x < 1 и y < 1 | x + y = 1 |
| IV | x ≥ 1 и y < 1 | x – y = 1 |
Ответ: рисунок 5.
На координатной плоскости фигуры могут задаваться и неравенствами.
Графиком неравенства с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого неравенства.
Рассмотрим алгоритм построения модели решений неравенства с двумя переменными:
- Записать уравнение, соответствующее неравенству.
- Построить график уравнения из пункта 1.
- Выбрать произвольную точку в одной из полуплоскостей. Проверить, удовлетворяют ли координаты выбранной точки данному неравенству.
- Изобразить графически множество всех решений неравенства.
Рассмотрим, прежде всего, неравенство ax + bx + c > 0. Уравнение ax + bx + c = 0 задает прямую, разбивающую плоскость на две полуплоскости. В каждой из них функция f(x) = ax + bx + c сохраняет знак. Для определения этого знака достаточно взять любую точку, принадлежащую полуплоскости, и вычислить значение функции в этой точке. Если знак функции совпадает со знаком неравенства, то эта полуплоскость и будет решением неравенства.
Если знак функции совпадает со знаком неравенства, то эта полуплоскость и будет решением неравенства.
Рассмотрим примеры графического решения наиболее часто встречающихся неравенств с двумя переменными.
1) ax + bx + c ≥ 0. Рисунок 6.
2) |x| ≤ a, a > 0. Рисунок 7.
3) x2 + y2 ≤ a, a > 0. Рисунок 8.
4) y ≥ x2. Рисунок 9.
5) xy ≤ 1. Рисунок 10.
Если у вас появились вопросы или вы хотите попрактиковаться изображать на плоскости модели множества всех решений неравенств с двумя переменными с помощью математического моделирования, вы можете провести бесплатное 25-минутное занятие с онлайн репетитором после того, как зарегистрируетесь. Для дальнейшей работы с преподавателем у вас будет возможность выбрать подходящий для вас тарифный план.
Остались вопросы? Не знаете, как изобразить фигуру на координатной плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Неравенства с двумя переменными
III. Закрепление ранее изученного материала.
Закрепление ранее изученного материала.
Определение: Выражения, составленные с помощью чисел, двух переменных, знаков действий и знаков сравнения называются неравенствами с двумя переменными.
1. С помощью приема «Кластер» — учащиеся составляют Алгоритм решения неравенств с двумя переменными. Выделяется 5 минут.
Поочерёдно группы у доски озвучивают свои ответы.
Затем учитель зачитывает Алгоритм и сравниваем ответы.
АЛГОРИТМ:
Заменить знак неравенства на равно;
Выразить одну переменную через другую;
Построить график полученного уравнения;
Выбрать по одной точке из полученных полуплоскостей.
Проверить, удовлетворяют ли их координаты неравенству.
Выбрать удовлетворяющую неравенству точку.
2. Ребята, а теперь давай те каждая группа, с помощью Алгоритма решений, на примерах вспомнит, как изображается множество решений неравенства с двумя переменными на координатной плоскости.
Каждая группа получает конверт с заданием и ватман.
1 группа
Изобразить на координатной плоскости XOY фигуру, состоящую из точек, координаты которых удовлетворяют неравенству 2у+3х≤6.
Решение.
1.Заменить знак неравенства на равно: 2у+3х=6
2. Выразить переменную у через переменную х:
2у=6-3х
у=3-1,5х
3. Построить график полученного уравнения
х | 0 | 2 |
у | 3 | 0 |
Прямая разбивает множество всех точек координатной плоскости на точки, расположенные ниже ее, и точки, расположенные выше ее. Возьмем из каждой области по контрольной точке: А(1;1), В(1;3).
Координаты точки А удовлетворяют данному неравенству 2у+3х≤6,
2·1+3·1≤6,
5≤6
Координаты точки В не удовлетворяют данному неравенству 2у+3х≤6,
2·3+3·1≤6
9≤6
2 группа
Изобразить на координатной плоскости XOY фигуру , состоящую из точек, координаты которых удовлетворяют неравенству у+1 ≥ х²
Решение.
1.Заменить знак неравенства на равно: у +1 = х²
2. Выразить переменную у через переменную х: у = х² — 1
3. Построить график полученного уравнения
х | -2 | -1 | 0 | 1 | 2 |
у | 3 | 0 | -1 | 0 | 3 |
В
А
Парабола разбивает множество всех точек координатной плоскости на точки, расположенные внутри ее, и точки, расположенные снаружи ее. Возьмем из каждой области по контрольной точке: А(1;3), В(3;1).
Координаты точки А удовлетворяют данному неравенству: 3+1 ˃ 1²
4 ˃ 1
Координаты точки В не удовлетворяют данному неравенству: 1 + 1 ˃ 3²
2 ˃ 9
3 группа
Изобразить на координатной плоскости XOY фигуру , состоящую из точек, координаты которых удовлетворяют неравенству х² + у²
Решение.
1.Заменить знак неравенства на равно: х² + у² = 4
2. Определить, какая фигура задаётся таким уравнением:
х2 + y2 = 4 – уравнение окружности, с центром в начале координат, R = 2
3. Построить данную фигуру в системе координат и выделить область, соответствующую знаку неравенства
В
А
Окружность разбивает множество всех точек координатной плоскости на точки, расположенные внутри ее, и точки, расположенные снаружи ее. Возьмем из каждой области по контрольной точке: А(-1;1), В(3;-1).
Координаты точки А удовлетворяют данному неравенству:
(-1)² + 1²
1 + 1
2
Координаты точки В не удовлетворяют данному неравенству: 3² + (-1)²
9 + 1
10
4 группа
Изобразить на координатной плоскости XOY фигуру , состоящую из точек, координаты которых удовлетворяют неравенству у – 2х
1.Заменить знак неравенства на равно: у – 2х = 1
2. Выразить переменную у через переменную х:
Выразить переменную у через переменную х:
у = 2х + 1
3. Построить график полученного уравнения
х | 0 | 3 |
у | 1 | 7 |
2
3
О
у
х
В
А
Прямая разбивает множество всех точек координатной плоскости на точки, расположенные ниже ее, и точки, расположенные выше ее. Возьмем из каждой области по контрольной точке: А(1;1), В(-2;2).
Координаты точки А удовлетворяют данному неравенству
1 — 2·1
-1
Координаты точки В не удовлетворяют данному неравенству : 2 – 2 · (-2)
2 + 4
6
Параграф 6
§ 6. ГРАФИКИ УРАВНЕНИЙ И НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
Таблица 12
1. Построение графиков функции вида y = f (x) + g (x)
Если нам известны графики функций y = f (x) и y = g (x), то эскиз графика функции y = f (x) + g (x) можно построить так: изобразить в одной системе координат графики функций f (x) и g (x), а потом построить искомый график по точкам, выполняя для каждого значения х (из области определения функции f (x) + g (x)) необходимые операции с отрезками, изображающими соответствующие ординаты f (x) и g (x).
Аналогично можно построить и схематические графики функций
y = f (x)-g (x) и y = -1-.
f (x)
86 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА
Продолж. табл. 12
Пример
Комментарий
Постройте график функции
2 1
у = х2 + -.
X
Построим в одной системе коор-динат графики функций-слагаемых: у = х2 и у = — (на рисунке они
X
показаны штриховыми линиями). Для каждого значения х (кроме х = 0, которое не принадлежит области определения заданной функции) справа от оси Оу прибавляем соответствующие отрезки — значения функций f (х) и g (х) (обе функции имеют одинаковые знаки), слева от оси Оу — вычитаем (функции имеют противоположные знаки). На рисунке синей линией изобра-
2 —
жен график функции у = х +—.
2. Графики уравнений и неравенств с двумя переменными
Определение. Графиком уравнения (неравенства) с двумя переменными х и у называется множество всех точек координатной плоскости с координатами (х; у), где пара чисел (х; у) является решением соответствующего уравнения (неравенства).
Графики некоторых уравнений и неравенств
У1 y>f(x) К&/ л/ y<f(x) У1 3 II * х>а У’ х<а в II н
0 X 0 а X 0 а х
у’ х2 + у2 > R2 \
1
1
\
\
\
\ о ; х t t *
-Д.’
х2 + у2 < R2
\R
§ 6. Графики уравнений и неравенств с двумя переменными 87
Продолж. табл. 12
3. Геометрические преобразования графика уравнения F (x; у) = 0
Преобразование
Пример
F (я — a; у — Ъ) = 0
Параллельный перенос графика уравнения F (x; у) = 0 на вектор n (a; b).
F (| я |; у) = 0
Часть графика уравнения F (х; у) = 0 справа от оси Оу (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси Оу.
F (я; | у |) = 0
Часть графика уравнения F (х; у) = 0 выше оси Ох (и на самой оси) остается без из-менений, и эта же часть гра-фика отображается симме-трично относительно оси Оx.
Объяснение и обоснование
1. — на с. 92 (в последнем случае
— на с. 92 (в последнем случае
f (x)
удобно строить графики функций y = f (x) и у = не в одной системе
f (x)
координат, а в разных, расположенных так, чтобы их оси ординат находились на одной прямой).
Заметим, что такой способ построения графика функции не всегда дает возможность определить все характерные особенности поведения графика (часто это можно сделать только в результате специального исследования функции, которое будет рассмотрено в учебнике для 11 класса), но во многих случаях приведенный способ позволяет получить определенное представление о виде графика заданной функции.
2. Графики уравнений и неравенств с двумя переменными. С понятием графика уравнения с двумя переменными вы ознакомились в курсе алгебры. Аналогично вводится и понятие графика неравенства с двумя переменными. Поэтому можно дать общее определение этих графиков:
Графиком уравнения (неравенства) с двумя переменными х и у называется множество всех точек координатной плоскости с координатами (х; у), где пара чисел (х; у) является решением соответствующего уравнения (неравенства).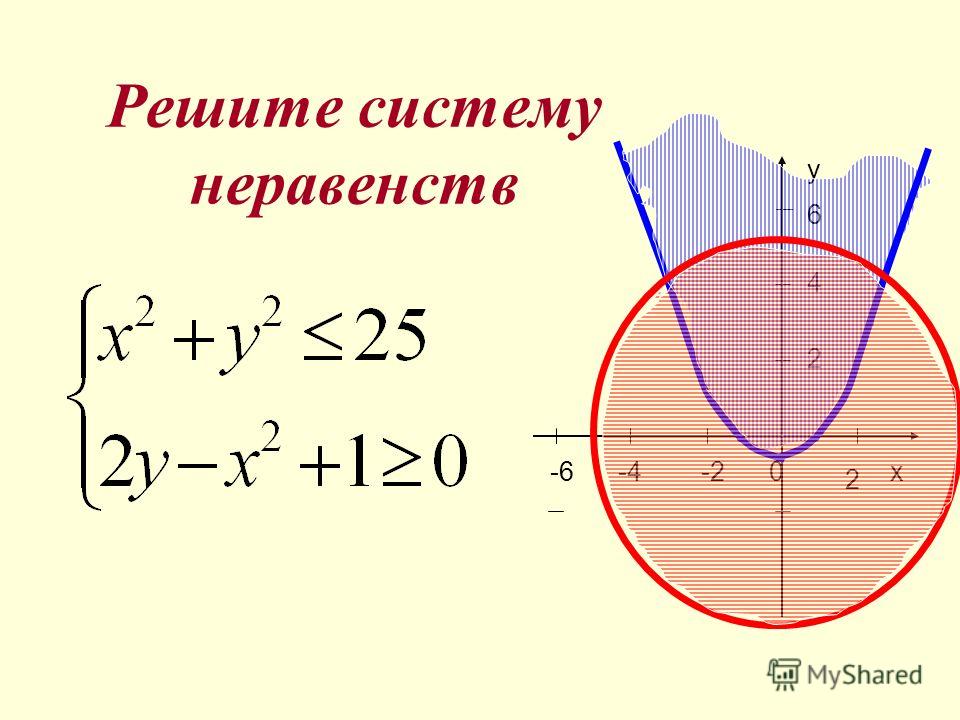
9 Для построения графика неравенства y > f (x) (или y < f (x)) достаточно иметь график функции y = f (x). Действительно, по определению график функции y = f (x) состоит из всех точек M координатной плоскости с координатами (x; y) = (x; f (x)). Тогда для каждого значения x точки, координаты которых удовлетворяют неравенству y > f (x), будут находиться выше точки M (рис. 42, а), а точки, координаты которых удовлетворяют неравенству y < f (x), будут находиться ниже точки M (рис. 42, б). Таким образом,
график неравенства y > f (x) состоит из всех точек координатной плоскости, находящихся выше графика функции y = f (я), а график неравенства y < f (я) состоит из всех точек координатной плоскости, находящихся ниже графика функции y = f (я). О
Например, на рисунке 43 изображен график неравенства y > x2, а на рисунке 44 — график неравенства y < x2. Поскольку точки графика y = x2 не принадлежат графику неравенства y > x2, то на первом графике парабола y = x2 изображена штриховой линией; а так как точки графика y = x2 принадлежат графику неравенства y < x2, то на втором графике парабола y = x2 изображена сплошной линией.
Аналогично, если на координатной плоскости есть прямая x = а, то графиком неравенства x > а будут все точки координатной плоскости, находящиеся справа от этой прямой, а графиком неравенства x < а будут все точки координатной плоскости, находящиеся слева от этой прямой.
§ 6. Графики уравнений и неравенств с двумя переменными 89
у\ 1
/(*)
*
*
* V>f(x) , А?’
1 0 х х
У f(x) У $ М%» y<f{x)
/
/
# 0 X
У1
1
1
1
1
t
1
1
V
V \
1
\
\
\ У > х21 1 1 1 1 1 1 1 / i / /
0 ж
Рис. 42
Рис. 43
Рис. 45
Например, на рисунке 45 изображен график неравенства x> 2, а на рисунке 46 — график неравенства x < —1.
Отметим, что в том случае, когда на координатной плоскости есть изо-бражение окружности x2 + y2 = R2, то
графиком неравенства x2 + y2 < R2 будут все точки координатной плоскости, находящиеся внутри окружности, а графиком неравенства x2 + y2 > R2 будут все точки координатной плоскости, находящиеся вне окружности.
0 Действительно, если на координатной плоскости рассмотреть точку M (x, y), то OM2 = x2 + y2 (O — начало координат). Если x2 + y2 = R2 (где R > 0), то OM2 = R2, таким образом, OM = R — точка M лежит на окружности радиуса R с центром в начале координат (рис. 47, а).
Если x2 + y2 < R2, то OM2 < R2, таким образом, OM< R. То есть неравенству x2 + y2 < R2 удовлетворяют координаты всех точек (и только этих точек), которые находятся внутри круга, ограниченного окружностью радиуса R с центром в начале координат (рис. 47, б).
Если x2 + y2 > R2, то OM2 >R2, таким образом, OM> R. То есть неравенству x2 + y2 > R2 удовлетворяют координаты всех точек (и только этих точек), которые находятся вне круга, ограниченного окружностью радиуса R (рис. 47, в).
Аналогично, если на плоскости есть изображение окружности (x — а)2 + + (y — b)2 = R2, то графиком неравенства (x — а)2 + (y — b)2 < R2 будут все точ
б
а
90 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА
ки координатной плоскости, находящиеся внутри этой окружности, а графиком неравенства (х — а)2 + (у — b)2 > R2 будут все точки координатной плоскости, находящиеся вне окружности.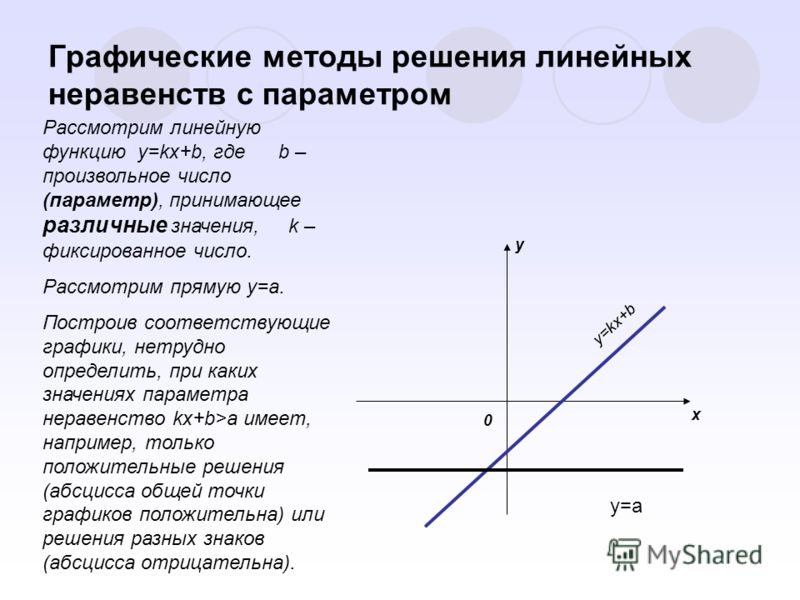 !Я 1 t * / ✓ и
!Я 1 t * / ✓ и
Рис. 47
У’ * * / / / 1 1 х2 + у2>9 ч ч ч \ \ 1 1
1
1
\
\
\
ч
ч о з: х t / / / г *
Рис. 48
3. Геометрические преобразования графика уравнения F (я; у) = 0.
О По определению график уравнения
F (х; у) = 0 (1)
состоит из всех точек М (х0; у0) координатной плоскости, координаты (х0; у0) которых являются решениями этого уравнения. Это означает, что при подстановке пары чисел (х0; у0) в данное уравнение оно обращается в верное числовое равенство, таким образом, F (х0; у0) = 0 — верное равенство.
Рассмотрим точку М1 (х0 + а; у0 + b). Если координаты этой точки подставить в уравнение
F (х — а; у — b) = 0, (2)
то получим верное равенство F (х0; у0) = 0. Поэтому координаты точки М1 являются решениями уравнения (2), значит, точка M1 принадлежит графику уравнения F (х — а; у — b) = 0.
Точку М1 (х0 + а; у0 + b) можно получить из точки М (х0; у0) параллельным переносом ее на вектор n (a; b). Поскольку каждая точка М1 графика
Поскольку каждая точка М1 графика
уравнения F (х — а; у — b) = 0 получается из точки М графика уравнения F (х; у) = 0 параллельным переносом ее на вектор n (a; b) (рис. 50), то и весь
I
график уравнения F (я — a; у — b) = 0 можно получить из графика уравнения F (х; у) = 0 параллельным переносом его на вектор
n (a; b). О
• Для обоснования связи между графиками F (х; у) = 0 и F (| х |; у) = 0 до-статочно заметить, что при х 1 0 уравнение F (| х |; у) = 0 совпадает с урав-нением F (х; у) = 0, таким образом, совпадают и их графики справа от оси Оу и на самой оси. Пусть точка M (х0; у0) (где х0 1 0) — одна из общих точек этих графиков. Тогда F (х0; у0) = 0 — верное равенство.
Рассмотрим точку М1 (-х0; у0 ). Если координаты этой точки подставить в уравнение F (| х |; у) = 0 и учесть, что х0 1 0, то получим равенство F (х0; у0) = 0. Поэтому координаты точки М1 являются решениями уравнения F (| х |; у) = 0, значит, точка M1 принадлежит графику этого уравнения. Учитывая, что точки М и М1 симметричны относительно оси Оу (рис. 51) , получаем:
Учитывая, что точки М и М1 симметричны относительно оси Оу (рис. 51) , получаем:
I
график уравнения F (| х |; у) = 0 можно получить из графика урав-нения F (х; у) = 0 следующим образом: часть графика уравнения F (х; у) = 0 справа от оси Оу (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси Оу. О
Аналогично обосновывается, что
1
для построения графика уравнения F (х; | у |) = 0 часть графика уравнения F (х; у) = 0 выше оси Ох (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси Ох.
В таблице 12 приведены простейшие примеры использования геометрических преобразований графиков уравнений. Указанные соотношения приходится применять в заданиях типа: построить график уравнения или неравенства или изобразить на координатной плоскости множество точек, координаты которых удовлетворяют заданному уравнению (неравенству).
92 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА
Задача 1*
Примеры решения задач
—
Постройте график функции у =
2
х — 9
Решение
► х2 — 9 = 0 при х = ±3. = ~2——. Поэтому
= ~2——. Поэтому
проведем через эти точки вертикаль- ные прямые, которые не пересекают
—
график функции у =
f (х)
Затем для
каждого значения х разделим 1 на соответствующее значение ординаты f (х) (используя то, что ординаты f (х) отмечены на верхнем графике). На рисунке синей линией изображен результат — график функции
у = ~2——. (Для построения этого гра-
х2 — 9
фика масштаб по осям Ох и Оу выбран разный.)
Задача 2
Покажите штриховкой на координатной плоскости множество
х2 + у m о, х — у < 2.
Комментарий
точек, координаты которых удовлетворяют системе
Решение ► Заданная система равносильна си-
\у m -х2,
стеме
у > х — 2.
Перепишем заданную систему так, чтобы было удобно изображать графики данных неравенств (то есть запишем неравенства в виде у > f (х)
§ 6. Графики уравнений и неравенств с двумя переменными 93
Изобразим штриховкой графики неравенств системы (первого — вер-тикальной штриховкой, второго — горизонтальной):
наты которых удовлетворяют системе, будет таким:
Задача 3*
или у < f (х)). Множество точек, ко-ординаты которых удовлетворяют неравенству у < -х2, является объ-единением точек параболы у = -х2 и точек координатной плоскости, находящихся ниже параболы (на ри-сунке это множество обозначено вер-тикальной штриховкой). Множество точек, координаты которых удовлет-воряют неравенству у > х — 2, состоит из точек координатной плоскости, находящихся выше прямой у = х — 2 (на рисунке это множество обозначено горизонтальной штриховкой).
Множество точек, ко-ординаты которых удовлетворяют неравенству у < -х2, является объ-единением точек параболы у = -х2 и точек координатной плоскости, находящихся ниже параболы (на ри-сунке это множество обозначено вер-тикальной штриховкой). Множество точек, координаты которых удовлет-воряют неравенству у > х — 2, состоит из точек координатной плоскости, находящихся выше прямой у = х — 2 (на рисунке это множество обозначено горизонтальной штриховкой).
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, заданных каждым из неравенств данной системы (на рисунке пересечению множеств соответствует та область, где штриховки наложились друг на друга).
Заметим, что в подобных заданиях можно не выполнять промежуточных рисунков, а сразу штриховать искомое множество точек координатной плоскости (выше прямой у = х — 2 и ниже параболы у = -х2 вместе с той частью параболы, которая лежит выше прямой).
Постройте график уравнения | х — у | + 2 | х+у | = х + 6. Ориентир
Ориентир
Для упрощения выражения с несколькими модулями с двумя переменными можно найти нули подмодульных выражений (то есть приравнять их к нулю) и разбить область определения рассматриваемого выражения на несколько частей, в каждой из которых знак каждого модуля раскрывается однозначно.
Используя этот ориентир, получаем план решения примера.
Приравняем к нулю подмодульные выражения х — у = 0 (отсюда у = х) и х + у = 0 (отсюда у = -х). Прямые у = х и у = -х разбивают координатную плоскость на четыре области. В каждой из этих областей знак каж
94 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА
дого модуля раскрывается однозначно, после преобразования полученного равенства строим соответствующую часть графика заданного уравнения.
Решение
► 1. Область определения: х — любое действительное число, у — любое действительное число.
2. х — у = 0 при у = х; х + у = 0 при у = -х.
3. Прямые у = х и у = -х разбивают координатную плоскость на четыре части, в каждой из которых обозначены знаки первого и второго под- модульных выражений (рис.
Вопросы для контроля
1. Объясните на примерах, как можно, имея графики функций y = f (х) и y = g (х), построить эскиз графика функции y = f (х) + g (х) и функции
_ 1 у _ f (х).
2. Что называется графиком уравнения с двумя переменными? Что называ-ется графиком неравенства с двумя переменными? Приведите примеры.
3. Как, зная график функции y = f (х), построить график неравенства y > f (х) и неравенства y < f (х)? Приведите примеры.
4. Как, зная график уравнения F (х; y) = 0, можно построить график урав-нения F (х — a; y — b) = 0 и уравнений F (| х| ; y) = 0 и F (х; | y |) = 0? При-ведите примеры.
5*. Обоснуйте правила геометрических преобразований графика уравнения F (х; y) = 0 для получения графиков уравнений F (х — a; y — b) = 0, F (| х |; y) = 0, F (х; | y |) = 0.
6. Объясните на примере, как можно найти на координатной плоскости мно-жество точек, координаты которых удовлетворяют системе неравенств с двумя переменными.
Упражнения
1. Постройте эскиз графика функции:
Постройте эскиз графика функции:
1) у _ х + —; 2) у _ х — —; 3*) у _ х3 + —; 4*) у _ х2 — —.
х х х х
2. Постройте график уравнения:
1) | y | = х — 2; 2) | y | = х2- х; 3) | х | = -y2;
4) | х | +| y | = 2; 5) | х | — | y | = 2.
3. Постройте график неравенства:
1) y > х2 — 3; 2) у < —; 3) х2 + y2 m 25;
х
4) (х — 2)2 + (y + 3 )2 > 4.
4. Покажите штриховкой на координатной плоскости множество точек, ко-ординаты которых удовлетворяют системе:
у m 5 — х,
у 1 х,
у m 2х + 4.
5*. Постройте график уравнения:
1) | х — у | — | х + у | = y + 3; 2) | х — 2у | + | 2х — у | = 2 — y;
3) | 3х + у | + | х — у | = 4.
Уравнения и неравенства — определение и вычисление с примерами решения
Содержание:
Уравнения и неравенства
О появлении посторонних корней и потере решений уравненийВы знаете, что далеко не каждое преобразование уравнения сохраняет неизменным множество его корней. В одном случае это множество может сузиться, то есть корни будут потеряны, в другом — расшириться, то есть появятся посторонние корни.
В одном случае это множество может сузиться, то есть корни будут потеряны, в другом — расшириться, то есть появятся посторонние корни.
Приведем несколько примеров.
При переходе от уравнения
Возведение обеих частей уравнения в квадрат приводит к появлению постороннего корня
Заменяя уравнение уравнением получаем посторонний корень
Метод решения уравнения, при котором данное уравнение заменяют на уравнение-следствие, а затем полученные корни подвергают проверке, называют методом следствий. Его применяют тогда, когда выполнить проверку несложно.
Однако так бывает не всегда. Например, число является корнем уравнения но чтобы в этом убедиться, надо провести довольно большую вычислительную работу.
Для подобных ситуаций возможен другой путь решения — метод равносильных преобразований. С этим методом вы ознакомились в 10 классе.
Подчеркнем, что, применяя как метод следствий, так и метод равносильных преобразований, важно знать причины потери корней и появления посторонних корней. Рассмотрим некоторые из этих причин.
Рассмотрим некоторые из этих причин.
Изменение области определения уравнения
Вне области определения уравнения корней нет (рис. 32.1). Поэтому преобразование уравнения, при котором расширяется область его определения, может привести к появлению посторонних корней.
Например, областью определения уравнения является множество Пользуясь определением логарифма, получаем уравнение , областью определения которого является множество Расширение области определения исходного уравнения привело к появлению постороннего корня
Пример:
Решите уравнение
Решение:
Если дробь в левой части данного уравнения сократить на то получим уравнение При таком преобразовании область определения исходного уравнения расширяется на множество чисел, которые являются корнями уравнения Поэтому на самом деле данное в условии уравнение равносильно системе
Найдем корни уравнения системы. Имеем:
Поскольку то получаем Отсюда Осталось заметить, что при значение выражения отлично от нуля.
Ответ:
Если расширение области определения уравнения может привести к появлению посторонних корней, то ее сужение — возможная причина потери корней.
Например, областью определения уравнения является множество а областью определения уравнения является множество Множество содержит корень первого уравнения. Поэтому при переходе от уравнения к уравнению этот корень потерян.
Часто причиной изменения множества корней уравнения является применение равенств, правая и левая части которых имеют разные области определения.
Приведем примеры таких равенств:
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области определения выражения, стоящего в левой части. Поэтому применение этих равенств слева направо может привести к потере корней, а справа налево — к появлению посторонних корней.
Пример:
Решите уравнение
Решение:
Областью определения данного уравнения является множество Очевидно, число 1 является корнем данного уравнения.
Однако применение формулы приводит к уравнению
область определения которого — множество Поэтому число 1 не является корнем полученного уравнения, то есть такой переход ведет к потере этого корня.
Решим данное уравнение методом равносильных переходов.
Данное в условии уравнение равносильно системе
Отсюда
Ответ:
Умножение обеих частей уравнения на выражение, содержащее переменнуюИногда бывает целесообразным умножить обе части уравнения на некоторое выражение. Рассмотрим последствия такого преобразования. Перейдем от уравнения
к уравнению
При таком переходе множество корней уравнения может измениться под влиянием двух факторов: области определения функции и множества корней уравнения Например, если обе части уравнения умножить
на выражение и перейти к уравнению то тем самым теряем корень Если же обе части этого уравнения умножить на то теряем корень и одновременно получаем посторонний корень
Следовательно, если при решении уравнения возникла потребность умножить обе его части на выражение то надо учитывать как область определения этого выражения, так и множество корней уравнения
Пример:
Решите уравнение
Решение:
Умножим обе части данного уравнения на выражение Поскольку то получим:
Это преобразование не изменяет области определения исходного уравнения. Появление же посторонних корней возможно за счет корней уравнения Следовательно, полученное уравнение — следствие уравнения, данного в условии.
Появление же посторонних корней возможно за счет корней уравнения Следовательно, полученное уравнение — следствие уравнения, данного в условии.
Уравнение равносильно совокупности
Решим второе уравнение совокупности. Его следствием будет уравнение Отсюда
Осталось выполнить проверку. Легко убедиться, что число 2 является корнем данного в условии уравнения, а число 0 — нет.
Ответ:
Переход от уравнения f (x) = g (x) к уравнению φ (f (x)) = φ (g (x))Переход от уравнения к уравнению
Почему уравнения
равносильны, а уравнения
не являются равносильными?
Дело в том, что свойства функции отличаются от свойств функции
Если определенная на функция обратима, то равенство выполняется тогда и только тогда, когда Поэтому в этом случае уравнения и равносильны.
Если же определенная на функция не является обратимой, то из равенства не обязательно следует, что Поэтому уравнение является следствием уравнения
Так, уравнения равносильны, потому что функция обратима. Поскольку функция не является обратимой, то уравнения не являются равносильными.
Поскольку функция не является обратимой, то уравнения не являются равносильными.
Вы знаете, что возведение обеих частей уравнения в четную степень приводит к уравнению-следствию, а возведение в нечетную степень — к равносильному уравнению.
Это связано с тем, что функция не является обратимой, а функция обратимая.
Функция обратима на множестве
В 10 классе вы пользовались этим фактом в виде такой теоремы.
Теорема 32.1. Если для любого выполняются неравенства то уравнения равносильны на множестве
Эту теорему вы использовали при решении иррациональных уравнений.
Рассмотрим пример, в котором появление постороннего корня связано с необратимостью функции
Пример:
Решите уравнение
Решение:
Поскольку определенная на функция не является обратимой, то уравнение следствие данного. Поэтому решение уравнения должно завершиться проверкой корней. Следовательно, можно не бояться далее переходить к новым уравнениям-следствиям.
Следовательно, можно не бояться далее переходить к новым уравнениям-следствиям.
Напомним, что имеют место равенства
и Поэтому можно записать:
Ответ:
Далее имеем:
Проверим полученные корни.
При имеем:
Следовательно, число корень исходного уравнения.
При имеем:
Следовательно, число не является корнем исходного уравнения.
Ответ:
Основные методы решения уравненийВ таблице приведены схемы решения некоторых типовых уравнений.
Часто решение уравнений сводится к решению типовых уравнений, приведенных в таблице. Это иллюстрируют упражнения №№ 33.1, 33.2. К тем уравнениям, которые не сводятся к типовым, применяют специальные методы и приемы. Рассмотрим некоторые из них.
Метод разложения на множителиХорошо, если удается левую часть уравнения представить в виде произведения нескольких выражений. Как правило, этот шаг полезен, поскольку позволяет вместо данного уравнения решить совокупность более простых уравнений.
Рассмотрим примеры.
Пример:
Решите уравнение
Решение:
Очевидно, что число 1 является корнем данного уравнения. Тогда левую часть уравнения можно представить в виде произведения где квадратный трехчлен. Для нахождения разделим «уголком» многочлен на двучлен
Получили, что
Имеем:
Это уравнение равносильно совокупности
Отсюда
Ответ:
Пример:
Решите уравнение
Решение:
Имеем:
Ошибочным было бы считать, что это уравнение равносильно совокупности
Действительно, корень второго уравнения совокупности не входит в область определения исходного уравнения. На самом деле исходное уравнение равносильно системе
Отсюда
Ответ:
Метод замены переменнойПример:
Решите уравнение
Решение:
Преобразуем данное уравнение так:
Сделав замену получаем уравнение
Отсюда
Ответ:
Пример:
Решите уравнение
Решение:
Поскольку число 0 не является корнем данного уравнения, то, разделив числитель и знаменатель каждой из дробей левой части уравнения на получаем уравнение, равносильное данному:
Сделаем замену Тогда
Имеем:
Ответ:
Пример:
Решите уравнение
Решение:
Пусть Тогда
Отсюда
Исходное уравнение принимает вид
Отсюда
Получаем, что исходное уравнение равносильно совокупности
Отсюда
Поскольку то получаем
Отсюда
Пример:
Решите уравнение
Решение:
Пусть Тогда
Теперь можно записать:
Ответ:
Применение свойств функций
Поиск области определения функции может быть ключом к решению уравнения
Пример:
Решите уравнение
Решение:
Применение любых приемов, связанных с преобразованием левой части данного уравнения, вряд ли приведет к успеху.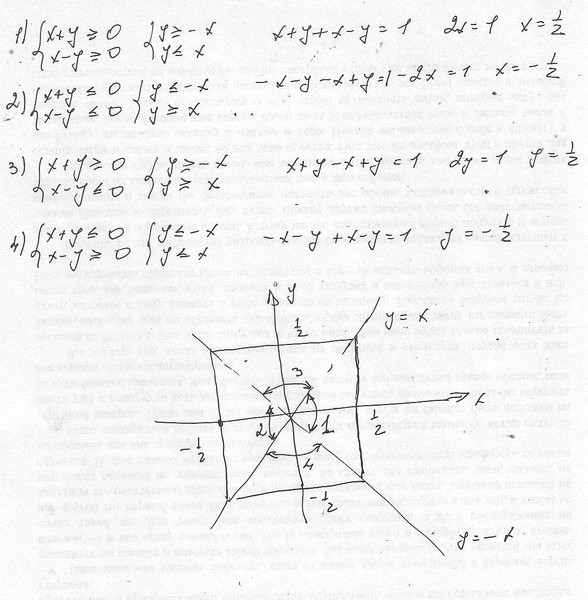 Вместе с тем нахождение области определения уравнения — путь вполне естественный.
Вместе с тем нахождение области определения уравнения — путь вполне естественный.
Имеем:
Решив эту систему, получим, что областью определения рассматриваемого уравнения является двухэлементное множество Проверка показывает, что число 1 не подходит, а число 3 является корнем исходного уравнения.
Ответ:
Пусть функции и таковы, что для любого выполняются неравенства и где некоторое число. Тогда уравнение равносильно системе
С помощью этих очевидных соображений можно решить целый ряд уравнений.
Пример:
Решите уравнение
Решение:
Поскольку
Отсюда В то же время
Поэтому исходное уравнение равносильно системе
Отсюда
Ответ:
Вы знаете, что если функция является возрастающей (убывающей), то уравнение имеет не более одного корня. Если удается корень угадать, то решение такого уравнения завершено.
Пример:
Решите уравнение
Решение:
Рассмотрим функцию
Имеем: Поскольку для любого выполняется неравенство то функция возрастает на Следовательно, уравнение имеет не более одного корня. Очевидно, что число 0 является корнем данного уравнения.
Очевидно, что число 0 является корнем данного уравнения.
Ответ:
Пример:
Решите уравнение
Решение:
Рассмотрим функцию
Легко определить, что
Каждая из функций и является возрастающей на Следовательно, функция также возрастает на
Очевидно, что число является корнем исходного уравнения. Этот корень единственный.
Ответ:
Основные методы решения неравенствВ таблице приведены схемы решения некоторых типовых неравенств.
Часто решение неравенств сводится к решению типовых неравенств, приведенных в таблице. Это иллюстрируют упражнения №№ 34.1-34.10. К тем неравенствам, которые не сводятся к типовым, применяют специальные методы и приемы. Рассмотрим некоторые из них.
Метод равносильных преобразованийПример:
Решите неравенство
Решение:
Заметим, что ошибочными являются следующие соображения: «Поскольку при выполняется неравенство то исходное неравенство равносильно системе Отсюда Несложно увидеть, что при таком «решении» теряется решение
Правильным решением данного неравенства является, например, переход к совокупности:
Решением уравнения совокупности являются числа 2 и 3, множеством решений неравенства — промежуток
Ответ:
Пример:
Решите неравенство
Решение:
Сразу возводить обе части неравенства в квадрат не является рациональным шагом, поскольку этот переход требует учитывать такое дополнительное условие:
Данное в условии неравенство целесообразно записать так:
Поскольку обе части последнего неравенства могут принимать только неотрицательные значения, то можно перейти к равносильному неравенству:
Далее получаем:
Отсюда
Ответ:
Метод интерваловПусть нули функции и ее точки разрыва разбивают область определения функции на некоторые промежутки (рис. 34.1). Тогда из следствия из теоремы Больцано-Коши (см. пункт 5) следует, что эти промежутки являются промежутками знакопостоянства функции. Определить знак функции на каждом из таких промежутков можно с помощью «пробных точек».
34.1). Тогда из следствия из теоремы Больцано-Коши (см. пункт 5) следует, что эти промежутки являются промежутками знакопостоянства функции. Определить знак функции на каждом из таких промежутков можно с помощью «пробных точек».
Эти соображения являются основой для решения широкого класса неравенств.
Пример:
Решите неравенство
Решение:
Рассмотрим функцию
Имеем: Найдем нули функции Для этого решим уравнение
Сделаем замену: Имеем:
Отсюда Получаем систему:
Отсюда
Эта система имеет три решения:
Теперь можно записать: Отсюда
Поскольку функция непрерывна, то ее нули, то есть числа 1, 2, 10, разбивают ее область определения на промежутки знакопостоянства:
Имеем:
Знаки функции на промежутках знакопостоянства показаны на рисунке 34.2. Ответ:
Применение свойств функцийПри решении примера 3 было использовано такое свойство функции, как непрерывность. Нередко ключом к решению могут быть и другие свойства функций: периодичность, четность (нечетность), возрастание (убывание), наибольшее и наименьшее значения функции и т. д.
Нередко ключом к решению могут быть и другие свойства функций: периодичность, четность (нечетность), возрастание (убывание), наибольшее и наименьшее значения функции и т. д.
Например, если и то множеством решений каждого из неравенств и является множество (рис. 34.3).
Еще один пример: если функция возрастает на промежутке и то множеством решений неравенства является промежуток (рис. 34.4). Рассмотрим примеры, иллюстрирующие вышесказанное.
- Заказать решение задач по высшей математике
Пример:
Решите неравенство
Решение:
Рассмотрим функцию
Имеем:
Решив уравнение получим
Сравнивая числа приходим к выводу, что
Тогда неравенство выполняется для всех
Ответ:
Пример:
Решите неравенство
Решение:
Областью определения данного неравенства является промежуток
Поскольку то
При получаем, что Тогда
Имеем: и Отсюда для всех выполняется неравенство
Ответ:
Пример:
Решите неравенство
Решение:
Рассмотрим функцию
Легко показать, что эта функция возрастает на Очевидно, что Тогда множеством решений неравенства является промежуток
Ответ:
—10клас
Графики уравнений и неравенств с двумя переменнымиПостроение графиков функции вида
Если нам известны графики функций и , то эскиз графика функции можно построить так: изобразить водной системе координат графики функций и , а потом построить искомый график по точкам, выполняя для каждого значения (из области определения функции) необходимые операции с отрезками, изображающими соответствующие ординаты и .
Аналогично можно построить и схематические графики функций
и
Пример:
Постройте график функции
Комментарий:
Построим в одной системе координат графики функций-слагаемых: и (на рисунке они показаны соответственно зеленой и синими линиями). Для каждого значения (кроме , которое не принадлежит области определения заданной функции) справа от оси прибавляем соответствующие отрезки — значения функций и (обе функции имеют одинаковые знаки), слева от оси — вычитаем (функции имеют противоположные знаки). На рисунке розовой линией изображен график функции
2. Графики уравнений и неравенств с двумя переменными
Определение: Графиком уравнения (неравенства) с двумя переменными и называется множество всех точек координатной плоскости с координатами , где пара чисел является решением соответствующего уравнения.
Графики некоторых уравнений и неравенств
3. Геометрические преобразования графика уравнения
Геометрические преобразования графика уравнения
Преобразование
Параллельный перенос графика уравнения на вектор
Часть графика уравнения справа от оси (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси .
Часть графика уравнения выше оси (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси .
Объяснение и обоснование:
Построение графиков функции вида y=f(x)+g(x)
Построение графиков функций вида .
Если известны графики функций и , то можно построить ориентировочный вид графика функции , или , или . Для этого достаточно изобразить в одной системе координат f М
графики функций и , а потом построить искомый график по точкам, выполняя для каждого значения (из области определения заданной функции) необходимые операции над отрезками (или над длинами этих отрезков), которые изображают соответствующие ординаты функций и .
Пример построения графика функции вида приведен
в таблице 13, а графика функции вида далее в задаче 1 (в последнем случае удобно строить графики функций и не в одной системе координат, а в разных, расположенных так, чтобы их оси ординат находились на одной прямой).
Заметим, что такой способ построения графика функции не всегда дает возможность определить все характерные особенности поведения графика (часто это можно сделать только в результате специального исследования функции, которое будет рассмотрено в учебнике для 11 класса), но во многих случаях приведенный способ позволяет получить определенное представление о виде графика заданной функции.
Графики уравнений и неравенств с двумя переменнымиС понятием графика уравнения с двумя переменными вы ознакомились в курсе алгебры. Аналогично вводится и понятие графика неравенства с двумя переменными. Поэтому можно дать общее определение этих графиков:
Графиком уравнения (неравенства) с двумя переменными и называется множество всех точек координатной плоскости с координатами , где пара чисел является решением соответствующего уравнения (неравенства).
Для построения графика неравенства (или ) достаточно иметь график функции . Действительно, по определению график функции состоит из всех точек координатной плоскости с координатами . Тогда для каждого значения точки, координаты которых удовлетворяют неравенству , будут находиться выше точки (рис. 55, а), а точки, координаты которых удовлетворяют неравенству , будут находиться ниже точки (рис. 55, б). Таким образом,
график неравенства состоит из всех точек координатной плоскости, находящихся выше графика функции , а график неравенства состоит из всех точек координатной плоскости, находящихся ниже графика функции .
Например, на рисунке 56 изображен график неравенства , а на рисунке 57 — график неравенства . Поскольку точки графика не принадлежат графику неравенства , то на первом графике парабола изображена штриховой линией; а так как точки графика принадлежат графику неравенства , то на втором графике парабола изображена сплошной линией.
Аналогично, если на координатной плоскости есть прямая , то графиком неравенства будут все точки координатной плоскости, находящиеся справа от этой прямой, а графиком неравенства будут все точки координатной плоскости, находящиеся слева от этой прямой.
Например, на рисунке 58 изображен график неравенства , а на рисунке 59 — график неравенства .
Отметим, что в том случае, когда на координатной плоскости есть изображение окружности , то
графиком неравенства будут все точки координатной плоскости, находящиеся внутри окружности, а графиком неравенства будут все точки координатной плоскости, находящиеся вне окружности.
Действительно, если на координатной плоскости рассмотреть точку , то ( — начало координат). Если (где ), то , таким образом, — точка лежит на окружности радиуса с центром в начале координат (рис. 60, а). Если , то , таким образом, . То есть неравенству удовлетворяют координаты всех точек (и только этих точек), которые находятся внутри круга, ограниченного окружностью радиуса с центром в начале координат (рис. 60, б).
Если , то , таким образом, . То есть неравенству удовлетворяют координаты всех точек (и только этих точек), которые находятся вне круга, ограниченного окружностью радиуса с центром в начале координат (рис. 60, в). Аналогично, если на плоскости есть изображение окружности , то графиком неравенства будут все точки координатной плоскости, находящиеся внутри этой окружности, а графиком неравенства будут все точки координатной плоскости, находящиеся вне окружности. Например, на рисунке 61 изображен график неравенства , а на рисунке 62 — график неравенства .
60, в). Аналогично, если на плоскости есть изображение окружности , то графиком неравенства будут все точки координатной плоскости, находящиеся внутри этой окружности, а графиком неравенства будут все точки координатной плоскости, находящиеся вне окружности. Например, на рисунке 61 изображен график неравенства , а на рисунке 62 — график неравенства .
Геометрические преобразования графика уравнения
По определению график уравнения
(1)
состоит из всех точек координатной плоскости, координаты которых являются решениями этого уравнения. Это означает, что при подстановке пары чисел в данное уравнение оно обращается в верное числовое равенство, таким образом, — верное равенство.
Рассмотрим точку . Если координаты этой точки подставить в уравнение
, (2)
то получим верное равенство . Поэтому координаты точки являются решениями уравнения (2), значит, точка принадлежит графику уравнения .
Точку можно получить из точки параллельным переносом ее на вектор . Поскольку каждая точка графика уравнения получается из точки графика уравнения параллельным переносом ее на вектор (рис. 63), то и весь
график уравнения можно получить из графика уравнения параллельным переносом его на вектор .
Для обоснования связи между графиками и достаточно заметить, что при уравнение совпадает с уравнением , таким образом, совпадают и их графики справа от оси и на самой оси. Пусть точка (где ) — одна из общих точек этих графиков. Тогда — верное равенство.
Рассмотрим точку . Если координаты этой точки подставить в уравнение и учесть, что , то получим верное равенство . Поэтому координаты точки являются решениями уравнения , значит, точка принадлежит графику этого уравнения. Учитывая, что точки и симметричны относительно оси (рис. 64):
график уравнения можно получить из графика уравнения следующим образом: часть графика уравнения справа от оси (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси .
Аналогично обосновывается, что
для построения графика уравнения часть графика уравнения выше оси (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси .
В таблице 13 приведены простейшие примеры использования геометрических преобразований графиков уравнений. Указанные соотношения приходится применять в заданиях типа: построить график уравнения или неравенства или изобразить на координатной плоскости множество точек, координаты которых удовлетворяют заданному уравнению (неравенству).
Примеры решения задач:
Пример №426Постройте график функции
Решение:
► при . Поэтому область определения заданной функции:
то есть
Комментарий:
Построим две системы координат так, чтобы оси ординат были у них на одной прямой. В тех точках, где функция равна нулю , не существует графика функции . Поэтому проведем через эти точки вертикальные прямые, которые не пересекают график функции
Поэтому проведем через эти точки вертикальные прямые, которые не пересекают график функции
Затем для каждого значения разделим 1 на соответствующее значение ординаты (используя то, что ординаты отмечены на верхнем графике). На рисунке розовой линией изображен результат — график функции . (Для построения этого графика масштаб по осям и выбран разный.)
Пример №427Покажите штриховкой на координатной плоскости множество точек, координаты которых удовлетворяют системе
Решение:
► Заданная система равносильна системе
Изобразим штриховкой графики неравенств системы (первого — вертикальной штриховкой, второго — горизонтальной):
Тогда множество точек, координаты которых удовлетворяют системе, будет таким:
Комментарий:
Перепишем заданную систему так, чтобы было удобно изображать графики данных неравенств (то есть запишем неравенства в виде или ). Множество точек, координаты которых удовлетворяют неравенству , является объединением точек параболы и точек координатной плоскости, находящихся ниже параболы (на рис. 65 это множество обозначено вертикальной штриховкой). Множество точек, координаты которых удовлетворяют неравенству , состоит из точек координатной плоскости, находящихся выше прямой (на рисунке это множество обозначено горизонтальной штриховкой).
65 это множество обозначено вертикальной штриховкой). Множество точек, координаты которых удовлетворяют неравенству , состоит из точек координатной плоскости, находящихся выше прямой (на рисунке это множество обозначено горизонтальной штриховкой).
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, заданных каждым из неравенств данной системы (на рисунке пересечению множеств соответствует та область, где штриховки наложились одна на другую).
Заметим, что в подобных заданиях можно не выполнять промежуточных рисунков, а сразу штриховать искомое множество точек координатной плоскости (выше прямой и ниже параболы вместе с той частью параболы, которая лежит выше прямой; рис. 66).
Пример №428Постройте график уравнения .
Ориентир
Для упрощения выражения с несколькими модулями с двумя переменными можно найти нули подмодульных выражений (то есть приравнять их к нулю) и разбить область определения рассматриваемого выражения на несколько частей, в каждой из которых знаки всех модулей раскрываются однозначно.
Используя этот ориентир, получаем план решения примера. Приравняем к нулю подмодульные выражения (отсюда ) и (отсюда ). Прямые и разбивают координатную плоскость на четыре области. В каждой из этих областей знак каждого модуля раскрывается однозначно, после преобразования полученного равенства строим соответствующую часть графика заданного уравнения.
Решение:
► 1. Область определения:
2. при при
3. Прямые и разбивают координатную плоскость на четыре части, в каждой из которых обозначены знаки первого и второго подмодульных выражений (рис. 67, а). (Будем считать, что каждая область берется вместе с лучами, которые ее ограничивают.) Действительно, если точки находятся в области I или на ее границе, то их координаты удовлетворяют системе неравенств которую можно записать так:
Тогда в области I первое подмодульное выражение отрицательно, а второе — положительно, поэтому данное уравнение имеет вид . Отсюда . Строим ту часть графика этой функции, которая находится в области I (рис. 67, б).
67, б).
Аналогично для точек области II: то есть
Таким образом, в области II данное уравнение имеет вид . Отсюда . Строим ту часть графика этой
функции, которая находится в области II.
Если точки находятся в области III, то то есть из данного уравнения получаем . Отсюда
Если точки находятся в области IV, то то есть из
данного уравнения имеем Отсюда
Окончательный вид графика уравнения приведен на рисунке 67, б.
Системы линейных неравенств | Математическое моделирование
Результаты обучения
- Поиск решений систем линейных неравенств
График системы двух неравенств
Помните из модуля по построению графиков, что график одного линейного неравенства разбивает координатную плоскость на две области. На одной стороне лежат все решения неравенства. С другой стороны решений нет. Рассмотрим график неравенства [latex]y<2x+5[/latex].
Пунктирная линия: [латекс]у=2х+5[/латекс]. Каждая упорядоченная пара в заштрихованной области под линией является решением [латекс]y<2x+5[/латекс], так как все точки под линией сделают неравенство верным. Если вы сомневаетесь в этом, попробуйте подставить в неравенство координаты x и y точек A и B; вы увидите, что они работают. Итак, заштрихованная область показывает все решения этого неравенства.
Каждая упорядоченная пара в заштрихованной области под линией является решением [латекс]y<2x+5[/латекс], так как все точки под линией сделают неравенство верным. Если вы сомневаетесь в этом, попробуйте подставить в неравенство координаты x и y точек A и B; вы увидите, что они работают. Итак, заштрихованная область показывает все решения этого неравенства.
Линия границы делит координатную плоскость пополам. В этом случае она показана пунктирной линией, так как точки на прямой не удовлетворяют неравенству. Если бы неравенство было [латекс]y\leq2x+5[/латекс], то граница была бы сплошной.
Теперь нарисуйте другое неравенство: [latex]y>−x[/latex]. Вы можете проверить пару точек, чтобы определить, какую сторону линии границы следует заштриховать. Проверка точек M и N дает верные утверждения. Итак, заштриховываем область над линией. Линия пунктирная, так как точки на прямой не соответствуют действительности.
Чтобы создать систему неравенств, вам нужно построить два или более неравенства вместе. Давайте использовать [latex]y<2x+5[/latex] и [latex]y>−x[/latex], так как мы уже построили график каждого из них.
Давайте использовать [latex]y<2x+5[/latex] и [latex]y>−x[/latex], так как мы уже построили график каждого из них.
Фиолетовая область показывает, где перекрываются решения двух неравенств. Эта область является решением системы неравенств. Любая точка в этой фиолетовой области будет верна как для [латекс]у>-х[/латекс], так и для [латекс]у<2x+5[/латекс].
В следующих видео-примерах показано, как построить график системы линейных неравенств и определить область решения.
В следующем разделе мы увидим, что точки могут быть решениями систем уравнений и неравенств. Алгебраически проверим, является ли точка решением линейного уравнения или неравенства.
Алгебраически проверим, является ли точка решением линейного уравнения или неравенства.
Определить, является ли упорядоченная пара решением системы линейных неравенств
На приведенном выше графике видно, что точки B и N являются решениями системы, поскольку их координаты делают оба неравенства верными.
Напротив, точки M и A лежат вне области решения (фиолетовый). Хотя точка M является решением неравенства [latex]y>−x[/latex], а точка A является решением неравенства [latex]y<2x+5[/latex], ни одна из точек не является решением система . В следующем примере показано, как проверить точку, чтобы увидеть, является ли она решением системы неравенств.
Вот график системы в приведенном выше примере. Обратите внимание, что [латекс](2, 1)[/латекс] находится в фиолетовой области, которая является областью перекрытия двух неравенств.
Вот график системы выше. Обратите внимание, что [латекс](2, 1)[/латекс] не находится в фиолетовой области, которая является перекрывающейся областью; это решение одного неравенства (красная область), но не решение второго неравенства (синяя область).
В следующем видео мы покажем еще один пример определения того, входит ли точка в решение системы линейных неравенств.
Как показано выше, решение системы неравенств можно найти, изобразив каждое неравенство в виде графика и указав область, которую они разделяют. Ниже приведены дополнительные примеры, показывающие весь процесс определения области решений на графе для системы двух линейных неравенств. Общие шаги описаны ниже:
- Изобразите каждое неравенство в виде линии и определите, будет ли она сплошной или пунктирной.
- Определите, какая сторона каждой граничной линии представляет решения неравенства, проверив точки на каждой стороне.
- Закрасьте область, представляющую решения для обоих неравенств.
Системы без решений
В следующем примере мы покажем решение системы двух неравенств, граничные линии которых параллельны друг другу. Когда графики системы двух линейных уравнений параллельны друг другу, мы обнаружили, что система не имеет решения. Аналогичный результат мы получим для следующей системы линейных неравенств.
Когда графики системы двух линейных уравнений параллельны друг другу, мы обнаружили, что система не имеет решения. Аналогичный результат мы получим для следующей системы линейных неравенств.
Примеры
График системы [латекс]\начало{массив}{с}у\ге2х+1\\у\lt2x-3\конец{массив}[/латекс]
Показать решение
Резюме
- Решениями систем линейных неравенств являются целые области точек.
- Вы можете проверить, является ли точка решением системы линейных неравенств, таким же образом, как вы проверяете, является ли точка решением системы уравнений.
- Системы неравенств не могут иметь решений, если граничные линии параллельны.
Графические неравенства | Начальная алгебра
Результаты обучения
- Определение графиков и решений уравнений и неравенств
- Определите сходства и различия между решениями линейных уравнений с двумя переменными и линейных неравенств с двумя переменными
- Определите сходства и различия между графиками линейных уравнений с двумя переменными и линейных неравенств с двумя переменными
- График неравенства двух переменных
- Определите и выполните шаги для построения графика линейного неравенства с двумя переменными
Определите разницу между графиком линейного уравнения и линейным неравенством
Вспомните, что решениями линейных неравенств являются целые наборы чисел, а не одно число, как вы находите с решениями равенств (уравнений).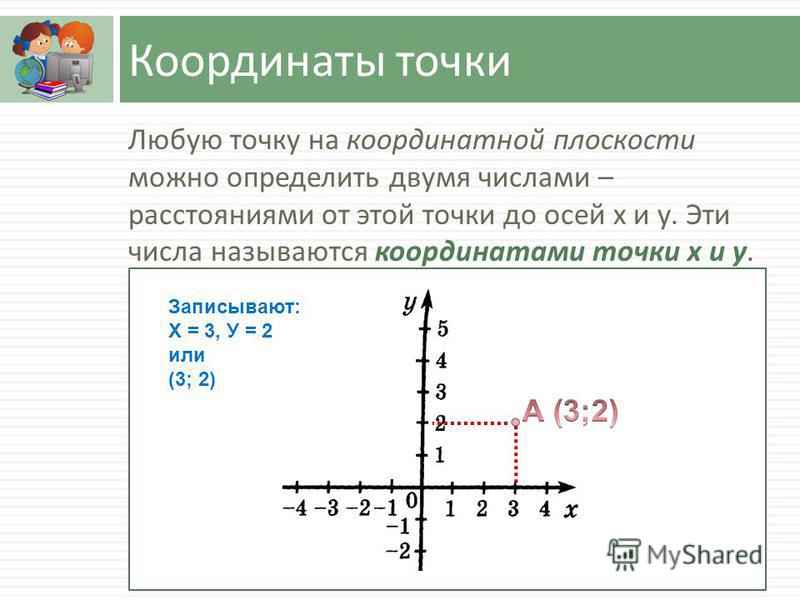
Вот пример из раздела о решении линейных неравенств:
Решить для p . [латекс]4p+5<29[/латекс]
[латекс] \displaystyle \begin{array}{l}4p+5<\,\,\,29\\\underline{\,\,\,\,\,\,\,\ ,\,-5\,\,\,\,\,\,\,-5}\\\подчеркивание{4p}\,\,\,\,\,\,\,\,<\,\, \подчеркнуть{24}\,\,\\4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,4\\\,\,\,\,\,\,\,\,\,\,\,p<6\end{array}[/latex]
Вы можете интерпретировать решение как p может быть любым числом меньше шести. Теперь вспомните, что мы можем построить уравнения линий, определив выходные данные y и входные данные x и написав уравнение.
Ранее мы показали, как изобразить линию, описываемую этим уравнением: [latex]y=2x+3[/latex] , и обнаружили, что можно построить бесконечную таблицу значений, которые образуют точки на линия — это некоторые решения уравнения [латекс]у=2х+3[/латекс].
| x значений | [латекс]2x+3[/латекс] | у значений |
|---|---|---|
| 0 | [латекс]2(0)+3[/латекс] | 3 |
| 1 | [латекс]2(1)+3[/латекс] | 5 |
| 2 | [латекс]2(2)+3[/латекс] | 7 |
| 3 | [латекс]2(3)+3[/латекс] | 9 |
Кроме того, мы узнали, как изобразить линию, представляющую все точки, которые делают [латекс]у=2х+3[/латекс] верным утверждением.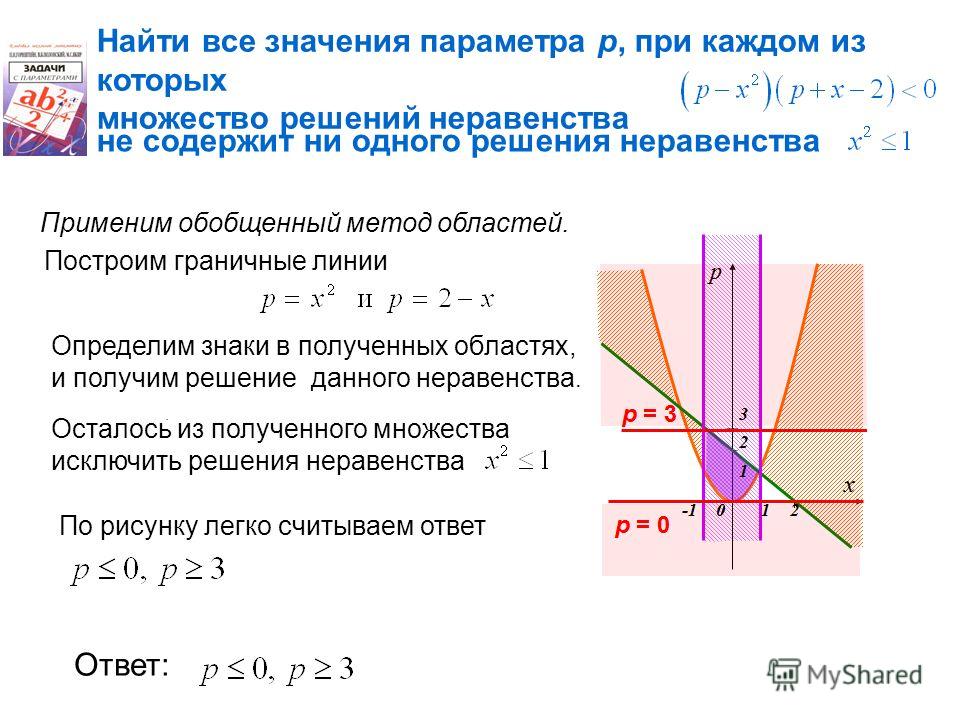
Что, если мы объединим эти две идеи — линейные неравенства и графы линий? Сначала переведите строку [latex]y=2x+3[/latex] в слова:
Вы получите х , умножив х на два и прибавив три. [latex]y=2x+3[/latex]
Как бы вы перевели это неравенство словами? [latex]y<2x+3[/latex]
Для каких значений x вы получите результат y, который на меньше, чем , умноженный на x плюс три?
ВАУ, это может показаться запутанным, но продолжайте читать, мы поможем вам разобраться.
Линейные неравенства отличаются от линейных уравнений, хотя вы можете применить свои знания об уравнениях, чтобы понять неравенства. Неравенства и уравнения — это математические операторы, которые сравнивают два значения. В уравнениях используется символ = ; помните, что неравенства представлены символами < , ≤ , > и ≥.
Один из способов визуализировать неравенства с двумя переменными — нанести их на координатную плоскость. Вот как выглядит неравенство [latex]x>y[/latex] .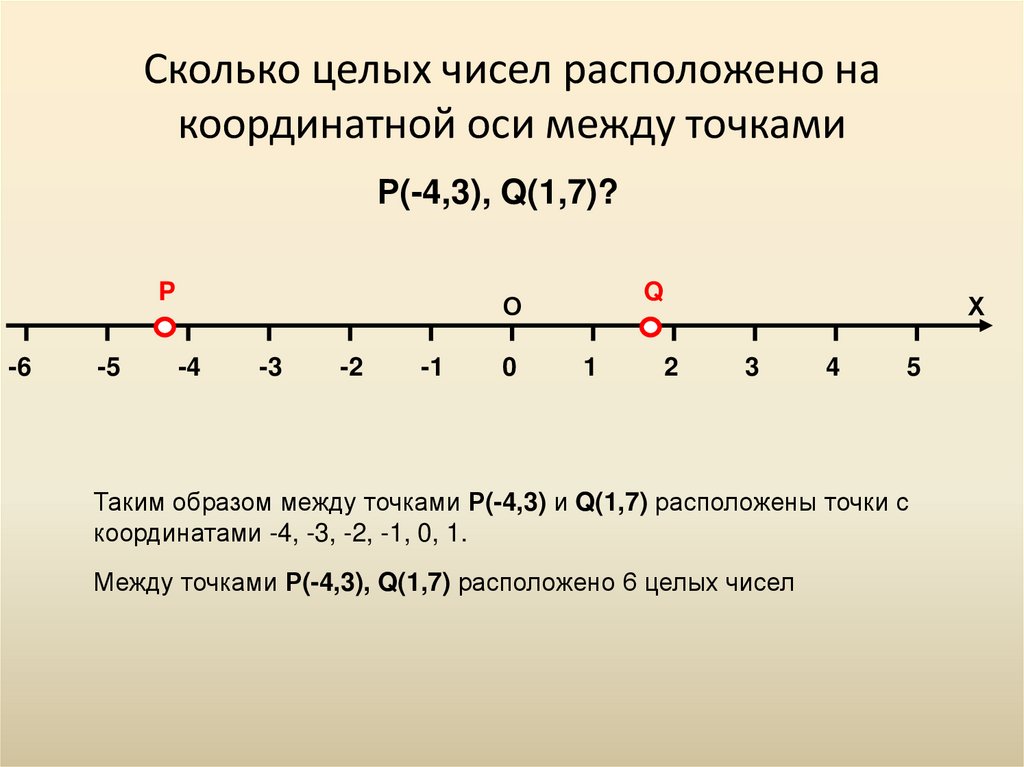 Решение представляет собой область, которая заштрихована. Эта область состоит из множества упорядоченных пар, каждая из которых делает утверждение [latex]x>y[/latex] верным.
Решение представляет собой область, которая заштрихована. Эта область состоит из множества упорядоченных пар, каждая из которых делает утверждение [latex]x>y[/latex] верным.
Здесь следует отметить несколько моментов. Во-первых, посмотрите на пунктирную красную граничную линию: это график соответствующего линейного уравнения [latex]x=y[/latex]. Затем посмотрите на светло-красную область справа от линии. Эта область (за исключением строки [latex]x=y[/latex]) представляет собой все множество решений неравенства [latex]x>y[/latex]. Помните, как все точки на строки являются решениями линейного уравнения линии? Итак, все точки в области являются решениями линейного неравенства , представляющего эту область.
Давайте задумаемся об этом на мгновение — если [латекс]x>y[/латекс], то график [латекс]х>у[/латекс] покажет все упорядоченные пары [латекс](х,у)[ /latex], для которого координата x- больше, чем координата y-.
На приведенном ниже графике показана область [латекс]x>y[/латекс], а также некоторые упорядоченные пары на координатной плоскости. Посмотрите на каждую заказанную пару. 9Координата 0015 x- больше, чем координата y-? Находится ли упорядоченная пара внутри или снаружи заштрихованной области?
Посмотрите на каждую заказанную пару. 9Координата 0015 x- больше, чем координата y-? Находится ли упорядоченная пара внутри или снаружи заштрихованной области?
Упорядоченные пары [латекс](4,0)[/латекс] и [латекс](0,−3)[/латекс] лежат внутри заштрихованной области. В этих упорядоченных парах координата x- больше, чем координата y-. Эти упорядоченные пары входят в набор решений уравнения [латекс]х>у[/латекс].
Упорядоченные пары [латекс](−3,3)[/латекс] и [латекс](2,3)[/латекс] находятся вне заштрихованной области. В этих упорядоченных парах 9Координата 0015 x- на меньше , чем координата y-, поэтому они не включены в набор решений неравенства.
Упорядоченная пара [латекс](−2,−2)[/латекс] находится на граничной линии. Это не решение, так как [латекс]-2[/латекс] не больше, чем [латекс]-2[/латекс]. Однако если бы неравенство было [латекс]x\geq y[/латекс] (читается как « x больше или равно y »), то [латекс](−2,−2)[/латекс ] был бы включен (и линия была бы представлена сплошной, а не пунктирной линией).
Разница между линейным уравнением и линейным неравенством (две переменные)
Рассмотрим еще один пример: неравенство [latex]3x+2y\leq6[/latex]. На приведенном ниже графике показана область значений, которая делает это неравенство верным (заштрихована красным), граничная линия [латекс]3x+2y=6[/латекс], а также несколько упорядоченных пар. Граничная линия на этот раз сплошная, потому что точки на граничной линии [latex]3x+2y=6[/latex] делают неравенство [latex]3x+2y\leq6[/latex] истинным.
Как и в предыдущем примере, вы можете подставить значения x- и y- в каждую из упорядоченных пар [latex](x,y)[/latex] в неравенство, чтобы найти решения . Хотя вы, возможно, смогли сделать это в уме для неравенства [latex]x>y[/latex], иногда создание таблицы значений имеет смысл для более сложных неравенств.
| Заказная пара | Делает неравенство [латекс]3x+2y\leq6[/латекс] верное утверждение | Делает неравенство [латекс]3x+2y\leq6[/латекс] ложное заявление |
|---|---|---|
| [латекс](−5, 5)[/латекс] | [латекс]\begin{array}{r}3\left(−5\right)+2\left(5\right)\leq6\\−15+10\leq6\\−5\leq6\end{array }[/латекс] | |
| [латекс](−2,−2)[/латекс] | [латекс]\begin{array}{r}3\left(−2\right)+2\left(–2\right)\leq6\\−6+\left(−4\right)\leq6\\ –10\leq6\end{массив}[/латекс] | |
| [латекс](2,3)[/латекс] | [латекс]\begin{массив}{r}3\влево(2\вправо)+2\влево(3\вправо)\leq6\\6+6\leq6\\12\leq6\end{массив}[/ латекс] | |
| [латекс](2,0)[/латекс] | [латекс]\begin{array}{r}3\left(2\right)+2\left(0\right)\leq6\\6+0\leq6\\6\leq6\end{array}[/ латекс] | |
| [латекс](4,−1)[/латекс] | [латекс]\begin{массив}{r}3\влево(4\вправо)+2\влево(-1\вправо)\leq6\\12+\влево(-2\вправо)\leq6\\10\ leq6\end{массив}[/латекс] |
Если подстановка [латекс](х,у)[/латекс] в неравенство дает верное утверждение, то упорядоченная пара является решением неравенства, и точка будет нанесена в заштрихованную область или точку будет частью сплошной граничной линии. Ложное утверждение означает, что упорядоченная пара не является решением, и точка будет находиться вне заштрихованной области или будет частью пунктирной граничной линии.
Ложное утверждение означает, что упорядоченная пара не является решением, и точка будет находиться вне заштрихованной области или будет частью пунктирной граничной линии.
Определите, удовлетворяют ли упорядоченные пары линейному неравенству
Используйте графический определение, определяемые упорядоченными парными решениями линейного неравенства в двух переменных
Определите, удовлетворяют ли упорядоченные пары линейное неравенство
График. алгебраическая форма неравенства, например [latex]y>3x+1[/latex], к графику этого неравенства? Построить неравенство довольно просто, если вы выполните пару шагов.

Графические неравенства
Чтобы построить график неравенства:
- Нарисуйте соответствующую граничную линию. Замените знак <, >, ≤ или ≥ в неравенстве на =, чтобы найти уравнение граничной линии.
- Определите хотя бы одну упорядоченную пару по обе стороны от линии границы и подставьте эти значения [латекс](х,у)[/латекс] в неравенство. Закрасьте область, содержащую упорядоченные пары, которые делают утверждение неравенства верным.
- Если точки на граничной линии являются решениями, используйте сплошную линию для рисования граничной линии. Это произойдет для ≤ или ≥ неравенств.
- Если точки на граничной линии не являются решениями, используйте пунктирную линию для граничной линии. Это произойдет для < или > неравенств.
Построим график неравенства [latex]x+4y\leq4[/latex].
Чтобы построить граничную линию, найдите не менее двух значений, лежащих на линии [latex]x+4y=4[/latex]. Вы можете использовать точки пересечения x и y для этого уравнения, подставив сначала 0 вместо x и найдя значение y ; затем подставьте 0 вместо y и найдите x .
| х | у |
| 0 | 1 |
| 4 | 0 |
Нанесите точки [латекс](0,1)[/латекс] и [латекс](4,0)[/латекс] и проведите линию через эти две точки в качестве граничной линии. Линия сплошная, потому что ≤ означает «меньше или равно», поэтому все упорядоченные пары вдоль линии включаются в набор решений.
Следующий шаг — найти область, содержащую решения. Это выше или ниже границы? Чтобы определить область, в которой справедливо неравенство, вы можете протестировать пару упорядоченных пар, по одной с каждой стороны от граничной линии.
Если заменить [латекс](−1,3)[/латекс] на [латекс]x+4y\leq4[/латекс]:
[латекс]\begin{array}{r}−1+4\ left(3\right)\leq4\\−1+12\leq4\\11\leq4\end{array}[/latex]
Это неверное утверждение, поскольку 11 не меньше или равно 4.
С другой стороны, если вы замените [латекс](2,0)[/латекс] на [латекс]x+4y\leq4[/латекс]:
[латекс]\begin{array}{r}2 +4\left(0\right)\leq4\\2+0\leq4\\2\leq4\end{массив}[/latex]
Это правда! Область, включающая [латекс](2,0)[/латекс], должна быть заштрихована, так как это область решений.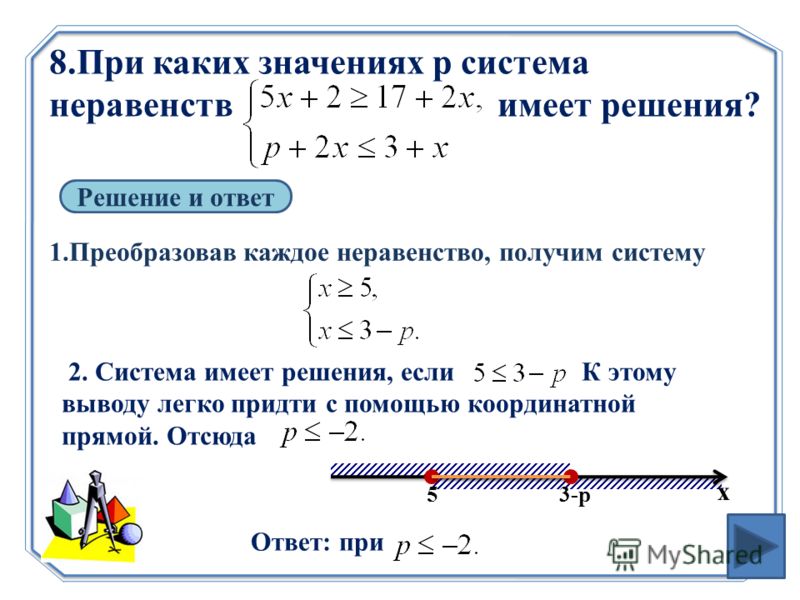
Вот и все — график множества решений для [latex]x+4y\leq4[/latex].
Графики линейных неравенств с двумя переменными
Небольшое примечание к описанной выше проблеме — обратите внимание, что вы можете использовать точки [латекс](0,−3)[/латекс] и [латекс](2,1)[/латекс] для построения линии границы, но это эти точки не входят в область решений, так как область не включает граничную линию!
Графики линейных неравенств с двумя переменными (форма пересечения наклона)
Резюме
Когда неравенства изображаются на координатной плоскости, решения располагаются в области координатной плоскости, которая представлена в виде заштрихованной области на самолет.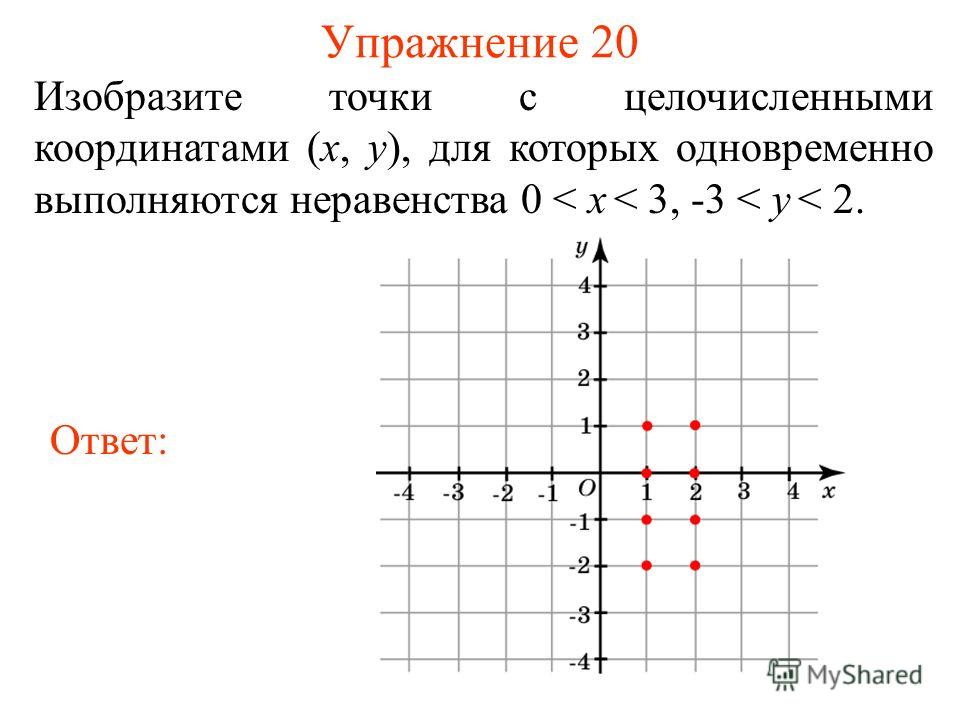 Граница неравенства рисуется сплошной линией, если точки на самой линии удовлетворяют неравенству, как в случаях ≤ и ≥. Она рисуется штриховой линией, если точки на прямой не удовлетворяют неравенству, как в случаях < и >. Вы можете сказать, какую область закрасить, проверив некоторые точки в неравенстве. Использование координатной плоскости особенно полезно для визуализации области решений неравенств с двумя переменными.
Граница неравенства рисуется сплошной линией, если точки на самой линии удовлетворяют неравенству, как в случаях ≤ и ≥. Она рисуется штриховой линией, если точки на прямой не удовлетворяют неравенству, как в случаях < и >. Вы можете сказать, какую область закрасить, проверив некоторые точки в неравенстве. Использование координатной плоскости особенно полезно для визуализации области решений неравенств с двумя переменными.
|
Линейные неравенства (с двумя переменными)
Решения линейных неравенств
Мы знаем, что линейное уравнение с двумя переменными имеет бесконечно много упорядоченных парных решений, которые на графике образуют линию. Линейное неравенство с двумя переменными. Неравенство, связывающее линейные выражения с двумя переменными. Множество решений представляет собой область, определяющую половину плоскости. С другой стороны, имеет множество решений, состоящее из области, определяющей половину плоскости.
Линейное неравенство с двумя переменными. Неравенство, связывающее линейные выражения с двумя переменными. Множество решений представляет собой область, определяющую половину плоскости. С другой стороны, имеет множество решений, состоящее из области, определяющей половину плоскости.
Для неравенства линия определяет одну границу заштрихованной области. Это указывает на то, что любая упорядоченная пара, находящаяся в заштрихованной области, включая граничную линию, будет удовлетворять неравенству. Чтобы убедиться, что это так, выберите несколько контрольных точек. Точка не на границе линейного неравенства, используемая как средство для определения того, в какой полуплоскости лежат решения. и подставить их в неравенство.
Также мы видим, что упорядоченные пары вне заштрихованной области не решают линейного неравенства.
График набора решений линейного неравенства всегда является областью. Однако граница не всегда может быть включена в этот набор. В предыдущем примере линия была частью набора решений из-за части «или равно» включающего неравенства ≤. Если у нас есть строгое неравенство <, мы будем использовать пунктирную линию, чтобы указать, что эти точки не включены в набор решений.
Если у нас есть строгое неравенство <, мы будем использовать пунктирную линию, чтобы указать, что эти точки не включены в набор решений.
Рассмотрим точку (0, 3) на границе; эта упорядоченная пара удовлетворяет линейному уравнению. Это часть инклюзивного неравенства «или равно», которая делает его частью набора решений.
До сих пор мы видели примеры неравенств со значением «меньше». Теперь рассмотрим следующие графики с одной и той же границей:
Что можно ожидать, учитывая приведенные выше графики, если мы используем начало координат (0, 0) в качестве контрольной точки?
Попробуйте! Какие из упорядоченных пар (−2, −1), (0, 0), (−2, 8), (2, 1) и (4, 2) решают неравенство y>−12x+2?
Ответ: (−2, 8) и (4, 2)
Решение для видео
(нажмите, чтобы посмотреть видео)Графические решения линейных неравенств
Решения линейных неравенств представляют собой заштрихованную полуплоскость, ограниченную сплошной или пунктирной линией. Эта граница либо входит в решение, либо нет, в зависимости от заданного неравенства. Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано включающее неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги построения графика набора решений для неравенства с двумя переменными показаны в следующем примере.
Эта граница либо входит в решение, либо нет, в зависимости от заданного неравенства. Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано включающее неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги построения графика набора решений для неравенства с двумя переменными показаны в следующем примере.
Пример 1: Постройте график набора решений: y>−3x+1.
Решение:
Шаг 1: Нарисуйте линию границы. В этом случае нарисуйте пунктирную линию y=−3x+1 из-за строгого неравенства. При осмотре мы видим, что наклон равен m=−3=−31=riserun, а точка пересечения y равна (0, 1).
Шаг 2: Проверьте точку , а не на границе. Обычной контрольной точкой является исходная точка (0, 0). Контрольная точка помогает нам определить, какую половину плоскости нужно заштриховать.
Шаг 3: Закрасьте область, содержащую решения. Поскольку контрольная точка (0, 0) не была решением, она не лежит в области, содержащей все упорядоченные парные решения. Поэтому заштрихуйте половину плоскости, не содержащую эту контрольную точку. В этом случае заштрихуйте выше линии границы.
Поскольку контрольная точка (0, 0) не была решением, она не лежит в области, содержащей все упорядоченные парные решения. Поэтому заштрихуйте половину плоскости, не содержащую эту контрольную точку. В этом случае заштрихуйте выше линии границы.
Ответ:
Рассмотрим задачу затенения выше или ниже граничной линии, когда неравенство имеет форму пересечения наклона. Если y>mx+b, то затемнить над линией. Если y Пример 2: Нарисуйте набор решений: 2x−5y≥−10. Решение: Здесь граница определяется линией 2x−5y=−10. Поскольку неравенство является всеобъемлющим, мы изображаем границу сплошной линией. В этом случае нарисуйте граничную линию, используя точки пересечения. Далее проверьте точку; это помогает решить, какую область затенить. Поскольку контрольная точка находится в наборе решений, заштрихуйте половину плоскости, в которой она находится. Ответ: Обратите внимание, что в этом примере набор решений состоит из всех упорядоченных пар ниже граничной линии. Это может быть нелогичным из-за исходного ≥ в неравенстве. Это показывает, что лучше всего проверить точку. Найдите и , и вы увидите, что штриховка правильная. В форме пересечения наклона вы можете видеть, что область ниже граничной линии должна быть затенена. Альтернативный подход состоит в том, чтобы сначала выразить границу в форме пересечения наклона, нанести ее на график, а затем заштриховать соответствующую область. Пример 3: Нарисуйте набор решений: y<2. Решение: Сначала нарисуйте граничную линию y=2 пунктирной линией из-за строгого неравенства. Затем проверьте точку. В этом случае заштрихуйте область, содержащую контрольную точку. Ответ: Попробуйте! Нарисуйте набор решений: 5x−y≤10. Ответ:
Решение для видео
(нажмите, чтобы посмотреть видео)
Ключевые выводы
- Линейные неравенства с двумя переменными имеют бесконечно много упорядоченных парных решений, которые можно изобразить, заштриховав соответствующую половину прямоугольной координатной плоскости.

- Чтобы построить график множества решений линейного неравенства с двумя переменными, сначала нарисуйте границу пунктирной или сплошной линией в зависимости от неравенства. Если задано строгое неравенство, используйте пунктирную линию для границы. Если дано инклюзивное неравенство, используйте сплошную линию. Затем выберите контрольную точку не на границе. Если контрольная точка решает неравенство, то заштрихуйте содержащую ее область; в противном случае заштрихуйте противоположную сторону.
- При графическом отображении наборов решений линейных неравенств рекомендуется тестировать значения в наборе решений и за его пределами в качестве проверки.
Упражнения по теме
Часть A: Решения линейных неравенств (две переменные)
Является ли упорядоченная пара решением данного неравенства?
1. у<5х+1; (0, 0)
2. y>−12x−4; (0, −2)
3. y≤23x+1; (6, 5)
4. y≥−13x−5; (−3, −8)
5. у<15х-13; (−13, −1)
у<15х-13; (−13, −1)
6. 4x−3y≤2; (−2, −1)
7. −x+4y>7; (0, 0)
8. 7x−3y<21; (5, −3)
9. у>−5; (−3, −1)
10. x≤0; (0, 7)
Часть B. Построение графиков решений линейных неравенств
Постройте график набора решений.
11. y<−3x+3
12. y<−23x+4
13. y≥−12x
14. y≥45x−8
1 3017. y>−x+4
18. y>x−2
19. y≥−1
20. y<−3
21. x<2
22. x≥2
10010 23. 12≤3090x 24. y>−32x+5225. −2x+3y>6
26. 7x−2y>14
27. 5x−y<10
28. x−y<0
29. 3x −2y≥0
30. x−5y≤0
31. −x+2y≤−4
32. −x+2y≤3
33. 2x−3y≥−1
34. 5x− 4y<−3
35. 12x−13y<1
36. 12x−110y≥12
37. x≥−2y
38. x<2y+3
39. 3x−y+2>0
40. 3−y−2x<0
41. −4x≤12−3y
42. 5x≤−4y−12
43. Запишите неравенство, описывающее все точки верхней полуплоскости выше оси x .
44. Запишите неравенство, описывающее все точки нижней полуплоскости ниже оси x .
45. Запишите неравенство, описывающее все точки полуплоскости слева от оси y .
46. Запишите неравенство, описывающее все точки полуплоскости справа от оси y .
47. Запишите неравенство, описывающее все упорядоченные пары, у которых y -координата не меньше 2.
48. Запишите неравенство, описывающее все упорядоченные пары, у которых x -координата не больше 5.
Ответы
1: Да
3: Да
5: Да
7: Нет
9: Да
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43: y>0
45: x<0
47: y≥2
404 — СТРАНИЦА НЕ НАЙДЕНА
Почему я вижу эту страницу?
404 означает, что файл не найден. Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Вы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.
Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.
Также возможно, что вы непреднамеренно удалили корневую папку документа или вам может потребоваться повторное создание вашей учетной записи. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.
Как найти правильное написание и папку
Отсутствующие или поврежденные файлы Когда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере. Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
http://example.com/example/Example/help.html
В этом примере файл должен находиться в папке public_html/example/Example/
Обратите внимание, что CaSe важен в этом примере. На платформах, которые обеспечивают чувствительность к регистру 9Пример 0126 e и пример E не совпадают.
Для дополнительных доменов файл должен находиться в папке public_html/addondomain.com/example/Example/, а имена чувствительны к регистру.
Неработающее изображениеЕсли на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным размером X , где отсутствует изображение. Щелкните правой кнопкой мыши на X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Это зависит от браузера. Если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши на странице, затем выберите «Просмотреть информацию о странице» и перейдите на вкладку «Мультимедиа».
http://example.com/cgi-sys/images/banner.PNG
В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/
Обратите внимание, что в этом пример. На платформах с учетом регистра PNG и png не совпадают.
404 Ошибки после перехода по ссылкам WordPress
При работе с WordPress часто могут возникать ошибки 404 Page Not Found, когда была активирована новая тема или когда были изменены правила перезаписи в файле .htaccess.
Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.
Вариант 1. Исправьте постоянные ссылки- Войдите в WordPress.
- В меню навигации слева в WordPress нажмите Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете пользовательскую структуру, скопируйте или сохраните ее где-нибудь.)
- Выберите По умолчанию .

- Нажмите Сохранить настройки .
- Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.
- Нажмите Сохранить настройки . 9index.php$ — [L]
- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Использовать SSH и текстовый редактор
- Используйте файловый менеджер в cPanel
- Войдите в cPanel.
- В разделе «Файлы» щелкните значок File Manager .
- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
- Убедитесь, что установлен флажок Показать скрытые файлы (точечные файлы) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
- Щелкните правой кнопкой мыши файл .htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода значок вверху страницы.
- Может появиться диалоговое окно с вопросом о кодировании.
 Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.
Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне. - При необходимости отредактируйте файл.
- Нажмите Сохранить изменения в правом верхнем углу, когда закончите. Изменения будут сохранены.
- Протестируйте свой веб-сайт, чтобы убедиться, что ваши изменения были успешно сохранены. Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает. 92 \leq 25$?
спросил
Изменено 5 лет, 1 месяц назад
Просмотрено 1к раз
$\begingroup$
У меня были эти вопросы с предыдущего экзамена, на которые я не мог ответить, я извиняюсь за любые английские ошибки или за любые глупые вопросы, я пытался их решить, я искал в Интернете, и я не мог найти ответы или, по крайней мере, те с пояснениями.
 92 \leq 25$$ Сколько INTEGER пар $x,y$ удовлетворяют неравенству?
92 \leq 25$$ Сколько INTEGER пар $x,y$ удовлетворяют неравенству?
*Я пытался думать о комбинаторике, но не знал, чем она может мне помочь, в конце концов мне пришлось применить грубую силу.Спасибо, что нашли время, чтобы прочитать вопрос, если у кого-то есть советы для моего экзамена или знает какие-либо сложные задачи, я был бы очень благодарен, если бы он/она мог рассказать мне о них!
Спасибо!неравенство алгебраического предварительного исчисления
$\endgroup$
7
$\begingroup$
В замкнутом круге радиуса $5$ есть $$\bigl\lfloor\sqrt{25}\bigr\rfloor+\bigl\lfloor\sqrt{24}\bigr\rfloor+\bigl\lfloor\sqrt{21}\bigr\rfloor+\bigl\lfloor\sqrt{16} \bigr\rfloor+\bigl\lfloor\sqrt{9}\bigr\rfloor=20$$ точек решетки, удовлетворяющих $x\geq0$, $y>0$. Таким образом, общее число точек решетки в этом круге равно $1+4\cdot20=81$.
 2}\right\rfloor=\color{red}{81}.\end{eqnarray*} $$ 92 = 5$ разрезает 16 узлов решетки
$(\pm 5,0), (0,\pm 5), (\pm3,\pm4)$
2}\right\rfloor=\color{red}{81}.\end{eqnarray*} $$ 92 = 5$ разрезает 16 узлов решетки
$(\pm 5,0), (0,\pm 5), (\pm3,\pm4)$Если мы построим неправильный восьмиугольник, соединяющий эти 8 точек. Его площадь будет немного меньше площади круга.
Площадь круга $25\pi$
Теорема Пика утверждает, что количество точек решетки внутри (I) $+ \frac 12$ количество точек решетки на периметре(E) $- 1$ равна площади любого замкнутого многоугольника.
$I+ 8 — 1 < 25\pi\\ Я < 71$
Далее симметрия к линии сетки. Центр стационарный. Для любой другой точки на решетке, если мы повернем ее на 90 градусов, мы найдем другую точку на решетке.
$I-1$ делится на $4$
$I=69$ — наибольшее число, удовлетворяющее двум имеющимся ограничениям.
$\endgroup$
$\begingroup$
Подход грубой силы, нарушающий симметрию. Заметьте, что если $(x,y)$ — решение, то $(y,x)$ — тоже, а если $(x,y)$ — решение, то $(\pm x,\pm y)$ — тоже.

RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule . /index.php [L]
# Конец WordPress
Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и перезапись URL-адресов — это две очень распространенные директивы, которые можно найти в файле . htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. В этом разделе рассматривается, как редактировать файл в cPanel, но не то, что может потребоваться изменить. статьи и ресурсы для этой информации.)
Существует множество способов редактирования файла .htaccessСамый простой способ редактирования файла .htaccess для большинства людей — через диспетчер файлов в cPanel.
Как редактировать файлы .htaccess в файловом менеджере cPanel Прежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.

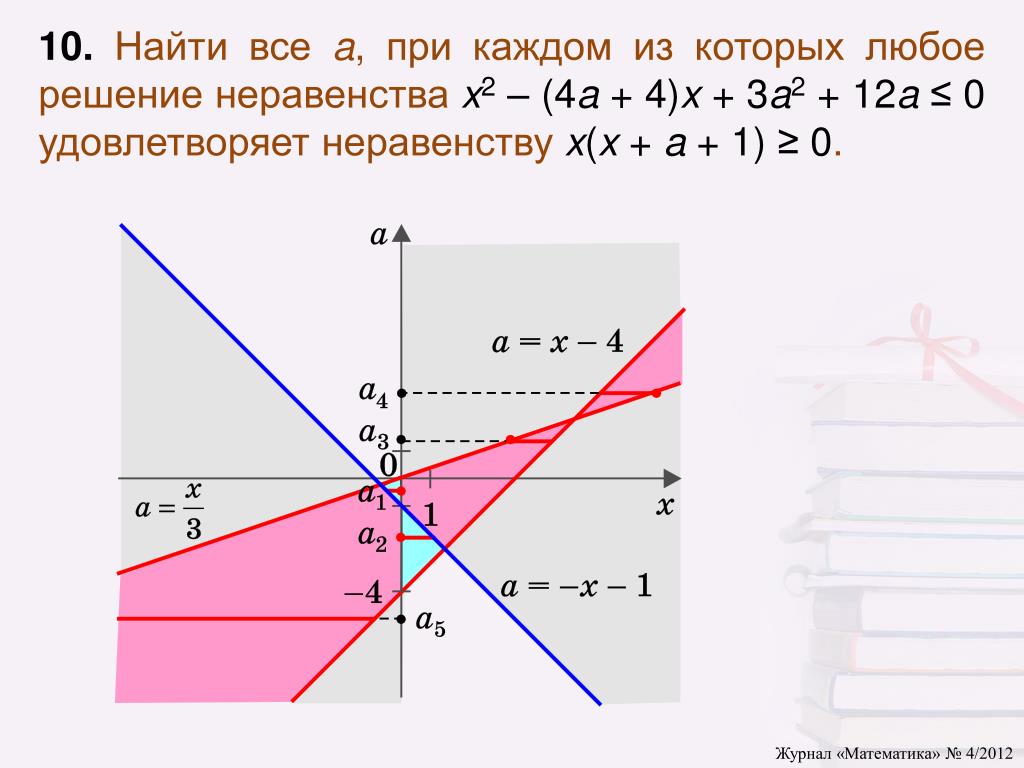 ед.
ед.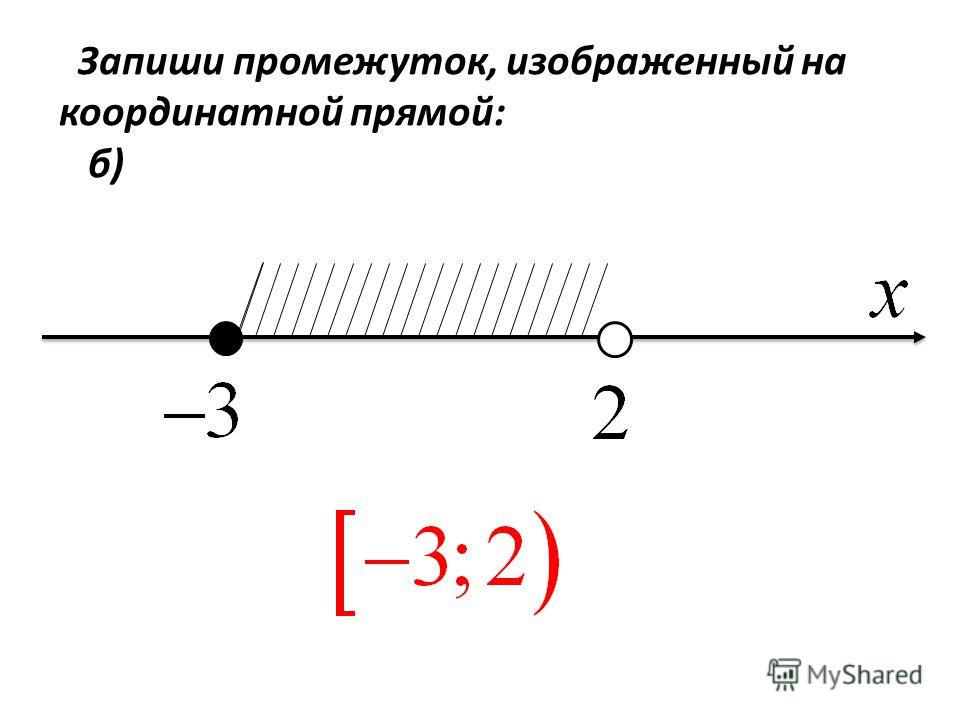


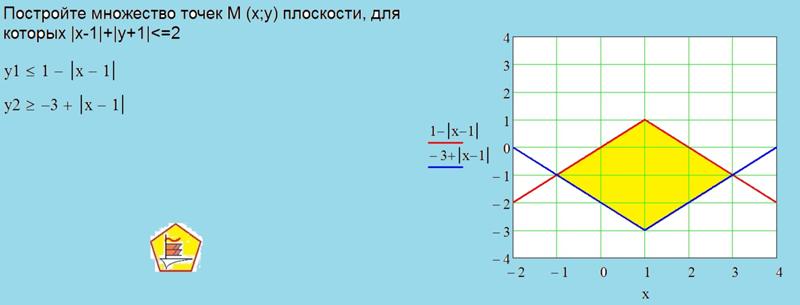
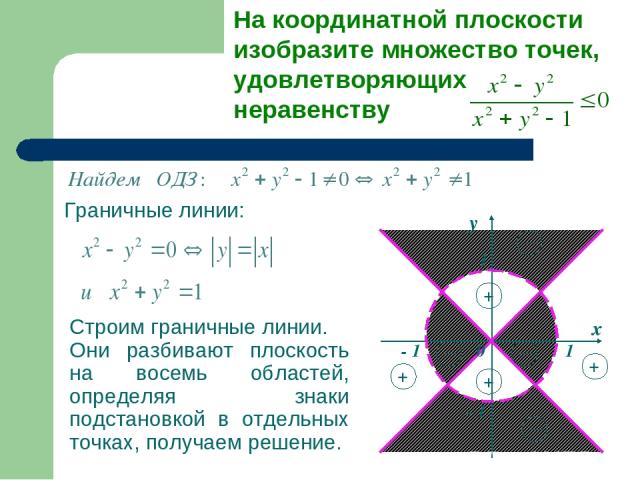 В плоской прямоугольной системе координат точка пересечения осей; график (0,0).
В плоской прямоугольной системе координат точка пересечения осей; график (0,0).