Формула тангенса половинного угла | это… Что такое Формула тангенса половинного угла?
В тригонометрии, формула тангенса половинного угла связывает тангенс половинного угла с тригонометрическими функциями полного угла:
Различные вариации этой формулы выглядят следующим образом:
В области определения угла θ имеем
Содержание
|
Геометрическое доказательство
Геометрическое доказательство формулы тангенса половинного угла
Универсальная тригонометрическая подстановка
Основная статья: Универсальная тригонометрическая подстановка
В различных приложениях полезно записывать тригонометрические функции (такие как синус и косинус) через рациональные функции новой переменной t, равной тангенсу половинного угла. Эти тождества полезны при вычислении первообразных.
Эти тождества полезны при вычислении первообразных.
Существование формулы тангенса половинного угла основано на том факте, что окружность является алгебраической кривой порядка 0. Поэтому можно ожидать, что ‘круговые функции’ могут быть сведены к рациональным функциям.
Геометрические построения выглядят следующим образом: на тригонометрическом круге для любой точки, имеющей координаты (cos φ, sin φ), проведём прямую, проходящую через круг и точку с координатами (−1,0). Эта прямая пересекает ось ординат (ось y) в некоторой точке с координатой y = t. Путём простых геометрических построений можно показать, что t = tg(φ/2). Уравнение проведённой прямой таково y = (1 + x)t. Уравнение для определения точек пересечения указанной прямой и окружности представляет собой квадратное уравнение относительно t. Два решения этого уравнения — это (−1, 0) и (cos φ, sin φ). Это позволяет нам записать (cos φ, sin φ) как рациональные функции от t (решения даны ниже).
Заметим также, что параметр t стереографическую проекцию точки (cos φ, sin φ) на ось y с центром проекции, расположенным в точке (−1,0). Поэтому формула тангенса половинного угла даёт нам переход от стереографической координаты t к тригонометрическому кругу и стандартной угловой координате φ.
Имеем
и
Из этих формул можно выразить арктангенс через натуральный логарифм
При нахождении первообразных от функций, содержащих sin(φ) и cos(φ), подстановка Вейерштрасса выглядит следующим образом. Принимая
получаем
и следовательно
Гиперболические тождества
Можно получить полностью аналогичные выводы для гиперболических функций. Точка на гиперболе (на её правой ветви) определяется координатами (ch
и тогда тождества для гиперболических функций таковы
и
Использование этих подстановок для нахождения первообразных было представлено Карлом Вейерштрассом.
Выражение θ через t приводит к следующим соотношениям между гиперболическим арктангенсом и натуральным логарифмом:
См. также
- Тригонометрические тождества
- Формула половины стороны
- Стереографическая проекция
- Функция Гудермана
Ссылки
- Тангенс половинного угла на Planetmath
Формулы приведения.
Тригонометрические функции углов вида ,,,могут быть выражены через функции углас помощью формул, которые называются формулами приведения.
Формулы приведения предназначены для того, чтобы выражать значения тригонометрических функций произвольных углов через функции острого угла.
Все
приводимые ниже формулы справедливы
при произвольных значениях угла(естественно, входящих в область
определения соответствующих функций),
хотя применяются преимущественно в
тех случаях, когда угол – острый.
Докажем сначала, что для любого
и
Для определённости предположим, что . Тогда для угласправедливо двойное неравенство. Рассмотрим радиусыи, образующие углыис положительным направлением осисоответственно (рис. 17). Опустим из точекиперпендикуляры на ось. Полученные треугольникииравны, поскольку они прямоугольные,, имеют равные гипотенузы () и равные острые углы:.
Из равенства треугольников следует, что и.Следовательно,, . Вторая формула получается с помощью аналогичных рассуждений.
Для тангенса и котангенса формулы приведения следуют из равенств
и .
Из формул , а также с учётом чётности и нечётности тригонометрических функций можно получить формулы
, ,,.
Например, .
Формулы приведения для синуса и косинуса угла выглядят так:
и
.
Для доказательства достаточно представить в видеи дважды воспользоваться формулами. Аналогичные формулы для тангенса и котангенса,можно получить с помощью формул приведения для синуса и косинуса.
Из формул (3) следует:
, ,,. (20.4)
Для доказательства достаточно представить в виде суммыи применить формулы (20.3).
Формулы приведения для углов имеют вид
, ,,.
Для доказательства этих формул надо представить и последовательно применить формулы (20.3) и (20.1).
Справедливы также формулы
, ,,.
Перечисленные выше формулы могут быть обобщены одним правилом:
Любая
тригонометрическая функция угла
по
абсолютной величине равна той же функции
угла,
если числоn —
чётное, и ко-функции этого же угла, если n –
нечётное.
Теорема (основное тригонометрическое тождество).
Для любого угла справедливо тождество.
Доказательство.
Пусть дан некоторый угол. Тогда координаты конца радиуса тригонометрического круга, составляющего уголс положительным направлением оси, будут равны по определению, (рис.18). Так как квадрат расстояния между любыми двумя точками плоскости, заданными своими координатами, равен сумме квадратов разностей одноимённых координат, то квадрат расстояния от точкидо точки(равный единице, поскольку- конец радиуса единичной длины) определяется равенством,
откуда
следует
.
Между основными тригонометрическими функциями произвольного аргумента αимеются следующие соотношения.
Основное тригонометрическое тождество
.
Доказательство тождества приведено выше.
По определению тангенса и котангенса выполнено
, для ,;
, для ,.
Перемножая последние два соотношения, получим
для ,.
4. Разделив основное тригонометрическое тождество почленно наии выполнив несложные преобразования, получим соответственно
для ,.
Аналогично для,.
2.3: Закон касательных
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3256
- Майкл Коррал
- Колледж Скулкрафт
Мы показали, как решить треугольник во всех четырех случаях, рассмотренных в начале этой главы. Альтернативой закону косинусов для случая 3 (две стороны и угол между ними) является Закон касательных :
Альтернативой закону косинусов для случая 3 (две стороны и угол между ними) является Закон касательных :
Теорема: Закон касательных
Если треугольник имеет длины сторон \(a \), \(b \) и \(c \), противоположные углам \(A \), \(B \) и \ (C \), соответственно, тогда
\[ \begin{align}\label{2.17}\frac{a-b}{a+b} ~&=~
\frac{\tan\;\frac{1} {2}(AB)}{\tan\;\frac{1}{2}(A+B)} ~,\\ \label{2.18}
\frac{b-c}{b+c} ~&=~
\frac{\tan\;\frac{1}{2}(BC)}{\tan\;\frac{1}{2}(B+C)} ~,\\ \label{2.19}
\ frac{c-a}{c+a} ~&=~
\ frac {\ tan \; \ frac {1} {2} (CA)} {\ tan \; \ frac {1} {2} (C + A)} ~. \\
\end{align} \]
Обратите внимание, что поскольку \(\tan\;(-\theta) = -\tan\;\theta \) для любого угла \(\theta \), мы можем переключать порядок букв в каждой из приведенных выше формул. Например, мы можем переписать уравнение \ref{2.17} как
. \[\label{2.20}
\frac{ba}{b+a}~=~\frac{\tan\;\frac{1}{2}(BA)}{\tan\;\frac{1 {2}(Б+А)}~,
\]
и аналогично для остальных формул. Если \(a > b \), то обычно удобнее использовать уравнение \ref{2.17}, а уравнение \ref{2.20} удобнее, когда \(b > a \). 9\круг = 0\)). Это означает, что
Если \(a > b \), то обычно удобнее использовать уравнение \ref{2.17}, а уравнение \ref{2.20} удобнее, когда \(b > a \). 9\круг = 0\)). Это означает, что
С законом касательных связаны Уравнения Моллвейде :
Уравнения Моллвейде
Для любого треугольника \(\triangle\,ABC \),
\[\begin{align}
\frac{a-b}{c} ~&=~
\frac{\sin\;\frac {1}{2}(AB)}{\cos\;\frac{1}{2}C} ~,~\text{and}\label{2.21}\\[4pt]
\frac{a+b }{c} ~&=~
\frac{\cos\;\frac{1}{2}(AB)}{\sin\;\frac{1}{2}C} ~.\label{2. 22}
22}
\end{align} \]
Обратите внимание, что все шесть частей треугольника входят в оба уравнения Моллвейда. По этой причине любое уравнение можно использовать для проверки решения треугольника. Если обе части уравнения совпадают (более или менее), то мы знаем, что решение правильное. 9\circ}\\ \nonumber
1.44 ~&=~ 1.86 \quad\times
\end{align*} \nonumber \]
Здесь разница слишком велика, поэтому мы заключаем, что треугольника с этими частями нет .
Мы докажем закон касательных и уравнения Моллвейде в главе 3, где мы сможем предоставить краткие аналитические доказательства.
Эта страница под названием 2.3: The Law of Tangents распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Майкл Коррал
- Лицензия
- ГНУ ФДЛ
- Версия лицензии
- 1,3
- Показать страницу TOC
- нет
- Теги
- Закон касательных
- Уравнения Моллвейде
- источник@http://www.
 mecmath.net/trig/index.html
mecmath.net/trig/index.html
Уравнения касательных — Высшая математика
Добро пожаловать на сайт , посвященный высшей математике.
Прохождение ускоренного курса высшей математики значительно увеличивает ваши карьерные возможности, помогая вам поступить в колледж/университет, пройти стажировку или даже найти работу. «Хороший» результат по высшей математике подготовит вас к курсу математики AH в следующем году, если вы заинтересованы. Пожалуйста, сделайте все возможное, чтобы продолжать учебу.
Для студентов, которым нужна дополнительная помощь по курсу высшей математики, вы можете рассмотреть возможность подписки на фантастические дополнительные ресурсы, ориентированные на экзамены, доступные в онлайн-пакете для изучения.
Чтобы получить доступ к множеству дополнительных бесплатных ресурсов по теме , воспользуйтесь расположенной выше панелью поиска или нажмите ЗДЕСЬ, выбрав тему, которую хотите изучить.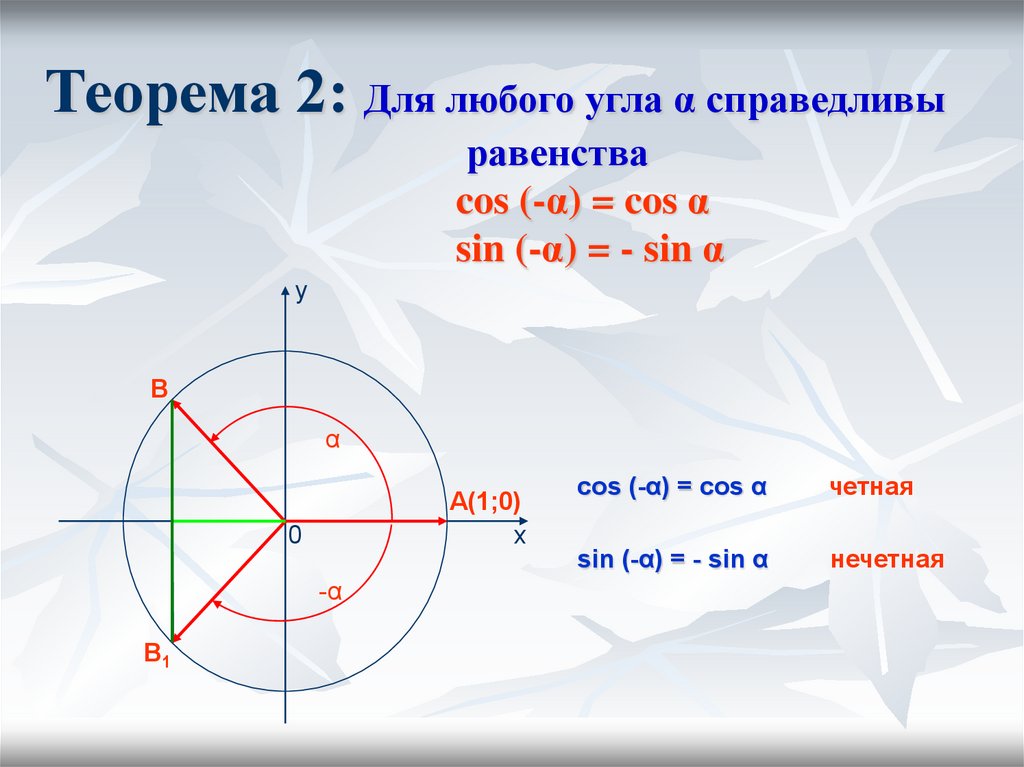
Мы надеемся, что вы найдете этот веб-сайт полезным, и желаем вам всего наилучшего в изучении курса высшей математики в 2023 году. Ниже вы найдете:
1. Об уравнениях касательных
2. Прямые линии и дифференцирование – рабочие листы
3. Прямые линии и дифференцирование – видео, руководства по теории и ментальные карты
4. Высшие математические навыки
Экзамен по математике по темам
6. Прошлые и практические статьи по высшей математике по темам
7. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы
8. Прошлые и практические статьи по высшей математике
9. 40 вопросов и ответов по высшей математике без калькулятора
10. 200 вопросов и ответов по высшей математике 13. Контрольные списки экзаменов по высшей математике
14. Старые вопросы к экзаменам по высшей математике по темам
15. Решения из учебников по высшей математике
16. Руководства по теории высшей математики
17. Интеллект-карты высшей математики
Интеллект-карты высшей математики
18. Оценки модулей по высшей математике – решения включены
19. Высшая математика: бумажные видеорешения
20. Рекомендуемый учебник по высшей математике
21. Онлайн-учебник, ориентированный на экзамен – для студентов, которым нужен «хороший» пропуск
Ресурсы по высшей математике
.
1. Об уравнениях касательных
Чтобы узнать об уравнениях касательных, нажмите на ссылку Теория прямых линий (HSN) и прочитайте со страницы 7, а также на ссылку Теория дифференцирования (HSN) и прочитайте с стр. 8 . Кроме того, в разделах 2 и 3 ниже вы найдете видеоролики (Дифференциация — уравнение касательных), ментальные карты (см. Перпендикулярные линии (в разделе «Прямые линии») и Уравнения касательных (в разделе «Дифференциация»)) и рабочие листы по этой теме, чтобы помочь вам понять. Настоятельно рекомендуется использовать рабочие листы основных навыков, а также рабочие листы, содержащие фактические вопросы экзамена SQA.
Если вам нужна дополнительная помощь в понимании Уравнения касательной , в Учебном онлайн-пакете вы найдете полные, простые для понимания, пошаговые решения десятков экзаменационных вопросов Higher Maths Past & Practice по всем темам. Пожалуйста, дайте себе все возможности для успеха, поговорите со своими родителями и подпишитесь на сосредоточенный на экзамене Online Study Pack сегодня.
Уравнения касательной
На экзамене по высшей математике вас могут попросить определить уравнение касательной. На приведенном ниже рисунке показана линия, касательная к окружности. Знаете ли вы, как найти уравнение касательной?
.
- Касательная – это прямая линия, перпендикулярная другой линии под прямым углом
- Для перпендикулярных уклонов m1m2 = -1
- Мы используем уравнения y – b = m(x – a) или y = mx + c, чтобы найти уравнение прямой
- Дифференциация — это скорость изменения функции по отношению к одной из ее переменных
- Если мы продифференцируем и заменим x, то это будет градиент касательной в этой точке
- «Уравнения касательных» входят в разделы «Прямые» и «Дифференциация» курса высшей математики
.
.
.
2. Прямые линии и дифференциация. Рабочие листы
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом.
Прямые линии. Рабочие листы
Четкие, простые в использовании пошаговые решения для всех приведенных ниже рабочих листов доступны в Онлайн-учебном пакете.
| Высшее Рабочие листы __________________________ | Рекомендуемый _____________ | Рабочий лист _________________________________ | Без ответов ________________ | Примечания/комментарии _____________ 5________________ | Предоставлено 3________________ |
| Heinemann Book — Straight Line | Ex 1A, 1B, 1D, 1E, 1F, 1G, 1I, 1K, 1M, 1N, 1O | Ответы по ссылкам | |||
| Практика экзамена по основным навыкам 1 | Прямая линия | Без ответов | Только ответы | Предоставлено Mr G Rennie | |
| Основные навыки 1 | Медиана треугольника | Без ответов | Только ответы | Предоставлено г-ном Г.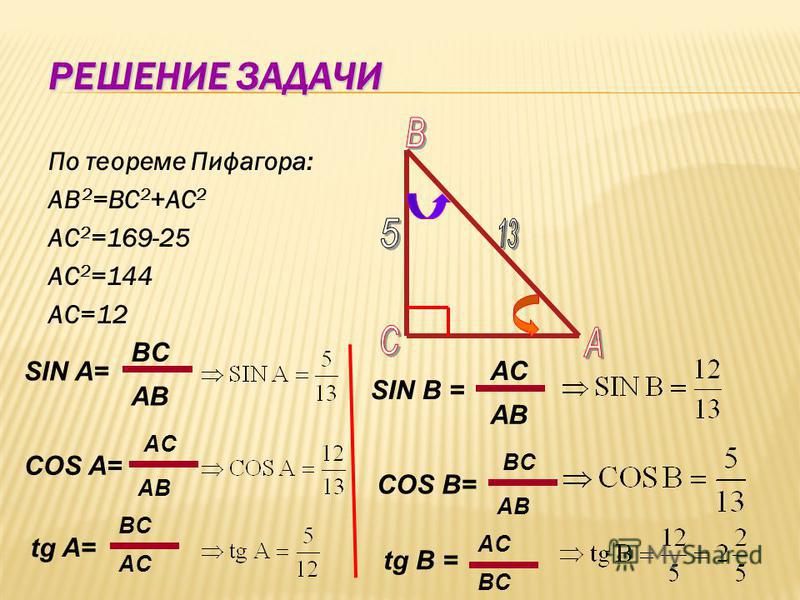 Ренни Ренни | |
| Основные навыки 2 | Биссектрисы | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни | |
| Основные навыки 3 | Высота треугольника | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни | |
| Основные навыки 4 | Уравнение касательной к кривой | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни | |
| Основные навыки 9 | Пересечение линий и окружностей | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни | |
| Основные навыки 29 | Угол между линией и осью X | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни | |
| Grade Booster Paper 5 | Прямые линии | Без ответов | Включены рабочие решения | ||
| Высшие экзаменационные вопросы | Рекомендуемые | Прямые линии 1 (2000–2022) | Без ответов | 2022 Вопросы включены! | Предоставлено SQA |
| Высшие экзаменационные вопросы | Прямые линии 2 | Без ответов | Предоставлено SQA | ||
| Высшие экзаменационные вопросы | Прямые линии 3 | Без ответов | Предоставлено SQA | ||
| Высшие экзаменационные вопросы | Прямые линии 4 (Старое высшее) | Без ответов | Предоставлено SQA | ||
| Высшие экзаменационные вопросы | Straight Lines 5 (2000–2013) | Схемы выставления оценок SQA | Предоставлено SQA | ||
| Экзаменационные вопросы более высокого уровня | Straight Lines 6 (множественный выбор) | Схемы оценки SQA | Предоставлено SQA | ||
| Рабочие листы 1 и 2 | Градиенты перпендикулярных линий 1, 2 | ||||
| Рабочий лист 3 | Формула расстояния | ||||
| Контрольный список экзаменов 11 | Прямые линии |
Дифференциация – Рабочие листы
Четкие, простые в использовании, пошаговые решения для всех рабочих листов, приведенных ниже, доступны в Онлайн-учебном пакете.
| Рабочие листы высшего уровня __________________________ | Рекомендуется _____________ | Рабочие листы ___________________________ | Без ответов ________________ | Примечания/комментарии _________________________ | Предоставлено ____________________ |
| HEINEMANN — Дифференциация | EX 6C, 6D, 6E, 6F, 6G, 6H, 6i, 6J, 6L, 6M , 6N, 6O, 6p, 6q, 6R, 6S | . | |||
| Heinemann — Дальнейшее исчисление | Ex 14B, 14C, 14E, 14G, 14H, 14I, 14J, 14K | Ответы по ссылкам | |||
| Практика экзамена по основным навыкам 3 | Дифференциация | Без ответов | Только ответы | Предоставлено Mr G Rennie | |
| Практика экзамена по основным навыкам 9 | Дальнейшее исчисление | Без ответов | Только ответы | Предоставлено Mr G Rennie | |
| Основные навыки 4 | Уравнение касательной к кривой | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни Ренни | |
| Основные навыки 5 | Стационарные баллы | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни | |
| Основные навыки 17 | Графики производных функций | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни | |
| Основные навыки 22 | Дальнейшая дифференциация | Без ответов | Только ответы | Предоставлено Mr G Rennie | |
| Основные навыки 23 | Дальнейшая интеграция | Без ответов | Только ответы | Предоставлено Mr G Rennie | |
| Бумага Grade Booster 4 | Стационарные точки | Без ответов | |||
| Grade Booster Paper 6 | Касательные к кривым | Без ответов | |||
| Grade Booster Paper 14 | Оптимизация | Без ответов | Включены рабочие решения | ||
| Высшие экзаменационные вопросы | Рекомендуемые | Дифференциация 1 (2000 — 2022) | Без ответов | 2022 Вопросы включены! | Предоставлено SQA |
| Высшие экзаменационные вопросы | Дифференциация 2 | Без ответов | Предоставлено SQA | ||
| Высшие экзаменационные вопросы | Дифференциация 3 | Без ответов | Предоставлено SQA | ||
| Высшие экзаменационные вопросы | Дифференциация 4 (оптимизация) | Без ответов | Предоставлено SQA | ||
| Экзаменационные вопросы высшего уровня | Дифференциация 5 (Старое высшее) | Без ответов | Предоставлено SQA | ||
| Вопросы экзамена высшего уровня | Дифференциация 6 (2000–2013) | Схемы выставления оценок SQA | Предоставлено SQA | ||
| Высшие экзаменационные вопросы | Рекомендуемые | Дальнейшее исчисление 1 (2000 — 2022) | Без ответов | 2022 Вопросы включены! | Предоставлено SQA |
| Высшие экзаменационные вопросы | Дальнейшее исчисление 2 | Без ответов | Предоставлено SQA | ||
| Высшие экзаменационные вопросы | Дальнейшее исчисление 3 (старое высшее) | Без ответов | Несколько вариантов ответа включены! | Предоставлено SQA | |
| Рабочий лист 1 | Дифференциация Введение — 1 | ||||
| Рабочий лист 2 | Дифференциация Введение — 2 | Без ответов | Только ответы | ||
| Рабочий лист 3 | Дифференциальное сопоставление | Без ответов | Только ответы | ||
| Контрольный список экзамена 3 | Дифференциация | ||||
| Контрольный список экзамена 5 | Дополнительные расчеты |
.
3. Прямые линии и дифференциация – видео, теоретические руководства и интеллект-карты
Спасибо авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом.
Прямые линии — видео, руководства по теории и ментальные карты
| Видео по математике Ларберта _____________ | maths180.com Video ___________________ | HSN Theory Guide ____________________________ | Mind Maps __________________ |
| Высоты | Прямые линии | Теория прямых линий (HSN) | Прямые линии (HSN) |
| Коллинеарность | Прямые линии 1 | ||
| Расстояние между точками | Прямые линии 2 | ||
| Уравнение прямой | |||
| Редакция градиента | |||
| Градиент от угла | |||
| Медианы | |||
| Средние точки | |||
| Биссектрисы | |||
| Перпендикулярные градиенты | |||
| Точки пересечения |
Differentiation – Videos, Theory Guides & Mind Maps
| Larbert Maths Videos __________________________________ | maths180. com Videos com Videos ______________________________________ | HSN Theory Guides ____________________________ | Mind Maps ____________________________ |
| Применение производных | Цепное правило — возрастание/убывание | Теория дифференциации (HSN) | Дифференциация (HSN) |
| Цепное правило | Оптимизация — более сложные примеры | Дальнейшая теория исчисления (HSN) | Дифференциация (подготовка к) |
| Замкнутые интервалы | Скорость изменения и касательная к кривой | Дифференциация 1 | |
| Комплексное дифференцирование | Триггерные функции и цепное правило | Дифференциация 2 | |
| Рисование кривой | Дифференциация (дальше) | ||
| Производные графики | |||
| Уравнения касательных | |||
| Дроби и корни | |||
| Функции возрастания и убывания | |||
| Введение в дифференциацию | |||
| Нотация Лейбница | |||
| Оптимизация | |||
| Стационарные точки | |||
| Sin x и Cos x |
.
4. Высшие математические навыки
Спасибо г-ну Г. Ренни за то, что он предоставил в свободный доступ приведенные ниже отличные ресурсы. Рабочие листы основных навыков можно использовать для общего повторения, выполнения домашних заданий, закрепления темы или подготовки к оцениванию, тестам и экзаменам. Четкие, простые в использовании, пошаговые решения для всех 33 рабочих листов основных навыков, приведенных ниже, доступны в пакете онлайн-обучения 9.0034
.
5. Рабочие листы экзамена по высшей математике по темам
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Рабочие листы по темам являются фантастическим учебным ресурсом, поскольку они являются реальными вопросами прошлых бумажных экзаменов. Четкие, простые в использовании, пошаговые решения для всех новых вопросов CfE по высшей математике, приведенных ниже, доступны в онлайн-пакете для изучения.
.
6. Прошлые и практические работы по высшей математике по темам
Спасибо SQA за предоставление бесплатного доступа к превосходным ресурсам, указанным ниже. Вопросы и ответы разделены по темам для удобства поиска. Четкие, простые в использовании, пошаговые решения всех приведенных ниже вопросов доступны в пакете онлайн-обучения.
| . Бумага _____________ | . Маркировка __________ | . Круги ______ | Дифференциация и оптимизация 9. Интеграция _________ | Полиномиалы & Quadratics ____________ | Рецидив Отношения __________ | СТРУКА _________ | TRIG. Векторы ________ | Волна Функция _________ | ||||||
| 2019 P1 | Marking P1 | Q3,16 | Q1 | Q14 | Q10,12 | Q6,11,17b | Q8 | Q2 | Q4 | Q5,7 | Q13, 15,17а | Q9 | ||
| 2019 P2 | Marking P2 | Q15 | Q7b,11 | Q9,12 | Q5,8 | Q2,13 | Q7,10 | Q4 | Q1 | Q6b | Q3,14 | Q6a | ||
| 2018 P1 | Marking P1 | Q4 | Q6,11 | Q2,11,15 | Q3,14 | Q10 | Q7 | Q1,8 | Q13 | Q5,9 ,12 | ||||
| 2018 P2 | Обозначение P2 | Q5c,12 | Q3,9 | Q11 | Q6 | 9,70355 Q24 | 7b,c | Q5a,b | Q2 | Q8 | ||||
| 2017 P1 | Marking P1 | Q2 | Q8,15c | Q12 | Q1,6,15a | Q3,13 | Q10,15b | Q4 | Q9 | Q7,11 | Q5 | Q14 | ||
| 2017 P2 | Маркировка P2 | Q3,10 | Q4,7 | Q9 | Q2 | 2 | 20352 | Q1 | Q6,11 | Q5 | ||||
| 2016 P1 | Marking P1 | Q4,8 | Q2,9 | Q14 | Q6,10,12 | Q5 | Q15 | Q3 | Q1 | Q13 | Q7,11 | |||
| 2016 P2 | Marking P2 | Q4 | Q7 | Q6 | Q10,11b | 3b,9 | Q2,3a | Q1 | Q8b,11a | Q5 | Q8a | |||
| 2015 P1 | Marking P1 | Q11,14 | Q2,7 | Q6 | Q4,5,13 | Q12,15 | Q3,8 | Q9 | Q10 | Q1 | ||||
| 2015 P2 | Marking P2 | Q5 | Q8 | Q2 | Q7a | Q4 | Q3 | Q1 | Q7b | Q6 | Q9 | |||
| Specimen P1 | Marking P1 | Q11 | Q8 | Q10 | Q1 | Q4,7 | Q2,5,9 | Q6,12 | Q3 | |||||
| Specimen P2 | Marking P2 | Q5 | Q3b,8 | Q4,7 | Q9 | Q3a | Q2 | Q1,6 | Q10 | |||||
| Exemplar P1 | Marking P1 | Q1 | Q8,11 | Q10 | Q3 | Q2,5 | Q6 | Q4,7 | Q9 | |||||
| Exemplar P2 | Marking P2 | Q2 | Q9,10 | Q7 | Q8 | Q4 | Q3 | Q1 | Q5,6 |
.
7. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы
Десятки видеороликов по высшей математике содержат качественные уроки по темам. Также включены отличные руководства по теории, интеллект-карты и рабочие листы с актуальными экзаменационными вопросами по высшей математике. Пожалуйста, нажмите на нашу новую страницу с видео и рабочими таблицами по высшей математике по темам.
.
8. Higher Maths Past & Practice Papers
Спасибо SQA за то, что они предоставили в свободном доступе превосходные ресурсы, указанные ниже. Четкие, простые в использовании, пошаговые решения для всех представленных ниже документов CfE Higher Papers доступны в пакете онлайн-обучения.
.
9. 40 Вопросы и ответы по высшей математике без калькулятора
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Начните с этих вопросов, чтобы укрепить свою уверенность. Закончив, вы можете перейти к 200 экзаменационным вопросам по высшей математике в следующем разделе, проверяя свои ответы по ходу дела. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые для понимания, пошаговые решения всех 40 приведенных ниже вопросов доступны в пакете онлайн-обучения.
Закончив, вы можете перейти к 200 экзаменационным вопросам по высшей математике в следующем разделе, проверяя свои ответы по ходу дела. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые для понимания, пошаговые решения всех 40 приведенных ниже вопросов доступны в пакете онлайн-обучения.
.
10. 200 вопросов и ответов по высшей математике
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, постарайтесь задать как можно больше вопросов, проверяя ответы по ходу. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые в использовании, пошаговые решения всех 200 приведенных ниже вопросов доступны в пакете онлайн-обучения.
.
11. Практические экзаменационные работы от A до H – ответы включены
Спасибо SQA и Larkhall Academy за предоставление нижеприведенных превосходных ресурсов в свободный доступ. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые решения для практических работ от A до E доступны в онлайн-пакете для изучения.
Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые решения для практических работ от A до E доступны в онлайн-пакете для изучения.
.
12. 264 SQA Exam Multiple Choice Questions & Answers
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Множественный выбор — это, прежде всего, вопросы уровня C, и это отличное место для начала проверки. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее.
.
13. Контрольные списки экзамена по высшей математике
Спасибо SQA и авторам за то, что они предоставили в свободный доступ приведенные ниже отличные ресурсы. Это фантастические контрольные списки для оценки ваших знаний по высшей математике. Пожалуйста, старайтесь регулярно использовать их для повторения перед тестами, предварительными экзаменами и выпускным экзаменом.
.
14. Старые экзаменационные вопросы по высшей математике по темам
Спасибо SQA за то, что они предоставили в свободном доступе превосходные ресурсы, указанные ниже. Рабочие листы по темам являются фантастическим дополнительным учебным ресурсом.
| Тема ________ | Название темы ___________________________ | Ссылка ________ | Примечания ___________________ |
| Тема 1 | Круги | ЗДЕСЬ | Ответы включены |
| Тема 2 | Дифференциация | ЗДЕСЬ | Ответы включены |
| Тема 3 | Экспоненты и логарифмы | ЗДЕСЬ | Ответы включены |
| Тема 4 | Функции | ЗДЕСЬ | Ответы включены |
| Тема 5 | Дальнейшее исчисление | ЗДЕСЬ | Ответы включены |
| Тема 6 | Графики функций | ЗДЕСЬ | Ответы включены |
| Тема 7 | Интеграция | ЗДЕСЬ | Ответы включены |
| Тема 8 | Многочлены | ЗДЕСЬ | Ответы включены |
| Тема 9 | Квадратика | ЗДЕСЬ | Ответы включены |
| Тема 10 | Рекуррентные соотношения | ЗДЕСЬ | Ответы включены |
| Тема 11 | Прямая линия | ЗДЕСЬ | Ответы включены |
| Тема 12 | Триггерные формулы сложения | ЗДЕСЬ | Ответы включены |
| Тема 13 | Триггерные графики и уравнения | ЗДЕСЬ | Ответы включены |
| Тема 14 | Векторы | ЗДЕСЬ | Ответы включены |
| Тема 15 | Волновая функция | ЗДЕСЬ | Ответы включены |
.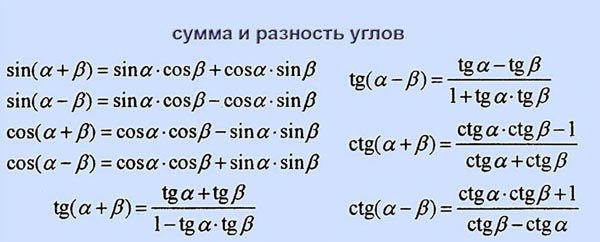
15. Решения для учебников по высшей математике
Спасибо AHS за предоставленные решения для учебников Heinemann по высшей математике, указанные ниже. Они окажутся чрезвычайно полезными для улучшения ваших знаний по высшей математике. Обратите внимание, что может быть нечетная арифметическая ошибка.
.
16. Руководства по высшей математике
Благодарим HSN за то, что они сделали превосходные руководства по высшей математике бесплатными для всех. Они окажутся фантастическим ресурсом, который поможет вам закрепить ваше понимание высшей математики.
| Пособия по теории _________________ | Тема ____________________________________________ | Ссылка _______ |
| Теоретическое руководство 1 | Все темы Раздел 1 Теория (HSN) | ЗДЕСЬ |
| Теоретическое руководство 2 | Все темы, часть 1 — краткое руководство на одной странице (HSN) | ЗДЕСЬ |
| Руководство по теории 3 | Все темы Раздел 2 Теория (HSN) | ЗДЕСЬ |
| Теоретическое руководство 4 | Все темы, раздел 2 — краткое руководство на одной странице (HSN) | ЗДЕСЬ |
| Руководство по теории 5 | Все темы Раздел 3 Теория (HSN) | ЗДЕСЬ |
| Теоретическое руководство 6 | Все темы, раздел 3 — краткое руководство на одной странице (HSN) | ЗДЕСЬ |
| Руководство по теории 7 | Все темы Разделы 1, 2 и 3 Теория (HSN) | ЗДЕСЬ |
| Руководство по теории 8 | Теория кругов (HSN) | ЗДЕСЬ |
| Руководство по теории 9 | Теория дифференцировки (HSN) | ЗДЕСЬ |
| Руководство по теории 10 | Теория экспонент и логарифмов (HSN) | ЗДЕСЬ |
| Руководство по теории 11 | Теория функций и графиков (HSN) | ЗДЕСЬ |
| Руководство по теории 12 | Дальнейшая теория исчисления (HSN) | ЗДЕСЬ |
| Руководство по теории 13 | Теория трансформации графиков (движение и отражение) | ЗДЕСЬ |
| Теоретическое руководство 14 | Сводная таблица преобразований графиков | ЗДЕСЬ |
| Руководство по теории 15 | Теория интеграции (HSN) | ЗДЕСЬ |
| Руководство по теории 16 | Теория многочленов и квадратичных уравнений (HSN) | ЗДЕСЬ |
| Руководство по теории 17 | Теория последовательностей (HSN) | ЗДЕСЬ |
| Руководство по теории 18 | Теория прямых линий (HSN) | ЗДЕСЬ |
| Руководство по теории 19 | Теория тригонометрии (HSN) | ЗДЕСЬ |
| Руководство по теории 19 | Теория векторов (HSN) | ЗДЕСЬ |
| Руководство по теории 20 | Теория волновых функций (HSN) | ЗДЕСЬ |
.
17. Интеллект-карты высшей математики
Спасибо авторам за предоставленные ниже отличные ресурсы. Они окажутся фантастическим ресурсом, помогающим вам подготовиться к оценкам, тестам и выпускному экзамену.
.
18. Оценки модулей по высшей математике – решения включены
Благодарим авторов за то, что они предоставили нижеприведенные превосходные ресурсы в свободный доступ для всех. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом.
.
19. Higher Maths Past Paper Video Solutions
Щелкните DLB Maths, чтобы просмотреть видеорешения Higher Maths Past Paper. Это отличный ресурс, который поможет вам подготовиться к оцениванию, тестам и выпускному экзамену.
.
20. Рекомендуемый учебник по высшей математике
Ниже вы найдете рекомендуемый учебник, который можно заказать, нажав на книгу/ссылку.

 mecmath.net/trig/index.html
mecmath.net/trig/index.html