§ Деление в столбик. Как делить столбиком без остатка
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность.
Площадь круга - Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Площадь кругаАлгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Надо учиться в школе, но ещё больше надо учиться по выходе из школы.
на главную
Введите тему
Русский язык Поддержать сайт
Сложение в столбик Вычитание в столбик Умножение в столбик Деление в столбик
Для деления чисел из двух и более цифр (знаков) применяют деление в столбик.
По традиции, разбираться как делить столбиком будем на примере.
Вычислить:
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра «8».
Начинаем делить «512» на «8» следующим образом:
- Определяем неполное частное. Для этого слева направо сравниваем цифры делимого и делитель. Берём «5». Цифра «5» меньше «8», значит нужно взять еще одну цифру из делимого.
- «51» больше «8». Значит это неполное частное. Ставим точку в частном (под уголком делителя).
Запомните!
Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.
Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас после «51» стоит только одно цифра «2». Значит и добавляем в результат ещё одну точку.
- Приступаем к делению. Вспоминая таблицу умножения на
«8», находим ближайшее к
«51» произведение.
«6 · 8 = 48»
Записываем цифру «6» в частное.Записываем «48» под «51».
При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.
Между «51» и «48» слева поставим «−» (минус).
Вычтем по правилам
вычитания в столбик «48» и под чертой запишем результат. - В остатке получилось «3».
Сравним остаток с делителем. «3» меньше «8».
Запомните!
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
Спишем из делимого «512» цифру «2» к «3».
Число «32» больше «8». И опять по таблице умножения на «8», найдем ближайшее произведение.
8 · 4 = 32
В остатке получился ноль. Значит числа разделились нацело (без остатка).
Значит это неполное частное. Ставим точку в частном (под уголком делителя).
Вычтем по правилам
вычитания в столбик «48» и под чертой запишем результат.Сложение в столбик Вычитание в столбик Умножение в столбик Деление в столбик
Внетабличное деление / Деление / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
- Внетабличное деление
Внетабличное деление на однозначное число
99 : 9 = ?
Рассуждай так:
В числе 99 – 9 десятков и 9 единиц; делю 9 десятков на 9, получаю 1 десяток, или это число 10; далее делю 9 единиц на 9 и получаю число 1.
Теперь к 10 прибавляю 1 и получаю 11. Тогда,
99 : 9 = 11
84 : 4 = ?
Рассуждай так:
В числе 84 – 8 десятков и 4 единицы; делю 8 десятков на 4, получаю 2 десятка, или это число 20; далее делю 4 единицы на 4 и получаю число 1. Теперь к 20 прибавляю 1 и получаю 21. Тогда,
84 : 4 = 11
Нахождение частного подбором
87 : 29 = ?
Пробуем в частном 2 и проверяем: 29 • 2 = 58, 58 < 87, число 2 не подходит.
Пробуем в частном 3 и проверяем: 29 • 3 = 87, 87 = 87, значит, 87 : 29 = 3.
Внетабличное деление на двузначное число
Если ты еще не умеешь решать такие примеры столбиком, то можно решать при помощи умножения.
Рассуждай так:
Деление суммы на число
Чтобы разделить сумму на число, можно вычислить сумму и разделить её на число или разделить на число каждое слагаемое и полученные результаты сложить.
Случай 1: (15 + 25) : 5 = ?Рассуждай так:
Способ 1:
Нахожу сумму чисел 15 и 25, получаю 40.
Теперь 40 делю на 5 и получаю 8.
Записываю так:
(15 + 25) : 5 = 40 : 5 = 8
Способ 2:
Каждое из слагаемых делю на 5 и результат складываю. Сначала делю первое слагаемое 15 на 5, получу 3, потом на 5 разделю второе слагаемое 25, получу 5, теперь полученные результаты 3 и 5 сложу и получу 8. Запишу так:
(15 + 25) : 5 = 15 : 5 + 25 : 5 = 3 + 5 = 8
Значит, (15 + 25) : 5 = 8
Случай 2: 36 : 2 = ?
Рассуждай так:
Число 36 представлю в виде суммы слагаемых, которые легко делятся на 2, например, 20 и 16. Эту сумму надо разделить на 2.
32 : 2 = (20 + 16) : 2 = ?
Сначала делю первое слагаемое 20 на 2, получу 10, потом на 2 разделю второе слагаемое 16, получу 8, теперь полученные результаты 10 и 8 сложу и получу 18.
32 : 2 = (20 + 16) : 2 = 20 : 2 + 16 : 2 = 10 + 8 = 18
Значит, 36 : 2 = 18
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное деление
Деление с остатком
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Деление
Правило встречается в следующих упражнениях:
2 класс
Страница 36.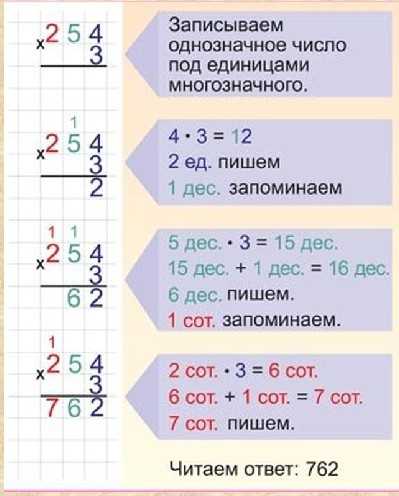
Урок 12,
Петерсон, Учебник, часть 3
Страница 70. Урок 26, Петерсон, Учебник, часть 3
Страница 73. Урок 27, Петерсон, Учебник, часть 3
Страница 78. Урок 29, Петерсон, Учебник, часть 3
Страница 81. Урок 31, Петерсон, Учебник, часть 3
Страница 82. Урок 31, Петерсон, Учебник, часть 3
Страница 88. Урок 34, Петерсон, Учебник, часть 3
Страница 108. Повторение, Петерсон, Учебник, часть 3
Страница 109. Повторение, Петерсон, Учебник, часть 3
Страница 110.
Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 80. Вариант 1. Проверочная работа 1, Моро, Волкова, Проверочные работы
Страница 21, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2
Страница 25, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2
Страница 100, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2
Страница 92. Урок 34, Петерсон, Учебник, часть 1
Страница 15. Урок 6, Петерсон, Учебник, часть 2
Страница 24.
Урок 11,
Петерсон, Учебник, часть 2
Страница 55. Урок 22, Петерсон, Учебник, часть 2
Страница 6. Урок 2, Петерсон, Учебник, часть 3
4 класс
Страница 18, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 40, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 78, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 13, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 30, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 20, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 26, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 67, Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Номер 241, Мерзляк, Полонский, Якир, Учебник
Номер 242, Мерзляк, Полонский, Якир, Учебник
Номер 254, Мерзляк, Полонский, Якир, Учебник
Номер 264, Мерзляк, Полонский, Якир, Учебник
Номер 291, Мерзляк, Полонский, Якир, Учебник
Номер 5, Мерзляк, Полонский, Якир, Учебник
Номер 317, Мерзляк, Полонский, Якир, Учебник
Номер 318, Мерзляк, Полонский, Якир, Учебник
Номер 362, Мерзляк, Полонский, Якир, Учебник
Номер 365, Мерзляк, Полонский, Якир, Учебник
Узнайте, как решить деление с десятичными числами
В этом посте мы узнаем, как решить деление с десятичными числами.
Мы увидим различные примеры.
Наконец, мы увидим, как решать задачи на деление до тех пор, пока остаток не станет равным нулю.
Деление десятичного числа на целоеВы делите, как если бы они были целыми числами. Просто поместите десятичную точку в частное прямо над ее позицией в делимом.
Мы рассмотрим пример деления 77,5 на 25.
77 разделить на 25 равно 3 с остатком 2.
Теперь выпадаем следующая цифра. Поскольку 5 — это первое десятичное число, мы запишем десятичную точку в частном и разделим 25 на 25, что равно 1.
1 x 25 = 25, таким образом, 25 входит один раз без остатка.
Результат этого десятичного деления на целое число равен 3,1, а остаток равен нулю.
Деление целого числа на десятичное числоНапример, мы собираемся разделить 278 на 3,6.
В делителе не может быть десятичных знаков; поэтому у делителя убираем запятую и прибавляем к делимому столько нулей, сколько цифр после запятой.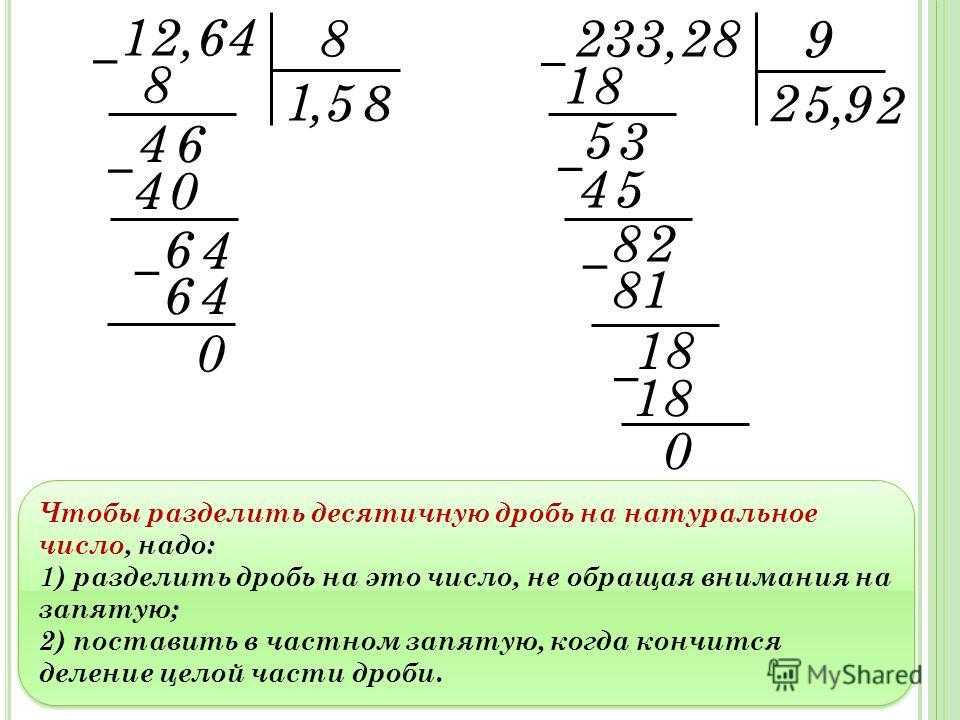
В этом случае мы должны добавить только один ноль. Итак, теперь мы должны разделить 2780 на 36.
36 входит в число 278 семь раз с остатком 26.9.0005
Теперь опустите 0, чтобы мы могли разделить 260 на 36, что равно 7 с остатком 8.
Решение деления 77 с остатком 8.
Деление d десятичное число на десятичное числоУдалить десятичную точку из делителя и переместить десятичную точку делимого вправо на столько знаков, сколько делитель имеет после запятой. При необходимости добавьте к делимому нули.
Теперь мы собираемся разделить 278,1 на 2,52.
Сначала удалите десятичную точку из делителя, и, поскольку делитель имеет два десятичных знака, вы должны переместить десятичную точку делимого на две позиции. Если делимое имеет только один десятичный знак, добавьте столько нулей, сколько осталось позиций. В этом случае мы добавляем один ноль и делим 27810 на 252.
на 252, что входит один раз, с остатком 9.
Мы опускаем следующее число, равное 0, так что теперь нам нужно разделить 90 на 252. Поскольку 90 меньше 252, мы должны записать 0 в частном и опустить следующую цифру.
Мы уже решили деление, потому что цифр больше нет. Решением будет 110 с остатком 90.
Теперь мы увидим как вынуть десятичные дроби . Если в конце деления остался остаток, то в частном пишем десятичную точку, а к делимому прибавляем ноль. Если мы хотим продолжать вычитать десятичные дроби, нам придется продолжать добавлять нули к делимому.
Мы увидим пример удаления десятичных дробей, деление 33 на 6.
6 входит в 33, 5 раз с остатком 3.Итак, если мы хотим сложить десятичные дроби, мы должны поставить десятичную точку в частном после 5.
Затем мы можем добавить ноль к остатку.
Теперь нам нужно разделить 30 на 6, что равно 5.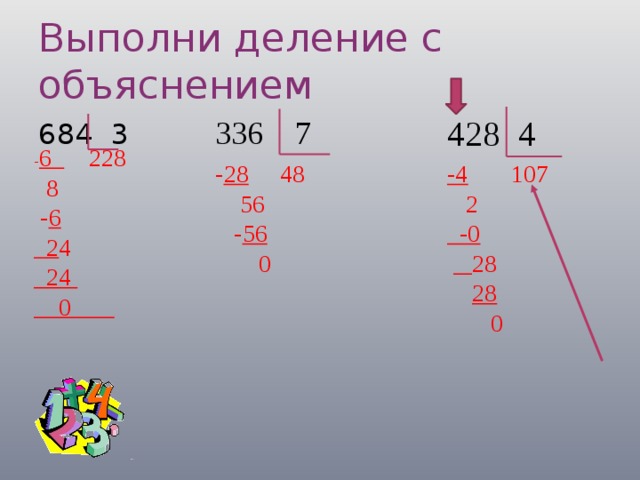
И решение 33 разделить на 6 равно 5,5.
Кроме того, теперь вы можете узнать больше о делении десятичных дробей!
- Изучите и попрактикуйтесь в делении десятичных дробей
- Как решить задачу, связанную с делением двухзначных чисел
Подпишитесь на бесплатную пробную версию Smartick уже сегодня!
Подробнее:
- Автор
- Последние сообщения
Smartick
Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Последние сообщения Smartick (посмотреть все)
Практика решения задач на деление — Элементарная математика
В этом посте мы научимся анализировать, думать и решать задачи, требующие деления: задачи на деление. В Smartick мы хотим подчеркнуть тот факт, что вы должны знать, как точно решить любую математическую задачу.
В результате мы предоставим вам множество задач, для решения которых требуется разделение.
Задачи отдела № 1
В старших классах некоторые учителя жаловались, что не хватает материалов, и в результате им пришлось разделить 18 коробок ластиков поровну между 9 классами. Сколько коробочек с ластиком получит каждый класс?
Это самый простой тип задачи на деление, с которой мы столкнемся. Задача говорит нам, что есть 18 ящиков, и они хотят разделить их на равные части между девятью классами. Когда мы говорим о делении на равные части, мы говорим о ДЕЛЕНИИ:
18 ÷ 9 = 2Каждый класс получит по 2 коробки ластиков.
Проблемы отдела № 2
В моем городе есть водопровод рядом с большими садами на самом высоком холме, чтобы обеспечить достаточное количество воды для орошения, но в настоящее время в запасе всего 56 галлонов воды. Если вся вода делится с получателями по 8 литров на каждого, то сколько получателей снабжается водой?
Эта проблема аналогична предыдущей.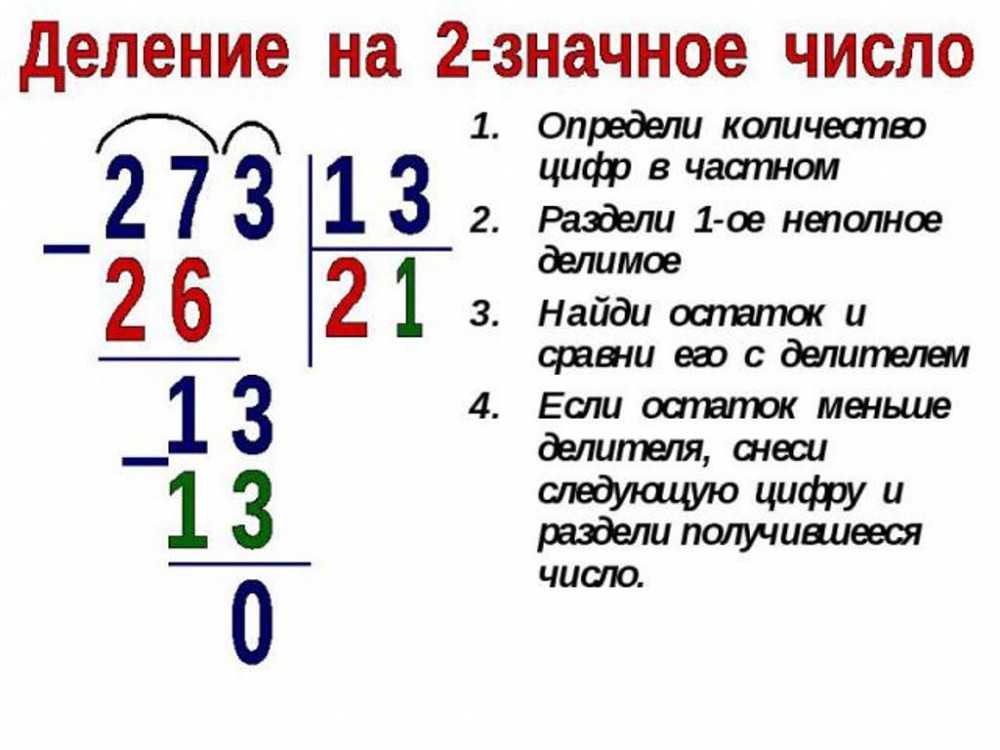
Опять же, вы должны разделить 56 галлонов воды между получателями, дав каждому по 8 литров. Следовательно, мы должны ДЕЛИТЬ:
Будет предоставлено 7 получателям.
Задачи отдела № 3
Как и каждое воскресное утро, Ричард и Кэтрин отправились прогуляться по полю. Так как они привыкли заниматься спортом, то идут быстро и без остановок на прогулке. Зная, что прогулка длится три часа, что в общей сложности они прошли 15 миль и что они прошли с семью людьми, подсчитайте, с какой скоростью они идут (при условии, что они идут с постоянной скоростью).
Вы должны начать разъяснять, что скорость в этой задаче измеряется в милях в час (читается как мили в час) и относится к количеству миль, пройденных за один час. Задача говорит нам, что 15 миль пройдено за три часа. То, что по ней шли семь человек, для этой задачи не имеет значения. Следовательно, если за 3 часа они пройдут 15 миль, сколько миль будет пройдено за один час? Чтобы найти его, мы должны РАЗДЕЛИТЬ:
15 ÷ 3 = 5 Они шли со скоростью 5 миль в час (5 миль в час).
Проблемы отдела № 4
Мы с Рэймондом копим деньги, чтобы купить игру и подарить ее Кармен на ее день рождения, который наступит через 5 дней. У него есть 9 долларов, а у меня уже есть 27 долларов. Во сколько раз больше денег я сэкономил, чем Рэймонд?
Формулировка задачи может привести к путанице, так что «больше» или «меньше» раз можно интерпретировать как сложение или вычитание. В случае этой задачи они говорят, что Рэймонд получил 9 долларов.и что у меня есть 27 долларов, и они спрашивают меня, на сколько умножить на больше, чем я сэкономил, чем он. У Раймонда меньше денег, чем у меня; следовательно, сумма, которую он имеет (9 долларов), умноженная на некоторое число, должна дать в результате деньги, которые есть у меня (27 долларов). Следовательно, нам нужно РАЗДЕЛИТЬ:
27 ÷ 9 = 3Я накопил в 3 раза больше, чем Рэймонд.
На этом мы закончили решать задачи с одной операцией: задачи на сложение, вычитание, умножение и деление.