Формулы синуса и косинуса двойного угла: Формулы двойного угла в тригонометрии, синус косинус двойного угла, вывод формул двойного угла

Формулы двойного угла в тригонометрии, синус косинус двойного угла, вывод формул двойного угла

Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2α, используя тригонометрические функции угла α. Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.

Список формул двойного угла

Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид nα записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin nαимеет то же значение, что и sin (nα). При обозначении sinn α имеем аналогичную запись(sin α)n. Использование записи применимо для всех тригонометрических функций со степенями n.

Ниже приведены формулы двойного угла:

sin 2α=2·sin α·cos αcos 2α=cos2 α-sin2 α,   cos 2α=1-2·sin2 α, cos 2α=2·cos2 α-1tg 2α=2·tg α1-tg2 αctg 2α-ctg2 α-12·ctg α

Отметим, что данные формулы sin и cos применимы с любым значением угла α. Формула тангенса двойного угла справедлива при любом значении α, где tg 2α имеет смысл, то есть α≠π4+π2·z, z является любым целым числом. Котангенс двойного угла существует при любом α, где ctg 2α определен на α≠π2·z.

Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.

Доказательство формул двойного угла

Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:

sin (α+β)=sin α ·cos β+cos α·sin βи косинуса суммы cos (α+β)=cos α ·cos β-sin α·sin β. Предположим, что β=α, тогда получим, что

sin (α+α)=sin α ·cos α+cos α·sin α=2·sin α·cos α и cos (α+α)=cos α ·cos α-sin α·sin α=cos2α-sin2α

Таким образом доказываются формулы синуса и косинуса двойного угла sin 2α= 2·sin α·cos α и cos 2α=cos2α-sin2α.

Остальные формулы cos 2α=1-2·sin2 α и cos 2α=2·cos2 α-1 приводят к виду cos 2α=cos 2α=cos2 α-sin2 α, при замене 1 на сумму квадратов по основному тождествуsin2 α+cos2 α=1. Получаем, что sin2 α+cos2 α=1.   Так 1-2·sin2 α=sin2 α+cos2 α-2·sin2 α=cos2 α-sin2 α и 2·cos2 α-1=2·cos2 α-(sin2 α+ cos2 α)=cos2 α-sin2 α.

Для доказательства формул двойного угла тангенса и котангенса применим равенства tg 2α=sin 2αcos 2α и ctg 2α=cos 2αsin 2α. После преобразования получим, что tg 2α=sin 2αcos 2α=2·sin α·cos αcos2 α-sin2 α и ctg 2α=cos 2αsin 2α=cos2 α-sin2 α2·sin α·cos α. Разделим выражение на cos2 α, где cos2 α≠0 с любым значением α, когда tg α определен. Другое выражение поделим на sin2 α, где sin2 α≠0 с любыми значениями α, когда ctg 2α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:

tg 2α=sin 2αcos 2α=2·sin α·cos αcos2 α-sin2 α=2·sin α·cos αcos2 αcos2 α-sin2 αcos2 α=2·sin2 αcos2 α1-sin2 αcos2 α=2·tg α1-tg2 αctg 2α=cos 2αsin 2α=cos2 α-sin2 α2·sin α·cos=cos2 α-sin2 αsin2 α2·sin α·cos αsin2 α=cos2 αsin2 α-12·cos αsin α=ctg2 α-12·ctg α

Примеры использования формул двойного угла

Данный пункт показывает несколько примеров решения с формулами двойного угла.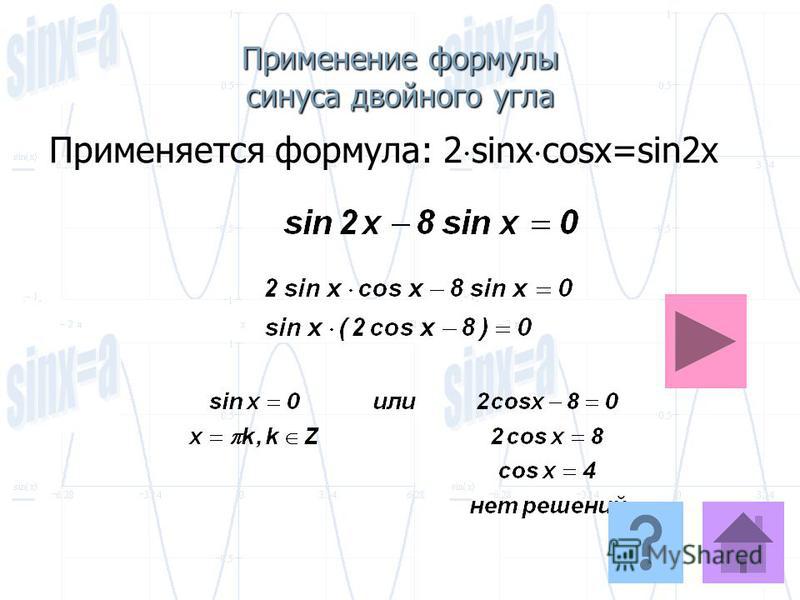 Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2α для α=30°, применим значения тригонометрических функций для этих углов. Если α=30°, тогда 2α=60°. Проверим значения sin 60°=2·sin 30°·cos 30°, cos 60°=cos2 30°-sin2 30°.

Подставив значения, получим tg 60°= 2·tg 30°1-tg2 30° и ctg 60°=ctg230°-12·ctg 30°..

Известно, что sin 30°=12, cos 30°=32, tg 30°=33, ctg 30°=3 и

sin 60°=32, cos 60°=12, tg 60°=3, ctg 60°=33, тогда отсюда видим, что

2·sin 30°·cos 30°=2·12·32=32, cos230°-sin230°=(32)2-(12)2=12,2·tg 30°1-tg230°=2·321-(33)=3 

и  ctg230°-12·ctg 30°=(3)2-12·3=33

Проведя вычисления, можно сделать вывод, что справедливость для α=30° подтверждена.

Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2α. В примере допускается применение формулы двойного угла 3π5. Тогда его необходимо преобразовать, в результате чего получим α=3π5:2=3π10.

Отсюда следует, что формула двойного угла для косинуса будет иметь видcos3π5=cos23π10-sin23π10.

Пример 1

Представить sin 2α3 через тригонометрические функции, при α6.

Решение

Заметим, что из условия имеем 2α3=4·α6. Тогда использовав 2 раза формулу двойного угла, выразим sin2α3 через тригонометрические функции угла α6. Применяя формулу двойного угла, получим sin 2α3=2·sin α3·cos α3. После чего к функциям sin α3 и cos α3применим формулы двойного угла: sin 2α2=2·sin α3·cosα3=2·(2·sinα5·cosα6)·(cos2α6-sinα6)==4·sinα6·cos3α6-4·sin3α6·cosα6

Ответ: sin2α3=4·sinα6·cos3α6-4·sin3α6·cosα6.

Формулы тройного, четверного и т.д. угла

Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.

sin 3α=sin(2α+α)=sin 2α·cos α+cos 2α·sin α=2·sin α·cosα·cos α+ (cos2 α-sin2α)·sin α==3·sin α·cos2α-sin3 α

При замене cos2α на 1-sin2α из формулы sin 3α=3·sin α·cos2α-sin3α, она будет иметь вид sin 3α=3·sin α-4·sin3 α.

Так же приводится формула косинуса тройного угла:

cos 3α=cos (2α+α)=cos 2α·cos α-sin 2α·sin α==(cos2 α-sin2 α)·cos α-2·sin α·cos α·sin α=cos3α-3·sin2α·cos α

При замене sin2 α на 1-cos2 α получим формулу вида cos 3α=-3·cos α+4·cos3 α.

При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:

tg 3α=sin 3αcos 3α=3·sin α·cos2 α-sin3 αcos3α-3·sin2α·cos α=3·sin α·cos2α-sin3αcos3αcos3α-3·sin2α·cos αcos3α==3·sin αcos α-sin3αcos3α1-3·sin2 αcos2 α=3·tg α-tg3α1-3·tg2α;ctg 3α=cos 3αsin 3α=cos3 α-3·sin2α·cosα3·sin α·cos2α-sin3α=cos3α-3·sin2α·cosαsin3α3·sin α·cos2α-sin3αsin3α==cos3αsin3α-3·cos αsin α3·cos2αsin2α-1=ctg3α-3·ctgα3·ctg2α-1

Чтобы выводить формулы четвертой степени, имеет смысл представить 4α как 2·2α, тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5α в виде 3α+2α, что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.

тригонометрические, синуса, косинуса, тангенса, примеры

Основные понятия по теме

Определение 

Формулы двойного аргумента являются представлением тригонометрической функции удвоенного аргумента и имеют вид выражения тригонометрических функций простого, или одинарного, аргумента.

С помощью формул двойного аргумента можно связать sin 2x, cos 2x, tg 2x и sin x,  cos x, tg x между собой. Данные закономерности полезны при решении задач на уроках тригонометрии в десятом классе и при выполнении самостоятельных работ. С их помощью можно значительно упростить тригонометрические выражения в любом задании.

Формулы синуса, косинуса, тангенса двойного аргумента

Данные формулы разработаны на основе уравнений суммы и разности двух аргументов тригонометрических функций.

Формула 1

Формула синуса двойного угла имеет вид:

Формула 2

Формула косинуса двойного угла записана таким образом:

Формула 3

Тангенс двойного угла можно вычислить, исходя из формулы:

Формула 4

Формула для определения котангенса двойного угла следующая:

Тригонометрические формулы двойного аргумента

В качестве объяснения вывода формул представим, что имеется некая окружность с углами \alpha и \beta:

Источник: shkolkovo. net

Предположим, что у данных углов существуют соответствующие точки А и В. Координаты рассматриваемых точек будут равны:

Проанализируем полученный треугольник AOB:

Вспомним теорему для косинусов углов. Тогда получим, что:

Заметим, что в данном выражении радиусом окружности является:

AO=BO=R

Насколько точки удалены друг от друга в пределах рассматриваемой плоскости, можно вычислить таким образом:

Если сопоставить между собой уравнения, которые записаны выше, получим, что:

Другие формулы суммы и разности углов можно вывести, используя записанную формулу, а также свойства четности и нечетности косинуса и синуса, формулы приведения, которые имеют вид:

Выполним вычисления:

Здесь следует поделить числитель и знаменатель дроби на выражение:

С учетом, что:

Получим:

В результате полученное уравнение является справедливым равенством при условии:

Вывести формулу котангенса суммы и разности двух углов можно аналогичным методом, но с помощью деления на выражение:

Записанные формулы помогут при выведении формул двойного угла:

Вспомним ключевое тождество из тригонометрии:

Тогда можно вывести еще пару формул для косинуса двойного угла:

Вычислим тангенс двойного угла:

Здесь целесообразно поделить числитель и знаменатель дроби на выражение:

В результате:

Заметим, что записанное уравнение является справедливым равенством, если выполняются следующие условия:

Рассмотрим формулу котангенса для двойного угла:

Условием является:

Примеры заданий с решениями

Задача 1

Необходимо вычислить синус двойного угла  при условии, что:

Решение

Здесь целесообразно возвести во вторую степень обе части выражения. Тогда получим:

Вспомним формулу упрощенного умножения «квадрат разности». Выполним соответствующие преобразования:

В этом случае пригодится основное тригонометрическое тождество, которое имеет вид:

Применим эту формулу к нашим вычислениям и получим в результате:

Далее потребуется использовать формулу синуса двойного угла:

Тогда получим, что:

Ответ  

Задача 2

Дано выражение, которое требуется записать в виде произведения:

Решение

В этом случае поможет формула синуса двойного угла. С ее помощью выполним преобразования:

Полученное выражение можно подставить в начальное выражение. В таком случае:

Ответ: 

Формулы двойного угла для синуса и косинуса

Формулы двойного угла для синуса и косинуса рассказывают, как найти синус и косинус дважды угла ($\,2x\,$),
через синус и косинус исходного угла ($\,x\,$):

• Формулы двойного угла являются тождествами. То есть они всегда верны .
  Каждому из них можно было бы предварять:   ‘Для всех действительных чисел $\,x\,$ … ’
• Напомним соглашение об использовании обозначения функций с многобуквенными именами функций (например, ‘$\,\sin\,$’ и ‘$\,\cos\,$’):
  круглых скобок можно опустить, если нет путаницы в порядке операций.

  Таким образом, вы обычно видите ‘$\,\sin 2x\,$’ (без скобок) вместо ‘$\,\sin(2x)\,$’ (со скобками).

  Оба ‘$\,\sin 2x\,$’ и ‘$\,\sin(2x)\,$’ представляют одно и то же: 92 x — 1\,$ версия с только косинус Обратите внимание, что эти описания относятся к тому, что происходит в правой части формул.

Вывод формул двойного угла

Формулы двойного угла доказываются просто, как только формулы сложения для синуса и косинуса будут на месте.
Для всех действительных чисел $\,x\,$:

2 х — 1} $$

Геометрическое доказательство формул двойного угла для малых углов

Для наброска и вывода ниже предположим, что $\,x\,$ измеряется в градусах, а $\,2x Это другая «укладка» треугольников, чем в предыдущий урок, показать альтернативные подходы к доказательству.

$\sin 2x$	$=$	$\sin(x+x)$	(переименовать $\,2x\,$ в $\,x + x\,$)
	$=$	$\sin x\,\cos x + \cos x\,\sin x$	(формула сложения синуса)
	$=$	$2\sinx\,\cosx$	(добавьте похожие термины)
$\cos 2x$	$=$	$\cos (х + х)$	(переименовать $\,2x\,$ в $\,x + x\,$)

Начните с прямоугольного треугольника $\,\треугольник ABC\,$ (желтый). Он имеет острый угол $\,x\,$ и гипотенузу длины $\,1\,.$ Таким образом: нижняя ветвь: $\,\cos x\,$ боковая нога: $\,\sin x\,$ Сложите прямоугольный треугольник $\,\треугольник ACD\,$ (в основном зеленый) на гипотенузе желтого треугольника. Он также имеет острый угол $\,x\,.$ Нижний катет имеет длину $\,1\,.$ Поскольку $\,\cos x = \frac{\text{ADJ}}{\text{HYP}} = \frac{1}{\text{HYP}}\,$ , гипотеза имеет длину $\,\ frac{1}{\cos x}\,. $ Таким образом, боковая ветвь $\,\frac{1}{\cos x}\cdot \sin x = \frac{\sin x}{\cos x}\,.$ 92 х}{\cos х}\,$ боковая нога: $\,\frac{\sin x}{\cos x}(\cos x) = \sin x\,$ Используя прямоугольный треугольник $\,\треугольник AFD\,$ 92 х}\кр\кр \end{выравнивание} $$

Снова используя правый $\,\треугольник AFD\,$ получаем формулу синуса двойного угла: $$ \cssId{s119}{\sin 2x} \ \cssId{s120}{=\ \frac{\text{OPP}}{\text{HYP}}} \ \cssId{s121}{=\ \frac{\sin x +\sin x}{1/\cos x}} \ \cssId{s122}{=\ 2\sin x\,\cos x} $$

Обзор: Определяет ли $\,\cos x\,$ однозначно $\,\sin x\,$? Нет!

Напомним, что каждое ненулевое действительное число однозначно определяется двумя вещами:

• его размер (расстояние от нуля)
• его знак (плюс-минус)

Этот факт часто имеет решающее значение при работе с тригонометрическими выражениями.

Часто знание значения тригонометрического выражения (например, $\,\cos x\,$)
позволяет правильно определить размер других тригонометрических выражений, но не знак .
Для получения правильного знака необходимо предоставить дополнительную информацию.

Например, предположим, что вы знаете, что $\,\cos x = \frac 45\,$ и ничего больше . Позволяет ли это однозначно определить $\,\sin x\,$? Нет! Он дает размер $\,\sin x\,$ , но не знак , следующим образом: Знание $\,\cos x = \frac 45\,$ помещает конечную точку для $\,x\,$ либо в квадрант I (точка $\,A\,$) , либо в квадрант IV (точка $\,B \,$), как показано справа. В поисках 92} \ \cssId{s144}{=\ \frac{25}{25} — \frac{16}{25}}\ \cssId{s145}{=\ \frac{9}{25}} $$ Таким образом, $\sin x = \pm \frac{3}{5}\,. $ Размер $\,\sin x\,$ равен $\,\frac 35\,.$ Знак неизвестен (без дополнительной информации).

Существует различная дополнительная информация, которая может быть предоставлена определить знак $\,\sin x\,.$ Вот несколько примеров: информация: следствие: информация: следствие: $\,x\,$ находится в квадранте I $\,\sin x\,$ положителен $\,x\,$ находится в квадранте IV $\,\sin x\,$ отрицательно $\csc х > 0$ косеканс есть величина, обратная синусу; , если косеканс положительный, то и синус; $\,\sin x\,$ положительно $\csc х косеканс есть величина, обратная синусу; , если косеканс отрицательный, то и синус; $\,\sin x\,$ отрицательно $\тангенс х > 0$ тангенс представляет собой синус над косинусом; если косинус положительный и тангенс положительный, то: $\,\sin x\,$ положительный $\загар х тангенс представляет собой синус над косинусом; , если косинус положительный , а тангенс отрицательный, то: $\,\sin x\,$ отрицательно

Пример: Использование формул двойного угла

Предположим, что $\displaystyle\,\cos x = \frac 45\,$ и $\,\csc x Найдите $\,\sin 2x\,$ $\,\cos 2x\,$ и $\,\tan 2x\,. $

Решение:

• По пифагорейской идентичности, 92} \ \cssId{s183}{=\ \frac{25}{25} — \frac{16}{25}}\ \cssId{s184}{=\ \frac{9}{25}}\,$
  , поэтому $\displaystyle\, \sin x = \pm \frac{3}{5}\,.$
• Поскольку $\displaystyle\,\csc x := \frac{1}{\sin x}
• Вместе $\,\displaystyle\sin x = -\frac{3}{5}\,.$
• $\displaystyle \cssId{s1892 — 1} \ \cssId{s196}{=\ 2\cdot\frac{16}{25} — \frac{25}{25}}\ \cssId{s197}{=\ \frac{7}{25}}$

  (Можно использовать любую из трех формул косинуса двойного угла.
  Выбранная здесь «наиболее безопасная», поскольку она использует только при — не вычисляется — информация. )

• $\displaystyle \cssId{s200}{\загар 2x} \ \cssId{s201}{:=\ \frac{\sin 2x}{\cos 2x}}\ \cssId{s202}{=\ \frac{-\frac{24}{25}}{\frac{7}{25}}\cdot \frac{25}{25}}\ \cssId{s203}{=\ -\frac{24}{7}}$

  Сложная дробь — это выражение, включающее «дроби внутри дробей», например $\,\displaystyle\frac{-\frac{24}{25}}{\frac{7}{25}}\,.$
  Вот метод, используемый для преобразования сложной дроби в простую:

  • Найдите наименьший общий знаменатель (НОД) всех простых дробей.
  • Умножить сложную дробь на $\,1\,$ в виде $\,\frac{\text{lcd}}{\text{lcd}}\,.$
  Это прекрасный пример «умножения на $\,1\,$ в соответствующей форме»!

  Вот как эта техника применялась выше:

  • Старшая дробь ($\,-\frac{24}{25}\,$) имеет знаменатель $\,25\,. $
  • Нижняя дробь ($\,\frac{7}{25}\,$) также имеет знаменатель $\,25\,.$
  • Наименьшее общее кратное $\,25\,$ и $\,25\,$ равно $\,25\,.$
    Таким образом, lcd всех задействованных простых дробей равен $\,25\,.$
  • Сложная дробь была умножена на $\,\frac{25}{25}\,$, и все «маленькие» дроби исчезли!

7.3 Двойной угол, полуугол и формулы редукции – предварительный расчет 2e

Цели обучения

В этом разделе вы:

• Используйте формулы двойного угла, чтобы найти точные значения.
• Используйте формулы двойного угла для проверки тождества.
• Используйте формулы сокращения для упрощения выражения.
• Используйте формулы половинного угла, чтобы найти точные значения.

Рисунок 1 Велосипедные рампы для опытных райдеров имеют более крутой наклон, чем для новичков.

Велосипедные рампы, изготовленные для соревнований (см. рис. 1), должны различаться по высоте в зависимости от уровня квалификации участников. Для продвинутых участников угол, образованный рампой и землей, должен быть θθ таким, чтобы tanθ=53.tanθ=53. Угол делится пополам для новичков. Какая крутизна пандуса для новичков? В этом разделе мы исследуем три дополнительные категории тождеств, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.

Использование формул двойного угла для нахождения точных значений

В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций. Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул сумм, где α=β.α=β. Вывод формулы двойного угла для синуса начинается с формулы суммы

.

sin(α+β)=sinαcosβ+cosαsinβsin(α+β)=sinαcosβ+cosαsinβ

Если мы допустим α=β=θ,α=β=θ, то мы имеем

sin(θ+θ)=sinθcosθ+cosθsinθ    sin(2θ)=2sinθcosθsin(θ+θ)=sinθcosθ+cosθsinθ    sin(2θ)=2sinθcosθ

Получение двойного угла для косинуса дает нам три варианта. Во-первых, исходя из формулы суммы, cos(α+β)=cosαcosβ−sinαsinβ,cos(α+β)=cosαcosβ−sinαsinβ и допуская α=β=θ,α=β=θ, мы имеем

cos(θ+θ)=cosθcosθ−sinθsinθ    cos(2θ)=cos2θ−sin2θcos(θ+θ)=cosθcosθ−sinθsinθ    cos(2θ)=cos2θ−sin2θ

Используя свойства Пифагора, мы можем расширить эту формулу двойного угла для косинуса и получить еще две интерпретации. Первый:

cos(2θ)=cos2θ−sin2θ            = (1−sin2θ)−sin2θ            = 1−2sin2θcos(2θ)=cos2θ−sin2θ                                      =1−2sin2θ

Вторая интерпретация:

.           =2cos2θ−1

Аналогично, чтобы вывести формулу тангенса двойного угла, заменив α=β=θα=β=θ в формуле суммы, получим

tan(α+β)=tanα+tanβ1−tanαtanβtan(θ+θ)=tanθ+tanθ1−tanθtanθtan(2θ)=2tanθ1−tan2θtan(α+β)=tanα+tanβ1−tanαtanβtan(θ+θ)=tanθ+ tanθ1−tanθtanθtan(2θ)=2tanθ1−tan2θ

Формулы двойного угла

Формулы двойного угла резюмируются следующим образом:           =2cos2θ−1cos(2θ)=cos2θ−sin2θ =1−2sin2θ            =2cos2θ−1

tan(2θ)=2tanθ1−tan2θtan(2θ)=2tanθ1−tan2θ

Как

Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение.

1. Нарисуйте треугольник, чтобы отразить предоставленную информацию.
2. Определите правильную формулу двойного угла.
3. Подставьте значения в формулу на основе треугольника.
4. Упростить.

Пример 1

Использование формулы двойного угла для нахождения точного значения, включающего тангенс

Учитывая, что tanθ=-34tanθ=-34 и θθ находится в квадранте II, найдите следующее:

1. ⓐ sin(2θ)sin(2θ)
2. ⓑ потому что (2θ) потому что (2θ)
3. ⓒ загар(2θ)загар(2θ)

Решение

Если мы нарисуем треугольник, чтобы отразить предоставленную информацию, мы сможем найти значения, необходимые для решения проблем на изображении. Нам заданы tanθ=−34,tanθ=−34, так что θθ находится в квадранте II. Тангенс угла равен стороне, противоположной соседней стороне, и, поскольку θθ находится во втором квадранте, смежная сторона находится на оси x и является отрицательной. Используйте теорему Пифагора, чтобы найти длину гипотенузы:

(−4)2+(3)2=c216+9=c225=c2c=5(−4)2+(3)2=c216+9=c225=c2c=5

Теперь мы можем нарисовать треугольник аналогичный изображенному на рис. 2.

Рис. 2

1. ⓐНачнем с написания формулы двойного угла для синуса.

   sin(2θ)=2sinθcosθsin(2θ)=2sinθcosθ

   Мы видим, что нам нужно найти sinθsinθ и cosθ.cosθ. На основании рисунка 2 мы видим, что гипотенуза равна 5, поэтому sinθ=35,sinθ=35 и cosθ=−45.cosθ=−45. Подставьте эти значения в уравнение и упростите.

   Итак,

   sin(2θ)=2(35)(−45)            =−2425sin(2θ)=2(35)(−45)                  =−2425

2. ⓑ Напишите формулу двойного угла для косинуса.

   cos(2θ)=cos2θ−sin2θcos(2θ)=cos2θ−sin2θ

   Снова подставьте значения синуса и косинуса в уравнение и упростите.

   cos(2θ)=(−45)2−(35)2            =1625−925            =725cos(2θ)=(−45)2−(35)2             =1625−925            =725 9 0008

3. ⓒ Запишите формулу тангенса двойного угла.

   tan(2θ)=2tanθ1−tan2θtan(2θ)=2tanθ1−tan2θ

   В этой формуле нам нужен тангенс, который мы получили как tanθ=−34.tanθ=−34. Подставьте это значение в уравнение и упростите.

   tan(2θ)=2(−34)1−(−34)2          =−321−916           = −32(167)           =−247tan(2θ)=2(−34)1−(−34)2           =− 321−916           =−32(167)           =−247

Попробуй #1

При заданных sinα=58,sinα=58 и θθ в квадранте I найдите cos(2α).cos(2α).

Пример 2

Использование формулы двойного угла для косинуса без точных значений

Используйте формулу двойного угла для косинуса, чтобы записать cos(6x)cos(6x) через cos(3x).cos(3x).

Решение

. )            =2cos2(3x)−1

Анализ

Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений. Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.

Использование формул двойного угла для проверки идентичности

Установление тождеств с помощью формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для вывода формул суммы и разности. Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной.

Пример 3

Использование формул двойного угла для установления тождества

Установите следующее тождество с помощью формул двойного угла:

1+sin(2θ)=(sinθ+cosθ)21+sin(2θ)=(sinθ+cosθ) 2

Решение

Мы будем работать с правой частью знака равенства и перепишем выражение, пока оно не совпадет с левой частью.

(sinθ+cosθ)2=sin2θ+2sinθcosθ+cos2θ                      =(sin2θ+cos2θ)+2sinθcosθ                      =1+2sin θcosθ                      =1+sin(2θ)(sinθ+cosθ)2=sin2θ+2sinθcosθ+cos2θ                                        = (sin2θ+cos2θ )+2sinθcosθ                      =1+2sinθcosθ                      =1+sin(2θ)

Анализ

Этот процесс не сложен, если вспомнить формулу совершенного квадрата из алгебры:

(a±b)2=a2±2ab+b2(a±b)2=a2±2ab+b2

где a=sinθa=sinθ и b=cosθ. b=cosθ. Частью успеха в математике является способность распознавать закономерности. Хотя термины или символы могут меняться, алгебра остается неизменной.

Попробуй #2

Установите тождество: cos4θ−sin4θ=cos(2θ).cos4θ−sin4θ=cos(2θ).

Пример 4

Проверка идентичности двойного угла для касательной

Проверка идентичности:

tan(2θ)=2cotθ−tanθtan(2θ)=2cotθ−tanθ

Решение

В этом случае мы будем работать с левой частью уравнения и упрощать или переписывать, пока оно не сравняется с правой частью уравнения.

tan(2θ)=2tanθ1−tan2θФормула двойного угла           = 2tanθ(1tanθ)(1−tan2θ)(1tanθ) Умножьте на член, который даст желаемый числитель. =21tanθ−tan2θtanθ           =2cotθ−tanθИспользовать взаимное тождество для 1tanθ.tan(2θ)=2tanθ1−tan2θФормула двойного угла                   =2tanθ(1tanθ)(1−tan2θ)(1tanθ)Умножить на a термин, который приводит к желаемому числителю. =21tanθ−tan2θtanθ           =2cotθ−tanθИспользуйте взаимное тождество для 1tanθ.

Анализ

Вот случай, когда более сложная часть исходного уравнения появилась справа, но мы решили работать с левой частью. Однако, если бы мы выбрали для перезаписи левую часть, мы бы работали в обратном направлении, чтобы получить эквивалентность. Например, предположим, что мы хотим показать

2tanθ1−tan2θ=2cotθ−tanθ2tanθ1−tan2θ=2cotθ−tanθ

Давайте поработаем с правой стороны.

2cotθ−tanθ=21tanθ−tanθ(tanθtanθ)                  =2tanθ1tanθ(tanθ)−tanθ(tanθ)                                             tanθ−tanθ(tanθtanθ)                  =2tanθ1tanθ(tanθ)−tanθ(tanθ)                  =2tanθ1−tan2θ

При использовании тождеств для упрощения тригонометрического выражения или решения тригонометрического уравнения обычно существует несколько путей к желаемому результату. Не существует установленного правила относительно того, какой стороной следует манипулировать. Тем не менее, мы должны начать с руководящих принципов, изложенных ранее.

Попробуй #3

Проверьте идентичность: cos(2θ)cosθ=cos3θ−cosθsin2θ.cos(2θ)cosθ=cos3θ−cosθsin2θ.

Использование формул сокращения для упрощения выражения

Формулы двойного угла можно использовать для вывода формул приведения, которые представляют собой формулы, которые мы можем использовать для уменьшения мощности данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны в курсах математики более высокого уровня, в частности исчисления. Также называемые формулами уменьшения степени, включены три тождества, которые легко выводятся из формул двойного угла.

Мы можем использовать две из трех формул двойного угла для косинуса, чтобы вывести формулы приведения для синуса и косинуса. Начнем с cos(2θ)=1−2sin2θ.cos(2θ)=1−2sin2θ. Найдите sin2θ:sin2θ:

cos(2θ)=1−2sin2θ2sin2θ=1−cos(2θ) sin2θ=1−cos(2θ)2cos(2θ)=1−2sin2θ2sin2θ=1−cos(2θ) sin2θ=1−cos(2θ)2

Далее используем формулу cos(2θ)=2cos2θ−1.cos(2θ)=2cos2θ−1. Найдите cos2θ:cos2θ:

       cos(2θ)=2cos2θ−11+cos(2θ)=2cos2θ1+cos(2θ)2=cos2θ       cos(2θ)=2cos2θ−11+cos(2θ)=2cos2θ1+cos(2θ)2=cos2θ

Последняя формула приведения получается путем записи тангенса через синус и косинус:

tan2θ=sin2θcos2θ        =1−cos(2θ)21+cos(2θ)2Подставьте формулы редукции. =(1−cos(2θ)2)(21+cos(2θ))         =1−cos(2θ)1+cos(2θ)tan2θ=sin2θcos2θ         =1−cos(2θ)21+cos(2θ)2 Подставляем сокращение формулы. =(1−cos(2θ)2)(21+cos(2θ))         =1−cos(2θ)1+cos(2θ)

Формулы приведения

Формулы приведения обобщаются следующим образом:

sin2θ=1−cos(2θ)2sin2θ=1−cos(2θ)2

cos2θ=1+cos(2θ)2cos2θ=1+cos(2θ)2

tan2θ=1−cos(2θ)1+ cos(2θ)tan2θ=1−cos(2θ)1+cos(2θ)

Пример 5

Написание эквивалентного выражения, не содержащего степени больше 1

Напишите эквивалентное выражение для cos4xcos4x, не содержащее степени синуса или косинуса больше 1.

Решение

Применим формулу приведения косинуса дважды.

cos4x=(cos2x)2          =(1+cos(2x)2)2Подставьте формулу приведения вместо cos2x. =14(1+2cos(2x)+cos2(2x))          =14+12cos(2x)+14(1+cos2(2x)2) Замените cos2x формулой приведения. =14+12cos(2x)+18+18cos(4x)          =38+12cos(2x)+18cos(4x)cos4x=(cos2x)2          = (1+cos(2x)2)2Подставьте формулу приведения вместо cos2x. =14(1+2cos(2x)+cos2(2x))          =14+12cos(2x)+14(1+cos2(2x)2) Замените cos2x формулой приведения. =14+12cos(2x)+18+18cos(4x)          =38+12cos(2x)+18cos(4x)

Анализ

Решение находится путем двойного использования формулы приведения, как уже отмечалось, и формулы полного квадрата из алгебры.

Пример 6

Использование формул понижения степени для доказательства тождества

Использование формул понижения мощности для доказательства

sin3(2x)=[12sin(2x)][1−cos(4x)]sin3(2x)=[12sin (2x)][1-cos(4x)]

Решение

Будем работать над упрощением левой части уравнения:

sin3(2x)=[sin(2x)][sin2(2x)]             =sin(2x)[1−cos(4x)2]Замените формулой уменьшения мощности. =sin(2x)(12)[1−cos(4x)]             =12[sin(2x)][1−cos(4x)]sin3(2x)=[sin(2x)][sin2(2x)]             = sin(2x)[1−cos(4x)2]Подставьте формулу уменьшения мощности. =sin(2x)(12)[1−cos(4x)]             =12[sin(2x)][1−cos(4x)]

Анализ

Обратите внимание, что в этом примере мы заменили

1-cos(4x)21-cos(4x)2

вместо sin2(2x).sin2(2x). Формула гласит

sin2θ=1−cos(2θ)2sin2θ=1−cos(2θ)2

Допустим θ=2x,θ=2x, поэтому 2θ=4x.2θ=4x.

Попробуй #4

Используйте формулы уменьшения мощности, чтобы доказать, что 10cos4x=154+5cos(2x)+54cos(4x).10cos4x=154+5cos(2x)+54cos(4x).

Использование формул половинного угла для нахождения точных значений

Следующий набор тождеств — это набор формул половинного угла, которые могут быть получены из формул приведения и могут использоваться, когда у нас есть угол, который в два раза меньше специального угла. Если мы заменим θθ на α2,α2, формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для sin(α2).sin(α2). Обратите внимание, что перед формулами половинного угла стоит знак ±±. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается α2α2.

Формула половинного угла для синуса получается следующим образом:

   sin2θ=1-cos(2θ)2sin2(α2)=1-cos(2⋅α2)2=1-cosα2sin(α2)=±1-cosα2   sin2θ=1-cos(2θ)2sin2(α2)=1- cos(2⋅α2)2=1−cosα2sin(α2)=±1−cosα2

Чтобы получить формулу половинного угла для косинуса, мы имеем

   cos2θ=1+cos(2θ)2cos2(α2)=1+cos(2⋅α2)2             =1+cosα2  cos(α2)=±1+cosα2   cos2θ=1+cos(2θ)2cos2(α2)=1 +cos(2⋅α2)2             =1+cosα2  cos(α2)=±1+cosα2

Для тождества касательной имеем

   tan2θ=1−cos(2θ)1+cos(2θ)tan2(α2)=1−cos(2⋅α2)1+cos(2⋅α2)             =1–cosα1+cosα  tan(α2)=±1− cosα1+cosα   tan2θ=1−cos(2θ)1+cos(2θ)tan2(α2)=1−cos(2⋅α2)1+cos(2⋅α2)            =1−cosα1+cosα  tan(α2)=± 1-cosα1+cosα

Формулы половинного угла

Формулы для половинного угла следующие:

tan(α2)=±1−cosα1+cosα=sinα1+cosα=1−cosαsinαtan(α2)=±1−cosα1+cosα=sinα1+cosα=1−cosαsinα

Пример 7

Использование формулы половинного угла для нахождения точного значения функции синуса

Найдите sin(15∘)sin(15∘) с помощью формулы половинного угла.

Решение

Так как 15∘=30∘2, 15∘=30∘2, используем формулу половинного угла для синуса:

sin30∘2=1−cos30∘2 2−34           = 2−32sin30∘2=1−cos30∘2           =1−322           =2−322           =2−34           =2−32

Анализ

Обратите внимание, что мы использовали только положительный корень, потому что sin(15o)sin(15o) положительный.

Как

Даны тангенс угла и квадрант, в котором находится угол, найти точные значения тригонометрических функций половины угла.

1. Нарисуйте треугольник для представления данной информации.
2. Определите правильную формулу половинного угла.
3. Подставьте значения в формулу на основе треугольника.
4. Упростить.

Пример 8

Нахождение точных значений с помощью тождеств половинных углов

Учитывая, что tanα=815tanα=815 и αα лежит в квадранте III, найдите точное значение следующего:

1. ⓐ sin(α2)sin(α2)
2. ⓑ потому что (α2) потому что (α2)
3. ⓒ загар(α2)загар(α2)

Решение

Используя данную информацию, мы можем нарисовать треугольник, показанный на рисунке 3. Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sinα=−817sinα=−817 и cosα=−1517.cosα=− 1517.

Рисунок 3

1. ⓐПрежде чем мы начнем, мы должны помнить, что если αα находится в квадранте III, то 180°<α<270°, 180°<α<270°, поэтому 180°2<α2<270°2,180°2 <α2<270°2. Это означает, что крайняя сторона α2α2 находится в квадранте II, так как 90°<α2<135°,90°<α2<135°.

   Чтобы найти sinα2,sinα2, начнем с записи формулы половинного угла для синуса. Затем подставляем значение найденного нами косинуса из треугольника на рисунке 3 и упрощаем.

   sinα2=±1−cosα2        =±1−(−1517)2        =±32172        =±3217⋅12        =±1617        =±417        =41717 sinα2=±1−cos α2        =±1−(−1517)2        =±32172        = ±3217⋅12        =±1617        =±417        =41717

   Мы выбираем положительное значение sinα2sinα2, потому что угол заканчивается в квадранте II, а синус положителен в квадранте II.

2. ⓑ Чтобы найти cosα2,cosα2, мы напишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника на рисунке 3, и упростим.

   cosα2=±1+cosα2        =±1+(−1517)2        =±2172        =±217⋅12        =±117        =−1717cosα2=±1+cosα2        =±1+( −1517)2        =±2172        =±217 ⋅12        =±117        =−1717

   Мы выбираем отрицательное значение cosα2cosα2, потому что угол находится в квадранте II, потому что косинус отрицателен в квадранте II.

3. ⓒ Чтобы найти tanα2,tanα2, запишем формулу половинного угла для тангенса. Снова подставляем значение найденного нами косинуса из треугольника на рисунке 3 и упрощаем.    =±1−(−1517) 1+(−1517)        =±3217217        =±322        =−16        =−4

   Мы выбираем отрицательное значение tanα2tanα2, потому что α2α2 лежит в квадранте II, а тангенс отрицателен в квадранте II.

Попробуй #5

Учитывая, что sinα=-45sinα=-45 и αα лежит в квадранте IV, найдите точное значение cos(α2).cos(α2).

Пример 9

Нахождение измерения половинного угла

Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа сконструирована для соревнований высокого уровня с углом θθ, образованным рампой и землей. Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если tanθ=53tanθ=53 для соревнований более высокого уровня, каково измерение угла для соревнований новичков?

Решение

Поскольку угол для соревнований новичков измеряет половину крутизны угла для соревнований высокого уровня, а tanθ=53tanθ=53 для соревнований высокого уровня, мы можем найти cosθcosθ из прямоугольного треугольника и теоремы Пифагора, чтобы мы могли использовать полуугловые тождества. См. рис. 4.

32+52=34          c=3432+52=34          c=34

Рисунок 4

Мы видим, что cosθ=334=33434.cosθ=334=33434. Мы можем использовать формулу половинного угла для тангенса: tanθ2=1−cosθ1+cosθ.tanθ2=1−cosθ1+cosθ. Поскольку tanθtanθ находится в первом квадранте, то же самое относится и к tanθ2.tanθ2. Таким образом,

tanθ2=1−334341+33434        =34−3343434+33434        =34−33434+334         ≈0,57tanθ2=1–334341+33434        =34 −3343434+33434        =34−33434+334        ≈0,57

Мы можем взять арктангенс для нахождения угла: tan−1(0,57)≈29,7∘. tan−1(0,57)≈29,7∘. Таким образом, угол рампы для соревнований новичков составляет ≈29,7∘.≈29,7∘.

7.3 Секционные упражнения

Вербальный

1.

Объясните, как определить редукционные тождества из тождества двойного угла cos(2x)=cos2x-sin2x.cos(2x)=cos2x-sin2x.

2.

Объясните, как определить формулу двойного угла для tan(2x)tan(2x), используя формулы двойного угла для cos(2x)cos(2x) и sin(2x).sin(2x).

3.

Мы можем определить формулу половинного угла для tan(x2)=1−cosx1+cosxtan(x2)=1−cosx1+cosx, разделив формулу для sin(x2)sin(x2) на cos(x2).cos (х2). Объясните, как определить две формулы для tan(x2)tan(x2) которые не содержат квадратных корней.

4.

Для формулы половинного угла, приведенной в предыдущем упражнении для tan(x2),tan(x2), объясните, почему деление на 0 не имеет значения. (Подсказка: проверьте значения cosxcosx, необходимые для того, чтобы знаменатель был равен 0.)

Алгебраический

Для следующих упражнений найдите точные значения a) sin(2x),sin(2x), b) cos(2x),cos(2x) и c) tan(2x)tan(2x) без решение для х.х.

5.

Если sinx=18,sinx=18 и xx находится в квадранте I.

6.

Если cosx=23,cosx=23 и xx находится в квадранте I.

7.

Если cosx=-12,cosx=-12 и xx находится в квадранте III.

8.

Если tanx=-8,tanx=-8 и xx находится в квадранте IV.

В следующих упражнениях найдите значения шести тригонометрических функций, если выполнены указанные условия.

9.

cos(2θ)=35cos(2θ)=35 и 90∘≤θ≤180∘90∘≤θ≤180∘

10.

cos(2θ)=12cos(2θ)=12 и 180∘≤θ≤270∘180∘≤θ≤270∘

Для следующих упражнений упростите до одного тригонометрического выражения.

11.

2sin(π4)2cos(π4)2sin(π4)2cos(π4)

12.

4sin(π8)cos(π8)4sin(π8)cos(π8)

Для следующих упражнений найдите точное значение, используя формулы половинного угла.

13.

грех (π8) грех (π8)

14.

cos(-11π12)cos(-11π12)

15.

грех(11π12)грех(11π12)

16.

потому что (7π8) потому что (7π8)

17.

тан (5π12) тан (5π12)

18.

тангенс (−3π12) тангенс (−3π12)

19.

тангенс (−3π8) тангенс (−3π8)

В следующих упражнениях найдите точные значения a) sin(x2),sin(x2), b) cos(x2),cos(x2) и c) tan(x2)tan(x2), не решая для x ,Икс, когда 0∘≤x≤360∘0∘≤x≤360∘

20.

Если tanx=-43,tanx=-43 и xx находится в квадранте IV.

21.

Если sinx=-1213,sinx=-1213 и xx находится в квадранте III.

22.

Если cscx=7,cscx=7 и xx находится в квадранте II.

23.

Если secx=-4, secx=-4 и xx находится в квадранте II.

В следующих упражнениях используйте рисунок 5, чтобы найти требуемые половинные и двойные углы.

Рисунок 5

24.

Найдите sin(2θ),cos(2θ),sin(2θ),cos(2θ) и tan(2θ).tan(2θ).

25.

Найти sin(2α),cos(2α),sin(2α),cos(2α) и tan(2α). tan(2α).

26.

Найти sin(θ2),cos(θ2),sin(θ2),cos(θ2) и tan(θ2).tan(θ2).

27.

Найдите sin(α2),cos(α2),sin(α2),cos(α2) и tan(α2).tan(α2).

В следующих упражнениях упростите каждое выражение. Не оценивайте.

28.

cos2(28∘)−sin2(28∘)cos2(28∘)−sin2(28∘)

29.

2cos2(37∘)−12cos2(37∘)−1

30.

1−2sin2(17∘)1−2sin2(17∘)

31.

cos2(9x)−sin2(9x)cos2(9x)−sin2(9x)

32.

4sin(8x)cos(8x)4sin(8x)cos(8x)

33.

6sin(5x)cos(5x)6sin(5x)cos(5x)

Для следующих упражнений подтвердите данное тождество.

34.

(sint-cost)2=1-sin(2t)(sint-cost)2=1-sin(2t)

35.

sin(2x)=-2sin(-x)cos(-x)sin(2x)=-2sin(-x)cos(-x)

36.

cotx-tanx=2cot(2x)cotx-tanx=2cot(2x)

37.

1+cos(2θ)sin(2θ)tan2θ=tanθ1+cos(2θ)sin(2θ)tan2θ=tanθ

Для следующих упражнений перепишите выражение с показателем степени не выше 1.

38.

cos2(5x)cos2(5x)

39.

cos2(6x)cos2(6x)

40.

sin4(8x)sin4(8x)

41.

sin4(3x)sin4(3x)

42.

cos2xsin4xcos2xsin4x

43.

cos4xsin2xcos4xsin2x

44.

tan2xsin2xtan2xsin2x

Технология

Для следующих упражнений уменьшите уравнения до степени единицы, а затем проверьте ответ графически.

45.

tan4xtan4x

46.

sin2(2x)sin2(2x)

47.

sin2xcos2xsin2xcos2x

48.

tan2xsinxtan2xsinx

49.

tan4xcos2xtan4xcos2x

50.

cos2xsin(2x)cos2xsin(2x)

51.

cos2(2x)sinxcos2(2x)sinx

52.

tan2(x2)sinxtan2(x2)sinx

Для следующих упражнений алгебраически найдите эквивалентную функцию только в терминах sinxsinx и/или cosx,cosx, а затем проверьте ответ, построив оба уравнения в виде графика.

53.

грех (4x) грех (4x)

54.

cos(4x)cos(4x)

Расширения

Для следующих упражнений докажите тождества.

55.

sin(2x)=2tanx1+tan2xsin(2x)=2tanx1+tan2x

56.

cos(2α)=1−tan2α1+tan2αcos(2α)=1−tan2α1+tan2α

57.

tan(2x)=2sinxcosx2cos2x−1tan(2x)=2sinxcosx2cos2x−1

58.

(sin2x−1)2=cos(2x)+sin4x(sin2x−1)2=cos(2x)+sin4x

59.

sin(3x)=3sinxcos2x-sin3xsin(3x)=3sinxcos2x-sin3x

60.

cos(3x)=cos3x−3sin2xcosxcos(3x)=cos3x−3sin2xcosx

61.

1+cos(2t)sin(2t)−cost=2cost2sint−11+cos(2t)sin(2t)−cost=2cost2sint−1

62.