Общая схема исследования функции и построения графиков (Лекция №11)
- Найти ОДЗ и точки разрыва функции.
- Найти точки пересечения графика функции с осями координат.
- Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.
- Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.
- Найти асимптоты графика функции: а) вертикальные, b) наклонные.
- На основании проведенного исследования построить график функции.
Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.
Вспомним, что функция
называется четной, если при изменении знака аргумента значение функции не
меняется: f(-x) = f(x) и функция называется
нечетной, если f(-x) = -f(x).
В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.
Примеры. Исследовать функции и построить их графики.
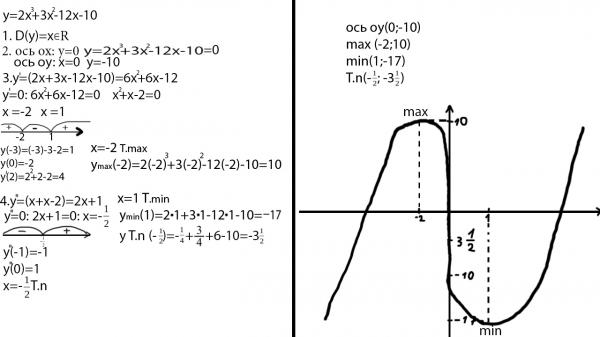
- .
1. Область определения функции D(у)= (–∞; +∞). Точек разрыва нет.
Пересечение с осью Ox: x = 0,у=0.
Функция нечетная, следовательно, можно исследовать ее только на промежутке [0, +∞).
2. . Критические точки: x1 = 1; x2= –1. 3. 4. а) Вертикальных асимптот нетб) . Асимптота – y = 0.
- .
- D(y)=(–∞; +∞). Точек
разрыва нет.

Пересечение с осью Ox: .
- .
- а) Вертикальных асимптот нет
б).
Наклонных асимптот нет.
- D(y)=(–∞; +∞). Точек
разрыва нет.
- .
- D(y)=(0; +∞). Функция
непрерывна на области определения.
Пересечение с осью :
- а) .
Вертикальная асимптота x = 0.
б).Наклонная асимптота y = 0.
- D(y)=(0; +∞). Функция
непрерывна на области определения.
- .
- D(y)=(
–∞;0)È(0;1)È(1;+∞).
Функция имеет две точки разрыва x= 0 и x= 1.
Точек пересечения с осями координат нет.
- при любых действительных значениях x. Поэтому функция возрастает на всей числовой прямой.
-
а)
Вертикальные асимптоты x = 0, x = 1.
б)
Наклонная асимптота y = x + 1.

- D(y)=(
–∞;0)È(0;1)È(1;+∞).
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Во многих приложениях математического анализа встречаются комбинации показательных функций. Эти комбинации рассматриваются как новые функции и обозначаются:
– гиперболический синус.
– гиперболический косинус.
С помощью этих функций можно определить еще две функции.
– гиперболический тангенс.
– гиперболический котангенс.
Функции sh x, ch x, th x определены, очевидно, для всех значений x, т.е. их область определения (–∞; +∞). Функция же cthx определена всюду за исключением точки x = 0.
Между гиперболическими функциями существуют следующие соотношения, аналогичные соответствующим соотношениям между тригонометрическими функциями.
Найдем: .
Т.е. .
.
Итак, .
Следовательно, .
Найдем производные гиперболических функций
.
Аналогично можно показать .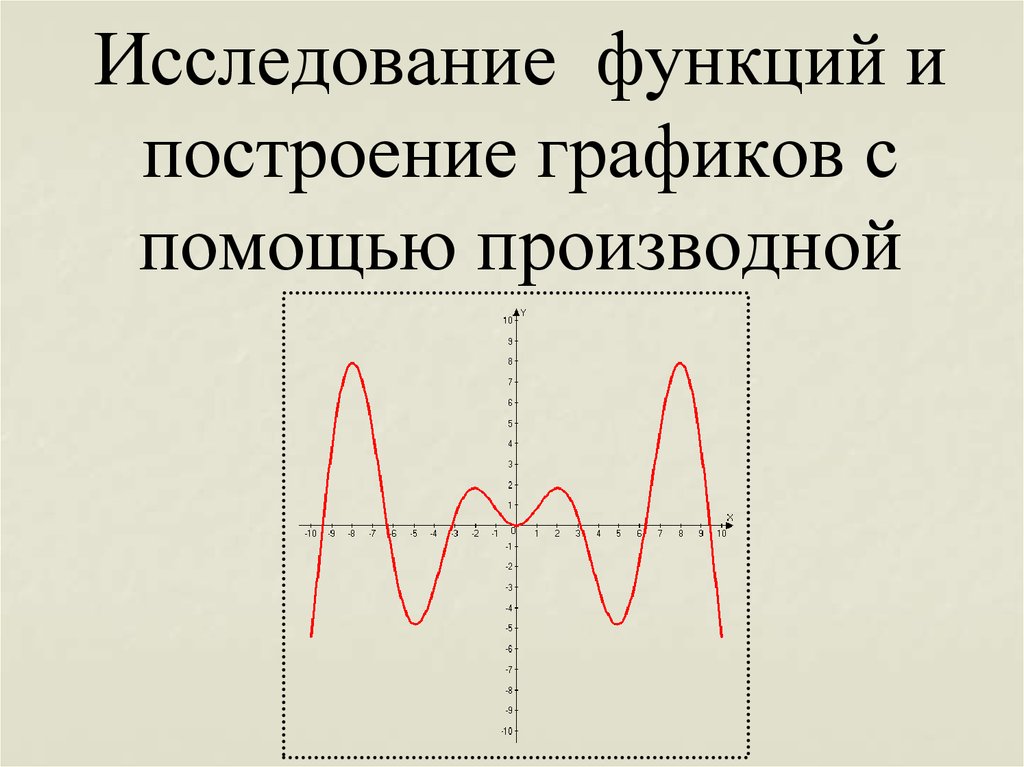
.
Т.е. и .
Графики гиперболических функций. Для того чтобы изобразить графики функций
shx и chx нужно вспомнить графики функций y = ex и y = e—x
Проведем исследования функции y = th x.
- D(f) = (–∞; +∞), точек разрыва нет.
- Точка пересечения с осями координат .
-
, функция возрастает на (–∞; +∞).
- Вертикальной асимптоты нет.
.
y = cth x
- D. Точка разрыва x = 0 cth x = 0 – нет
-
убывает на .
- При x → +∞
Полное исследование функции и построение графика, примеры решений
При построении графика функции необходимо провести ее предварительное исследование. Примерная схема исследования функции с
целью построения ее графика имеет следующую структуру:
Примерная схема исследования функции с
целью построения ее графика имеет следующую структуру:
- Область определения $D(y)$ и область допустимых значений $E(y)$ функции.
- Четность, нечетность функции.
- Точки пересечения с осями.
- Асимптоты функции.
- Экстремумы и интервалы монотонности.
- Точки перегиба и промежутки выпуклости, вогнутости.
- Сводная таблица.
Замечание
Схема представлена как примерная. Пункты исследования можно опускать, если они дают банальную информацию, или переставлять, если обнаруживаются интересные особенности поведения графика.
Замечание
Для уточнения графика можно найти некоторые дополнительные точки, но иногда удается обойтись и без них.
Замечание
Рекомендуется строить график одновременно с исследованием функции, нанося на координатную плоскость информацию по завершении каждого пункта исследования.
Пример
Задание. Исследовать функцию $y(x)=\frac{x^{2}-x-1}{x^{2}-2 x}$ и построить ее график. {\prime \prime}=0 : x=1$ ; при $x=0$ и
$x=2$ вторая производная не существует.
{\prime \prime}=0 : x=1$ ; при $x=0$ и
$x=2$ вторая производная не существует.
Таким образом, на промежутках $(0 ; 1)$ и $(2 ;+\infty)$ функция вогнута, а на промежутках $(-\infty ; 0)$ и $(1 ; 2)$ — выпукла. Так как при переходе через точку $x=1$ вторая производная поменяла знак, то эта точка является точкой перегиба.
7) Эскиз графика.
Читать первую тему — понятие производной, раздела производные.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
1.5: Интерпретация, оценка и использование производной
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4296
- Мэтью Болкинс, Дэвид Остин и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли
Цели обучения
В этом разделе мы стремимся понять идеи, порожденные следующими важными вопросами:
- В контексте, отличном от положения движущегося объекта, что измеряет производная функции?
- Каковы единицы измерения производной функции \(f’\) и как они связаны с единицами исходной функции \(f\)?
- Что такое центральное различие и как его можно использовать для оценки значения производной в точке по заданным данным функции?
- Зная значение производной функции в точке, какой вывод мы можем сделать о том, как изменяется значение функции поблизости?
Введение
Интересной и мощной особенностью математики является то, что ее часто можно рассматривать как в абстрактных, так и в прикладных терминах. Например, исчисление может быть разработано почти полностью как абстрактный набор идей, сосредоточенных на свойствах произвольных функций. В то же время исчисление также может быть очень непосредственно связано с нашим опытом физической реальности, рассматривая функции, которые представляют значимые процессы. Мы уже видели, что для функции положения \(y=s(t)\), скажем, для мяча, подброшенного прямо вверх в воздух, скорость мяча в момент времени \(t\) определяется выражением \(v(t )=s'(t)\), производная функции положения.
Например, исчисление может быть разработано почти полностью как абстрактный набор идей, сосредоточенных на свойствах произвольных функций. В то же время исчисление также может быть очень непосредственно связано с нашим опытом физической реальности, рассматривая функции, которые представляют значимые процессы. Мы уже видели, что для функции положения \(y=s(t)\), скажем, для мяча, подброшенного прямо вверх в воздух, скорость мяча в момент времени \(t\) определяется выражением \(v(t )=s'(t)\), производная функции положения.
Далее, напомним, что если \(s(t)\) измеряется в футах в момент времени \(t\), то единицей измерения \(v(t)=s'(t)\) являются футы в секунду. Далее в этом разделе мы исследуем несколько различных функций, каждая из которых имеет определенный физический смысл, и подумаем о том, как единицы измерения независимой переменной, зависимой переменной и производной функции дополняют наше понимание. Для начала рассмотрим известную задачу о функции положения движущегося объекта.
Активность предварительного просмотра \(\PageIndex{1}\)
Один из самых длинных участков прямой (и ровной) дороги в Северной Америке можно найти на Великих равнинах в штате Северная Дакота на государственной автомагистрали 46, которая проходит к югу от межштатной автомагистрали I-94 и проходит через город Гакле. Автомобиль выезжает из города (в момент времени \(t=0\)) и направляется на восток по шоссе 46; его положение в милях от Гакла в момент времени \(t\) в минутах определяется графиком функции на рис. 1.22. На графике отмечены три важные точки; где кривая выглядит линейной, предположим, что это действительно прямая линия.
. минут.
- Обыденным языком опишите поведение автомобиля на указанном интервале времени. В частности, обсудим, что происходит на временных интервалах [57, 68] и [68, 104].
- Найдите наклон прямой между точками (57, 63,8) и (104, 106,8). Какие единицы находятся на этом склоне? Что представляет наклон?
- Найти среднюю скорость изменения положения автомобиля на отрезке [68, 104].
 Включите единицы в свой ответ.
Включите единицы в свой ответ. - Оценить мгновенную скорость изменения положения автомобиля в момент \(t=80\). Напишите предложение, объясняющее ваши рассуждения и значение этого значения.
Единицы производной функции
Как мы теперь знаем, производная функции \(f\) при фиксированном значении \(x\) определяется выражением \[f'(x)=\lim_{h\ до 0} \frac{f(x+h)-f(x)}{h}\],
и это значение имеет несколько различных интерпретаций. Если мы установим \(x=a\), одним из значений \(f'(a)\) будет наклон касательной в точке \((a, (f(a))\).
In альтернативные обозначения, мы также иногда эквивалентно пишем \(\frac{df}{dx}\) или \(\frac{dy}{dx}\) вместо \(f'(x)\), и эти обозначения помогают нам чтобы далее увидеть единицы (и, следовательно, значение) производной, поскольку она рассматривается как t мгновенная скорость изменения \(f\) по отношению к \(х\). Обратите внимание, что единицы наклона секущей, \(\frac{f(x+h)-f(x)}{h}\), являются «единицами \(f\) на единицу \(x \)».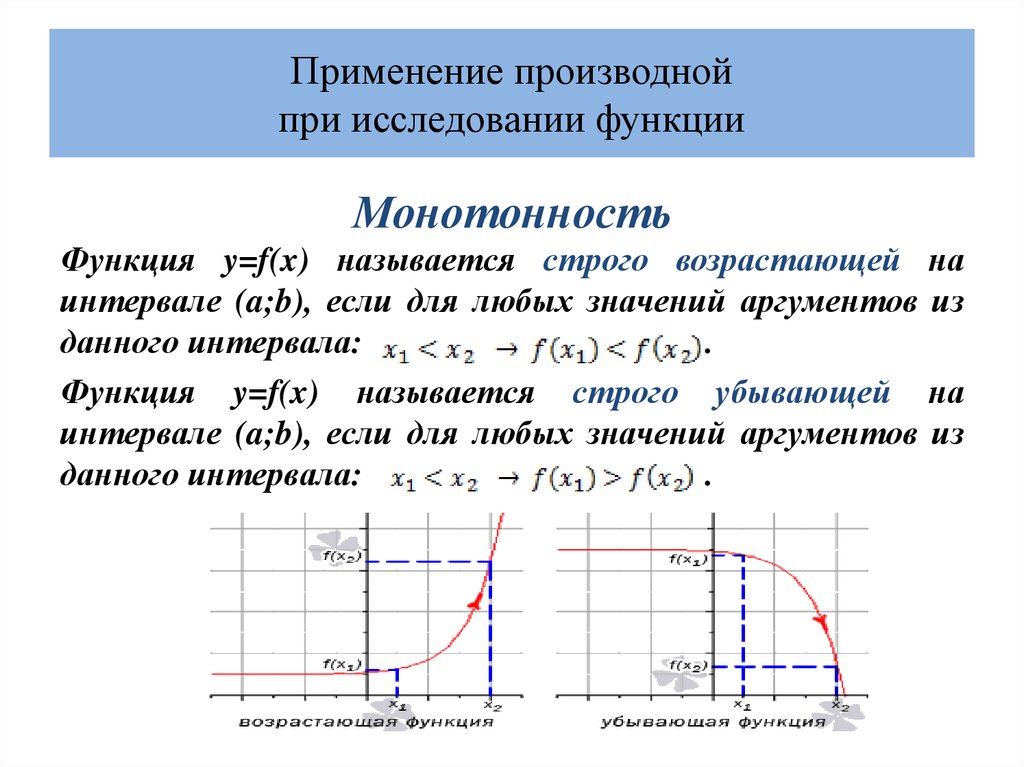 Таким образом, когда мы используем предел, чтобы получить \(f'(x)\), мы получаем те же самые единицы на производной \(f'(x)\): единицы \(f\) на единицу \( Икс\). Независимо от рассматриваемой функции \(f\) (и независимо от используемых переменных), полезно помнить, что единицами производной функции являются «единицы выпуска на единицу ввода» с точки зрения входных и вывод исходной функции.
Таким образом, когда мы используем предел, чтобы получить \(f'(x)\), мы получаем те же самые единицы на производной \(f'(x)\): единицы \(f\) на единицу \( Икс\). Независимо от рассматриваемой функции \(f\) (и независимо от используемых переменных), полезно помнить, что единицами производной функции являются «единицы выпуска на единицу ввода» с точки зрения входных и вывод исходной функции.
Например, у нас есть функция \(y=P(t)\), где \(P\) измеряет численность населения города (в тысячах) в начале года \(t\) (где \(t=0\) соответствует 2010 году нашей эры), и нам говорят, что \(P'(2)=21,37\). В чем смысл этого значения? Ну а поскольку \(P\) измеряется в тысячах, а \(t\) — в годах, то можно сказать, что мгновенная скорость изменения численности населения города по отношению ко времени на начало 2012 г. составляет 21,37 тыс. чел./чел. год. Поэтому мы ожидаем, что в наступающем году к населению города добавится около 21 370 человек.
К более точным оценкам производных
К более точным оценкам производных Полезно также вспомнить, как мы впервые убедились в разделе 1.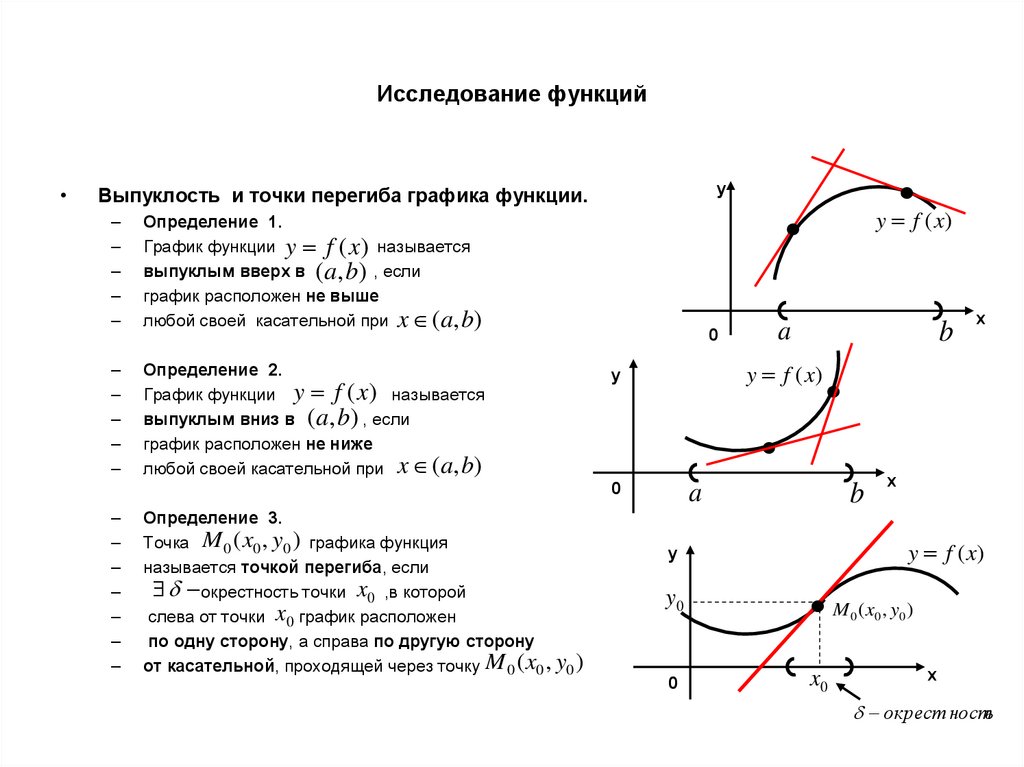 3, что когда мы хотим оценить значение \(f'(x)\) при заданном \(x\), мы можем использовать разностный коэффициент \(\frac{f(x+h)-f(x)}{h}\) с относительно небольшим значением \(h\). При этом мы должны использовать как положительные, так и отрицательные значения \(h\), чтобы убедиться, что мы учитываем поведение функции по обе стороны от точки интереса. С этой целью мы рассмотрим следующий краткий пример, демонстрирующий понятие центральная разность и ее роль в оценке производных.
3, что когда мы хотим оценить значение \(f'(x)\) при заданном \(x\), мы можем использовать разностный коэффициент \(\frac{f(x+h)-f(x)}{h}\) с относительно небольшим значением \(h\). При этом мы должны использовать как положительные, так и отрицательные значения \(h\), чтобы убедиться, что мы учитываем поведение функции по обе стороны от точки интереса. С этой целью мы рассмотрим следующий краткий пример, демонстрирующий понятие центральная разность и ее роль в оценке производных.
Пример \(\PageIndex{1}\)
Предположим, что \(y=f(x)\) — функция, для которой известны три значения: \(f(1)=2,5\), \(f (2)=3,25\) и \(f(3)=3,625\). Оценка \(f'(2)\).
Решение .
Мы знаем, что \(f'(2)=\lim_{h\to 0} \frac{f(2+h)-f(2)}{h}\). Но поскольку у нас нет ни графика для \(y=f(x)\), ни формулы для функции, мы не можем ни нарисовать касательную, ни точно оценить предел. Мы даже не можем использовать все меньшие и меньшие значения \(h\) для оценки предела.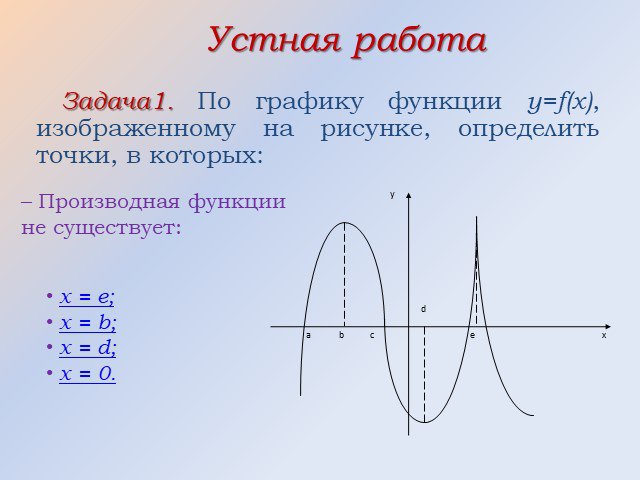 Вместо этого у нас есть только два варианта: использовать \(h=-1\) или \(h=1\), в зависимости от того, какую точку мы соединяем с (2, 3.25). Таким образом, одна оценка равна \[f'(2) \приблизительно \frac{f(1)-f(2)}{1-2}=\frac{2,5-3,25}{-1}=0,75.\]
Вместо этого у нас есть только два варианта: использовать \(h=-1\) или \(h=1\), в зависимости от того, какую точку мы соединяем с (2, 3.25). Таким образом, одна оценка равна \[f'(2) \приблизительно \frac{f(1)-f(2)}{1-2}=\frac{2,5-3,25}{-1}=0,75.\]
Другой равен \[f'(2) \приблизительно \frac{f(3)-f(2)}{3-2}=\frac{3,625-3,25}{1}=0,375.\]
Поскольку первое приближение смотрит только назад из точки (2, 3.25), а второе приближение смотрит только вперед из (2, 3.25), имеет смысл усреднить эти два значения, чтобы учесть поведение по обе стороны от точки интерес. При этом мы находим, что \[f'(2) \приблизительно \frac{0,75+0,375}{2}=0,5625.\]
Интуитивный подход к усреднению двух оценок, найденных в примере 1.4, на самом деле является наилучшим из возможных. оценка \(f'(2)\), когда у нас есть только два значения функции для \(f\) на противоположных сторонах точки интереса. Чтобы понять почему, обратимся к диаграмме на рис. 1.23, которая
Рисунок 1.23: Слева график \(y=f(x)\) вместе с секущей через (1, 2. 5) и (2, 3.25), секущая через (2, 3.25) ) и (3, 3.625), а также касательная. Справа тот же график вместе с секущей, проходящей через (1, 2,5) и (3, 3,625), плюс касательная.
5) и (2, 3.25), секущая через (2, 3.25) ) и (3, 3.625), а также касательная. Справа тот же график вместе с секущей, проходящей через (1, 2,5) и (3, 3,625), плюс касательная.
показывает возможную функцию \(y=f(x)\), которая удовлетворяет данным, приведенным в примере 1.4. Слева мы видим две секущие линии с наклоном, полученным в результате вычисления назад разность \(\frac{f(1)-f(2)}{1-2}=0,75\) и из вперед разность \(\frac{f(3)-f(2)} {3-2}=0,375\). Обратите внимание, что наклон первой такой линии завышает наклон касательной в точке \((2, f(2))\), а наклон второй линии занижает \(f'(2)\). Однако справа мы видим секущую, наклон которой определяется центральной разностью \[ \frac{f(3)-f(1)}{3-1}=\frac{3,625-2,5}{ 2}=\frac{1,125}{2}=0,5625.\]
Обратите внимание, что эта центральная разность имеет то же значение, что и среднее значение прямой и обратной разности (и нетрудно объяснить, почему это всегда выполняется) , и, кроме того, центральная разность дает очень хорошее приближение к значению производной, отчасти потому, что секущая линия, которая использует точку до и после точки касания, дает линию, которая ближе к параллельной линии касательной.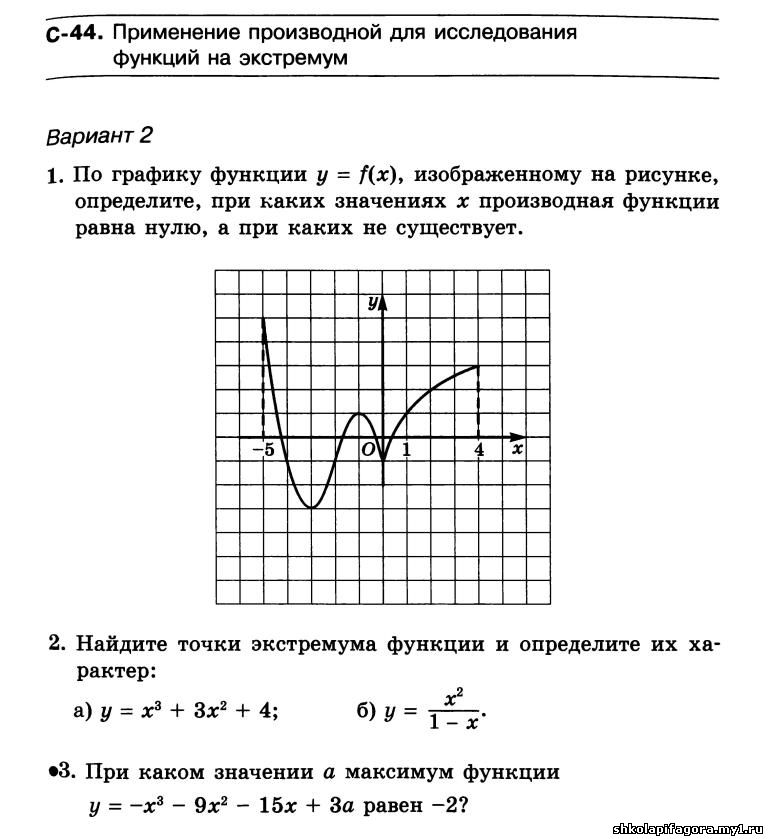
В общем случае центрально-разностная аппроксимация значения первой производной определяется выражением \[f'(a) \ приблизительно \frac{f(a+h)-f(a-h)}{2h}\],
, и эта величина измеряет наклон секущей к \(y=f(x)\) через точки \((a-h, f(a-h))\) и \((a+h, f(a+h ))\). Каждый раз, когда у нас есть симметричные данные, окружающие точку, в которой мы хотим оценить производную, центральная разность является идеальным выбором для этого.
В следующих упражнениях будет дополнительно изучено значение производной в нескольких различных контекстах, а также рассмотрена производная с графической, числовой и алгебраической точек зрения.
Действие \(\PageIndex{2}\)
Картофель помещают в печь, измеряют температуру картофеля \(F\) (в градусах по Фаренгейту) в различные моменты времени и записывают в следующую таблицу. Время \(t\) измеряется в минутах.
| \(т\) | \(Ф(т)\) |
|---|---|
| 0 | 70 |
| 15 | 180,5 |
| 30 | 251 |
| 45 | 296 |
| 60 | 324,5 |
| 75 | 342,8 |
| 90 | 354,5 |
- Используйте центральную разность для оценки мгновенной скорости изменения температуры картофеля при \(t=30\).
 Включите единицы в свой ответ.
Включите единицы в свой ответ. - Используйте центральную разность для оценки мгновенной скорости изменения температуры картофеля при \(t=60\). Включите единицы в свой ответ.
- Без каких-либо вычислений, что вы ожидаете больше: \(f'(75)\) или \(f'(90)\)? Почему?
- Предположим, что задано \(F(64)=330,28\) и \(f'(64)=1,341\). Каковы единицы измерения этих двух величин? Какой, по вашему мнению, будет температура картофеля при \(t=65\)? когда \(t=66\)? Почему?
- Напишите пару аккуратных предложений, описывающих поведение температуры картофеля на интервале времени \([0, 90]\), а также поведение мгновенной скорости изменения температуры картофеля на тот же интервал времени.
Вид деятельности \(\PageIndex{3}\)
Компания производит веревку, и общие затраты на производство \(r\) футов веревки составляют \(C(r)\) долларов.
- Что значит сказать, что \(C(2000)=800\)?
- Каковы единицы измерения \(C'(r)\)?
- Предположим, что \(C(2000)=800\) и \(C'(2000)=0,35\).
 Оцените \(C(2100)\) и обоснуйте свою оценку, написав хотя бы одно предложение, объясняющее ваши мысли.
Оцените \(C(2100)\) и обоснуйте свою оценку, написав хотя бы одно предложение, объясняющее ваши мысли. - Какое из следующих утверждений вы считаете верным и почему?
- \(С'(2000) < С'(3000)\)
- \(С'(2000)=С'(3000)\)
- \(С'(2000) > С'(3000)\)
- Предположим, кто-то утверждает, что \(C'(5000)=-0,1\). Что практическое значение этой производной может сказать вам о приблизительной стоимости следующего фута веревки? Это возможно? Почему или почему нет?
Activity \(\PageIndex{4}\)
Исследователи крупной автомобильной компании нашли функцию, связывающую расход бензина со скоростью для конкретной модели автомобиля. В частности, они установили, что расход \(С\) в литров на км при заданной скорости \(с\) определяется функцией \(С=f(с)\), где \ (с\) скорость автомобиля в километров в час .
- Данные, предоставленные автомобильной компанией, говорят нам, что \(f(80)=0,015\), \(f(90)=0,02\) и \(f(100)=0,027\).
 Используйте эту информацию, чтобы оценить мгновенную скорость изменения расхода топлива по отношению к скорости при \(s=90\). Будьте максимально точными, используйте правильные обозначения и включайте единицы измерения в свой ответ.
Используйте эту информацию, чтобы оценить мгновенную скорость изменения расхода топлива по отношению к скорости при \(s=90\). Будьте максимально точными, используйте правильные обозначения и включайте единицы измерения в свой ответ. - Написав полное предложение, интерпретируйте значение (в контексте расхода топлива) «\(f(80)=0,015\)».
- Напишите хотя бы одно полное предложение, интерпретирующее значение \(f'(90)\), которое вы оценили в (а). 9{\ circ} Ф / мин \). Во всех случаях, когда мы работаем с функциями, имеющими прикладной контекст, полезно и поучительно тщательно подумать о задействованных единицах и о том, как они дополнительно влияют на смысл наших вычислений.
Резюме
В этом разделе мы столкнулись со следующими важными идеями:
- Независимо от контекста данной функции \(y=f(x)\), производная всегда измеряет мгновенную скорость изменения выхода переменная по отношению к входной переменной.
- Единицами производной функции \(y=f'(x)\) являются единицы \(f\) на единицу \(x\).
 Опять же, это измеряет, насколько быстро изменяется выход функции \(f\) при изменении входа функции.
Опять же, это измеряет, насколько быстро изменяется выход функции \(f\) при изменении входа функции. - Аппроксимация центральной разности значения первой производной задается выражением \[f'(a) \ приблизительно \frac{f(a+h)-f(a-h)}{2h},\], и эта величина измеряет наклон секущей к \(y=f(x)\) через точки \((a-h, f(a-h))\) и \((a+h, f(a+h))\). Центральная разность дает хорошее приближение значения производной каждый раз, когда у нас есть симметричные данные, окружающие интересующую точку.
- Зная значения производной и функции в одной точке, мы можем оценить значения других функций поблизости. Если, например, мы знаем, что \(f'(7)=2\), то мы знаем, что при \(x\)=7 функция \(f\) возрастает с мгновенной скоростью 2 единицы выпуска на каждую единицу ввода. Таким образом, мы ожидаем, что \(f(8)\) будет примерно на 2 единицы больше, чем \(f(7)\). Значение является приблизительным, потому что мы не знаем, остается ли скорость изменения неизменной при изменении \(x\).
Эта страница под заголовком 1.
 5: Интерпретация, оценка и использование производной доступна в соответствии с лицензией CC BY-SA 4.0, ее авторами, ремикшированием и/или кураторами являются Мэтью Болкинс, Дэвид Остин и Стивен Шликер (ScholarWorks @Grand Valley State университета) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
5: Интерпретация, оценка и использование производной доступна в соответствии с лицензией CC BY-SA 4.0, ее авторами, ремикшированием и/или кураторами являются Мэтью Болкинс, Дэвид Остин и Стивен Шликер (ScholarWorks @Grand Valley State университета) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Активное исчисление
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- источник@https://activecalculus.
 org/single
org/single
- источник@https://activecalculus.
3.2 Производная как функция. Исчисление, том 1
Цели обучения
- 3.2.1 Определите производную функцию данной функции.
- 3.2.2 График производной функции по графику заданной функции.
- 3.2.3 Укажите связь между производными и непрерывностью.
- 3.2.4 Назовите три условия, при которых функция не имеет производной.
- 3.2.5 Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы продифференцируем функцию положения в данный момент времени, мы получим скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке даст ценную информацию о поведении функции. Однако процесс нахождения производной даже при нескольких значениях с использованием методов из предыдущего раздела быстро стал бы довольно утомительным.
 В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.Производные функции
Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная. Мы можем формально определить производную функцию следующим образом.
Определение
Пусть ff — функция. Производная функция, обозначаемая f′,f′, представляет собой функцию, область определения которой состоит из таких значений xx, что существует следующий предел:
f′(x)=limh→0f(x+h)−f(x )h.f′(x)=limh→0f(x+h)−f(x)h.
(3.9)
Функция f(x)f(x) называется дифференцируемой в п.в., если f′(a)f′(a) существует. В более общем смысле функция называется дифференцируемой на SS, если она дифференцируема в каждой точке открытого множества S, S, а дифференцируемая функция — это функция, в которой f′(x)f′(x) существует в своей области определения.

В следующих нескольких примерах мы используем уравнение 3.9 для нахождения производной функции.
Пример 3.11
Нахождение производной функции квадратного корня
Найдите производную f(x)=x.f(x)=x.
Решение
Начните непосредственно с определения функции производной. Используйте уравнение 3.1.
f′(x)=limh→0x+h−xhЗаменитьef(x+h)=x+handf(x)=xintof′(x)=limh→0f(x+h)−f(x)h.= limh→0x+h−xh·x+h+xx+h+xУмножить числитель и знаменатель наx+h+x без распределения в знаменателе.=limh→0hh(x+h+x)Умножить числители и упростить.=limh→01 (x+h+x)Отменить h.=12xВычислить предел.f′(x)=limh→0x+h−xhЗаменитьef(x+h)=x+handf(x)=xintof′(x)=limh→0f (x+h)−f(x)h.=limh→0x+h−xh·x+h+xx+h+xУмножить числитель и знаменатель наx+h+x без распределения в знаменателе.=limh→0hh(x+h +x)Умножить числители и упростить.=limh→01(x+h+x)Отменить h.=12xВычислить предел.
Пример 3.12
Нахождение производной квадратичной функции
Нахождение производной функции f(x)=x2−2x.
 f(x)=x2−2x.
f(x)=x2−2x.Решение
Выполните ту же процедуру здесь, но без умножения на сопряженное.
f′(x)=limh→0((x+h)2−2(x+h))−(x2−2x)hПодставитьef(x+h)=(x+h)2−2(x+ h)иf(x)=x2−2xintof′(x)=limh→0f(x+h)−f(x)h.=limh→0x2+2xh+h3−2x−2h−x2+2xhExpand(x+h )2−2(x+h).=limh→02xh−2h+h3hУпростить.=limh→0h(2x−2+h)hМножитель hвыпадает из числителя.=limh→0(2x−2+h)Отменить общий множитель ofh.=2x−2Вычислить предел.f′(x)=limh→0((x+h)2−2(x+h))−(x2−2x)hПодставитьef(x+h)=(x+h )2−2(x+h) и f(x)=x2−2xintof′(x)=limh→0f(x+h)−f(x)h.=limh→0x2+2xh+h3−2x−2h− x2+2xhExpand(x+h)2−2(x+h).=limh→02xh−2h+h3hУпростить.=limh→0h(2x−2+h)hМножитель hиз числителя.=limh→0(2x−2 +h)Отменить общий множитель h.=2x−2Вычислить предел.
Контрольно-пропускной пункт 3,6
Найдите производную f(x)=x2.f(x)=x2.
Мы используем различные обозначения для выражения производной функции. В примере 3.12 мы показали, что если f(x)=x2−2x,f(x)=x2−2x, то f′(x)=2x−2.f′(x)=2x−2.
 Если бы мы представили эту функцию в виде y=x2−2x,y=x2−2x, мы могли бы выразить производную как y′=2x−2y′=2x−2 или dydx=2x−2.dydx=2x− 2. Мы могли бы передать ту же информацию, написав ddx(x2−2x)=2x−2.ddx(x2−2x)=2x−2. Таким образом, для функции y=f(x),y=f(x) каждое из следующих обозначений представляет собой производную от f(x):f(x):
Если бы мы представили эту функцию в виде y=x2−2x,y=x2−2x, мы могли бы выразить производную как y′=2x−2y′=2x−2 или dydx=2x−2.dydx=2x− 2. Мы могли бы передать ту же информацию, написав ddx(x2−2x)=2x−2.ddx(x2−2x)=2x−2. Таким образом, для функции y=f(x),y=f(x) каждое из следующих обозначений представляет собой производную от f(x):f(x):f′(x),dydx,y′,ddx(f(x)).f′(x),dydx,y′,ddx(f(x)).
Вместо f′(a)f′(a) мы также можем использовать dydx|x=adydx|x=a Использование нотации dydxdydx (называемой нотацией Лейбница) довольно распространено в технике и физике. Чтобы лучше понять эти обозначения, вспомним, что производная функции в точке — это предел наклона секущих по мере приближения секущих к касательной. Наклоны этих секущих часто выражаются в виде ΔyΔxΔyΔx, где ΔyΔy — разность значений yy, соответствующая разнице значений xx, которая выражается как ΔxΔx (рис. 3.11). Таким образом, производная, которую можно рассматривать как мгновенную скорость изменения yy по отношению к x,x, выражается как
dydx=limΔx→0ΔyΔx.
 dydx=limΔx→0ΔyΔx.
dydx=limΔx→0ΔyΔx.Рисунок 3.11 Производная выражается как dydx=limΔx→0ΔyΔx.dydx=limΔx→0ΔyΔx.
График производной
Мы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить график. Учитывая оба, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку f′(x)f′(x) дает скорость изменения функции f(x)f(x) (или наклон кривой). касательная к f(x)).f(x)).
В примере 3.11 мы обнаружили, что для f(x)=x,f′(x)=1/2x.f(x)=x,f′(x)=1/2x. Если мы изобразим эти функции на тех же осях, как на рис. 3.12, мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями. Во-первых, мы замечаем, что f(x)f(x) возрастает по всей своей области, а это означает, что наклоны ее касательных во всех точках положительны. Следовательно, мы ожидаем, что f′(x)>0f′(x)>0 для всех значений xx в его области определения. Кроме того, по мере увеличения xx наклоны касательных линий к f(x)f(x) уменьшаются, и мы ожидаем увидеть соответствующее уменьшение f′(x).
 f′(x). Заметим также, что f′(0)f′(0) не определено и что limx→0+f′(x)=+∞, limx→0+f′(x)=+∞, что соответствует вертикальной касательной к f(x)f(x) при 0,0.
f′(x). Заметим также, что f′(0)f′(0) не определено и что limx→0+f′(x)=+∞, limx→0+f′(x)=+∞, что соответствует вертикальной касательной к f(x)f(x) при 0,0.Рисунок 3.12 Производная f′(x)f′(x) везде положительна, поскольку функция f(x)f(x) возрастает.
В примере 3.12 мы нашли, что для f(x)=x2−2x,f′(x)=2x−2.f(x)=x2−2x,f′(x)=2x−2. Графики этих функций показаны на рис. 3.13. Обратите внимание, что f(x)f(x) убывает при x<1.x<1. Для этих же значений x,f′(x)<0.x,f′(x)<0. Для значений x>1,f(x)x>1,f(x) возрастает, а f′(x)>0.f′(x)>0. Кроме того, f(x)f(x) имеет горизонтальную касательную в точке x=1x=1 и f′(1)=0.f′(1)=0.
Рисунок 3.13 Производная f′(x)<0f′(x)<0, где функция f(x)f(x) убывающая и f′(x)>0f′(x)>0, где f(x)f(x) ) повышается. Производная равна нулю там, где функция имеет горизонтальный тангенс.
Пример 3.13
Набросок производной с помощью функции
Используйте следующий график f(x)f(x) для построения графика f′(x).
 f′(x).
f′(x).Решение
Решение показано на следующем графике. Заметим, что f(x)f(x) возрастает и f′(x)>0f′(x)>0 на (–2,3).(–2,3). Кроме того, f(x)f(x) убывает и f′(x)<0f′(x)<0 на (−∞,−2)(−∞,−2) и на (3,+∞). (3,+∞). Также обратите внимание, что f(x)f(x) имеет горизонтальные касательные в точках –2–2 и 3,3, а также f′(−2)=0f′(−2)=0 и f′(3)=0.f ′(3)=0.
Контрольно-пропускной пункт 3,7
Нарисуйте график функции f(x)=x2−4.f(x)=x2−4. На каком интервале находится график функции f′(x)f′(x) над осью xx?
Производные и непрерывность
Теперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков. Сначала рассмотрим связь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в точке, не обязательно должна быть дифференцируемой в этой точке. На самом деле функция может быть непрерывной в точке и не быть дифференцируемой в этой точке по одной из нескольких причин.

Теорема 3.1
Дифференцируемость подразумевает непрерывность
Пусть f(x)f(x) — функция, aa — в ее области определения. Если f(x)f(x) дифференцируема в точках а, а, то функция ff непрерывна в точках а.
Доказательство
Если f(x)f(x) дифференцируема в точках a,a, то f′(a)f′(a) существует и
f′(a)=limx→af(x)−f(a)x−a.f′(a)=limx→af(x)−f(a)x−a.
Мы хотим показать, что функция f(x)f(x) непрерывна в точке aa, показав, что limx→af(x)=f(a).limx→af(x)=f(a). Таким образом,
limx→af(x)=limx→a(f(x)−f(a)+f(a))=limx→a(f(x)−f(a)x−a·(x−a) +f(a)) Умножить и разделить f(x)−f(a)наx−a.=(limx→af(x)−f(a)x−a)·(limx→a(x−a))+ limx→af(a)=f′(a)·0+f(a)=f(a).limx→af(x)=limx→a(f(x)−f(a)+f(a) )=limx→a(f(x)−f(a)x−a·(x−a)+f(a)) Умножить и разделить f(x)−f(a)наx−a.=(limx→af (x)−f(a)x−a)·(limx→a(x−a))+limx→af(a)=f′(a)·0+f(a)=f(a).
Следовательно, поскольку f(a)f(a) определено и limx→af(x)=f(a),limx→af(x)=f(a), мы заключаем, что ff непрерывен в п.
 в.
в.□
Мы только что доказали, что дифференцируемость влечет непрерывность, но теперь мы рассмотрим, влечет ли непрерывность дифференцируемость. Чтобы найти ответ на этот вопрос, мы исследуем функцию f(x)=|x|.f(x)=|x|. Эта функция всюду непрерывна; однако f′(0)f′(0) не определено. Это наблюдение приводит нас к мысли, что непрерывность не влечет дифференцируемости. Давайте исследовать дальше. Для f(x)=|x|,f(x)=|x|,
f′(0)=limx→0f(x)−f(0)x−0=limx→0|x|−|0|x−0=limx→0|x|x.f′(0)=limx→ 0f(x)−f(0)x−0=limx→0|x|−|0|x−0=limx→0|x|x.
Это ограничение не существует, так как
limx→0−|x|x=−1и limx→0+|x|x=1.limx→0−|x|x=−1иlimx→0+|x|x=1.
См. рис. 3.14.
Рисунок 3.14 Функция f(x)=|x|f(x)=|x| непрерывна в точке 00, но не дифференцируема в точке 0,0.
Рассмотрим некоторые дополнительные ситуации, в которых непрерывная функция не может быть дифференцируемой. Рассмотрим функцию f(x)=x3:f(x)=x3:
f′(0)=limx→0x3−0x−0=limx→01×23=+∞.
 f′(0)=limx→0x3−0x−0=limx→01×23=+∞.
f′(0)=limx→0x3−0x−0=limx→01×23=+∞.Таким образом, f′(0)f′(0) не существует. Беглый взгляд на график f(x)=x3f(x)=x3 проясняет ситуацию. Функция имеет вертикальную касательную в точке 00 (рис. 3.15).
Рисунок 3.15 Функция f(x)=x3f(x)=x3 имеет вертикальную касательную в точке x=0.x=0. Он непрерывен в точке 00, но не дифференцируем в точке 0,0.
Функция f(x)={xsin(1x)ifx≠00ifx=0f(x)={xsin(1x)ifx≠00ifx=0 также имеет производную, которая демонстрирует интересное поведение при 0,0. Мы видим, что
f′(0)=limx→0xsin(1/x)−0x−0=limx→0sin(1x).f′(0)=limx→0xsin(1/x)−0x−0=limx→0sin( 1х).
Этого предела не существует, в основном потому, что наклоны секущих постоянно меняют направление по мере приближения к нулю (рис. 3.16).
Рисунок 3.16 Функция f(x)={xsin(1x)ifx≠00ifx=0f(x)={xsin(1x)ifx≠00ifx=0 не дифференцируема при 0,0.
Итого:
- Заметим, что если функция не непрерывна, она не может быть дифференцируемой, так как каждая дифференцируемая функция должна быть непрерывной.
 Однако, если функция непрерывна, она может не быть дифференцируемой.
Однако, если функция непрерывна, она может не быть дифференцируемой. - Мы видели, что f(x)=|x|f(x)=|x| не мог быть дифференцируем в 00, потому что предел наклонов касательных слева и справа не был одинаковым. Визуально это привело к появлению острого угла на графике функции в точке 0.0. Отсюда заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть «гладкой» в этой точке.
- Как мы видели на примере f(x)=x3,f(x)=x3, функция не может быть дифференцируемой в точке, где есть вертикальная касательная.
- Как мы видели с f(x)={xsin(1x)ifx≠00ifx=0f(x)={xsin(1x)ifx≠00ifx=0 функция может не быть дифференцируемой в точке и более сложными способами .
Пример 3.14
Кусочная функция, которая является непрерывной и дифференцируемой
Компания по производству игрушек хочет разработать траекторию для игрушечной машинки, которая начинается с параболической кривой, а затем переходит в прямую линию (рис.
 3.17). Функция, описывающая дорожку, должна иметь вид −10, где xx и f(x)f(x) указаны в дюймах. Чтобы автомобиль двигался плавно по трассе, функция f(x)f(x) должна быть одновременно непрерывной и дифференцируемой при −10,−10. Найдите значения bb и cc, которые делают f(x)f(x) непрерывным и дифференцируемым.
3.17). Функция, описывающая дорожку, должна иметь вид −10, где xx и f(x)f(x) указаны в дюймах. Чтобы автомобиль двигался плавно по трассе, функция f(x)f(x) должна быть одновременно непрерывной и дифференцируемой при −10,−10. Найдите значения bb и cc, которые делают f(x)f(x) непрерывным и дифференцируемым.Рисунок 3.17 Чтобы автомобиль двигался плавно по трассе, функция должна быть одновременно и непрерывной, и дифференцируемой.
Решение
Чтобы функция была непрерывной при x=−10,limx→−10−f(x)=f(−10).x=−10,limx→−10−f(x)=f(−10). Таким образом, поскольку
limx→−10−f(x)=110(−10)2−10b+c=10−10b+climx→−10−f(x)=110(−10)2−10b+c =10−10b+c
и f(−10)=5,f(−10)=5, мы должны иметь 10−10b+c=5,10−10b+c=5. Эквивалентно, мы имеем c=10b−5.c=10b−5.
Чтобы функция была дифференцируемой при −10, −10,
f′(-10)=limx→−10f(x)−f(−10)x+10f′(-10)=limx→−10f(x)−f(−10)x+10
обязательно существовать. Поскольку f(x)f(x) определяется по разным правилам справа и слева, мы должны вычислить этот предел справа и слева, а затем приравнять их друг другу:
limx→−10−f( x)−f(−10)x+10=limx→−10−110×2+bx+c−5x+10=limx→−10−110×2+bx+(10b−5)−5x+10Substitutec=10b−5.
 = limx→−10−x2−100+10bx+100b10(x+10)Умножить числитель и знаменатель на 10.=limx→−10−(x+10)(x−10+10b)10(x+10)Множитель на группировка.=b−2.limx→−10−f(x)−f(−10)x+10=limx→−10−110×2+bx+c−5x+10=limx→−10−110×2+bx+( 10b−5)−5x+10Substitutec=10b−5.=limx→−10−x2−100+10bx+100b10(x+10)Умножить числитель и знаменатель на 10.=limx→−10−(x+10)( x−10+10b)10(x+10) Фактор по группировке.=b−2.
= limx→−10−x2−100+10bx+100b10(x+10)Умножить числитель и знаменатель на 10.=limx→−10−(x+10)(x−10+10b)10(x+10)Множитель на группировка.=b−2.limx→−10−f(x)−f(−10)x+10=limx→−10−110×2+bx+c−5x+10=limx→−10−110×2+bx+( 10b−5)−5x+10Substitutec=10b−5.=limx→−10−x2−100+10bx+100b10(x+10)Умножить числитель и знаменатель на 10.=limx→−10−(x+10)( x−10+10b)10(x+10) Фактор по группировке.=b−2.У нас также есть
limx→−10+f(x)−f(−10)x+10=limx→−10+−14x+52−5x+10=limx→−10+−(x+10 )4(x+10)=−14.limx→−10+f(x)−f(−10)x+10=limx→−10+−14x+52−5x+10=limx→−10+− (х+10)4(х+10)=-14.
Это дает нам b−2=−14.b−2=−14. Таким образом, b=74b=74 и c=10(74)−5=252.c=10(74)−5=252.
Контрольно-пропускной пункт 3,8
Найдите значения aa и bb, которые делают f(x)={ax+bifx<3x2ifx≥3f(x)={ax+bifx<3x2ifx≥3 непрерывными и дифференцируемыми в 3.3.
Производные высшего порядка
Производная функции сама по себе является функцией, поэтому мы можем найти производную производной.
 Например, производная функции положения — это скорость изменения положения или скорость. Производная скорости — это скорость изменения скорости, то есть ускорение. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать брать производные, чтобы получить третью производную, четвертую производную и так далее. В совокупности они называются производными более высокого порядка. Обозначение производных высшего порядка от y=f(x)y=f(x) может быть выражено в любой из следующих форм:
Например, производная функции положения — это скорость изменения положения или скорость. Производная скорости — это скорость изменения скорости, то есть ускорение. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать брать производные, чтобы получить третью производную, четвертую производную и так далее. В совокупности они называются производными более высокого порядка. Обозначение производных высшего порядка от y=f(x)y=f(x) может быть выражено в любой из следующих форм:f″(x),f‴(x),f(4)(x),…,f(n)(x)f″(x),f‴(x),f(4)(x), …,f(n)(x)
y″(x),y‴(x),y(4)(x),…,y(n)(x)y″(x),y‴(x),y(4)(x), …,у(п)(х)
d2ydx2,d3ydx3,d4ydx4,…,dnydxn.d2ydx2,d3ydx3,d4ydx4,…,dnydxn.
Интересно отметить, что нотация для d2ydx2d2ydx2 может рассматриваться как попытка выразить ddx(dydx)ddx(dydx) более компактно. Аналогично, ddx(ddx(dydx))=ddx(d2ydx2)=d3ydx3.ddx(ddx(dydx))=ddx(d2ydx2)=d3ydx3.
Пример 3.15
Нахождение второй производной
Для f(x)=2×2−3x+1,f(x)=2×2−3x+1 найдите f″(x).
 f″(x).
f″(x).Решение
Сначала найдите f′(x).f′(x).
f′(x)=limh→0(2(x+h)2−3(x+h)+1)−(2×2−3x+1)hПодставить f(x)=2×2−3x+1andf(x+ h)=2(x+h)2−3(x+h)+1intof′(x)=limh→0f(x+h)−f(x)h.=limh→04xh+2h3−3hhУпростим числитель. =limh→0(4x+2h−3) Вынести в числитель и сократить в знаменателе.=4x−3 Возьмем предел. f′(x)=limh→0(2(x+h)2−3(x+ h)+1)−(2×2−3x+1)hПодставитьef(x)=2×2−3x+1andf(x+h)=2(x+h)2−3(x+h)+1intof′(x)= limh→0f(x+h)−f(x)h.=limh→04xh+2h3−3hhУпростить числитель.=limh→0(4x+2h−3)Вынести из числителя в множитель и сократить в знаменателе.=4x− 3Возьмите лимит.
Затем найдите f″(x)f″(x), взяв производную от f′(x)=4x−3.f′(x)=4x−3.
f″(x)=limh→0f′(x+h)−f′(x)hUsef′(x)=limh→0f(x+h)−f(x)hс f′(x) на месте off( x).=limh→0(4(x+h)−3)−(4x−3)hПодставьте f′(x+h)=4(x+h)−3 и f′(x)=4x−3.=limh →04Упростить.=4Возьмем предел. (x) вместо off(x).=limh→0(4(x+h)−3)−(4x−3)hПодставить f′(x+h)=4(x+h)−3andf′(x)= 4x−3.=limh→04Упростить.=4Возьмем предел.
Контрольно-пропускной пункт 3,9
Найдите f″(x)f″(x) для f(x)=x2.
 f(x)=x2.
f(x)=x2.Пример 3.16
Определение ускорения
Положение частицы вдоль координатной оси в момент времени tt (в секундах) определяется выражением s(t)=3t2−4t+1s(t)=3t2−4t+1 (в метрах). Найдите функцию, описывающую его ускорение в момент времени t.t.
Решение
Поскольку v(t)=s′(t)v(t)=s′(t) и a(t)=v′(t)=s″(t), a(t)=v′(t) =s″(t), начнем с нахождения производной от s(t):s(t):
s′(t)=limh→0s(t+h)−s(t)h=limh→03 (t+h)2−4(t+h)+1−(3t2−4t+1)h=6t−4.s′(t)=limh→0s(t+h)−s(t)h= limh→03(t+h)2−4(t+h)+1−(3t2−4t+1)h=6t−4.
Далее,
s″(t)=limh→0s′(t+h)−s′(t)h=limh→06(t+h)−4−(6t−4)h=6.s ″(t)=limh→0s′(t+h)−s′(t)h=limh→06(t+h)−4−(6t−4)h=6.
Таким образом, a=6м/с2.a=6м/с2.
Контрольно-пропускной пункт 3.10
Для s(t)=t3,s(t)=t3 найти a(t).a(t).
Раздел 3.2 Упражнения
В следующих упражнениях используйте определение производной, чтобы найти f′(x).
 f′(x).
f′(x).54.
f(x)=6f(x)=6
55.
f(x)=2−3xf(x)=2−3x
56.
f(x)=2×7+1f(x)=2×7+1
57.
f(x)=4x2f(x)=4×2
58.
f(x)=5x−x2f(x)=5x−x2
59.
f(x)=2xf(x)=2x
60.
f(x)=x−6f(x)=x−6
61.
f(x)=9xf(x)=9x
62.
f(x)=x+1xf(x)=x+1x
63.
f(x)=1xf(x)=1x
В следующих упражнениях используйте график y=f(x)y=f(x), чтобы начертить график его производной f′(x).f′(x).
64.
65.
66.

67.
Для следующих упражнений заданный предел представляет собой производную функции y=f(x)y=f(x) при x=a.x=a. Найти f(x)f(x) и п.в.
68.
limh→0(1+h)2/3−1hlimh→0(1+h)2/3−1h
69.
limh→0[3(2+h)2+2]−14hlimh→0[3(2+h)2+2]−14h
70.
limh→0cos(π+h)+1hlimh→0cos(π+h)+1h
71.
limh→0(2+h)4−16hlimh→0(2+h)4−16h
72.
limh→0[2(3+h)2−(3+h)]−15hlimh→0[2(3+h)2−(3+h)]−15h
73.
limh→0eh−1hlimh→0eh−1h
Для следующих функций,
- эскиз графика и
- используют определение производной, чтобы показать, что функция не дифференцируема при x=1.x=1.
74.
f(x)={2x,0≤x≤13x−1,x>1f(x)={2x,0≤x≤13x−1,x>1
75.

f(x)={3,x<13x,x≥1f(x)={3,x<13x,x≥1
76.
f(x)={−x2+2,x≤1x,x>1f(x)={−x2+2,x≤1x,x>1
77.
f(x)={2x,x≤12x,x>1f(x)={2x,x≤12x,x>1
Для следующих графиков
- определить, для каких значений x=ax=a существует limx→af(x)limx→af(x), но ff не является непрерывным при x=a,x=a, и
- определить, при каких значениях x=ax=a функция непрерывна, но не дифференцируема при x=a.x=a.
78.
79.
80.
Используйте график для оценки a. f'(-0,5),f'(-0,5), б. f′(0),f′(0), в. f′(1),f′(1), д. f′(2),f′(2) и e. f′(3),f′(3), если он существует.
Для следующих функций используйте f″(x)=limh→0f′(x+h)−f′(x)hf″(x)=limh→0f′(x+h)−f′(x)h чтобы найти f″(x).f″(x).
81.
f(x)=2−3xf(x)=2−3x
82.

f(x)=4x2f(x)=4×2
83.
f(x)=x+1xf(x)=x+1x
В следующих упражнениях используйте калькулятор для построения графика f(x).f(x). Определите функцию f′(x),f′(x), затем используйте калькулятор для построения графика f′(x).f′(x).
84.
[Т] f(x)=−5xf(x)=−5x
85.
[Т] f(x)=3×2+2x+4.f(x)=3×2+2x+4.
86.
[Т] f(x)=x+3xf(x)=x+3x
87.
[Т] f(x)=12xf(x)=12x
88.
[Т] f(x)=1+x+1xf(x)=1+x+1x
89.
[Т] f(x)=x3+1f(x)=x3+1
В следующих упражнениях опишите, что представляют два выражения в терминах каждой из данных ситуаций.
 Обязательно укажите единицы измерения.
Обязательно укажите единицы измерения.- f(x+h)−f(x)hf(x+h)−f(x)h
- f′(x)=limh→0f(x+h)−f(x)hf′(x)=limh→0f(x+h)−f(x)h
90.
P(x)P(x) обозначает население города в момент времени xx в годах.
91.
C(x)C(x) обозначает общую сумму денег (в тысячах долларов), потраченную на уступки xx клиентам в парке развлечений.
92.
R(x)R(x) обозначает общую стоимость (в тысячах долларов) изготовления xx радиочасов.
93.
g(x)g(x) обозначает оценку (в процентах), полученную за тест при xx часах обучения.
94.
B(x)B(x) обозначает стоимость (в долларах) учебника по социологии в университетских книжных магазинах США в xx лет, начиная с 1990.1990.
95.
p(x)p(x) обозначает атмосферное давление в торрах на высоте xx футов.

96.
Нарисуйте график функции y=f(x)y=f(x) со всеми следующими свойствами:
- f′(x)>0f′(x)>0 для −2≤x<1−2≤x<1
- f'(2)=0f'(2)=0
- f′(x)>0f′(x)>0 для x>2x>2
- f(2)=2f(2)=2 и f(0)=1f(0)=1
- limx→−∞f(x)=0limx→−∞f(x)=0 и limx→∞f(x)=∞limx→∞f(x)=∞
- f′(1)f′(1) не существует.
97.
Предположим, что температура TT в градусах Фаренгейта на высоте xx в футах над землей равна y=T(x).y=T(x).
- Дайте физическую интерпретацию с единицами измерения T′(x).T′(x).
- Если мы знаем, что T′(1000)=−0,1,T′(1000)=−0,1, объясни физический смысл.
98.
Предположим, что общая прибыль компании составляет y=P(x)y=P(x) тысяч долларов при продаже xx единиц товара.
- Что измеряет P(b)−P(a)b−aP(b)−P(a)b−a для 0
- Что измеряет P′(x)P′(x) и в каких единицах?
- Предположим, что P'(30)=5, P'(30)=5, как приблизительно изменится прибыль, если количество проданных товаров увеличится с 30 до 31?30 до 31?
99.

График на следующем рисунке моделирует количество людей N(t)N(t), заболевших гриппом tt недель после его первоначальной вспышки в городе с населением 50 000 50 000 жителей.
- Опишите, что представляет собой N'(t)N'(t) и как она ведет себя при увеличении tt.
- Что эта производная говорит нам о том, как этот город пострадал от вспышки гриппа?
Для следующих упражнений используйте следующую таблицу, в которой указана высота hh ракеты Saturn VV для миссии Apollo 1111 через tt секунд после запуска.
Время (секунды) Высота (метры) 00 00 11 22 22 44 33 1313 44 2525 55 3232 100.

Каков физический смысл h'(t)?h'(t)? Что такое единицы?
101.
[T] Постройте таблицу значений для h'(t)h'(t) и отобразите h(t)h(t) и h'(t)h'(t) на одном графике. ( Подсказка: для внутренних точек, оцените как левый предел, так и правый предел и усредните их. Внутренняя точка интервала I — это элемент I, который не является конечной точкой I.)
102.
[T] Наилучшая линейная аппроксимация данных дается формулой H(t)=7,229t−4,905,H(t)=7,229t−4,905, где HH — высота ракеты (в метрах) и tt — время, прошедшее с момента взлета. Из этого уравнения определите H′(t).H′(t). График H(t)H(t) с заданными данными и на отдельной координатной плоскости график H′(t).H′(t).
103.
[T] Наилучшее квадратичное соответствие данным определяется выражением G(t)=1,429t2+0,0857t−0,1429,G(t)=1,429t2+0,0857t−0,1429, где GG — высота ракеты (в метрах) и tt — время, прошедшее с момента взлета.




 Включите единицы в свой ответ.
Включите единицы в свой ответ. Включите единицы в свой ответ.
Включите единицы в свой ответ. Оцените \(C(2100)\) и обоснуйте свою оценку, написав хотя бы одно предложение, объясняющее ваши мысли.
Оцените \(C(2100)\) и обоснуйте свою оценку, написав хотя бы одно предложение, объясняющее ваши мысли. Используйте эту информацию, чтобы оценить мгновенную скорость изменения расхода топлива по отношению к скорости при \(s=90\). Будьте максимально точными, используйте правильные обозначения и включайте единицы измерения в свой ответ.
Используйте эту информацию, чтобы оценить мгновенную скорость изменения расхода топлива по отношению к скорости при \(s=90\). Будьте максимально точными, используйте правильные обозначения и включайте единицы измерения в свой ответ. Опять же, это измеряет, насколько быстро изменяется выход функции \(f\) при изменении входа функции.
Опять же, это измеряет, насколько быстро изменяется выход функции \(f\) при изменении входа функции. 5: Интерпретация, оценка и использование производной доступна в соответствии с лицензией CC BY-SA 4.0, ее авторами, ремикшированием и/или кураторами являются Мэтью Болкинс, Дэвид Остин и Стивен Шликер (ScholarWorks @Grand Valley State университета) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
5: Интерпретация, оценка и использование производной доступна в соответствии с лицензией CC BY-SA 4.0, ее авторами, ремикшированием и/или кураторами являются Мэтью Болкинс, Дэвид Остин и Стивен Шликер (ScholarWorks @Grand Valley State университета) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу. org/single
org/single В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
/ModulBM/ModBM/Praktika/Rechen/pract(IssF_2pr).files/image214.jpg) f(x)=x2−2x.
f(x)=x2−2x. Если бы мы представили эту функцию в виде y=x2−2x,y=x2−2x, мы могли бы выразить производную как y′=2x−2y′=2x−2 или dydx=2x−2.dydx=2x− 2. Мы могли бы передать ту же информацию, написав ddx(x2−2x)=2x−2.ddx(x2−2x)=2x−2. Таким образом, для функции y=f(x),y=f(x) каждое из следующих обозначений представляет собой производную от f(x):f(x):
Если бы мы представили эту функцию в виде y=x2−2x,y=x2−2x, мы могли бы выразить производную как y′=2x−2y′=2x−2 или dydx=2x−2.dydx=2x− 2. Мы могли бы передать ту же информацию, написав ddx(x2−2x)=2x−2.ddx(x2−2x)=2x−2. Таким образом, для функции y=f(x),y=f(x) каждое из следующих обозначений представляет собой производную от f(x):f(x): dydx=limΔx→0ΔyΔx.
dydx=limΔx→0ΔyΔx. f′(x). Заметим также, что f′(0)f′(0) не определено и что limx→0+f′(x)=+∞, limx→0+f′(x)=+∞, что соответствует вертикальной касательной к f(x)f(x) при 0,0.
f′(x). Заметим также, что f′(0)f′(0) не определено и что limx→0+f′(x)=+∞, limx→0+f′(x)=+∞, что соответствует вертикальной касательной к f(x)f(x) при 0,0. f′(x).
f′(x).
 в.
в. f′(0)=limx→0x3−0x−0=limx→01×23=+∞.
f′(0)=limx→0x3−0x−0=limx→01×23=+∞. Однако, если функция непрерывна, она может не быть дифференцируемой.
Однако, если функция непрерывна, она может не быть дифференцируемой. 3.17). Функция, описывающая дорожку, должна иметь вид −10, где xx и f(x)f(x) указаны в дюймах. Чтобы автомобиль двигался плавно по трассе, функция f(x)f(x) должна быть одновременно непрерывной и дифференцируемой при −10,−10. Найдите значения bb и cc, которые делают f(x)f(x) непрерывным и дифференцируемым.
3.17). Функция, описывающая дорожку, должна иметь вид −10, где xx и f(x)f(x) указаны в дюймах. Чтобы автомобиль двигался плавно по трассе, функция f(x)f(x) должна быть одновременно непрерывной и дифференцируемой при −10,−10. Найдите значения bb и cc, которые делают f(x)f(x) непрерывным и дифференцируемым. = limx→−10−x2−100+10bx+100b10(x+10)Умножить числитель и знаменатель на 10.=limx→−10−(x+10)(x−10+10b)10(x+10)Множитель на группировка.=b−2.limx→−10−f(x)−f(−10)x+10=limx→−10−110×2+bx+c−5x+10=limx→−10−110×2+bx+( 10b−5)−5x+10Substitutec=10b−5.=limx→−10−x2−100+10bx+100b10(x+10)Умножить числитель и знаменатель на 10.=limx→−10−(x+10)( x−10+10b)10(x+10) Фактор по группировке.=b−2.
= limx→−10−x2−100+10bx+100b10(x+10)Умножить числитель и знаменатель на 10.=limx→−10−(x+10)(x−10+10b)10(x+10)Множитель на группировка.=b−2.limx→−10−f(x)−f(−10)x+10=limx→−10−110×2+bx+c−5x+10=limx→−10−110×2+bx+( 10b−5)−5x+10Substitutec=10b−5.=limx→−10−x2−100+10bx+100b10(x+10)Умножить числитель и знаменатель на 10.=limx→−10−(x+10)( x−10+10b)10(x+10) Фактор по группировке.=b−2. Например, производная функции положения — это скорость изменения положения или скорость. Производная скорости — это скорость изменения скорости, то есть ускорение. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать брать производные, чтобы получить третью производную, четвертую производную и так далее. В совокупности они называются производными более высокого порядка. Обозначение производных высшего порядка от y=f(x)y=f(x) может быть выражено в любой из следующих форм:
Например, производная функции положения — это скорость изменения положения или скорость. Производная скорости — это скорость изменения скорости, то есть ускорение. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать брать производные, чтобы получить третью производную, четвертую производную и так далее. В совокупности они называются производными более высокого порядка. Обозначение производных высшего порядка от y=f(x)y=f(x) может быть выражено в любой из следующих форм: f″(x).
f″(x). f(x)=x2.
f(x)=x2. f′(x).
f′(x).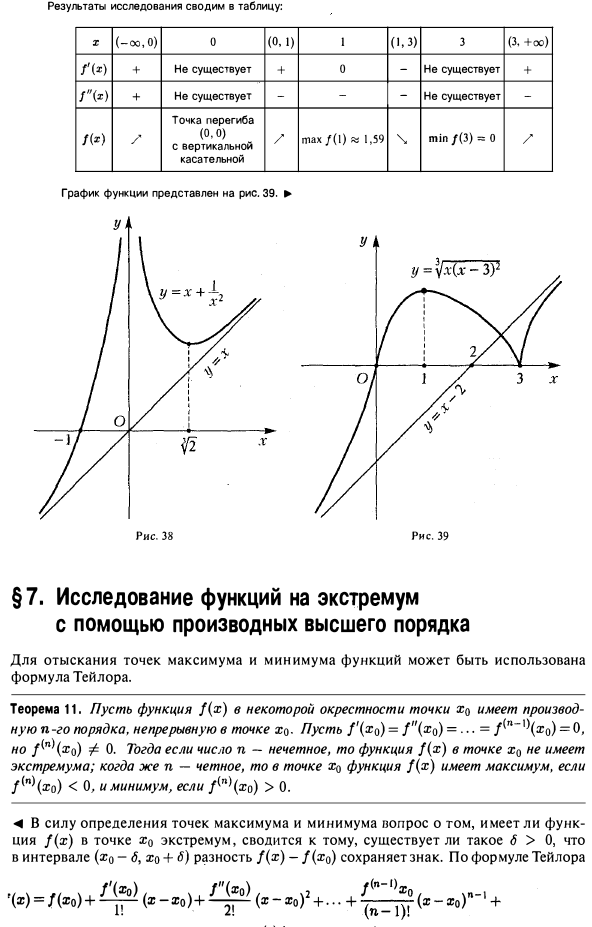

 Обязательно укажите единицы измерения.
Обязательно укажите единицы измерения.


