Сравнение обыкновенных дробей. Онлайн калькулятор
- Сравнение дробей с одинаковыми знаменателями
- Сравнение дробей с одинаковыми числителями
- Сравнение дробей с разными знаменателями и числителями
- Сравнение дроби с натуральным числом
- Равенство дробей
- Онлайн калькулятор сравнения дробей
Сравнить две дроби — значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
Пример. Дробь больше чем дробь , потому что доли в обеих дробях одинаковы, но в первой дроби их больше, чем во второй.
Если изобразим единицу отрезком и разделим его на 8 долей, то легко увидеть, что дробь больше :
Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.
Пример. Дробь больше чем дробь , потому что число долей в обеих дробях одинаково, но в первой дроби доли крупнее, чем во второй.
Изобразим две единицы в виде кругов, один разделим на 4 доли, второй на 6 долей. Теперь можно увидеть, что дробь больше :
Сравнение дробей с разными знаменателями и числителями
Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.
Пример. Сравните дроби: и .
Решение: приводим данные дроби к общему знаменателю:
Теперь сравниваем их по правилу сравнения дробей, у которых одинаковые знаменатели. Так как , значит .
Приведём ещё один способ сравнения дробей с разными знаменателями и числителями. Рассмотрим сначала числовой пример.
Пример. Сравним дроби и .
Решение: приводим данные дроби к общему знаменателю:
Решая данный пример можно заметить, что, после приведения дробей к общему знаменателю, задача сравнения свелась фактически к сравнению произведений
2 · 7 и 4 · 3.
Так как 2 · 7 = 14, а 4 · 3 = 12, то
2 · 7 > 4 · 3.
Значит, .
Теперь решим эту же задачу в общем виде, используя буквенную запись.
Пример. Пусть даны дроби и , где a и c — нуль или натуральные числа, b и d — натуральные числа. Приведём дроби к общему знаменателю:
Следовательно:
- если a · d > c · b, то
- если a · d < c · b, то
- если a · d = c · b, то
Таким образом мы получили следующее правило сравнения обыкновенных дробей:
Чтобы сравнить две обыкновенные дроби, можно числитель одной дроби умножить на знаменатель другой и полученные произведения сравнить.
Это правило называется перекрёстным правилом сравнения дробей.
Сравнение дроби с натуральным числом
Любая правильная дробь меньше любого натурального числа.
Пример.
Сравнение неправильной дроби с натуральным числом сводится к сравнению двух дробей.
Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби со знаменателем 1, затем их можно сравнить одним из двух способов: используя перекрёстное правило, либо привести дроби к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.
Пример. Сравните дробь с числом 5.
Решение: представим число 5 в виде дроби со знаменателем 1:
Приводим дроби к общему знаменателю:
Сравниваем числители, так как 11 < 15, то , значит, .
Равенство дробей
Две обыкновенные дроби считаются равными, если равны их числители и знаменатели или если они выражают одну и ту же часть единицы.
Пример.
Онлайн калькулятор сравнения дробей
Данный калькулятор поможет вам сравнить обыкновенные дроби. Просто введите две дроби и нажмите кнопку
Просто введите две дроби и нажмите кнопку Сравнить
.
Линейные диофантовы уравнения онлайн
Линейным диофантовым уравнением с двумя неизвестными называется уравнение вида:
В основе нашего калькулятора лежит расширенный алгоритм Евклида, записанный в виде цепной дроби. Однако, в некоторых случаях (например, когда коэффициент ) применяются более простые подходы. Также калькулятор не рассматривает случаи, когда хотя бы один из коэффициентов или равен , так как они приводят к обычному линейному уравнению.
Если коэффициент не делится нацело на , то линейное диофантово уравнение с двумя неизвестными не имеет решений. Напротив, если делится нацело на , то указанное уравнение имеет бесконечное множество целых решений.
Для решения линейного диофантового уравнения с двумя неизвестными сначала необходимо найти частное решение и , а затем записать общее решение, используя формулы:
Рассмотрим пример решения линейного диофантового уравнения с двумя неизвестными:
Коэффициенты уравнения:
.
Поскольку делится нацело на , то данное уравнение имеет решения в целых числах.
Далее, найдём какое-нибудь конкретное (частное) решение и исходного уравнения. Для этого, сначала необходимо найти частное решение и вспомогательного уравнения с коэффициентом :
а затем умножить найденное частное решение и вспомогательного уравнения на и получить частное решение и исходного уравнения:
Чтобы найти частное решение вспомогательного уравнения используем цепные дроби. Для этого составим дробь
, числителем которой будет коэффициент
, а знаменателем коэффициент
.
Преобразуем данную дробь в цепную дробь:
В полученной цепной дроби отбросим последнюю дробь :
Полученная дробь является отношением частных решений и выбранных с правильным знаком:
Подставляя четыре значения во вспомогательное уравнение, определяем его частное решение:
Теперь, чтобы найти частное решение и исходного уравнения, умножим найденное частное решение и вспомогательного уравнения на :
Используя формулы для общего решения, запишем конечный ответ:
Наш онлайн калькулятор может решить любое линейное диофантово уравнение с двумя неизвестными с описанием подробного хода решения на русском языке.
В описании подробного решения встречается функция которая означает — наибольший общий делитель чисел и .
Калькулятор диофантовых уравнений
Переменная-1: xyztupqnms
Переменная-2: xyztupqnms
Дано линейное диофантово уравнение:5x6y19Найти:x- ?y- ?Установить калькулятор на свой сайт
Другие полезные разделы:
Разложение на множители онлайнМетод Ньютона онлайн
Оставить свой комментарий:
Сложные дроби и уравнения с рациональными выражениями
Сложные дроби и уравнения с рациональными выражениями
Сложные дроби
Сначала мы начнем со сложной дроби, которая не содержит переменных.
Пример
1
5
1
5
—
12 —
12
2 6
2
6
«=»
Умножить
Числитель и
1 2
1
2
Знаменатель на 12
+ 12 +
12
4
3
4 3
6 —
10
4
«=»
«=»
—
3 +
8
11
Обратите внимание, что сначала мы умножаем на общий наименьший общий знаменатель, а затем упрощенный.
Сложные дроби, включающие выражения
Когда у нас есть сложная дробь с рациональными выражениями в качестве числителя и знаменатель, мы делаем аналогичные шаги, за исключением, конечно, разложения на множители ключевую роль.
Шаг 1 Учитывать все.

Шаг 2 Определить общий наименьший общий знаменатель, используя максимальная мощность каждого фактора.
Шаг 3 Умножьте все термины на ЖК-дисплее.
Шаг 4 Объедините похожие термины.
Шаг 5 Умножить и отменить.
Примечание: Обычно вам не нужно выполнять все шаги.
Пример:
7
7
1 –
1(х + 1) —
(x + 1)
x
+ 1
х + 1
«=»
Умножить
Числитель и
4
4
Знаменатель на (x+1)
+
1
(Икс
+ 1) + 1(х + 1)
х +
1
х +
1
х + 1 —
7
х — 6
«=»
=
4 +
х + 1
х + 5
Перекрестное умножение
Напомним, что если
а c
=
б г
затем
ad = bc
То же верно для функций:
f g
=
ч к
затем
fg = hk
Пример
Решать.
3x — 1 x + 2
=
5x —
2 3x + 4
Раствор
Скрещиваем множим
(3x — 1)(3x + 4) = (5x — 2)(x + 2)
9x 2 + 12x — 3x — 4 = 5x 2 + 10х — 2х — 4
9x 2 + 9x — 4 = 5x 2 + 8x — 4
4x 2 + х = 0
х (4х + 1) = 0
1
x = 0 или x = —
Внимание! Всегда проверяйте работоспособность решения, подключая его к исходному уравнение!
Уравнения с рациональными выражениями
Чтобы решить уравнения, включающие рациональные выражения, мы следуем следующему шаги:
Шаг 1 Умножить, если возможно.

Шаг 2 Умножьте левую и правую части на ЖК-дисплей.
Шаг 3 Объедините похожие термины.
Шаг 4 Перенесите все в левую часть уравнения.
Шаг 5 Решите методом нулевого произведения или элементарной алгеброй.
Шаг 6 Вновь подключитесь к исходному уравнению, чтобы проверить посторонние решения.
Пример
Решить
3 4
48
—
=
Икс —
6 х +
6 x 2 — 36
Решение
Первый фактор.
3
4 48
—
=
Икс —
6 х +
6 (x —
6)(x + 6)
Затем умножьте на LCD (x
— 6)(х+6).
3 4 48
(х — 6)(х + 6) —
(х — 6)(х + 6) =
(х — 6)(х + 6)
Икс —
6 x +
6 (x — 6)(x + 6)
3(х + 6) — 4(х — 6) = 48
3x + 18 — 4x + 24 = 48
-x + 42 = 48
-х = 6
х = -6
Обратите внимание, что -6 нельзя вернуть в исходное уравнение, поскольку будет ноль в знаменателе. Можно сделать вывод, что это уравнение не имеет решение.
Назад на страницу факторинга и рациональных выражений
Назад на страницу Основы алгебры, часть II
Назад к математике Домашняя страница отдела
электронная почта Вопросы и предложения
Дроби с обеих сторон Уравнения
Источник изображения: http://www. blogspot.com
blogspot.com
В этом уроке мы рассмотрим, как решать уравнения с дробями с обеих сторон.
Прежде чем приступить к этому уроку, вам необходимо научиться решать уравнения с буквами и/или скобками с обеих сторон.
Если вам нужно узнать, как делать уравнения с переменными буквами на обеих сторонах, то пройдите наш предыдущий урок по этому вопросу по следующей ссылке:
Решение букв с переменной на обеих сторонах Урок
Метод «Дроби с обеих сторон» в основном то же самое, что и решение уравнений с буквой с обеих сторон, за исключением того, что нам нужно сделать дополнительный шаг перекрестного умножения в начале.
Перед прохождением нашего урока «Дроби с обеих сторон»:
Мы также рекомендуем вам проверить, что вы поняли материал из следующих предыдущих уроков:
Уравнения по перекрестному умножению Уравнения
Расширяющиеся кронштейны с использованием урока правила распределения
Фракции Обе стороны уравнения
. Вот типичное уравнение «Фракции обе стороны».
Вот типичное уравнение «Фракции обе стороны».
Image Copyright 2013 by Passy’s World of Mathematics
Эти типы уравнений выполняются так же, как уравнения «Переменная буква с обеих сторон», но у нас есть один дополнительный начальный шаг в начале.
Дроби с обеих сторон Этапы разработки
Image Copyright 2013 by Passy’s World of Mathematics
Перекрестное умножение такое же, как и для отношений.
Напр. Уравнение отношения 3/4 = 6/8, умноженное на крест, дает
8×3 = 6×4, что является истинным уравнением,
, и поэтому метод перекрестного умножения является законным.
Дроби с обеих сторон – Пример 1
Вот как мы выполняем шаг перекрестного умножения для типичного уравнения «Дроби с обеих сторон»:
Image Copyright 2013 by Passy’s World of Mathematics
Обратите внимание, что нам нужно использовать скобки, чтобы убедиться, что ВСЕ термины в верхней строке «числитель» умножаются.
После того, как мы завершили перекрестное умножение, нам осталось решить обычное уравнение «Переменная буква с обеих сторон».
Решаем это следующим образом:
Image Copyright 2013 by Passy’s World of Mathematics
Если вы не знаете, как найти переменную букву с обеих сторон, то посмотрите наш предыдущий урок на эту тему по следующей ссылке:
Решение буквы переменной с обеих сторон Урок
Дроби с обеих сторон – пример второй
В этом примере дробь есть только на одной стороне.
Мы проделываем небольшой «трюк», который заключается в том, чтобы представить не дробную часть как дробь, которая равна / 1
Затем мы можем выполнить шаг перекрестного умножения.
Вот пример, показывающий шаг перекрестного умножения
Изображение Copyright 2013 by Passy’s World of Mathematics
Вот оставшиеся шаги, необходимые для получения окончательного ответа:
Изображение Copyright 2013 by Passy’s World of Mathematics
Видео о дробях Уравнения обеих сторон видео показывают, как использовать Пропорции Метод перекрестного умножения для решения уравнений.
А вот и второе видео, которое нужно посмотреть.
Связанные элементы
Решение уравнений с переменной буквой на обеих сторонах
Раскрытие скобок с использованием распределительного правила
Как преобразовать текстовые задачи в уравнения
Решение одношаговых уравнений сложения
Одношаговое решение уравнений вычитания
Решение одношаговых уравнений — все типы
Двухшаговые уравнения с использованием блок-схем и обратное отслеживание
Двухшаговые уравнения с использованием обратных операций
Трехшаговые уравнения с использованием блок-схем и обратного отслеживания
Уравнения балансира
Решение уравнений с использованием методов луковой шелухи
Эквивалентные уравнения
Уравнения дробей
Решение задач в виде слов
Транспонирование и преобразование уравнений в формулах
Задача eBay, решенная с помощью уравнений алгебры
Microsoft Mathematics Equations Solver
Реальные математические формулы и уравнения
Игры в уравнения
Подписаться
Если вам понравилось этот урок, почему бы не получить бесплатную подписку на наш сайт.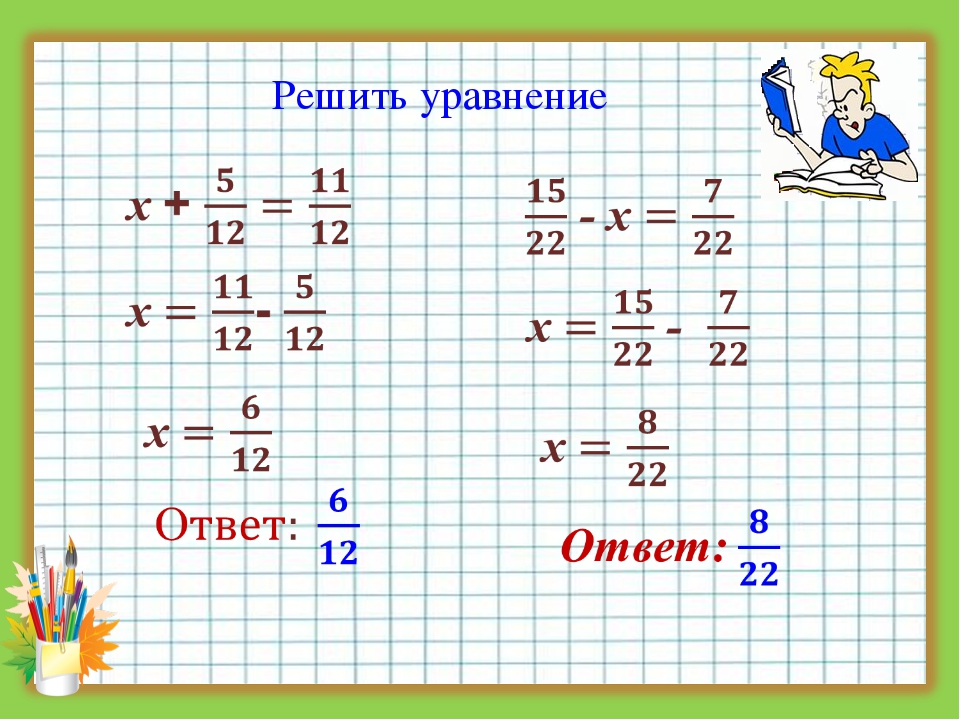
После этого вы сможете получать уведомления о новых страницах прямо на свой адрес электронной почты.
Перейдите в область подписки на правой боковой панели, введите свой адрес электронной почты и нажмите кнопку «Подписаться».
Чтобы точно узнать, как работает бесплатная подписка, нажмите на следующую ссылку:
Как работает бесплатная подписка
Если вы хотите предложить идею для статьи или стать приглашенным автором на нашем веб-сайте, напишите нам по адресу адрес горячей почты, показанный в правой части этой страницы.
Если вы являетесь подписчиком Passy’s World of Mathematics и хотели бы получить бесплатную версию этого урока в PowerPoint, которая на 100 % бесплатна для вас как подписчика, напишите нам по следующему адресу:
Пожалуйста, укажите в своем электронном письме, что вы хотите получить бесплатную копию подписки «Дроби в уравнениях обеих сторон» Powerpoint.
Не стесняйтесь размещать ссылки на любые наши уроки, делиться ими в социальных сетях или использовать их в системах управления обучением в школах.
Нравится нам на Facebook
На нашей странице Facebook есть много дополнительных элементов, которые не размещены на этом сайте.
Сюда входят предметы, представляющие математический интерес, забавные математические картинки и мультфильмы, а также случайные зарисовки из личной жизни «Пасси».
Проверьте это по следующей ссылке:
https://www.facebook.com/PassysWorldOfMathematics
Пока вы там, ставьте НРАВИТСЯ странице, чтобы вы могли получать наши обновления FB в своей ленте новостей Facebook.
Помогите Passy’s World расти
Каждый день Passy’s World предоставляет сотням людей бесплатные уроки математики.
Помогите нам поддерживать этот бесплатный сервис и поддерживать его рост.
Пожертвуйте любую сумму от $2 и выше через PayPal, щелкнув изображение PayPal ниже. Спасибо!
PayPal принимает кредитные карты, но вам нужно будет указать адрес электронной почты и пароль, чтобы PayPal мог создать для вас учетную запись PayPal для обработки транзакции.


