Как различать перестановки размещения и сочетания
Статьи › Карточка › Сколько различных буквосочетаний можно получить перестановкой карточек со следующими буквами колокол
Теория:
- Размещения — это упорядоченные наборы.
- Комбинации, при составлении которых важно знать только то, какие элементы выбраны, но их порядок не имеет значения, называются сочетаниями. В сочетаниях все элементы равноправны. Например, два дежурных, два куска хлеба.
- Сочетания не являются упорядоченными наборами.
- Что называется перестановки размещения сочетания
- Как определить число комбинаций
- Как считать перестановки
- Как понять когда порядок важен
- Как считать размещения
- Что называют размещением
- В чем разница между размещением и сочетанием
- Сколько комбинаций из цифр 1 2 3 4
- Сколько вариантов комбинаций из 24 цифр
- Чем перестановка отличается от подстановки
- Как находится размещение с повторением
- Как понять четная перестановка или нет
- Что называется сочетаниями
- Сколько перестановок
- Что такое сочетание в теории вероятности
- Какая из формул определяет число перестановок
- Как понять Комбинаторику
- Какие выборки называются размещениями
- Сколько комбинаций из 4 цифр может быть
- Сколько комбинаций из 5 цифр от 1 до 5
- Сколько комбинаций из 6 цифр может быть
- Какие бывают перестановки
- Что такое число размещений
- Что означает перестановка в тексте
- Что такое сочетание размещение
- Что такое перестановки из n элементов
- Что такое сочетание с повторениями
Что называется перестановки размещения сочетания
Классическими понятиями комбинаторики являются перестановки, размещения и сочетания.
Перестановкой называется какой-либо способ упорядочения данного множества.
Как определить число комбинаций
Количество сочетаний обозначается как C n m (читается: сочетания из \(n\) по \(m\)). Сочетания вычисляются по формуле C n m = n! M! (n − m)!.
Как считать перестановки
Перестановками называются такие выборки элементов, которые отличаются только порядком расположения элементов, но не самими элементами. Если перестановки производятся на множестве из n элементов, их число определяется по формуле Pn = n·(n−1)·(n−2) 3·2·1 = n!
Как понять когда порядок важен
Порядок элементов важен, т. к., если поменять местами людей, обязанности их изменятся.
Как считать размещения
Формула числа размещений
Akn=Ckn⋅k! =Ckn⋅Pk.
Что называют размещением
Ряд, заполненный объектами данного множества, называется размещением, т. е. мы разместили объекты на данных местах.
В чем разница между размещением и сочетанием
Размещения — это упорядоченные наборы.
Комбинации, при составлении которых важно знать только то, какие элементы выбраны, но их порядок не имеет значения, называются сочетаниями. В сочетаниях все элементы равноправны. Например, два дежурных, два куска хлеба.
Сколько комбинаций из цифр 1 2 3 4
Следовательно комбинаций будет: 4 * 3 * 2 * 1 = 4! = 24.
Сколько вариантов комбинаций из 24 цифр
Вы немного ошиблись, комбинаций не 12, а из 24 чисел по 12 есть почти 3 млн. комбинаций, точнее 2 704 156 комбинаций.
Чем перестановка отличается от подстановки
Более существенное отличие состоит в том, что подстановка — это непосредственно функция, а перестановка — результат применения этой функции к элементам последовательности.)
Как находится размещение с повторением
Упорядоченные выборки \(k\) элементов с повторениями, которые составлены из основного множества \(n\) элементов, называются размещениями с повторениями из \(n\) элементов по \(k\) элементов. Их количество обозначается как A ¯ n k и находится по формуле: A ¯ n k = n k.
Как понять четная перестановка или нет
Перестановка называется четной, если она содержит четное число инверсий элементов. Нечетная перестановка содержит нечетное число инверсий.
Что называется сочетаниями
Каждое множество, содержащее m элементов из числа n заданных, называется сочетанием из n элементов по m. Подчеркнем, что сочетание определено как множество некоторых элементов без рассмотрения порядка, в котором они расположены. Число всех сочетаний из n элементов по m обозначается.
Сколько перестановок
Количество перестановок обозначается как P n, где \(n\) — количество элементов множества. Перестановки вычисляются по формуле P n = n!
Что такое сочетание в теории вероятности
Определение. Неупорядоченные подмножества (комбинации), т. е. такие, порядок следования элементов в которых не играет роли и которые отличаются друг от друга хотя бы одним элементом, называются сочетаниями.
Какая из формул определяет число перестановок
Общая формула, которая позволяет найти число перестановок из n элементов, имеет вид (она же — формула для факториала числа n): Pn=n! =1⋅2⋅3⋅ ⋅(n−1)⋅n.
5 = 100,000. Логически подумайте — каждая из комбинаций от 000,001 до 100,000 повышают общее число комбинаций на одну, итого кол-во комбинаций равно собственно числу.
Сколько комбинаций из 6 цифр может быть
Допустим, есть шесть цифр. То есть N=6, и число возможных комбинации N!, 6!= 720 вариантов.
Какие бывают перестановки
Перестановка называется четной, если число инверсий в ней четно, и нечетной — если инверсий в ней нечётное количество.
Что такое число размещений
Числом размещений из по (обозначается) называется количество способов расположить некоторые из различных объектов на пронумерованных местах, при условии что каждое место занято в точности одним объектом.
Что означает перестановка в тексте
Перестановка — это изменение порядка следования языковых элементов в тексте перевода по сравнению с текстом оригинала. Перестановке подвергаются языковые единицы абсолютно на разных уровнях. Это могут быть слова, словосочетания, части сложного предложения, самостоятельные предложения в строе текста [2, 3].
Что такое сочетание размещение
Размещения — это упорядоченные наборы. Комбинации, при составлении которых важно знать только то, какие элементы выбраны, но их порядок не имеет значения, называются сочетаниями. В сочетаниях все элементы равноправны. Например, два дежурных, два куска хлеба.
Что такое перестановки из n элементов
Напомним, что перестановкой из N элементов (еще говорят порядка N) называется упорядоченный набор из N различных чисел от 1 до N. Количество различных перестановок порядка N равно PN = N! Пусть у нас есть упорядоченное множество из N элементов. Перестановка задает преобразование этого множества.
Что такое сочетание с повторениями
Определение: Сочетания с повторениями (англ. combinations with repetitions) — те же сочетания, только теперь даны типов элементов, из которых нужно выбрать элементов, причем элементов каждого типа неограниченное количество, и элементы одного типа должны стоять подряд друг за другом.
алгебра размещение
Вы искали алгебра размещение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь.
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как алгебра размещение,алгебра сочетание,алгебра сочетания,задачи на перестановку размещение и сочетание,количество перестановок из n по m,количество перестановок из n по n,количество размещений,комбинаторика перестановки размещения сочетания,комбинаторика размещение,комбинаторика размещение формула,комбинаторика размещения,комбинаторика размещения перестановки сочетания,комбинаторика размещения сочетания перестановки,комбинаторика сочетания перестановки размещения,комбинаторика сочетания размещения перестановки,комбинаторика формула размещение,математика перестановки,математика размещение,основные формулы комбинаторики перестановки сочетания размещения,основные формулы комбинаторики размещения сочетания перестановки,перестановка комбинаторика,перестановка размещение сочетание,перестановка размещение сочетание формулы,перестановка сочетание размещение,перестановка сочетание размещение формулы,перестановки и размещения,перестановки комбинаторика,перестановки размещения сочетания,перестановки размещения сочетания формулы,перестановки сочетания размещения,размещение алгебра,размещение комбинаторика,размещение комбинаторика формула,размещение математика,размещение перестановка сочетание,размещение перестановка сочетание формулы,размещение сочетание перестановка,размещение сочетание перестановка формулы,размещение теория вероятности,размещение формула,размещение формула комбинаторика,размещений,размещения и перестановки,размещения и сочетания,размещения комбинаторика,размещения перестановки и сочетания,размещения перестановки сочетания,размещения сочетания и перестановки,размещения формулы,сочетание алгебра,сочетание перестановка размещение,сочетание перестановка размещение формулы,сочетание размещение перестановка,сочетание размещение перестановка формулы,сочетания алгебра,сочетания и размещения формулы,сочетания перестановки размещения,сочетания примеры,сочетания размещения перестановки,сочетания размещения перестановки формулы,теория вероятности размещение,формула размещение,формула размещений,формула размещения,формула размещения в комбинаторике,формулы перестановка размещение сочетание,формулы перестановки размещения сочетания,формулы перестановки сочетания размещения,формулы размещения,формулы размещения перестановки сочетания,формулы размещения сочетания перестановки,формулы сочетания размещения перестановки,число размещений из n по k формула,элементы комбинаторики перестановки размещения сочетания,элементы комбинаторики перестановки сочетания размещения,элементы комбинаторики размещения перестановки сочетания,элементы комбинаторики сочетания размещения перестановки.
Решить задачу алгебра размещение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Перестановки и комбинации – определение, различие и формула
Вы когда-нибудь замечали, что используемый вами мобильный PIN-код может быть нарисован в нескольких вариантах?
Ну, это один из примеров перестановок и комбинаций.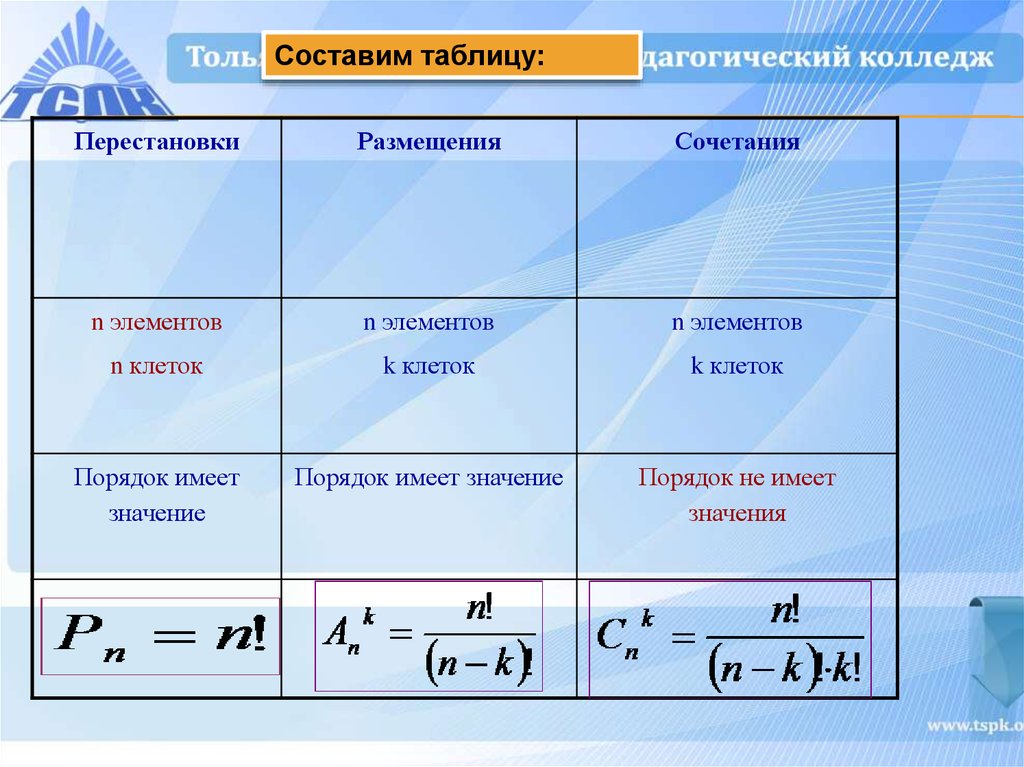
Говоря простым языком, комбинация — это когда порядок не важен, а перестановка — когда важен порядок. С помощью комбинаций перестановок можно выразить группу данных в виде наборов и подмножеств.
Это относится к различным способам организации определенной группы данных. Обе эти концепции жизненно важны не только на ваших экзаменах на доске, но и на всех конкурсных экзаменах, таких как CAT, JEE и т. д. Таким образом, вам необходимо понимать обе концепции, а также разницу между перестановкой и комбинацией.
Определение перестановки и комбинации
Чтобы начать изучать эту главу, вам сначала нужно понять определение перестановки и комбинации и связь между перестановкой и комбинацией.
Перестановка
Перестановка — это организация набора данных в определенном порядке или последовательности. Более того, если данные уже расположены по порядку, вы можете изменить их порядок, используя формулу перестановки.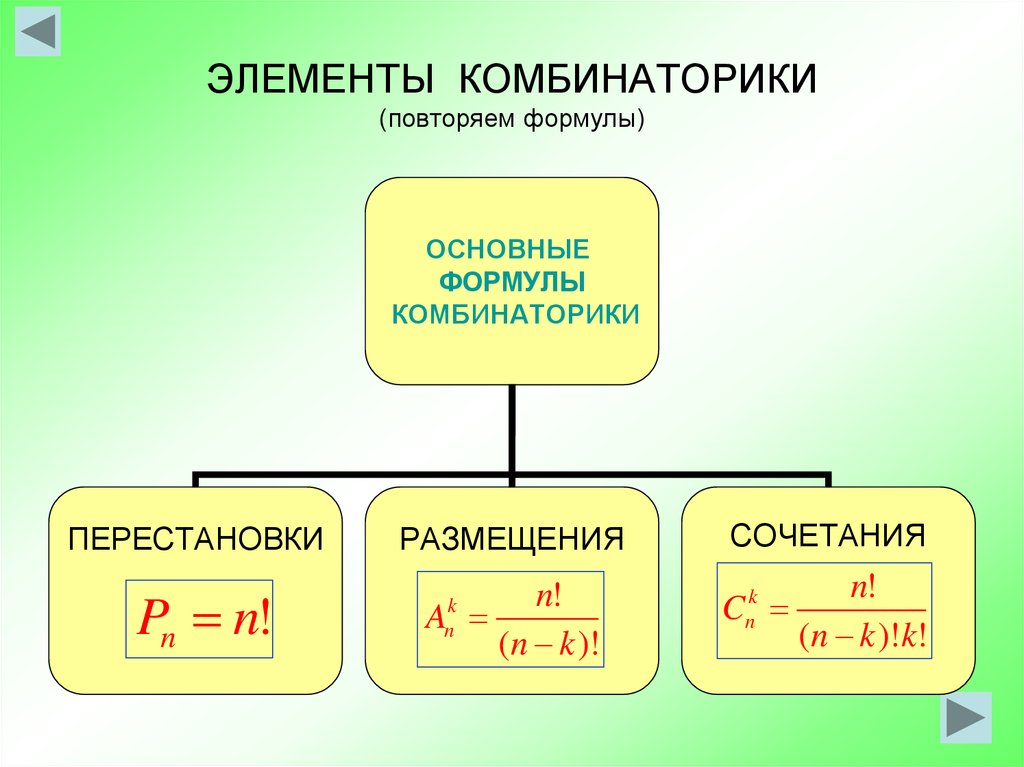
В большинстве областей математики происходит перестановка.
Комбинация
В отличие от перестановки, комбинация — это когда вы выбираете данные из группы без какого-либо порядка или последовательности. Если группа данных относительно меньше, вы можете рассчитать количество возможных комбинаций.
Разработаем эти определения с примерами перестановок и комбинаций. Например, у вас есть группа из четырех букв P, Q, R и S. Теперь сколькими способами вы можете выбрать три буквы из этой группы? Каждое возможное расположение может быть комбинацией.
Однако способы группировки P, Q, R и S являются перестановками. Итак, PQRS, PRSQ, PSQR, PRQS и т. д. являются перестановками. Если значение перестановки и комбинации неясно, попробуйте пример из реальной жизни.
Согласно примерам комбинаций перестановок из реальной жизни, вы можете сказать, что выбор победителей, таких как 1-й, 2-й и 3-й, является перестановкой.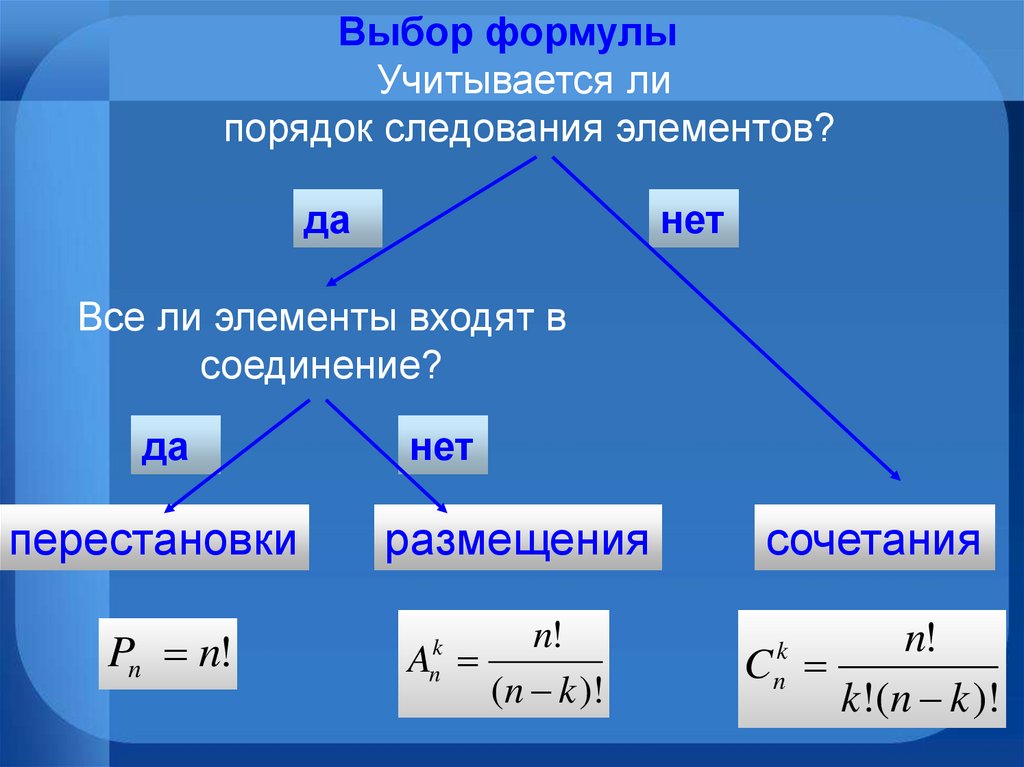
А выбор трех победителей — это комбинация.
Разница между перестановкой и комбинацией
До сих пор вы знали ответ на вопрос «определить комбинацию и перестановку», и это может помочь вам отличить перестановку от комбинации. Согласно их определениям и примерам, основное различие между перестановкой и комбинацией заключается в том, что комбинации представляют собой разные способы выбора без учета последовательности. А перестановки — это различные способы расположения по порядку.
Это ключевое различие комбинаций перестановок, которое вы должны понимать, чтобы закрепить концепцию.
Базовая формула перестановки и комбинации
В математике есть множество способностей к формуле перестановки и комбинации. Однако большинство этих формул комбинаций перестановок основаны на двух основных формулах. Вот эти базовые формулы перестановки и комбинации –
Формула перестановки
Если общее количество данных равно «n» и выбор из «r» вещей, то перестановка будет (без замены и относительно порядка)-
nPr = (n!) / (n-r)!
Формула комбинирования
Из группы «n» данных выбор «r» вещей без учета порядка и замены-
nCr = (nr) = nPr / r! = п! / {р! (n-r)!}
Это ключевые формулы для определения вероятностных перестановок и комбинаций.
Более того, соотношение между ними nCr = nPr / r!.
Теперь давайте решим несколько вопросов о перестановках и комбинациях, чтобы рассеять ваши сомнения.
Проблемы с перестановкой и комбинацией Word
Решая следующие задачи с перестановкой и комбинацией, вы можете понять, как получить эти формулы для решений NCERT с перестановкой и комбинацией.
Как рассчитать количество комбинаций и перестановок, если n = 14 и r = 3
Класс 11 перестановок и комбинаций решений:
Согласно вопросу, n = 14
r = 3
По вывод формулы перестановки-
nPr = (n!) / (n-r)! = 14! / (14 — 3)! = 14! / 11! = (14 х 13 х 12 х 11!) / 11! = 2184
Теперь из формулы комбинации-
nCr = (nr) = nPr/r! = п! / {р! (н-р)!} = 14! / 3! (14 — 3)! = 14! / 3! (11!) = 14 х 13 х 12 х 11! / 2! Х 11!
1092
Сколько четырехзначных чисел можно составить из цифр 1, 2, 3 и 4 –
- 9 0070 С повторением?
Без повторения?
NCERT Класс 11 Перестановка и Комбинация Решение:
Поскольку будет 4-значное число, пусть цифра будет ABCD.
Здесь D — единица, C — 10-е место, B — 100-е место, а A — тысячное место.
Теперь, с повторением, на месте D возможное количество цифр равно 4. Кроме того, на
месте A, B и C вероятное количество цифр равно 5.
Таким образом, общее количество четырехзначных чисел равно – 4 х 4 х 4 х 4 = 256
Возможное количество цифр на месте D равно 4; следовательно, это единичное место. Теперь
Без повторений одна цифра занята в D. Таким образом, для места C возможная цифра будет 3, и будет 2 возможных цифры для B и 1 для A.
Следовательно, общее количество возможных 4- числа без повторения – 4 X 3 X 2 X 1 = 24.
Из приведенных выше вопросов о перестановке и комбинации с решением вы должны были понять структуру вопросов, которые могут появиться на ваших экзаменах.
Тем не менее, если вам нужно еще несколько решений NCERT для перестановок и комбинаций, вы можете зайти на наш веб-сайт Vedantu и проверить все учебные материалы по перестановкам и комбинациям ответов. Они также сопровождаются анкетами и упражнениями. Кроме того, вы также можете изучить перестановку и комбинацию онлайн на наших онлайн-сессиях.
Получите наше приложение Vedantu сейчас для обновленных решений NCERT, класс 11 перестановок и комбинаций.
Различные концепции, в которых используются перестановки и комбинации, помогут нам различать их. Перестановки и комбинации помогают нам получить группу данных в виде наборов и подмножеств, а также могут быть определены как различные способы организации определенных групп данных.
Перестановка используется, когда объекты и вещи относятся к разным видам. Меньшие группы, которые могут быть образованы из элементов большей группы, — это Комбинация.
Когда нам нужно упорядочить последовательность вещей, нам нужны перестановки, тогда как для того, чтобы найти, сколько возможных групп можно сформировать, нам нужны комбинации.
Для списка данных, где порядок данных важен, у нас есть перестановка и группа данных, где нам не нужен какой-либо порядок, это комбинация.
Формулы перестановки и комбинации помогают нам понять расчеты разницы между этими двумя. Две важные формулы:
Перестановка — это выбор вещей ‘r’ из набора вещей n без какой-либо замены, а также там, где важен порядок:
nPr = (n!) / (n-r)
Комбинация есть выбор вещей ‘r’ из множества вещей ‘n’ без замены, но где порядок не требуется и не имеет значения:
nCr = (nr) = nPr / r! = п! / {р! (н-р)!}
Возьмем пример из NCERT. Решение:
В. Сколько четырехзначных чисел можно составить из 1, 2, 3 и 4 –
С повторением?
Без повторения?
NCERT Класс 11 Перестановка и Комбинация Решение:
Поскольку будет 4-значное число, пусть цифра будет ABCD.
Здесь D — единица, C — 10-е место, B — 100-е место, а A — тысячное место.
Теперь, с повторением, на месте D возможные номера цифры равны 4. Кроме того, на месте A, B и C вероятное количество цифр равно 5. Таким образом, всего возможно 4- числа цифр – 4 X 4 X 4 X 4 = 256.
Возможное количество цифр на месте D равно 4; следовательно, это единичное место. Теперь, без повторений, одна цифра занята в D. Итак, для места C возможная цифра будет 3, и будет 2 возможных цифры для B и 1 для A. Следовательно, общее количество возможных 4-значных чисел без повторений равно – 4 х 3 х 2 х 1 = 24,
Из приведенных выше двух примеров из вопросов и решений NCERT мы можем получить более четкое представление о перестановке и комбинации, а также получить небольшое представление о структуре вопросов, которые мы можем ожидать во время экзаменов.
Основные понятия перестановки и комбинирования — Hitbullseye
В этой статье мы обсудим основные понятия перестановки и комбинирования и формулы, необходимые для решения задач на них. Эта тема затрагивается на всех конкурсных экзаменах, поэтому вы не можете позволить себе рисковать и избегать ее. Прочитав эту статью, вы познакомитесь с основными понятиями перестановки и комбинации.
Предлагаемое действие
БЕСПЛАТНЫЕ живые мастер-классы от нашего звездного факультета с более чем 20-летним опытом. Зарегистрируйтесь сейчас
- Перестановка f формула: Перестановка определяется как расположение r вещей, которые можно сделать из всего n вещей. Это обозначается n P r , что равно n!/(n-r)!
- Комбинированная формула
- Комбинация определяется как выбор r вещей, которые можно сделать из общего количества n вещей.
Это обозначается n C r , что равно n!/r!(n-r)! - В соответствии с основным принципом счета, если одно действие может быть выполнено 90 226 m 90 227 способами, а другое действие может быть выполнено 90 226 n 90 227 способами, то любое из двух действий может быть выполнено за 90 226 m + 90 227 90 226 n 90 227 способами, и оба они могут быть выполнены в 90 226 м × 90 227 90 226 n способов.
- Комбинация определяется как выбор r вещей, которые можно сделать из общего количества n вещей.
Это обозначается n C r , что равно n!/r!(n-r)!
Пример 1: Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6 (повторение цифр не допускается)?
Решение: Тысячное число можно заполнить 6 способами. Место сотни можно заполнить 5 способами. Место десятки может быть заполнено 4 способами. Место юнита можно заполнить 3 способами. Итак, используя основной принцип счета, мы получаем ответ как 6 × 5 × 4 × 3 = 360. Или, используя формулу перестановок, нам нужно расположить 4 цифры из 6 цифр.
Это можно сделать в 6 P 4 = 360 способов.
Пример 2: У человека есть 6 друзей, которых нужно пригласить на ужин с помощью пригласительных билетов, и у него есть 3 слуги. Сколькими способами он может продлить пригласительный билет?
Решение: Мы видим, что у друга 1 st есть 3 варианта получения карты, т.е. либо от слуги 1 st , либо от 2 st или 3 rd . Точно так же у 2-го друга также есть 3 варианта получения карты, т.е. либо от 1 ст слуга или 2 й или 3 й . Таким образом, можно сказать, что у каждого из 6 друзей есть 3 варианта получения карты. Следовательно, ответ будет 3 × 3 × 3 × 3 × 3 × 3 = 3 6 = 729 способов.
Пример 3: В экзамене 10 вопросов. Сколькими способами человек может попытаться ответить хотя бы на один вопрос?
Решение: Человек может попытаться ответить на 1 вопрос или 2 вопроса или .
….до всех 10 вопросов. Ответить на один вопрос из десяти можно за 9 0209 10 C 1 = 10 контактов. Точно так же на два вопроса из десяти можно ответить 10 C 2 = 45 способами. Следуя той же логике, можно попытаться ответить на все десять вопросов 10 C 10 = 1 способом. Следовательно, общее количество способов = 10 + 45 + 120 +…..10 + 1 = 1023 способа (используя формулу Комбинации).
Или можно применить некоторую логику: У каждого вопроса есть 2 варианта, либо попытка, либо нет. Продолжая эту логику, поскольку есть 10 вопросов, и каждый вопрос имеет 2 варианта, поэтому общее количество случаев = 2 10 = 1024. Но этот подсчет включает один случай, в котором не было предпринято ни одной попытки задать вопрос. Это нарушение предоставленной информации. Так что этот случай нужно вычесть. Следовательно, общее количество случаев будет 1024 — 1 = 1023.
Рекомендуемое действие:
Начните подготовку с БЕСПЛАТНОГО доступа к более чем 25 макетам, 75+ видео и 100+ тестам по главам.