Вычитание чисел — Служба поддержки Майкрософт
Excel
Формулы и функции
Формулы
Формулы
Вычитание чисел
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Предположим, вы хотите узнать, сколько складских запасов невыгодно (вычитайте прибыльные позиции из общего запаса). Или, возможно, вам нужно узнать, сколько сотрудников приближаются к возрасту выхода на пенсию (вычесть из общего числа сотрудников количество сотрудников в возрасте до 55 лет).
Что необходимо сделать
Существует несколько способов вычитания чисел, в том числе:
- org/ListItem»>
-
Вычитание чисел в диапазоне
Вычитание чисел в ячейке
Вычитание чисел в ячейке
Для простого вычитания используйте арифметические операторы — (минус).
Например, если ввести в ячейку формулу =10-5, в результате в ячейке отобразится 5.
Вычитание чисел в диапазоне
При добавлении отрицательного числа все равно, что вычитать одно число из другого. С помощью функции СУММ
можно складывать отрицательные числа в диапазоне.Примечание: В Excel не существует функции ВЫЧЕСТЬ. Используйте функцию СУММ, преобразуя все числа, которые необходимо вычесть, в их отрицательные значения. Например, функция СУММ(100,-32,15,-6) возвращает результат 77.
Используйте функцию СУММ, преобразуя все числа, которые необходимо вычесть, в их отрицательные значения. Например, функция СУММ(100,-32,15,-6) возвращает результат 77.
Пример
Чтобы вычесть числа различными способами, выполните указанные здесь действия.
-
Выберите все строки в приведенной ниже таблице, а затем нажмите клавиши CTRL+C.
Данные
15000
9000
-8000
Формула =A2-A3
Вычитает 9000 из 15000 (что равно 6000).

-СУММ(A2:A4)
Добавляет все число в списке, включая отрицательные (чистый результат — 16 000).
Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.
-
Чтобы переключиться между просмотром результатов и просмотром формул, нажмите клавиши CTRL+’ (ударение) на клавиатуре. Можно также нажать кнопку Показать формулы (на вкладке Формулы).
Использование функции СУММ
Функция СУММ суммирует все числа, которые вы указали в качестве аргументов. Каждый аргумент может быть диапазон, ссылка на ячейку, массив, константа или формулалибо результатом выполнения другой функции. Например, СУММ(A1:A5) суммирует все числа в диапазоне ячеек A1–A5. Другим примером является сумм(A1, A3, A5), которая суммирует числа, содержащиеся в ячейках A1, A3 и A5 (аргументы — A1, A3 и A5).
Каждый аргумент может быть диапазон, ссылка на ячейку, массив, константа или формулалибо результатом выполнения другой функции. Например, СУММ(A1:A5) суммирует все числа в диапазоне ячеек A1–A5. Другим примером является сумм(A1, A3, A5), которая суммирует числа, содержащиеся в ячейках A1, A3 и A5 (аргументы — A1, A3 и A5).
Сложение, вычитание, умножение и деление в Excel
Редактор таблиц Microsoft Excel имеет очень широкий набор возможностей для решения задач самой разной сложности в различных сферах деятельности. Именно благодаря этому Эксель стал таким популярным среди пользователей по всему миру. Одним из базовых навыков работы с программой является проведение простейших вычислений и математических операций. В этой статье подробно разберём, как выполнять сложение, вычитание, умножение и деление в Excel. Давайте же начнём! Поехали!
Математические операции выполняются без использования калькулятора
Все расчёты в Экселе основаны на построении простых формул, с помощью которых программа и будет производить вычисления. Для начала необходимо создать таблицу со значениями. Обратите внимание на то, что каждая ячейка таблицы имеет свой адрес, который определяется буквой и цифрой. Каждая буква соответствует столбцу, а каждая цифра — строке.
Для начала необходимо создать таблицу со значениями. Обратите внимание на то, что каждая ячейка таблицы имеет свой адрес, который определяется буквой и цифрой. Каждая буква соответствует столбцу, а каждая цифра — строке.
Начнём с самых простых операций — сложения и вычитания. Для сложения чисел можно использовать, так называемую функцию «Автосумма». Ей удобно пользоваться в случаях, когда необходимо посчитать сумму чисел, которые стоят подряд в одной строке, столбце либо в выделенной вами области. Чтобы воспользоваться этим инструментом, перейдите во вкладку «Формулы». Там вы обнаружите кнопку «Автосумма». Выделив участок таблицы со значениями, которые нужно сложить, кликните по кнопке «Автосумма». После этого появится отдельная ячейка, содержащая результат вычисления. Это был первый подход.
Второй подход заключается в том, что формула для расчёта вводится вручную. Допустим, перед вами стоит задача вычислить сумму чисел, разбросанных по таблице. Для этого сделайте активной (кликните по ней левой кнопкой мыши) ячейку, в которую желаете поместить результат вычисления. Затем поставьте знак «=» и по очереди вводите адрес каждой ячейки, содержимое которой нужно просуммировать, не забывая ставить знак «+» между ними. К примеру, у вас должно получиться: «=A1+B7+C2+B3+E5». После того как будет введён адрес последней ячейки, нажмите на клавиатуре «Enter» и вы получите сумму всех отмеченных чисел. Необязательно вводить каждый адрес вручную. Достаточно кликнуть по определённой ячейке и в поле для формул сразу отобразится её адрес, ставьте после него «+» и переходите к следующей.
Затем поставьте знак «=» и по очереди вводите адрес каждой ячейки, содержимое которой нужно просуммировать, не забывая ставить знак «+» между ними. К примеру, у вас должно получиться: «=A1+B7+C2+B3+E5». После того как будет введён адрес последней ячейки, нажмите на клавиатуре «Enter» и вы получите сумму всех отмеченных чисел. Необязательно вводить каждый адрес вручную. Достаточно кликнуть по определённой ячейке и в поле для формул сразу отобразится её адрес, ставьте после него «+» и переходите к следующей.
Существует ещё один подход — использование функции «Специальная вставка». Этот способ удобен тем, что позволяет суммировать данные из нескольких отдельных таблиц, при условии, что все их графы одинаковые. Для начала создайте сводную таблицу, в которую вы будете вставлять скопированные данные. Выделите числа одной таблицы и вставьте их в сводную, далее поступите так же со значениями второй таблицы, только в этот раз кликните по ячейке правой кнопкой мыши и выберите пункт «Специальная вставка». В открывшемся окне в разделе «Вставить» отметьте «Значения», а в разделе «Операция» выберите сложить. В результате все данные просуммируются.
В открывшемся окне в разделе «Вставить» отметьте «Значения», а в разделе «Операция» выберите сложить. В результате все данные просуммируются.
Вычитание в Excel выполняется таким же способом, как и сложение. Вам понадобится ввести формулу, указав необходимые ячейки, только вместо знака «+» между адресами ставится «–».
Чтобы умножить числа в Экселе, напишите формулу, отмечая нужные данные и ставя между ними знак «*». Формула будет иметь следующий вид: «=A3*A7*B2».
Деление производится аналогичным образом, только используется знак «/». Также вы можете выполнять несколько арифметический операций сразу. Формулы строятся по математическим правилам. Например: «=(B2-B4)*E8/(A1+D1)*D4». Построенная вами формула может быть любой сложности, главное, не забывать основные математические правила, чтобы расчёт был выполнен верно.
Владея навыками простых арифметических вычислений в программе Microsoft Excel, вы уже сможете упростить себе процесс решения некоторых задач и сэкономить время. Эксель позволяет решать сложные уравнения, выполнять инженерный и статистический анализ. Постепенно овладевая базовыми функциями и инструментами программы, вы научитесь выполнять всё больше операций в редакторе Excel. Пишите в комментариях помогла ли вам статья разобраться с возникшими вопросами и делитесь своим опытом с другими пользователями.
Эксель позволяет решать сложные уравнения, выполнять инженерный и статистический анализ. Постепенно овладевая базовыми функциями и инструментами программы, вы научитесь выполнять всё больше операций в редакторе Excel. Пишите в комментариях помогла ли вам статья разобраться с возникшими вопросами и делитесь своим опытом с другими пользователями.
7.2: Идентичности сложения и вычитания
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 13871
- Дэвид Липпман и Мелони Расмуссен
- The OpenTextBookStore
Раздел 7.2 Тождества сложения и вычитания
В этом разделе мы начинаем расширять наш репертуар тригонометрических тождеств.
Тождества суммы и разности
\[\cos (\alpha -\beta )=\cos (\alpha )\cos (\beta )+\sin (\alpha )\sin (\beta )\]
\[\cos (\alpha +\beta)=\cos (\alpha)\cos (\beta)-\sin (\alpha)\sin (\beta)\]
\[\sin (\alpha +\ бета)=\sin (\alpha)\cos (\beta)+\cos (\alpha)\sin (\beta)\]
\[\sin (\alpha -\beta )=\sin (\alpha )\cos (\beta )-\cos (\alpha )\sin (\beta )\]
Докажем тождество разности углов для косинуса. Остальные тождества могут быть получены из этого.
Доказательство тождества разности углов для косинуса
Рассмотрим две точки на единичной окружности:
\(P\) под углом \(\alpha\) от положительной оси \(x\) с координаты \(\left(\cos (\alpha ),\sin (\alpha )\right)\) и \(Q\) под углом \(\beta\) с координатами \(\left(\cos (\beta),\sin (\beta)\right)\).
Обратите внимание, что мера угла \(POQ\) равна \(\alpha\) – \(\beta\). Обозначьте еще две точки:
\(C\) под углом \(\alpha\) – \(\beta\), с координатами \(\left(\cos (\alpha -\beta ),\sin ( \alpha -\beta )\right)\),
\(D\) в точке (1, 0).
Обратите внимание, что расстояние от \(C\) до \(D\) такое же, как расстояние от \(P\) до \(Q\), потому что треугольник \(COD\) является вращением треугольника \( ПОК\).
Использование формулы расстояния для нахождения расстояния от \(P\) до \(Q\) дает 9{2} (\alpha -\beta )}\nonumber\]
Применение тождества Пифагора и упрощение
\[\sqrt{-2\cos (\alpha -\beta )+2}\nonumber\]
Поскольку два расстояния одинаковы, мы устанавливаем эти две формулы равными друг другу и упрощаем
\[\sqrt{2-2\cos (\alpha)\cos (\beta)-2\sin (\alpha)\sin (\beta)} =\sqrt{-2\cos (\alpha -\beta)+2}\nonumber\]
\[2-2\cos (\alpha)\cos (\beta)-2\sin ( \alpha )\sin (\beta )=-2\cos (\alpha -\beta )+2\nonumber\]
\[\cos (\alpha )\cos (\beta )+\sin (\alpha )\ sin (\beta)=\cos (\alpha -\beta)\nonumber\]
Это позволяет установить личность.
Упражнение \(\PageIndex{1}\)
Записав \(\cos (\alpha +\beta )\) как \(\cos \left(\alpha -\left(-\beta \right)\ справа)\), тождество суммы углов для косинуса следует из доказанного выше тождества разности углов.
- Ответить
\[\ begin {array}{l} {\ cos (\ alpha + \ beta) = \ cos (\ alpha — (- \ beta))} \\ {\ cos (\ alpha) \ cos (- \ beta ) + \ грех (\ альфа) \ грех (- \ бета)} \\ {\ соз (\ альфа) \ соз (\ бета) + \ грех (\ альфа) (- \ грех (\ бета))} \\ {\ cos (\ alpha) \ cos (\ beta) — \ sin (\ alpha) \ sin (\ beta)} \ end {array} \ nonumber \] 9\circ )\nonumber\] Вычислить
\[=\dfrac{\sqrt{3} }{2} \cdot \dfrac{\sqrt{2} }{2} -\dfrac{1}{2} \cdot \ dfrac{\sqrt{2} }{2}\nonumber\] Просто
\[=\dfrac{\sqrt{6} -\sqrt{2} }{4}\nonumber\]Упражнение \(\PageIndex{ 2}\)
Найдите точное значение \(\sin\left(\dfrac{\pi }{12}\right)\).
- Ответить
\[\ sin \left(\dfrac{\pi }{12} \right)=\sin \left(\dfrac{\pi }{3} -\dfrac{\pi }{4} \right)=\ sin \left(\dfrac{\pi} {3} \right)\cos \left(\dfrac{\pi} {4} \right)-\cos \left(\dfrac{\pi} {3} \right )\sin\left(\dfrac{\pi }{4} \right)\nonumber\]
\[=\dfrac{\sqrt{3} }{2} \dfrac{\sqrt{2} }{2} -\dfrac{1}{2} \dfrac{\sqrt{2}} {2}\ четырехъядерный \dfrac{\sqrt{6} -\sqrt{2} }{4}\номер\]
Пример \(\PageIndex{2}\)
Переписать \(\sin \left(x-\dfrac{\pi }{4} \right)\) через sin(\(x\)) и потому что (\ (х \)).

Решение
\[\sin \left(x-\dfrac{\pi }{4} \right)\nonumber\]Использовать тождество разности углов для синуса
\[=\sin \left(x \right)\cos \left(\dfrac{\pi} {4} \right)-\cos \left(x\right)\sin \left(\dfrac{\pi} }{4} \right)\nonumber\ ] Оцените косинус и синус и переставьтеКроме того, эти тождества можно использовать для упрощения выражений или доказательства новых тождеств.
Пример \(\PageIndex{3}\)
Докажите )} = \ dfrac {\ tan (a) + \ tan (b)} {\ tan (a) — \ tan (b)} \).
Решение
Как и с любой личностью, нам нужно сначала решить, с какой стороны начать. Поскольку левая часть включает сумму и разность углов, мы могли бы начать с нее.0034
\[\dfrac{\sin (a+b)}{\sin (a-b)}\nonumber\] Применить сумму и разность тождеств углов
\[=\dfrac{\sin (a)\cos (b )+\cos (a)\sin (b)}{\sin (a)\cos (b)-\cos (a)\sin (b)}\nonumber\]Поскольку сразу не очевидно, как продолжайте, мы могли бы начать с другой стороны и посмотреть, будет ли путь более очевидным.

\[\dfrac{\tan (a)+\tan (b)}{\tan (a)-\tan (b)}\nonumber\] Переписывание касательных с использованием тождества касательных
\[=\dfrac{ \ dfrac {\ sin (a)} {\ cos (a)} + \ dfrac {\ sin (b)} {\ cos (b)}} {\ dfrac {\ sin (a)} {\ cos (a) } -\dfrac{\sin (b)}{\cos (b)} }\nonumber\]Умножение вершины и низа на cos(\(a\))cos(\(b\))
\[=\dfrac{\left(\dfrac{\sin (a)}{\cos (a)} +\dfrac{\sin (b)}{\cos (b)} \right)\cos (a )\cos (b)}{\left(\dfrac{\sin (a)}{\cos (a)} -\dfrac{\sin (b)}{\cos (b)} \right)\cos ( a)\cos (b)}\nonumber\]Распределение и упрощение
\[=\dfrac{\sin (a)\cos (b)+\sin (b)\cos (a)}{\sin (a) \cos (b)-\sin (b)\cos (a)}\nonumber\]Из приведенного выше мы узнаем это
\[=\dfrac{\sin (a+b)}{\sin (ab)}\ nonumber\]Установление тождестваЭти тождества также можно использовать для решения уравнений.
Пример \(\PageIndex{4}\)
Решить \(\sin (x)\sin (2x)+\cos (x)\cos (2x)=\dfrac{\sqrt{3}} {2} \).
Решение
Признав левую часть уравнения результатом тождества разности углов для косинуса, мы можем упростить уравнение
\[\sin (x)\sin (2x)+\cos ( x)\cos (2x)=\dfrac{\sqrt{3} }{2}\nonumber\]Применить разность углов тождества
\[\cos (x-2x)=\dfrac{\sqrt{3} } {2}\nonumber\]
\[\cos (-x)=\dfrac{\sqrt{3} }{2}\nonumber\]Используйте тождество отрицательного угла
\[\cos (x)=\dfrac{\sqrt{3} }{2}\nonumber\]Поскольку это особое значение косинуса, которое мы узнаем из единичного круга, мы можем быстро записать ответы:
\[\begin{array}{l} {x=\dfrac{\pi }{6} +2\pi k} \\ {x=\dfrac{11\pi }{6} +2\pi k} \ end{array}\nonumber\], где \(k\) — целое число
Объединение волн одинакового периода
Синусоидальная функция вида \(f(x)=A\sin (Bx+C)\) можно переписать, используя тождество суммы углов.

Пример \(\PageIndex{5}\)
Перепишите \(f(x)=4\sin\left(3x+\dfrac{\pi }{3}\right)\) как сумму синуса и косинуса.
Решение
\[4\sin \left(3x+\dfrac{\pi }{3} \right)\nonumber\]Использование суммы углов тождества
\[=4\left(\sin \left (3x\right)\cos\left(\dfrac{\pi}{3}\right)+\cos\left(3x\right)\sin\left(\dfrac{\pi}{3}\right)\ right)\nonumber\]Вычисление синуса и косинуса
\[=4\left(\sin \left(3x\right)\cdot \dfrac{1}{2} +\cos \left(3x\right)\cdot \dfrac{\sqrt{3} }{2} \right)\nonumber\]Распределите и упростите
\[=2\sin \left(3x\right)+2\sqrt{3} \cos \left(3x\right)\nonumber\]Обратите внимание, что результат представляет собой удлинение синуса, добавленное к другому растяжение косинуса, но оба имеют одинаковое горизонтальное сжатие, что приводит к одному и тому же периоду.
Теперь мы можем спросить, можно ли обратить этот процесс вспять – может ли комбинация синуса и косинуса одного периода быть записана как одна синусоидальная функция? Чтобы изучить это, мы рассмотрим в целом процедуру, использованную в приведенном выше примере.

\[f(x)=A\sin (Bx+C)\nonumber\]Использовать тождество суммы углов
\[=A\left(\sin (Bx)\cos (C)+\cos (Bx )\sin (C)\right)\nonumber\]Распределите \(A\)
\[=A\sin (Bx)\cos (C)+A\cos (Bx)\sin (C)\nonumber\ ] Немного переставьте термины
\[=A\cos (C)\sin (Bx)+A\sin (C)\cos (Bx)\nonumber\]На основе этого результата, если у нас есть выражение форму \(m\sin (Bx)+n\cos (Bx)\), мы могли бы переписать ее как единую синусоидальную функцию, если бы мы могли найти значения A и C 9{2}\quad \cos (C)=\dfrac{m}{A}\text{ и }\sin (C)=\dfrac{n}{A}\]
Вы можете использовать любой из двух последних уравнения для возможных значений C . Поскольку обычно будет два возможных решения, нам нужно будет рассмотреть оба, чтобы определить, в каком квадранте находится C , и определить, какое решение для C удовлетворяет обоим уравнениям.
Пример \(\PageIndex{6}\)
Перепишите \(4\sqrt{3} \sin (2x)-4\cos (2x)\) как одну синусоидальную функцию.
 9{2} =16\cdot 3+16=64\), поэтому \(A = 8\).
9{2} =16\cdot 3+16=64\), поэтому \(A = 8\).Решение для \(C\),
\[\cos (C)=\dfrac{4\sqrt{3} }{8} =\dfrac{\sqrt{3} }{2}\text{ так }C=\dfrac{\pi }{6}\text{ или }C=\dfrac{11\pi }{6}\nonumber\]
Однако обратите внимание \(\sin (C)=\dfrac{- 4}{8} =-\dfrac{1}{2}\). Синус отрицательный в третьем и четвертом квадранте, поэтому угол, который работает для обоих, равен \(C=\dfrac{11\pi }{6}\).
Объединение этих результатов дает нам выражение
\[8\sin \left(2x+\dfrac{11\pi }{6} \right)\nonumber\] 9{2} =36\quad A=6\nonnumber\]
\[\cos (C)=\dfrac{-3\sqrt{2} }{6} =\dfrac{-\sqrt{2} }{2 } \ quad \ sin (C) = \ dfrac {3 \ sqrt {2}} {6} = \ dfrac {\ sqrt {2}} {2} \ quad C = \ dfrac {3 \ pi} {4} \ нечисло\]
\[6\sin \left(5x+\dfrac{3\pi }{4} \right)\нечисло\]
Преобразование комбинации синуса и косинуса с равными периодами в виде одной синусоидальной функции обеспечивает подход к решению некоторых уравнений.
Пример \(\PageIndex{7}\)
Решите \(3\sin (2x)+4\cos (2x)=1\), чтобы найти два положительных решения. 9{-1} \left(\dfrac{3}{5} \right)\приблизительно 0,927\text{ или }C=2\pi -0,927=5,356\nonnumber\]
9{-1} \left(\dfrac{3}{5} \right)\приблизительно 0,927\text{ или }C=2\pi -0,927=5,356\nonnumber\]
Так как \(\sin (C)= \dfrac{4}{5}\), положительное значение, нам нужен угол в первом квадранте, \(C = 0,927\).
Используя это, наше уравнение принимает вид
\[5\sin \left(2x+0,927\right)=1\nonnumber\] Разделить на 5
\[\sin \left(2x+0,927\right)=\dfrac {1}{5}\nonumber\] Сделайте замену \(u = 2x + 0,927\)
\[\sin \left(u\right)=\dfrac{1}{5}\nonumber\] Обратное дает первое решение 9{-1} \left(\dfrac{1}{5} \right)\приблизительно 0,201\nonumber\] По симметрии второе решение равно
\[u=\pi -0,201=2,940\nonumber\] Третье решение будет
\[u=2\pi +0.201=6.485\nonnumber\]
Отменив подстановку, мы можем найти два положительных решения для \(x\).
\[\begin{array}{ccccc}{2x+0,927=0,201}&{\text{или}}&{2x+0,927=2,940}&{\text{или}}&{2x+0,927=6,485 }\\{2x=-0,726}&{}&{2x=2,013}&{}&{2x=5,558}\\{x=-0,363}&{}&{x=1,007}&{}&{x =2,779}\end{array}\nonumber\]
Поскольку первое из них отрицательное, мы исключаем его и сохраняем два положительных решения, \(x=1,007\) и \(x=2,779\).
Тождества произведения на сумму и суммы на произведение
Тождества произведения на сумму
\[\begin{array}{l} {\sin (\alpha )\cos (\beta ) = \ dfrac {1} {2} \ влево (\ грех (\ альфа + \ бета) + \ грех (\ альфа — \ бета) \ вправо)} \\ {\ грех (\ альфа) \ грех (\ бета ) = \ dfrac {1} {2} \ влево (\ соз (\ альфа — \ бета) — \ соз (\ альфа + \ бета) \ справа)} \\ {\ соз (\ альфа) \ соз (\ бета )=\dfrac{1}{2} \left(\cos (\alpha +\beta )+\cos (\alpha -\beta )\right)} \end{array}\]
Докажем первое из них, используя тождества суммы и разности углов из начала раздела. Доказательства двух других тождеств аналогичны и оставлены в качестве упражнения.
Доказательство идентичности произведения на сумму для sin(\(\alpha\))cos(\(\beta\))
Вспомнить тождества суммы и разности углов из предыдущих
\[\sin (\alpha +\beta)=\sin (\alpha)\cos (\beta)+\cos (\alpha)\sin (\beta)\nonumber\]
\[\sin (\alpha -\beta)= \sin (\alpha)\cos (\beta)-\cos (\alpha)\sin (\beta)\nonumber\]
Складывая эти два уравнения, мы получаем
\[\sin (\alpha +\beta )+\sin (\alpha -\beta )=2\sin (\alpha )\cos (\beta )\nonumber\]
Разделив на 2, получаем тождество
\[\sin (\alpha )\cos (\beta )=\dfrac{1}{2} \left(\sin (\alpha +\beta )+\sin (\alpha -\beta )\right)\nonumber\]
Пример \(\PageIndex{8}\)
Запишите \(\sin (2t)\sin (4t)\) в виде суммы или разности.
Решение
Использование тождества произведения синусов
\[\sin (2t)\sin (4t)=\dfrac{1}{2} \left(\cos (2t-4t)-\cos (2t+4t)\right)\nonumber\]
\ [=\dfrac{1}{2} \left(\cos (-2t)-\cos (6t)\right)\nonumber\]При желании примените тождество отрицательного угла
\[=\dfrac{1}{ 2} \left(\cos (2t)-\cos (6t)\right)\nonumber\]Распределить
\[=\dfrac{1}{2} \cos (2t)-\dfrac{1}{2} \cos (6t)\nonumber\]
Упражнение \(\PageIndex{4}\)
Вычислить \(\cos \left(\dfrac{11\pi }{12} \right)\cos \left(\ dfrac{\pi }{12} \right)\).
- Ответить
\[\cos \left(\dfrac{11\pi }{12} \right)\cos \left(\dfrac{\pi }{12} \right)=\dfrac{1}{2} \left( \cos \left(\dfrac{11\pi} }{12} +\dfrac{\pi }{12} \right)+\cos \left(\dfrac{11\pi} }{12} -\dfrac{\pi }{12} \right)\right)\nonumber\]
\[=\dfrac{1}{2} \left(\cos \left(\pi \right)+\cos \left(\dfrac{5\) pi }{6} \right)\right)=\dfrac{1}{2} \left(-1-\dfrac{\sqrt{3} }{2} \right)\nonumber\]
\[=\ dfrac{-2-\sqrt{3} }{4}\номер\]
Тождества суммы и произведения
\[\sin \left(u\right)+\sin \left(v\right)=2\sin \left(\dfrac{u+v}{2} \ right)\cos\left(\dfrac{u-v}{2} \right)\]
\[\sin\left(u\right)-\sin\left(v\right)=2\sin\left(\ dfrac{u-v}{2} \right)\cos \left(\dfrac{u+v}{2} \right)\]
\[\cos \left(u\right)+\cos \left(v\ справа) = 2\cos \left(\dfrac{u+v}{2} \right)\cos \left(\dfrac{u-v}{2} \right)\]
\[\cos \left(u\ вправо)-\cos\влево(v\вправо)=-2\sin\влево(\dfrac{u+v}{2}\вправо)\sin\влево(\dfrac{u-v}{2}\вправо)\ ]
Мы снова докажем одно из них, а остальное оставим в качестве упражнения.
Доказательство идентичности суммы и произведения для функции синуса
Мы определяем две новые переменные:
\[\begin{array}{l} {u=\alpha +\beta } \\ {v= \alpha -\beta } \end{array}\nonumber\]
Сложение этих уравнений дает \(u+v=2\alpha\), что дает \(\alpha =\dfrac{u+v}{2}\ )
Вычитание уравнений дает \(u-v=2\beta\) или \(\beta =\dfrac{u-v}{2}\)
Подстановка этих выражений в тождество произведения на сумму
\[\sin (\alpha)\cos (\beta)=\dfrac{1}{2} \left(\sin (\alpha +\beta)+\sin (\alpha -\beta)\right) \nonumber\] дает
\[\sin \left(\dfrac{u+v}{2} \right)\cos \left(\dfrac{u-v}{2} \right)=\dfrac{1}{ 2} \left(\sin \left(u\right)+\sin \left(v\right)\right)\nonumber\]Умножить на 2 с обеих сторон
\[2\sin \left(\dfrac{ u+v}{2} \right)\cos \left(\dfrac{u-v}{2} \right)=\sin \left(u\right)+\sin \left(v\right)\nonumber\] Установление личности
Упражнение \(\PageIndex{5}\)
Обратите внимание, что при использовании тождества отрицательного угла \(\sin \left(u\right)-\sin \left(v\right)=\sin (u)+\sin (-v)\). Используйте это вместе с идентичностью суммы синусов, чтобы доказать идентичность суммы и произведения для \(\sin\left(u\right)-\sin\left(v\right)\).
Используйте это вместе с идентичностью суммы синусов, чтобы доказать идентичность суммы и произведения для \(\sin\left(u\right)-\sin\left(v\right)\).
- Ответить
\[\sin (u)-\sin (v)\nonumber\]Использовать тождество отрицательного угла для синуса
\[\sin (u) + \sin (-v)\nonumber\]Использовать тождество суммы к произведению для синуса
\[2\text{sin} (\dfrac{u + (-v)}{2}) \text{cos} (\dfrac{u — (-v)}{2})\nonumber\] Удалить скобки 9\circ \right)\nonumber\]Вычислить
\[=-2\cdot \dfrac{\sqrt{2} }{2} \cdot \dfrac{-1}{2} =\dfrac{\sqrt{2} }{2}\nonumber\]Пример \(\PageIndex{10}\)
Докажите тождество \(\dfrac{\cos (4t)-\cos (2t)}{\sin (4t)+\ sin (2t)} =-\tan (t)\).
Решение
Поскольку левая часть кажется более сложной, мы можем начать с нее и упростить.
\[\dfrac{\cos (4t)-\cos (2t)}{\sin (4t)+\sin (2t)}\nonumber\]Используйте тождества суммы-произведения
\[=\dfrac {-2\sin\left(\dfrac{4t+2t}{2}\right)\sin\left(\dfrac{4t-2t}{2}\right)}{2\sin\left(\dfrac{ 4t+2t}{2} \right)\cos \left(\dfrac{4t-2t}{2} \right)}\nonumber\]Упростить
\[=\dfrac{-2\sin\left(3t\right)\sin\left(t\right)}{2\sin\left(3t\right)\cos\left(t\right)}\ nonumber\]Упростить еще
\[=\dfrac{-\sin \left(t\right)}{\cos \left(t\right)}\nonumber\]Переписать как касательную
\[=-\tan ( t)\nonumber\]Установление идентичностиПример \(\PageIndex{11}\)
Решить \(\sin \left(\pi {\kern 1pt} t\right)+\sin \left(3\ pi {\kern 1pt} t\right)=\cos (\pi {\kern 1pt} t)\) для всех решений с \(0\le t<2\).

Решение
В таком уравнении не сразу понятно, как действовать. Одним из вариантов было бы объединить две синусоидальные функции в левой части уравнения. Другим было бы переместить косинус в левую часть уравнения и объединить его с одним из синусов. Без особой веской причины мы начнем с объединения синусов в левой части уравнения и посмотрим, как все получится.
\[\sin \left(\pi {\kern 1pt} t\right)+\sin \left(3\pi {\kern 1pt} t\right)=\cos (\pi {\kern 1pt} t )\nonumber\]Применить сумму к идентификатору продукта слева
\[2\sin \left(\dfrac{\pi {\kern 1pt} t+3\pi {\kern 1pt} t}{2} \right)\cos \left(\dfrac{\pi {\kern 1pt} t-3\pi {\kern 1pt} t}{2} \right)=\cos (\pi {\kern 1pt} t)\nonumber\]Упростить
\[2\sin \left(2\pi {\kern 1pt} t\right)\cos \left(-\pi {\kern 1pt} t\right)=\cos (\pi {\kern 1pt} t)\nonumber\] Применить тождество отрицательного угла
\ [2\sin\left(2\pi {\kern 1pt} t\right)\cos \left(\pi {\kern 1pt} t\right)=\cos (\pi {\kern 1pt} t)\nonumber \] Измените уравнение так, чтобы оно равнялось 0 с одной стороны
\[2\sin \left(2\pi {\kern 1pt} t\right)\cos \left(\pi {\kern 1pt} t\right)-\ cos (\pi {\kern 1pt} t)=0\nonumber\]Вычтем косинус
\[\cos \left(\pi {\kern 1pt} t\right)\left(2\sin \left(2\pi {\kern 1pt} t\right)-1\right)=0\nonnumber\ ]Используя теорему о нулевом произведении, мы знаем, что по крайней мере один из двух множителей должен быть равен нулю.
 Первый фактор, \(\cos\left(\pi {\kern 1pt} t\right)\), имеет период \(P=\dfrac{2\pi}{\pi} =2\), поэтому решение интервал \(0\le t<2\) представляет собой один полный цикл этой функции.
Первый фактор, \(\cos\left(\pi {\kern 1pt} t\right)\), имеет период \(P=\dfrac{2\pi}{\pi} =2\), поэтому решение интервал \(0\le t<2\) представляет собой один полный цикл этой функции.\[\cos \left(\pi {\kern 1pt} t\right)=0\nonnumber\]Подстановка \(u=\pi {\kern 1pt} t\)
\[\cos \left(u\right)=0\nonumber\]За один цикл это имеет решения
\[u=\dfrac{\pi }{2}\text{ или }u=\dfrac{3 \pi }{2}\nonumber\]Отмените замену
\[\pi {\kern 1pt} t=\dfrac{\pi} {2}\text{, так что }t=\dfrac{1}{2} \nonumber\]
\[\pi {\kern 1pt} t=\dfrac{3\pi}{2}\text{, поэтому }t=\dfrac{3}{2}\nonumber\]Второй фактор, \(2\sin\left(2\pi {\kern 1pt} t\right)-1\), имеет период \(P=\dfrac{2\pi}{2\pi} =1\) , поэтому интервал решения \(0\le t<2\) содержит два полных цикла этой функции.
\[2\sin \left(2\pi {\kern 1pt} t\right)-1=0\nonnumber\] Изолировать синус
\[\sin \left(2\pi {\kern 1pt} t \right)=\dfrac{1}{2}\nonumber\] Замените \(u=2\pi {\kern 1pt} t\)
\[\sin (u)=\dfrac{1}{2}\ nonumber\] На одном цикле это имеет решения
\[u=\dfrac{\pi }{6}\text{или}u=\dfrac{5\pi}{6}\nonumber\] На втором цикле решения:
\[u=2\pi +\dfrac{\pi }{6} =\dfrac{13\pi }{6}\text{или}u=2\pi +\dfrac{5\pi} {6} =\dfrac{17\pi }{6}\nonumber\] Отменить замену
\[2\pi {\kern 1pt} t=\dfrac{\pi} {6}\text{, поэтому} t=\dfrac{1}{12}\nonumber\]
\[2\pi {\ kern 1pt} t=\dfrac{5\pi }{6}\text{, поэтому }t=\dfrac{5}{12}\nonumber\]
\[2\pi {\kern 1pt} t=\dfrac {13\pi} {6}\text{, поэтому} t=\dfrac{13}{12}\nonumber\]
\[2\pi {\kern 1pt} t=\dfrac{17\pi} {6 }\text{, поэтому }t=\dfrac{17}{12}\nonumber\]Всего мы нашли шесть решений для \(0\le t<2\), что можно подтвердить, посмотрев на график .

\[t=\dfrac{1}{12},\dfrac{5}{12},\dfrac{1}{2},\dfrac{13}{12},\dfrac{3}{2} ,\dfrac{17}{12}\номер\]
Важные темы этого раздела
- Тождества суммы и разности
- Объединение волн равных периодов
- Тождества произведение-сумма
- Тождества суммы и произведения
- Завершение корректуры
Эта страница под названием 7.2: Сложение и вычитание идентификаторов распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Дэвидом Липпманом и Мелони Расмуссен (The OpenTextBookStore) через исходный контент, отредактированный в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дэвид Липпман и Мелони Расмуссен
- Лицензия
- СС BY-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- источник@http://www.
 opentextbookstore.com/details.php?id=30
opentextbookstore.com/details.php?id=30
- источник@http://www.
Доказательство формулы сложения и вычитания для тригонометрических функций: CCSS.Math.Content.HSF-TF.C.9- Common Core: High School
All Common Core: High School — Functions Resources
6 диагностических тестов 82 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Common Core: High School — Помощь по функциям » Тригонометрические функции » Докажите формулу сложения и вычитания для тригонометрических функций: CCSS.Math.Content.HSF-TF.C.9
Используя формулу сложения для вычисления синуса и специальных опорных углов,
.
Возможные ответы: Правильный ответ: Объяснение:Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами.
 Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным опорным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Чтобы рационализировать знаменатель, умножьте числитель и знаменатель на квадратный корень из двух.
Сообщить об ошибке
Используя формулу сложения для вычисления синуса и специальных опорных углов,
.
Возможные ответы: Правильный ответ: Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным опорным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.

Сообщить об ошибке
Используя формулу сложения для вычисления синуса и специальных опорных углов,
.
Возможные ответы: Правильный ответ: Объяснение:Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным опорным углам.

Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Сообщить об ошибке
Используя формулу сложения для синуса и вычисления специальных опорных углов,
.
Возможные ответы: Правильный ответ: Объяснение:Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.

Шаг 1: Разбейте угол на два угла, которые соответствуют специальным опорным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Сообщить об ошибке
Используя формулу сложения для вычисления синуса и специальных опорных углов,
.
Возможные ответы: Правильный ответ: Объяснение:Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.
 MATH. СОДЕРЖАНИЕ.HSF.TF.C).
MATH. СОДЕРЖАНИЕ.HSF.TF.C).Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным опорным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Сообщить об ошибке
Используя формулу вычитания для синуса и вычисления специальных опорных углов,
.
Возможные ответы: Правильный ответ: Объяснение:Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.

В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным опорным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Теперь, чтобы рационализировать знаменатель, умножьте числитель и знаменатель на квадратный корень из двух.
Сообщить об ошибке
Используя формулу вычитания для косинуса и вычисления специальных опорных углов,
.
Возможные ответы: Правильный ответ: Объяснение:Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами.
 Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным опорным углам.
Шаг 2: Напишите общую формулу сложения для косинуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для косинуса.
Чтобы рационализировать знаменатель, умножьте числитель и знаменатель на квадратный корень из двух.
Сообщить об ошибке
Используя формулу сложения для косинуса и вычисления специальных опорных углов,
.
Возможные ответы: Правильный ответ: Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным опорным углам.
Шаг 2: Напишите общую формулу сложения для косинуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для косинуса.

Чтобы рационализировать знаменатель, умножьте числитель и знаменатель на квадратный корень из двух.
Сообщить об ошибке
Используя формулу сложения для косинуса и вычисления специальных опорных углов,
.
Возможные ответы: Правильный ответ: Объяснение:Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.
 HSF.TF.C).
HSF.TF.C).Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным опорным углам.
Шаг 2: Напишите общую формулу сложения для косинуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для косинуса.
Сообщить об ошибке
Используя формулу сложения для косинуса и вычисления специальных опорных углов,
Возможные ответы: Правильный ответ: Объяснение:Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.






 9{2} =16\cdot 3+16=64\), поэтому \(A = 8\).
9{2} =16\cdot 3+16=64\), поэтому \(A = 8\).
 Первый фактор, \(\cos\left(\pi {\kern 1pt} t\right)\), имеет период \(P=\dfrac{2\pi}{\pi} =2\), поэтому решение интервал \(0\le t<2\) представляет собой один полный цикл этой функции.
Первый фактор, \(\cos\left(\pi {\kern 1pt} t\right)\), имеет период \(P=\dfrac{2\pi}{\pi} =2\), поэтому решение интервал \(0\le t<2\) представляет собой один полный цикл этой функции.
 opentextbookstore.com/details.php?id=30
opentextbookstore.com/details.php?id=30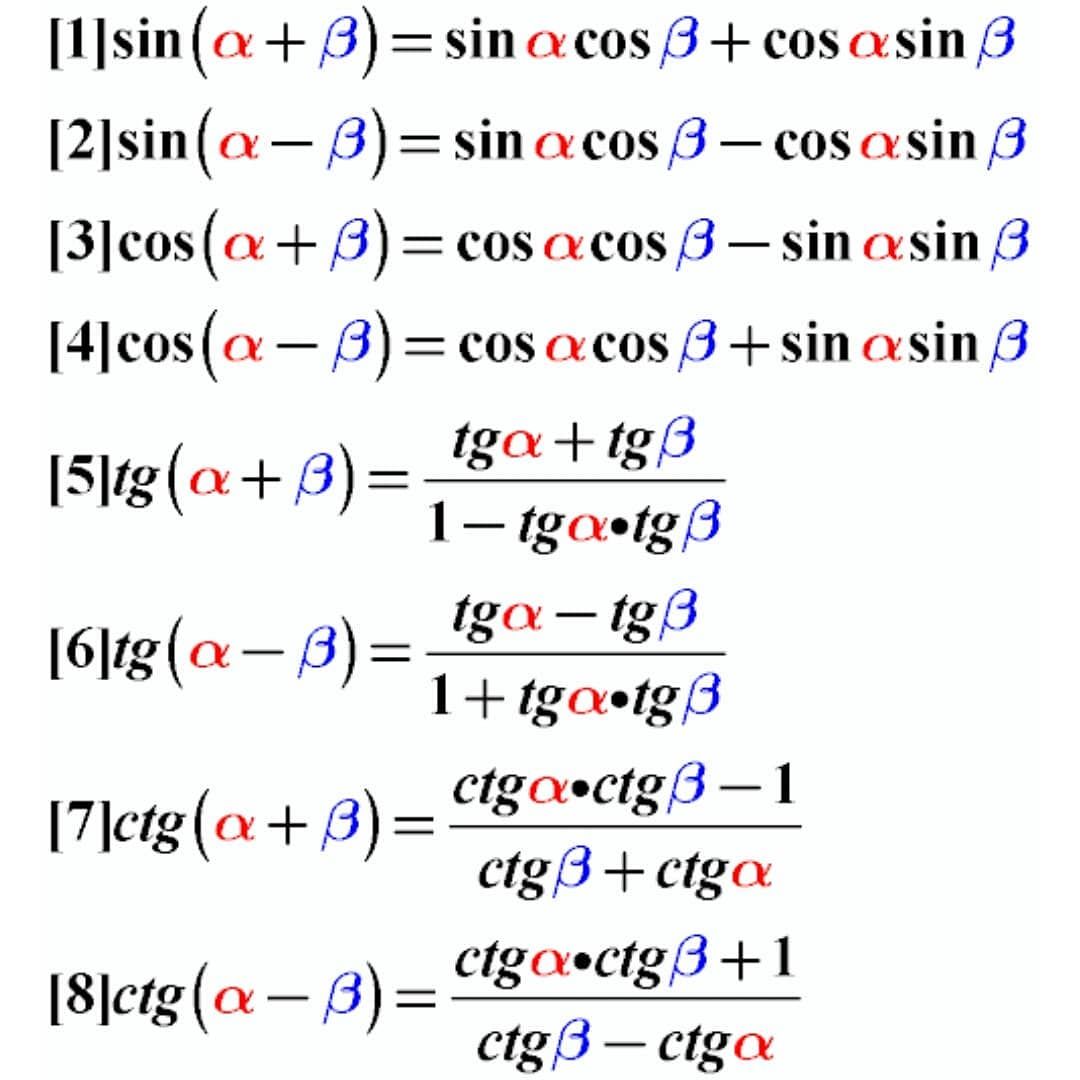 Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.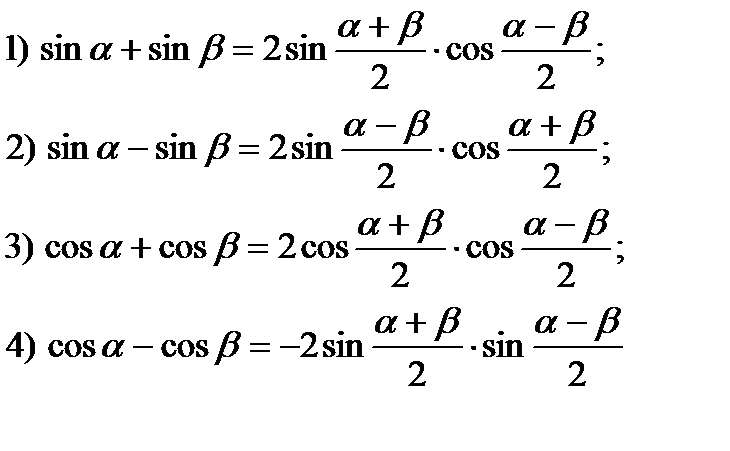


 MATH. СОДЕРЖАНИЕ.HSF.TF.C).
MATH. СОДЕРЖАНИЕ.HSF.TF.C).
 Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.

 HSF.TF.C).
HSF.TF.C).