Формулы высоты треугольника: Как найти высоту треугольника зная его площадь и сторону на которую проведено основание?

найти онлайн, формулы и примеры

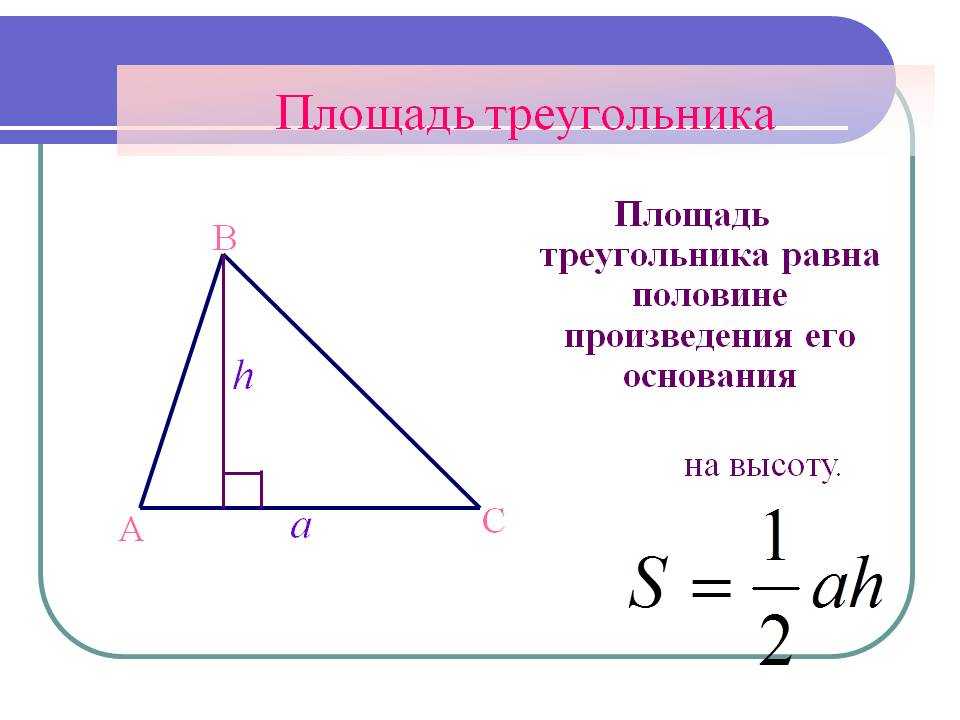
Здесь рассмотрены все возможные способы нахождения высоты треугольников разных типов. Высота треугольника – отрезок, проведенный из вершины треугольника перпендикулярно к противоположной стороне. В задачах нахождение высоты часто является промежуточным звеном для поиска других значений. Она и является катетом в треугольнике, который сама же образует, и участвует во многих формулах, например, для нахождения площади.

• Высота разностороннего треугольника через площадь и длину стороны
• Высота разностороннего треугольника через длины всех сторон
• Высота разностороннего треугольника через длину прилежащей стороны и синус угла
• Высота разностороннего треугольника через стороны и радиус описанной окружности
• Высота равнобедренного треугольника через основание и боковые стороны
• Высота прямоугольного треугольника через длины отрезков, образованных на гипотенузе
• Высота прямоугольного треугольника через все стороны треугольника
• Высота равностороннего треугольника через сторону треугольника

Через площадь и длину стороны разностороннего треугольника

Через площадь и длину высота находится по формуле:

h = 2S / a

где S – площадь треугольника, а – сторона треугольника.

Площадь (S):

мм²см²дм²м²

Сторона (a):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Согласно этой формуле высота равна удвоенной площади, деленной на длину стороны, к которой она проведена.

Пример.  Найдите высоту разностороннего треугольника, проведенную к стороне а, площадь которого равна 27 см, а длина стороны а составляет одну треть от площади. Решение: Найдем сторону а. Так как известно, что она составляет треть от площади, а = 27 / 3 = 9 см. Теперь воспользуемся формулой для нахождения высоты: h = 2S / a. Подставим известные значения. h = 2 * 27 / 9 = 6 см. Ответ: 6 см

Через длины всех сторон разностороннего треугольника

Через длины всех сторон высота разностороннего треугольника ищется по формуле:

h = (2 √(p (p-a)(p-b)(p-c))) / 2
p = (a + b + c) / 2

где h – высота, а, b, c – стороны треугольника, p – полупериметр треугольника.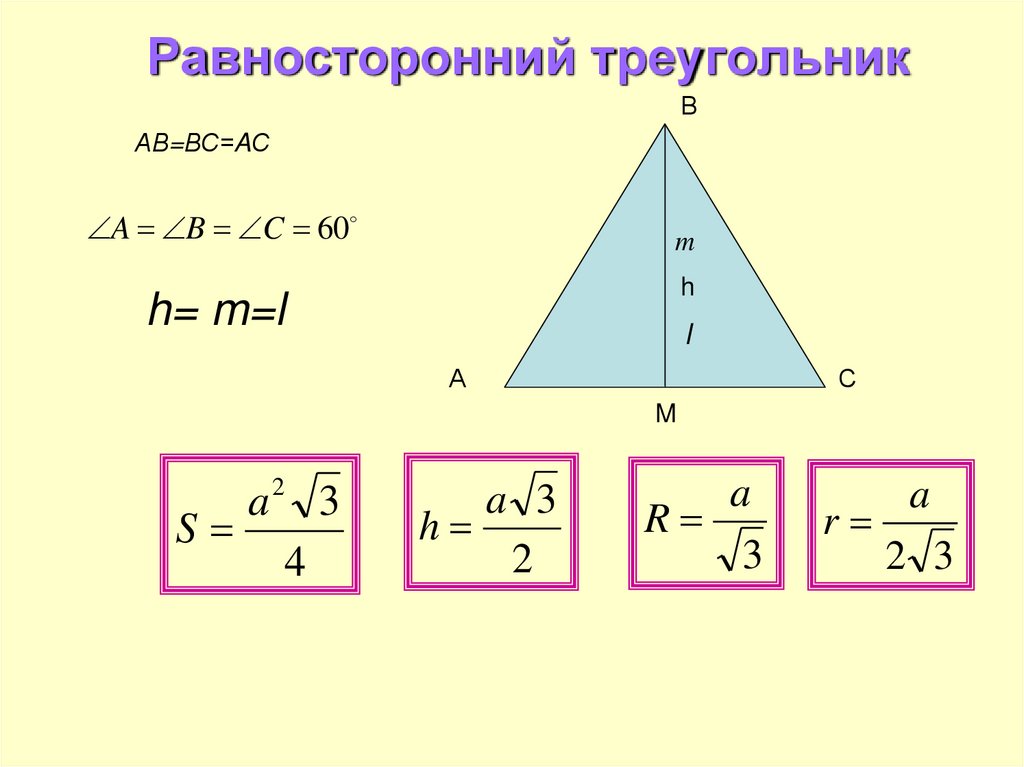

Сторона (a):

ммсмдмм

Сторона (b):

ммсмдмм

Сторона (c):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Полупериметр треугольника можно найти либо в два этапа через периметр, либо сразу по формуле. Этим способом удобно пользоваться, когда треугольник разносторонний.

Пример. Периметр разностороннего треугольника равен 18 см. Длины сторон 6 см и 8 см. Найдите высоту, проведенную к стороне а. Решение: P = a + b + c, значит с = P – a – b , то есть c = 18 – 8 – 6 = 4 см. Для нахождения h будем использовать формулу h = (2 √(p (p-a)(p-b)(p-c))) / 2. Сначала найдем полупериметр (p): p = p / 2 = 18 / 2 = 9 см. Подставим, найденные значения в формулу высоты: h = (2 √(9 (9 — 6)(9 — 8)(9 — 4))) / 2 = √135 / 3 = 2,12 см

Через длину прилежащей стороны и синус угла разностороннего треугольника

Через длину прилежащей стороны и синус угла высота ищется по следующей формуле:

h = a * sin α

где а – длина стороны, sin α – синус прилежащей стороны.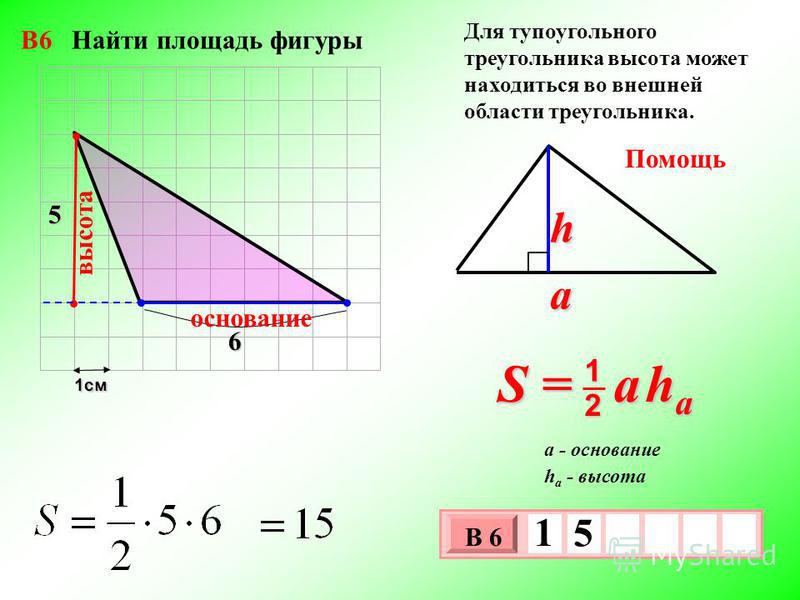

Сторона (a):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. В разностороннем треугольнике высота проведена к стороне AB. Угол ACH равен 30˚, а длина стороны AB 12 см. Найдите длину высоты CH в треугольнике ABC. По теореме о сумме углов в треугольнике найдем угол САН. ∠САН = 180 – (∠АСН + ∠АНС). ∠САН = 180 – 90 – 30 = 60˚  sin 60º = 1/2. СН = AB * sin ∠САН, СН = 12 * 1/2 = 6 см. Ответ: 6 см

Через стороны и радиус описанной окружности разностороннего треугольника

Через стороны и радиус описанной окружности высоту можно найти по следующей формуле:

h = bc / 2R

где r – радиус описанной около треугольника окружности, b,c – стороны треугольника

Сторона (b):

ммсмдмм

Сторона (c):

ммсмдмм

Радиус (R):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример.  Вокруг разностороннего треугольника описана окружность с радиусом 3 см. Из вершины между сторонами b и с проведена высота. Стороны b и с соответственно равны 5 см и 6 см. Найдите высоту. Решение: Найдем высоту, используя формулу h = 5 * 6 / 2 * 3 = 30 / 6 = 5 см. Ответ: 5 см.

Через длины отрезков прямоугольного треугольника, образованных на гипотенузе

Через длины отрезков образованных на гипотенузе высоту можно найти по следующей формуле:

h = √(C1 * C2)

где: C1, C2 — отрезки, образованные проведением высоты к гипотенузе.

Отрезок (C1):

ммсмдмм

Отрезок (C2):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. В прямоугольном треугольнике катеты равны 4 см и 3 см. Угол BAH равен 30˚. Найдите высоту. По теореме Пифагора найдём сторону BC, которая является гипотенузой в треугольнике ABC. BC² = AB² = AC²,  BC² = 4² + 3² = 16+9 = 25 см², BC = √25 = 5 см. Угол АНВ равен 90˚, так как АН является высотой, то есть, проведена перпендикулярно к стороне ВС. Следовательно, треугольник АНВ – прямоугольный. Сторона ВН лежит напротив угла 30˚ в прямоугольном треугольнике, значит, ее длина равна половине длины гипотенузы. Найдем ВН. BH = 1/2 AB. BH = 1/2 × 4 = 2 см. BC = BH + HC, значит, HC = BC – BH, HC = 5 – 2 = 3 см. По формуле найдем высоту (АН). АН = √(2 * 3) = √6 = 2,4 см. Ответ: 2,4 см.

Через основание и боковые стороны равнобедренного треугольника

Через основание и боковые стороны высота равнобедренного треугольника находится по формуле:

h = √(b² — a²/4)

где а – основание треугольника, b – боковая сторона. Для равнобедренного треугольника.

Основание (a):

ммсмдмм

Сторона (b):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример.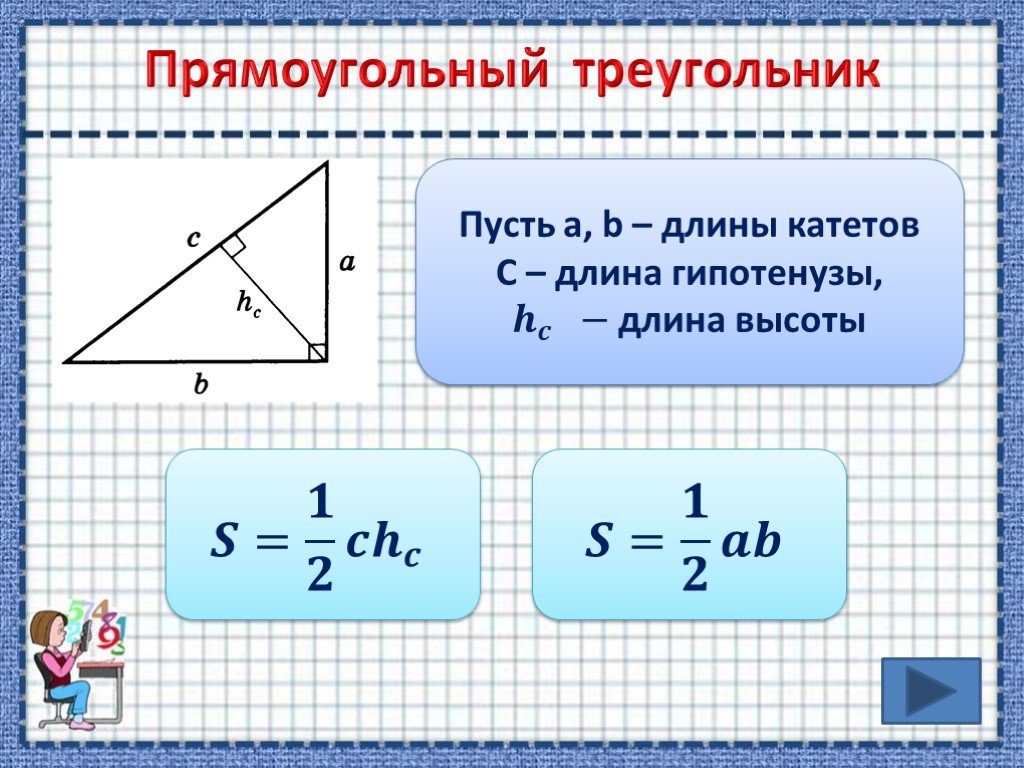  В равнобедренном треугольнике АВС боковая сторона равна 8 см. Из вершины В к основанию АС проведена высота ВН. Отрезок АН равен 5 см. Найдите высоту. Решение: Так как по условию треугольник АВС равнобедренный по условию, то АВ = ВС = 8 см высота ВН, является и медианой, и биссектрисой. Значит, АН = НС, а АС = НС + АН, АС = 5 + 5 = 10 см. По формуле найдем высоту ВН = √(АВ² — АС² / 4). ВН = √(8² — 10² / 4) = √(64 — 100 / 4) = √39 = 6 см. Ответ: 6 см.

Высота прямоугольного треугольника через все стороны треугольника

Если известны все стороны прямоугольного треугольника, то можно найти его высоту по следующей формуле:

h = ab / c

где a,b,c – стороны треугольника.

Сторона (a):

ммсмдмм

Сторона (b):

ммсмдмм

Сторона (c):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. В прямоугольном треугольнике угол между катетом и гипотенузой равен 45˚. Длина стороны АС равна 6 см. Найти высоту АН. Решение: По теореме о сумме углов в треугольнике найдем угол АСВ. ∠АСВ = 180˚ – (45˚ + 90˚) = 45˚. Так как АСВ = АСВ, то треугольник АВС равнобедренный с основанием ВС. Таким образом, АС = АВ = 6 см. По теореме Пифагора найдем гипотенузу ВС. BC² = AB² + AC². BC² = 6² + 6² = 36 +36 = 72 см². ВС = √72 = 6√2 см. Найдем высоту по формуле AH = AB * AC / BC. АН = 6 * 6 / 6√2= см. Домножим полученное значение на √2: (6 * √2) / √2 * √2 = 6√2 / 2 = 3√2 см. Ответ: 3√2 см

Через сторону равностороннего треугольника

Высота равностороннего треугольника через сторону треугольника ищется по следующей формуле:

h = a√3 / 2

где a – сторона треугольника.

Сторона (a):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример: Найдите высоту в равностороннем треугольнике, если известно, что его сторона равна 4√3 см.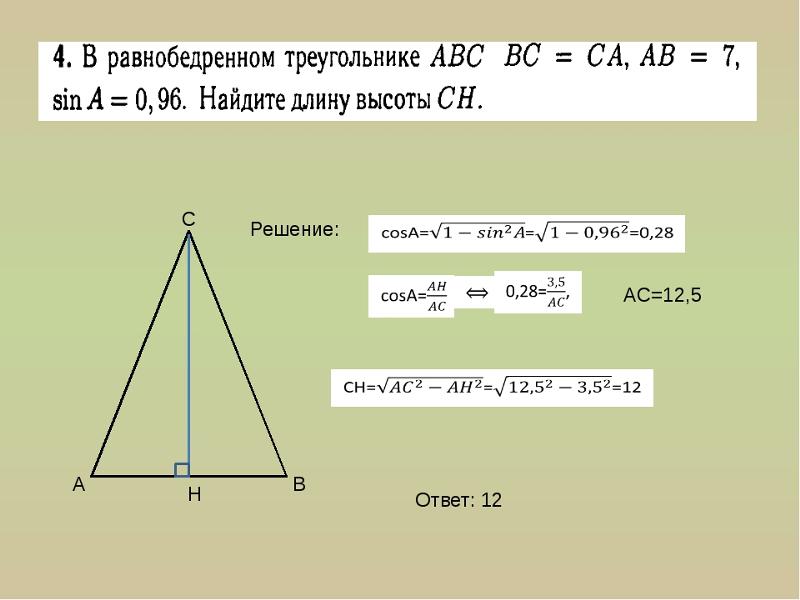  Решение: Для нахождения высоты воспользуемся формулой h = a√3 / 2 = √3 * 4 √3 / 2 = 4 * 3 / 2 = 6 см. Ответ: 6 см

В зависимости от типа треугольника высота может располагаться по-разному:

1. Например, в треугольнике KGM высота GH, проведённая из вершины G к стороне находится внутри треугольника, так как треугольник является остроугольным. Кроме того, треугольник в данном примере равнобедренный, значит, она же является биссектрисой и медианой. Знание этого пригодится при решении задач, например таким образом можно будет найти основание.
2. В тупоугольном треугольнике высота будет выходить за его пределы и для того чтобы её провести понадобится сначала продлить сторону. Например, на рисунке сторона ВС продлена до НС.
3. В случае, когда треугольник имеет прямой угол – высота совпадёт с одним из катетов, либо будет внутри треугольника (как в первом рассмотренном варианте) и проведена к гипотенузе.

что такое высота в геометрии, ее свойства, определение

Определение высоты треугольника

Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.

Определение 1

Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.

Треугольники могут быть:

• разными по величине углов: прямоугольными, тупоугольными и остроугольными;
• разными по числу равных сторон: равносторонними, равнобедренными и разносторонними.

Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.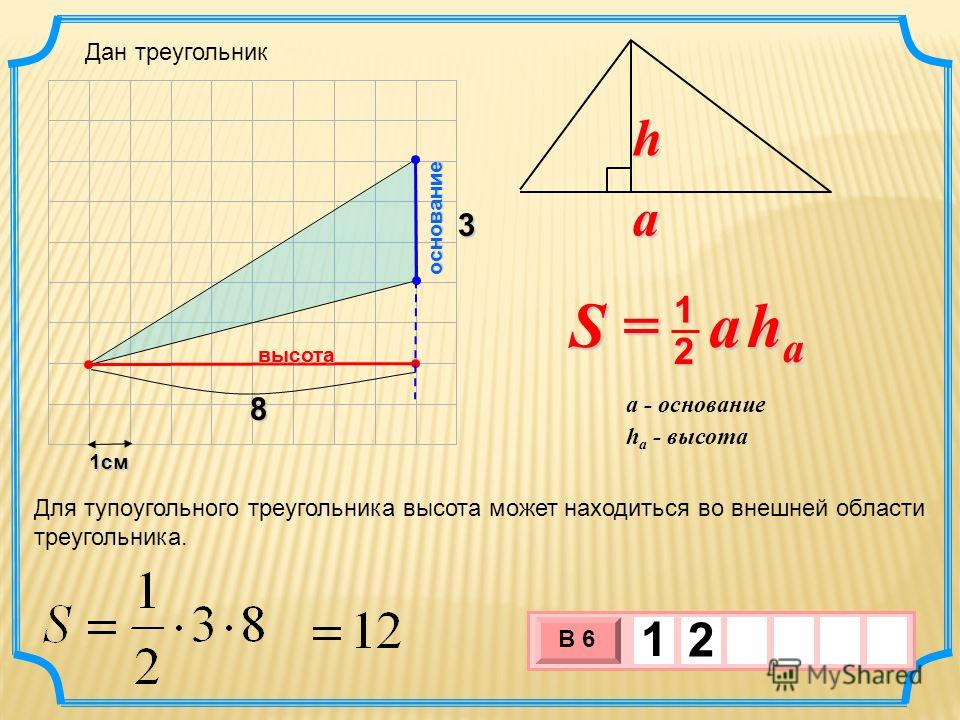

Определение 2

Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.

В геометрии высота треугольника обозначается буквой h.

В зависимости от типа треугольника высота может:

• падать на противоположную сторону — у остроугольного треугольника;
• находиться вне треугольника — у тупоугольного треугольника;
• совпадать с одной из сторон — у прямоугольного треугольника.

Источник: tmath.ru

Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.

Для того чтобы определить графическое начертание высоты треугольника, необходимо:

1. Найти вершину фигуры.
2. Опустить вниз перпендикулярную линию к противоположной стороне.
3. Продлить противоположную сторону до пересечения с высотой, если требуется.

Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.

Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:

A×HA÷B×HB÷C×HC=1BC÷1AC÷1AB

Выглядеть графически это будет так:

Источник: youclever.org

Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.

Через площадь и длину стороны, к которой опущена высота:

Формула 1

h=2Sa

где S — уже известная площадь треугольника,

а — сторона.

Через длины всех сторон:

Формула 2

h=2pp×ap×bp×ca

где a, b и c — стороны треугольника,

p — его полупериметр.

p=a+b+c2

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длину прилежащей стороны и синус угла:

Формула 3

h=a×sina

где a — сторона,

sina — синус угла прилежащей стороны.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через стороны и радиус описанной окружности.

Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:

Формула 4

h=bc2R

где b, c — стороны разностороннего треугольника, к которым не опущена высота,

R — радиус описанной окружности.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:

Формула 5

h=С1×С2

где C1 и С2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.

Данная формула подходит только для нахождения высоты прямоугольного треугольника.

Нахождение высоты равнобедренного треугольника через основание и боковые стороны

Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.

Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.

Формула для нахождения высоты в этом случае:

Формула 6

h=b2-a24

где a — основание,

b — равные боковые стороны.

Свойства высоты в равностороннем треугольнике

Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.

Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.

Высоту в таком треугольнике можно найти с помощью следующей формулы:

Формула 7

h=a32

где а — сторона равностороннего треугольника.

Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:

h=m=l=32a

где h — высота,

m — медиана,

l — биссектриса,

а — сторона правильного равностороннего треугольника.

Нахождение высоты прямоугольного треугольника через его катеты

Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.

Важно отметить, что две другие высоты будут совпадать с катетами треугольника.

Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).

Причем гипотенуза также легко находится через катеты по теореме Пифагора:

c² = a² + b²

Расчет высоты идет следующим образом:

Формула 8

h=abc

где a, b и c — вышеупомянутые стороны треугольника.

Как найти высоту треугольника (прямоугольного, равностороннего, равнобедренного)

Автор:

Малкольм МакКинси

11 января 2023 г.

a треугольник

Высота треугольника  является длиной отрезка перпендикулярной линии, начинающегося на стороне и пересекающего противоположный угол. Каждый треугольник имеет три высоты или высоты, потому что у каждого треугольника три стороны.

В равностороннем треугольнике, таком как △SUN  ниже, каждая высота представляет собой отрезок, который делит сторону пополам, а также является биссектрисой противоположного угла. Это произойдет только в равностороннем треугольнике.

Три высотные линии — равносторонний треугольник

По определению равностороннего треугольника вы уже знаете, что все три стороны конгруэнтны и все три угла равны 60° .

Если △SUN  на одной стороне обозначено 24 см , то все три стороны  24 см . Каждый отрезок, показывающий высоту с каждой стороны, также делит равносторонний треугольник на два прямоугольных треугольника.

Вы можете видеть, что отрезок линии, показывающий высоту, делит сторону пополам, поэтому короткая сторона только что созданного прямоугольного треугольника равна 12 см . Мы уже знаем, что гипотенуза равна 24 см .

Формула высоты треугольника

Вы можете взять любую сторону нашего великолепного  △SUN  выше и увидеть, что отрезок, показывающий его высоту, делит сторону пополам, поэтому каждая короткая сторона только что созданного прямоугольного треугольника равна  12 см , и мы уже знаем, что гипотенуза нашего нового прямоугольного треугольника равна 24 см .

Зная все три угла и две стороны прямоугольного треугольника, какова длина третьей стороны? Это работа для теоремы Пифагора.

Использование теоремы Пифагора

Сосредоточьтесь на длинах; углы не важны в теореме Пифагора. Подставьте то, что вы знаете:

Большинство людей с радостью назовут высоту (сторону) b ) примерно равно 20,78 , или b ≈ 20,78 .

Вы сами можете решить, сколько значащих цифр нужно для ответа, поскольку десятичная дробь будет продолжаться и дальше. Не забудьте использовать для ответа линейные измерения!

Решение теоремы Пифагора работает для прямоугольных, равнобедренных и равносторонних треугольников. Это не будет работать на разносторонних треугольниках!

Использование формулы площади для определения высоты

Формула для  площадь  треугольника равна  12(основание×высота)\frac{1}{2}(основание\умножить на высоту)21​(основание×высота) или 12bh\frac{1}{2}bh31​bh. Зная площадь и длину основания, можно вычислить высоту.

В отличие от метода теоремы Пифагора, если у вас есть две из трех частей, вы можете найти высоту любого треугольника!

Здесь у нас есть масштаб △ZIG  с основанием, показанным как 56 ярдов , и площадью 987 квадратных ярдов , но нет сведений об углах и двух других сторонах:

Используя формулу площади, чтобы найти высоту треугольника

Вспоминая формулу площади, где A  означает площадь, b  это основание, а h

4 :положим 900, мы помним в наших известных значениях:

Помните, как мы говорили, что каждый треугольник имеет три высоты? Если мы возьмем △ZIG и повернем его по часовой стрелке так, чтобы сторона GZ была горизонтальной, и построим высоту до ∠I , мы также можем получить высоту для этой стороны.

Как найти высоту треугольника пример

Высота треугольника Формула

Перпендикуляр, проведенный из вершины к противоположной стороне треугольника, называется    высотой треугольника. Формула высоты треугольника дает нам высоту треугольника. Интерпретируется формула высоты треугольника, и для разных типов треугольников даны разные формулы. Высота используется для расчета площади треугольника.

Какова высота формулы треугольника?

Формула высоты треугольника может быть выражена следующим образом. Здесь высота представлена ​​буквой h. Кроме того, мы также можем видеть ниже разные высоты формул треугольника для разных треугольников.

Общая формула высоты треугольника (h) = (2 × площадь) ÷ основание

Высота треугольника Формула для различных треугольников

Мы знаем, что треугольники классифицируются на основе сторон и углов. Давайте изучим разные формулы высоты в разных условиях для разных типов треугольников.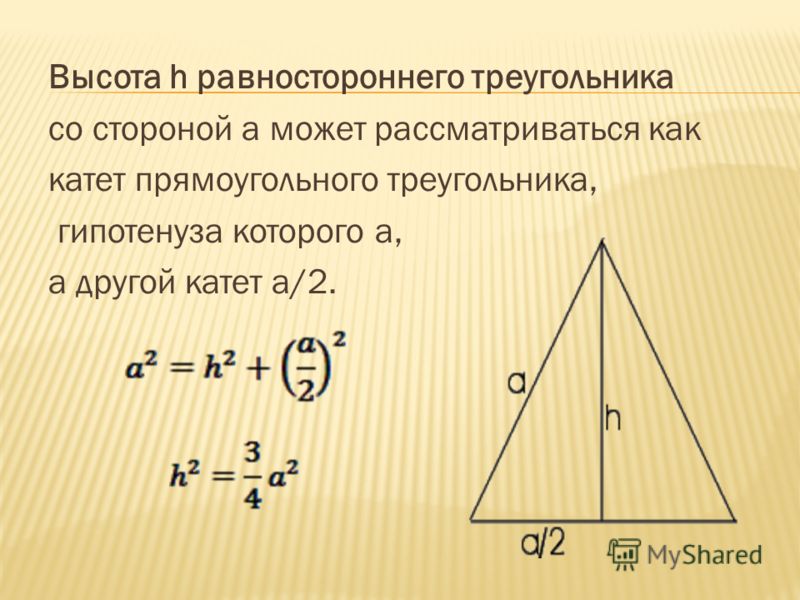

Высота треугольника Формула для разностороннего треугольника

Высота разностороннего треугольника определяется как: \(h_a = \dfrac{2 \sqrt{s(s-a)(s-b)(s-c)}}{a}\), \(h_b = \dfrac{2 \sqrt{s(s-a)(s-b)(s-c)}}{b}\) и \(h_c = \dfrac{2 \sqrt{s(sa)(s-b)(s-c) }}{c}\)Где a,b,c — стороны треугольника, а s — полупериметр

Высота треугольника Формула для равностороннего треугольника

Высота равностороннего треугольника определяется как: \( h= \dfrac{a\sqrt{3}}{2}\)

92}{4}}\), где a и b — стороны треугольника.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Примеры формулы высоты треугольника

Давайте рассмотрим несколько примеров, чтобы понять формулу высоты треугольника

Пример 1:  Площадь прямоугольной доски равна 720 кв.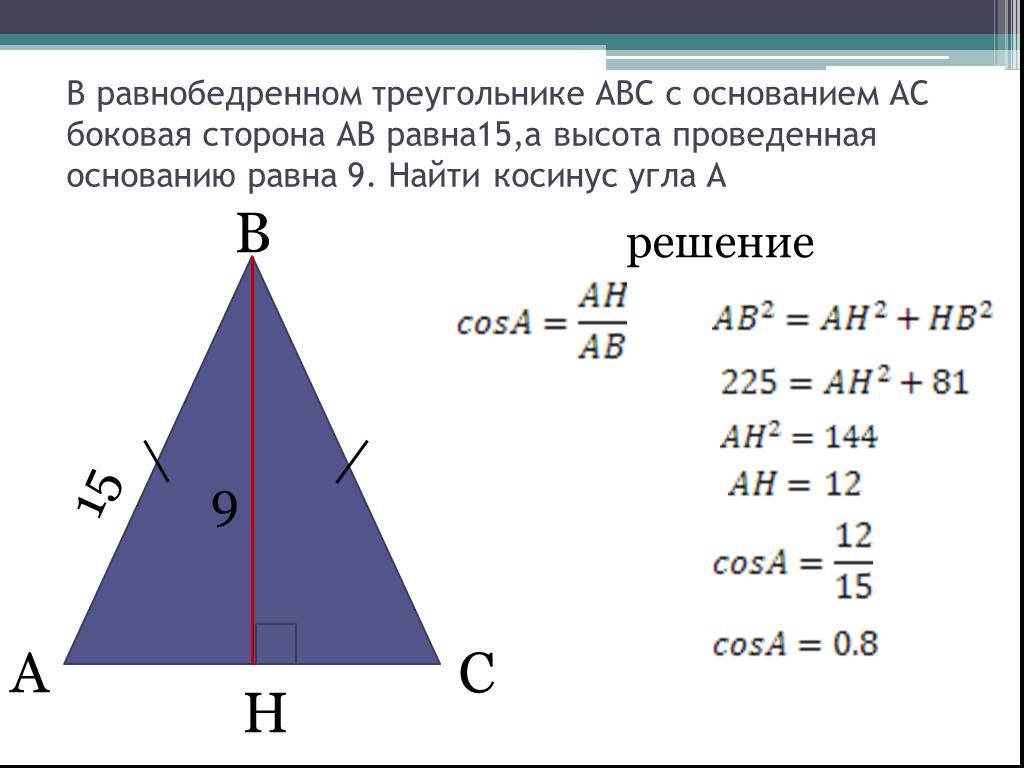 ед. Найдите длину высоты, если длина основания равна 9.0 единиц.

Решение:    Найти: Длина высоты.

Площадь прямоугольной доски = 720 кв. ед. (данные)
Длина основания = 90 ед.
Используя формулу высоты треугольника, 90 177 Высота треугольника (h) = (2 × Площадь) ÷ основание 90 177 =(2 × 720)/90 90 177 = 16 единиц

Ответ: Длина высоты треугольной доски 16 единиц.

Пример 2:  Вычислите длину высоты треугольника, проведенного из вершины A, стороны которого a, b.c равны 8 футам, 7 футам, 9футов соответственно.  

Решение:  Найти: Высота треугольника.
Полупериметр = s = (9 + 7 + 8)/2 = 24/2 = 12 футов 90 177 Используя формулу высоты треугольника, 90 177 Высота треугольника (h) = \(\dfrac{2 \sqrt{s(sa)(sb)(sc)}}{a}\)
Высота \(h_a= \dfrac{2 \sqrt{12(12-8)(12-7)(12-9)}}{8}\)
= \(\dfrac{2 \sqrt{12\\times 4\\times 5\\times 3}}{8}\)
= (12√ 5)/4
= 3 √ 5 футов

Ответ: Длина высоты треугольника, проведенного из вершины А, равна 3√ 5 футов.

Пример 3: Найдите высоту равностороннего треугольника, длина стороны которого равна 8 единицам.

Решение:    Найти: длину высоты равностороннего треугольника.
Использование формулы высоты треугольника для равностороннего треугольника h= (a√ 3)/2, где «a» – сторона треугольника 90 177 h = (8√ 3)/2 фута = 6,928 единиц.

Ответ:   Длина высоты равностороннего треугольника – 6,928 единицы.

Часто задаваемые вопросы о формуле высоты треугольника

Какова высота формулы равностороннего треугольника?

Формула высоты треугольника для равностороннего треугольника выражается как:  h= (a√ 3)/2. Где «а» – сторона равностороннего треугольника.

Какова высота формулы треугольника для прямоугольного треугольника?

Высота в формуле прямоугольного треугольника задается как h= √xy, где x и y – длины отрезков гипотенузы, деленные на высоту. Высота прямоугольного треугольника равна среднему геометрическому отрезков гипотенузы, образованных этой высотой.

No related posts.