Фотон рассеялся под углом 120 на покоившемся свободном электроне: Задачи по физике и математике с решениями и ответами

alexxlab / / Разное

StudyPort.Ru — Квантовая природа излучения

Страница 1 из 3

173. Определите, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость Re ослабилась в 16 раз.

 

174. Температура внутренней поверхности муфельной печи при открытом отверстии площадью 30 см2 равна 1,3 кК. Принимая, что отверстие печи излучает как черное тело, определите, какая часть мощности рассеивается стенками, если потребляемая печью мощность составляет 1,5 кВт.

175. Энергетическая светимость черного тела Re = 10 кВт/м2. Определите длину волны, соответствующую максимуму спектральной плотности энергетической светимости этого тела.

176. Определите, как и во сколько раз изменится мощность излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с λ1 = 720 нм до λ2 = 400 нм.

177. Черное тело находится при температуре T1 = 3 кК. При остывании тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на Δλ = 8 мкм. Определите температуру T2, до которой тело охладилось.

178. Черное тело нагрели от температуры T1 = 600 К до T2 = 2400 К. Определите: 1) во сколько раз увеличилась его энергетическая светимость; 2) как изменилась длина волны, соответствующая максимуму спектральной плотности энергетической светимости.

179. Площадь, ограниченная графиком спектральной плотности энергетической светимости rλ,T черного тела, при переходе от термодинамической температуры T1 к температуре T2 увеличилась в 5 раз. Определите, как изменится при этом длина волны Lmax , соответствующая максимуму спектральной плотности энергетической светимости черного тела.

180. В результате нагревания черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилась с λ1 = 2,7 мкм до λ2 = 0,9 мкм. Определите, во сколько раз увеличилась: 1) энергетическая светимость тела; 2) максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного тела возрастает по закону (rλ,T)max = CT5, где C = 1,3*10-5 Вт/(м3*К5).

181. Определите, какая длина волны соответствует максимальной спектральной плотности энергетической светимости (rλ,T)max, равной 1,3*1011 Вт/м3.

182. Считая никель черным телом, определите мощность, необходимую для поддержания температуры расплавленного никеля 1453 °С неизменной, если площадь его поверхности равна 0,5 см2. Потерями энергии пренебречь.

183. Металлическая поверхность площадью S = 15 см2, нагретая до температуры T = 3 кК, излучает в одну минуту 100 кДж. Определите: 1) энергию, излучаемую этой поверхностью, считая ее черной; 2) отношение энергетических светимостей этой поверхности и черного тела при данной температуре.

184. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определите: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения.

185. Определите температуру тела, при которой оно при температуре окружающей среды t0 = 23 °С излучало энергии в 10 раз больше, чем поглощало.

186. Считая, что тепловые потери обусловлены только излучением, определите, какую мощность необходимо подводить к медному шарику диаметром d = 2 см, чтобы при температуре окружающей среды t0 = -13 °С поддерживать его температуру равной t = 17 °С. Примите поглощательную способность меди AT = 0,6.

187. Определите силу тока, протекающего по вольфрамовой проволоке диаметром d = 0,8 мм, температура которой в вакууме поддерживается постоянной и равной t = 2800 °С. Поверхность проволоки считать серой с поглощательной способностью AT = 0,343. Удельное сопротивление проволоки при данной температуре ρ = 0,92*10-4 Ом*см. Температура окружающей проволоку среды t0 = 17 °С.

192. Используя формулу Планка, определите спектральную плотность потока излучения единицы поверхности черного тела, приходящегося на узкий интервал длин волн Δλ = 5 нм около максимума спектральной плотности энергетической светимости, если температура черного тела T = 2500 К.

194. Для вольфрамовой нити при температуре T = 3500 К поглощательная способность AT = 0,35. Определите радиационную температуру нити.

196. Определите максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U0 = 3,7 В.

198. Красная граница фотоэффекта для некоторого металла равна 500 нм. Определите минимальное значение энергии фотона, вызывающего фотоэффект.

200. Фотоэлектроны, вырываемые с поверхности металла, полностью задерживаются при приложении обратного напряжения U0 = 3 В. Фотоэффект для этого металла начинается при частоте падающего монохроматического света ν0 = 6*1014 с-1. Определите: 1) работу выхода электронов из этого металла; 2) частоту применяемого излучения.

 

Квантовые свойства излучения и частиц

    Представления о дискретной структуре материи зародилось в XIX веке.
    В 1811 г. А. Авогадро предположил, что в равных объемах различных газов при одинаковой температуре содержится одинаковое количество молекул. Гипотеза Авогадро объяснила многие макроскопические свойства вещества на основе молекулярной теории. В данном представлении материя является не сплошной средой, а дискретной, состоящей из отдельных молекул, то есть квантованной.
    Следующий важный шаг в представлении о дискретной структуре вещества был сделан на основе работ М. Фарадея (1833 г.) по электролизу. Из опытов Фарадея следовало, что электрический заряд, как и материя, не является непрерывным, а состоит из отдельных частиц, имеющих минимальный электрический заряд.
    В 1897 г., изучая явление электрического разряда в газах, Дж. Томсон открыл электрон – мельчайшую частицу, имеющую единый отрицательный заряд. Заряд электрона был измерен Р. Милликеном в 1912 г. Важный шаг в понимании квантовой дискретной структуры излучения был сделан М. Планком. Явление дифракции электронов подтвердило корпускулярно-волновую природу частиц.

3.1. Излучение абсолютно черного тела. Формула Планка
3.2. Фотоэффект
3.3. Эффект Комптона
3.4. Корпускулярно-волновой дуализм
3.5. Дифракция электронов
3.6. Принцип неопределенности В. Гейзенберга
       Задачи

2.1. Излучение абсолютно черного тела. Формула Планка


Рис. 2.1. Распределение энергии в спектре теплового излучения абсолютно черного тела.

    В классической физике плотность излучения абсолютно черного тела описывается законом Рэлея-Джинса

ρ(ν) ≈ 8πν2kT/c3,(2.1)

где ν − частота излучения, k − постоянная Больцмана, T − абсолютная температура. В области низких частот формула Рэлея-Джинса хорошо описывает экспериментальные данные. Однако в области высоких частот расхождения с экспериментом были настолько существенны, что возникшую ситуацию стали называть «ультрафиолетовой катастрофой».
    В 1900 г. была опубликована работа М. Планка, посвященная проблеме теплового излучения тел. Планк моделировал вещество как совокупность гармонических осцилляторов различной частоты ν. Предположив, что излучение происходит не непрерывно, а порциями – квантами hν, он получил формулу распределения плотности энергии в спектре теплового излучения U(T,ν), которая хорошо согласовывалась с опытными данными

(2. 2)

 где k – постоянная Больцмана, T – абсолютная температура, ν – частота излучения, h – постоянная Планка

h = 6.62·10-34 Дж·с = 6.62·10-27 эрг·с.

В квантовой теории чаще используют приведенную постоянную Планка ћ

ћ = h/2π = 1.05·10-34Дж·с = 6.58×10-22 МэВ·с,

которая также называется постоянной Планка.

Закон распределения Планка для излучения абсолютно черного тела

Плотность энергии в интервале dν при частоте ν: dU(ν) = r(ν)dν,

.

Закон Релея-Джинса (низкочастотный предел распределения Планка)

ρ(ν) ≈ 8πν2kT/c3, hν << kT.

Закон Стефана-Больцмана (полная плотность энергии)

. = 2

Закон Вина (высокочастотный предел распределения Планка)

hν >> kT.

    Через пять лет А. Эйнштейн, обобщив идею Планка, показал, что квантованность является общим свойством электромагнитного излучения. Согласно идеям Эйнштейна электромагнитное излучение состоит из квантов, названных позднее фотонами. Каждый фотон имеет определенную энергию E и импульс :

Е = ћω, = ћ//, ω = 2πν(2.3)

где и ω − приведенная длина волны и частота фотона, − единичный вектор в направлении распространения волны.

= λ/2π,  ω = 2πν.(2.4)

Необходимо помнить, что истинной длиной волны является λ, а не .

3.2. Фотоэффект

    Фотоэффект был открыт Г. Герцем в 1887 г. и подробно исследован А.Г. Столетовым. При облучении металлической поверхности светом из неё вылетают электроны. Было установлено, что энергии вылетающих электронов не зависят от интенсивности излучения и определяются только его частотой. Кинетическая энергия электрона Te, вылетающего из металла под действием фотона с энергией ћω

ћω = Aвых + Te,(3.5)

где Aвых – работа выхода металла. Эта формула была написана Эйнштейном в 1905 г. примерно через полтора десятка лет после первых экспериментов А.Г. Столетова. Представления о квантованности электромагнитного излучения позволили объяснить закономерности фотоэффекта.

3.3. Эффект Комптона

    На основе квантовой теории А.  Комптоном было объяснено явление упругого рассеяния электромагнитного излучения на свободных электронах, сопровождающееся увеличением длины волны излучения (эффект Комптона). Из законов сохранения энергии и импульса следует формула Комптона для изменения длины волны фотона Δλ, рассеянного под углом θ,

Δλ = λ‘ – λ = λ0(1 – cosθ),(2.6)

где λ и λ‘ – соответственно длины волн падающего и рассеянного фотона,
λ0 = h/mec = 2.4·10-10 см = 0.024 Å – комптоновская длина волны электрона. Изменение длины волны фотона Δλ не зависит от длины волны падающего фотона. Оно определяется только углом рассеяния фотона θ. При комптоновском рассеянии увеличивается длина волны фотона, т. е. уменьшается его частота. Это уменьшение частоты очевидное с точки зрения корпускулярной теории (уменьшение энергии фотона происходит за счёт передачи части энергии электрону отдачи) не удавалось объяснить в классической электродинамике, где частота света при рассеянии не должна изменяться.

Рис. 2.2 Спектры рассеянного излучения для трех углов рассеяния. Абсцисса пропорциональна длине излучения, ордината – интенсивности излучения. а) Спектр падающего излучения; б) – г) спектры рассеянного на графите излучения.

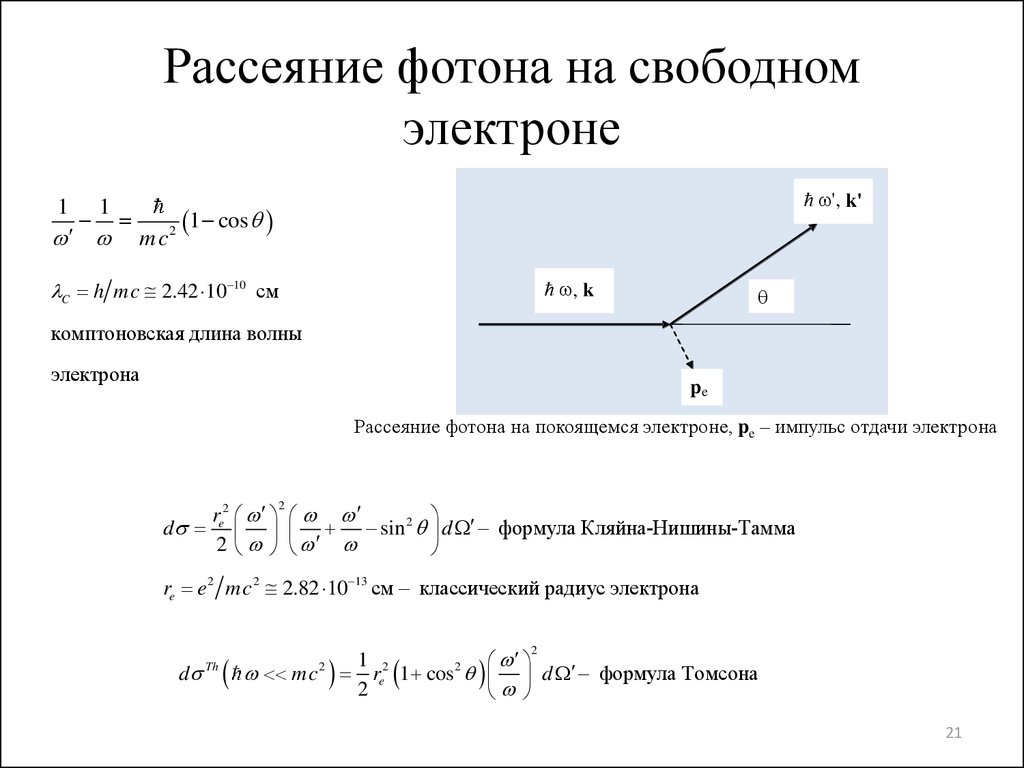
Пики слева на всех графиках отвечают фотонам с исходной длиной волны λ, которые рассеиваются на сильно связанных электронах с эффективной массой, равной массе атома. Максимумы справа имеют длину волны λ’, соответствующую формуле Комптона.

Эффект Комптона

Упругое рассеяние фотона на электроне.
Законы сохранения энергии и импульса:

Eγ + E0 = E‘γ + Ee,
γ = ‘γ + e,

Eγ = hc/λ – энергия налетающего фотона,
E0 = mec2 = 0.

511 МэВ — энергия покоя электрона,
E‘γ = hc/λ‘ – энергия рассеянного фотона,
Ee – энергия электрона отдачи,
p = h/λ – величина импульса налетающего фотона,
p‘ = h/λ‘ – величина импульса рассеянного фотона,
pe – величина импульса электрона отдачи,
θ – угол рассеяния фотона,
φ – угол рассеяния электрона отдачи

Δλ = λ‘ – λ = λ0(1 – cosθ),

λ0 = h/(mec) = 0.024 Å – комптоновская длина волны электрона.

3.4. Корпускулярно-волновой дуализм

    Важным этапом в становлении современного понимания структуры материи стала выдвинутая де Бройлем в 1924 г. гипотеза об универсальности корпускулярно-волнового дуализма. Согласно этой гипотезе не только фотоны, но и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами. Де Бройль предложил, что каждой частице, движущейся с импульсом

р, следует приписать определённую длину волны – дебройлевскую длину волны. Соотношения, связывающие корпускулярные и волновые свойства частиц те же, что были установлены ранее для фотонов

Е = ћω, р = ћk = ћ/.(2.7)

    Опытами, подтверждающими идею корпускулярно-волнового дуализма, были опыты по дифракции электронов на монокристаллах.

3.5. Дифракция электронов

    В 1927 г. Дж. Томсон исследовал прохождение электронов с энергией от 10 до 40 кэВ через тонкую металлическую фольгу и наблюдал дифракционную картину, аналогичную дифракционной картине фотонов соответствующих энергий.

 

Рис. 3.3. Опыт Томсона. а) Схема установки для наблюдения дифракции на поликристаллической алюминиевой мишени. б) Дифракционная картина, полученная при рассеянии рентгеновских лучей λ = 0.071 нм. в) Дифракционная картина, полученная при рассеянии электронов с энергией 600 эВ (увеличена в 1. 6 раза для сравнения с б)).

    Дифракционная картина наблюдалась в опытах К. Дэвиссона и Л. Джермера (1927 г.) по изучению отражения электронов от монокристалла никеля. Дифракция появлялась в результате рассеяния электронов на атомах в узлах кристаллической решетки.
    Позднее наблюдалась дифракция нейтронов и других частиц. Метод дифракции частиц в настоящее время широко используется в изучении строения и свойств вещества. Атомные ядра являются объектом с характерным размером ~ 10–12 см. Поэтому рассеяние частиц с длиной волны де Бройля
λ < 10–12 см позволяет исследовать эти объекты. Наиболее точные измерения размеров ядер были выполнены при рассеянии электронов и протонов высоких энергий.
Длина волны λ частицы зависит от ее массы m и кинетической энергии T:

(2.8)

3.

6. Принцип неопределенности Гейзенберга

    Экспериментальное подтверждение идеи корпускулярно-волнового дуализма привело к пересмотру привычных представлений о движении частиц и способа описания частиц. Для классических материальных точек характерно движение по определенным траекториям, так, что их координаты и импульсы в любой момент времени точно определены. Для квантовых частиц это утверждение неприемлемо, так как для квантовой частицы импульс частицы связан с ее длиной волны, а говорить о длине волны в данной точке пространства бессмысленно. Для квантовой частицы нельзя одновременно точно определить значения ее координат и импульса. Неопределенность в значении координаты частицы Δx и неопределенность в значении компоненты импульса частицы Δрx связаны соотношением неопределенности, установленным В. Гейзенбергом в 1927 году

Δx·Δрx ≥ ћ.(2.9)

    Физический смысл соотношения неопределённости (принципа неопределенности) состоит в том, что невозможно одновременно точно определить положение частицы (x,y,z) и её импульс

4.2: Комптоновское рассеяние — Physics LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    9728
    • Paul D’Alessandris
    • Общественный колледж Монро

    Комптоновское рассеяние относится к рассеянию света на свободных электронах. Экспериментально невозможно создать мишень из полностью свободных электронов. Однако, если падающие фотоны имеют энергию, намного превышающую типичные энергии связи электронов с атомами, электроны будут «выбиваться» фотонами из атомов и действовать как свободные частицы. Следовательно, комптоновское рассеяние обычно относится к рассеянию фотонов высокой энергии от атомных мишеней.

    Если бы свет был чисто волновым явлением, падающая волна с определенной частотой заставляла бы электрон колебаться с той же частотой. Тогда колеблющийся электрон будет излучать электромагнитные волны этой частоты. Таким образом, рассеянный свет и падающий свет будут иметь, с точностью до небольшой вариации из-за эффекта Доплера, одинаковую частоту. Это не то, что видно экспериментально. 92 = Е’ + Е_е\]

    \(x\)-сохранение импульса:

    \[ pc + 0 = p’c \cos \theta + p_e c \cos \phi\]

    и \(y\)-сохранение импульса:

    \[ 0 + 0 = p’c \sin \theta + p_e c \sin \phi\]

    Для фотонов \(E = pc\), поэтому уравнения импульса можно записать так:

    \[ p_x: E = E’ \cos \theta + p_e \cos \phi\]

    \[ p_x: 0 = E’ \cos \theta — p_e \sin \phi\]

    Экспериментально легче обнаружить рассеянный фотон, чем рассеянный электрон, поэтому мы исключим параметры электрона и выведем взаимосвязь между различными параметрами фотона. Чтобы исключить \(\phi\), решите \(x\)-импульс и \(y\)-импульс для \(\cos \phi\) и \(\sin \phi\), а затем возведите их в квадрат и добавьте вместе: 92 — 2EE’ = -2EE’ \cos \theta\]

    Перестановка дает

    Этот результат напрямую связывает приходящую длину волны с длиной волны рассеяния и углом рассеяния. Все эти параметры легко измеряются экспериментально. За теоретическое объяснение и экспериментальную проверку рассеяния фотонов высоких энергий американец Артур Комптон был удостоен Нобелевской премии в 1927 г.

    Фотон с энергией 800 кэВ сталкивается с покоящимся электроном. После столкновения регистрируется фотон с энергией 650 кэВ. Найти кинетическую энергию и угол рассеяния электрона. 92}( 1- \cos \theta)\]

    где

    • \(\lambda’\) длина волны рассеянного фотона,
    • \(\lambda \) — длина волны падающего фотона,
    • и \(\theta\) — угол рассеяния фотона.

    Для нахождения кинетической энергии рассеянного электрона не требуется использование формулы Комптона. Если фотон изначально имеет \(800\, \text{кэВ}\), а после рассеяния имеет \(650 \text{кэВ}\), то \(150\, \text{кэВ}\) должен был перейти в электрон. Таким образом, \(KE_{электрон} = 150 \text{кэВ}\). 9{-3} = \lambda = \frac{1240 \text{eVnm}}{511 \text{кэВ}}(1-\cos\theta)\]

    \[0,1484 = (1-\cos\theta) \]

    \[\theta = 31,6°\]

    Однако это угол рассеяния фотона, а не электрона!

    Чтобы найти угол рассеяния электрона, примените закон сохранения импульса в направлении, перпендикулярном начальному направлению фотона.

    \[0 = p_{\text{рассеянный фотон}}c(\sin\theta)-p_{электрон}c(\sin\phi)\]

    \[p_{\text{рассеянный фотон}}c (\sin\theta) =p_{электрон}c(\sin\phi)\] 92}(\sin\phi)\]

    \[\sin\phi =0,813\]

    \[\phi = 54,4\]

    Эта страница под названием 4.2: Compton Scattering распространяется под лицензией CC BY-NC-SA 4.0, ее автор, ремикс и/или куратор Пол Д’Алессандрис.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        Поль Д’Алессандрис
        Лицензия
        CC BY-NC-SA
        Версия лицензии
        4,0
        Показать оглавление
        нет
      2. Теги
        1. Комптоновское рассеяние

      [Решено] Рентгеновские лучи с длиной волны 0,4500 нм рассеиваются на свободных электронах

      Рентгеновские лучи с длиной волны 0,4500 нм рассеиваются на свободных электронах в мишени. Какова длина волны фотонов, рассеянных под углом 60° к падающим лучам? (h = 6,63 × 10 -34 Дж, м e = 9,11 × 10 -31 кг, c = 3 × 10 8 м/с)

      1. 0,4476 нм
      2. 0,4512 нм
      3. 0,4524 нм
      4. 0,4488 нм

      Вариант 2 : 0,4512 нм

      March AI Junior 5 Junior 2 ATC

      2 90 1 официальный документ (смена 1)

      6,3 тыс. пользователей

      120 вопросов

      120 баллов

      120 минут

      Концепция:

      Комптоновское рассеяние: Это рассеяние фотона заряженной частицей, обычно электроном. Это приводит к уменьшению энергии (или увеличению длины волны) фотона (обычно это рентгеновский или гамма-фотон).

      Соотношение Комптона определяется как: \;\left( {1 — \cos \theta } \right)\)

      где, λ = начальная длина волны, λ’ = длина волны после & рассеяния, h = постоянная Планка, m e = масса покоя электрона, c = скорость света, θ = угол рассеяния

      \(\frac{h}{{{m_e}c}}\) известен как комптоновская длина волны электрона и равен 2,43 × 10 -12 м.

      99}\;\)

      λ’ = 0,45 + 0,0012 = 0,4512 нм

      Скачать решение PDF

      Поделиться в WhatsApp

      Последние обновления AAI JE ATC

      Последнее обновление: 20 апреля 2023 г.

      Выпущена система показателей AAI JE ATC!   Компьютерный тест был проведен 21 февраля 2023 года. Это относится к циклу 2022 года. Ранее были объявлены даты экзаменов AAI JE ATC для проверки приложений, теста Viva и психоактивных веществ. Тест будет запланирован на период с 1 по 4 мая 2023 года, с 8 по 12 мая 2023 года и 15 мая 2023 года. Ранее были объявлены результаты AAI JE ATC для письменного теста. Набор AAI JE ATC Recruitment был выпущен для общего количества вакансий 356. Процесс подачи заявок был активен с 22 декабря 2022 года по 21 января 2023 года. Отбор кандидатов осуществляется на основе компьютерного теста, голосового теста и теста на употребление психоактивных веществ.

      No related posts.

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *