модуль числа на примерах с int и float, синтаксис функции
Встроенная функция abs(x) в Python возвращает абсолютное значение аргумента x, который может быть целым или числом с плавающей точкой, или же объектом, реализующим функцию __abs__(). Для комплексных чисел функция возвращает их величину. Абсолютное значение любого числового значения -x или +x — это всегда соответствующее положительное +x.
| Аргумент | x | целое число, число с плавающей точкой, комплексное число, объект, реализующий __abs__() |
| Возвращаемое значение | |x| | возвращает абсолютное значение входящего аргумента |
Пример abs() с целым числом
Следующий код демонстрирует, как получить абсолютное значение 42 положительного числа 42.
Копировать Скопировано Use a different Browser
x = 42 abs_x = abs(x) print(f"Абсолютное значение {x} это {abs_x}") # Вывод: Абсолютное значение 42 это 42
Вывод: «Абсолютное значение 42 это 42».
То же самое, но уже с отрицательным -42.
Копировать Скопировано Use a different Browser
x = -42 abs_x = abs(x) print(f"Абсолютное значение {x} это {abs_x}") # Вывод: Абсолютное значение -42 это 42
Пример с числом float
Вот как получить абсолютное значение 42.42 и для -42.42:
Копировать Скопировано Use a different Browser
x = 42.42 abs_x = abs(x) print(f"Абсолютное значение {x} это {abs_x}") # Абсолютное значение 42.42 это 42.42 x = -42.42 abs_x = abs(x) print(f"Абсолютное значение {x} это {abs_x}") # Абсолютное значение -42.42 это 42.42
Комплексное число
Абсолютное значение комплексного числа (3+10j).
Копировать Скопировано Use a different Browser
complex_number = (3+10j) abs_complex_number = abs(complex_number) print(f"Абсолютное значение {complex_number} это {abs_complex_number}") # Абсолютное значение (3+10j) это 10.44030650891055
abs() vs fabs()
abs(x) вычисляет абсолютное значение аргумента x. По аналогии функция
По аналогии функция fabs(x) модуля math вычисляет то же значение. Разница лишь в том, что math.fabs(x) возвращает число с плавающей точкой, а abs(x) вернет целое число, если в качестве аргумента было целое число. Fabs расшифровывается как float absolute value.
Пример c fabs():
Копировать Скопировано Use a different Browser
x = 42 print(abs(x)) # 42 import math print(math.fabs(x)) # 42.0
abs() vs. np.abs()
И abs() в Python, и np.abs() в NumPy вычисляют абсолютное значение числа, но есть два отличия. np.abs(x) всегда возвращает число с плавающей точкой. Также np.abs(x) принимает массив NumPy, вычисляя значение для каждого элемента коллекции.
Пример:
Копировать Скопировано Use a different Browser
x = 42 print(abs(x)) # 42 import numpy as np print(np.fabs(x)) # 42.0 a = np.array([-1, 2, -4]) print(np.abs(a)) # [1 2 4]
abs и np.abs абсолютно идентичны. Нет разницы какой использовать. У первой преимущество лишь в том, что ее вызов короче.
Вывод
Функция abs() — это встроенная функция, возвращающая абсолютное значение числа. Она принимает целые, с плавающей точкой и комплексные числа на вход.
Если передать в n и сохранит тип. Для целого числа — целое число. Для числа с плавающей точкой — число с плавающей точкой.
Копировать Скопировано Use a different Browser
>>> abs(20) 20 >>> abs(20.0) 20.0 >>> abs(-20.0) 20.0
Комплексные числа состоят из двух частей и могут быть записаны в форме a + bj, где a и b — это или целые числа, или числа с плавающей точкой. Абсолютное значение a + bj вычисляется математически как math.sqrt(a**2 + b**2).
Копировать Скопировано Use a different Browser
>>> abs(3 + 4j) 5.0 >>> math.sqrt(3**2 + 4**2) 5.0
Таким образом, результат всегда положительный и всегда является числом с плавающей точкой.
Максим
Я создал этот блог в 2018 году, чтобы распространять полезные учебные материалы, документации и уроки на русском. На сайте опубликовано множество статей по основам python и библиотекам, уроков для начинающих и примеров написания программ.
Python Q https://yandex.ru/q/loves/python Online
Python QCEO [email protected]://secure.gravatar.com/avatar/b16f253879f7349f64830c64d1da4415?s=96&d=mm&r=gCEO PythonruPythonАлександрРедакторhttps://t.me/cashncarryhttps://pythonru.com/https://yandex.ru/q/profile/cashnc/[email protected] Zabrodin2018-10-26OnlinePython, Programming, HTML, CSS, JavaScriptДля вычисления модуля числа х используется функция
Содержание
- 1 Модуль числа
- 2 Вычисление
- 2.
 1 Свое решение
1 Свое решение
- 2.
- 3 Модуль комплексного числа
- 4 Страницы
- 5 четверг, 7 апреля 2011 г.
- 5.1 Модуль числа
- 6 Аннотация научной статьи по математике, автор научной работы — Аглиуллин И.Н., Кирпичников А.П., Чони Ю.И.
- 7 Похожие темы научных работ по математике , автор научной работы — Аглиуллин И.Н., Кирпичников А.П., Чони Ю.И.
- 8 Текст научной работы на тему «Аппроксимация комплекснозначных функций с использованием приближенных формул для вычисления модуля комплексного числа»
Очень часто возникает необходимость вычисления модуля числа в Python. Рассмотрим, что такое модуль числа, какие есть способы его вычисления. Так же отдельно коснемся комплексных чисел.
Модуль числа
Часто в программировании требуется вычислить абсолютное значение числа. Иначе говоря, отбросить знак.
При вычислении модуля возможны 3 ситуации:
- Когда число больше 0. Если взять его по модулю — не изменится.

- Модуль нуля так же равен нулю.
- У отрицательного числа отбрасываем знак. То есть умножаем его на -1.
Но это все справедливо только для действительных чисел. Чему же тогда будет равен модуль комплексных?
Комплексное число состоит из действительной составляющей и мнимой. Геометрически это можно представить как 2 ортогональные оси: действительную и мнимую. Отмечаем на координатных осях требуемую точку. Модулем будет длина отрезка, проведенного из начала координат в эту точку.
Вычисление
Вычислять модуль можно следующими способами:
- Используя стандартную функцию abs.
- С помощью функции fabs библиотеки math.
- При помощи самостоятельно написанной функции.
Все эти функции работают как в Python 2, так и в Python 3.
Для вычисления в Python модуля числа используется функция abs. Результат функции того же типа, которого был аргумент.
Можно так же воспользоваться функцией fabs из библиотеки math.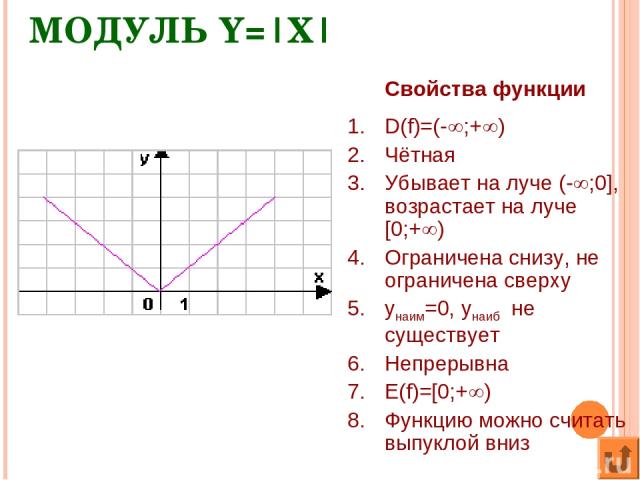
Свое решение
Если по каким то причинам нет возможности или желания использовать стандартные функции, то можно написать свое решение.
Например, можно вычислить воспользоваться тернарным оператором.
На основе такого условия сделаем свою функцию.
Модуль комплексного числа
Мы разобрались как происходит вычисление с действительными числами. Теперь посмотрим, как в языке программирования Python можно получить модуль комплексного.
Функцией fabs мы не сможем воспользоваться. Если попытаемся это сделать, то получим ошибку приведения комплексного числа к действительному (TypeError).
А вот с помощью abs преобразование удается.
Или же напишем свою функцию:
Результаты получились одинаковыми. Но нам все равно пришлось подключить библиотеку math для вычисления квадратного корня.
Простая математика, Excel. Как минимум. Но не только.
Страницы
четверг, 7 апреля 2011 г.
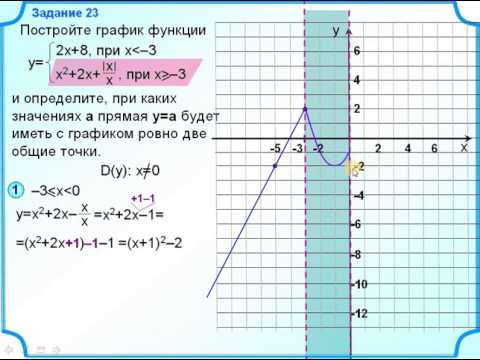
Модуль числа
Пример .
Формула =ABS(55-62) вернет число 7
Для вычисления модуля комплексного числа используется инженерная функция МНИМ.ABS(комплексное число) . Комплексное число записывается в виде «x+yi» (кавычки обязательно).
Пример .
Формула =МНИМ.ABS(«3+4i») вернет число 5
Аннотация научной статьи по математике, автор научной работы — Аглиуллин И.Н., Кирпичников А.П., Чони Ю.И.
Рассмотрена задача аппроксимации комплекснозначной функции с использованием минимаксного критерия . Для вычисления модуля комплексного числа предлагаются приближенные формулы, являющиеся кусочно-линейными зависимостями, которые облегчают вычисления коэффициентов аппроксимации . Предложен специальный алгоритм решения задачи.
Похожие темы научных работ по математике , автор научной работы — Аглиуллин И.Н., Кирпичников А.П., Чони Ю.И.
Текст научной работы на тему «Аппроксимация комплекснозначных функций с использованием приближенных формул для вычисления модуля комплексного числа»
ИНФОРМАТИКА, ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА И УПРАВЛЕНИЕ
И. Н. Аглиуллин, А. П. Кирпичников, Ю. И. Чони
Н. Аглиуллин, А. П. Кирпичников, Ю. И. Чони
АППРОКСИМАЦИЯ КОМПЛЕКСНОЗНАЧНЫХ ФУНКЦИЙ С ИСПОЛЬЗОВАНИЕМ ПРИБЛИЖЕННЫХ ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ МОДУЛЯ КОМПЛЕКСНОГО ЧИСЛА
Ключевые слова: аппроксимация, минимаксный критерий, кусочно-линейная функция.
Рассмотрена задача аппроксимации комплекснозначной функции с использованием минимаксного критерия. Для вычисления модуля комплексного числа предлагаются приближенные формулы, являющиеся кусочно-линейными зависимостями, которые облегчают вычисления коэффициентов аппроксимации. Предложен специальный алгоритм решения задачи.
Keywords: approximation, minimax criterion, a piecewise linear function.
The paper is devoted to the problem of complex-valued function approximation with using the minimax criterion. Several formulas for estimating the amplitude of a complex value on the base of piecewise linear relations have been analyzed. As a result, calculations of the approximation coefficients can be greatly facilitated. A specific algorithm is proposed for solving the problem under consideration.
В задачах аппроксимации функций по результатам наблюдений наиболее
распространенным и удобным с вычислительной точки зрения является метод наименьших квадратов [1]. Статистические методы обработки наблюдений используются в различных областях знаний [2,3]. В некоторых случаях, однако, оптимизация проектируемых устройств требует минимаксного подхода. Например, в интересах ограничения осцилляций переходного процесса в системах регулирования технологических процессов (в химической промышленности в том числе) или ограничения уровня побочного излучения в акустике и радиоэлектронике. Т.к. функционал, отражающий соответствующий критерий, не линеен и не дифференцируется, то при вычислении коэффициентов аппроксимации появляются определенные трудности. В ряде случаев эти трудности удается обойти, используя приближенные формулировки критерия, сводящиеся к системе линейных ограничений.
Рассмотрим следующую задачу. Не нарушая общности рассуждений, будем считать, что в некоторых точках (¿ = 1,т) интервала [0,Т] наблюдается комплекснозначная функция
действительного аргумента 1. По результатам наблюдений необходимо построить
По результатам наблюдений необходимо построить
аппроксимирующую зависимость по заданной системе функций
Гк (о = Гк (о +;/к (о, (к = ю (2)
Неизвестные коэффициенты аппроксимации ск =ск +Усй будем определять из выражения
Функция (3) не дифференцируема, поэтому для вычисления коэффициентов аппроксимации нельзя использовать градиентные методы поиска экстремума. Кроме того, чрезвычайно актуальной является проблема сокращения времени решения задачи с точки зрения принятия решений в реальном масштабе времени, например в технических (радиоэлектронных) системах обнаружения объекта. Поэтому, оправдан интерес к поиску приближенных алгоритмов решения поставленной задачи аппроксимации комплекснозначной функции. В частности, в формуле (3) модуль комплексного числа достаточно сложно зависит от неизвестных коэффициентов аппроксимации. Рассмотрим некоторые приближенные методы вычисления модуля комплексного числа.
Пусть г = х+ ]’у, комплексное число, тогда |г| = -Ух2 +у2 . Рассмотрим другую приближенную формулу вычисления модуля комплексного числа, например:
— Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Здесь ср — аргумент комплексного числа. Очевидно, что приведенная формула вычисления модуля комплексного числа является кусочно-линейной зависимостью. Если положить |z| = 1 и учесть, что х = cos Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Теперь при любом значении аргумента 1
В этом случае получаем следующую уточненную геометрическую иллюстрацию оценки модуля комплексного числа с использованием дуг четырех окружностей (рис. 1).
Множитель « в формуле (7) необходимо подобрать так, чтобы приближенная формула вычисления модуля давала как можно меньшую погрешность вычислений. При этом для определения « можно воспользоваться несколькими способами.
Определим« из условия, чтобы максимальная погрешность была как можно меньше. В этом случае для зависимости р = a cos Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Рис. 2 — Аппроксимация модуля комплексного числа четырьмя дугами
После некоторых преобразований получаем
Для вычисления « третьим способом можно использовать условие, что окружности р = 1 и р = a cos Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы. сш/а б -аиу/а б))
сш/а б -аиу/а б))
13. Вычисляется очередное приближение
14. Далее либо возврат к шагу 8, либо завершение вычислений.
Завершение вычислений происходит, когда все значения Ut достаточно малы или тогда, когда активными станут 2n неравенств и система уравнений на 10 м шаге будет несовместна.
1. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической обработки наблюдений, М., Физматгиз, 1958. — С. 340.
2. Исмагилов И.И., Кирпичников А.П., Костромин А.В., Хасанова С. Ф. Применение быстрого дискретного преобразования к фазовому сплайн-анализу макроэкономической динамики // Вестник Казанского технологического университета. — 2015. — Т. 18. № 7. -С. 228-231.
3. Емалетдинова Л.Ю., Катасёв А.С., Кирпичников А.П. Нейронечеткая модель аппроксимации сложных объектов с дискретным выходом// Вестник Казанского технологического университета. — 2014. — Т. 17. № 1. -С. 295-300.
Для вычисления модуля числа х используется функция
Очень часто возникает необходимость вычисления модуля числа в Python.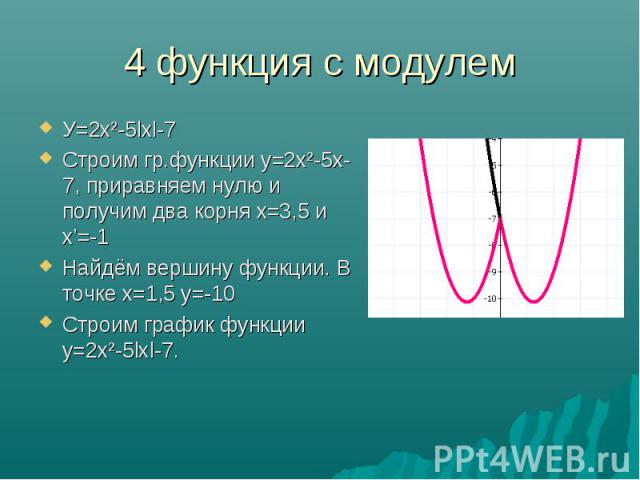 Рассмотрим, что такое модуль числа, какие есть способы его вычисления. Так же отдельно коснемся комплексных чисел.
Рассмотрим, что такое модуль числа, какие есть способы его вычисления. Так же отдельно коснемся комплексных чисел.
Модуль числа
Часто в программировании требуется вычислить абсолютное значение числа. Иначе говоря, отбросить знак.
При вычислении модуля возможны 3 ситуации:
- Когда число больше 0. Если взять его по модулю — не изменится.
- Модуль нуля так же равен нулю.
- У отрицательного числа отбрасываем знак. То есть умножаем его на -1.
Но это все справедливо только для действительных чисел. Чему же тогда будет равен модуль комплексных?
Комплексное число состоит из действительной составляющей и мнимой. Геометрически это можно представить как 2 ортогональные оси: действительную и мнимую. Отмечаем на координатных осях требуемую точку. Модулем будет длина отрезка, проведенного из начала координат в эту точку.
Вычисление
Вычислять модуль можно следующими способами
- Используя стандартную функцию abs.

- С помощью функции fabs библиотеки math.
- При помощи самостоятельно написанной функции.
Все эти функции работают как в Python 2, так и в Python 3.
Для вычисления в Python модуля числа используется функция abs. Результат функции того же типа, которого был аргумент.
Можно так же воспользоваться функцией fabs из библиотеки math. Библиотеку можно подключить с помощью from math import fabs .
Свое решение
Если по каким то причинам нет возможности или желания использовать стандартные функции, то можно написать свое решение.
Например, можно вычислить воспользоваться тернарным оператором.
На основе такого условия сделаем свою функцию.
Модуль комплексного числа
Мы разобрались как происходит вычисление с действительными числами. Теперь посмотрим, как в языке программирования Python можно получить модуль комплексного.
Функцией fabs мы не сможем воспользоваться. Если попытаемся это сделать, то получим ошибку приведения комплексного числа к действительному (TypeError).
А вот с помощью abs преобразование удается.
Или же напишем свою функцию:
Результаты получились одинаковыми. Но нам все равно пришлось подключить библиотеку math для вычисления квадратного корня.
Простая математика, Excel. Как минимум. Но не только.
Страницы
четверг, 7 апреля 2011 г.
Модуль числа
Пример .
Формула =ABS(55-62) вернет число 7
Для вычисления модуля комплексного числа используется инженерная функция МНИМ.ABS(комплексное число) . Комплексное число записывается в виде «x+yi» (кавычки обязательно).
Пример .
Формула =МНИМ.ABS(«3+4i») вернет число 5
Рассмотрена задача аппроксимации комплекснозначной функции с использованием минимаксного критерия . Для вычисления модуля комплексного числа предлагаются приближенные формулы, являющиеся кусочно-линейными зависимостями, которые облегчают вычисления коэффициентов аппроксимации . Предложен специальный алгоритм решения задачи.
Похожие темы научных работ по математике , автор научной работы — Аглиуллин И.
 Н., Кирпичников А.П., Чони Ю.И.
Н., Кирпичников А.П., Чони Ю.И.Текст научной работы на тему «Аппроксимация комплекснозначных функций с использованием приближенных формул для вычисления модуля комплексного числа»
ИНФОРМАТИКА, ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА И УПРАВЛЕНИЕ
И. Н. Аглиуллин, А. П. Кирпичников, Ю. И. Чони
АППРОКСИМАЦИЯ КОМПЛЕКСНОЗНАЧНЫХ ФУНКЦИЙ С ИСПОЛЬЗОВАНИЕМ ПРИБЛИЖЕННЫХ ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ МОДУЛЯ КОМПЛЕКСНОГО ЧИСЛА
Ключевые слова: аппроксимация, минимаксный критерий, кусочно-линейная функция.
Рассмотрена задача аппроксимации комплекснозначной функции с использованием минимаксного критерия. Для вычисления модуля комплексного числа предлагаются приближенные формулы, являющиеся кусочно-линейными зависимостями, которые облегчают вычисления коэффициентов аппроксимации. Предложен специальный алгоритм решения задачи.
Keywords: approximation, minimax criterion, a piecewise linear function.
The paper is devoted to the problem of complex-valued function approximation with using the minimax criterion. Several formulas for estimating the amplitude of a complex value on the base of piecewise linear relations have been analyzed. As a result, calculations of the approximation coefficients can be greatly facilitated. A specific algorithm is proposed for solving the problem under consideration.
Several formulas for estimating the amplitude of a complex value on the base of piecewise linear relations have been analyzed. As a result, calculations of the approximation coefficients can be greatly facilitated. A specific algorithm is proposed for solving the problem under consideration.
В задачах аппроксимации функций по результатам наблюдений наиболее
распространенным и удобным с вычислительной точки зрения является метод наименьших квадратов [1]. Статистические методы обработки наблюдений используются в различных областях знаний [2,3]. В некоторых случаях, однако, оптимизация проектируемых устройств требует минимаксного подхода. Например, в интересах ограничения осцилляций переходного процесса в системах регулирования технологических процессов (в химической промышленности в том числе) или ограничения уровня побочного излучения в акустике и радиоэлектронике. Т.к. функционал, отражающий соответствующий критерий, не линеен и не дифференцируется, то при вычислении коэффициентов аппроксимации появляются определенные трудности. В ряде случаев эти трудности удается обойти, используя приближенные формулировки критерия, сводящиеся к системе линейных ограничений.
В ряде случаев эти трудности удается обойти, используя приближенные формулировки критерия, сводящиеся к системе линейных ограничений.
Рассмотрим следующую задачу. Не нарушая общности рассуждений, будем считать, что в некоторых точках (¿ = 1,т) интервала [0,Т] наблюдается комплекснозначная функция
действительного аргумента 1. По результатам наблюдений необходимо построить
аппроксимирующую зависимость по заданной системе функций
Гк (о = Гк (о +;/к (о, (к = ю (2)
Неизвестные коэффициенты аппроксимации ск =ск +Усй будем определять из выражения
Функция (3) не дифференцируема, поэтому для вычисления коэффициентов аппроксимации нельзя использовать градиентные методы поиска экстремума. Кроме того, чрезвычайно актуальной является проблема сокращения времени решения задачи с точки зрения принятия решений в реальном масштабе времени, например в технических (радиоэлектронных) системах обнаружения объекта. Поэтому, оправдан интерес к поиску приближенных алгоритмов решения поставленной задачи аппроксимации комплекснозначной функции. В частности, в формуле (3) модуль комплексного числа достаточно сложно зависит от неизвестных коэффициентов аппроксимации. Рассмотрим некоторые приближенные методы вычисления модуля комплексного числа.
В частности, в формуле (3) модуль комплексного числа достаточно сложно зависит от неизвестных коэффициентов аппроксимации. Рассмотрим некоторые приближенные методы вычисления модуля комплексного числа.
Пусть г = х+ ]’у, комплексное число, тогда |г| = -Ух2 +у2 . Рассмотрим другую приближенную формулу вычисления модуля комплексного числа, например:
— Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Здесь ср — аргумент комплексного числа. Очевидно, что приведенная формула вычисления модуля комплексного числа является кусочно-линейной зависимостью. Если положить |z| = 1 и учесть, что х = cos Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Теперь при любом значении аргумента 1
В этом случае получаем следующую уточненную геометрическую иллюстрацию оценки модуля комплексного числа с использованием дуг четырех окружностей (рис. 1).
Множитель « в формуле (7) необходимо подобрать так, чтобы приближенная формула вычисления модуля давала как можно меньшую погрешность вычислений. При этом для определения « можно воспользоваться несколькими способами.
При этом для определения « можно воспользоваться несколькими способами.
Определим« из условия, чтобы максимальная погрешность была как можно меньше. В этом случае для зависимости р = a cos Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Рис. 2 — Аппроксимация модуля комплексного числа четырьмя дугами
После некоторых преобразований получаем
Для вычисления « третьим способом можно использовать условие, что окружности р = 1 и р = a cos Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
ау, Т у = sin ц>) и при замене окружности восемью дугами необходимо а и р подобрать так, чтобы уменьшить погрешности вычислений модуля комплексного числа по приближенной формуле (10). Для определения а и р можно воспользоваться теми же тремя способами, которые использовались ранее.
Определим а и р из условия, чтобы отклонения окружностей р = acos
При графическом изображении формул (9) можно убедиться в том, что при значениях Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы. сш/а б -аиу/а б))
сш/а б -аиу/а б))
13. Вычисляется очередное приближение
14. Далее либо возврат к шагу 8, либо завершение вычислений.
Завершение вычислений происходит, когда все значения Ut достаточно малы или тогда, когда активными станут 2n неравенств и система уравнений на 10 м шаге будет несовместна.
1. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической обработки наблюдений, М., Физматгиз, 1958. — С. 340.
2. Исмагилов И.И., Кирпичников А.П., Костромин А.В., Хасанова С. Ф. Применение быстрого дискретного преобразования к фазовому сплайн-анализу макроэкономической динамики // Вестник Казанского технологического университета. — 2015. — Т. 18. № 7. -С. 228-231.
3. Емалетдинова Л.Ю., Катасёв А.С., Кирпичников А.П. Нейронечеткая модель аппроксимации сложных объектов с дискретным выходом// Вестник Казанского технологического университета. — 2014. — Т. 17. № 1. -С. 295-300.
Определение модуля числа. Математика , 6 класс.
- Форум
- Архив
- Школы, Олимпиады, Вузы
Родители, кто в теме, какое определение модуля дают вашим детям?
По учебнику или учитель из своих источников? Если не трудно, напишите, на какой учебник опираетесь в своем ответе.
Меня что-то смущает, что в Петерсон модуль — это расстояние. По-моему, модуль это в первую очередь число. А то что он еще и расстояние — это практический (физический, геометрический … ) смысл модуля.
Поговорите со мной, может, я напрасно смущаюсь.
Специально залезла в учебник Петерсон, посмотреть что это за новое определение модуля.
Оказалось , что с г-жой Петерсон все нормально все-таки. Это Вы несколько спутали курицу и яйцо. Смотрю Дорофеев. Петерсон 2010 г . часть 2 стр. 79 Петерсон не модуль называет расстоянием, как вы пишите, такого у нее даже нет в помине, а расстояние от начала отсчета до точки, означающей данное число ( на числовой прямой) называет модулем. Это имхо две большие разницы.
Ну это примерно как если бы в учебнике было написано — Москва — это столица . А Вы бы вдруг запереживали, что в учебнике неправильно написано: столица — это ведь не только Москва, Москва лишь частный случай столицы… В принципе вы правы — Москва — это лишь частный случай столицы, но ведь в учебнике и не утверждается что только Москва -столица.
Про Москву-столицу согласна. Но если следовать этой логике, у Петерсон получается, что всякое расстояние от начала отсчета до точки — модуль, но не всякий модуль — расстояние. И это неправильно.
И ничего другого про модуль не сказано. Это меня тревожит.
Вообще-то модуль — это в первую очередь функция . Которая по определённым правилам переводит одно множество (область определения) в другое множество (область значений). Все остальные определения — от лукавого (в вашем случае — от Петерсон).
Ну, про функцию детям в 6ом еще рано. Я хотела бы, чтобы до них донесли, что есть понятие модуля числа и модуль числа — это число. автор.
Все это чудесно и если бы я допустим полностью утратив знания о модуле, то посмотрев на функцию, ее свойства скорее всего смогла бы для себя уложить в голове , что такое модуль.
Но Вы правда думаете, что это под силу среднему шестикласснику? По моему мнению для шестиклассника абсолютно от лукавого определения модуля через функцию, а вот методики Петерсон вполне подходит для первого знакомства с модулем.
Кстати Петерсон вообще не дает определения модуля как такого , она расписывает как определить модуль числа через расстояние на числовой прямой
«Я хотела бы, чтобы до них донесли, что есть понятие модуля числа и модуль числа — это число» — вот и донесите. Заодно вам придётся «доносить», что модуль определён для любого вещественного числа (область определения), что это новое число (сиречь модуль) вычисляется по определённым правилам (т.е. рассказать про преобразование), что он (модуль) всегда положительный (область значений). Т.е. рассказать про функцию . Видите, сколько мороки? Детям то ещё рано! Поэтому Петерсон (которой даже если рано и нельзя, но очень хочется — значит можно) прибегает к своему любимому приёму: объясним как-нибудь, пока все маленькие, им и так сгодится. Поэтому — «расстояние». Которое ведь в сущности тоже число . И мамы довольны — «наши уже модуль прошли»!
Думаю, что среднему шестикласснику не под силу.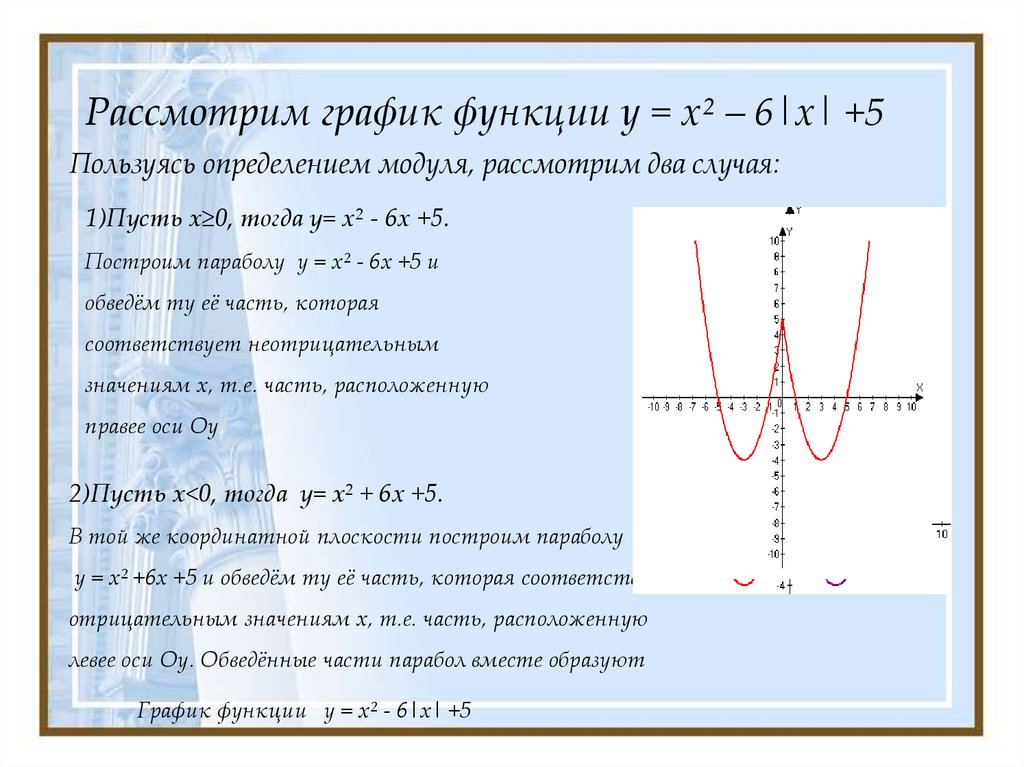 За это и не понимаю восторгов вокруг Петерсон .
За это и не понимаю восторгов вокруг Петерсон .
(Потому что если совсем по-честному, то это расстояние в математике определяется через модуль, а не наоборот, но что не позволено быку, то позволено Людмиле Георгиевне ).
Давайте предметно. Вот я смотрю вот этот учебник за 6 класс — у Вас этот? Что конкретно в рассуждениях авторов Вам кажется неправильным?
http://vklasse.org/6-klass/uchebniki/matematika/gv-dorofeev-lg-peterson-2010-chast-2/stranitsa-79
То, что у неё тележка впереди лошадки .
Ну геометрически на координатной прямой расстояние как раз себе модуль. Вот Петерсон видимо выдает этот частный случай модуля. Более подробно как функцию наверное определение модуля буду давать позднее.
Просто я так предполагаю, что математика в школе, особенно в начальной и средней это некий компромисс между математикой и педагогикой, причем педагогикой, которая рассчитана совсем не на будущих математиков.
Я сейчас точно не скажу, такой ли, но очень похож учебник, только год позже. Не нравится, что понятие модуля вводится без нормального объяснения. Далее идут упражнения, включающие модуль, и дети будут их решать, не будучи в состоянии сказать, а что же такое модуль.
Попался мне учебник Никольского, в нем, как надо все. Но не знаю, используют ли его в школе. Если у кого используют, напишите, пожалуйста.
«Ну геометрически на координатной прямой расстояние как раз себе модуль.» — вы не понимаете, где вы сама себе противоречите? А расстояние — это действительно модуль. Я вам про это и написала.
Можно сказать Москва — это столица. А в частном случае можно сказать, что столица — это Москва. Но нельзя давать определение столицы через понятие Москвы . Хотя если очень хочется, то можно: Вот, дети, Москва, это очень большой город, в котором расположены органы управления страной, многие другие важные учреждения, а также дипломатические представительства разных стран. Так вот, города других стран, которые как Москва — это столицы. Мило, но к 6-ому классу эти бирюльки уже наверное можно и прекратить.
Так вот, города других стран, которые как Москва — это столицы. Мило, но к 6-ому классу эти бирюльки уже наверное можно и прекратить.
Нельзя сводить компромисс к комиксу. Даже если рассчитываешь на нематиматиков ни разу. Т.е. если рассчитывать именно на них — то лучше не выпендриваться.
Объяснить как раз не сложно, можно и функцию упомянуть. 6-ой класс для функции — самое время, имхо. Но вполне можно и без функции, как у выше упомянутого мной Никольского.
Для меня сложность в том, что в школе говорят одно, а дома другое, при том, что математика — точная наука и в школе полностью однозначная. Здесь подумать надо, прежде чем по-своему объяснять.
Ни разу не гнушались мы с мужем дома говорить про математику другое, отличное от того, что говорят в школе . Причем с подробными пояснениями, что там в школе говорят неточно или даже неправильно. Вырастили хорошего сильного математика .
— не туда
Поделитесь опытом, возникали ли противоречия с учителем на этой почве? Если ребенок решает не так, как объяснял учитель или ребенок не мог увязать между собой два варианта объяснения? Мне кажется, это очень тонкий момент.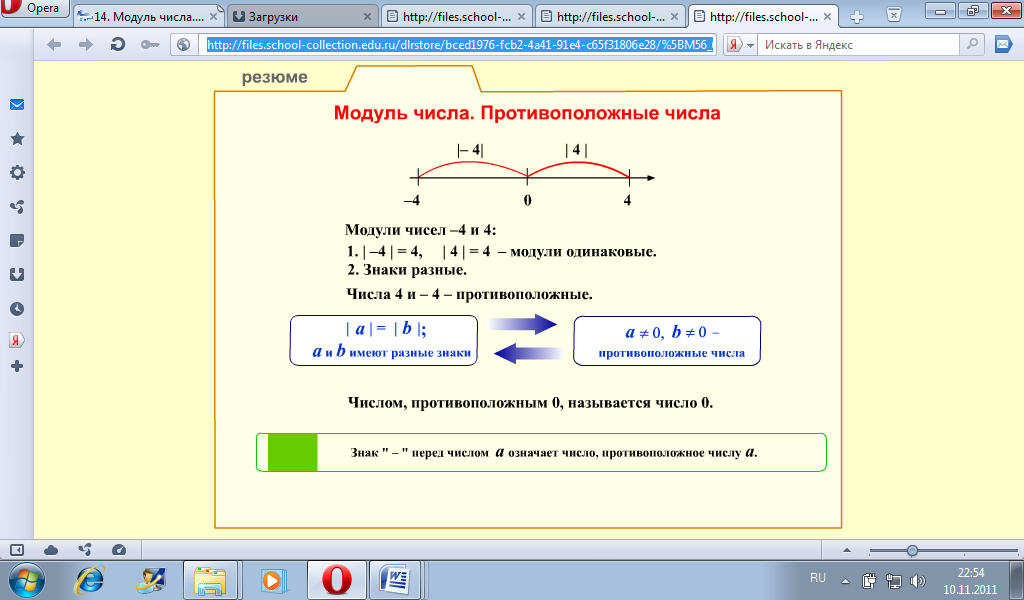
Повезло с ребёнком (или ребёнку с родителями): с увязать между собой два варианта объяснений проблем не было. Ну и мы, честное слово, никогда не пытались принизить авторитет учителя. В том числи и объяснив про компромисс между математикой и педагогикой .
А насчёт противоречий в оформлении решения: в младших классах оформлял так, как требовал учитель. А в старших повезло с учителями: там можно уже было решать так, как решиться. Главное, чтобы правильно. Граница между младшими и старшими у меня в голове лежит в районе 8-ого класса. Ну и на самом деле, чем старше, тем ближе к математике становится то, что преподают в школе.
На 88 странице второй части Петерсон дан алгебраический смысл модуля. Но понять его дано 5% шестиклассников от силы. А понятие модуля как расстояния дается именно как геометрический смысл. Как то Вы учебник через страницу читаете. Вот у Виленкина четко написано, что модуль — это расстояние (стр. 159). Не надо на Петерсон бочку катить. Нормальный у нее учебник, что касается 5-6 классов. Зубарева, Мордкович подойдут как авторитеты? Так они прямо модуль называют расстоянием в шестом классе (стр. 22 учебника). Для того, что бы вдолбить в головы нынешних двенадцатилеток, что значение модуля — это ПОЛОЖИТЕЛЬНОЕ число вполне подойдет такое определение.
Нормальный у нее учебник, что касается 5-6 классов. Зубарева, Мордкович подойдут как авторитеты? Так они прямо модуль называют расстоянием в шестом классе (стр. 22 учебника). Для того, что бы вдолбить в головы нынешних двенадцатилеток, что значение модуля — это ПОЛОЖИТЕЛЬНОЕ число вполне подойдет такое определение.
Учитывая, что учебник 6 класс и выше Петерсон используется в ФИЗМАТ отобранных школах, там не должно быть у детей никаких проблем с пониманием модулей. И если ребенок этого не понял, то родителям надо подумать, а нужна ли такая школа ребенку.
Я не понимаю с кем общаюсь и кто мне пишет. Вот выше один аноним написал, что модуль — это функция в глобальном смысле. Я полностью с этим согласна, при этом считаю, что геометрически модуль это расстояние. Это не противоречит первому утверждению. Именно этот частный случай в геометерическом смысле рассматривает учебник Дорофеева-Петерсон. И я не понимаю где я противоречу самой себе. Поясните, мне без подколов интересно, что не так в моих рассуждениях.
Про столицу это Вы вообще мои слова повторили. Я именно этими словами и писала, что расстояние — это частный случай модуля, как Москва — частный случай столицы… Вы считаете, что геометрическое расстояние — это общий случай модуля? Как вы тогда объясните понятие модуля как величины вектора например силы или скорости?
Конкретно про учебник, я бы еще отметила, что Дорофеев- Петерсон тактично обходят определения модуля, давая не полное определение модуля как функции, а определение расстояния на координатной прямой ( кстати даже не физического расстояния) как модуля.
И я понимаю что это достаточно наглядное понятие модуля гораздо проще воспринять, а главное запомнить и употреблять без ошибок средней массе, чем ненаглядное |x|= х для х>=0 и |x|=-х, для х<0 . Хотя для детей с развитым абстрактным воображением это дополнение будет абсолютно не лишним….
А вот давать полные свойства функции модуля с описанием области значений, определений, нули функции, четность /нечетность — это по-моему однозначно задача не для обычных шестиклассников. …
…
я с вами совершенно согласна. Оппоненты не учитывают ни детскую психологию, ни возраст в принципе.
Люблю Петерсон и благодарна ей. Да учебник не для среднего ученика, но способный ребенок по нему учится обычно без каких либо проблем. Бывают вопросы, на которые надо чуть больше времени, но в массе темы очень легко понимаемы ребенком, и при самостоятельном изучении. А уж с учителем, не вижу проблем.
О спасибо, я хоть тоже убедилась , что я не верблюд, и что расстояние, как я и думала раньше — это частный случай модуля с геометрической точки зрения, о чем честно и откровенно признаются авторы учебника на 88 странице.
И действительно нормально расписан алгебраический смысл модуля… Так что я считаю учебник в итоге угодил всем: и той массе, которой нужно объяснять на палочках и картинках, и тем, у кого с абстрактным мышлением все в порядке….
Но видимо учебник действительно нужно читать внимательно, а то у кого-то в голове останется, что модуль — это расстояние.
6 класс, Виленкин, Жохов. «Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки а.» Насколько я понимаю, это и до появления Петерсон было так в советской школе.
Виленкин, математика 5 класс, издание 1971 года: «Модулем числа называется расстояние от начала отсчета до точки, которой соответствует это число.»
Про 6%, это я от общего числа всех учеников и в защиту Петерсон.
Спросила у своей дочки только что.
Ответила, что геометрически модуль — это число, равное расстоянию от нуля, но вообще модуль х равен х при х>=0 и -х при х<0
Вроде по Петерсон учат их.
Вообще не поняла, в чем может быть проблема с модулем и что так смутило
Да, именно это определение я и хотела увидеть, но справедливо ожидала найти его в разделе о модуле , а не в разделе «сравнение чисел» (наши еще не дошли до него, а примеры с модулем уже вовсю решают).
Не знаю, почему тут многие считают, что шестиклассникам такое определение не по зубам. Это же чистый алгоритм, вообще не требуется думать.
Это же чистый алгоритм, вообще не требуется думать.
чем ненаглядное |x|= х для х>=0 и |x|=-х, для х<0 .
куда уж нагляднее? Это определение — как инструкция для дураков ) имхо.
А вот давать полные свойства функции модуля с описанием области значений, определений, нули функции, четность /нечетность — это по-моему однозначно задача не для обычных шестиклассников…. — так они еще и фунцию толком не проходили, тем более свойства функции. Конечно, им рано еще давать модуль как функцию.
Открыть тему в окнах
Обобщённое понятие модуля числа
В данном уроке мы рассмотрим понятие модуля числа более подробно.
Что такое модуль?
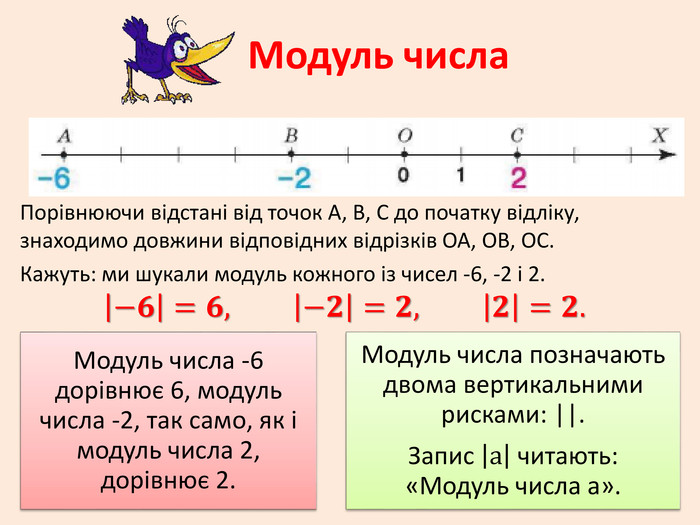
Модуль — это расстояние от начала координат до какого-нибудь числа на координатной прямой. Поскольку расстояние не бывает отрицательным, то и модуль всегда неотрицателен. Так, модуль числа 3 равен 3, как и модуль числа −3 равен 3
| 3 |= 3
|−3|= 3
Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу. Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:
Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:
Модуль это не только расстояние от начала координат до какого-нибудь числа. Модуль это также расстояние между любыми двумя числами на координатной прямой. Такое расстояние выражается в виде разности между этими числами, заключенной под знак модуля:
|x1 − x2|
Где x1 и x2 — числа на координатной прямой.
Например, отметим на координатной прямой числа 2 и 5.
Расстояние между числами 2 и 5 можно записать с помощью модуля. Для этого запишем разность из чисел 2 и 5 и заключим эту разность под знак модуля:
|2 − 5| = |−3| = 3
Видим, что расстояние от числа 2 до числа 5 равно трём шагам:
Если расстояние от 2 до 5 равно 3, то и расстояние от 5 до 2 тоже равно 3
То есть, если в выражении |5 − 2| поменять числа местами, то результат не изменится:
|5 − 2| = | 3 | = 3
Тогда можно записать, что |2 − 5| = |5 − 2|.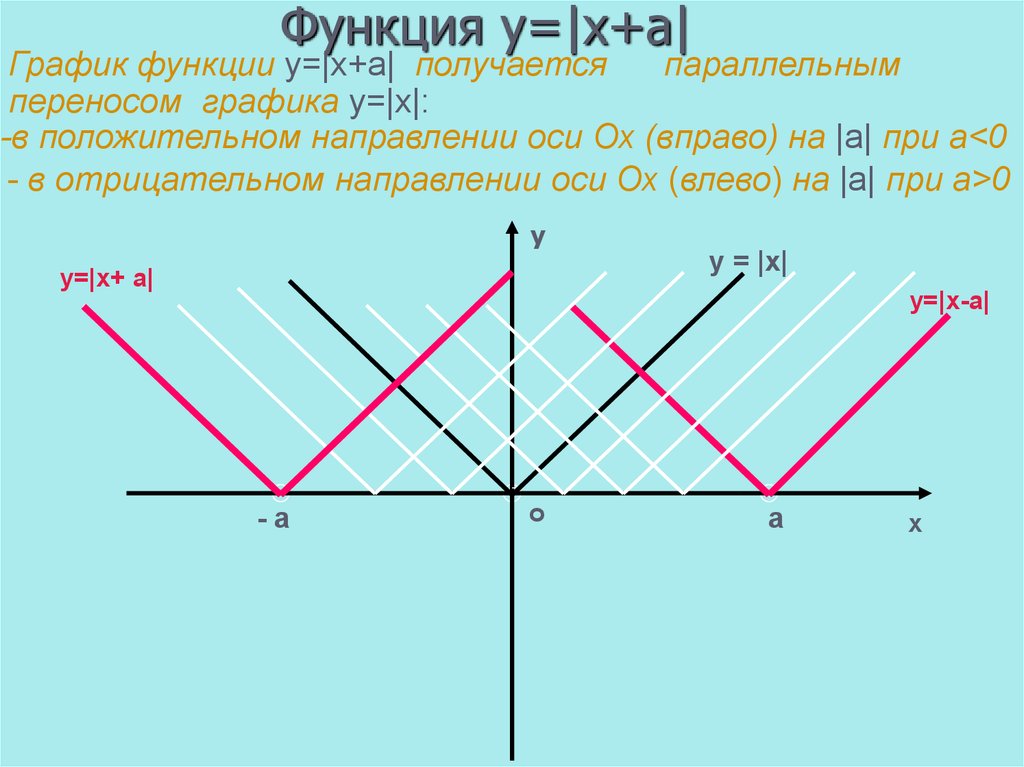 Вообще, справедливо следующее равенство:
Вообще, справедливо следующее равенство:
|x1 − x2| = |x2 − x1|
Это равенство можно прочитать так: Расстояние от x1 до x2 равно расстоянию от x2 до x1.
Раскрытие модуля
Когда мы говорим, что |3|= 3 или |−3|= 3 мы выполняем действие называемое раскрытием модуля.
Правило раскрытия модуля выглядит так:
Такую запись мы ранее не использовали. Дело в том, что равенство можно задавать несколькими формулами. Фигурная скобка указывает, что возможны два случая в зависимости от условия. В данном случае условиями являются записи «если x ≥ 0» и «если x < 0».
В зависимости от того что будет подставлено вместо x, выражение |x| будет равно x, если подставленное число больше или равно нулю. А если вместо x подставлено число меньшее нуля, то выражение |x| будет равно −x.
Второй случай на первый взгляд может показаться противоречивым, поскольку запись |x| = −x выглядит будто модуль стал равен отрицательному числу. Следует иметь ввиду, что когда x < 0, то под знáком модуля располагается отрицательное число. После знака равенства нужно подстáвить данное отрицательное число вместо x и раскрыть скобки.
Например, найдём модуль числа −7, используя правило раскрытия модуля:
Итак, x = −7
|−7|
В данном случае выполняется второе условие x < 0, ведь −7 < 0
Поэтому используем вторую формулу. А именно |x| = −x. Подстáвим вместо x число −7
Отсюда:
Поэтому |−7| = 7.
Пример 2. Пусть x = 5. То есть мы рассматриваем модуль числа 5
| 5 |
В данном случае выполняется первое условие x ≥ 0, ведь 5 ≥ 0
Поэтому используем первую формулу. А именно | x | = x.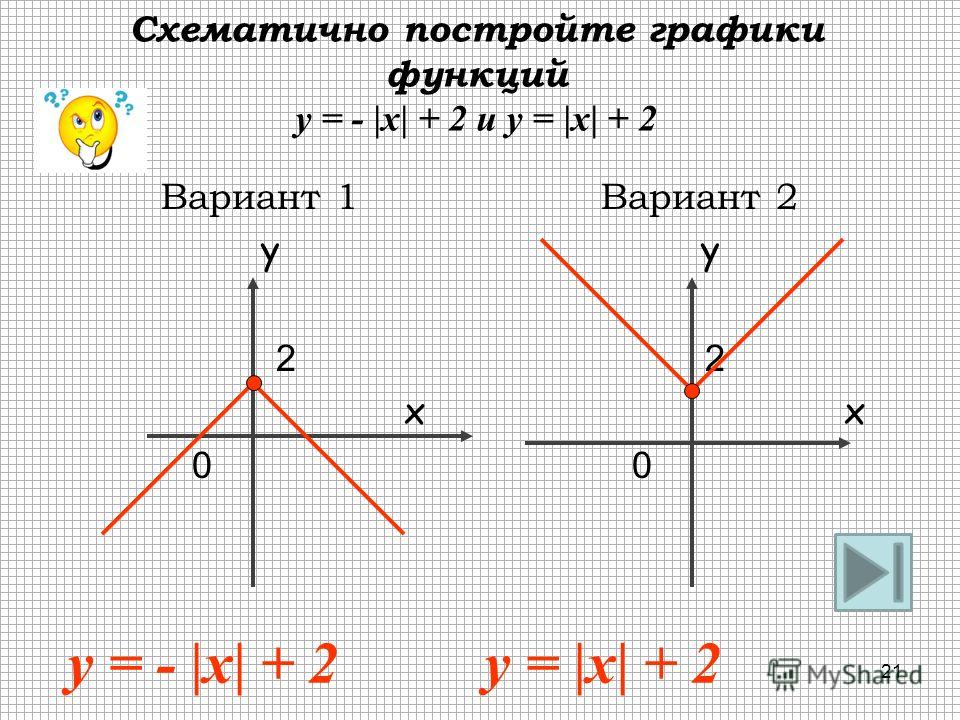 Получаем | 5 | = 5.
Получаем | 5 | = 5.
Ноль это своего рода точка перехода, в которой модуль меняет свой порядок раскрытия и далее сохраняет свой знак. Визуально это можно представить так:
На рисунке красные знаки минуса и плюса указывают как будет раскрываться модуль |x| на промежутках x < 0 и x ≥ 0.
К примеру, если взять числа 1, 9 и 13, а они принадлежат промежутку x ≥ 0, то согласно рисунку модуль |x| раскроется со знаком плюс:
| 1 | = 1
| 9 | = 9
| 13 | = 13
А если возьмём числа, меньшие нуля, например −3, −9, −15, то согласно рисунку модуль раскроется со знаком минус:
|−3| = −(−3) = 3
|−9| = −(−9) = 9
|−15| = −(−15) = 15
Пример 3. Пусть x = √4 − 6. То есть мы рассматриваем модуль выражения √4 − 6,
|√4 − 6|
Корень из числа 4 равен 2. Тогда модуль примет вид
|√4 − 6| = |2 − 6| = |−4|
x который был равен √4−6 теперь стал равен −4. В данном случае выполняется второе условие x < 0, ведь −4 < 0
В данном случае выполняется второе условие x < 0, ведь −4 < 0
Следовательно, используем вторую формулу |x| = −x. Продолжаем решение в исходном примере:
|√4 − 6| = |2 − 6| = |−4| = −(−4) = 4
На практике обычно рассуждают так:
«Модуль раскрывается со знаком плюс, если подмодульное выражение больше или равно нулю; модуль раскрывается со знаком минус, если подмодульное выражение меньше нуля».
Примеры:
|2| = 2 — модуль раскрылся со знаком плюс, поскольку 2 ≥ 0
|−4| = −(−4) = 4 — модуль раскрылся со знаком минус, поскольку −4 < 0
В некоторых учебниках можно встретить следующую запись правила раскрытия модуля:
В этой записи первое условие которое ранее выглядело как x ≥ 0 расписано подробнее, а именно сказано что если x > 0, то выражение |x| будет равно x, а если x=0, то выражение |x| будет равно нулю.
Пример 4. Пусть x = 0. То есть мы рассматриваем модуль нуля:
| 0 |
В данном случае выполняется условие x=0, ведь 0 = 0
Отсюда: |0| = 0
Пример 5. Раскрыть модуль в выражении |x|+ 3
Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид x + 3.
Если x < 0, то модуль раскроется со знаком минус, и тогда исходное выражение примет вид −x + 3. Чтобы сделать это выражение более удобным для восприятия, поменяем местами его члены, полýчим 3 − x
Теперь запишем решение так:
Проверим это решение при произвольных значениях x.
Допустим, требуется найти значение выражения |x|+ 3 при x = 5. Поскольку 5 ≥ 0, то модуль, содержащийся в выражении |x|+ 3 раскрóется со знаком плюс и тогда решение примет вид:
|x|+ 3 = x + 3 = 5 + 3 = 8
Найдём значение выражения |x|+ 3 при x = −6. Поскольку −6 < 0, то модуль содержащийся в выражении |x|+ 3 раскроется со знаком минус и тогда решение примет вид:
Поскольку −6 < 0, то модуль содержащийся в выражении |x|+ 3 раскроется со знаком минус и тогда решение примет вид:
|x| + 3 = 3 − x = 3 − (−6) = 9
Пример 6. Раскрыть модуль в выражении x +|x + 3|
Если x + 3 ≥ 0, то модуль |x + 3| раскроется со знаком плюс и тогда исходное выражение примет вид x + x + 3, откуда 2x + 3.
Если x + 3 < 0, то модуль |x + 3| раскроется со знаком минус и тогда исходное выражение примет вид x − (x + 3), откуда x − x − 3 = −3.
Запишем решение так:
Заметим, что условия x + 3 ≥ 0 и x + 3 < 0 являются неравенствами. Их можно привести к более простому виду, решив их:
Тогда условия из решения можно заменить на равносильные x ≥ −3 и x < −3
Во втором случае когда x строго меньше −3 выражение x +|x + 3| всегда будет равно постоянному числу −3.
Например, найдём значение выражения x +|x + 3| при x = −5. Поскольку −5 < −3, то согласно нашему решению значение выражения x +|x + 3| будет равно −3
При x = −5,
x +|x + 3| = x − x − 3 = −5 − (−5) − 3 = −3
Найдём значение выражения x +|x + 3| при x = 4. Поскольку 4 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив 4 получим 11
При x = 4,
x +|x + 3| = 2x+3 = 2 × 4 + 3 = 8 + 3 = 11
Найдём значение выражения x +|x + 3| при x=−3.
Поскольку −3 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив −3 получим −3
x +|x + 3| = 2x + 3 = 2 × (−3) + 3 = −6 + 3 = −3
Пример 3.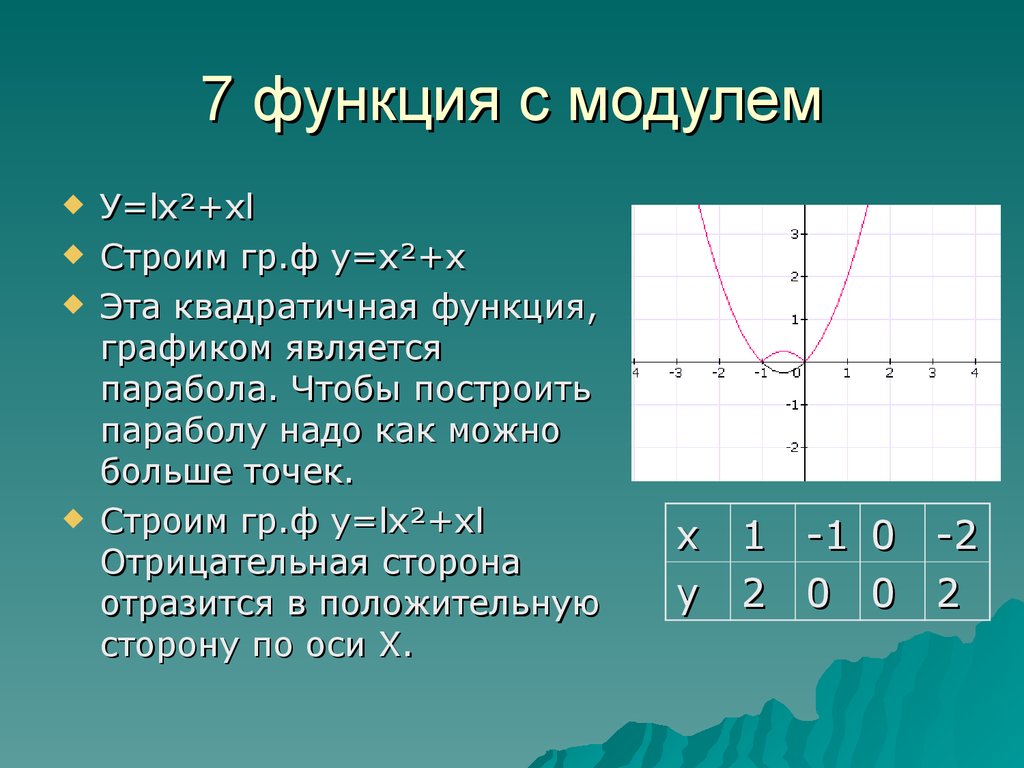 Раскрыть модуль в выражении
Раскрыть модуль в выражении
Как и прежде используем правило раскрытия модуля:
Но это решение не будет правильным, поскольку в первом случае написано условие x ≥ 0, которое допускает что при x = 0 знаменатель выражения обращается в ноль, а на ноль делить нельзя.
В данном примере удобнее использовать подробную запись правила раскрытия модуля, где отдельно рассматривается случай при котором x = 0
Перепишем решение так:
В первом случае написано условие x > 0. Тогда выражение станет равно 1. Например, если x = 3, то числитель и знаменатель станут равны 3, откуда полýчится 1
И так будет при любом x, бóльшем нуля.
Во втором случае написано условие x = 0. Тогда решений не будет, потому что на ноль делить нельзя.
В третьем случае написано условие x < 0. Тогда выражение станет равно −1. Например, если x = −4, то числитель станет равен 4, а знаменатель −4, откуда полýчится единица −1
Пример 4. Раскрыть модуль в выражении
Раскрыть модуль в выражении
Если x ≥ 0, то модуль, содержащийся в числителе, раскроется со знаком плюс, и тогда исходное выражение примет вид , которое при любом x, бóльшем нуля, будет равно единице:
Если x < 0, то модуль раскроется со знаком минус, и тогда исходное выражение примет вид
Но надо учитывать, что при x = − 1 знаменатель выражения обращается в ноль. Поэтому второе условие x < 0 следует дополнить записью о том, какие значения может принимать x
Преобразование выражений с модулями
Модуль, входящий в выражение, можно рассматривать как полноценный множитель. Его можно сокращать и выносить за скобки. Если модуль входит в многочлен, то его можно сложить с подобным ему модулем.
Как и у обычного буквенного множителя, у модуля есть свой коэффициент. Например, коэффициентом модуля |x| является 1, а коэффициентом модуля −|x| является −1. Коэффициентом модуля 3|x+1| является 3, а коэффициентом модуля −3|x+1| является −3.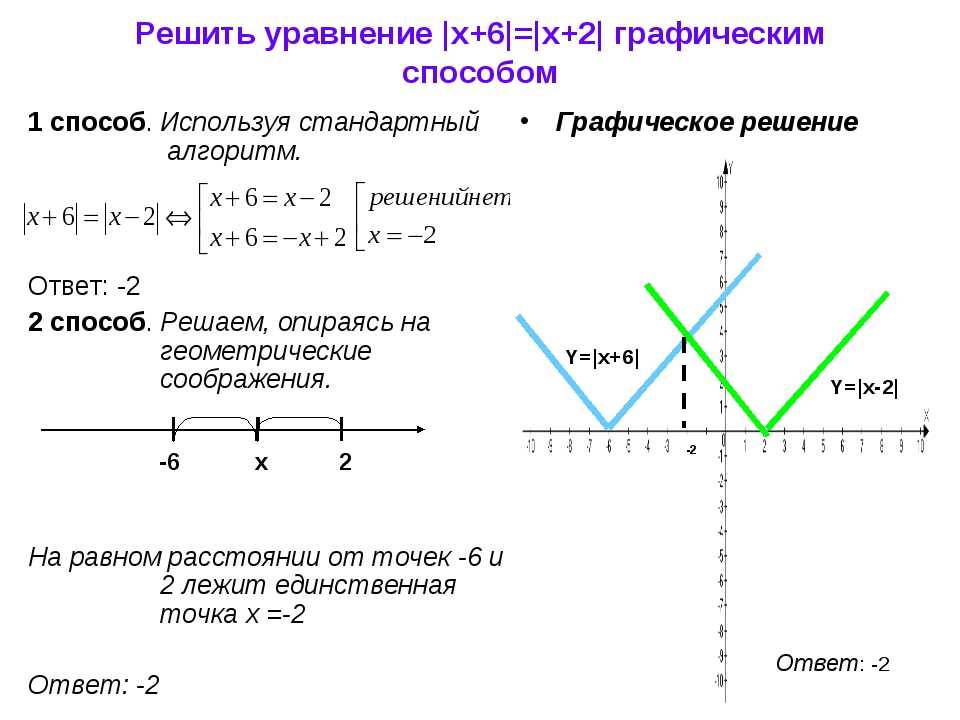
Пример 1. Упростить выражение |x| + 2|x| − 2x + 5y и раскрыть модуль в получившемся выражении.
Решение
Выражения|x| и 2|x| являются подобными членами. Слóжим их. Остальное оставим без изменений:
Раскроем модуль в получившемся выражении. Если x ≥ 0, то получим 3x − 2x + 5y, откуда x + 5y.
Если x < 0, то получим −3x − 2x + 5y, откуда −5x + 5y. Вынесем за скобки множитель −5, получим −5(x − y)
В итоге имеем следующее решение:
Пример 2. Раскрыть модуль в выражении: −|x|
Решение
В данном случае перед знаком модуля стоит минус. Его можно понимать как минус единицу перед знаком модуля. Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид −x
Если x < 0, то модуль раскроется со знаком минус, и тогда исходное выражение примет вид −(−x) откуда получим просто x
Задания для самостоятельного решения
Задание 1. Раскройте модуль:
Раскройте модуль:
Решение:
Показать решение
Задание 2. Раскройте модуль:
Решение:
Показать решение
Задание 3. Раскройте модуль:
Решение:
Показать решение
Задание 4. Раскройте модуль:
Решение:
Показать решение
Задание 5. Раскройте модуль:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Как взять модуль числа в python
Функция модуль ABS для арифметических операций с отрицательными числами со знаком минус. Вычисление абсолютного значения для отрицательных чисел.
Модуль числа
Часто в программировании требуется вычислить абсолютное значение числа. Иначе говоря, отбросить знак.
Иначе говоря, отбросить знак.
При вычислении модуля возможны 3 ситуации:
- Когда число больше 0. Если взять его по модулю — не изменится.
- Модуль нуля так же равен нулю.
- У отрицательного числа отбрасываем знак. То есть умножаем его на -1.
Но это все справедливо только для действительных чисел. Чему же тогда будет равен модуль комплексных?
Комплексное число состоит из действительной составляющей и мнимой. Геометрически это можно представить как 2 ортогональные оси: действительную и мнимую. Отмечаем на координатных осях требуемую точку. Модулем будет длина отрезка, проведенного из начала координат в эту точку.
Определение модуля числа
Алгебра дает четкое определения модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой «A» — расстояние от точки «A» до начала отсчёта (то есть до нуля, длина отрезка «OA») будет называться модулем числа «a».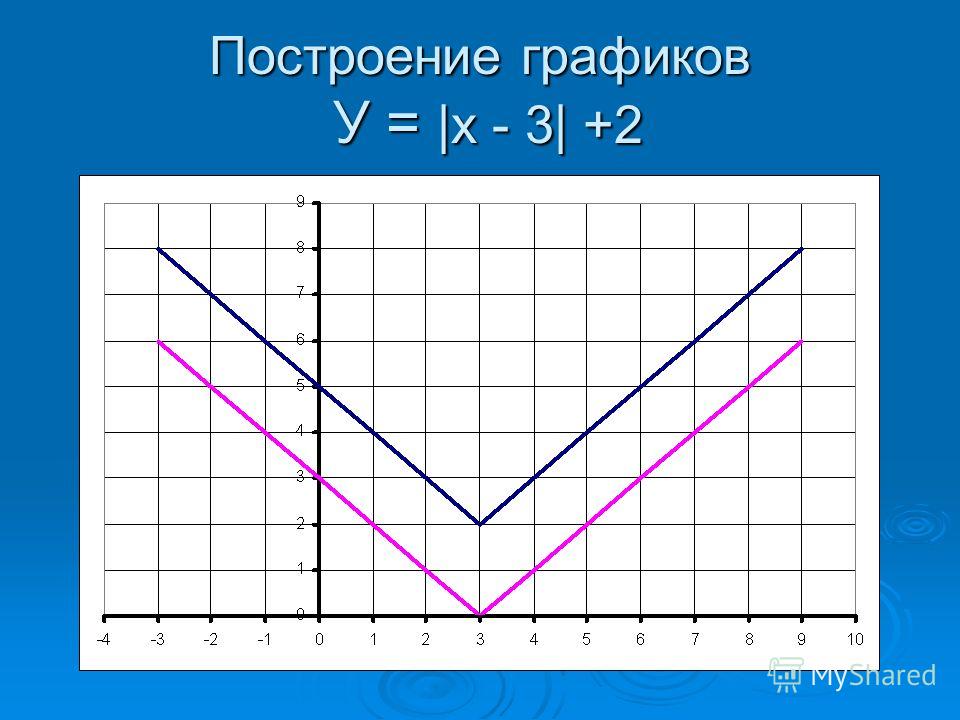
Знак модуля: |a| = OA
Разберем на примере:
Точка «В», которая соответствует числу «−3», находится на расстоянии 3 единичных отрезков от точки 0 (то есть от начала отсчёта). То есть длина отрезка «OB» равна 3 единицам.
Число 3 (длина отрезка «OB») называют модулем числа «−3».
Обозначение модуля: |−3| = 3
Читают символы выше следующим образом: «модуль числа минус три равен трем».
Точка «С», которая соответствует числу «+4», находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка «OС» равна четырем единицам.
Число 4 называют модулем числа «+4» и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Пример abs() с целым числом
Следующий код демонстрирует, как получить абсолютное значение 42 положительного числа 42.
Вывод: «Абсолютное значение 42 это 42».
То же самое, но уже с отрицательным -42.
Немного теории
Итак, поехали.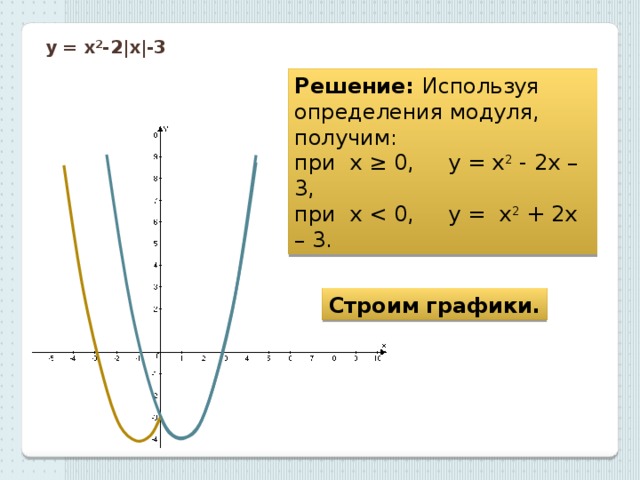 Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
[left| -a right|=left| a right|]
Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
[left| a right|=left& a,quad age 0, \& -a,quad a lt 0. \end right.]
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
График модуля и пример решения уравнения
Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: $_>$ и $_>$, но об этом мы поговорим позже.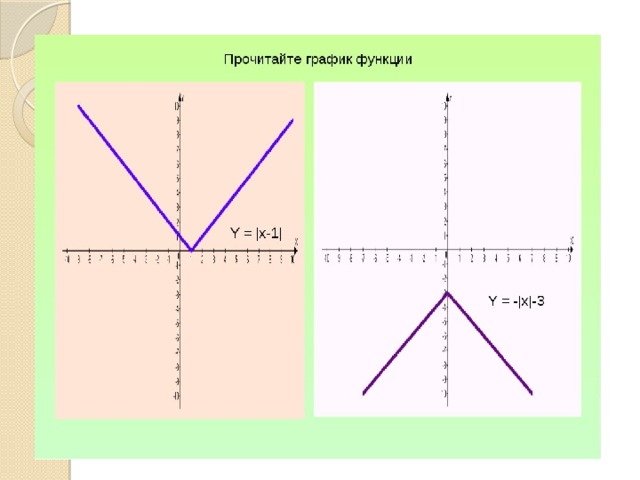 🙂
🙂
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: $_>$ и $_>$. В этом случае выражение $left| _>-_> right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
Модуль — это расстояние между точками на числовой прямой
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Вычисление
Вычислять модуль можно следующими способами:
- Используя стандартную функцию abs.
- С помощью функции fabs библиотеки math.
- При помощи самостоятельно написанной функции.
Все эти функции работают как в Python 2, так и в Python 3.
Для вычисления в Python модуля числа используется функция abs. Результат функции того же типа, которого был аргумент.
Можно так же воспользоваться функцией fabs из библиотеки math. Библиотеку можно подключить с помощью from math import fabs .
Библиотеку можно подключить с помощью from math import fabs .
Свое решение
Если по каким то причинам нет возможности или желания использовать стандартные функции, то можно написать свое решение.
Например, можно вычислить воспользоваться тернарным оператором.
На основе такого условия сделаем свою функцию.
Расчет разницы между наименьшим отрицательным и положительным числом
Пример 2. Найти разность между наименьшим и наименьшим абсолютным значениями элементов массива.
Для расчета используем следующую формулу (формула массива CTRL+SHIFT+Enter):
Функция МИН выполняет поиск наименьшего значения в диапазоне. Для поиска наименьшего неотрицательного числа используется выражение МИН(ABS(B3:B12)).
График функции
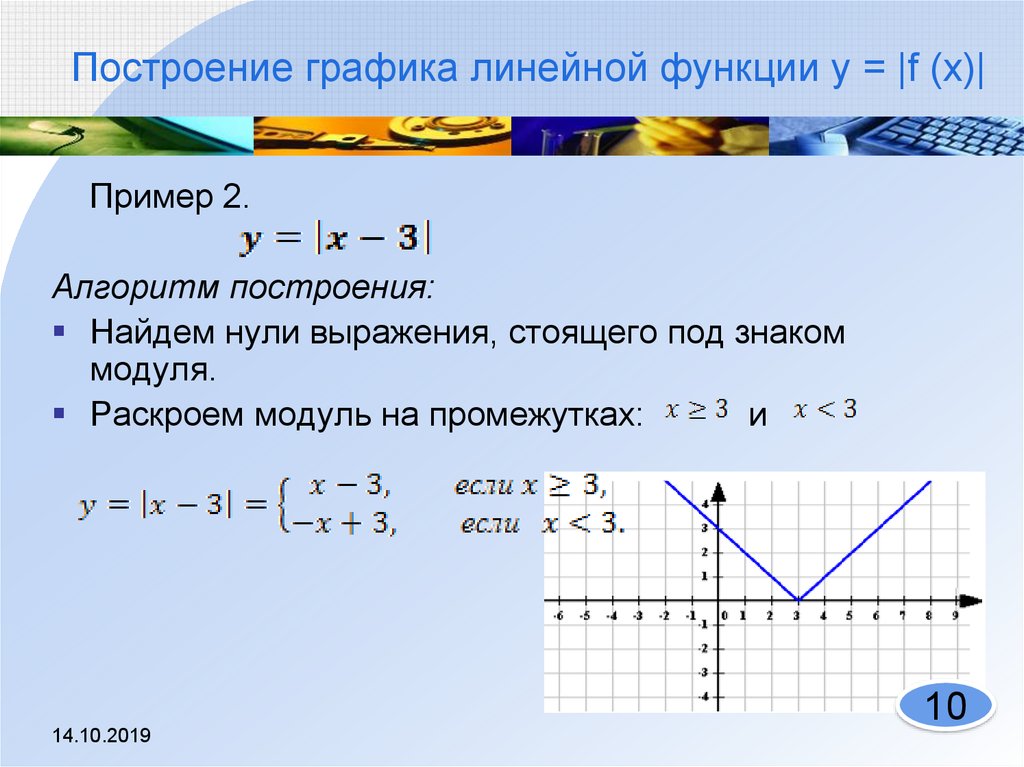
График функции равен y = |х|.
Для x 0 имеем y = x.
Для x < 0 имеем y = −x. В результате получаем:
Этот график можно использовать при решении уравнений и неравенств.
четверг, 7 апреля 2011 г.

Модуль числа
Пример .
Формула =ABS(55-62) вернет число 7
Для вычисления модуля комплексного числа используется инженерная функция МНИМ.ABS(комплексное число) . Комплексное число записывается в виде “x+yi” (кавычки обязательно).
Пример .
Формула =МНИМ.ABS(“3+4i”) вернет число 5
Корень из квадрата
В контрольной или задаче ЕГЭ может встретиться задачка, в которой просят вычислить √ a2 , где a – некоторое число или выражение.
При этом, √ a2 = |a|.
По определению арифметического квадратного корня √ a2 — это такое неотрицательное число, квадрат которого равен a2 .
В Python для нахождения модуля числа применяются две функции: fabs() из подключаемой библиотеки math и встроенная функция abs() .
Как вычислить модуль в Python?
Для вычисления в Python модуля числа используется функция abs. Результат функции того же типа, которого был аргумент.
Как определить является ли число целым Python?
Для проверки целого числа в Python 2. x вам действительно нужно использовать isinstance(x, (int, long)) . Ведь long — это тоже целое число!
x вам действительно нужно использовать isinstance(x, (int, long)) . Ведь long — это тоже целое число!
Как взять по модулю в Excel?
Как получить модуль числа
Для вычисления модуля используется функция ABS(). Найти ее очень легко, в списке математических функций она стоит первой. В качестве аргумента может служить число, содержимое ячейки, другая функция или математическое выражение. Покоряйте Excel и до новых встреч!
Как вывести остаток от деления Python?
Для получения остатка от деления в Python 3 используется операция, обозначающаяся символом процента «%». Остаток — это оставшаяся после целочисленного деления часть числа. Операция взятия остатка используется для решения различных видов задач.
Как определить тип переменной в Python?
- Введение В Python есть две функции type() и isinstance() с помощью которых можно проверить к какому типу данных относится переменная.
- Разница между type() и isinstance() type() возвращает тип объекта .

- type() .
- Пример использования type() .
- isinstance() .
- Пример использования
Как добавить модуль в Python?
Подключать модули желательно в самом вверху скрипта, используя ключевое слово «import», например import random . После подключения программа получает доступ ко всем функциям, методам и классам, содержащимся в нём. Программист может вызвать любую функцию из подключенной библиотеки используя префикс « имя_модуля. «.
Как посчитать длину числа в Питоне?
- python count integer. .
- Если вы хотите, чтобы длина целого числа была равна числу цифр в целом числе, вы всегда можете преобразовать его в строку, например, str(133) , и найти ее длину, например, len(str(123)) . .
- Python 2.
Как найти квадрат числа в Питоне?
Как получить квадрат числа в Python? Для возведения числа в квадрат, нужно указать 2 в качестве степени. Встроенной функции для получения квадрата в Python нет. Например, квадрат числа 6 — 6**2 —> 36.
Как определить является ли число простым в Python?
- Проверка того, является ли число простым числом в Python.
- Ваша функция возвращает True , как только видит, что число не делится ни на какое j . .
- int() усекает, а не округляет, так что int(math.sqrt(3) + 1) == 2 . .
- Квадратный корень из 3 меньше 2, поэтому цикл никогда не вводится и ничего не возвращается.
Как определить целое число или нет?
Вещественное число является целым, если его десятичное представление не содержит дробной части (но может содержать знак). Примеры вещественных чисел: Числа 142857; 0; −273 являются целыми. Числа 5½; 9,75 не являются целыми.
Что такое целые числа пример?
Определение целых чисел
Что такое целое число — это натуральное число, а также противоположное ему число и нуль. Примеры целых чисел: -7, 222, 0, 569321, -12345 и др. Что важно знать о целых числах: Сумма, разность и произведение целых чисел в результате дают целые числа. n, где e – это число Эйлера, а n – степень возведения. Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP . Кроме того, эту функцию можно отобразить в виде графика.
n, где e – это число Эйлера, а n – степень возведения. Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP . Кроме того, эту функцию можно отобразить в виде графика.
Для вычисления модуля числа в языке программирования Python можно использовать несколько способов.
Вычисление модуля числа с помощью модуля Math
Самый простой из них — подключить встроенный модуль, предназначенный для работы с математическими операциями — Math.
Для подключения модуля введем:
И после воспользуемся командой:
Рассмотрим конкретный пример вычисления модуля на языке программирования Python:
Вычисление модуля числа написанием собственной функции
Для вычисления модуля вещественного числа можно написать простую собственную функцию:
Здесь в первой строке мы объявляем новую функцию module. Далее в функции проверяем, отрицатильное ли число получает функция на входе, и, если это так, то умножаем его на -1. Не зависимо от результата, в конце функция возвращает результат с помощью команды return.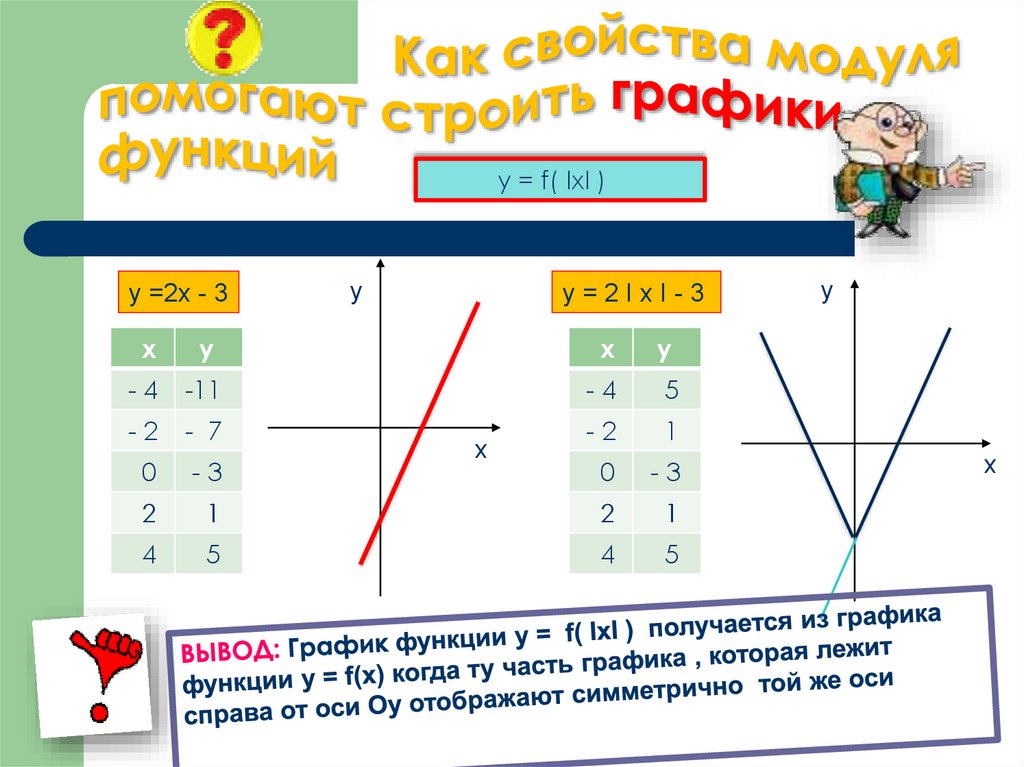
Datetime — важный элемент любой программы, написанной на Python. Этот модуль позволяет управлять датами и временем, представляя их в таком виде, в котором пользователи смогут их понимать.
datetime включает различные компоненты. Так, он состоит из объектов следующих типов:
- date — хранит дату
- time — хранит время
- datetime — хранит дату и время
Как получить текущие дату и время?
С помощью модуля Python это сделать очень просто. Сначала нужно импортировать класс datetime из модуля datetime , после чего создать объект datetime . Модуль предоставляет метод now() , который возвращает текущие дату и время с учетом локальных настроек.
А вот результат:
Получить текущую дату в Python
Класс date можно использовать для получения или изменения объектов даты. Например, для получения текущей с учетом настроек подойдет следующее:
Текущая дата — 2020-11-14 в формате год-месяц-день соответственно.
Получить текущее время
Для получения текущего локального времени сперва нужно получить текущие дату и время, а затем достать из этого объекта только время с помощью метода time() :
Компоненты datetime в Python
Модуль datetime в Python может использоваться для получения разных версий времени. Для этого нужно ознакомиться с атрибутами модуля. Используем для этого функцию dir() .
Для этого нужно ознакомиться с атрибутами модуля. Используем для этого функцию dir() .
В этом руководстве речь пойдет о следующих элементах:
- date — объекты даты
- datetime — объекты даты и времени
- time — объекты времени
- timedelta — этот атрибут покрывает интервалы и используется для определения прошлых или будущих событий
- Tzinfo — этот атрибут отвечает за часовые пояса
Как создавать объекты даты и времени
Для создания объекта времени используется класс time из модуля datetime в Python. Синтаксис следующий: datetime.time(hour, minutes, seconds) .
В этом примере создается объект времени представленный следующим образом (8, 48, 45).
Сначала импортируется модуль datetime . После этого создается экземпляр класса (объект time ). Затем ему присваивается значение datetime.time(8, 48, 45) , где параметры 8, 48 и 45 представляют собой часы, минуты и секунды соответственно.
Для создания объекта даты нужно передать дату с использованием следующего синтаксиса:
Вернет вот такой результат:
Timedelta
timedelta представляет длительность (даты или времени). Модуль datetime включает атрибут timedelta() , который используется для управления датой в Python. Объект timedelta выглядит следующим образом:
Модуль datetime включает атрибут timedelta() , который используется для управления датой в Python. Объект timedelta выглядит следующим образом:
Все аргументы опциональные и их значения по умолчанию равно 0. Они могут быть целыми или числами с плавающей точкой, как положительными, так и отрицательными. Благодаря этому можно выполнять математические операции, такие как сложение, вычитание и умножение.
Как вычислить разницу для двух дат
Посмотрим на несколько примеров вычисления разницы во времени. Предположим, есть два объекта datetime :
Для получения разницы нужно лишь вычесть значение одного объекта из второго:
Таким образом между 2 и 30 октября 2020 года 28 дней.
Как вычислить разницу двух объектов datetime.time
С помощью timedelta нельзя выполнять манипуляции над объектами time . Например:
Такой код вернет следующую ошибку:
Как получать прошлые и будущие даты с помощью timedelta
Поскольку timedelta — это длительность, то для получения прошлой или будущей даты нужно добавить объект timedelta к существующему или вычесть из него же. Вот пример нескольких уравнений, где n — это целое число, представляющее количество дней:
Вот пример нескольких уравнений, где n — это целое число, представляющее количество дней:
Если нужно, например, получить дату за прошлые две недели, то достаточно вычесть 14 дней из текущей даты:
Предположим, вы задумали практиковать определенный навык в течение 21 дня. Для получения будущей даты нужно добавить 21 день к текущей дате:
Другие арифметические операции с timedelta
Значения даты и времени могут сравниваться для определения того, какая из них была раньше или позже. Например:
Часовые пояса
Пока что мы работали с datetime без учета часовых поясов и летнего времени. Но прежде чем переходить к следующим пунктам, нужно разобраться с разницей в абсолютных (naive) и относительных (aware) датах.
Абсолютные даты не содержат информацию, которая бы могла определить часовой пояс или летнее время. Однако с такими намного проще работать.
Относительные же содержат достаточно информации для определения часового пояса или отслеживания изменений из-за летнего времени.
Разница между DST, GMT и UTC
- GMT
Официальный часовой пояс, используемый в некоторых странах Европы и Африки. Он может быть представлен как в 24, так и в 12-часовом форматах. GMT используется для того, чтобы задавать местное время. Например, местное время для Берлина 2020–10–17 09:40:33.614581+02:00 GMT. Для Найроби же это — 2020–10–17 10:40:33.592608+03:00 GMT. - DST (летнее время)
Страны, которые переходят на летнее время, делают это для того, чтобы дневное время длилось как можно дольше. Во время летнего времени они переводят стрелки своих часов на час вперед и возвращаются обратно осенью. - UTC (всемирное координированное время)
Временной стандарт для часовых поясов во всем мире. Он позволяет синхронизировать время во всем мире и служит отправной точкой для остальных.
Как работать с часовыми поясами
Рассмотрим, как создать простой относительный объект datetime :
Эта программа возвращает объект с абсолютным значением datetime .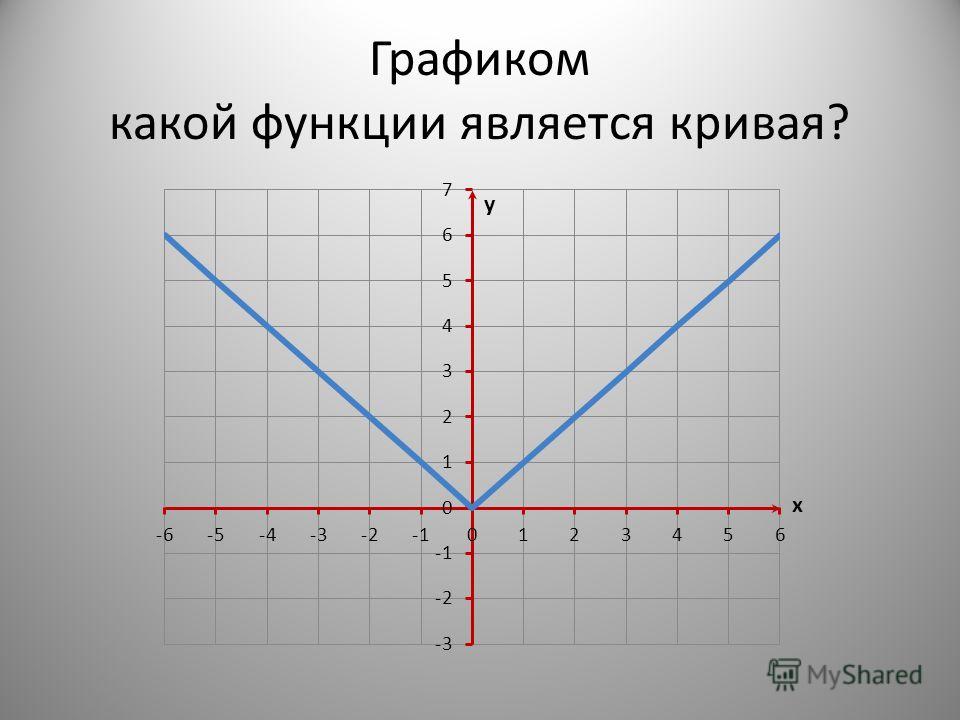 Если же нужно сделать его абсолютным, то нужно явно указать часовой пояс. Как это сделать? В библиотеке datetime в Python нет модуля для работы с часовыми поясами. Для этого нужно использовать другие библиотеки. Одна из таких — pytz.
Если же нужно сделать его абсолютным, то нужно явно указать часовой пояс. Как это сделать? В библиотеке datetime в Python нет модуля для работы с часовыми поясами. Для этого нужно использовать другие библиотеки. Одна из таких — pytz.
Предположим, нужно получить текущее время для Найроби. Для этого нужно использовать конкретный часовой пояс. Для начала можно с помощью pytz получить все существующие часовые пояса.
Вот некоторые из них:
Для получения времени в Найроби:
А вот так можно получить время Берлина:
Здесь можно увидеть разницу в часовых поясах разных городов, хотя сама дата одна и та же.
Конвертация часовых поясов
При конвертации часовых поясов в первую очередь нужно помнить о том, что все атрибуты представлены в UTC. Допустим, нужно конвертировать это значение в America/New_York :
Другие практические примеры
Всегда храните даты в UTC. Вот примеры:
Результат для этого кода — 2020-11-14 14:38:46.462397+00:00 , хотя локальное время может быть, например, таким 2020-11-14 16:38:46.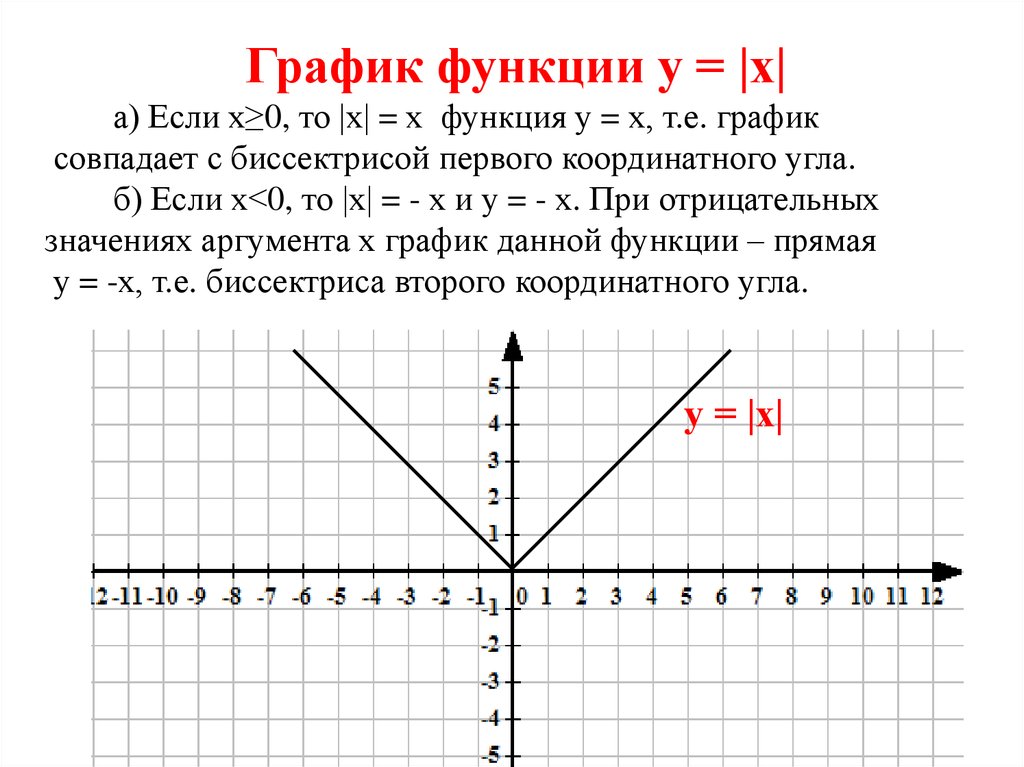 462397+00:00 . А уже при демонстрации даты пользователю стоит использовать метод localize с местными настройками:
462397+00:00 . А уже при демонстрации даты пользователю стоит использовать метод localize с местными настройками:
Вернет текущее локальное время — 2020-11-14 16:42:38.228528+00:00 .
Как конвертировать строки в datetime
strptime() в Python — это метод из модуля datetime. Вот его синтаксис:
Аргументы формата необязательные и являются строками. Предположим, нужно извлечь текущие дату и время:
Функциональные модули ABAP
Функциональные модули для создания программ (Полезно при создании программ)RS_PROGRAM_CHECK_NAME : Для проверки имен программ, если вы их создаете.
RS_CORR_INSERT : Для вставки запроса на исправление в репозиторий.
REPS_OBJECT_ACTIVATE : Для активации объектов репозитория, например — для активации только что сгенерированной программы.
RS_DELETE_PROGRAM: Чтобы удалить программу.
RS_ACCESS_PERMISSION : Чтобы заблокировать или разблокировать программу.
CALCULATE_DATE: Вычисляет будущую дату на основе ввода.
DATE_TO_DAY : Возвращает день для введенной даты.
DATE_COMPUTE_DAY: Возвращает день недели для даты
DATE_GET_WEEK: Возвращает неделю для даты
Function Modules related to (ALV) ADVANCED LIST VIEWERREUSE_ALV_LIST_DISPLAY: ABAP List viewer (LIST DISPLAY)
REUSE_ALV_GRID_DISPLAY: ALV GridControl full screen
REUSE_ALV_FIELDCATALOG_MERGE: Create field catalog from dictionary structure или внутреннюю таблицу
Функциональный модуль, связанный с отслеживанием измененийCHANGEDOCUMENT_READ_HEADERS : Чтение и форматирование документов об изменениях
DAY_ATTRIBUTES_GET : Возвращает атрибуты для указанного диапазона дат
MONTHS_BETWEEN_TWO_DATES : Чтобы получить количество месяцев между двумя датами.
END_OF_MONTH_DETERMINE_2 : Определяет конец месяца.
HR_HK_DIFF_BT_2_DATES : Найдите разницу между двумя датами в годах, месяцах и днях.
FIMA_DAYS_AND_MONTHS_AND_YEARS : Найти разницу между двумя датами в годах, месяцах и днях.
месяц_NAMES_GET: Получите имена месяца
Week_get_first_day: Получить первый день недели
hrgpbs_hesa_date_format: Format Дата в DD/MM/yyyy Format_.100069
9 . между двумя датами/временем и сообщить разницу в часах
L_MC_TIME_DIFFERENCE : Найти разницу во времени между двумя датами/временем
HR_99S_INTERVAL_BETWEEN_DATES : Разница между двумя датами в днях, неделях, месяцах
LAST_DAY_OF_MONTHS : Возвращает последний день месяца
DATE_CHECK_PLAUSIBILITY : Проверить недопустимую дату.
DATE_2D_TO_4D_CONVERSION : Ввод года: 2-символьный в 4-символьный.
DAY_IN_WEEK : Введите дату и название дня 1-понедельник, 2-вторник….
Подробнее о SAP ABAP
Функциональные модули, связанные с форматированиемCLOI_PUT_SIGN_IN_FRONT: Отображает отрицательный знак перед цифрой
RKD_WORD_WRAP: Текст упаков число слева
Функциональные модули, относящиеся к диалоговым подсказкамPOPUP_TO_CONFIRM : Отображает всплывающее диалоговое окно с определяемым пользователем сообщением для подтверждения
POPUP_TO_GET_VALUE : Отображает всплывающее диалоговое окно, запрашивающее значение для определенного имени поля таблицы получить имя файла сервера презентаций
F4_DATE : Отображает всплывающее диалоговое окно для выбора даты
GUI_UPLOAD : Загрузить файл с сервера презентаций
POPUP_TO_SELECT_MONTH : Display a pop-up to select a month
Function modules related to RFC communicationRFC_CONNECTION_CLOSE : Close a RFC connection
RFC_GET_SYSTEM_INFO : Give system’s information of a remote system
Функциональные модули, относящиеся к чтению/записи файловFILE_READ_AND_CONVERT_SAP_DATA: Загружает файл с сервера презентаций или приложений во внутреннюю таблицу
SUBST_GET_FILE_LIST: Чтобы получить список файлов с сервера приложений.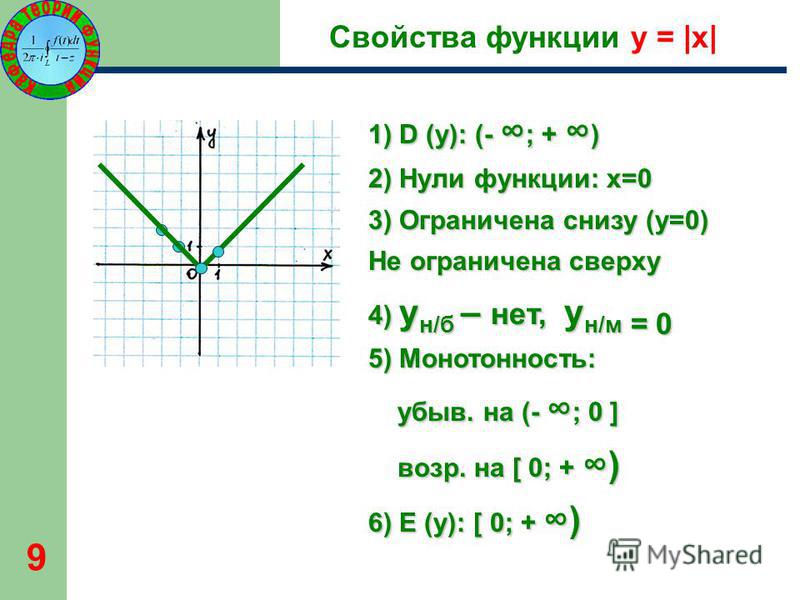
ALSM_EXCEL_TO_INTERNAL_TABLE: УСТАНОВКА ПЕРЕДАЧА ДАННЫХ W/ EXCEL
Функциональные модули, связанные с отправкой электронных писемSO_NEW_DOCUMENT_ATT_SEND_API1 — SENDAS с текстовыми и приложениями
9
9 3 SENDSERSERI_PI1 — .
Функциональные модули, относящиеся к справке F4F4IF_INT_TABLE_VALUE_REQUEST — F4 help также возвращает значение для отображения во внутренней таблице
Читать здесь Функциональный модуль для шифрования и дешифрования
Как создать функциональный модуль в ABAP
Что такое функциональный модуль?
Функциональные модули — это набор кодов, которые могут повторно использоваться другими программами. Вместо того, чтобы копировать одни и те же операторы внутри программ, гораздо полезнее и проще в сопровождении создать функциональный модуль. Функциональные модули создаются с импортом, экспортом, изменением параметров и исключениями.
Функциональные модули могут выполняться независимо и вызываться из любой программы.
Так выглядит функциональный модуль:
Из чего состоит функциональный модуль?
Параметры импорта : входные данные функционального модуля, отправленные из основной программы.
Параметры экспорта : являются выходами функционального модуля. Параметры отправляются из основной программы пустыми и возвращаются в основную программу с выходным значением.
Изменение параметров : входные параметры, значения которых в конце процесса изменяются и становятся выходными параметрами функционального модуля.
Параметры исключения : это параметр, вызывающий определенные исключения, ожидаемые нашим кодом.
Исходный код : здесь место для реализации фактической логики
Как создать функциональный модуль, шаг за шагом
Мы собираемся создать функциональный модуль, который вычисляет два операнда:
- IV_OPERAND_1 и
- IV_OPERAND_2.

Результат расчета зависит от операции, которая хранится в параметре IV_OPERATION. Возможны 2 операции:
- добавление (+) или
- вычитание (-).
Результат расчета сохраняется в параметре EV_RESULT.
Если IV_OPERATION не является ни сложением (+), ни вычитанием (-), функциональный модуль вызывает исключение с именем OPERATION_NOT_SUPPORTED.
Шаги для создания функционального модуля:
В SAP easy access откройте транзакцию SE37, чтобы открыть Function Builder.
Примечание: /OSE37, /O означает открытие нового сеанса/окна для транзакции SE37.
Появится следующее окно «Конструктор функций».
Введите имя нового функционального модуля. В моем случае я назову его: ZAS_LIB_HPL_CALCULATE_DEMO.
Почему название начинается с ZAS?
В SAP имя функционального модуля начинается с Z или Y, а AS — мои инициалы. Это соглашение об именах очень важно для удобочитаемости и удобства сопровождения.
… и нажмите кнопку «Создать», чтобы продолжить.
Войдите в «Функциональную группу». Функциональная группа должна быть определена до создания функционального модуля.
Примечание: чтобы узнать больше о том, что такое функциональная группа и как ее создать, нажмите здесь Как создать функциональную группу.
Введите «Краткий текст», чтобы описать функциональный модуль, например. «ABAP Academy Demo Calculate FM»
… и нажмите кнопку «Сохранить», чтобы продолжить.
Отображается информационное диалоговое окно со следующим сообщением. Нажмите на зеленую кнопку, чтобы продолжить.
Вкладка «Атрибуты»
Выбираем переключатель «Обычный функциональный модуль».
Вкладка «Импорт»
На этой вкладке мы предоставляем все параметры импорта для функционального модуля.
Флажок «Необязательный» означает, что текущий параметр является необязательным и не требует заполнения.
Есть 3 параметра импорта для этого функционального модуля расчета, а именно:
- IV_OPERAND_1
- IV_ОПЕРАЦИЯ
- IV_OPERAND_2
Импортируемый параметр начинается с «IV», что означает «Импортируемая переменная». Это соглашение об именах важно для удобочитаемости и удобства сопровождения. Делая это, мы знаем, что все параметры, начинающиеся с «IV», являются параметрами импорта.
Определите их следующим образом:
Типы IV_OPERAND_1 и IV_OPERAND_2 — Integer, поскольку они содержат числовое значение.
Тип IV_OPERATION — одиночный символ, так как он будет содержать знаки «+» или «-«.
Вкладка «Экспорт»
На этой вкладке мы предоставляем все параметры экспорта для функционального модуля. У нас есть только один параметр экспорта для этого функционального модуля расчета, который называется EV_RESULT. Тип — Integer, так как он содержит результат вычисления.
Имя параметра экспорта начинается с EV, что означает «Экспортируемая переменная».
Вкладка «Изменение»
На этой вкладке представлены все изменяемые параметры функционального модуля. Функциональный модуль расчета не имеет изменяемых параметров.
Чтобы продемонстрировать вам, как создать один изменяемый параметр, я создал, например, CV_DEMO. Изменение параметра начинается с CV, что означает «Изменение переменной».
Примечание: Просто убедитесь, что вы удалили этот параметр, потому что мы не будем использовать его в этом примере.
Вкладка «Исключение»
На этой вкладке мы создаем исключения для обнаружения определенных типов ошибок. Поскольку наш функциональный модуль вычислений будет использовать только сложение (+) и вычитание (-), нам необходимо создать исключение ошибки, когда операция, отправленная основной программой, не поддерживается.
Мы создаем следующее исключение:
Вкладка «Исходный код»
Это настоящий редактор ABAP, в котором мы реализуем логику функционального модуля.
ABAP предоставляет предварительно сгенерированные комментарии, содержащие все параметры: Импорт, Экспорт, Изменение параметров и Исключения следующим образом:
Реализация кода
Этот код вычисляет два операнда: IV_OPERAND_1 и IV_OPERAND_2.
Значение операции в IV_OPERATION может быть сложением (+) или вычитанием (-).
Результат сохраняется в EV_RESULT.
Сначала я очищаю параметр экспорта EV_RESULT. Причина этого в том, чтобы визуально показать, что этот параметр экспортируется, и я не ожидаю, что он будет иметь какое-либо значение, когда запустится логика.
Затем я ищу операцию в IV_OPERATION.
Если значением IV_OPERATION является сложение (+), добавить IV_OPERAND_1 и IV_OPERAND_2.
Если значением IV_OPERATION является вычитание (-), вычтите IV_OPERAND_1 на IV_OPERAND_2.
Если значение IV_OPERATION не является ни сложением (+), ни вычитанием (-), вызвать исключение.
Проверить согласованность (CTRL+F2) и активировать функцию (CTRL+F3).
Функциональный модуль ZAS_LIB_HPL_CALCULATE_DEMO создан.
Чтобы протестировать функциональный модуль, нажмите (F8) для выполнения, и появится экран, показанный ниже:
Введите значения IV_OPERAND_1, IV_OPERATION и IV_OPERAND_2 для выполнения вычислений и нажмите Execute (F8).
EV_RESULT заполняется результатом расчета, как показано ниже:
Если введенная IV_OPERATION является умножением (*), возникает исключение, поскольку операция не поддерживается.
Наиболее часто используемый функциональный модуль в SAP ABAP
В sap abap разные требования к использованию другого функционального модуля. Если вы используете функциональный модуль, то сначала вы узнаете, как работает этот функциональный модуль. Ниже приведены различные функциональные модули и их использование.
| Функциональные модули | Применение |
|---|---|
| REUSE_ALV_GRID_DISPLAY | Показать данные в формате таблицы. |
| REUSE_ALV_LIST_DISPLAY | Показать данные в формате таблицы. |
| REUSE_ALV_FIELDCATALOG_MERGE | Преобразование таблицы в fieldcat. |
| LVC_FIELDCATALOG_MERGE | Преобразование таблицы в fieldcat . |
| HR_IN_CHG_INR_WRDS | Преобразовать сумму в слово (только индийские рупии) |
| SPELL_AMOUNT | Преобразование суммы в слово (сумма для любой страны) |
| FI_CONVERT_FIRSTCHARS_TOUPPER | Преобразовать первую букву в верхний регистр. |
| GET_CURRENT_YEAR | Показать текущий финансовый год. |
| RP_CALC_DATE_IN_INTERVAL | Добавить две даты или месяца |
| ДОБАВИТЬ_ВРЕМЯ_ДО_ДАТЫ | Добавить два раза |
| SD_DATETIME_DIFFERENCE | Разница двух даты и времени |
| G_POSTING_DATE_OF_PERIOD_GET | Найти дату формы и текущую дату. |
| HR_JP_MONTH_BEGIN_END_DATE | Найти дату начала и окончания месяца. |
| C14Z_MESSAGES_SHOW_AS_POPUP | Показать всплывающее сообщение. |
| FORMAT_MESSAGE | Показать сообщение на весь экран. |
| VRM_SET_VALUES | Показать раскрывающееся меню. |
| F4_FILENAME | Выберите файл в локальной системе. |
| DSYS_SHOW_FOR_F1HELP | Показать справку любого поля. |
| F4IF_INT_TABLE_VALUE_REQUEST | Показать справку по запросу значения. |
| CONVERSION_EXIT_ALPHA_INPUT | Добавить нули в пользовательский ввод. |
| CONVERSION_EXIT_ALPHA_OUTPUT | Удалить нули в поле вывода. |
| ПРЕОБРАЗОВАНИЕ_ВЫХОД_MATN1_INPUT | Добавьте нули в номер материала. |
| CONVERSION_EXIT_MATN1_OUTPUT | Удалить нули в номере материала. |
| GUI_DOWNLOAD | Перенос данных внутренней таблицы в файл |
| MS_EXCEL_OLE_STANDARD_DAT | Перенос данных внутренней таблицы в файл |
| ТЕКСТ_ПРЕОБРАЗОВАТЬ_XLS_TO_SAP | Перенос данных файла Excel во внутреннюю таблицу |
| GUI_UPLOAD | Передача данных текстового файла во внутреннюю таблицу |
| SSF_FUNCTION_MODULE_NAME | Создать функциональный модуль в соответствии с именем смарт-формы |
| SSF_OPEN | Открыть задание как распечатать несколько интеллектуальных форм |
| SSF_CLOSE | Закрыть задание как распечатать несколько интеллектуальных форм |
| SSFCOMP_PDF_PREVIEW | Прямой предварительный просмотр перед печатью |
| CONVERT_OTF | Преобразование в формат OTF |
| SX_OBJECT_CONVERT_OTF_PDFF | Преобразование в формат OTF TO PDF |
| SO_NEW_DOCUMENT_ATT_SEND_API1 | Отправить документ по почте |
| READ_TEXT | Получить сведения о тексте |
| BAPI_FIXEDASSET_OVRTAKE_CREATE | Создать BAPI |
| BAPI_TRANSACTION_COMMIT | Сохранить или зафиксировать BAPI |
| УДАЛИТЬ_ВСЕ | Разблокировка замков LUW |
| BAPI_ACC_DOCUMENT_POSTL | Проводка документа счета для GL/AP/AR |
| BAPI_ACC_INVOICE_RECEIPT_POST | Проводка документа счета для AP |
| BAPI_ACC_GL_POSTING_POST | Проводка единственного основного счета |
| BAPI_SALESORDER_CREATEFROMDAT2 | Создать заказ на продажу |
| RFC_READ_TABLE | Чтение таблицы базы данных из другой системы |
| GET_GLOBALS_FROM_SLVC_FULLSCR | Обновление ALV после модификации |
| ENQUE_READ2 | Чтение записей блокировки клиента |
| SAPGUI_PROGRESS_INDICATOR | ПРОГРЕСС ГРАФИЧЕСКОГО ИНТЕРФЕЙСА В ПРОЦЕНТАХ |
| DP_CREATE_URL | Создает временный URL-адрес |
| /ISDFPS/EXEC_TRANSACTION | Функциональный модуль для вызова T-кода |
| NUMBER_GET_NEXT | Получить следующий номер из диапазона номеров |
| POPUP_TO_CONFIRM | Задать вопрос во всплывающем диалоговом окне |
| ADDR_GET_NEXT_COMM_TYPE | Найти тип связи |
| CONVERT_COMM_TYPE_DATA | Преобразование данных типа связи |
| NAST_PROTOCOL_UPDATE | Обновление протокола Nast выполнено успешно или нет |
| SX_ADDRESS_TO_DEVTYPE | Адрес отправителя для доставки почты |
| FP_FUNCTION_MODULE_NAME | Создать функциональный модуль в соответствии с именем формы Adobe |
| FP_JOB_OPEN | Открыть задание как печать нескольких форм Adobe |
| FP_JOB_CLOSE | Закрыть задание как напечатать несколько форм Adobe |
| ARCHIV_GET_PRINTFORMAT | Установить формат печати архива |
| ARCHIV_CREATE_OUTGOINGDOCUMENT | Создание архивного документа |
| FP_GET_LAST_ADS_ERRSTR | Ошибка проверки последнего адреса формы Adobe |
| ICON_CREATE | Создать значок |
REUSE_ALV_GRID_DISPLAY
Используется для отображения данных в формате таблицы на экране вывода. Эти данные отображаются на выходе. Эти данные сначала сохраняются во внутренней таблице, и эта внутренняя таблица передается функциональному модулю REUSE ALV GRID DISPLAY. Знаете ли вы, как использовать функциональный модуль REUSE_ALV_GRID_DISPLAY в программе отчетов.
Эти данные отображаются на выходе. Эти данные сначала сохраняются во внутренней таблице, и эта внутренняя таблица передается функциональному модулю REUSE ALV GRID DISPLAY. Знаете ли вы, как использовать функциональный модуль REUSE_ALV_GRID_DISPLAY в программе отчетов.
Используется для отображения данных в формате таблицы на экране вывода. Эти данные отображаются на выходе. Эти данные сначала сохраняются во внутренней таблице, и эта внутренняя таблица передается функциональному модулю ПОВТОРНОЕ ИСПОЛЬЗОВАНИЕ СПИСКА ИЗОБРАЖЕНИЙ. Знаете ли вы, как использовать REUSE_ALV_LIST_DISPLAY функциональный модуль в программе отчета. Использование обоих функциональных модулей REUSE_ALV_GRID_DISPLAY и REUSE_ALV_LIST_DISPLAY одинаково, но отображение макета вывода является небольшой разницей.
REUSE_ALV_FIELDCATALOG_MERGE Используется для создания fieldcat с использованием пользовательской таблицы. Если вы создаете fieldcat вручную, основные данные, которые вам нужны, это имя поля, описание поля или другие данные, которые есть в пользовательской таблице, затем используйте пользовательскую таблицу. Этот fieldcat для использования как функционального модуля REUSE ALV GRID, так и LIST DISPLAY. Знаете ли вы, как использовать REUSE_ALV_FIELDCATALOG_MERGE функциональный модуль в программе отчета и почему вы используете этот функциональный модуль.
Если вы создаете fieldcat вручную, основные данные, которые вам нужны, это имя поля, описание поля или другие данные, которые есть в пользовательской таблице, затем используйте пользовательскую таблицу. Этот fieldcat для использования как функционального модуля REUSE ALV GRID, так и LIST DISPLAY. Знаете ли вы, как использовать REUSE_ALV_FIELDCATALOG_MERGE функциональный модуль в программе отчета и почему вы используете этот функциональный модуль.
Используется для создания fieldcat с использованием пользовательской таблицы. Если вы создаете fieldcat вручную, основные данные, которые вам нужны, это имя поля, описание поля или другие данные, которые есть в пользовательской таблице, затем используйте пользовательскую таблицу. Этот fieldcat для использования как функционального модуля REUSE ALV GRID, так и LIST DISPLAY. Знаете ли вы, как использовать LVC_FIELDCATALOG_MERGE функциональный модуль в программе отчета и почему вы используете этот функциональный модуль.
Он используется для преобразования количества в слово означает только преобразование индийских рупий в слово. Если вам нужно преобразовать сумму другой страны в слово, например, доллар в слово, используйте функциональный модуль SPELL_AMOUNT . Знаете ли вы, как использовать функциональный модуль HR_IN_CHG_INR_WRDS в программе отчета или пуле модулей.
SPELL_AMOUNTОн используется для преобразования суммы в слово означает не только преобразование индийских рупий, но и преобразование суммы любой страны, такой как доллар, фунт, ринггит, иена и т. д., в слово в соответствии с валютой. Знаете ли вы, как использовать функциональный модуль SPELL_AMOUNT в программе отчетов и другой пример использования функционального модуля или пула модулей количества заклинаний.
FI_CONVERT_FIRSTCHARS_TOUPPER Используется для преобразования первого символа в верхний регистр. В некоторых местах требуется вывод первого символа в верхнем регистре, тогда в этом месте используется функциональный модуль. Знаете ли вы, как использовать FI_CONVERT_FIRSTCHARS_TOUPPER функциональный модуль в программе отчета или пуле модулей.
В некоторых местах требуется вывод первого символа в верхнем регистре, тогда в этом месте используется функциональный модуль. Знаете ли вы, как использовать FI_CONVERT_FIRSTCHARS_TOUPPER функциональный модуль в программе отчета или пуле модулей.
Используется для отображения текущего финансового года. Финансовый год некоторых компаний начинается с 1 апреля по 31 марта, а финансовый год других компаний начинается с 1 января по 31 декабря, поэтому используйте этот функциональный модуль. Знаете ли вы, как использовать функциональный модуль GET_CURRENT_YEAR в программе отчета или пуле модулей.
RP_CALC_DATE_IN_INTERVAL Он используется для добавления двух дат или месяцев. Это означает, что если одна компания продает какой-либо товар другой компании и говорит, что компании-плательщику вы платите 21 марта, но компания-плательщик говорит: «Мы не можем заплатить за это». дата и, пожалуйста, продлить более 20 дней. Тогда предыдущая дата выплаты 21 марта и продление еще на 20 дней означает 21 марта + 20 дней = 10 апреля этот тип расчета для использования этого функционального модуля. Знаете ли вы, как использовать функциональный модуль RP_CALC_DATE_IN_INTERVAL в программе отчетов или пул модулей.
дата и, пожалуйста, продлить более 20 дней. Тогда предыдущая дата выплаты 21 марта и продление еще на 20 дней означает 21 марта + 20 дней = 10 апреля этот тип расчета для использования этого функционального модуля. Знаете ли вы, как использовать функциональный модуль RP_CALC_DATE_IN_INTERVAL в программе отчетов или пул модулей.
Он используется для добавления времени к дате. Это означает , если вы добавите 36 часов 15 мая, тогда результат будет 12 часов 16 мая этот тип расчета для использования этого функционального модуля. Знаете ли вы, Как использовать функциональный модуль ADD_TIME_TO_DATE в программе отчета или пуле модулей.
SD_DATETIME_DIFFERENCE Используется для расчета разницы двух дат и времени. Это означает , если вы вычисляете разницу дней с 3 марта по 21 апреля. Результат равен 49.дней этот тип расчета для использования этого функционального модуля. Знаете ли вы, как использовать функциональный модуль SD_DATETIME_DIFFERENCE в программе отчета или пуле модулей.
Знаете ли вы, как использовать функциональный модуль SD_DATETIME_DIFFERENCE в программе отчета или пуле модулей.
Используется для поиска даты первой и последней публикации. Знаете ли вы, как использовать функциональный модуль G_POSTING_DATE_OF_PERIOD_GET в программе отчета или пуле модулей.
HR_JP_MONTH_BEGIN_END_DATEИспользуется для нахождения даты начала и даты окончания месяца. Если пользователь вводит только месяц и год и использует этот месяц и год, чтобы найти дату начала и дату окончания этого месяца. Один пример: если пользователь вводит месяц «8» и год «2022», тогда дата начала будет 1-08-2022, а дата окончания — 31-08-2022. Знаете ли вы, как использовать функциональный модуль HR_JP_MONTH_BEGIN_END_DATE в программе отчета или пуле модулей.
C14Z_MESSAGES_SHOW_AS_POPUP Используется для отображения всплывающего сообщения. Если в каком-либо месте требуется проверка, то в этом месте используйте этот функциональный модуль. Показывать различные типы сообщений, такие как сообщение об ошибке, сообщение об успешном завершении, предупреждающее сообщение и т. д. Знаете ли вы, как использовать функциональный модуль C14Z_MESSAGES_SHOW_AS_POPUP в программе отчета или пуле модулей.
Если в каком-либо месте требуется проверка, то в этом месте используйте этот функциональный модуль. Показывать различные типы сообщений, такие как сообщение об ошибке, сообщение об успешном завершении, предупреждающее сообщение и т. д. Знаете ли вы, как использовать функциональный модуль C14Z_MESSAGES_SHOW_AS_POPUP в программе отчета или пуле модулей.
Используется для отображения выпадающего меню. Если какое-либо поле требует раскрывающегося меню, используйте этот функциональный модуль. Элементы раскрывающегося меню являются пользовательским выбором, что означает, что пользовательские элементы добавляются через пользовательскую таблицу или внутреннюю таблицу. Знаете ли вы, как использовать VRM_SET_VALUES функциональный модуль в программе отчета или пуле модулей.
DSYS_SHOW_FOR_F1HELP Используется для отображения справки любого поля. Это означает, что если пользователь выбирает или щелкает справку по любому конкретному полю, затем показывает новый экран, и этот экран описывает это конкретное поле и информацию, отображаемую на этом экране по вашему выбору. Знаете ли вы, как использовать функциональный модуль DSYS_SHOW_FOR_F1HELP в программе отчета или пуле модулей.
Знаете ли вы, как использовать функциональный модуль DSYS_SHOW_FOR_F1HELP в программе отчета или пуле модулей.
Используется для отображения справки по запросу значения. Это означает, что вы не знаете, какое значение вводить в том или ином поле. Если вы используете справку по запросу значения, то покажите как маленькое поле в правой части поля. Если вы нажмете на это поле, затем отобразите несколько рекомендуемых значений и используйте любое значение за раз. Эти рекомендуемые значения выбираются по вашему выбору. Знаете ли вы, как использовать функциональный модуль F4IF_INT_TABLE_VALUE_REQUEST в программе отчета или пуле модулей.
CONVERSION_EXIT_ALPHA_INPUT Используется для добавления нулей в пользовательский ввод. Знаете ли вы, как использовать функциональный модуль CONVERSION_EXIT_ALPHA_INPUT в программе отчета или пуле модулей.
Используется для удаления нулей в поле вывода. Знаете ли вы, как использовать функциональный модуль CONVERSION_EXIT_ALPHA_OUTPUT в программе отчета или пуле модулей.
CONVERSION_EXIT_MATN1_INPUTИспользуется для добавления нулей в номер материала. Знаете ли вы, как использовать функциональный модуль CONVERSION_EXIT_MATN1_INPUT в программе отчета или пуле модулей.
CONVERSION_EXIT_MATN1_OUTPUTИспользуется для удаления нулей в номере материала. Знаете ли вы, как использовать функциональный модуль CONVERSION_EXIT_MATN1_OUTPUT в программе отчета или пуле модулей.
GUI_DOWNLOAD Используется для передачи данных внутренней таблицы в файл. Знаете ли вы, как использовать GUI_DOWNLOAD функциональный модуль в программе отчета или пуле модулей.
Используется для передачи данных внутренней таблицы в файл. Знаете ли вы, как использовать функциональный модуль MS_EXCEL_OLE_STANDARD_DAT в программе отчета или пуле модулей.
TEXT_CONVERT_XLS_TO_SAPИспользуется для передачи данных файла excel во внутреннюю таблицу. Знаете ли вы, как использовать TEXT_CONVERT_XLS_TO_SAP функциональный модуль в программе отчета или пуле модулей.
GUI_UPLOADИспользуется для передачи данных текстового файла во внутреннюю таблицу. Знаете ли вы, как использовать функциональный модуль GUI_UPLOAD в программе отчета или пуле модулей.
SSF_FUNCTION_MODULE_NAME Используется для создания функционального модуля в соответствии с именем смарт-формы. Знаете ли вы, как использовать функциональный модуль SSF_FUNCTION_MODULE_NAME в программе отчета или пуле модулей.
Используется для открытия задания, например печати нескольких интеллектуальных форм. Знаете ли вы, как использовать функциональный модуль SSF_OPEN в программе отчета или пуле модулей.
SSF_CLOSEИспользуется для закрытия задания, например печати нескольких интеллектуальных форм. Знаете ли вы, как использовать функциональный модуль SSF_CLOSE в программе отчета или пуле модулей.
SSFCOMP_PDF_PREVIEWИспользуется для прямого предварительного просмотра печати. Знаете ли вы, как использовать SSFCOMP_PDF_PREVIEW функциональный модуль в программе отчета или пуле модулей.
CONVERT_OTF Используется для преобразования в формат OTF. Знаете ли вы, как использовать функциональный модуль CONVERT_OTF в программе отчета или пуле модулей.
Используется для преобразования в формат OTF TO PDF. Знаете ли вы, как использовать функциональный модуль SX_OBJECT_CONVERT_OTF_PDFF в программе отчета или пуле модулей.
SO_NEW_DOCUMENT_ATT_SEND_API1Используется для отправки документа или текста по почте. Знаете ли вы, как использовать функциональный модуль SO_NEW_DOCUMENT_ATT_SEND_API1 в программе отчета или пуле модулей.
READ_TEXTИспользуется для извлечения сведений о тексте. Знаете ли вы, как использовать функциональный модуль READ_TEXT в программе отчета или пуле модулей.
BAPI_FIXEDASSET_OVRTAKE_CREATE Используется для создания BAPI. Знаете ли вы, как использовать BAPI_FIXEDASSET_OVRTAKE_CREATE функциональный модуль в программе отчета или пуле модулей.
Используется для сохранения или фиксации BAPI. Знаете ли вы, как использовать функциональный модуль BAPI_TRANSACTION_COMMIT в программе отчета или пуле модулей.
DEQUEUE_ALLИспользуется для снятия блокировок LUW. Знаете ли вы, как использовать функциональный модуль DEQUEUE_ALL в программе отчета или пуле модулей.
BAPI_ACC_DOCUMENT_POSTLИспользуется для проводки документа счета. Знаете ли вы, как использовать функциональный модуль BAPI_ACC_DOCUMENT_POSTL в программе отчета или пуле модулей.
BAPI_ACC_GL_POSTING_POSTИспользуется для проводки единственного основного счета. Знаете ли вы, как использовать функциональный модуль DSYS_SHOW_FOR_F1HELP в программе отчета или пуле модулей.
BAPI_SALESORDER_CREATEFROMDAT2 Используется для создания заказа на продажу. Знаете ли вы, как использовать функциональный модуль BAPI_SALESORDER_CREATEFROMDAT2 в программе отчета или пуле модулей.
Знаете ли вы, как использовать функциональный модуль BAPI_SALESORDER_CREATEFROMDAT2 в программе отчета или пуле модулей.
Используется для чтения таблицы базы данных из другой системы. Знаете ли вы, как использовать функциональный модуль RFC_READ_TABLE в программе отчета или пуле модулей.
GET_GLOBALS_FROM_SLVC_FULLSCRИспользуется для обновления ALV после модификации. Знаете ли вы, как использовать GET_GLOBALS_FROM_SLVC_FULLSCR функциональный модуль в программе отчета или пуле модулей.
ENQUE_READ2Используется для чтения записей блокировки клиента. Знаете ли вы, как использовать функциональный модуль ENQUE_READ2 в программе отчета или пуле модулей.
SAPGUI_PROGRESS_INDICATOR Используется для GUI PROGRESS PROCENTAGE. Знаете ли вы, как использовать функциональный модуль SAPGUI_PROGRESS_INDICATOR в программе отчета или пуле модулей.
Знаете ли вы, как использовать функциональный модуль SAPGUI_PROGRESS_INDICATOR в программе отчета или пуле модулей.
Используется для создания временного URL-адреса. Знаете ли вы, как использовать функциональный модуль DP_CREATE_URL в программе отчета или пуле модулей.
/ISDFPS/EXEC_TRANSACTIONИспользуется в функциональном модуле для вызова T-кода. Знаете ли вы, как использовать функциональный модуль /ISDFPS/EXEC_TRANSACTION в программе отчета или пуле модулей.
NUMBER_GET_NEXTИспользуется для извлечения следующего номера из диапазона номеров. Знаете ли вы, как использовать NUMBER_GET_NEXT функциональный модуль в программе отчета или пуле модулей.
POPUP_TO_CONFIRM Используется, чтобы задать вопрос через всплывающее диалоговое окно. Знаете ли вы, как использовать функциональный модуль POPUP_TO_CONFIRM в программе отчета или пуле модулей.
Знаете ли вы, как использовать функциональный модуль POPUP_TO_CONFIRM в программе отчета или пуле модулей.
Используется для поиска типа связи. Знаете ли вы, как использовать функциональный модуль ADDR_GET_NEXT_COMM_TYPE в программе отчета или пуле модулей.
CONVERT_COMM_TYPE_DATAИспользуется для преобразования данных типа связи. Знаете ли вы, как использовать функциональный модуль CONVERT_COMM_TYPE_DATA в программе отчета или пуле модулей.
NAST_PROTOCOL_UPDATEИспользуется для проверки успешности обновления протокола Nast. Знаете ли вы, как использовать функциональный модуль NAST_PROTOCOL_UPDATE в программе отчета или пуле модулей.
SX_ADDRESS_TO_DEVTYPE Используется для адреса отправителя для доставки почты. Знаете ли вы, как использовать функциональный модуль SX_ADDRESS_TO_DEVTYPE в программе отчета или пуле модулей.
Знаете ли вы, как использовать функциональный модуль SX_ADDRESS_TO_DEVTYPE в программе отчета или пуле модулей.
Используется для создания функционального модуля в соответствии с именем формы Adobe. Знаете ли вы, как использовать функциональный модуль FP_FUNCTION_MODULE_NAME в программе отчета или пуле модулей.
FP_JOB_OPENИспользуется для открытия задания, например, для печати нескольких форм Adobe. Знаете ли вы, как использовать FP_JOB_OPEN функциональный модуль в программе отчета или пуле модулей.
FP_JOB_CLOSEИспользуется для закрытия задания, как при печати нескольких форм Adobe. Знаете ли вы, как использовать функциональный модуль FP_JOB_CLOSE в программе отчета или пуле модулей.
ARCHIV_GET_PRINTFORMAT Используется для установки формата печати архива. Знаете ли вы, как использовать функциональный модуль ARCHIV_GET_PRINTFORMAT в программе отчета или пуле модулей.
Знаете ли вы, как использовать функциональный модуль ARCHIV_GET_PRINTFORMAT в программе отчета или пуле модулей.
Используется для создания архивного документа. Знаете ли вы, как использовать функциональный модуль ARCHIV_CREATE_OUTGOINGDOCUMENT в программе отчета или пуле модулей.
FP_GET_LAST_ADS_ERRSTRИспользуется для проверки ошибки последнего адреса формы Adobe. Знаете ли вы, как использовать функциональный модуль FP_GET_LAST_ADS_ERRSTR в программе отчета или пуле модулей.
ICON_CREATEИспользуется для создания значка на кнопке. Знаете ли вы, как использовать функциональный модуль ICON_CREATE в программе отчета или пуле модулей.
Макросы, подпрограммы и функциональные модули
ByScott Livingston
ЧасыОбновлено
Когда вы модульизуете исходный код, вы помещаете последовательность операторов ABAP в модуль. Затем, вместо размещения всех операторов в основной программе, вы просто вызываете модуль. Когда программа генерируется, исходный код модуля модульности обрабатывается так, как если бы он действительно физически присутствовал в основной программе.
В этом руководстве вы узнаете:
- Макрос SAP-ABAP
- Включить программы
- Подпрограммы
- Функциональные модули
- Функциональные группы
Необходимость модульности
- Улучшить структуру программы.
- Легко читаемый код
- Простота обслуживания, код
- Избегайте избыточности и поощряйте повторное использование кода
Различные методы модуляции
- Использование макросов
- Использование включаемых файлов
- Подпрограммы
- Функциональные модули
Давайте подробно рассмотрим каждый из них:
Макрос SAP-ABAP
Если вы хотите повторно использовать один и тот же набор операторов более одного раза в программе, вы можете включить их в макрос.
Вы можете использовать макрос только в программе, в которой он определен, и его можно вызывать только в строках программы, следующих за его определением.
Макросы могут быть полезны для длинных вычислений или сложных операторов WRITE.
Синтаксис
DEFINE <имя_макроса> 'Макрооператоры КОНЕЦ ОПРЕДЕЛЕНИЯ
Макросы могут использовать параметры &N , где N = 1,2,3…
Пример:-
ДАННЫЕ: номер 1 ТИП I ЗНАЧЕНИЕ 1. ОПРЕДЕЛИТЕ приращение. ДОБАВЬТЕ 1 к &1. НАПИСАТЬ &1. КОНЕЦ ОПРЕДЕЛЕНИЯ. Приращение №1. НАПИШИТЕ номер 1.
Вывод: 2
Включаемые программы
Включаемые программы предназначены исключительно для модуляции исходного кода и не имеют интерфейса параметров.
Включаемые программы позволяют использовать один и тот же исходный код в разных программах. Они могут быть полезны, если у вас есть длинные объявления данных, которые вы хотите использовать в разных программах.
Синтаксис
Включить <имя программы включения>
Указывает на примечание
- Включить программы не могут вызывать сами себя.
- Включаемые программы должны содержать полные операторы.
Пример:
ВКЛЮЧИТЬ ZILX0004. НАПИСАТЬ: / «Пользователь», SY-UNAME,/ «Дата», SY-DATUM. ================================= ПРОГРАММА ZRPM0001. ВКЛЮЧИТЕ ZILX0004.
Подпрограммы
Подпрограммы — это процедуры, которые можно определить в любой программе ABAP, а также вызывать из любой программы. Подпрограммы обычно вызываются внутри, то есть они содержат участки кода или алгоритмы, которые часто используются локально. Если вы хотите, чтобы функцию можно было повторно использовать во всей системе, используйте функциональный модуль.
Синтаксис-
FORM <Подпрограмма> []. <Блок операторов>. КОНЕЦ.
<Подпрограмма> = Имя подпрограммы
Типы Подпрограмм
- Внутренние
- Подпрограмма определена в той же вызываемой программе.

- Может получить доступ ко всем объектам данных, объявленным в основной программе ABAP/4.
- Подпрограмма определена в той же вызываемой программе.
- Внешний
- Подпрограмма, определенная вне вызываемой программы.
- Необходимо использовать параметр
или объявить объекты данных в общих частях памяти.
Вызов подпрограммы
Внутренние подпрограммы
Выполнить[ ]
. в основной программе автоматически доступен.
Внешние подпрограммы
ВЫПОЛНИТЬ <подпрограмма>(<Программа>) [<проход>]. ВЫПОЛНИТЬ <подпрограмма> (<Программа>) [<пароль>] [ЕСЛИ НАЙДЕНА]. ВЫПОЛНИТЬ (<подпрограмма>) IN PROGRAM (<Программа>) [] [IF FOUND]. ВЫПОЛНИТЬ <индекс> OF <подпрограмма1> <подпрограмма2> <подпрограмма3> [<проход>].
Обратите внимание
- В подпрограммах разрешены вложенные вызовы (например, PERFORM внутри FORM … ENDFORM ).

- Также возможны рекурсивные вызовы.
- Чтобы определить локальные данные, используйте оператор DATA после FORM. Каждый раз, когда вы входите в подпрограмму, данные создаются заново (с начальным значением) и высвобождаются в конце (из стека).
- Чтобы определить глобальные данные, используемые внутри подпрограммы, используйте оператор LOCAL после FORM. Значения сохраняются при входе в подпрограмму и освобождаются в конце (из стека)
Функциональные модули
Функциональные модули — это подпрограммы ABAP/4 общего назначения, которые может использовать каждый. На самом деле, доступно большое количество стандартных функциональных модулей.
Функциональные модули организованы в функциональные группы: наборы логически связанных функций. Функциональный модуль всегда принадлежит функциональной группе.
Синтаксис-
FUNCTION <функциональный модуль> <Утверждения> КОНЕЦ ФУНКЦИИ.
Важная информация, связанная с функциональным модулем
- Администрация
- Импорт/Изменение/Экспорт параметров.

- Табличные параметры/исключения.
- Документация
- Исходный код — L
U01 . — функциональная группа - Глобальные данные – L
TOP .Глобальные данные для функциональной группы – доступны для всех функциональных модулей в функциональной группе. - Основная программа – SAPL
Вызов функционального модуля
Чтобы вызвать функциональный модуль, используйте оператор CALL FUNCTION:
CALL FUNCTION[ЭКСПОРТ f1 = a 1.... f n = a n] [ИМПОРТ f1 = a 1.... f n = a n] [ИЗМЕНЕНИЕ f1 = a 1.... f n = a n] [ТАБЛИЦЫ f1 = a 1.... f n = a n] [ИСКЛЮЧЕНИЯ e1 = r 1.... e n = r n [ERROR_MESSAGE = r E] [ДРУГИЕ = ro]].
Функциональные группы
Функциональные группы — это контейнеры для функциональных модулей. На самом деле существует большое количество стандартных функциональных групп.
Все функциональные модули в функциональной группе могут получить доступ к глобальным данным группы.
Подобно исполняемым программам (тип 1) и пулам модулей (тип M), группы функций могут содержать экраны, экраны выбора и списки.
Обратите внимание
- Функциональные группы не могут быть выполнены.
- Имя функциональной группы может содержать до 26 символов.
- При создании функциональной группы или функционального модуля основная программа и включаемые программы генерируются автоматически.
- Группы функций инкапсулируют данные.
Как создать группу функций
- Перейти к транзакции SE80.
- Выберите программу в раскрывающемся списке.
- Напишите имя функциональной группы, которую вы хотите создать. Обычно пользовательские группы функций начинаются с «Z». например –
. Нажмите клавишу ввода. - Обратите внимание, что TOP Include создается по умолчанию, если пользователь выбирает опцию создания TOP include.

Как создать функциональный модуль
- Создайте группу функций (например, « ZCAL »).
- Создайте функциональный модуль, установите такие атрибуты, как (Функциональная группа, Приложение, Краткий текст и Тип процесса) и Сохранить.
- Включаемый файл « LZCALU01 » будет содержать исходный код первого функционального модуля.
- Включаемый файл « LZCALTOP » будет содержать глобальные данные.
- Основная программа « SAPLZCAL » содержит
- Глобальные данные Включить файл » LZCALTOP »
- Функциональные модули включают файл « LZCALUXX »
- Включаемые файлы, определяемые пользователем « LZCALF ..», « LZCALO ..» и « LZCALI ..»
- Определение параметров интерфейса и исключений
- Напишите исходный код
- Активировать функциональный модуль
- Тестирование функционального модуля — одиночное тестирование и отладка
- Документирование и выпуск функционального модуля
Это все, что касается модульности в ABAP.
Поддержка SAP для функционального модуля
Поддержка SAP для функционального модуляПоддержка SAP для функционального модуля
Имеется два атрибута (отображается на вкладке Атрибуты функционального модуля) следует учитывать перед использованием функционального модуля:
- Если функциональный модуль не выпускается (отображается в общих данных), это внутренний к SAP, и пользователь должен использовать его с особой осторожностью. Из выпуска для выпуска этот функциональный модуль может быть удален или его поведение изменены без предварительного уведомления SAP.
- Атрибуты нормального функционального модуля или с дистанционным управлением функциональный модуль, описанный на вкладке Тип обработки не имеет технической разницы для интерфейса. Однако, если функциональный модуль поддерживает RFC, это может показать, что SAP принял некоторые шаги по экстернализации этого функционального модуля.
Интерфейс доступен только для чтения. Вы должны проверить, что любая функция
модуль, вызываемый из интерфейса, доступен только для чтения. Нет способа
сервер, чтобы проверить, доступен ли функциональный модуль только для чтения. Этот
ответственность должна быть возложена на пользователя.
Вы должны проверить, что любая функция
модуль, вызываемый из интерфейса, доступен только для чтения. Нет способа
сервер, чтобы проверить, доступен ли функциональный модуль только для чтения. Этот
ответственность должна быть возложена на пользователя.
Также следует уделить внимание безопасности системы. Если функция модуль поддерживает RFC, это не означает, что он привязан к Безопасность САП. По нашему собственному опыту, только подмножество функций модули с именем, начинающимся с BAPI, могут включать безопасность SAP.
- Создать синоним времени
А функциональный модуль может иметь набор таблиц Import/Export/Changing/Tables параметры. Он также может включать набор исключений. (см. текущие ограничения ниже).
Каждый параметр должен быть прототипирован для тип данных, который можно преобразовать в тип данных сервера WebFOCUS. Если параметр не может быть отображен, выдается предупреждение (FOC44492), и параметр будет отклонен.
 Примером является LOCAL_CAT.
импортировать параметр в функциональном модуле READ_TEXT.
Примером является LOCAL_CAT.
импортировать параметр в функциональном модуле READ_TEXT.Параметры может быть прототипирован как LIKE или TYPE. В случае TYPE этот тип должен быть экстернализованным, то есть определяться вне сферы действия функции группа, в которой определен функциональный модуль. Пример, где ТИП не может быть найден в параметре таблицы SELKZ_KUPAV в Функциональный модуль SD_PARTNER_SELECTION. Этот параметр имеет вид LV09A_TY_PRTNR_ITAB, определенный в группе типов LV09A. В таком случае, будет выдано сообщение об ошибке (FOC44488), и параметр быть отвергнутым.
Интерфейс может обрабатывать либо отдельные поля, или одноуровневые структуры, но он не может обрабатывать составные структуры, например, параметр импорта IT_COMP_SIMUPARAM_RANGES в ACEDS_ACCRUAL_FOR_ACRTYPE_CALC функциональный модуль. В этом случае будет выдано сообщение об ошибке (FOC44491), и параметр будет отклонен.
Когда структура параметр таблицы содержит только четыре смежных поля с именем SIGN, ОПЦИЯ, содержит (НИЗКИЙ) и содержит (ВЫСОКИЙ) эту конкретную таблицу рассматривается как таблица опций выбора и будет объявлена как таковая в файле доступа.
 Это, помимо импорта с одним значением,
наиболее эффективный способ передать набор ограничений функциональному модулю.
Это, помимо импорта с одним значением,
наиболее эффективный способ передать набор ограничений функциональному модулю. - Ограничения
- В настоящее время адаптер не поддерживает ИЗМЕНЕНИЕ параметров.
- Прототипы типов данных должны быть преобразованы в настоящий уникальный тип данных ABAP. Таким образом, ЛЮБОЙ, ЛЮБАЯ ТАБЛИЦА, СТАНДАРТНАЯ ТАБЛИЦА и ТАБЛИЦА не поддерживаются в качестве типа данных. прототипы.
- ТИП C по умолчанию А1.
- ТИП СТРОКИ по умолчанию A80. Для этих двух типов (C и STRING) это будет зависеть от пользователя, с помощью редактора синонимов, настроить длину определенных полей в соответствии с индивидуальными потребностями.
- Тип данных должен быть тот, который поддерживается. Неподдерживаемые типы данных: VARC, PREC, LCHR, LRAW, РАСШИРЕННАЯ СТРУНА.
- ИМПОРТ параметров
может быть сопоставлен с одним единственным полем (используя либо LIKE, либо TYPE).

- ЭКСПОРТ параметров
могут быть либо отдельными полями, либо структурой (используя либо LIKE, либо
ТИП). Когда параметр EXPORT является структурой, определенной с помощью TYPE,
возможны два варианта:
- Параметр упоминается в словаре данных как структура (например, БАПИРЕ 2).
- Упоминается как табличный тип (например, BAPIRET2_T).
- Хотя синоним может быть создан во всех случаях, табличный тип, как параметр экспорта не поддерживается.
- Сообщения об ошибках/предупреждениях
- (E) (FOC44488) ТИП ДАННЫХ тип_данных НЕ НАЙДЕН ДЛЯ ПАРАМЕТРА имя_параметра
- (Е) (FOC44489) DDIF_FIELDINFO_GET ВНУТРЕННЯЯ ОШИБКА ДЛЯ имя_параметра
- (E) (FOC44490) DDIF_FIELDINFO_GET НЕДОКУМЕНТИРОВАННАЯ ОШИБКА ДЛЯ имя_параметра
- (E) (FOC44491) ВНУТРЕННИЙ
НЕ ПОДДЕРЖИВАЕМЫЕ КОНСТРУКЦИИ.
 ПАРАМЕТР имя_параметра
ПАРАМЕТР имя_параметра - (E) (FOC44492) ПАРАМЕТР имя_параметра НЕ ИМЕЕТ ТИП ДАННЫХ
- (W) (FOC44493) ВОЗМОЖНО SELECT OPTION TABLE имя_таблицы (имя_параметра) БУДЕТ ОТОБРАЖЕНО В ВНУТРЕННЯЯ ТАБЛИЦА
При ошибке, если параметр, на котором возникшая ошибка необязательна, синоним все равно будет создан без соответствующего параметра. Если параметр является обязательным, создание синонима будет прервано.
Примечание: свойства для заданного параметра находятся с помощью функции DDID_FIELDINFO_GET модуль. Если этот функциональный модуль не может получить свойства для параметр, параметр помечен (FOC44488).
ABAP исключения, сгенерированные функциональным модулем SAP, теперь перехватываются в ТАБЛИЦА время работы.
В результате появится ошибка:
(FOC1695) ОШИБКА ЗАПРОСА SAP/R3: [необязательное сообщение об ошибке, отправленное функциональным модулем](FOC1736) ОШИБКА SAP/R3 ПРИ ВЫПОЛНЕНИИ ПРОГРАММЫ ABAP4: имя_модуля_функции
| Программное обеспечение iWay |
АВАР-СОВЕТЫ ПРЕДЫДУЩАЯ СЛЕДУЮЩИЙ СЛУЧАЙНЫЙ Поскольку ваш веб-браузер не поддерживает JavaScript, вот версия слайд-шоу изображений без JavaScript: |

 abs(a))
# [1 2 4]
abs(a))
# [1 2 4]
 1 Свое решение
1 Свое решение