Как найти радиус конуса если известен объем. Как найти радиус основания конуса
В данной статье рассмотрим четыре задачи по стереометрии. Дана комбинация тел – конус и шар. Во всех заданиях речь идёт о конусе, который . Отмечу, что в условии взаимное расположение данных тел озвучено может быть по разному, например: «Конус вписан в шар» или «Около конуса описана сфера».
Суть одна – если сказать простым (нематематическим) языком, то конус находится «внутри» сферы, она содержит окружность его основания и вершину. Посмотрите на эскиз:
При решении необходимо знать формулы объёмов шара и конуса.
Объём шара:
Объём конуса:
*Эти формулы необходимо знать!
Площадь основания конуса является кругом, она равна:
Рассмотрим частный случай! Если высота конуса будет равна радиусу его основания, то формула объёма конуса будет иметь вид:
Эскиз:
Понятно, что центральным сечением такого конуса будет являться прямоугольный равнобедренный треугольник, причём высота проведённая из прямого угла разбивает его также на два прямоугольных равнобедренных треугольника:
Вспомним понятие образующей, оно часто используется в задачах с конусами, будет и в заданиях ниже.
Образующая конуса – это отрезок, соединяющий вершину конуса с точкой его основания. На предыдущем эскизе она обозначена буквой l .
Напрашивается простой вывод: образующих у конуса имеется бесконечное количество и все они равны.
На блоге, кстати, уже есть пара статей с шарами, можете посмотреть их « » и « » .
Теперь рассмотрим задачи:
245351. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Так как сказано, что радиус основания конуса равен радиусу шара, то становится понятно, что основание конуса совпадает с плоскостью центрального сечения шара.
Построим эскиз данной комбинации для наглядности (это осевое сечение):
Сказано, что высота конуса равна радиусу его основания (и, разумеется, радиусу шара). Запишем формулы объёмов шара и конуса:
Так как объём шара известен (он равен 28), можем вычислить радиус. Вернее, нам понадобится не сам радиус, а его куб:
Таким образом, объём конуса будет равен:
*Можно было обойтись без вычислений. Посмотрите, если сопоставить две формулы:
Посмотрите, если сопоставить две формулы:
то видно, что объём шара в 4 раза больше объёма конуса.
Значит объём конуса будет равен 28/4 = 7.
То есть, задача решается практически устно.
Ответ: 7
245352. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Задача обратная предыдущей, рисунок тот же.
Формулы:
Из формул понятно, что объём шара в 4 раза больше объёма конуса:
Таким образом, искомый объём равен 24.
Ответ: 24
316555. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна . Найдите радиус сферы.
Здесь условие звучит по-другому, но тела расположены относительно друг друга абсолютно также, как и в предыдущих задачах – конус вписан в сферу, основание конуса совпадает с центральным сечением сферы.
Эскиз тот же, отметим радиус, высоту равную радиусу и образующую:
«Конус геометрия» — Вершина. Конус. Образующие. Основание. С конусом люди знакомы с глубокой древности. H-высота. Применение конуса и усеченного конуса в повседневной жизни. R-радиус основания. Центр основания. Конус в переводе с греческого «konos» означает «сосновая шишка». L-образующая.
Конус. Образующие. Основание. С конусом люди знакомы с глубокой древности. H-высота. Применение конуса и усеченного конуса в повседневной жизни. R-радиус основания. Центр основания. Конус в переводе с греческого «konos» означает «сосновая шишка». L-образующая.
«Атмосферное давление и высота» — Слон использует атмосферное давление всякий раз, когда хочет пить. 5. Ливер – предназначен для взятия проб различных жидкостей. Изучение новой темы. Организационный момент: приветствие, постановка цели и мотивация урока. Опускаем шприц в жидкое лекарственное средство. То же самое наблюдается и в природе – в водоеме.
«Конус 11 класс» — Площадь полной поверхности конуса. Площадь боковой поверхности усечённого конуса. Конус. Площадь боковой поверхности конуса. V = 1/3sосн.h. Объём усечённого конуса. Sбок= п(r+r1)l. Геометрия 11 класс. Объём конуса. Усечённый конус. Конус- тело ограниченное конической поверхностью и кругом с границей L.
«Медиана биссектриса и высота треугольника» — На каком рисунке изображена высота? отрезок, соединяющий вершину треугольника с серединой противолежащей стороны Биссектриса треугольника Медиана треугольника Высота треугольника. Медиана, биссектриса и высота треугольника. отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны Медиана треугольника Высота треугольника Биссектриса треугольника.
Медиана, биссектриса и высота треугольника. отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны Медиана треугольника Высота треугольника Биссектриса треугольника.
«Цилиндр конус шар» — Сечения цилиндра. Объёмы и поверхности тел вращения. Найти объём и площадь поверхности шара. Определение цилиндра. Оглавление. Объёмы тел вращения. Тела вращения. Объём шарового сегмента. Задача № 3. Площади поверхностей тел вращения. Определение шара. Виды тел вращения. Сечение конуса. — Шаровые сегменты.
«Громкость и высота звука» — Что такое звук? Механические колебания каких частот называются звуковыми? Громкость и высота звука. Контрольный тест. Кто в полёте чаще машет крыльями: муха или комар? Назовите физические характеристики звука. Балалайка. Уровень звукового давления, дБ. Назовите причины возникновения звука. Звук. Саксофон.
Прямой конус — это тело, которое получается при вращении прямоугольного треугольника вокруг одного из катетов.
Спонсор размещения P&G Статьи по теме «Как найти радиус основания конуса» Как найти площадь конуса Как найти площадь треугольника Как найти площадь прямоугольной призмы Как найти площадь грани в пирамиде Как найти перпендикуляр в треугольнике
Инструкция
Если вам известны объем V и высота конуса H, выразите его радиус основания R из формулы V=1/3 ?R?H. Получите: R?=3V/?H, откуда R=v(3V/?H). Если вам известны площадь боковой поверхности конуса S и длина его образующей L, выразите радиус R из формулы: S=?RL. Вы получите R=S/?L.
Следующие способы нахождения радиуса основания конуса базируются на утверждении, что конус образован при вращении прямоугольного треугольника вокруг одного из катетов к оси. Так, если вам известны высота конуса H и длина его образующей L, то для нахождения радиуса R вы можете воспользоваться теоремой Пифагора: L?=R?+H?.
Пример: образующая конуса L равна 20 см и угол? между образующей и высотой конуса равен 15?. Найдите радиус основания конуса. Решение: В прямоугольном треугольнике с гипотенузой L и острым углом? противолежащий этому углу катет R вычисляется по формуле R=L sin?. Подставьте соответствующие значения, получите: R=L sin?=20 sin15?. Sin15? находится из формул тригонометрических функций половинного аргумента и равен 0,5v(2–v3).
Другие новости по теме:
Если вблизи вершины конуса провести сечение, можно получить идентичную, но иную по форме и размерам фигуру, называемую усеченным конусом. Она имеет не один, а два радиуса, один из которых меньше другого. Как и у обычного конуса, у этой фигуры имеется высота. Спонсор размещения P&G Статьи по теме
Усеченным конусом называется геометрическое тело, которое получилось в результате сечения полного конуса плоскостью, параллельной его основанию. Согласно другому определению, усеченный конус образован вращением прямоугольной трапеции вокруг той ее боковой стороны, которая перпендикулярна
Тем, кто занимается моделированием и бумажной пластикой, необходимо уметь делать развертки разнообразных геометрических тел. В школьной геометрии конус определяют как геометрическое тело, которое получается в результате объединения всех лучей, исходящих из одной точки, называемой вершиной конуса,
В школьной геометрии конус определяют как геометрическое тело, которое получается в результате объединения всех лучей, исходящих из одной точки, называемой вершиной конуса,
Площадью основания конуса является круг. Для нахождения его площади надо знать радиус окружности, содержащей этот круг, либо какие-нибудь другие данные, расчеты которых математически связаны с площадью основания конуса. Спонсор размещения P&G Статьи по теме «Как найти площадь основания конуса» Как
Конус представляет собой геометрическое тело, основание которого представляет собой круг, а боковая поверхности — все отрезки, проведенные из точки, находящейся вне плоскости основания, к этому основанию. Прямой конус, который обычно рассматривается в школьном курсе геометрии, можно представить как
Конус — это тело, в основании которого лежит круг. Вне плоскости этого круга находится точка, называемая вершиной конуса, а отрезки, которые соединяют вершину конуса с точками окружности основания, называются образующими конуса. Вам понадобится Бумага, карандаш, калькулятор Спонсор размещения P&G
Вам понадобится Бумага, карандаш, калькулятор Спонсор размещения P&G
Конус. Формулы, признаки и свойства
Навигация по странице: Определение конуса Элементы конуса Объём конуса Площадь поверхности конуса Уравнение конуса Основные свойства кругового конуса
Определение.
Конус — это геометрическое тело, которое образовано совокупностью всех лучей, исходящих из точки и пересекающих любую плоскую поверхность. В месте пересечения образуется основание конуса.
| Рис.1 | Рис.2 | |
| Рис.3 | Рис. 4 4 |
Элементы конуса
Определение. Вершина конуса — это точка (K), из которой исходят лучи.
Определение. Основание конуса — это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.
Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):
L2 = R2 + H2
Определение. Направляющая конуса — это кривая, которая описывает контур основания конуса.
Определение. Боковая поверхность конуса — это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.
Определение. Высота конуса (H) — это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
Определение. Ось конуса (a) — это прямая, проходящая через вершину конуса и центр основания конуса.
Определение. Конусность (С) конуса — это отношение диаметра основания конуса к его высоте. В случае усеченного конуса — это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:
| C = | D | и C = | D — d |
| H | h |
где C — конусность, D — диаметр основания, d — диаметр меньшего основания и h — расстояние между основаниями.
Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса.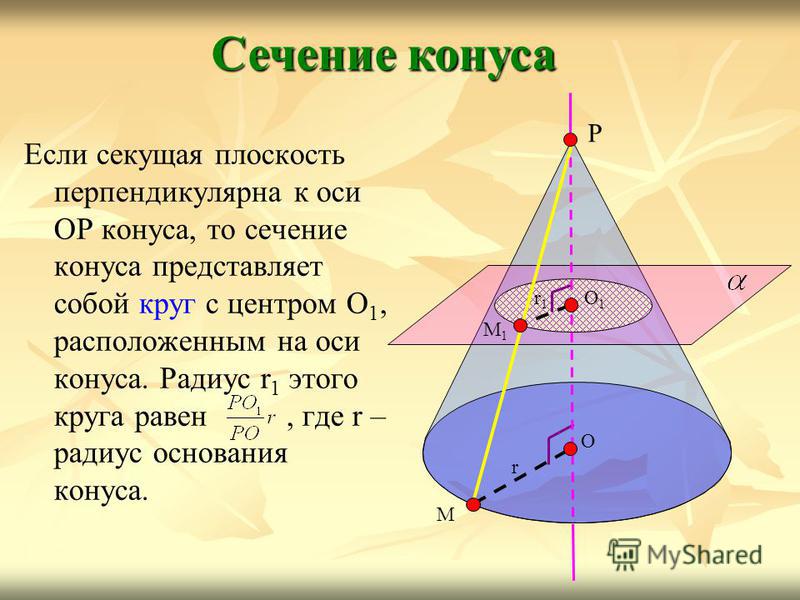 Чем больше конусность, тем острее угол наклона. угол конуса α будет:
Чем больше конусность, тем острее угол наклона. угол конуса α будет:
| α = 2arctg | R |
| H |
где R — радиус основы, а H — высота конуса.
Определение. Осевое сечение конуса — это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника — это диаметр основания конуса.
Определение. Касательная плоскость к конусу — это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.
Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).
Определение. Прямой конус — это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Прямой конус — это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Формула. Объём кругового конуса:
| V = | 1 | πHR2 |
| 3 |
Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:
Sb = πRL
Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:
Sp = πRL + πR2
Определение. Косой (наклонный) конус — это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.
Формула. Объём любого конуса:
| V = | 1 | SH |
| 3 |
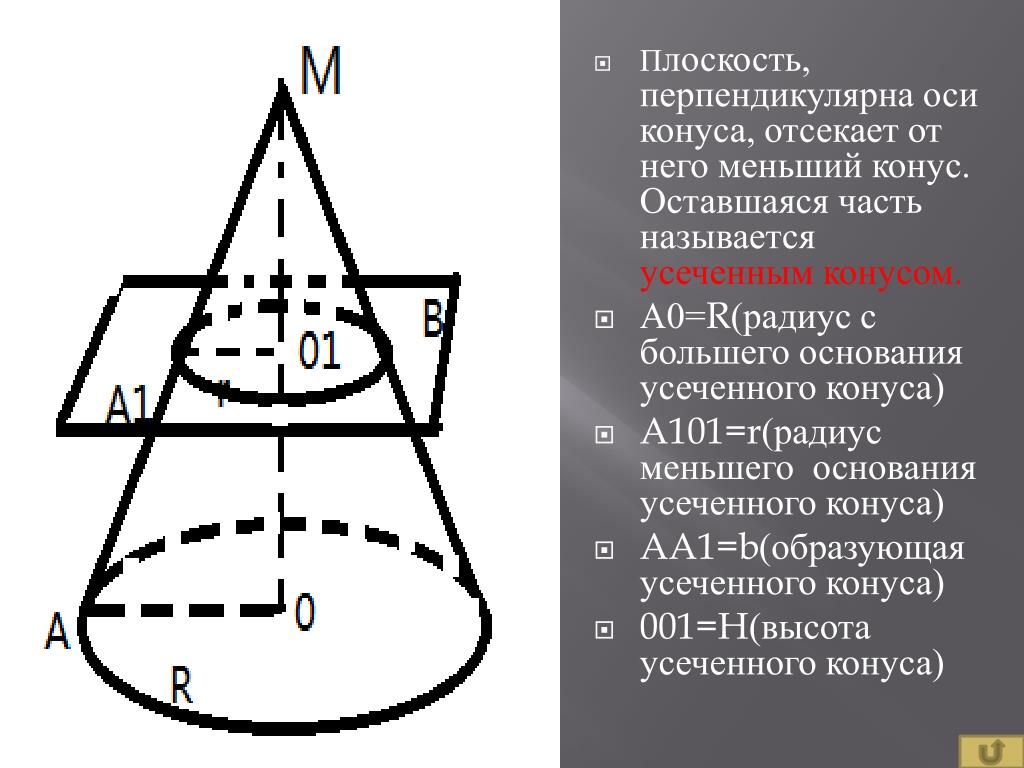
Определение. Усеченный конус — это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.
Формула. Объём усеченного конуса:
| V = | 1 | (S2H — S1h) |
| 3 |
Уравнение конуса
1. Уравнение прямого кругового конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | — | z2 | = 0 |
| a2 | a2 | c2 |
2. Уравнение прямого эллиптического конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | = | z2 |
| a2 | b2 | c2 |
Основные свойства кругового конуса
1.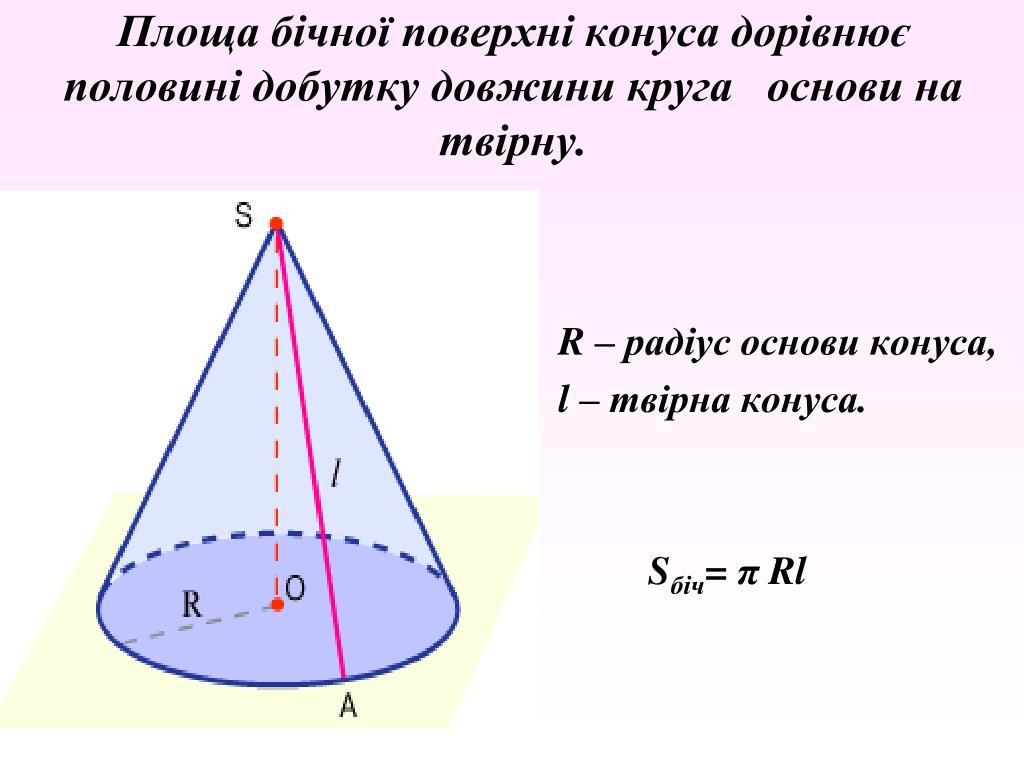 Все образующие прямого кругового конуса равны между собой.
Все образующие прямого кругового конуса равны между собой.
2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.
4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).
7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.
Все таблицы и формулы
Геометрия Площадь поверхности конуса
Материалы к уроку
Конспект урока
Площадь поверхности конуса
|
Вспомним, что такое конус. Тело, ограниченное конической поверхностью и кругом радиусом R, называется конусом.
|
Тело, ограниченное конической поверхностью и кругом радиусом R, называется конусом.
|
|
Боковую поверхность конуса можно развернуть на плоскость, разрезав ее по одной из образующих. Пусть дан конус с радиусом ОА. В результате получим круговой сектор, радиус которого равен образующей конуса, а длина дуги АА´ сектора равна длине окружности основания конуса. |
AA´ = 2πr. |
|
За площадь боковой поверхности конуса принимается площадь его развертки (кругового сектора).
Площадь сектора вычисляется по формуле: пи эль квадрат на угол фи, деленное на 360 градусов, где φ (фи) — градусная мера дуги АА´. Теперь выразим φ через l и r.
Длина дуги АА´ равна с одной стороны длине окружности, а с другой стороны длине кругового сектора в фи градусов, поэтому получаем формулу: Выразим из нее φ: 360 умножить на эр и разделить все на эль. |
|
|
Подставим это выражение в формулу площади боковой поверхности конуса, получим, что площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
|
Sбок. = πrl
|
|
Можно эту формулу выразить через радиус и высоту конуса: Площадь боковой поверхности конуса равна произведению числа π на радиус и на квадратный корень из суммы квадратов радиуса и высоты. |
r–радиус основания h–высота кунуса
|
|
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Основанием конуса является круг. |
Sполн. = πr (r + l) где r — радиус окружности основания,
|
|
Можно эту формулу выразить через радиус и высоту конуса: |
|
|
Задача. Найти высоту конуса, если площадь его осевого сечения равна 6 дм2, а площадь основания
Вспомним, что собой представляет осевое сечение конуса: сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. Решение
1.Осевое сечение конуса представляет собой треугольник РАВ, который является равнобедренным. Выразим площадь осевого сечения через высоту и радиус основания: площадь треугольника равна половине произведения основания на высоту. АВ равно двум радиусам, подставим в формулу и получим: площадь сечения равна произведению радиуса на высоту конуса. 2. Из этой формулы выразим высоту.
Из формулы площади основания выражаем радиус. Получим, что радиус равен корень квадратный из площади основания деленное на пи. Высота равна три корня из пи, деленное на корень из двух дм. |
Дано конус, РАВ–осевое сечение, SΔPAB=6дм2, Sосн=8дм2 Найти h. |
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Урок 10. комбинации тел вращения — Геометрия — 11 класс
Геометрия, 11 класс
Урок №10. Комбинации тел вращения
Перечень вопросов, рассматриваемых в теме:
- комбинации конуса и цилиндра, конуса и усеченного конуса, цилиндра и усеченного конуса, нескольких сфер;
- цилиндр, описанный около конуса, конус, описанный около цилиндра, усеченный конус, описанный около конуса и цилиндра;
- цилиндр, вписанный в конус, конус, вписанный в цилиндр, усеченный конус, вписанный в конус и цилиндр.

Глоссарий по теме
Определение
Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.
Определение
Конус вписан в цилиндр, если основание конуса совпадает с основанием цилиндра, а вершина совпадает с центром другого основания цилиндра. Цилиндр, соответственно, в этом случае называется описанным около конуса.
Определение
Конус вписан в другой конус, если его вершина лежит в центре основания второго конуса, а основание лежит на боковой поверхности.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-147.
Дополнительная литература:
Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.
: учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
1. Комбинации цилиндра и конуса
Определение
Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.
В любой конус можно вписать цилиндр.
Оси конуса и вписанного в него цилиндра совпадают. Верхнее основание цилиндра совпадает с сечением конуса плоскостью, параллельной основанию.
Осевое сечение цилиндра, вписанного в конус — представляет собой равнобедренный треугольник с вписанным в него прямоугольником.
SO=H — высота конуса
OA=OB=R — радиус конуса
OF=OM=r — радиус цилиндра
OO1=h — высота цилиндра
SA=SB=L — образующие конуса
NF=KM=h (l)— образующие цилиндра.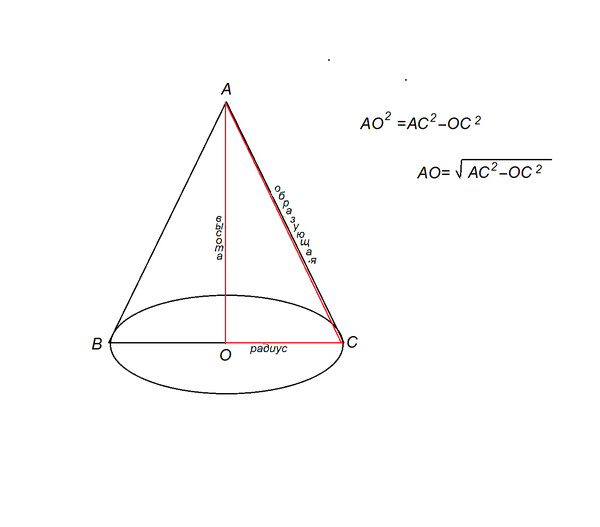
∆SOB и ∆KMB — прямоугольные
∆SOB∆KMB (по общему острому углу B)
Поэтому:
, то есть: .
Отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра (через радиусы основания и образующие)
, то есть .
Таким образом:
.
Определение
Конус вписан в цилиндр, если основание конуса совпадает с основанием цилиндра, а вершина совпадает с центром другого основания цилиндра. Цилиндр, соответственно, в этом случае называется описанным около конуса.
В любой цилиндр можно вписать конус.
OS — ось цилиндра и ось конуса, высота цилиндра и конуса
OA — радиус конуса и радиус цилиндра
SA=SB=L — образующие конуса,
CA=DB=l — образующие цилиндра
∆SOA, ∆SCA, ∆SDB и ∆SOB — прямоугольные
∆SOA=∆SCA, ∆SDB = ∆SOB, поэтому 2S∆ASB=2SACDB.
Отношение боковой поверхности конуса к боковой поверхности описанного около него цилиндра (через радиус основания и высоту)
, то есть .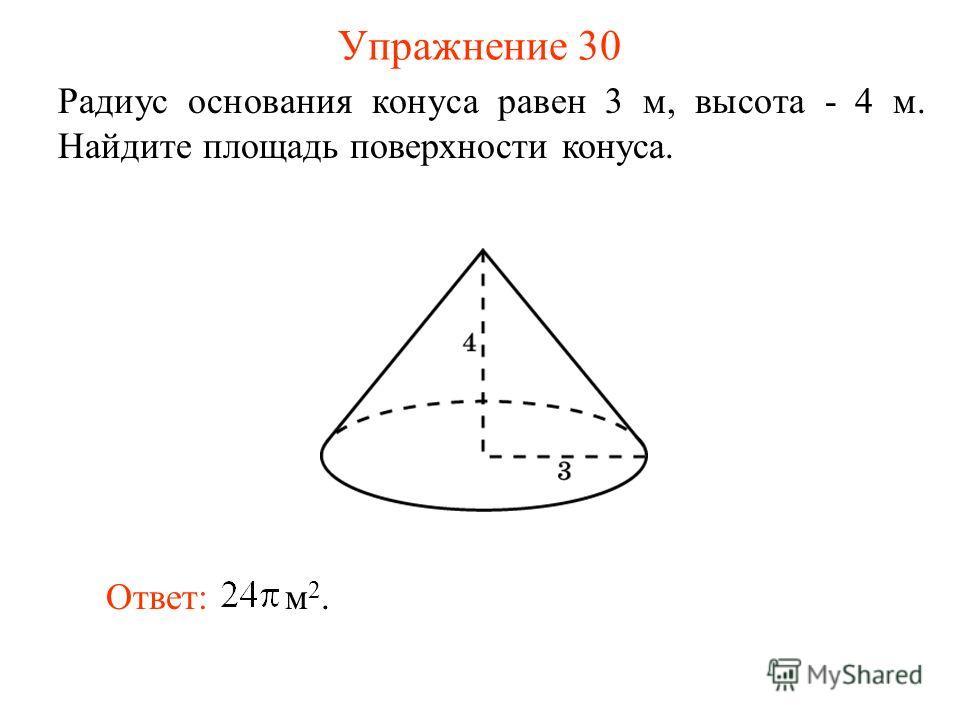
.
2. Комбинация двух конусов
Определение
Конус вписан в другой конус, если его вершина лежит в центре основания второго конуса, а основание лежит на боковой поверхности.
OS — ось конусов, высота большого конуса
OH — высота малого конуса
OA — радиус большого конуса
CH — радиус малого конуса
AS=SB=L
OC=OD=l
Задача
В дне кашпо, имеющего форму конуса с площадью боковой поверхности 15π дм и радиусом основания 3 дм, сделано отверстие для того чтобы в него можно было вставить горшок для цветов, имеющий форму цилиндра. Определите радиус этого отверстия так, чтобы горшок для цветов был вписан в конус и имел форму равностороннего цилиндра.
Дано:
Цилиндр вписан в конус
Sб.п.к.=15π дм
R=3дм
dц =lц
Найти r.
Решение:
AS=L — образующая конуса
KC=l — образующая цилиндра
AO=R – радиус основания конуса
KO=r — радиус цилиндра
πRL=15π
L=15π: (3π)=5
Рассмотрим подобные треугольники AKC и AOS.
В них: .
АО=3 (по условию)
KA=3-r
OS=4 (из прямоугольного треугольника AOS с катетом 3 и гипотенузой 5.
KC=2r
6r=4(3-r)
6r=12-4r
10r=12
r=1,2 (дм)
Ответ: r=1,2 (дм)
Примеры и разбор решения заданий тренировочного модуля
1. В конус, осевым сечением которого является прямоугольный треугольник, вписан равносторонний цилиндр. Найдите отношение площадей полных поверхностей конуса и цилиндра.
Решение:
Сделаем чертеж осевого сечения
Обозначим радиус цилиндра ЕО= r. Выразим через него все остальные элементы тел вращения.
Так как цилиндр равносторонний, то высота цилиндра равна h=СЕ=2r.
Так как сечение конуса ASB — прямоугольный треугольник и SO — его высота, то SO=OB. То есть высота конуса H равна радиусу R.
Образующая конуса равна L=SA=R .
∆SHD∆DKB∆OSB — прямоугольные равнобедренные треугольники.
Радиус конуса R=OB=OK+KB.
OK=r, KB=h=2r.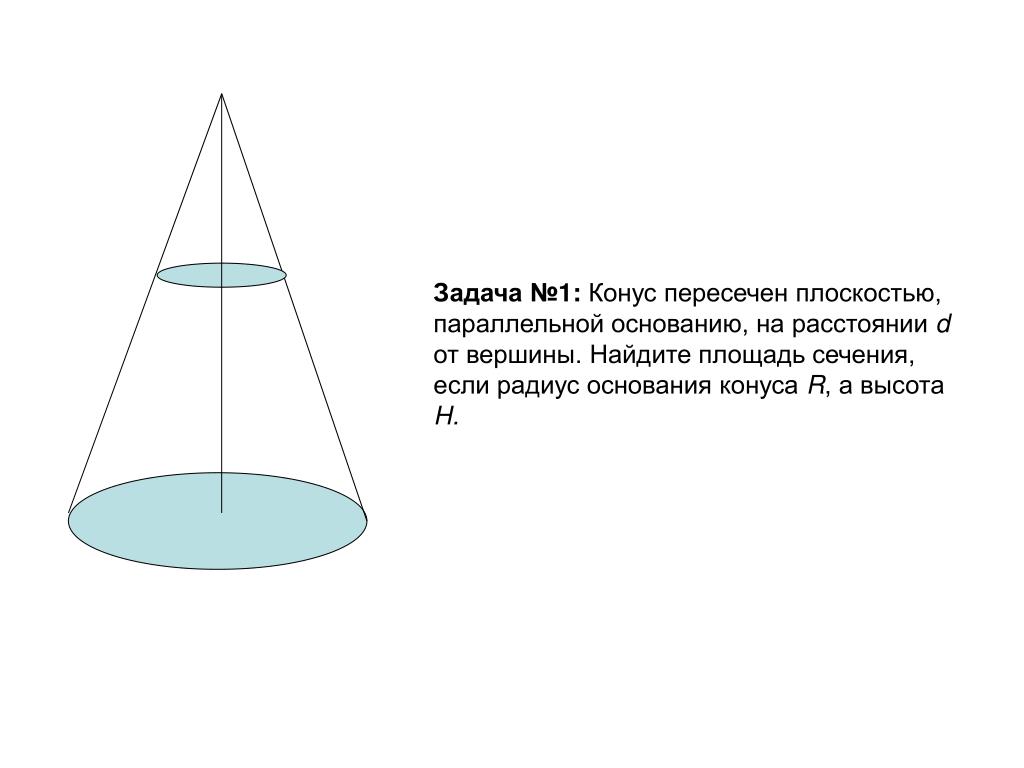
Поэтому R=3r, образующая конуса равна SA=3r .
Выразим площади полных поверхностей конуса и цилиндра.
Sп.п.ц. =2πr(r+h)= 2πr(r+2r)=6πr2.
Sп.п.к. =πR(R+L)= π3r(3r+3r)=9πr2(1+ )
Теперь найдем отношение: .
Ответ: .
2. Усеченный конус вписан в цилиндр. Найдите площадь полной поверхности усеченного конуса, если радиус цилиндра равен 16, высота равна 6 а радиус меньшего основания усеченного конуса в два раза меньше радиуса цилиндра.
Решение:
Сделаем чертеж осевого сечения:
O1B — радиус меньшего основания усеченного конуса.
OC- радиус большего основания усеченного конуса и радиус цилиндра.
BH — высота цилиндра и высота усеченного конуса
По условию OC=2O1B, ОС=16, BH=6.
Так как OC=2O1B и ОС=16, то O1B=8.
Рассмотрим треугольник BHC.
В нем HC=OC-OH=8, BH=6. По теореме Пифагора BC=10.
Теперь нам известен радиус меньшего основания усеченного конуса: он равен 8, радиус большего основания усеченного конуса: он равен 16, образующая усеченного конуса: она равна 10.
Найдем площадь боковой поверхности:
Sб.п.у.к. =πL(r+R)
Sб.п.у.к. =10π(8+16)=240π
Площадь полной поверхности найдем, прибавив две площади оснований:
Sп.п.у.к. =240π+64π+256π=560π
Ответ: Sп.п.у.к. =560π
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.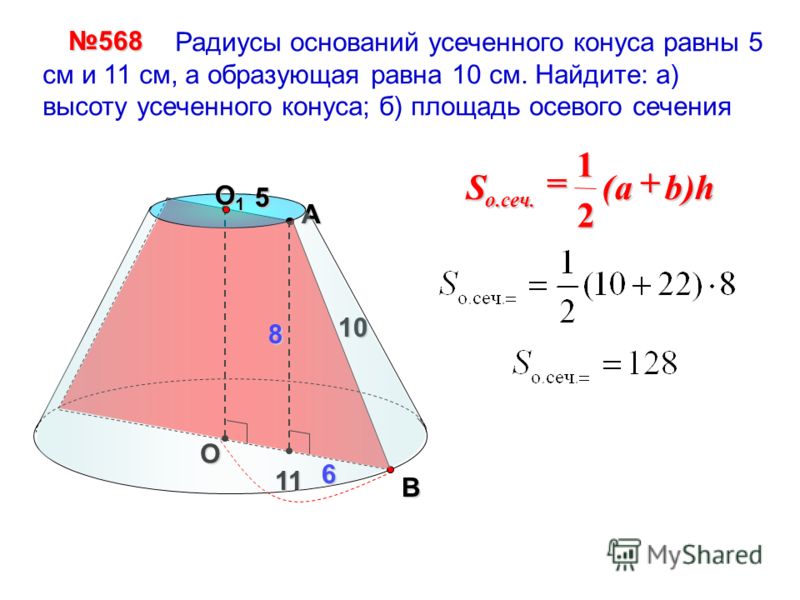 75 . Найдите АС.
75 . Найдите АС.
Решено
На полке было 12 книг. Несколько книг взяли с полки. После этого осталось на 4 книги больше, чем взяли. Сколько книг взяли с полки?
Решено
Ледокол 3 дня пробивал себе путь во льдах.В первый день он проплыл 2/5всего пути,во второй день 5/8 оставшегося пути, а в третий день оставшиеся 90км.Чему равен путь, который проплыл ледокол за 3 дня
Решено
На аэродроме 20 самолетов.Сколько всего троек самолетов может подняться в воздух?Сколько при этом самолетов останется?
Дано: геометрическая прогрессия (bn) задана условиями: b1=-2 , bn+1=3bn. Найдите b6. Объясните пожалуйста, как это решить?
Пользуйтесь нашим приложением
Конус имеет объем \ При каком радиусе основания \ и высоте \ площадь боковой поверхности конуса является наименьшей?
8 класс
Конус имеет объем \(V.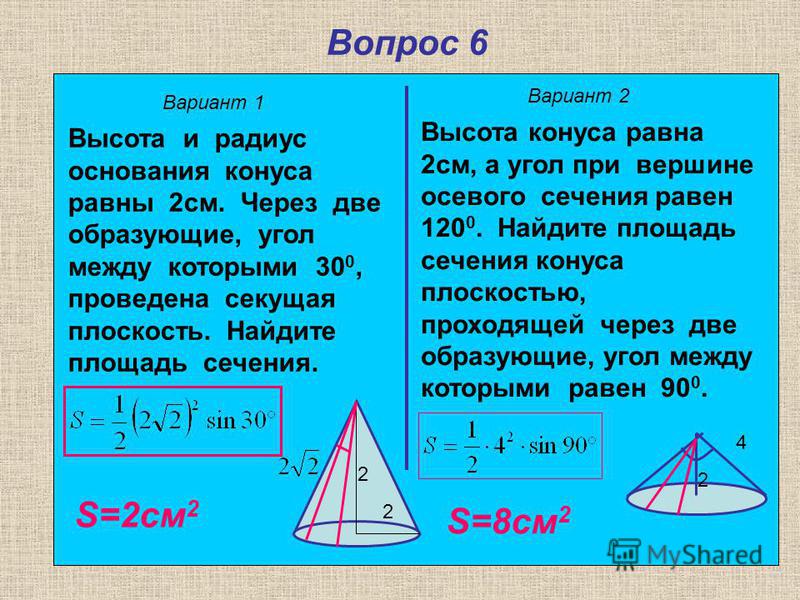 {\large\frac{1}{2}\normalsize}} = \sqrt 2 .}
\]
Таким образом, высота конуса с наименьшей площадью боковой поверхности должна быть примерно в \(1,4\) раза больше радиуса основания.
{\large\frac{1}{2}\normalsize}} = \sqrt 2 .}
\]
Таким образом, высота конуса с наименьшей площадью боковой поверхности должна быть примерно в \(1,4\) раза больше радиуса основания.
Интересно, каково отношение высоты к радиусу основания такого мегасооружения конусообразной формы как Хан Шатыр (рисунок \(15b\))? Если площадь боковой поверхности являлась одним из критических факторов при проектировании, то, вероятно, его форма должна быть близка к полученному решению.
8 класс Математика Простая 2120
Продолжить чтение
Геометрические задачи на оптимизацию
Ещё по теме
Диагональ равнобокой трапеции является биссектрисой ее острого угла и делит среднюю линию трапеции на отрезки длиной 15 см и 33 см. Вычислить (в см2) площадь трапеции.
8 класс Математика Простая 4078
В шар радиусом \(a\) вписан цилиндр.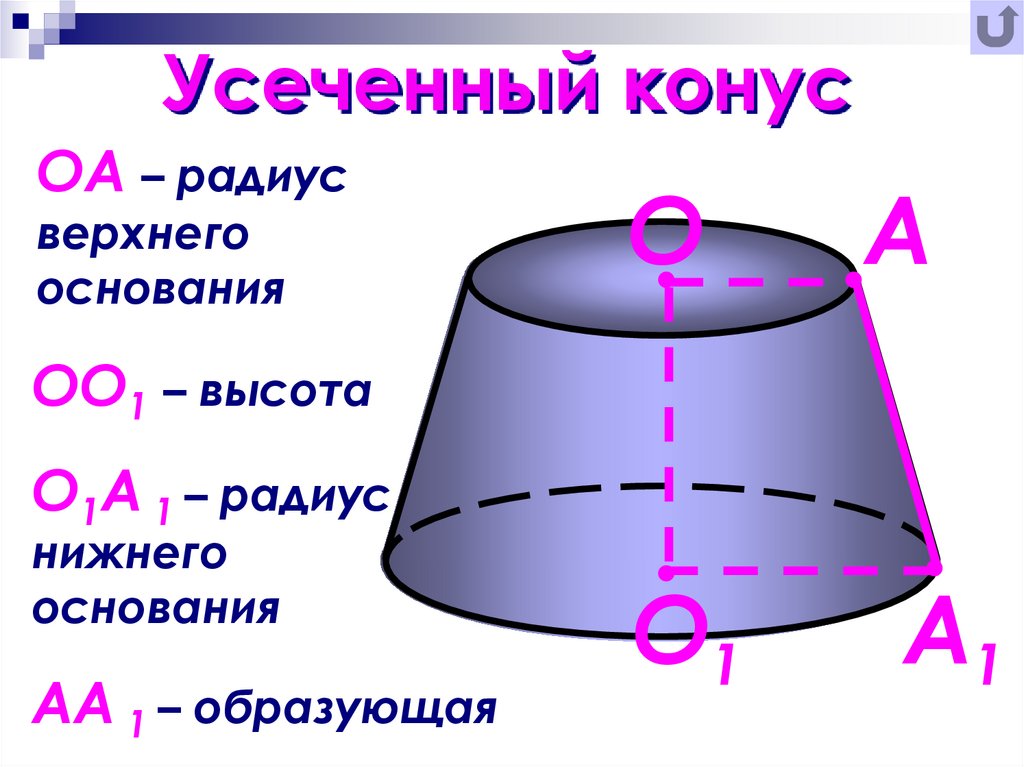 Найти радиус основания \(R\) и высоту \(H\) цилиндра, имеющего наибольший объем.
Найти радиус основания \(R\) и высоту \(H\) цилиндра, имеющего наибольший объем.
8 класс Математика Простая 8732
На координатной плоскости в первой четверти задана точка \(A\left( {a,b} \right).\) Провести через эту точку прямую, отсекающую треугольник наименьшей площади, ограниченный данной прямой и осями координат (рисунок \(1\)).
8 класс Математика Простая 1992
Равнобедренная трапеция описана вокруг окружности радиуса \(R\) (рисунок \(2\)). При каком угле при основании \(\alpha\) площадь заштрихованной области будет наименьшей?
8 класс Математика Простая 1176
Два канала шириной \(a\) и \(b\) соединяются друг с другом под прямым углом (рисунок \(5\)). Определить наибольшую длину бревен, которые можно
сплавлять по данной системе каналов.
Определить наибольшую длину бревен, которые можно
сплавлять по данной системе каналов.
8 класс Математика Простая 2704
Картина высотой \(a\) подвешена на стене таким образом, что ее нижний край выше уровня глаз наблюдателя на \(h\) единиц. На каком расстоянии \(x\) от стены должен находиться наблюдатель, чтобы угол обзора картины был наибольшим (рисунок \(7a\))?
8 класс Математика Простая 3116
Найти цилиндр с наименьшей площадью поверхности.
8 класс Математика Простая 4954
Окно имеет форму прямоугольника, ограниченного сверху полукругом (рисунок \(3\)). Периметр окна равен \(P.\) Определить радиус полукруга \(R,\) при котором площадь окна является наибольшей.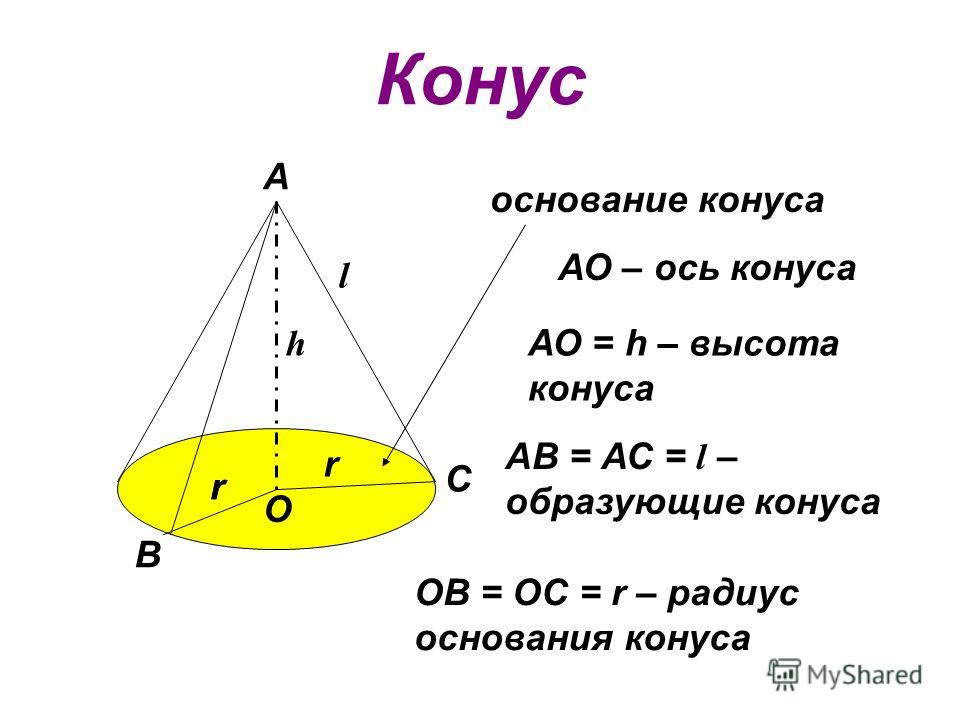
8 класс Математика Простая 3788
Площадь ромба равна \( 10.8 \) см2, а площадь круга, вписанного в этот ромб — \( 2.25\pi \) см2.
1. Определите длину радиуса круга, вписанного в ромб (в см).
2. Вычислить длину стороны ромба (в см).
8 класс Математика Простая 3230
Найти конус наибольшего объема, вписанный в шар радиуса \(R.\)
8 класс Математика Простая 5849
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Калькулятор радиуса конуса
Создано Komal Rafay
Отзыв от Gabriela Diaz
Последнее обновление: 02 июня 2022 г. Пропорционален ли радиус конуса его высоте?
Пропорционален ли радиус конуса его высоте?
Вы застряли в геометрической задаче и нужна помощь калькулятора радиуса конуса? Вы пришли в нужное место.
Наш калькулятор радиуса конуса поможет вам определить радиус конуса, используя различные размеры и формулы конуса .
Вы также узнаете:
- Как вычислить радиус конуса?; и
- Формула радиуса конуса.
Калькулятор радиуса конуса
Калькулятор радиуса конуса является эффективным и экономящим время инструментом. Он вычисляет радиус конуса , в основном используя высоту и наклонную высоту конуса . Другими размерами, в которых используется радиус или высота, являются площадь поверхности, объем, площадь боковой поверхности и площадь основания. Таким образом, эти размеры можно использовать и для оценки радиуса конуса.
Инструмент прост в использовании. Все, что вам нужно сделать, это:
Все, что вам нужно сделать, это:
- Введите высоту конуса .
- Введите наклонную высоту конуса . У вас также есть возможность выбрать другие единицы измерения высоты. По умолчанию сантиметры (см).
- Результатом является радиус правильного кругового конуса вместе с другими измерениями.
Если у вас есть площадь поверхности конуса и вы хотите определить радиус, вы можете ввести площадь поверхности и высоту наклона , и результатом будет радиус вместе со всеми другими размерами конуса.
Точно так же в калькуляторе есть и другие измерения, которые можно использовать для вычисления радиуса конуса.
Продолжайте читать, и вы поймете, как использовать все остальные формулы. 92}}r=l2−h3
где:
Это самая простая из всех других формул радиуса конуса. Это также основная формула, используемая в нашем инструменте.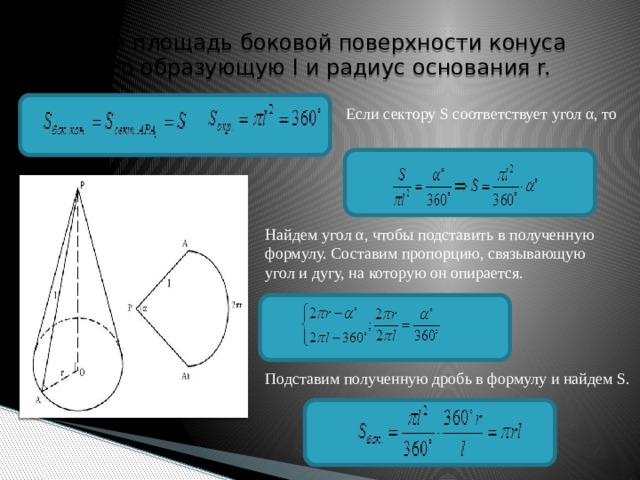
Используя объем
Следующая формула должна найти радиус конуса, используя его объем и высоту. Это выглядит так:
r=3×Vπ×h\large{r = \sqrt{\frac{3 \times V}{\pi \times h}}}r=π×h4×Vгде:
ВВВ — Том.
Если вы решите использовать объем для определения радиуса, вы можете введите объем и высоту конуса в инструменте, а результатом будет радиус в сантиметрах.
Использование боковой площади
Радиус конуса играет роль в определении боковой площади , поэтому, перетасовав формулу, вы можете получить радиус, учитывая боковую площадь конуса.r=ALπ×l\large{r = \frac{A_L}{\pi \times l}}r=π×lAL
- ALA_LAL — Боковая область.
Итак, если вам интересно как рассчитать радиус конуса , теперь у вас есть ответ и так много вариантов для его расчета, лучший вариант — использовать калькулятор радиуса конуса, мы сделали это только для вас .
Пропорционален ли радиус конуса его высоте?
Нет, высота и радиус конуса не пропорциональны друг другу.
Когда нам нужно использовать как высоту, так и радиус конуса для определения любого другого размера конуса, это происходит, когда радиус и высота взаимосвязаны. В остальном радиус и высота конуса не зависят друг от друга, и вы не сможете предсказать одно на основе другого.
Например, чтобы определить объем, наклонную высоту, боковую площадь и площадь поверхности , вам нужны радиус и высота.
Удивительное измерение конуса
Радиус конуса — это одно из многих измерений конуса. Ознакомьтесь с некоторыми другими нашими инструментами, чтобы узнать больше о каждом из них.
- Правый круговой конус;
- Высота конуса;
- Боковая часть конуса;
- Наклонная высота конуса; и
- Диаметр конуса.
Часто задаваемые вопросы
Как рассчитать радиус конуса?
Простейшая формула для расчета радиуса конуса:
r = √(l² - h²)
где:
-
r— радиус; -
l— Высота наклона; и -
h— Высота.
Итак, для расчета радиуса:
- Возведите в квадрат боковую высоту.
- Возведите высоту в квадрат.
- Вычесть квадрат высоты из квадрата боковой высоты .
- Найдите квадратный корень из результата третьего шага.
- Результатом является радиус конуса.
Каков радиус конуса с площадью основания 34 см²?
Радиус равен 3,29 см если площадь основания конуса составляет 34 см² .
Формула для определения радиуса конуса с известной площадью основания:
r = AB / π
где:
-
AB— Базовая площадь; -
π— Константа со значением 3,14159; и -
r— Радиус.
Итак, чтобы определить радиус из площади основания:
- Разделите площадь основания на число пи.
- Результат — радиус конуса.
Komal Rafay
Высота (h)
Наклонная высота (l)
Радиус (r)
Другие размеры
Площадь поверхности (A)
Объем (V)
Площадь боковой поверхности (A_L)
Площадь основания (A_B)
Посмотреть 20 похожих калькуляторов 3D-геометрии 📦
Площадь полушарияCubeCube Calc: найти v, a, d… 17 еще
3 Конусы
Горячая математика А конус представляет собой твердое тело, состоящее из
круг
и его интерьер( база ), данная точка не лежит на плоскости окружности ( вершина ) и все отрезки от точки до окружности.
радиус конуса — это радиус основания. высота конуса — перпендикулярный отрезок, проведенный из вершины к плоскости основания. высота конуса есть длина высоты.
ось конуса — это отрезок, концами которого являются вершина и центр основания. Если ось перпендикулярна плоскости окружности, то конус представляет собой правый конус в противном случае это косой конус .
Наклонной высотой прямого конуса называется длина отрезка от вершины конуса до окружности основания. Наклонная высота не определяется для наклонных конусов.
Конус тесно связан с
пирамида
. Таким образом, формулы их площадей и объемов связаны между собой.
Помните, формулы для боковой площадь поверхности пирамиды является 1 2 п л а общая площадь поверхности 1 2 п л + Б .
Поскольку основанием конуса является круг, подставляем
2
π
р
за
п
а также
π
р
2
за
Б
куда
р
это радиус основания конуса.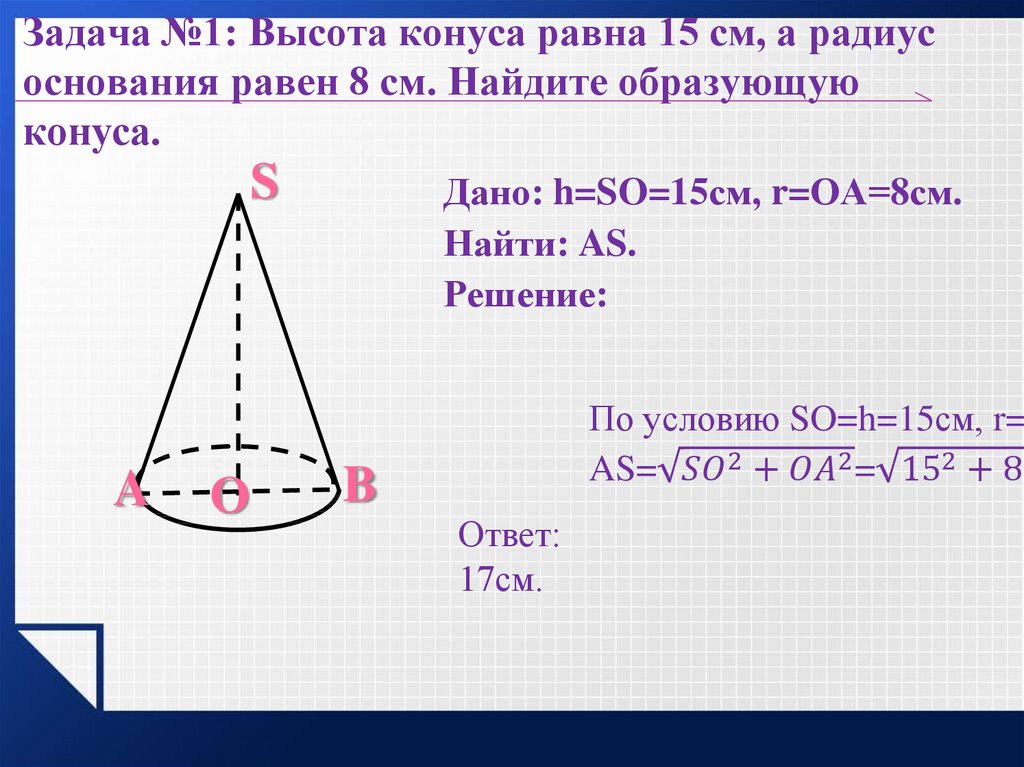
Итак, формула бокового площадь поверхности прямого конуса это Л. С. А. = π р л , куда л — наклонная высота конуса.
Пример 1:
Найдите площадь боковой поверхности прямого конуса, если радиус 4 см, а наклонная высота 5 см.
л .С .А . знак равно π ( 4 ) ( 5 ) знак равно 20 π ≈ 62,8 см 2
Формула для общая площадь поверхности прямого конуса
Т
. С
.А
.
знак равно
π
р
л
+
π
р
2
.
С
.А
.
знак равно
π
р
л
+
π
р
2
.
Пример 2:
Найдите площадь полной поверхности прямого конуса, если радиус 6 дюймов, а наклонная высота 10 дюймы.
Т .С .А . знак равно π ( 6 ) ( 10 ) + π ( 6 ) 2 знак равно 60 π + 36 π знак равно 96 π в 2 ≈ 301,59в 2
Поскольку наклонная высота для наклонного конуса не определена, формул для площадей наклонных конусов не существует.
объем круглого конуса составляет одну треть произведения его высоты и площади его основания. ( В знак равно 1 3 Б час ) .
Пример 3:
Найдите объем конуса, высота которого равна 15 м и радиус которого 8 м.
В
знак равно
1
3
(
8
)
2
(
π
)
(
15
)
знак равно
320
π
≈
1005. 31
31
Следовательно, объем конуса примерно 1005.31 м 3 .
Площадь поверхности конуса
Горячая математикаобщий площадь поверхности из конус есть сумма площадей его основания и боковой (боковой) поверхности.
площадь боковой поверхности конуса – это площадь только боковой или боковой поверхности.
Поскольку конус тесно связан с пирамида , формулы для их площадей связаны.
Помните, формула площади боковой поверхности пирамиды
1
2
п
л
а общая площадь поверхности
1
2
п
л
+
Б
.
Поскольку основанием конуса является круг, подставляем 2 π р за п а также π р 2 за Б куда р это радиус основания цилиндра.
Итак, формула для площадь боковой поверхности прямого конуса
л
.
С
.
А
знак равно
π
р
л
, куда
л
— наклонная высота конуса .
Пример 1:
Найдите площадь боковой поверхности прямого конуса, если радиус 4 см, а наклонная высота 5 см.
л . С . А знак равно π ( 4 ) ( 5 ) знак равно 20 π ≈ 62,82 см 2
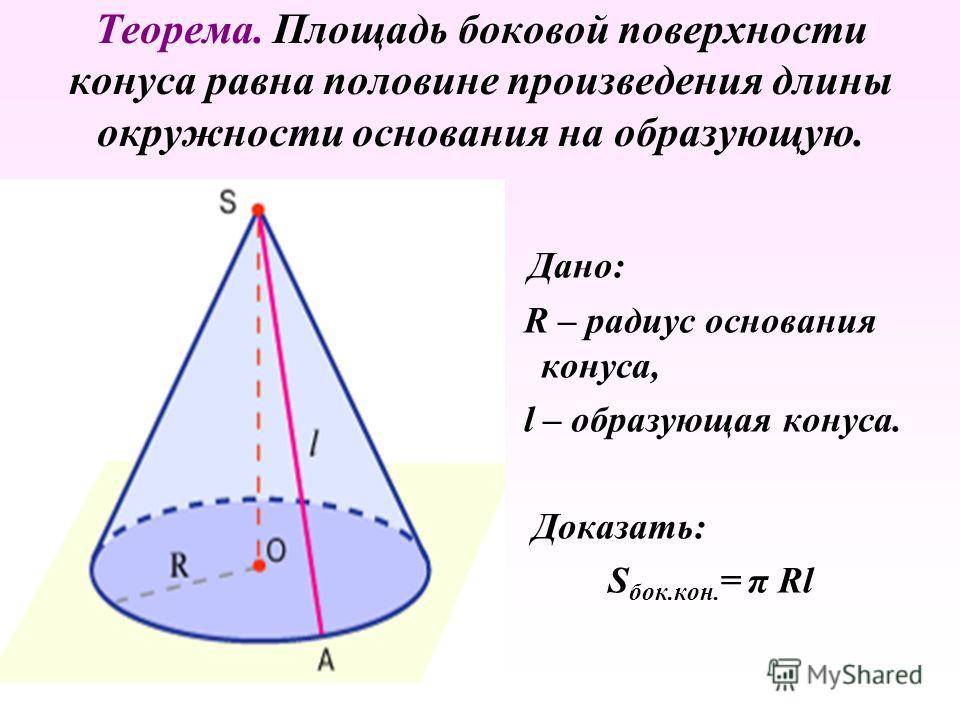
Формула для общая площадь поверхности прямого конуса
Т
. С
.
А
знак равно
π
р
л
+
π
р
2
.
С
.
А
знак равно
π
р
л
+
π
р
2
.
Пример 2:
Найдите площадь полной поверхности прямого конуса, если радиус 6 дюймов, а наклонная высота 10 дюймы.
Т . С . А знак равно π ( 6 ) ( 10 ) + π ( 6 ) 2 знак равно 60 π + 36 π знак равно 96 π дюймы 2 ≈ 301,59 дюймы 2
Площадь поверхности конуса
Первым шагом в определении площади поверхности конуса является измерение радиуса круглой части конуса.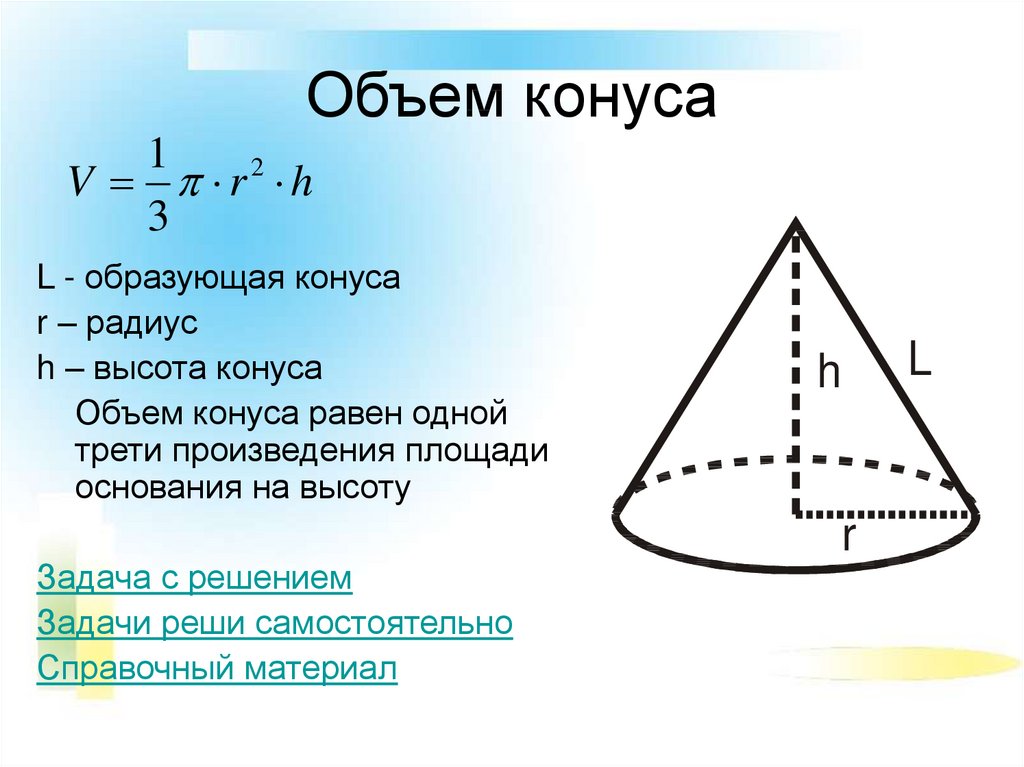 Следующим шагом является нахождение площади круга или основания. Площадь круга в 3,14 раза больше квадрата радиуса ( πr 2 ). Теперь вам нужно найти площадь самого конуса. Для этого необходимо измерить сторону (наклонную высоту) конуса. Убедитесь, что вы используете ту же форму измерения, что и радиус.
Следующим шагом является нахождение площади круга или основания. Площадь круга в 3,14 раза больше квадрата радиуса ( πr 2 ). Теперь вам нужно найти площадь самого конуса. Для этого необходимо измерить сторону (наклонную высоту) конуса. Убедитесь, что вы используете ту же форму измерения, что и радиус.
Теперь вы можете использовать измерение стороны, чтобы найти площадь конуса. Формула площади конуса в 3,14 раза больше радиуса, умноженного на сторону ( πrl ).
Таким образом, площадь поверхности конуса равна площади круга плюс площадь конуса, и окончательная формула определяется как:
SA = πr 2 + πrl
Где
r – радиус
h – высота
l – наклонная высота
Площадь криволинейной (боковой) поверхности конуса = πrl
Примечание:
Конус не имеет однородных (или конгруэнтных) поперечных сечений. (подробнее о коническом сечении здесь)
Пример 1: Конус имеет радиус 3 см и высоту 5 см, найдите общую площадь поверхности конуса.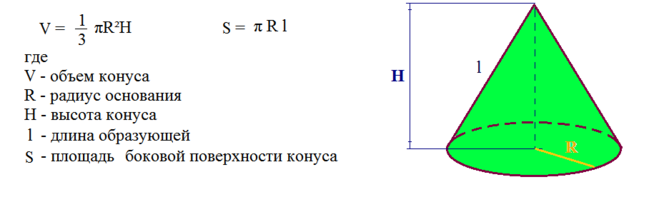
Решение :
Для начала нам нужно найти наклонную высоту конуса, которая определяется с помощью Пифагора, так как поперечное сечение представляет собой прямоугольный треугольник.
l 2 = h 2 + r 2
l 2 = 5 2 + 3 2
l 2 = 25 + 9
l = √(34)
l = 5.83 cm
And the total surface area of the cone is:
SA = πr 2 + πrl
SA = π · r · (r + l)
SA = π · 3 · (3 + 5,83)
SA = 83,17 см 2
Следовательно, общая площадь поверхности конуса равна 3·3·17 см 8
Пример 2: Общая площадь поверхности конуса составляет 375 квадратных дюймов. Если его наклонная высота в четыре раза больше радиуса, то каков диаметр основания конуса? Используйте π = 3,
Решение :
Общая площадь поверхности конуса = πrl + πr 2 = 375 дюймов 2
Slant height: l = 4 × radius = 4r
Substitute l = 4r and π = 3
3 × r × 4 r + 3 × r 2 = 375
12r 2 + 3r 2 = 375
15r 2 = 375
r 2 = 25
r = 25
r = 5
Таким образом, радиус основания конуса составляет 5 дюймов.
А диаметр основания конуса = 2 × радиус = 2 × 5 = 10 дюймов.
Пример 3: Какова общая площадь поверхности конуса, если его радиус = 4 см, а высота = 3 см.
Решение :
Как упоминалось ранее, формула площади поверхности конуса имеет вид:
SA = πr 2 + πrl
SA = πr(r + l)
Как и в предыдущем примере, наклон можно определить с использованием Pythagoras:
L 2 = H 2 + R 2
L 2 = 3909 2 2 2
2
2
2
2
2 2
2 2 2
2 2
2 2
2 2
2 2
2 2 2.
l 2 = 9 + 16
l = 5 Вставить l = 5 получим: +5)
SA = 113,04 см 2
Пример 4: Наклонная высота конуса 20см. диаметр основания 15см. Найдите площадь криволинейной поверхности конуса.
Найдите площадь криволинейной поверхности конуса.
Решение :
Учитывая это,
Наклонная высота: l = 20см
Диаметр: d = 15см
Radius: r = d/2 = 15/2 = 7.5cm
Curved surface area = πrl
CSA = πrl
CSA =π · 7.5 · 20
CSA =471.24 cm 2
Пример 5: Высота и радиус конуса 5 ярдов и 7 ярдов. Найдите площадь боковой поверхности данного конуса.
Решение :
Площадь боковой поверхности конуса = πrl
Шаг 1 :
Высота наклона конуса:
L 2 = H 2 + R 2
L 2 = 7 2 + 5 2 = 7 2 + 5 2 = 7 2 + 5 2 = 7 2 .0409 = 49 + 25
l = 8.6
Step 2 : Lateral surface area:
LSA = πrl
LSA = 3. 14 × 7 × 8.6
14 × 7 × 8.6
LSA =189.03 yd 2
Итак, площадь боковой поверхности конуса = 189,03 квадратных ярда.
Пример 6: Круглый конус имеет высоту 15 дюймов и радиус основания 20 дюймов. Какова площадь боковой поверхности конуса?
Решение:
The lateral surface area of cone is given by:
LSA = π × r × l
LSA =3.14 × 20 × 15
LSA = 942 inch 2
Example 7: Найдите полную площадь поверхности конуса, радиус основания которого равен 3 см, а высота перпендикуляра равна 4 см.
Решение :
Учитывая, что:
г = 3 см
h = 4 см
Чтобы найти общую площадь поверхности конуса, нам нужна наклонная высота конуса, а не перпендикулярная высота.
Наклонную высоту l можно найти по теореме Пифагора.
l 2 = h 2 + r 2
l 2 = 3 2 + 4 2
l 2 = 9 + 16
l = 5
Таким образом, общая площадь поверхности конуса составляет:
SA = πr(r + l)
SA = 3,14 · 3 · (3+5)
SA = 75,36 см 9 20003
Калькулятор площади поверхности онлайн
youtube.com/v/UyesG4M7jBo&hl=en_US&fs=1&color1=0x006699&color2=0x54abd6″ allowfullscreen=»true» allowscriptaccess=»always»>
Формула высоты конуса — Что такое формула высоты конуса? Примеры
Конус представляет собой трехмерную форму, образованную набором отрезков или линий, которые соединяются в общей точке, называемой вершиной или вершиной, со всеми точками круглого основания (которое не содержит вершина). Мы также можем определить конус как пирамиду с круглым поперечным сечением, в отличие от пирамиды с треугольным поперечным сечением. Изучим формулу высоты конуса на решённых примерах в конце страницы.
Что такое формула высоты конуса?
Формула высоты конуса помогает вычислить расстояние от вершины конуса до основания конуса. Высоту конуса можно рассчитать, используя либо объем куба и радиус, либо наклонную высоту и радиус конуса.
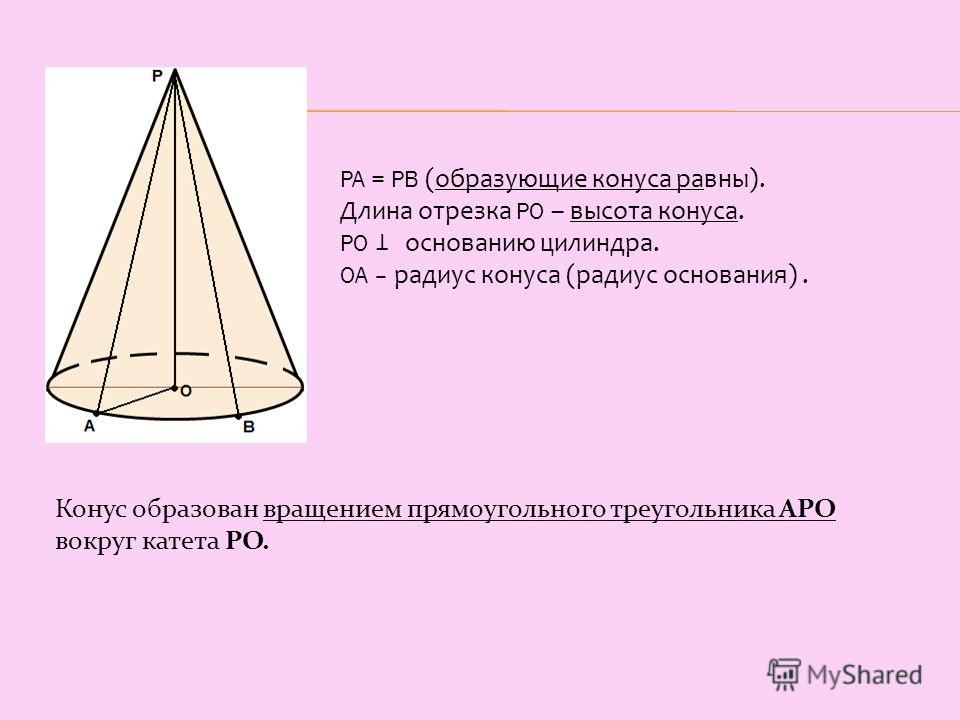
Формула высоты конуса
Формула высоты конуса для конуса может быть выражена как
Формула 1: h = 3V/πr 2
где, 90 008
объем конуса0010
r = радиус конуса Эта формула получена из формулы объема конуса.
Формула 2: h = √l 2 — r 2
где,
- l = высота наклона конуса
- r = Радиус конуса
Эта формула получена с использованием теоремы Пифагора.
Рассмотрим применение формулы высоты конуса в следующем разделе.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Записаться на бесплатный пробный урок
Примеры с использованием формулы высоты конуса
Пример 1: Шапка на день рождения имеет коническую форму, объем 20 единиц 3 , а ее радиус основания составляет 5 единиц. Какая высота шапки?
Решение:
Чтобы найти: Высота конуса.
Given:
volume = 20 units 3
Radius = 5 units
Using cone height formula,
h = 3V/πr 2
= (3 × 20)/π × 5 2
= (60)/ (π × 25)
= 0,76 единицы
Ответ: Высота конуса 0,76 единицы
Пример 2: = чему равна высота конуса 3 единицы и объем = 50 кубических единиц?
Решение:
Найти: Высота конуса.
Приведено:
Том = 50 кубических единиц
Радиус = 3 единицы
с использованием формулы высоты конуса,
H = 3V/πr 2
= (3 × 50)/π 3
= (3 × 50)/× 3 2
4304 = (3 × 50).
= (150)/(π × 9)
= 5,305 единицы
Ответ: Высота конуса равна 5,305 единицы.
Пример 3: Определить высоту конуса с радиусом = 5 единиц и наклонной высотой = 13 единиц?
Решение:
Найти: Высота конуса.
Given:
Slant height = 13 units
Radius = 5 units
Using cone height formula,
h = √l 2 — r 2
= √(13) 2 — ( 5) 2
= √169-25
= √144
= 12 единиц
Ответ: Высота конуса равна 12 единицам.
Часто задаваемые вопросы о формуле высоты конуса
Что такое формула высоты конуса в геометрии?
Формула высоты конуса вычисляет высоту конуса. Высота конуса с использованием формул высоты конуса: h = 3V/πr 2 и h = √l 2 — r 2 , где V = объем конуса, r = радиус конуса, и l = наклонная высота конуса.
Как использовать формулу высоты конуса?
Для определения высоты конуса воспользуемся формулой конуса следующим образом
- Шаг 1. Проверьте заданные параметры, объем и радиус или наклонную высоту и радиус.
- Шаг 2: Подставьте значения в соответствующую формулу, h = 3V/πr 2 или h = √l 2 — r 2
Что такое r в формуле высоты конуса?
В формуле высоты конуса либо h = 3V/πr 2 , либо h = √l 2 — r 2 , r представляет радиус конуса.
Что такое формула высоты конуса с использованием наклонной высоты?
Формула высоты конуса с использованием наклонной высоты: √l 2 — r 2 , где l — наклонная высота, а r — радиус конуса.
2
2 2
2 2 2.
l 2 = 9 + 16
l = 5 Вставить l = 5 получим: +5)
SA = 113,04 см 2
Пример 4: Наклонная высота конуса 20см. диаметр основания 15см. Найдите площадь криволинейной поверхности конуса.
Найдите площадь криволинейной поверхности конуса.
Решение :
Учитывая это,
Наклонная высота: l = 20см
Диаметр: d = 15см
Radius: r = d/2 = 15/2 = 7.5cm
Curved surface area = πrl
CSA = πrl
CSA =π · 7.5 · 20
CSA =471.24 cm 2
Пример 5: Высота и радиус конуса 5 ярдов и 7 ярдов. Найдите площадь боковой поверхности данного конуса.
Решение :
Площадь боковой поверхности конуса = πrl
Шаг 1 :
Высота наклона конуса:
L 2 = H 2 + R 2
L 2 = 7 2 + 5 2 = 7 2 + 5 2 = 7 2 + 5 2 = 7 2 .0409 = 49 + 25
l = 8.6
Step 2 : Lateral surface area:
LSA = πrl
LSA = 3. 14 × 7 × 8.6
14 × 7 × 8.6
LSA =189.03 yd 2
Итак, площадь боковой поверхности конуса = 189,03 квадратных ярда.
Пример 6: Круглый конус имеет высоту 15 дюймов и радиус основания 20 дюймов. Какова площадь боковой поверхности конуса?
Решение:
The lateral surface area of cone is given by:
LSA = π × r × l
LSA =3.14 × 20 × 15
LSA = 942 inch 2
Example 7: Найдите полную площадь поверхности конуса, радиус основания которого равен 3 см, а высота перпендикуляра равна 4 см.
Решение :
Учитывая, что:
г = 3 см
h = 4 см
Чтобы найти общую площадь поверхности конуса, нам нужна наклонная высота конуса, а не перпендикулярная высота.
Наклонную высоту l можно найти по теореме Пифагора.
l 2 = h 2 + r 2
l 2 = 3 2 + 4 2
l 2 = 9 + 16
l = 5
Таким образом, общая площадь поверхности конуса составляет:
SA = πr(r + l)
SA = 3,14 · 3 · (3+5)
SA = 75,36 см 9 20003
Калькулятор площади поверхности онлайн
youtube.com/v/UyesG4M7jBo&hl=en_US&fs=1&color1=0x006699&color2=0x54abd6″ allowfullscreen=»true» allowscriptaccess=»always»>
Формула высоты конуса — Что такое формула высоты конуса? Примеры
Конус представляет собой трехмерную форму, образованную набором отрезков или линий, которые соединяются в общей точке, называемой вершиной или вершиной, со всеми точками круглого основания (которое не содержит вершина). Мы также можем определить конус как пирамиду с круглым поперечным сечением, в отличие от пирамиды с треугольным поперечным сечением. Изучим формулу высоты конуса на решённых примерах в конце страницы.
Что такое формула высоты конуса?
Формула высоты конуса помогает вычислить расстояние от вершины конуса до основания конуса. Высоту конуса можно рассчитать, используя либо объем куба и радиус, либо наклонную высоту и радиус конуса.
Формула высоты конуса
Формула высоты конуса для конуса может быть выражена как
Формула 1: h = 3V/πr 2
где, 90 008
объем конуса0010
r = радиус конуса Эта формула получена из формулы объема конуса.
Формула 2: h = √l 2 — r 2
где,
- l = высота наклона конуса
- r = Радиус конуса
Эта формула получена с использованием теоремы Пифагора.
Рассмотрим применение формулы высоты конуса в следующем разделе.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Записаться на бесплатный пробный урок
Примеры с использованием формулы высоты конуса
Пример 1: Шапка на день рождения имеет коническую форму, объем 20 единиц 3 , а ее радиус основания составляет 5 единиц. Какая высота шапки?
Решение:
Чтобы найти: Высота конуса.
Given:
volume = 20 units 3
Radius = 5 units
Using cone height formula,
h = 3V/πr 2
= (3 × 20)/π × 5 2
= (60)/ (π × 25)
= 0,76 единицы
Ответ: Высота конуса 0,76 единицы
Пример 2: = чему равна высота конуса 3 единицы и объем = 50 кубических единиц?
Решение:
Найти: Высота конуса.
Приведено:
Том = 50 кубических единиц
Радиус = 3 единицы
с использованием формулы высоты конуса,
H = 3V/πr 2
= (3 × 50)/π 3
= (3 × 50)/× 3 2
4304 = (3 × 50).
= (150)/(π × 9)
= 5,305 единицы
Ответ: Высота конуса равна 5,305 единицы.
Пример 3: Определить высоту конуса с радиусом = 5 единиц и наклонной высотой = 13 единиц?
Решение:
Найти: Высота конуса.
Given:
Slant height = 13 units
Radius = 5 units
Using cone height formula,
h = √l 2 — r 2
= √(13) 2 — ( 5) 2
= √169-25
= √144
= 12 единиц
Ответ: Высота конуса равна 12 единицам.
Часто задаваемые вопросы о формуле высоты конуса
Что такое формула высоты конуса в геометрии?
Формула высоты конуса вычисляет высоту конуса. Высота конуса с использованием формул высоты конуса: h = 3V/πr 2 и h = √l 2 — r 2 , где V = объем конуса, r = радиус конуса, и l = наклонная высота конуса.
Как использовать формулу высоты конуса?
Для определения высоты конуса воспользуемся формулой конуса следующим образом
- Шаг 1. Проверьте заданные параметры, объем и радиус или наклонную высоту и радиус.
- Шаг 2: Подставьте значения в соответствующую формулу, h = 3V/πr 2 или h = √l 2 — r 2
Что такое r в формуле высоты конуса?
В формуле высоты конуса либо h = 3V/πr 2 , либо h = √l 2 — r 2 , r представляет радиус конуса.
Что такое формула высоты конуса с использованием наклонной высоты?
Формула высоты конуса с использованием наклонной высоты: √l 2 — r 2 , где l — наклонная высота, а r — радиус конуса.
l 2 = 9 + 16
l = 5
Вставить l = 5 получим: +5)
SA = 113,04 см 2
Пример 4: Наклонная высота конуса 20см. диаметр основания 15см. Найдите площадь криволинейной поверхности конуса.
Найдите площадь криволинейной поверхности конуса.
Решение :
Учитывая это,
Наклонная высота: l = 20см
Диаметр: d = 15см
Radius: r = d/2 = 15/2 = 7.5cm
Curved surface area = πrl
CSA = πrl
CSA =π · 7.5 · 20
CSA =471.24 cm 2
Пример 5: Высота и радиус конуса 5 ярдов и 7 ярдов. Найдите площадь боковой поверхности данного конуса.
Решение :
Площадь боковой поверхности конуса = πrl
Шаг 1 :
Высота наклона конуса:
L 2 = H 2 + R 2
L 2 = 7 2 + 5 2 = 7 2 + 5 2 = 7 2 + 5 2 = 7 2 .0409 = 49 + 25
l = 8.6
Step 2 : Lateral surface area:
LSA = πrl
LSA = 3. 14 × 7 × 8.6
14 × 7 × 8.6
LSA =189.03 yd 2
Итак, площадь боковой поверхности конуса = 189,03 квадратных ярда.
Пример 6: Круглый конус имеет высоту 15 дюймов и радиус основания 20 дюймов. Какова площадь боковой поверхности конуса?
Решение:
The lateral surface area of cone is given by:
LSA = π × r × l
LSA =3.14 × 20 × 15
LSA = 942 inch 2
Example 7: Найдите полную площадь поверхности конуса, радиус основания которого равен 3 см, а высота перпендикуляра равна 4 см.
Решение :
Учитывая, что:
г = 3 см
h = 4 см
Чтобы найти общую площадь поверхности конуса, нам нужна наклонная высота конуса, а не перпендикулярная высота.
Наклонную высоту l можно найти по теореме Пифагора.
l 2 = h 2 + r 2
l 2 = 3 2 + 4 2
l 2 = 9 + 16
l = 5
Таким образом, общая площадь поверхности конуса составляет: 0003 Калькулятор площади поверхности онлайн youtube.com/v/UyesG4M7jBo&hl=en_US&fs=1&color1=0x006699&color2=0x54abd6″ allowfullscreen=»true» allowscriptaccess=»always»> Конус представляет собой трехмерную форму, образованную набором отрезков или линий, которые соединяются в общей точке, называемой вершиной или вершиной, со всеми точками круглого основания (которое не содержит вершина). Мы также можем определить конус как пирамиду с круглым поперечным сечением, в отличие от пирамиды с треугольным поперечным сечением. Изучим формулу высоты конуса на решённых примерах в конце страницы. Формула высоты конуса помогает вычислить расстояние от вершины конуса до основания конуса. Высоту конуса можно рассчитать, используя либо объем куба и радиус, либо наклонную высоту и радиус конуса. Формула высоты конуса для конуса может быть выражена как Формула 1: h = 3V/πr 2 где, 90 008 объем конуса0010 Эта формула получена из формулы объема конуса. Формула 2: h = √l 2 — r 2 где, Эта формула получена с использованием теоремы Пифагора. Рассмотрим применение формулы высоты конуса в следующем разделе. Разбивайте сложные концепции с помощью простых визуальных средств. Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath. Записаться на бесплатный пробный урок Пример 1: Шапка на день рождения имеет коническую форму, объем 20 единиц 3 , а ее радиус основания составляет 5 единиц. Какая высота шапки? Решение: Чтобы найти: Высота конуса. Given: volume = 20 units 3 Radius = 5 units Using cone height formula, h = 3V/πr 2 = (3 × 20)/π × 5 2 = (60)/ (π × 25) = 0,76 единицы Ответ: Высота конуса 0,76 единицы Пример 2: = чему равна высота конуса 3 единицы и объем = 50 кубических единиц? Решение: Найти: Высота конуса. Приведено: Том = 50 кубических единиц Радиус = 3 единицы с использованием формулы высоты конуса, H = 3V/πr 2 = (3 × 50)/π 3
SA = πr(r + l)
SA = 3,14 · 3 · (3+5)
SA = 75,36 см 9 2 Формула высоты конуса — Что такое формула высоты конуса? Примеры
Что такое формула высоты конуса?
Формула высоты конуса
Примеры с использованием формулы высоты конуса

= (3 × 50)/× 3 2
4304 = (3 × 50).
= (150)/(π × 9)
= 5,305 единицы
Ответ: Высота конуса равна 5,305 единицы.
Пример 3: Определить высоту конуса с радиусом = 5 единиц и наклонной высотой = 13 единиц?
Решение:
Найти: Высота конуса.
Given:
Slant height = 13 units
Radius = 5 units
Using cone height formula,
h = √l 2 — r 2
= √(13) 2 — ( 5) 2
= √169-25
= √144
= 12 единиц
Ответ: Высота конуса равна 12 единицам.
Часто задаваемые вопросы о формуле высоты конуса
Что такое формула высоты конуса в геометрии?
Формула высоты конуса вычисляет высоту конуса. Высота конуса с использованием формул высоты конуса: h = 3V/πr 2 и h = √l 2 — r 2 , где V = объем конуса, r = радиус конуса, и l = наклонная высота конуса.
Как использовать формулу высоты конуса?
Для определения высоты конуса воспользуемся формулой конуса следующим образом
- Шаг 1. Проверьте заданные параметры, объем и радиус или наклонную высоту и радиус.
- Шаг 2: Подставьте значения в соответствующую формулу, h = 3V/πr 2 или h = √l 2 — r 2
Что такое r в формуле высоты конуса?
В формуле высоты конуса либо h = 3V/πr 2 , либо h = √l 2 — r 2 , r представляет радиус конуса.
Что такое формула высоты конуса с использованием наклонной высоты?
Формула высоты конуса с использованием наклонной высоты: √l 2 — r 2 , где l — наклонная высота, а r — радиус конуса.





 02.17
02.17