Что такое функция общего вида. График четной и нечетной функций
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
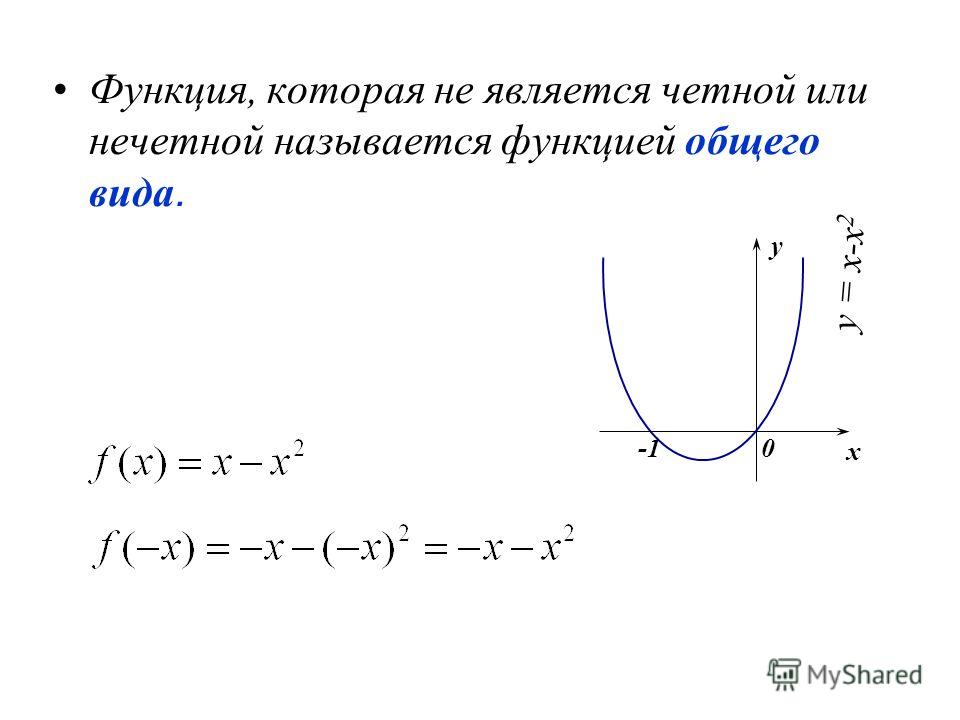
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как : пусть x 1a ;b , а x 2a ;b .
Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией. Для обозначения используют запись y=f(x). У каждой функции существует ряд основных свойств, таких как монотонность, четность, периодичность и другие.
Рассмотри подробнее свойство четности.
Функция y=f(x) называется четной, если она удовлетворяет следующим двум условиям:
2. 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.
Чётные и нечётные функции | это… Что такое Чётные и нечётные функции?
Толкование
- Чётные и нечётные функции
f(x) = x — пример нечётной функции.
f(x) = x2 — пример чётной функции.
f(x) = x3, нечётная
f(x) = x3 + 1 ни чётная, ни нечётная
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Или по-другому
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.
Содержание
- 1 Определения
- 2 Свойства
- 3 Примеры
- 3.
 1 Нечётные функции
1 Нечётные функции - 3.2 Чётные функции
- 3.
- 4 Вариации и обобщения
Определения
- Функция называется нечётной, если справедливо равенство
- Функция f называется чётной, если справедливо равенство
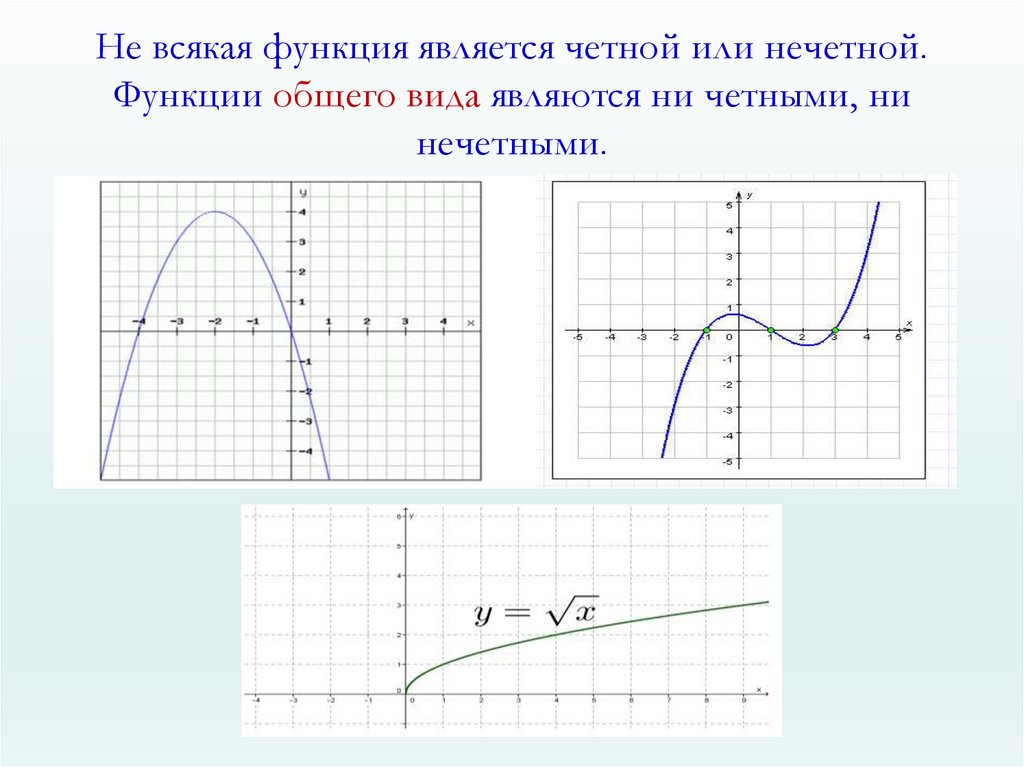
- Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.
Свойства
- График нечётной функции симметричен относительно начала координат
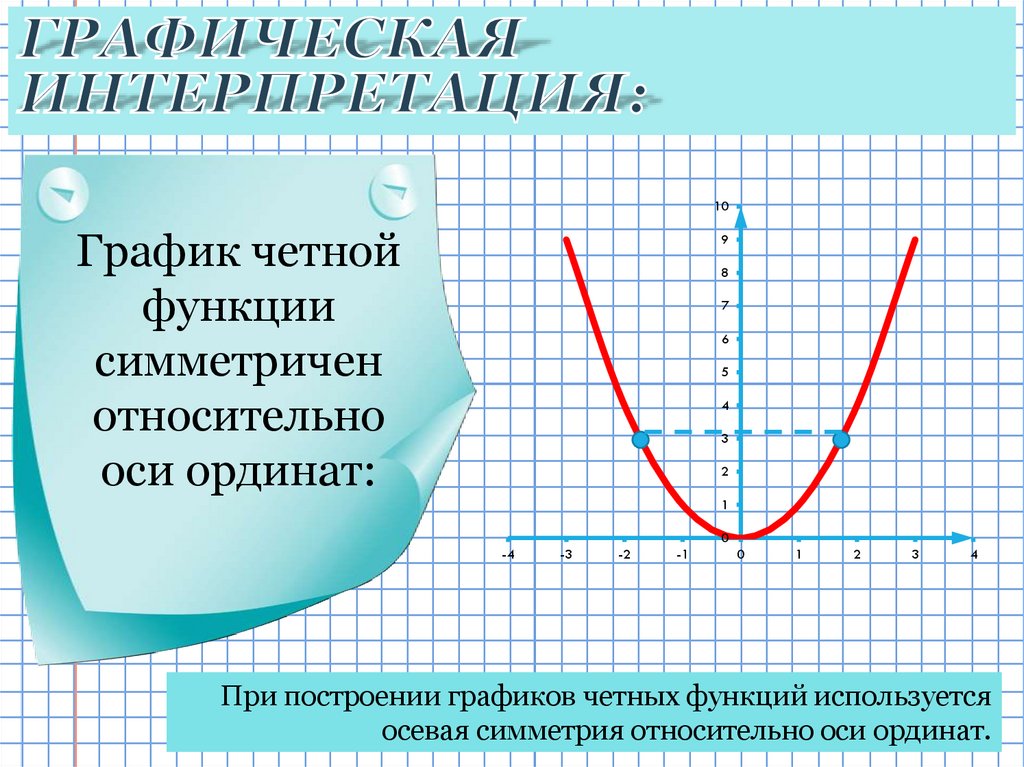
- График чётной функции симметричен относительно оси ординат Oy.
- Произвольная функция может быть представлена в виде суммы нечётной и чётной функций:
- f(x) = g(x) + h(x),
где
- Функция — единственная функция, одновременно являющаяся нечётной и чётной.
- Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.

- Произведение или дробь двух нечётных функций чётно.
- Произведение или дробь двух чётных функций чётно.
- Произведение или дробь нечётной и чётной функций нечётно.
- Композиция двух нечётных функция нечётна.
- Композиция двух чётных функций чётна.
- Композиция чётной функции с нечётной чётна.
- Композиция любой функции с чётной чётна (но не наоборот).
- Функция, обратная чётной, чётна, а нечётной — нечётна.
- Производная чётной функции нечётна, а нечётной — чётна.
- То же верно про производную третьего, пятого и вообще любого нечётного порядка.
- Производная чётного порядка сохраняет чётность.
Примеры
Нечётные функции
- Нечётная степень где — произвольное целое число.
- Синус .
- Тангенс .
Чётные функции
- Чётная степень где — произвольное целое число.
- Косинус .
Вариации и обобщения
- Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами.
 {\circ}$ вокруг начала координат. 92$ и $\cosx$.
{\circ}$ вокруг начала координат. 92$ и $\cosx$.Свойства
Некоторые основные свойства нечетных и четных функций:
- Единственная функция, областью определения которой являются все действительные числа, как нечетные, так и четные, — это постоянная функция, тождественно равная нулю, $f(x) =0$.
- Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.
- Разность двух четных функций четна, а разность двух нечетных функций нечетна.
- Произведение двух четных функций четно, а произведение двух нечетных функций четно.
- Произведение четной функции на нечетную является нечетной функцией.
- Частное двух четных функций четно, а частное двух нечетных функций четно.
- Частное четной функции и нечетной функции является нечетной функцией.
- Производная четной функции нечетна, а производная нечетной функции четна.
- Композиция двух четных функций четна, а композиция двух нечетных функций нечетна.

- Композиция четной функции и нечетной функции четна.
Примечание : сумма четной и нечетной функции не является ни четной, ни нечетной, если только одна из функций не равна нулю в данной области.
Периодические функции
Определение
Периодическая функция — это функция, которая повторяется через равные промежутки времени или периодов . Функция $f$ называется периодической с периодом $P$, если: \[f(x+P)=f(x)\] для всех значений $x$ и где $P$ — ненулевая константа.
Периодические функции используются для описания колебаний и волн, а наиболее важными периодическими функциями являются тригонометрические функции. Любая непериодическая функция называется апериодической .
Пример : Функция синуса является периодической с периодом $2\pi$, поскольку $\sin(x+2\pi)=\sin x$ для всех значений $x$. Функция повторяется на интервалах длины $2\pi$, что также хорошо видно на графике.

Рабочие тетради
Эти рабочие тетради, созданные HELM, являются хорошими вспомогательными средствами, содержащими ключевые моменты для повторения и множество рабочих примеров.
- Периодические функции
- Четные и нечетные функции
- Характеристика функций, включая рабочие примеры периодических, нечетных и четных функций.
Состав четных и нечетных функций и их результат
спросил
Изменено 6 лет, 1 месяц назад
Просмотрено 42к раз
$\begingroup$
Приведите пример четной функции. Приведите пример нечетной функции. Если f(x) равно нечетно, а g(x) четно, должно ли f(g(x)) быть четным? Должен ли g(f(x)) быть четным?
Я пробовал общие функции, такие как
92Обе композиции (переход к f(g(x)) и g(f(x)) дают одинаковые результаты)
Однако, когда я использую триггерные функции, происходит нечто другое.

f(x) = sin(x) g(x) = cos(x)
f(g(x)) = четный
и
g(f(x)) = четный.
Следовательно, могу ли я предположить, что комбинация любой функции (не являющейся ни нечетной, ни четной) будет четной?
- функции
$\endgroup$
0
$\begingroup$
Вы можете доказать правила композиции четных и нечетных функций прямо из определений. Функция $f: \mathbb{R} \rightarrow \mathbb{R}$ четна, если $f(-x)=f(x)$ для всех $x$; нечетно, если $f(-x)=-f(x)$ для всех $x$. Теперь рассмотрим $f$ нечетным, а $g$ четным: $f\circ g(-x)=f(g(-x))=f(g(x)),$, поскольку $g$ четно.
Но по определению $f(g(x))=f\circ g(x)$, поэтому $f \circ g$ четно.
Аналогичное доказательство показывает, что $g \circ f$ четно.
Безусловно, неверно, что состав любых двух функций будет четным. Возьмем $f$, определяемый $f(x)=x+1$ и $g(x)=x+4$.
 Тогда $g\circ f(-x) = g(-x+4)=-x+5$, а $g \circ f(x)=x+5$.
Тогда $g\circ f(-x) = g(-x+4)=-x+5$, а $g \circ f(x)=x+5$.Заметим, что $f(x)$ — это не функция, а значение функции $f$ на конкретном элементе $x$. Функция от действительных чисел к действительным числам — это правило, которое присваивает каждому вещественному числу $x$ другое число, которое мы записываем как $f(x)$. Так что не имеет смысла говорить о том, что значение $f(x)$ является нечетным или четным — четность и нечетность — это свойство правила, самой функции. 92$ для всех $x \in \mathbb{R}$», но, как видите, это более громоздко.
$\endgroup$
$\begingroup$
Каждый раз, когда вы составляете реальные функции, если какая-то из них четная, а остальные нечетные, то композиция четная. Это происходит потому, что нечетные функции «сохраняют» отрицание, а четные функции «избавляются» от него. Например, если $f$ четное, а $g$ нечетное,
$g(f(-x) = g(f(x))$ (четное)
$f(g(-x) = f( -g(x)) = f(g(x))$ (четное)
$\endgroup$
$\begingroup$
Попробуйте сделать это в общем случае.

- Единственная функция, областью определения которой являются все действительные числа,

 1 Нечётные функции
1 Нечётные функции
 {\circ}$ вокруг начала координат. 92$ и $\cosx$.
{\circ}$ вокруг начала координат. 92$ и $\cosx$.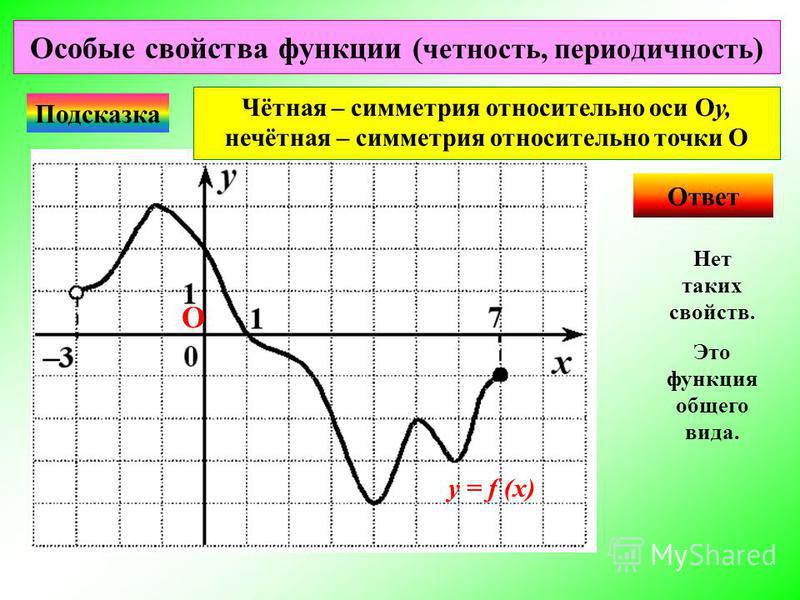

 Тогда $g\circ f(-x) = g(-x+4)=-x+5$, а $g \circ f(x)=x+5$.
Тогда $g\circ f(-x) = g(-x+4)=-x+5$, а $g \circ f(x)=x+5$.